自主空中加油会合问题,可以描述为一个航路规划、轨迹跟踪以及无人机控制的问题[1]。在突发的空中加油任务中,由于无人机自身携带油量的限制,必须在尽可能短的时间内完成会合并进行加油作业。为此,优化会合航路使无人机以最短的路径最小的时间与加油机会合成了一项重要的研究目标。因为自主空中加油过程中需要无人机进行完全自主飞行,所以会合对接过程的制导与控制系统有高精度、抗干扰的要求[2]。
文献[3]提出了一种在恒定风影响下且转弯速率有限制的优化的轨迹规划方法,该方法应用Dubins路径思想通过一种迭代算法计算出无人机从以初始位置到一有方向限制的最终位置的最短路径。文献[4]提出了一种固定翼飞机的Dubins轨迹的生成方法,根据不同的初始位置和方向以及不同的最终位置和方向,确定圆弧与直线的组合形式并计算直线与圆弧的切点。文献[5]设计了一种基于Dubins路径的最小时间会合控制器,算出从受油机当前位置到加油机预定飞行轨迹上目标点的Dubins路径,受油机以该Dubins路径飞向会合点,基于Buckinghan Pi理论的仿真结果达到了最小时间会合要求。文献[6]提出了一种基于三维Dubins轨迹的无人机最优路径生成算法,这为最小时间会合问题提供了一个新思路。
在无人机会合飞行过程中,动态模型中的气动参数可能出现变化,外部未知干扰也有较大的不确定性,这些因素的存在可能对系统的控制性能产生一定的影响。Backstepping控制在处理具有严格反馈形式的非线性系统是有着巨大优势,它是飞行器控制系统设计的常用方法之一[7]。文献[8]设计了自适应backstepping飞行控制系统,并使用了神经网络对战斗机飞行中的气动参数误差等不确定性因素导致的系统误差进行动态补偿。设计经典的backstepping控制器,需要对虚拟控制律进行反复求导使得 backstepping设计过程中存在微分膨胀问题[9-10]。
针对无人机自主空中加油会合过程中的制导与控制问题,本文采用Dubins路径方法计算会合点位置以满足最小时间会合要求,并考虑系统模型的不确定性影响,设计神经网络backstepping控制器,最后对整个空中加油会合制导与控制系统进行了综合仿真验证。
1 加油机与受油机数学模型在空中加油过程中,加油机通常作匀速直线平飞运动,故将加油机看作质点运动,其运动的数学模型为
| $\left\{ \begin{align} & {{{\dot{X}}}_{T}}={{V}_{T}}\cdot cos~{{\chi }_{T}} \\ & {{{\dot{Y}}}_{T}}={{V}_{T}}\cdot sin~{{\chi }_{T}} \\ & {{{\dot{\chi }}}_{T}}={{\omega }_{T}} \\ & {{{\dot{V}}}_{T}}={{a}_{T}} \\ \end{align} \right.$ | (1) |
式中:VT为飞行速度,χT为航迹方位角,XT、YT为惯性坐标系下的水平位置。
无人机运动的数学模型采用非线性六自由度的非线性方程描述如下:
| $\dot{V}=\frac{1}{m}(-D+Tsin~\alpha cos~\beta +m{{g}_{1}})$ | (2) |
| $\begin{align} & \dot{\alpha }=q-(pcos~\alpha +rsin~\alpha )tan~\beta + \\ & \frac{1}{mVcos~\beta }(-L-Tsin~\alpha +m{{g}_{3}}) \\ \end{align}$ | (3) |
| $\begin{align} & \dot{\beta }=psin~\alpha -rcos~\alpha + \\ & \frac{1}{mV}(Y-Tcos~\alpha sin~\beta +m{{g}_{3}}) \\ \end{align}$ | (4) |
| $\dot{p}={{I}_{2}}pq+{{I}_{1}}qr+{{I}_{3}}\bar{L}+{{I}_{4}}N$ | (5) |
| $\dot{q}={{I}_{5}}pr-{{I}_{6}}({{p}^{2}}-{{r}^{2}})+{{I}_{7}}M$ | (6) |
| $\dot{r}=-{{I}_{2}}qr+{{I}_{8}}pq+{{I}_{4}}\bar{L}-+{{I}_{9}}N$ | (7) |
| $\dot{\phi }=p+tan~\theta \left( qsin\phi +rcos\phi \right)$ | (8) |
| $\dot{\theta }=qcos~\phi -rsin\text{ }\phi $ | (9) |
| $\dot{\psi }=\frac{qsin\text{ }\phi +rcos~\phi }{cos~\theta }$ | (10) |
式中:V、α、β为飞机的空速,迎角和侧滑角,p、q、r为飞机的滚转、俯仰和偏航角速率,φ、θ、ψ为飞机的滚转角、俯仰角和偏航角,L为飞机所受的升力,T为发动机的推力,D为飞机所受阻力,L、M、N为飞机所受空气动力矩,I1…I9为与转动惯量有关的参数,g1、g2、g3为重力加速度在气流坐标系三轴上的分量。
| $\left\{ \begin{align} & {{g}_{1}}=g(-sin~\theta cos~\alpha cos~\beta +sin\text{ }\varphi cos~\theta sin~\beta + \\ & cos~\varphi cos~\theta sin~\alpha cos~\beta ) \\ & {{g}_{2}}=g(sin~\theta cos~\alpha sin~\beta +sin\text{ }\varphi cos~\theta cos~\beta - \\ & cos~\varphi cos~\theta sin~\alpha sin~\beta ) \\ & {{g}_{3}}=g(sin~\theta sin~\alpha +cos~\varphi cos~\theta cos~\alpha ) \\ \end{align} \right.$ | (11) |
水平面内受油机各状态量为
| $\left\{ \begin{align} & {{V}_{p}}=Vcos~\gamma \\ & {{{\dot{X}}}_{R}}={{V}_{p}}cos~\chi \\ & {{{\dot{Y}}}_{R}}={{V}_{p}}sin~\chi \\ \end{align} \right.$ | (12) |
式中:γ为飞机的航迹倾斜角,γ=θ-α;χ为飞机的航迹方位角,χ=ψ+β。
2 最小时间会合制导律设计空中加油过程中需要受油机与加油机在尽可能短的时间内完成会合,进行空中加油。故需要设计一条最短的会合路径,这样,就把研究最小时间的会合问题,转化成研究最短飞行路径的问题。假设加油机的运动可知或者可预测。
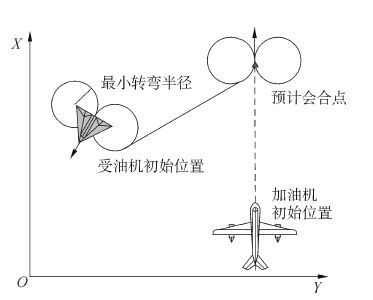
2.1 Dubins路径的生成Dubins路径的原理是,在二维平面中两个矢量之间最短的路径就是圆弧及其切线组成[11]。空中加油会合阶段,受油机将从较远的位置飞向加油机,其Dubins路径如图 1所示,由圆弧直线圆弧组合而成。
|
| 图1 空中加油会合Dubins路径示意图 Figure 1 Dubins path in aerial refueling rendezvous |
受油机采用协调转弯方式,其转弯半径的计算公式为
| $R=\frac{{{V}^{2}}}{gtan~\varphi }$ | (13) |
即滚转角φ有限制的情况下,可以计算出受油机的最小转弯半径Rmin。
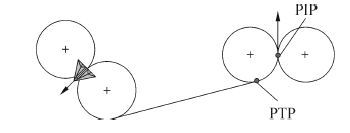
2.2 路径点的生成导航路径点估计器是会合制导控制中的重要部分。它计算出从受油机当前位置到会合点的Dubins路径,并给出曲线上的两个导航路径点。第一个导航点是Dubins路径第二段圆弧的起始点,受油机将从该点开始转向飞向会合点,该点记做PTP(predicted turn point)。第二个导航点是Dubins路径第二段圆弧的终止点,受油机飞至该点时完成与加油机的会合,该点记做PIP(predicted intercept point)。
|
| 图2 跟踪导航路径点切换 Figure 2 Tracking different guidance waypoint |
假设加油机的飞行速度与航向保持不变,其飞行轨迹可以确定,则其轨迹上的任意位置可以表示为时间的函数。也就是说,到达该轨迹上某一位置即预计会合点所消耗的时间TT可知。对于受油机来说任意时刻,可以得到一条到“加油机将来位置(也就是预计会合点PIP)”的Dubins路径并且可以计算出以恒定速度飞过这段路径所需要的时间TR。当TT=TR时,意味着将来的这个加油机的位置就是最小时间会合目标达到时,受油机和加油机的会合点。若TT≠TR,说明受油机和加油机不能同步到达,需要重新计算。根据时间差ΔT=TR-TT,更新会合预计耗时Ttot=TR+ΔT,根据会合预计耗时在加油机固定航线上更新预计会合点,加油机到该点耗时为TT=Ttot。计算从受油机当前位置到预计会合点的路径长度和时间消耗,比较TT和TR,直到TT-TR <εT,认为加油机和受油机将在容许的时间差εT内到达最终的会合点的位置。这时,整个会合航路点的计算过程结束,得到Dubins路径终止圆弧上的转弯点和会合点的具体位置,将这两个航路点作为受油机的跟踪目标。
2.3 受油机平面制导律设计平面轨迹制导律设计的目的是使得受油机能够精确地跟踪到Dubins路径生成的导航路径点,为此制导律要有良好的精确性。
从受油机指向加油机的目标视线方位角为χ*,并有
| ${{\chi }^{*}}=arctan(\frac{{{Y}_{R}}-{{Y}_{T}}}{{{X}_{R}}-{{X}_{T}}})$ | (14) |
可以求得χ*的一阶导数:
| ${{{\dot{\chi }}}^{*}}=\frac{({{{\dot{Y}}}_{R}}-{{{\dot{Y}}}_{T}})({{X}_{R}}-{{X}_{T}})-({{{\dot{X}}}_{R}}-{{{\dot{X}}}_{T}})({{Y}_{R}}-{{Y}_{T}})}{{{({{X}_{R}}-{{X}_{T}})}^{2}}+{{({{Y}_{R}}-{{Y}_{T}})}^{2}}}$ | (15) |
制导律采用PN导引方法时的,制导律的形式为
| ${{{\dot{\chi }}}_{d}}=\kappa {{{\dot{\chi }}}^{*}}$ | (16) |
对于任意的κ>2,拦截轨迹将最终变为直线,并且

|
| 图3 制导律原理图 Figure 3 Plane geometry relationship |
|
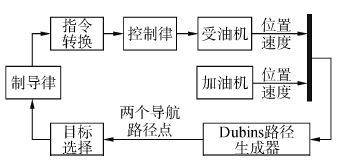
| 图4 制导与控制系统结构图 Figure 4 Guidance and control structure |
Dubins路径生成器给出两个导航路径点,转弯点PTP和会合点PIP,受油机首先跟踪PTP点然后切换跟踪目标为PIP,所以航向控制回路中加入一个目标选择模块。会合过程中,以一定的时间间隔计算更新导航路径点,直到受油机飞至与PTP相距0.15倍的最小转弯半径[5]的距离内的位置时,控制器将目标切换至下一个路径点PIP。这时,导航路径点不再更新,直到受油机飞至与PIP相距小于0.15个最小转弯半径的距离内时,计算结束。
| ${{P}_{waypoint}}=\left\{ \begin{align} & PTP\left| {{p}_{r}}-PTP \right|\ge 0.15{{R}_{min}} \\ & PIP{{p}_{r}}-PTP~ <0.15{{R}_{min}} \\ \end{align} \right.$ | (17) |
进行空中加油会合过程中,需要控制受油机飞行高度,最终与加油机保持在同一高度以便进行下一阶段的对接操作。因此设计垂直制导律,其形式为
| $\begin{align} & {{{\dot{\gamma }}}_{d}}={{k}_{\gamma }}({{\gamma }_{d}}-\gamma ) \\ & {{\gamma }_{d}}={{k}_{h}}({{H}_{T}}-{{H}_{R}}) \\ \end{align}$ | (18) |
式中:HT是加油机的高度,HR是受油机的高度,γ·d为航迹倾斜角速率指令,kγ和kh为比例系数。
2.5 指令转换制导系统所生成的制导指令为航迹角指令,需要将其转换成姿态角指令以输入飞行控制系统。
滚转角指令为
| ${{\varphi }_{d}}=arctan(\frac{{{{\dot{\chi }}}_{d}}cos~\gamma }{{{{\dot{\gamma }}}_{d}}}+gcos~\gamma )$ | (19) |
受油机所受的升力表达式为
| ${{L}_{des}}=mV{{{\dot{\gamma }}}_{d}}-Tsin~\alpha +mgcos~\gamma $ | (20) |
可以得到期望的升力系数:
| $$ | (21) |
根据迎角与升力系数的计算公式可以得出迎角指令为
| ${{\alpha }_{d}}=\frac{({{C}_{ldes}}-({{C}_{l0}}+{{C}_{lq}}\frac{{\bar{c}}}{V}\frac{q}{2}+{{C}_{l\delta e}}{{\delta }_{e}}))}{{{C}_{l\alpha }}}-{{\alpha }_{0}}$ | (22) |
以前面建立的受油机非线性动态模型为基础,选取系统状态变量x1,x2∈R3,系统控制输入u∈R3。即角度状态变量x1=αβφT,角速度状态变量x2=pqrT,等效控制舵偏角u=δeδaδrT,则其非线性动态模型可以表示为
| $\left\{ \begin{align} & {{{\dot{x}}}_{1}}={{f}_{1}}({{x}_{1}})+{{g}_{1}}({{x}_{1}}){{x}_{2}}+{{h}_{1}}({{x}_{1}})u \\ & {{{\dot{x}}}_{2}}={{f}_{2}}({{x}_{1}},{{x}_{2}})+{{g}_{2}}({{x}_{1}},{{x}_{2}})u \\ \end{align} \right.$ | (23) |
具体表示为
| $\begin{align} & {{f}_{1}}({{x}_{1}})=\left[ \begin{matrix} \frac{-Tsin~\alpha -L+m{{g}_{1}}}{mVcos~\beta } \\ \frac{-Tcos~\alpha sin~\beta +Y+m{{g}_{2}}}{mV} \\ 0 \\ \end{matrix} \right] \\ & {{g}_{1}}({{x}_{1}})=\left[ \begin{matrix} -cos~\alpha tan~\beta & 1 & -sin~\alpha tan~\beta \\ sin\alpha & 0 & -cos~\alpha \\ 1 & sin\varphi tan~\theta & cos~\varphi tan~\theta \\ \end{matrix} \right] \\ & {{f}_{2}}({{x}_{1}},{{x}_{2}})=\left[ \begin{matrix} {{I}_{1}}rq+{{I}_{2}}pq+{{I}_{3}}{{{\bar{L}}}_{ax}}+{{I}_{4}}{{N}_{ax}} \\ {{I}_{5}}pr-{{I}_{6}}({{p}^{2}}-{{r}^{2}})+{{I}_{7}}{{M}_{ax}} \\ {{I}_{8}}pq-{{I}_{2}}rq+{{I}_{4}}{{{\bar{L}}}_{ax}}+{{I}_{9}}{{N}_{ax}} \\ \end{matrix} \right]~ \\ & {{g}_{2}}({{x}_{2}})=\left[ \begin{matrix} 0 & ({{I}_{3}}{{C}_{L-{{\delta }_{a}}}}+{{I}_{4}}{{C}_{N{{\delta }_{a}}}})\bar{q}bS & ({{I}_{4}}{{C}_{N{{\delta }_{r}}}}+{{I}_{3}}{{C}_{L-{{\delta }_{r}}}})\bar{q}bS \\ {{I}_{7}}{{C}_{M{{\delta }_{e}}}}\bar{q}S\bar{c} & 0 & 0 \\ 0 & ({{I}_{4}}{{C}_{L-{{\delta }_{a}}}}+{{I}_{9}}{{C}_{N{{\delta }_{a}}}})\bar{q}bS & ({{I}_{9}}{{C}_{N{{\delta }_{r}}}}+{{I}_{4}}{{C}_{L-{{\delta }_{r}}}})\bar{q}bS \\ \end{matrix} \right] \\ \end{align}$ |
其中
| $\begin{align} & {{{\bar{L}}}_{ax}}=\bar{q}bS({{C}_{\bar{L}0}}+{{C}_{\bar{L}\beta }}\beta +{{C}_{\bar{L}p}}\frac{bp}{2V}+{{C}_{\bar{L}r}}\frac{br}{2V}) \\ & {{M}_{ax}}=\bar{q}Sc-({{C}_{M0}}+{{C}_{M\alpha }}\alpha +{{C}_{Mq}}\frac{\bar{c}q}{2V}) \\ & {{N}_{ax}}=\bar{q}bS({{C}_{N0}}+{{C}_{N\beta }}\beta +{{C}_{Np}}\frac{bp}{2V}+{{C}_{Nr}}\frac{br}{2V}) \\ \end{align}$ |
考虑到系统的不确定性,并引入未知有界干扰,式(23)可以写成
| $\left\{ \begin{align} & {{{\dot{x}}}_{1}}={{f}_{1}}({{x}_{1}})+\Delta {{f}_{1}}({{x}_{1}})+[{{g}_{1}}({{x}_{1}})+\Delta {{g}_{1}}({{x}_{1}})]{{x}_{2}}+ \\ & \left[ {{h}_{1}}\left( {{x}_{1}} \right)+\Delta {{h}_{1}}\left( {{x}_{1}} \right) \right]u+{{d}_{1}} \\ & {{{\dot{x}}}_{2}}={{f}_{2}}\left( {{x}_{1}},{{x}_{2}} \right)+\Delta {{f}_{2}}\left( {{x}_{1}},{{x}_{2}} \right)+[{{g}_{2}}\left( {{x}_{1}},{{x}_{2}} \right)+ \\ & \Delta {{g}_{2}}({{x}_{1}},{{x}_{2}})]u+{{d}_{2}} \\ \end{align} \right.$ | (24) |
式中:d1和d2为未知有界干扰。
系统式(24)中由于含有d1和d2,且控制尾舵的变化对气动力影响很小或可以忽略不计[8],即h1(x1)u≈0。将其转化为一类“标准块控制形”的MIMO纯反馈系统。
| $\left\{ \begin{align} & {{{\dot{x}}}_{1}}={{f}_{1}}({{x}_{1}})+{{g}_{1}}({{x}_{1}}){{x}_{2}}+{{\Delta }_{1}}\left( x \right) \\ & {{{\dot{x}}}_{2}}={{f}_{2}}({{x}_{1}},{{x}_{2}})+{{g}_{2}}({{x}_{1}},{{x}_{2}})u+{{\Delta }_{2}}\left( x \right) \\ \end{align} \right.$ | (25) |
其中
| $\left( \begin{align} & {{\Delta }_{1}}\left( x \right)=\Delta {{f}_{1}}({{x}_{1}})+\Delta {{g}_{1}}({{x}_{1}}){{x}_{2}}+ \\ & [{{h}_{1}}({{x}_{1}})+\Delta {{h}_{1}}({{x}_{1}})]u+{{d}_{1}} \\ & {{\Delta }_{2}}\left( x \right)=\Delta {{f}_{2}}({{x}_{1}},{{x}_{2}})+\Delta {{g}_{2}}({{x}_{1}},{{x}_{2}})u+{{d}_{2}} \\ \end{align} \right.$ | (26) |
根据RBF神经网络逼近理论对系统中的不确定性Δ1(x)和Δ2(x)进行估计,有
| $\begin{align} & {{\Delta }_{1}}\left( x \right)=W_{1}^{*}{{\zeta }_{1}}+{{\varepsilon }_{1}}\left( x \right) \\ & {{\Delta }_{2}}\left( x \right)=W_{2}^{*T}{{\zeta }_{2}}+{{\varepsilon }_{2}}\left( x \right) \\ \end{align}$ | (27) |
在采用RBF神经网络对不确定性进行逼近时,引入如下合理假设[14]。假设,神经网络理想权值矩阵W*1和W*2有界,即存在正常数W1M和W2M∈R,有‖W*1‖F≤W1M,‖W*2‖F≤W2M。
1) 考虑系统式(25)中的第一个子系统,
| ${{{\dot{x}}}_{1}}={{f}_{1}}({{x}_{1}})+{{g}_{1}}({{x}_{1}}){{x}_{2}}+{{\Delta }_{1}}\left( x \right)$ | (28) |
定义误差状态变量
选择该系统的虚拟控制律为
| ${{x}_{2d}}=-g_{1}^{-1}(x1)[k1{{{\tilde{x}}}_{1}}+f1(x1)+\hat{W}_{1}^{^{T}}\zeta 1-{{{\dot{x}}}_{1d}}]$ | (29) |
式中:k1为正的系统设计参数;
选取神经网络权值调整自适应律为
| ${{{\dot{\hat{W}}}}_{1}}={{\Xi }_{1}}({{\zeta }_{1}}\tilde{x}_{1}^{T}-{{\sigma }_{1}}{{{\hat{W}}}_{1}})$ | (30) |
式中:Ξ1为可逆正增益矩阵,且σ1>0为修正因子。
为避免对x2d求导出现“微分膨胀”问题。采用一阶滤波器来得到x2d的近似x2d和${{{\dot{\bar{x}}}}_{2d}}$,即
| $\tau {{{\dot{\hat{x}}}}_{2d}}+{{{\bar{x}}}_{2d}}={{x}_{2d}},{{{\bar{x}}}_{2d}}\left( 0 \right)={{x}_{2d}}\left( 0 \right)$ | (31) |
式中τ>0为设计的滤波器时间常数。
2) 考虑系统式(25)中的第二个子系统,
| ${{{\dot{x}}}_{2}}={{f}_{2}}\left( {{x}_{1}},{{x}_{2}} \right)+{{g}_{2}}\left( {{x}_{1}},{{x}_{2}} \right)u+{{\Delta }_{2}}\left( x \right)$ | (32) |
定义误差状态变量
该系统式的虚拟控制律选取为
| $\begin{align} & u=-g_{2}^{-1}\left( {{x}_{1}},{{x}_{2}} \right)\left[ {{k}_{2}}{{{\tilde{x}}}_{2}} \right.+{{f}_{2}}\left( {{x}_{1}},{{x}_{2}} \right)+ \\ & g_{1}^{T}\left( {{x}_{1}} \right){{{\tilde{x}}}_{1}}+\hat{W}_{2}^{T}{{\zeta }_{2}}-\left. {{{\dot{x}}}_{2d}} \right] \\ \end{align}$ | (33) |
式中:k2为正的系统设计参数;${\hat{W}}$2为RBF神经网络理想权值矩阵W2*的估计值,权值估计误差
神经网络权值调整自适应律选取为
| ${{{\dot{\hat{W}}}}_{2}}={{\Xi }_{2}}({{\zeta }_{2}}\tilde{x}_{2}^{T}-{{\sigma }_{2}}{{{\hat{W}}}_{2}})$ | (34) |
式中:Ξ2为可逆正增益矩阵,且σ2>0为修正因子。
3.2 稳定性分析通过Lyapunov稳定性理论来讨论闭环控制系统的稳定性。
首先定义误差动态,对${{{\tilde{x}}}_{1}}$求导并结合系统式(25),得到
| ${{{\dot{\tilde{x}}}}_{1}}={{{\dot{x}}}_{1}}-{{{\dot{x}}}_{1d}}={{f}_{1}}\left( {{x}_{1}} \right)+{{g}_{1}}\left( {{x}_{1}} \right){{x}_{2}}+{{\Delta }_{1}}\left( x \right)-{{{\dot{x}}}_{1d}}$ | (35) |
将不确定性估计值式(27)代入式(35)中得到
| ${{{\dot{\tilde{x}}}}_{1}}={{f}_{1}}\left( {{x}_{1}} \right)+{{g}_{1}}\left( {{x}_{1}} \right){{x}_{2}}+W_{1}^{*T}{{\zeta }_{1}}+{{\varepsilon }_{1}}\left( x \right)-{{{\dot{x}}}_{1d}}$ | (36) |
同理,对${{{\tilde{x}}}_{2}}$求导并结合系统式(25),得到
| ${{{\dot{\tilde{x}}}}_{2}}={{f}_{2}}\left( {{x}_{1}},{{x}_{2}} \right)+{{g}_{1}}\left( {{x}_{1}},{{x}_{2}} \right)u+{{\Delta }_{2}}\left( x \right)-{{{\dot{x}}}_{2d}}$ | (37) |
将不确定估计值式(27)代入式(37)中可以得到
| $\begin{align} & {{{\dot{\tilde{x}}}}_{2}}={{f}_{2}}\left( {{x}_{1}},{{x}_{2}} \right)+g2\left( {{x}_{1}},{{x}_{2}} \right)u+W_{2}^{*T}{{\zeta }_{2}}+{{\varepsilon }_{2}}(x)- \\ & {{{\dot{\bar{x}}}}_{2d}}={{f}_{2}}\left( {{x}_{1}},{{x}_{2}} \right)-({{k}_{2}}{{{\tilde{x}}}_{2}}+{{f}_{2}}\left( {{x}_{1}},{{x}_{2}} \right)+g_{1}^{T}(x1){{{\tilde{x}}}_{1}}+ \\ & \hat{W}_{2}^{T}{{\zeta }_{2}}-{{{\dot{\bar{x}}}}_{2d}})+W_{2}^{*T}{{\zeta }_{2}}+{{\varepsilon }_{2}}(x)-{{{\dot{\bar{x}}}}_{2d}}= \\ & -{{k}_{2}}{{{\tilde{x}}}_{2}}-g_{1}^{T}({{x}_{1}}){{{\tilde{x}}}_{1}}-\hat{W}_{2}^{T}{{\zeta }_{2}}+{{\varepsilon }_{2}}(x) \\ \end{align}$ | (38) |
定义滤波器的滤波误差为
| $z={{{\bar{x}}}_{2d}}-{{x}_{2d}}$ | (39) |
式(39)对时间求导有
| $\dot{z}={{{\dot{\bar{x}}}}_{2d}}-{{{\dot{x}}}_{2d}}={{\tau }^{-1}}\left( {{x}_{2d}}-{{{\bar{x}}}_{2d}} \right)-{{{\dot{x}}}_{2d}}=-{{\tau }^{-1}}z-{{{\dot{x}}}_{2d}}$ | (40) |
当存在滤波器滤波误差时,将式(36)改写为
| $\begin{align} & {{{\dot{\tilde{x}}}}_{1}}={{f}_{1}}\left( {{x}_{1}} \right)+{{g}_{1}}\left( {{x}_{1}} \right)\left( {{{\tilde{x}}}_{1}}+{{x}_{2d}}+z \right)+W_{1}^{*T}{{\zeta }_{1}}+ \\ & {{\varepsilon }_{1}}-{{{\dot{\bar{x}}}}_{1d}}={{f}_{1}}\left( {{x}_{1}} \right)+{{g}_{1}}\left( {{x}_{1}} \right){{x}_{2d}}+W_{1}^{*T}{{\zeta }_{1}}+{{\varepsilon }_{1}}- \\ & {{{\dot{x}}}_{1d}}+{{g}_{1}}({{x}_{1}})({{{\tilde{x}}}_{2}}+z)={{f}_{1}}\left( {{x}_{1}} \right)-({{k}_{1}}{{{\tilde{x}}}_{1}}+{{f}_{1}}\left( {{x}_{1}} \right)+ \\ & \hat{W}_{1}^{T}{{\zeta }_{1}}-{{{\dot{x}}}_{1d}})+W_{1}^{*T}\zeta +{{\varepsilon }_{1}}-{{{\dot{x}}}_{1d}}+{{g}_{1}}\left( {{x}_{1}} \right)\left( {{{\tilde{x}}}_{2}}+z \right)= \\ & -{{k}_{1}}{{{\tilde{x}}}_{1}}-W_{1}^{T}{{\zeta }_{1}}+{{\varepsilon }_{1}}+{{g}_{1}}\left( {{x}_{1}} \right)({{{\tilde{x}}}_{1}}+z) \\ \end{align}$ | (41) |
可以考虑如下的控制Lyapunov函数:
| $V\left( t \right)=\frac{1}{2}[\sum\limits_{i=1}^{2}{\tilde{x}_{i}^{T}{{{\tilde{x}}}_{i}}}+\sum\limits_{i=1}^{2}{tr}(\tilde{W}_{i}^{T}\Xi _{i}^{-1}{{{\tilde{W}}}_{i}})+{{z}^{T}}z]$ | (42) |
对于闭环系统,在前述假设条件下,通过选取适当的设计参数k1、k2和τ,有V·(t) <0。V(t)是有界的,且可知闭环系统内的所有信号均有界。采用控制律式(29)和式(33),神经网络调整规则式(30)和式(34),可使得系统在控制信号的作用下,对指令信号x1d的跟踪误差,指数收敛于零的一个小邻域内。证明过程与文献[14]中的定理类似,此处证明略。
4 前向速度控制为了实现受油机跟踪加油机并实现会合,需要控制受油机的飞行速度,根据式(2)速度方程可改写为
| ${{{\dot{V}}}_{R}}=\frac{Tsin~\alpha cos~\beta -D}{m}+{{g}_{1}}$ | (43) |
由式(39)可以得到
| $T=\frac{m{{U}_{a}}-m{{g}_{1}}+D}{sin~\alpha cos~\beta }$ | (44) |
式中Ua为受油机的前飞加速度指令。
| ${{U}_{a}}={{K}_{R}}\left( R-{{R}_{d}} \right)+{{K}_{V}}({{V}_{T}}-{{V}_{R}})$ | (45) |
KR、KV为比例系数,Rd为会合最终期望的受油机与加油机的相对距离。实际控制中,需要对受油机的加速度指令进行限幅。
由于Dubins路径生成器在计算预计会合点的过程中,需要根据受油机的速度来预估会合时间,且受油机最后存在一个减速过程,所以不直接用当前飞行速度,通过估算受油机完成会合过程中的平均速度来解决这个问题[5]。
5 制导与控制系统综合仿真为验证所设计的制导与控制系统的效果,进行数值仿真研究。受油机的数学模型采用某无人战斗机六自由度动力学模型,为研究方便加油机采用简化的质点动力学模型。在Matlab/Simulink仿真环境中通过飞行仿真对所设计的控制器进行验证。
仿真过程中,飞机模型气动参数摄动30%,增加干扰量sin(πt)[0.050.010.05]T 。控制器的参数选取为:k1=2;k2=5; Ξ1=diag(0.5,0.5,0.5,0.5,,0.5,0.5,0.5,0.5,0.5);Ξ2=[0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1];σ1=1;σ2=1;τ=0.01。RBF神经网络采用3-9-3的结构,αβφTd 、pqrTd分别为两个RBF神经网络的输入,径向基函数为高斯函数,参数分别选取为
| $B=\left[ \begin{matrix} -1/2 & -3/8 & -1/4 & -1/8 & 1/8 & 1/4 & 3/8 & 1/2 \\ \end{matrix} \right]$ |
C=ones(3,9) ,其中ones(3,9)表示3行9列的所有元素为1的矩阵。神经网络初始权值矩阵为均匀分布的随机矩阵,
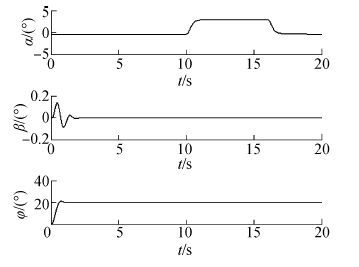
假定加油机在5 500 m高度,以150 m/s的速度沿正北方向直线平飞。受油机初始位置在加油机前方2 000 m,左侧13 000 m处。受油机的初始飞行高度为5 000 m,初始飞行速度为230 m/s,初始航向角为0。首先验证受油机的控制系统的性能,图 5是给定迎角指令α=3°,侧滑角指令β=0和滚转角指令φ=20°后,受油机的状态响应,其中迎角指令在10 s时刻加入,持续6 s。可以看出受油机能够有效跟踪指令信号。
|
| 图5 指令跟踪曲线 Figure 5 Command tracking curve |
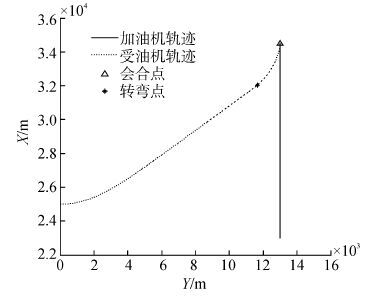
当受油机接收到会合指令后,根据受油机和加油机当前的相对位置和速度,Dubins路径生成器给出响应的导航路径点,制导系统生成相应的指令信号,通过飞控系统,控制受油机与加油机会合。图 6为受油机与加油机在地面坐标系下的三维飞行轨迹。图 7为受油机与加油机会合的平面飞行轨迹,可以看出,该轨迹由圆弧直线圆弧组成,符合Dubins最短路径中的“CLC”模式。图 8为受油机会合过程中的速度,迎角及侧滑角响应曲线。无人机的速度在起始阶段达到最大值并保持,当距离小于一定值后再逐渐减小最终与加油机一致。迎角一开始由于受油机转弯爬升而增加;18 s开始受油机直线飞向转弯点时,无滚转,迎角曲线平稳,45 s后受油机减速,迎角增加;60 s开始受油机进入最后一段圆弧轨迹,有滚转,迎角增大。侧滑角保持为0。

|
| 图6 三维会合曲线 Figure 6 3-D View of rendezvous trajectory |
|
| 图7 平面会合曲线 Figure 7 2-D View of rendezvous trajectory in X-Y plane |

|
| 图8 速度、迎角及侧滑角曲线 Figure 8 Velocity,angle of attack and sliding angle |
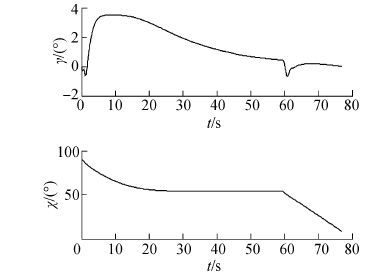
图 9和图 10为受油机飞行过程中的姿态角响应曲线和轨迹角响应曲线,仿真表明,所设计的系统能够根据受油机与加油机之间的位置,规划Dubins路径并给出受油机需要跟踪的导航点,通过飞行控制系统,最终控制受油机飞行并与加油机实现会合,会合过程受油机飞行轨迹平滑,飞行状态平稳。为下一步实现受油机受油插头与加油机加油锥套的对接奠定基础。

|
| 图9 滚转角、俯仰角及偏航角曲线 Figure 9 Roll angle,pitch angle and yaw angle |
|
| 图10 轨迹角曲线 Figure 10 Flight path angle and azimuth angle |
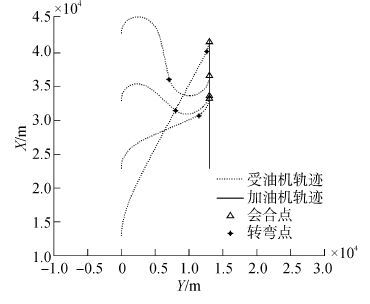
图 11和图 12为受油机不同初始航向角情况下,与加油机位于不同初始位置关系的会合平面飞行轨迹。受油机初始条件设置见表 1。反映出不同初始条件对Dubins路径规划的影响,并显示出所设计的制导与控制系统能够引导受油机按照最短路径飞行,实现最短时间会合。
|
| 图11 受油机不同初始条件平面会合曲线 Figure 11 2-D View of rendezvous trajectory in X-Y plane with different initial position of receiver |

|
| 图12 受油机不同初始条件平面会合曲线 Figure 12 2-D View of rendezvous trajectory in X-Y plane with different initial position of receiver |
| X/m | Y/m | χ/(°) |
| 13 000 | 0 | 0 |
| 23 000 | 0 | 0 |
| 33 000 | 0 | 0 |
| 43 000 | 0 | 0 |
| 23 000 | 0 | 180 |
| 33 000 | 0 | 180 |
| 43 000 | 0 | 180 |
| 53 000 | 0 | 180 |
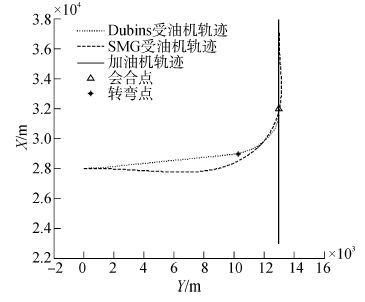
文献[15]根据受油机与加油机之间的视线向量和受油机的速度矢量之间的关系,设计了一种滑模追踪制导律(SMG),实验表明该方法最终能引导受油机飞至加油机正后方完成会合。图 13为将采用本文方法得出的最短飞行轨迹与采用SMG得出的飞行轨迹进行比较的图线。可以看出,SMG中的受油机轨迹的先偏向加油机,最终飞至加油机后方再慢慢接近加油机;本文中,受油机先向预计转弯点飞去再飞至预计会合点,会合轨迹明显短于滑模方法的轨迹。在加入速度控制的条件下,飞过会合轨迹所消耗的时间小于采用滑模追踪制导律会合飞行所消耗的时间。
|
| 图13 与滑模制导方法比较曲线 Figure 13 Comparision to sliding⁃mode guidance |
研究了空中加油的最小时间会合中的制导与控制问题,所设计的系统具有如下特点:
1) 借鉴Dubins最短路径的思想,设计了最小会合控制器,根据受油机与加油机之间的初始位置关系,生成Dubins最短路径并给出受油机需要跟踪的两个导航点,能够实现不同位置及航向初始条件下的跟踪会合制导要求。
2) 借鉴导弹制导的思想,采用比例导引方法设计了受油机与加油机会合制导的侧向加速度指令,设计了高度保持指令,并根据动力学关系转化为会合跟踪要求的飞行控制角指令。
3) 采用Backstepping方法设计了受油机的飞行控制系统,实现了对迎角、侧滑角及滚转角控制;采用RBF神经网络对系统的不确定性进行补偿。
4) 基于六自由度非线性动力学模型的仿真表明,受油机会合轨迹遵循了Dubins最短路径的原理,飞行轨迹平滑,飞行状态稳定,具有良好的动态性能。
| [1] |
郭军, 董新民, 徐跃鉴, 等. 无人机空中加油自主会合控制器设计[J].
控制与决策, 2010, 25(4): 567–571.
GUO Jun, DONG Xinmin, XU Yuejian, et al. Design of UAV autonomous controller for rendezvous in aerial refueling[J]. Control and decision, 2010, 25(4): 567–571. |
| [2] | XU Wenlong, LUO Delin, YANG Lei, et al. Guidance law research for autonomous aerial refueling of UAV[C]//Proceedings of the 2013 IEEE 3rd Annual International Conference on Cyber Technology in Automation, Control and Intelligent Systems (CYBER). Nanjing:IEEE, 2013:440-445. |
| [3] | MCGEE T G, SPRY S, HEDRICK J K. Optimal path planning in a constant wind with a bounded turning rate[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit. San Francisco, California:AIAA, 2005:1-11. |
| [4] | LUGO-CÁRDENAS I, FLORES G, SALAZAR S, et al. Dubins path generation for a fixed wing UAV[C]//Proceedings of 2014 International Conference on Unmanned Aircraft Systems (ICUAS). Orlando, FL:IEEE, 2014:339-346. |
| [5] | BURNS B S. Autonomous unmanned aerial vehicle rendezvous for automated aerial refueling[R]. Ohio:Air Force Inst of Tech Wright-Patterson AFB OH DEPT of Aeronautics and Astronautics, 2007. |
| [6] | WILBURN J N, PERHINSCHI M G, WILBURN B K. Implementation of a 3-Dimensional Dubins-Based UAV Path Generation Algorithm[C]//Proceedings of the AIAA Guidance, Navigation, and Control (GNC) Conference. Boston, MA:AIAA, 2013:1-18. |
| [7] | LUNGU M, LUNGU R. Adaptive backstepping flight control for a mini-UAV[J]. International journal of adaptive control and signal processing, 2013, 27(8): 635–650. |
| [8] | LEE T, KIM Y. Nonlinear adaptive flight control using backstepping and neural networks controller[J]. Journal of guidance, control, and dynamics, 2001, 24(4): 675–682. |
| [9] |
张强, 吴庆宪, 姜长生, 等. 基于Backstepping的非仿射非线性系统鲁棒控制[J].
控制与决策, 2014, 29(1): 19–26.
ZHANG Qiang, WU Qingxian, JIANG Changsheng, et al. Robust control for nonaffine nonlinear systems based on Backstepping[J]. Control and decision, 2014, 29(1): 19–26. |
| [10] |
马正华, 张倩倩, 陈岚萍. 四旋翼飞行器自适应反演姿态控制[J].
智能系统学报, 2015, 10(3): 454–459.
MA Zhenghua, ZHANG Qianqian, CHEN Lanping. Attitude control of quadrotor aircraft via adaptive back-stepping control[J]. CAAI transactions on intelligent systems, 2015, 10(3): 454–459. |
| [11] | HOTA S, GHOSE D. A modified Dubins method for optimal path planning of a Miniature Air Vehicle converging to a straight line path[C]//Proceedings of the American Control Conference. St. Louis, MO:IEEE, 2009:2397-2402. |
| [12] | LU Ping. Intercept of nonmoving targets at arbitrary time-varying velocity[J]. Journal of guidance, control, and dynamics, 1998, 21(1): 176–178. |
| [13] | LU Ping, DOMAN D B, SCHIERMAN J D. Adaptive terminal guidance for hypervelocity impact in specified direction[J]. Journal of guidance, control, and dynamics, 2006, 29(2): 269–278. |
| [14] |
冯福沁, 张胜修, 曹立佳, 等. 基于RBF神经网络的自适应反演大机动飞行控制器设计[J].
电光与控制, 2013, 20(5): 63–68.
FENG Fuqin, ZHANG Shengxiu, CAO Lijia, et al. Design of adaptive backstepping controller for high maneuvering flight based on RBF neural network[J]. Electronics optics & control, 2013, 20(5): 63–68. |
| [15] | YAMASAKI T, BALAKRISHNAN S N. Sliding mode-based pure pursuit guidance for unmanned aerial vehicle rendezvous and chase with a cooperative aircraft[J]. Proceedings of the institution of mechanical engineers, part G:journal of aerospace engineering, 2010, 224(10): 1057–1067. |



