The Logging-While-Dilling(LWD)acoustic technology was developed in recent years as a replacement of wireline logging(Tang and Cheng, 2004). Many studies have been done on LWD multipole acoustic wave propagation along a borehole surrounded by an isotropic formation(Tang et al., 2002; Cui, 2004; Su et al., 2006; Wang et al., 2009). The simulations of anisotropic formation in the LWD environment have got great progress(Wang et al., 2012; Li et al., 2013). The LWD acoustic technology now has been applied widely in exploration and production of unconventional oil-gas resources(Hao et al., 2012).
The universal presence of cracks and pores in formation can significantly affect the propagation of elastic waves. Tang(2011) and Tang et al.(2012)have recently developed an elastic wave theory for cracked porous rocks and used it to interpret acoustic log data from tight s and and shale gas formations. The theory has also been applied to model multipole acoustic wave propagation along a borehole surrounded by a cracked porous formation(Chen et al., 2012; Chen et al., 2013). In the modeling, Chen et al. simulate the velocity dispersion, attenuation, sensitivity, spectral excitation and waveforms of multipole wave modes for different crack parameters. They also analyzed the difference between the impermeable and permeable borehole wall conditions of wireline logging in a cracked porous formation.
This paper extends the study above to the LWD environment, modeling the acoustic wave propagation in a cracked porous formation in the presence of an LWD acoustic tool that occupies a large portion of the borehole. The multipole elastic wavefield for a cracked porous formation follows from Chen et al.’s formulation; the modeling of an LWD tool in borehole has been described in Tang and Cheng’s book as well as in Su et al.(2006). To the authors’ knowledge, suhc LWD modeling work has not been reported. In this paper, we describe the main characteristics of LWD multipole acoustic logging for tight rocks with low permeability and porosity but with abundant cracks. In the following, we present the calculated waveform characteristics for different pore fluids in tight formation rocks. The modeling results can provide theoretical support for interpreting LWD acoustic data logged in cracked porous formations.
2 LWD ELASTIC WAVEFIELD IN A CRACKED POROUS MEDIUMIn the acoustic LWD situation, the drill collar occupies a large portion of the borehole. The source called a multipole acoustic ring source are implemented as a distribution of the point sources placed on the rim of the collar. We use a pore-crack model in Fig. 1 to analyze the LWD multipole wave characteristics. In this model, an LWD drill collar of radius ra, rb, R is centered at the borehole of radius which is surrounded by a cracked porous formation.

|
Fig.1 A pore-crack model for acoustic LWD |
There are only incoming waves traveling from the outer to the inner boundary in the inner fluid. Using cylindrical coordinates(r, θ, z)the inner fluid wavefield(Φ')for the nth multipole is yielded:

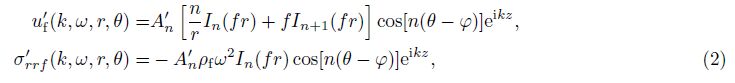
Drill collar is a special elastic medium in which exit compressional waves, SH-type shear-waves and SV-type shear-waves. Each of the potentials is the solution of a scalar wave equation

Considering both outgoing waves and incoming waves, the solution of Eq.(3)is

The drill collar displacement and stress elements are calculated by the following formulae:

There are incoming waves and outgoing waves for the outer fluid. The outer fluid wavefield(Φ)for the nth multipole is yielded

The radial displacement uf and stress σrrf of the outer fluid are given by

The constitutive equation for the average stress for a cracked porous formation is given by(Tang et al., 2012)


 is parameters combination; $\xi $ = [3$\phi $/(4πε)]1/3 is poreto-crack size ratio; η is pore fluid viscosity, ε is crack density and γ is crack aspect radio; and μ0 and υ0 are the shear modulus and Poisson’s ration in the absence of squirt flow, respectively. μ and Kd can be calculated by the Biot-consistent theory(Thomsen, 1985).
is parameters combination; $\xi $ = [3$\phi $/(4πε)]1/3 is poreto-crack size ratio; η is pore fluid viscosity, ε is crack density and γ is crack aspect radio; and μ0 and υ0 are the shear modulus and Poisson’s ration in the absence of squirt flow, respectively. μ and Kd can be calculated by the Biot-consistent theory(Thomsen, 1985).
Three wave modes(fast-, slow-compressional and shear waves)can propagate in a cracked porous formation. The displacements of these three waves can be expressed as

The stresses and displacements of the cracked porous formation can be calculated by Eqs.(8)to(10). The potentials are expressed as follows(Chen et al, 2013):


The displacement components, pore stress and stress components are obtained by

In the theory above, we provide detail theoretical elastic wavefield formulations of different portions in Fig. 1. By employing the boundary conditions, we relate the wave motion of these portions. We use a multipole acoustic ring source on the rim of the collar to model source excitation.
2.5.1 Inner fluid and drill collar boundary



The formulation above is a stress source(Cui, 2004). It is worth mentioning that the expression of the source can also be described as a displacement source(Tang and Cheng, 2004).
2.5.3 Outer fluid and formation boundaryConsidering the boundary condition as an open-pore case, which means that the borehole pressure equals the pore fluid pressure and there is a free hydraulic exchange between the borehole and formation(Tang and Cheng, 2004).
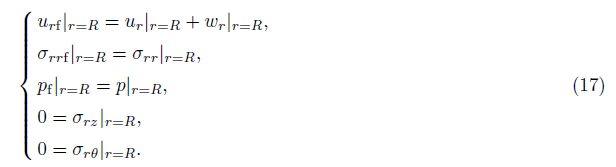
Substituting the stress and displacement components from Eqs.(1)-(13)into the boundary conditions from Eqs.(14)-(17), we give rise to a matrix equation

The details of components of H are given in Appendix A.
3 DISPERSION AND ATTENUATION CHARACTERISTICS OF LWD MULTIPOLE ACOUSTIC LOGGING IN CRACKED POROUS FORMATIONAccording to the theoretical formulation above, the main characteristics of LWD multipole acoustic logging for different crack density values and different pore fluids in cracked porous formation are simulated. The model parameters of drill collar and borehole fluid are listed in Table 1. Table 2 shows two sets of formation parameters of different pore fluids.
| Table 1 Parameters of the fluid and the collar |
| Table 2 Parameters of formation containing pores and cracks |
The determinant D of the matrix in Eq.(18)leads to dispersion equation,

By solving the Eq.(19), the phase velocity and attenuation of the wave mode are calculated:

The sensitivity of velocity or attenuation to a model parameter p, which is defined as the normalized partial derivative of the wave’s phase velocity(attenuation)to q(Tang and Cheng, 2004)is

Figure 2 shows the Stoneley wave velocity(Fig. 2a) and attenuation(Fig. 2b)in a water-saturated formation for various crack density values. The model parameters are listed in Table 1 and Table 2, respectively. The Stoneley velocity decreases and attenuation increases with crack density increasing from 0.00 to 0.25. The sensitivity of velocity to crack density analysis(Tang and Cheng, 2004)increases with crack density increasing(Fig. 2c). The modeling results show that the LWD Stoneley waves are significantly affected by the presence of cracks in tight rocks.

|
Fig.2
Simulation of LWD monopole for different crack density values (a) Phase velocity dispersion curves; (b) Attenuation curves; (c) Velocity sensitivity to ε; (d) Attenuation Sensitivity to ε. |
The sensitive to fluid saturation showing in the cracked porous theory can be utilized for hydrocarbon detection. Therefore, we present the calculated characteristics for different pore fluids in cracked porous formation. The fluid is a mixture of water and gas. The density, modulus and viscosity of the mixed fluid are given by(Brie et al, 1995)


|
Fig.3
Simulation of LWD monopole for different gas saturations (a)Phase velocity dispersion curves;(b)Attenuation curves;(c)Velocity sensitivity to Sg;(d)Attenuation sensitivity to Sg. |
The wave with azimuthal order number n = 1 in Eq.(18)is the dipole wave. Fig. 4 shows the flexural wave velocity(Fig. 4a) and attenuation(Fig. 4b)in a water-saturated formation for various crack density values. The velocity decreases and attenuation increases with crack density increasing from 0.00 to 0.25. It is also interesting to note that there is a minimum of the group velocity in the low-frequency range(3 kHz), which can produce a phenomenon in the waveform called the “Airy phase”. Meanwhile, a maximum of the attenuation exists among the same frequency range. Compared with the wireline logging(WL), the LWD dipole wave characteristics of the dispersion and attenuation vary very much at the high-frequency range. This is because the drill collar occupies a large portion of the borehole substantially influencing the acoustic wave propagation characteristics(Tang and Cheng, 2004), especially in the high-frequency range. It is also noted that the sensitivity of dipole wave velocity to crack density is severely decreased. It can be increased with frequency increasing because of the drill collar(Fig. 4c). The sensitivity of velocity to crack density is the minimum area coincidently in conventional logging-frequency. From this point of view we also demonstrate the drawback of acoustic dipole in LWD, which shows strong dispersion and low sensitivity to crack density in conventional logging-frequency. Fig. 5 shows the flexural wave velocity(Fig. 5a) and attenuation(Fig. 5b)in a various gas-saturated formation. The modeling results show that with gas saturation increasing, the flexural velocity decreases, but not clearly.

|
Fig.4
Simulation of LWD dipole for different crack density values (a)Phase velocity dispersion curves;(b)Attenuation curves;(c)Velocity sensitivity to ε;(d)Attenuation sensitivity to ε. |

|
Fig.5
Simulation of LWD dipole for different gas saturations (a)Phase velocity dispersion curves;(b)Attenuation curves;(c)Velocity sensitivity to Sg;(d)Attenuation sensitivity to Sg. |
The wave with azimuthal order number n = 2 in Eq.(18)is the quadrupole wave. Because the LWD quadrupole tool has become a st and ard technology for shear measurement(Tang and Cheng, 2004), it is particularly important to study the LWD quadrupole wave characteristics. Fig. 6 shows the wave’s velocity(Fig. 6a), attenuation(Fig. 6b) and the sensitivity analysis in a water-saturated formation for various crack density values. It is noted that increasing crack density decreases the velocity and increases the attenuation. The maximum of attenuation curves correspond to the Airy phase in the dispersion curves. The dispersion and attenuation characteristics of LWD quadrupole waves are similar to that of WL dipole waves, which shows some properties common of the S-type guided waves(depending strongly on the S-wave velocity of the formation). Fig. 7 shows the screw wave velocity(Fig. 7a) and attenuation(Fig. 7b)in a cracked formation(ε = 0.2)for various degrees of gas saturation. It is noted that increasing crack density decreases the velocity and increases the attenuation. However, increasing gas saturation has little effect on this S-type guided wave but significantly increases the attenuation.

|
Fig.6
Simulation of LWD quadrupole for different crack density values (a)Phase velocity dispersion curves;(b)Attenuation curves;(c)Velocity sensitivity to ε;(d)Attenuation sensitivity to ε. |

|
Fig.7
Simulation of LWD quadrupole for different gas saturation (a)Phase velocity dispersion curves;(b)Attenuation curves;(c)Velocity sensitivity to Sg;(d)Attenuation sensitivity to Sg. |
The goal of LWD acoustic measurement is to determine formation compressional and shear velocities(Tang and Cheng, 2004). For this reason, we show the LWD multipole acoustic waveform characteristics in connection with formation cracks. The model parameters are listed in Table 1 and Table 2, respectively.
4.1 LWD Monopole WaveformFigure 8 shows the LWD monopole waveforms in a fluid-filled borehole surrounded by a cracked porous formation with crack density values ranging from 0.00 to 0.25. We assign a 9 kHz center-frequency source to the rim of the tool.(The source implementation follows from Cui’s approach(Cui Z W, 2004)). The source-toreceiver distance is 5 m. Because the waveforms are dominated by the S-wave and Stoneley waves with strong amplitude, we multiply the early portion of the data that contains the collar and formation P-waves by a factor of 100 for visualization. The P- and collar-waves overlap for this fast formation is tight. We then increase the collar-wave attenuation(Q-1 = 0.2)in the simulation to simulate the effects of an acoustic isolator between the source and receiver. The waveforms are displayed from crack density values ranging from 0 to 0.25 for comparison. We also simulate the effects of water saturation(Sg = 0, black) and gas saturation(Sg = 1.0, red)on the waveforms. It is noted that the velocities of P-, S-, and Stoneley waves decrease with increasing crack density. Meanwhile, the Stoneley-wave attenuation increases the amplitude decrease as crack density increases. It is also noted that the P-wave arrival time for gas saturation, as denoted by a reline, lags behind that for water saturation(denoted by a black line). This well demonstrates that gas saturation lowers the P-wave velocity for a tight formation containing cracks. The higher the crack density value, the more pronounced this phenomenon becomes. In comparison, the S-wave velocity shows little changes, showing S waves are insensitive to formation fluid. A remarkable phenomenon is that Stoneley-wave amplitude is dramatically different between the two saturation conditions, the amplitude being strongly attenuation by gas. In addition, P wave amplitude is also significantly attenuated by gas saturation. A useful conclusion from the modeling is that one can use compressional-to-shear velocity ratio(VP/VS) and P- and Stoneley-wave amplitude from the LWD measurement for hydrocarbon detection in tight formations.

|
Fig.8 Simulation of LWD monopole waveforms for different crack density values and saturation conditions for water (black) and gas (red) |
Figure 9 shows the LWD quadrupole waveforms excited by a 3 kHz source in a fluid-filled borehole surrounded by a cracked porous formation with crack density values ranging from 0 to 0.25. The source-to-receiver distance is 3 m. The S-wave velocity decreases with increasing crack density. Both water(black) and gas(red)saturation conditions are calculated. The wave onset for both situations is the same, showing that S-wave velocity is insensitive to fluid saturation, consistent with the monopole modeling result of Fig. 8. It is noted that the later dispersive portion of waveform corresponding to the “Airy phase” is severely attenuated by gas saturation, in agreement with the attenuation modeling of Fig. 7b and Fig. 7d. This phenomenon can be used as a characteristic for hydrocarbon detection from LWD quadrupole wave data. Fig. 8 Simulation of LWD monopole waveforms for different crack density values and saturation conditions for water(black) and gas(red)Fig. 9 Simulation of LWD quadrupole waveforms for different crack density values and saturation conditions for water(black) and gas(red)

|
Fig.9 Simulation of LWD quadrupole waveforms for different crack density values and saturation conditions for water (black) and gas (red) |
The crossplot method of the compressional-to-shear velocity ratio(VP/VS)versus compressional-wave slowness is usually used in the fluid identification of the acoustic data interpretation. Tang et al.(2011)has used this method to interpret acoustic log data from tight s and and shale gas formations.
We use a field data of acoustic LWD(the tool only has the monopole acquisition mode)to compare with the theoretical modeling results above. Fig. 10 shows the LWD acoustic data of a horizontal well with a fast formation. We get a high quality data because of the successful construction. Track 1 shows the monopole acoustic waveform data(VD images). Track 2 shows the slowness-time coherence processed of the waveform. The data is respectively processed to give the compressional(DTP) and shear(DTS)slowness curves in track 3.

|
Fig.10 Field LWD data example |
We use crossplot analysis with the slowness data in track 3 to interpret the theory(Fig. 11). The green data of Fig. 11 are from 3283 m to 3309 m. The lithologic character of this gas containing section is in common, with abundant cracks, but little changes of the crack density values. The Stoneley-wave of this section is attenuated. The variation of gas saturations lead to the different of VP/VS. The orange data of Fig. 11 are from 3321 m to 3324 m with high gas saturations. The severe changes of the compressional-wave slowness shows the crack variations of this section. The processed results are in agreement with the attenuation modeling of Fig. 2 and Fig. 3.

|
Fig.11 A crossplot of VP/VS ratio versus compressional slowness using a field LWD data |
As an example, Fig. 12 shows LWD monopole acoustic waveforms of different gas saturations. We pick up three depths(a: 3308.30 m; b: 3295.35 m; c: 3286.51m)from the same lithologic character section(3283~3309 m). The red data of Fig. 11 shows that the gas saturation of these three depths increases, respectively. The characteristics of waveforms show that the gas saturation lowers the velocity and amplitude of P-wave while the S-wave velocity shows little changes. As we all know, the porosity of shale is usually below 10%. It is difficult to interpret the waveform characteristics above using the previous poroelastic wave theory. The result of Fig. 12 shows that the cracks cause the field-data waveform to be very sensitive to gas saturation which is in agreement with the cracked porous theory. This phenomenon can be used as a characteristic for the exploration and development of shale gas resources.

|
Fig.12 Comparison of LWD monopole waveform data for different saturation conditions |
We have analyzed the characteristics of LWD multipole acoustic waves(Stoneley, flexural and quadrupole waves)for a cracked porous formation as a function of crack density and gas saturation. The conclusions are as follows:
(1)The velocity of LWD Stoneley waves in cracked-porous tight formation is more sensitive to crack density while the attenuation is more sensitive to gas saturation.
(2)The minimum of the group velocity of LWD dipole and quadrupole called the “Airy phase” is corresponding to the maximum of the attenuation. The later dispersive portion of waveform corresponding to the “Airy phase” is severely attenuated by gas saturation, which can be used as a characteristic for hydrocarbon detection from LWD wave data.
(3)The variation of the crack density or gas saturation can significantly change the P- and S-wave characteristics of waveforms. These wave characteristics can be utilized for hydrocarbon detection from LWD acoustic data.
ACKNOWLEDGMENTSThis research was supported by Natural Science Foundation of China(41204070, 41174088), 973 program(2014CB239006) and the Fundamental Research Funds for the Central Universities(14CX06076A).
APPENDIX A We describe here the detail components of  in Eq.(18). To make the formula more simple, we use the following combinations of Bessel functions:
in Eq.(18). To make the formula more simple, we use the following combinations of Bessel functions:

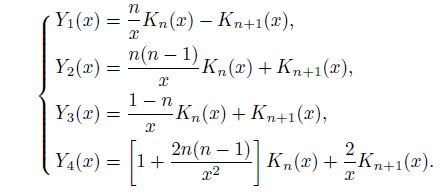
The detail expressions for the elements of H are given as follows:
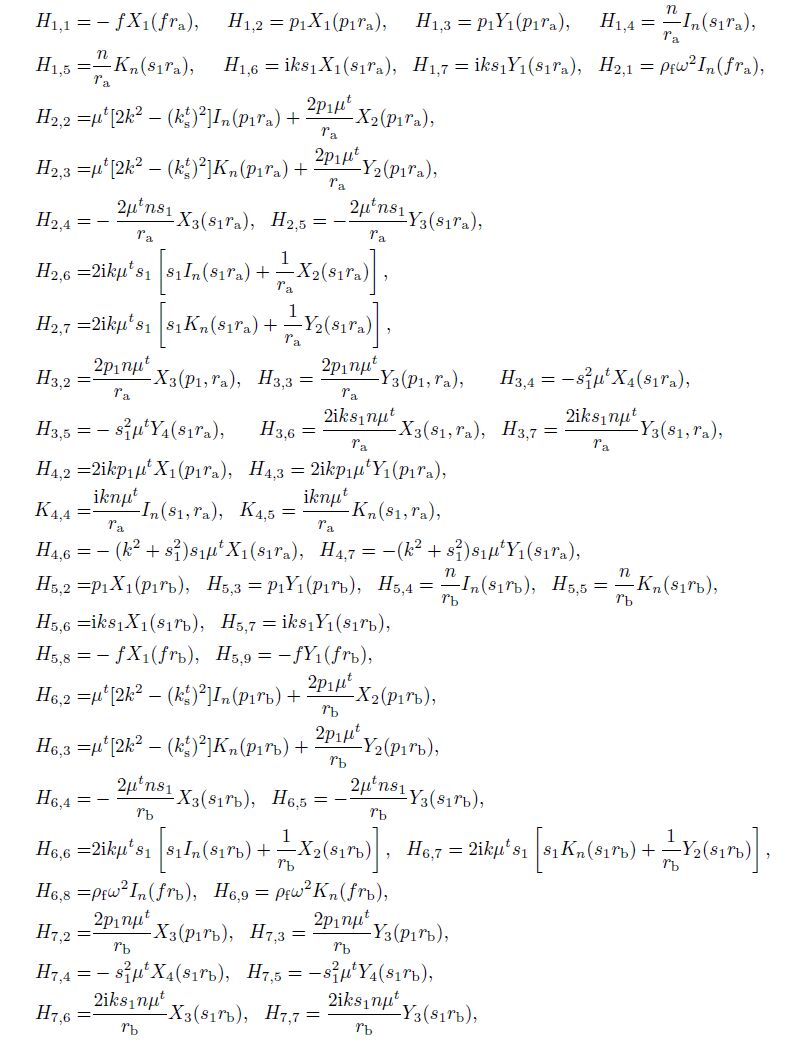

| [1] | Brie A, Pampuri F, Marsala A F, et al. 1995. Shear sonic interpretation in gas-bearing sands. SPE Annual Technical Conference and Exhibition, 701-710. |
| [2] | Chen X L, Tang X M. 2012. Numerical study on the characteristics of acoustic logging response in the fluid-filled borehole embedded in crack-porous medium. Chinese J. Geophysics. (in Chinese), 55(6):2139-2140. |
| [3] | Chen X L, Tang X M, Qian Y P. 2013. Simulation of multipole acoustic logging in cracked porous formations. Geophysics, 79(1):D1-D10. |
| [4] | Cui Z W. 2004. Theoretical and numerical study of modified Biots models, acous to electric well logging and acoustic logging while drilling excited by multipole acoustic source[Ph. D. thesis] (in Chinese). Changchun:Jilin University. |
| [5] | Hao Jian-fei, Zhou Can-can, Li Xia, et al. 2012. Summary of shale gas evaluation applying geophysical logging. Progress in Geophysics, 27(4):1624-1632. |
| [6] | Li X Q, Chen H, He X, et al. 2013. Analyses on mode waves of acoustic logging while drilling in transversely isotropic formations. Chinese J. Geophysics. (in Chinese), 56(9):3212-3222. |
| [7] | Su Y D, Sun J M, Fan Y R, et al. 2006. On numerical study of the LWD multipole source propagation characteristics in slow formation. Well Logging Technology, 30(3):205-207. |
| [8] | Tang X M. 2011. A unified theory for elastic wave propagation through porous media containing cracks-An extension of Biot's poroelastic wave theory. Sci China Earth Sci, 41(6):784-795. |
| [9] | Tang X M, Chen X L, Xu X K. 2012. A cracked porous medium elastic wave theory and its application to interpreting acoustic data from tight formations. Geophysics, 77(6):D245-D252. |
| [10] | Tang X M, Qian Y P, Chen X L. 2013. Laboratory study of elastic wave theory for a cracked porous medium using ultrasonic velocity data of rock samples. Chinese J. Geophysics. (in Chinese), 56(12):4226-4233. |
| [11] | Tang X M, Wang T, Patterson D. 2002. Multipole acoustic logging-while-drilling. 72nd Annual International Meeting, SEG, Expanded Abstracts, 364-368. |
| [12] | Tang X M, Zheng C H. 2004. Quantitative Borehole Acoustic Methods (in Chinese). Beijing:Petroleum Industry Press:20-39. |
| [13] | Thomsen L. 1985. Biot-consistent elastic moduli of porous rocks; low-frequency limit. Geophysics, 50(12):2797-2807. |
| [14] | Wang R J, Qiao W X, Ju X D. 2012. Numerical study of formation anisotropy evaluation using cross dipole acoustic LWD. Chinese J. Geophys. (in Chinese), 55(11):3870-3882. |
| [15] | Wang H, Tao G, Wang B, et al. 2009. Wave field simulation and data acquisition scheme analysis for LWD acoustic tool. Chinese J. Geophys. (in Chinese), 52(9):2402-2409. |
 2014, Vol. 57
2014, Vol. 57




