扩展功能
文章信息
- 常云涛, 王奕彤
- CHANG Yun-tao, WANG Yi-tong
- 连续流交叉口信号配时优化模型
- An Optimal Timing Model for Continuous Flow Intersection
- 公路交通科技, 2018, 35(4): 93-101
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(4): 93-101
- 10.3969/j.issn.1002-0268.2018.04.012
-
文章历史
- 收稿日期: 2016-12-29
常规平面交叉口的交通问题主要由左转车流与对向直行车流之间的冲突引起。通常设置左转专用相位,实现左转车流与对向直行车流的时空分离。然而,分析表明,在四相位信号控制模式下,交叉口的通行能力仅能达到相交道路的35%~40% [1]。为此,美国交通工程学者于2002年提出了连续流交叉口设计模式。连续流交叉口又称左转转移交叉口,是一种非传统的交叉口设计模式,该模式通过在主交叉口上游设置次级交叉口,将左转车流提前在次级交叉口行至对向直行车流左侧(见图 1),从而消除主交叉口范围内两者冲突,实现主交叉口两相位信号控制,大大提高其通行效率[2]。同时,通过主次交叉口信号绿时差优化设计,可以实现主次交叉口的协调控制,提高车辆通过交叉口系统的连续性,减少延误[3]。连续流交叉口设计模式与传统四相位渠化模式相比,通行能力可以提高50%以上,但占地需求变化不大,对于不便修建立交设施或资金有限的大型交叉口扩容改建具有较好的适用性[4-5]。

|
| 图 1 连续流交叉口交通运行[6] Fig. 1 Traffic operation of CFI |
| |
相比常规平面交叉口,虽然连续流交叉口建设费用较高,但在减少车均延误、排队长度和提高通行能力等方面有显著的成效[7-9]。但是当前针对连续流交叉口信号配时的研究大多为预设方案的对比分析,缺乏对其内部交通流运行的系统分析和最优方案的建模求解,大都是针对某一常规交叉口进行连续流设计,再手动生成信号配时方案并通过仿真平台进行交通效益评价,以表明连续流交叉口时空资源分配的优越性[10-14]。
近年来出现了有关主次交叉口信号协调理论模型的研究。X. Wu等[15]给出了延误最小、排队约束的信号配时优化模型,但文中假定所有车辆随机到达,通过到达-离去曲线分析排队长度,所生成的配时方案在实际应用中可能造成排队溢出。X. You等对主次交叉口车辆排队进行深入研究,给出了信号周期最短而非延误最小的优化模型,同时,约束主次交叉口范围内均为连续流,限制了模型的优化空间[16]。综合上述,本研究在分析连续流交叉口延误组成的基础上,建立延误最小、排队约束的信号配时优化模型,并通过相位差分析,简化求解流程和方法,最后用案例分析验证优化模型的有效性和准确性。
1 信号配时优化模型 1.1 模型假定(1) 各进口直行车道数与下游出口车道数相同,左转转移车道数不大于下游出口车道数,设置分离的右转专用车道和慢行过街设施(如天桥、地道等)[17]。
(2) 各进口直行车流量大于左转车流量(一般情况),由于篇幅限制,暂不考虑右转车流和慢行交通。
1.2 参数设定为方便建模,设定道路条件、交通条件和控制条件相关参数如表 1所示。其中,下标m表示主交叉口;下标s表示次级交叉口;下标i表示主次交叉口方向,i= 1, 2, 3, 4分别表示东、南、西、北4个进口;i表示当前进口,则i+1, i+2, i+3分别表示其左侧、对向、右侧进口。
| 参数 | 含义 |
| nmti/nmli | 主交叉口直行/左转车道数 |
| nmei/nsei | 主交叉口出口车道数。 |
| nsli | 次级交叉口左转车道数。 |
| Lmti/Lmli | 主交叉口直行/左转的行驶距离。 |
| Lsli | 次级交叉口左转的行驶距离。 |
| Lui | 主次交叉口间蓄车空间长度。 |
| Lv | 1辆车辆排队所需空间长度,通常取7 m。 |
| qti/qli | 各进口直行/左转交通需求。 |
| H0 | 饱和车头时距,通常取2.0~2.5 s。 |
| hm0i | 主交叉口左转等效车头时距,hm0i=H0/nmli。 |
| hs0i | 次级交叉口直行等效车头时距,hs0i=H0/nsti。 |
| V | 主次交叉口范围内期望车速。 |
| C | 信号周期时长。 |
| gmti/gmli | 主交叉口直行/左转绿灯时长。 |
| omti/omli | 主交叉口直行/左转绿灯启亮时刻,omli=omti。 |
| gsti/gsli | 次级交叉口直行/左转绿灯时长。 |
| Lm/Ls | 主信号绿灯损失, 每相位取[4 s, 5 s];次级信号绿灯损失,取[3 s, 4 s]。 |
| osti/osli | 次级交叉口直行/左转启亮时刻, |
| xsti | 主次信号(直行)相位差, |
| 注:信号配时相关参数取值范围均为[0, C]。 | |
设定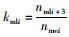
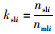
基于以下原则,对主次交叉口进行信号协调控制:
(1) 主次交叉口信号周期保持一致,均为两相位信号控制,绿灯时长根据两个相位关键车流的流量比进行比例分摊。
(2) 设定次级交叉口的左转车流饱和度为0.85~0.90来分配绿灯时间,以确保直行车流(即驶入出口道的车流)及时疏散。
(3) 通过主次信号协调控制,实现直行和左转车流的车均延误最小。
(4) 对于主交叉口左转车流和次级交叉口直行车流,其排队长度不得溢出至上游交叉口。
1.4 目标函数将延误定义为停车时间。优化目标为直行和左转车流的车均延误最小:

|
(1) |
式中,Dmti和Dmli分别为信号周期内主交叉口直行、左转延误;Dsti和Dsli分别为信号周期内次级交叉口直行、左转延误。
主交叉口直行车流和次级交叉口左转车流随机到达停车线,采用HCM2010延误模型计算,其延误值由周期时长决定。以主交叉口直行为例,其车均延误和周期延误为:

|
(2) |
式中,主交叉口直行绿信比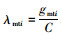


|
(3) |
考虑到主交叉口左转车流和次级交叉口直行车流受到上游信号交叉口的影响,采用波动理论进行分析,其延误值由周期时长和主次信号相位差决定。以主交叉口左转为例,在信号周期既定的情况下,其每周期内延误随相位差的变化情况分析如图 2所示。

|
| 图 2 主交叉口左转延误分析 Fig. 2 Analysis of left-turn movement delay at main intersection |
| |
当相位差xsti的取值为


|
(4) |

|
(5) |
式中,wmli和umli分别为延误梯形上下底边;Xm0i为主交叉口直行饱和车流的通过时间。其计算公式为:

|
(6) |

|
(7) |

|
(8) |

|
(9) |
当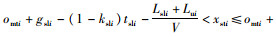


|
(10) |

|
(11) |

|
(12) |

|
(13) |
当


|
(14) |

|
(15) |
当


|
(16) |

|
(17) |

|
(18) |

|
(19) |

|
(20) |
综上所述,主交叉口直行延误和次级交叉口左转延误由周期时长决定,主交叉口左转延误和次级交叉口直行延误由周期时长和相位差决定,目标函数可以表示为:

|
(21) |
为确保连续流交叉口的可靠运行,主交叉口左转和次级交叉口直行的车辆排队不得溢出至上游交叉口;同样地,采用波动理论分析,其排队长度由周期时长和主次信号相位差决定。因此,上游交叉口车辆排队约束可以表示为:

|
(22) |

|
(23) |
式中,Qmli和Qsti分别为周期内主交叉口左转、次级交叉口直行车辆排队。
2 优化模型求解第1节给出了主次交叉口的信号配时优化模型,其决策变量为周期时长和主次信号相位差。其中,周期时长采用等步距枚举法进行搜索。对于既定的周期时长,主交叉口直行和次级交叉口左转的延误值可以确定,而主交叉口左转和次级交叉口直行的延误还受相位差的影响。因此,模型求解的关键在于相位差的优化。
2.1 最优相位差分析由第1节的延误分析,在信号周期既定的情况下,主交叉口左转随相位差的变化可以分为4种场景,其延误和排队的变化趋势如图 3(a)所示。其中,场景(3)所对应的延误和排队恒为零,即所有左转车直接通过主交叉口。

|
| 图 3 相位差优化分析 Fig. 3 Analysis of offset optimization |
| |
由于交通流叠加,次级交叉口直行可以分为7种场景,其延误和排队的变化趋势如图 3(b)所示。其中,场景(2)中延误和排队取得最小值,对应对向进口直行车全部直接通过刺激交叉口,右侧进口左转车全部停车排队[18]。
对于任一次级交叉口,最优相位差对应次级交叉口直行和主交叉口左转的总延误最小。如图 3(c)~(e)所示,设定



式中,tmti+2为主交叉口对向进口直行车流的通过时间;tmli+3为主交叉口左侧进口左转车流的通过时间。
设定L,M,R分别表示场景的相对位置;kBiL, kBiM,kBiR分别为主交叉口左转在场景(2)~(4)中延误的变化率;kAiL, kAiM,kAiR为次级交叉口直行在场景(1)~(3)中延误的变化斜率,可以根据延误公式求解。考虑到交通流叠加,次级交叉口直行流量通常会大于主交叉口左转,可以假定kAiL和kAiR的绝对值大于kBiL和kBiR。因此,最优相位差应对应次级交叉口最优场景,其取值范围为[AiL, AiR],再根据主交叉口左转最优场景的相位差取值,可以分为以下3种情况:
(1) BiL>AiR(图 3(c)):当kAiM≥|kBiL|时,最优相位差xsti为AiL,否则xsti=AiR。
(2) AiL<BiL≤AiR(图 3(d)):当kAiM≥|kBiL|时,xsti=BiL,否则xsti=AiR。
(3) BiL≤AiL(图 3(e)):xsti=AiL。
因此,只需分别计算相位差取值为AiL,BiL,AiR对应的主交叉口左转和次级交叉口直行的总延误,其最小值对应的即为最优相位差。
2.2 优化流程和求解方法基于上节所建信号配时优化模型,对周期时长和相位差进行优化,并求解配时参数。具体流程和方法如图 4所示。

|
| 图 4 信号配时优化流程 Fig. 4 Flowchart of signal timing optimization |
| |
图中,Cmin为周期时长的最小值,ΔS为搜索步距,d为车均延误,通过枚举法求解延误最低的协调配时优化方案。考虑到左转蓄车道长度(通常50~150 m)和信号效率,将周期时长的取值范围设定为[40 s,120 s],ΔS设定为5 s,以保证足够的精度。周期时长既定,根据2.3中的配时原则,计算主交叉口直行gmti和左转的绿灯时长gmli,并设定次级交叉口左转饱和度Sat1为0.8,分配其左转、直行的绿灯时长gsli和gsti。

|
(24) |

|
(25) |

|
(26) |

|
(27) |
式中,y1, 3和y2, 4分别为东西、南北向进口直行和左转的最大流量比;S为单车道通行能力;Y为关键流量比之和。
按照3.1中的优化原理,分别计算当前信号周期的相位差AiL,AiR,BiL所对应的主交叉口左转和次级交叉口直行的总延误,其最小值即对应最优相位差,再计算主次交叉口直行和左转的车均延误,进而判断主交叉口左转和次级交叉口直行的车辆排队是否满足蓄车道空间的约束,满足排队约束就继续循环,否则结束循环。
通过对比所有循环的车均延误,其最小值对应最优周期时长C,并输出相应的最优相位差、主次信号直行和左转绿灯时长等信号配时参数,以及车均延误、排队长度等反映交叉口运行的评价参数。
3 案例分析以位于江西南昌某干道交叉口为例(图 5(a)),采用常规渠化和四相位控制。由于存在过饱和车流,当前信号周期为236 s,经实地观测,高峰时段车均延误为260 s,南北进口车辆排队长度大于400 m。对东、南进口进行拓宽,增加直行车道数,周期时长设为120 s,理论上车均延误降至72.9 s,服务水平仍为E级。

|
| 图 5 案例交叉口 Fig. 5 CFI in case study |
| |
保持车道功能划分及车道数不变,对其进行连续流交叉口设计(图 5(b)):除东进口设有2条直行车道,其他进口都设有3条直行车道;东进口、南进口设有2条左转转移车道,西进口、北进口设有1条左转转移车道,各出口车道数与对向进口直行车道数相同;东、南、西、北4个进口的蓄车空间长度分别为160,140,80,130 m。
经计算,信号周期的取值范围为[45 s, 90 s]。设定步长为5 s,根据第2节的优化流程和求解方法,输出所有循环的车均延误和排队长度如图 6所示。随着周期时长的增加,车均延误先减后增,当周期时长取50 s时,车均延误取得最小值32.6 s,相比同样进口道设置(数量和车道功能划分)的传统四相位控制交叉口设计模式,车均延误减少55%,排队长度也远小于蓄车空间长度。相应的信号配时参数(包括绿灯启亮时刻和绿信比)如表 2所示。

|
| 图 6 交叉口运行指标随周期时长变化 Fig. 6 Intersection operation index varying with cycle length |
| |
| 序号 | 进口 | omti/omli | osti | osli | λmti/λmli | λsti | λsli |
| 1 | 东 | 0 | 9 | 34 | 0.54 | 0.44 | 0.44 |
| 2 | 南 | 32 | 25 | 50 | 0.32 | 0.44 | 0.44 |
| 3 | 西 | 0 | 5 | 41 | 0.54 | 0.66 | 0.22 |
| 4 | 北 | 32 | 16 | 1 | 0.32 | 0.64 | 0.24 |
基于上述连续流交叉口设计,采用微观交通仿真软件Vissim建立路网模型。根据优化模型计算结果,设定配时参数。根据高峰时段交通调查,设定各进口流量水平。将交叉口范围内饱和车头时距校准为2.48 s,目标车速为50 km/h。批量仿真20次,输出车均延误和排队长度作为评价指标,见表 3。
| 指标 | d/s | Qml1/ m |
Qml2/ m |
Qml3/ m |
Qml4/ m |
Qst1/ m |
Qst2/ m |
Qst3/ m |
Qst4/ m |
| 模型计算 | 33.9 | 0 | 0 | 0 | 0 | 21 | 28 | 21 | 14 |
| 仿真输出 | 32.6 | 0 | 2 | 0 | 8 | 14 | 35 | 14 | 10 |
整个仿真过程中,连续流交叉口运行稳定,未出现交通拥堵及车辆排队溢出现象(图 5(c))。表 3中的模型计算与仿真输出的评价指标接近,车均延误的精度高达95%,排队长度差别基本在1辆车长以内(7 m)。
4 结论连续流交叉口是一种非立体交叉口,但能有效提高交叉口通行能力的交通设计模式。目前针对该模式的研究大多为基于具体案例的预设方案的对比分析。在研究连续流交叉口延误组成与周期时长、相位差关系的基础上,建立了具有普遍适应性的连续流交叉口信号配时优化模型及最优相位差模型,并给出了简单易行的模型求解流程和方法。案例分析表明:所提出的模型与方法行之有效,所生成的配时方案能够有效降低延误、改善交叉口通行能力,且延误和排队长度的模型计算值与仿真输出相符。
| [1] |
陈亦新, 贺玉龙, 孙小端. 信号交叉口左弯待转区对左转车道通行能力的影响[J]. 长安大学学报:自然科学版, 2015, 35(6): 111-116. CHEN Yi-xin, HE Yu-long, SUN Xiao-duan. Impact of Left-turn Waiting Areas on the Capacity of Left-turn Lane in Signalized Intersection[J]. Journal of Chang'an University:Natural Science Edition, 2015, 35(6): 111-116. |
| [2] |
HUMMER J E. Unconventional Left-turn Alternative for Urban and Suburban Arterials:Part Two[J]. ITE Journal, 2000, 68(9): 26-29. |
| [3] |
顾九春. 非传统平面交叉口方案的设计研究进展[J]. 道路交通与安全, 2006(4): 41-45. GU Jiu-chun. The Research Evolution of Unconventional At-grade Intersection Design[J]. Road Traffic and Safety, 2006(4): 41-45. |
| [4] |
ESAWEY M E, SAYED T. Unconventional USC Intersection Corridors:Evaluation of Potential Implementation in Doha, Qatar[J]. Journal of Advanced Transportation, 2011, 45(1): 38-53. |
| [5] |
TABERNERO V, SAYED T. Upstream Signalized Crossover Intersection:An Unconventional Intersection Scheme[J]. Journal of Transportation Engineering, 2006, 132(11): 907-911. |
| [6] |
FONTAINE M D. Operational Comparison of a Continuous Flow Intersection to Conventional Alternatives[C]//ITE 2009 Annual Meeting and Exhibit. San Antonio: ITE, 2009.
|
| [7] |
GOLDBLATT R, MIER F, FRIEDMAN J. Continuous Flow Intersections[J]. Journal of Institute of Transportation Engineers, 1994, 64(7): 35-35. |
| [8] |
JAGANNATHAN R, BARED J. Design and Operational Performance of Crossover Displaced Left-turn Intersections[J]. Transportation Research Record, 2004, 1881: 1-10. |
| [9] |
PITAKSRINGKAR J P. Measures of Effectiveness for Continuous Flow Intersection: A Maryland Intersection Case Study[C]//ITE 2005 Annual Meeting and Exhibit. Melbourne: ITE, 2005.
|
| [10] |
OLARTE C, KAISAR E. Operational Performance Comparison between Three Unconventional Intersection Designs: Left-turn Bypass, Diverging Flow and Displaced Left-turn[C]//The 9th Latin American and Caribbean Conference. Medellin: LACCEI, 2011.
|
| [11] |
CHEONG S, RAHWANGI S, CHANG G L. Comparison of Three Unconventional Arterial Intersection Designs: Continuous Flow Intersection, Parallel Flow Intersection, and Upstream Signalized Crossover[C]//Proceedings of 11th International IEEE Conference on Intelligent Transportation Systems. Beijing: IEEE, 2008.
|
| [12] |
AUTEY J, SAYED T, ESAWEY M. Guidelines for the Use of Some Unconventional Intersection Designs[C]//The 4th International Symposium on Highway Geometric Design. Valenci: [s. n. ], 2010.
|
| [13] |
刘秋晨, 张轮, 杨文臣. 城市道路新型连续流交叉口的设计及仿真[J]. 交通信息与安全, 2013, 31(2): 122-127. LIU Qiu-chen, ZHANG Lun, YANG Wen-chen. Design and Simulation of a New Continuous Flow Intersection for Urban Road[J]. Journal of Transport Information and Safety, 2013, 31(2): 122-127. |
| [14] |
周亚平, 陈凤权, 王永. 基于两种非传统交叉口通行能力的综合优化模型[J]. 公路交通科技, 2016, 33(4): 134-141. ZHOU Ya-ping, CHEN Feng-quan, WANG Yong. An Integrated Capacity Optimization Model Based on Two Unconventional Intersections[J]. Journal of Highway and Transportation Research and Development, 2016, 33(4): 134-141. |
| [15] |
WU X, JUAREZ D, JIA X. Optimal Signal Timing Models for the FHWA and Mexico 4-legged Continuous Flow Intersections[C]//Transportation Research Board 93rd Annual Meeting. Washington, D. C. : TRB, 2014.
|
| [16] |
YOU X, LI L, MA W. Coordinated Optimization Model for Signal Timings of Full Continuous Flow Intersections[J]. Transportation Research Record, 2013, 2356: 23-33. |
| [17] |
PARK S, RAKHA H. Continuous Flow Intersections: A Safety and Environmental Perspective[C]//Proceedings of 13th International IEEE Conference on Intelligent Transportation Systems. Funchal, Portugal: IEEE, 2010: 85-90.
|
| [18] |
CHANG Y, DENG X. Study on Four-leg Intersection Continuous Flow Intersection Optimal Timing Modeling[C]//Transportation Research Board 94th Annual Meeting. Washington, D. C. : TRB, 2015.
|
 2018, Vol. 35
2018, Vol. 35
