扩展功能
文章信息
- 王威娜, 秦煜, 李小飞, 陈辉强, 王迪
- WANG Wei-na, QIN Yu, LI Xiao-fei, CHEN Hui-qiang, WANG Di
- 季节冻土地区阴阳坡路基温度场及变形发育数值模拟
- Numerical Simulation of Temperature Field and Deformation Development of Subgrade with Sunny-shady Slopes in Seasonal Frozen Region
- 公路交通科技, 2017, 34(2): 20-28
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(2): 20-28
- 10.3969/j.issn.1002-0268.2017.02.004
-
文章历史
- 收稿日期: 2015-12-30
2. 重庆交通大学 土木工程学院, 重庆 400074;
3. 中铁二院重庆勘察设计研究院有限责任公司, 重庆 400023;
4. 布伦瑞克工业大学, 路面工程中心, 德国 布伦瑞克 38106
2. School of Civil Engineering, Chongqing Jiaotong University, Chongqing 400074, China;
3. CREEC (Chongqing) Survey, Design and Research Co. Ltd., Chongqing 400023, China;
4. Pavement Engineering Centre, Technical University of Braunschweig, Braunschweig 38106, Germany
季节冻土地区路基内部温度场、水分场随外界环境发生剧烈变化。特别是路基阴阳坡效应强烈时,温度差异所引起的水分不均匀分布更加明显,路基两侧边坡出现不平衡冻融状态,导致路基不可避免的发生不均匀变形,引起路基纵向、横向裂缝等病害,加速了路基路面破坏。因此,开展季节冻土地区路基变形研究将为该地区路基设计与养护提供理论指导。
研究人员曾对多年冻土地区路基阴阳坡面温度差异所引起的路基变形进行了试验与理论研究[1-3],具有一定的成果积累。但由于环境温度的差异,多年冻土地区路基内部水、热、力状态与季节冻土地区路基内部状态不尽相同,其变形特性存在差异。国内外研究人员也对季节冻土地区路基进行了较多研究。杜兆成[4]基于吉林省长余高速公路路基两年来的冻胀观测资料,分析了路基冻胀量及其沿冻深的分布。Evans[5]对美国季节冻土地区森林道路进行了6年的变形观测,分析了路基冻结深度及变形特性。许健、牛富俊[6]采用非稳态相变温度场的数学模型和热弹塑性冻胀模型,分析了沈哈线换填试验段冻土路基冻融过程温度场及变形场,但较少研究涉及阴阳坡温度差异对季节冻土地区路基变形特性的影响。而张玉芝、杜彦良[7]采用热弹性力学理论,分析了季节冻土地区哈大高速铁路路基冻融变形,指出了阴阳坡效应导致阴坡冻胀融沉压缩变形更严重,但铁路路基的断面形式、填筑方式与公路路基并不相同,阴阳坡面温度差异所引起的不均匀变形可能有所差异。因此,有必要针对季节冻土地区实际状况,分析具有阴阳坡效应的公路路基温度场及变形发育特性。
本文以黑龙江鸡西地区作为研究对象,结合实际气候条件,通过有限元方法,建立季节冻土地区公路路基温度场计算模型并分析温度分布规律,在此基础上,考虑冻结锋面位置和形状,引入土体的冻胀率和融沉系数,建立路基变形场计算模型,研究由路基阴阳坡温度差异引起的路基变形发育。
1 基本理论 1.1 基本假设(1) 土体为均质各向同性材料;(2)土颗粒、冰及未冻水不可压缩;(3)土体为线弹性、小变形体;(4)路基土体仅在重力及土体冻结产生的膨胀力作用下发生变形。
1.2 伴有相变的路基非稳态温度场的控制方程伴随有相变的平面非稳态导热微分方程为[8]:
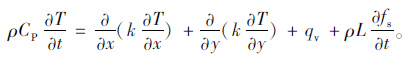
|
(1) |
式中,T为相变区内节点温度;t为过程进行的时间;k为材料的导热系数;ρ为材料的密度;CP为材料的定压比热;qv为材料的内热源强度;x, y为直角坐标;fs为该节点的固相率。
在非相变区内,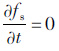
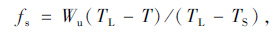
|
(2) |
式中,Wu为未冻水的体积含水量;TL,TS分别为融化及冻结温度。
1.3 本构方程在自重作用下,冻土路基土体的应力-应变关系[8]:
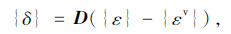
|
(3) |
式中,{δ}={δx δy τxy}T,D为弹性矩阵,对于平面应变问题,
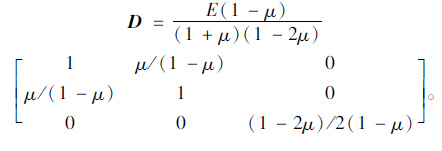
|
体变形εv可由式(4)确定,正为膨胀变形,负为压缩变形。
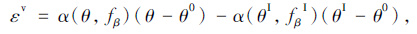
|
(4) |
式中,α(θ, fβ)为热变形系数;θ为现有温度;θI为初始温度;fβ为当前预定义的场变量;fβI为初始值的场变量;θ0为热变形系数的参考温度。
由于假定土体为各向同性体,因此体变形在每个方向是相等的,即:
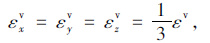
|
(5) |
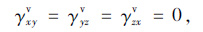
|
(6) |
式中,εxv,εyv,εzv分别为变形引起的正应变分量;γxyv,γyzv,γzxv分别为变形引起的剪应变分量。
2 计算方法与模型 2.1 计算方法路基温度随着环境发生周期性的变化,其温度场为瞬态温度场。在温度作用下,路基中水分将随着温度的变化而变化。研究表明[9]:已冻区土体中水分迁移量很小,含水率无明显变化,水分迁移主要出现在未冻区和冻结锋面附近的剧烈相变区。在温度梯度的作用下,路基土体中水分向冻结锋面迁移,冻结锋面附近的含水率将巨增。因此,本文基于路基温度场变化,考虑在地下水补给条件下,仅冻结锋面发生冻胀或融沉,采用冻胀率η表征土体的冻胀能力,融沉系数δ0表征土体的压缩程度,建立季节冻土地区路基位移场数值模型,以分析由于路基阴阳坡所引起的变形发育,具体步骤如下:
(1) 建立路基温度场计算模型,根据气象参数,在考虑大气温度、太阳辐射和地面有效辐射的基础上,建立第Ⅱ类与第Ⅲ类热边界条件叠加的有限元模型,计算1年内路基内部温度场,生成计算结果文件。
(2) 在此基础上,建立路基位移场计算模型(网格与温度场计算模型相同),定义随温度变化的材料参数,引入冻结锋面上下限温度的概念,得到在不同的温度边界条件作用下冻结锋面的位置及形状,假设土体冻胀率或融沉系数,导入温度场结果文件,进行路基位移场计算,得到发生冻胀或融沉时路基变形情况。
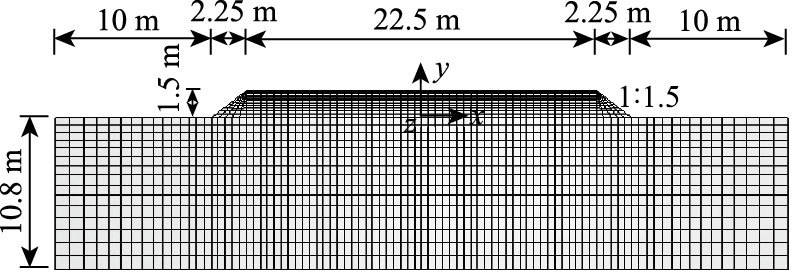
2.2 计算模型 2.2.1 模型建立路基高度采用1.5 m,路基边坡坡率采用1:1.5,路基顶面宽度为22.5 m。相关文章[10]指出:对于大面积填土来说,其影响深度为填土厚度的7.2倍,就本模型而言,即10.8 m。因此,地基深度取为10.8 m。研究表明[11]:路基对边坡10 m以外的天然土的影响很小,所以地基的研究宽度取路基两侧10 m,模型如图 1所示。本文基于有限元通用软件,使用FORTRAN语言编写子程序定义温度与变形的耦合作用本构关系,选取8节点四面体热传导单元进行非稳态温度场分析,采用8节点位移和温度耦合单元进行变形场分析。
|
| 图 1 路基数值计算模型 Fig. 1 Numerical computation model of subgrade |
| |
2.2.2 边界条件
1温度场边界条件
根据传热学原理,本文考虑第Ⅱ、Ⅲ类热边界条件的叠加。
(1) 太阳辐射及地面有效辐射
一天内太阳辐射的强度可近似的用正弦曲线表示[12]:
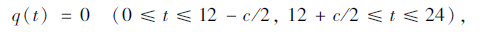
|
(7) |
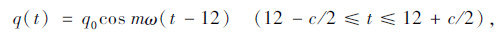
|
(8) |
式中,q0为中午最大辐射,q0=0.131mQd;Qd为日太阳辐射总量;m为系数,m=12/c,c为实际日照时间;ω为角频率,ω=0.2618。
路基边坡坡面为斜面,故引入坡面系数ε,计算坡面的太阳辐射量[13]:
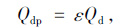
|
(9) |
式中,Qdp为坡面每平方米受到的太阳辐射量;ε为坡面系数。
坡面系数计算公式:
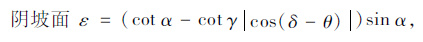
|
(10) |
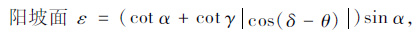
|
(11) |
式中,α为边坡坡角;γ为太阳高度角;δ为路基走向角;θ为太阳方位角。
地面有效辐射主要与地面温度、云量等诸多因素相关,其实测和计算都较困难。本文采用Barber提出的将太阳辐射的1/3近似视为地面有效辐射[14],实现地面有效辐射边界条件。
(2) 对热交换
大气温度与路表温度差引起的对流热交换,可利用牛顿放热定律确定:
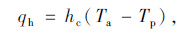
|
(12) |
式中,qh为地面有效辐射;hc为对流换热系数;Ta为空气温度;Tp为路表温度。
严作人[15]采用正弦函数的线性组合模拟了气温的日变化过程:
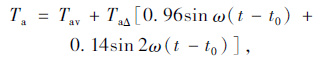
|
(13) |
式中,Ta为日平均温度;TaΔ为日气温振幅;TaΔ=(Tamax-Tamin)/2; Tamax,Tamin为日最高、低气温;ω为角频率,ω=0.261 8;t0为初相位,则本文设初相位为9,则计算时间起点与一天的时间起点一致为零点。
(3) 初始条件及底部边界条件
本文以新建道路为模拟对象,计算初始时间为10月1日,假设模型初始温度为15 ℃。研究表明[16]:路表下10 m处地温基本恒定,约为15 ℃。所以本文取15 ℃为结构底部采用恒温边界条件。
2应力场边界条件
模型左右边界水平方向位移为0,模型下边界水平及竖直方向位移为0。
2.2.3 参数选取(1) 热特性参数
参考相似土体实测资料与文献,土体各项热物理参数如表 1所示[17],假设路基土与地基土热物理参数一致。
| 温度/℃ | -20 | -5 | -0.2 | -0.1 | +5 | 20 |
| 导热系数/ [J·(h·m· ℃)-1] | 3 816 | 3 816 | 3 736 | 3 418 | 3 384 | 3 384 |
| 比热/ [J·(kg·℃)-1] | 1 380.1 | 1 380.1 | 1 345.5 | 1 628.3 | 1 672.8 | 1 672.8 |
| 相变潜热/ (J·kg-1) | 43 088 | |||||
| 密度/(kg·m-3) | 1 800 | |||||
| 注:相变潜热只有在相变发生时才有效,在本文计算中,取[-0.2, -0.1]为相变区间。 | ||||||
本文收集了道路所在的黑龙江鸡西地区的气象资料,见表 2[18]。
| 月份 | 日平均 气温/℃ | 日最高 气温/℃ | 日最低 气温/℃ | 日太阳 总辐射量/ (MJ·m-2) | 日有效日照 时间/h | 日平均风速/ (m·s-1) |
| 1 | -16.4 | -5.2 | -20.9 | 18.9 | 7.2 | 3.5 |
| 2 | -12.1 | -2.8 | -14.1 | 26.2 | 8.3 | 3.7 |
| 3 | -3.5 | -0.3 | -8.8 | 43.6 | 9.5 | 3.8 |
| 4 | 6.4 | 10.8 | 3.3 | 50.6 | 10.7 | 4.0 |
| 5 | 13.6 | 18.2 | 8.6 | 59.1 | 11.7 | 3.6 |
| 6 | 18.7 | 26.7 | 15.5 | 59.2 | 11.8 | 2.5 |
| 7 | 20.9 | 25.9 | 16.0 | 56.8 | 11.2 | 2.2 |
| 8 | 21.7 | 27.1 | 17.1 | 50.3 | 10.2 | 2.1 |
| 9 | 14.2 | 20.9 | 11.1 | 42.4 | 8.9 | 2.4 |
| 10 | 5.8 | 12.7 | 1.1 | 31.3 | 8.5 | 3.2 |
| 11 | -4.8 | 1.0 | -8.8 | 20.4 | 8.4 | 3.5 |
| 12 | -13.6 | -5.9 | -13.8 | 15.3 | 7.5 | 3.3 |
考虑北半球路线东西走向,阴阳坡效应强烈,所以选取东西走向的路基为研究对象,根据式(10)、式(11)计算坡面系数,见表 3。
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 南坡 | 2.09 | 1.75 | 1.45 | 1.16 | 1.07 | 1.06 | 1.12 | 1.25 | 1.36 | 1.63 | 1.99 | 2.23 |
| 北坡 | 0 | 0.01 | 0.22 | 0.43 | 0.55 | 0.61 | 0.58 | 0.49 | 0.31 | 0.06 | 0 | 0 |
式(12)中土体表面与大气的热交换系数hc可用hc=4.1v+5.7近似表示[12]。风速v根据气象资料及前人研究成果[19]加以确定,如表 4所示。
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 地基风速/(m·s-1) | 3.50 | 3.70 | 3.80 | 4.00 | 3.60 | 2.50 | 2.20 | 2.10 | 2.40 | 3.20 | 3.50 | 3.30 |
| 边坡风速/(m·s-1) | 2.63 | 2.78 | 2.85 | 3.01 | 2.70 | 1.90 | 1.69 | 1.62 | 1.83 | 2.40 | 2.63 | 2.48 |
| 路基顶面风速/(m·s-1) | 3.62 | 3.82 | 3.93 | 4.14 | 3.72 | 2.60 | 2.30 | 2.20 | 2.50 | 3.31 | 3.62 | 3.41 |
(2) 力学参数
为了简化计算,本文假定在冻胀模型中冻结区土体冻胀率较小,处于不冻胀或弱冻胀状态,在计算时忽略其冻胀率,仅考虑冻结锋面处土体的冻胀。假设在地下水补充的情况下冻结锋面处的土体含水量较大,根据黏性冻土的工程分类[20],取强冻胀率η=0.05。在融化模型中,本文考虑路基中的冻结土刚刚融化,而表层土体中的水分又来不及排除的最不利状态。考虑含水率较大的土体融沉变形较大,根据黏性冻土的工程分类[20],取较大的融沉系数δ0=0.05。本文选取相似土体冻结锋面产生时上下限温度区间0~-1.5 ℃[21]作为判断模型中冻结锋面位置及形状时所调用的温度。土体力学参数如表 5所示[8]。
| 土体 | 回弹模量/MPa | 泊松比 | 干密度/(kg·m-3) |
| 冻结土体 | 100 | 0.2 | - |
| 未冻结土体 | 60 | 0.35 | 1800 |
| 冰锋带处融化土体 | 10 | 0.35 | - |
3 计算结果与分析 3.1 模型验证
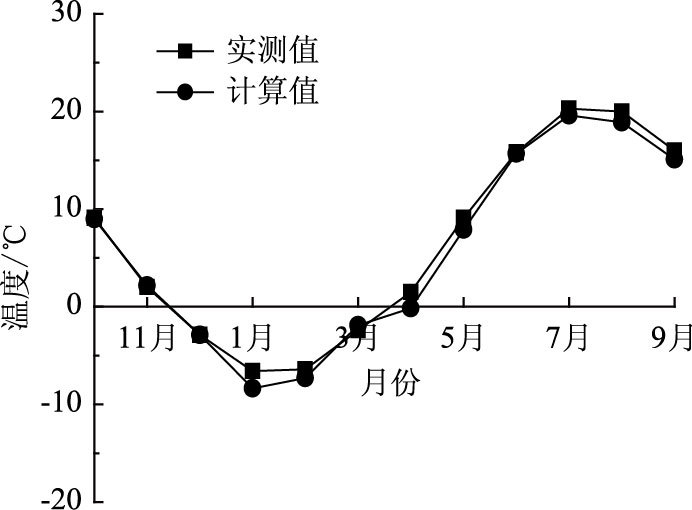
为了验证本文所建温度模型的正确性,将数值模拟的土基下0.4 m深处温度值与国家气象局数据中心提供的黑龙江鸡西地区0.4 m深处的多年月平均实测典型代表值进行比较。结果如图 2所示:计算值略低于实测值,但二者变化规律一致,所以温度场模型是合理的。
|
| 图 2 地基下0.4 m深度计算值与实测值对比 Fig. 2 Comparison of 0.4 m depths underground between calculated and measured values |
| |
根据现场调查,在有地下水补给的情况下,季节冻土地区路基变形可达到48 mm,并可能更大[4];本文所建模型计算得到的路基最大冻胀变形为38 mm,在实际调查范围内。就融沉而言,前人研究结果表明:在封闭系统内,冻胀与融沉关系密切,冻胀量大,其融沉量也大[22];而本文建模计算所得的路基最大融沉变形区域与最大冻胀变形区域大体一致,与前人研究规律相符。综上所述,本文建立的变形发育模型较合理。
3.2 温度分析(1) 路基温度场分析
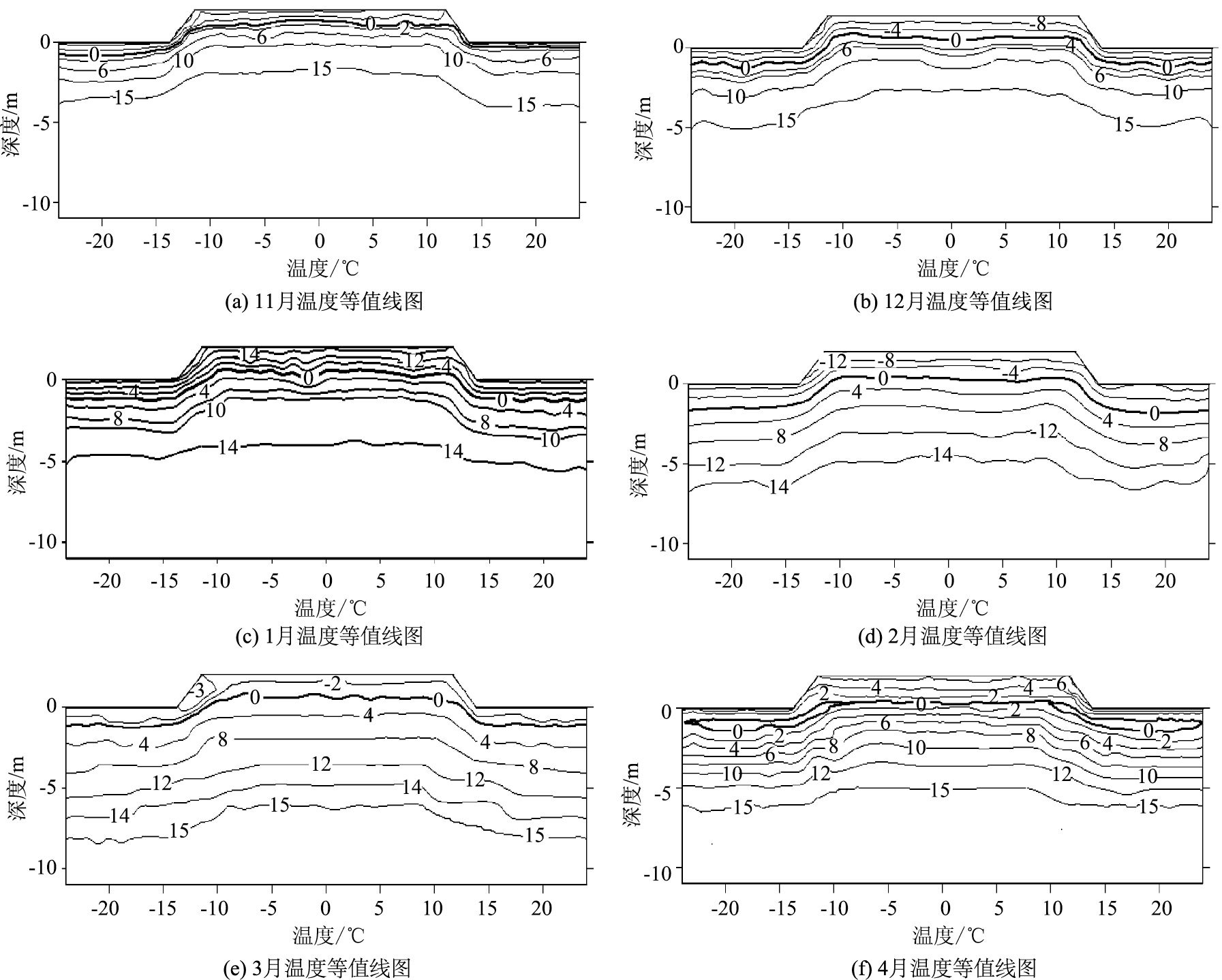
由于温度梯度的作用,热量由高温区域向低温区域传递。路基的温度将随着大气温度和太阳辐射的周期性变化而变化。随着温度的降低,太阳辐射量的减小,路基处于从边界表面向下冻结状态。本文所分析的温度值为该月中旬的温度。如图 3(a)所示,11月路基及地基浅层土体开始发生冻结,冻结锋面大致位于0 ℃等温线附近,整体向阳坡面略有偏移。由图 3(b)~(c)可知,12月~1月,冻结锋面的位置会随着温度的降低而逐渐下移,可达地下1.2 m左右。路基温度场也呈规则的层状分布,但由于路线走向的关系,受阴阳坡效应的影响,路基温度场的横向分布并不对称,向阳坡(右侧)略有倾斜,这就导致了路基变形的不均匀性。而1月路基各边界处的日均温度可达到年最小值,其中阴坡(左侧)的温度最低,约为-20 ℃。到2, 3月温度逐渐上升,但环境温度还是处于负温阶段。由图 3(d)可知,2月虽然温度上升,但由于温度还处于负温阶段,所以冻结锋面略有下降,但路基表面温度却已升高至-10 ℃。进入3月,如图 3(e)所示,冻结锋面位置较2月略有上升,而路基表面温度却已升高至-2 ℃,但阴坡温度还是较低,约为-3 ℃。4月,随着大气温度的不断回升和太阳辐射量的进一步增加,路基将处于吸热状态,路基土体从边界向下单向融化。从图 3(f)可知,阳坡(右侧)日温度升高至8.6 ℃,且其他边界处的温度也不同程度地增加,只是较阳坡面(右侧)增加幅度小。阳坡(右侧)一侧的地温明显高于阴坡一侧(左侧),路基内部存在未融区,由于阴阳坡效应,未融区也是不均匀分布的。
|
| 图 3 路基温度场 Fig. 3 Temperature field of subgrade |
| |
(2) 路基阴阳坡面温度差异分析
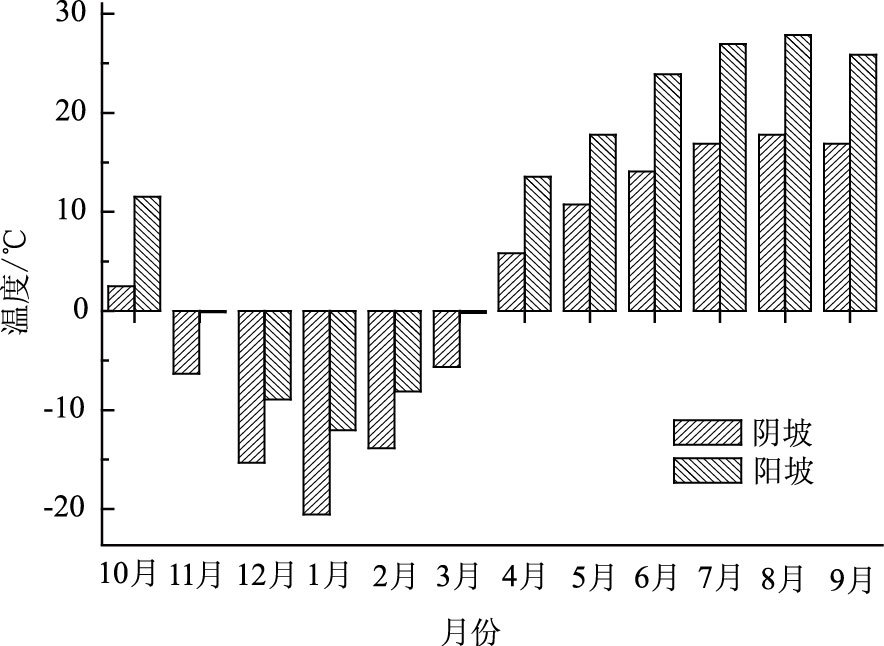
由图 4可知,冬季阴阳坡温差较夏季小,但无论冬季或是夏季,阴阳坡效应均很强烈。由于阴阳坡温度的不同,导致阳坡冻结开始时间迟于阴坡,而融化时间却早于阴坡,阴阳坡冻结深度与融化时间会有一定差异,而阴阳坡差异也会引起冻结锋面分布的不均匀,这些都可能引起路基的不均匀变形。
|
| 图 4 阴阳坡坡面平均温度比较 Fig. 4 Comparison of average temperatures between sunny and shady slopes |
| |
3.3 变形分析
(1) 冻结过程中路基顶面及边坡表面变形特性
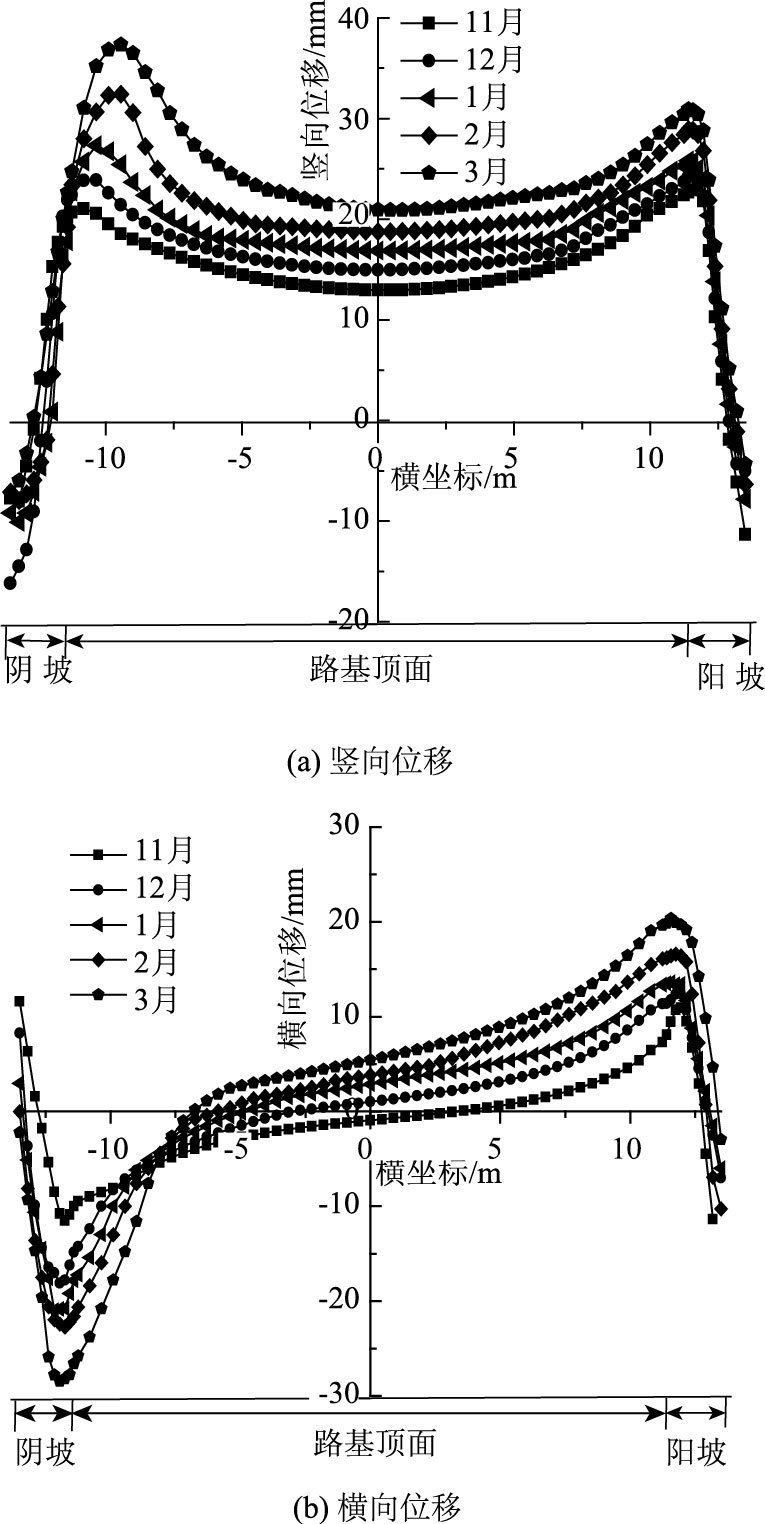
本文定义竖向位移正为隆起,负为凹陷,定义横向位移正为向阳坡方向移动的位移,负为向阴坡方向移动的位移。由图 5(a)可知,自11月外界环境进入负温阶段,路基顶面逐渐隆起,呈盆状隆起,且靠近边坡处隆起较大。11月由于阳坡温度较阴坡高,阳坡处的冻结冰锋带较为靠近土表,且土体冻结层厚度较浅,导致阳坡面的冻胀略大于阴坡面。而随着外界温度的进一步降低,自12月开始,阴坡处温度进一步降低,阴坡处水分积聚越积越多,所以靠近阴坡的路肩隆起逐渐高于靠近阳坡面的路肩。从12月至3月,最大竖向位移均发生在靠近阴坡的路肩,而随着时间的推移,最大位移有向路基中部逐渐移动的趋势。路基表面的隆起会引起水泥混凝土路面板的不均匀支撑,在行车荷载的作用下,导致水泥混凝土路面断板等破坏,或引起沥青路面隆起,严重影响行车安全及行车舒适性。1月温度最低,但是路基顶面冻胀并不是最大,这说明路基的变形较温度的变化有滞后现象,这与冻土路基实测规律相一致[2]。
|
| 图 5 冻结过程中路基顶面位移 Fig. 5 Deformations of subgrade top in freezing process |
| |
由图 5(b)可知,随着温度的降低,水分不断积聚,在冻胀力作用下,冻结锋面产生的冻胀力会使阴、阳坡面隆起,且由于阴坡面的温度较阳坡低,水分积聚也较多,所以靠近阴坡面的路肩横向位移也较靠近阳坡面的路肩大。路基顶面及坡脚均有相背离的横向位移,可能会发生拉裂等破坏。从11月到3月,路基顶面相背离的横向位移逐渐向阴坡靠近,且横向位移的斜率逐渐增大,即拉应力逐渐增大。路基顶面的拉裂破坏,使路基产生纵向裂缝; 边坡处或者坡脚处的拉裂破坏,使边坡产生滑塌现象或由于边坡的裂缝影响到路基的稳定性,这与文献[7]的结论相一致。路基横向位移的规律与竖向位移相似,也有滞后现象,最大横向位移不会出现在温度最低的月份。
(2) 融化过程中路基顶面及边坡表面变形特性
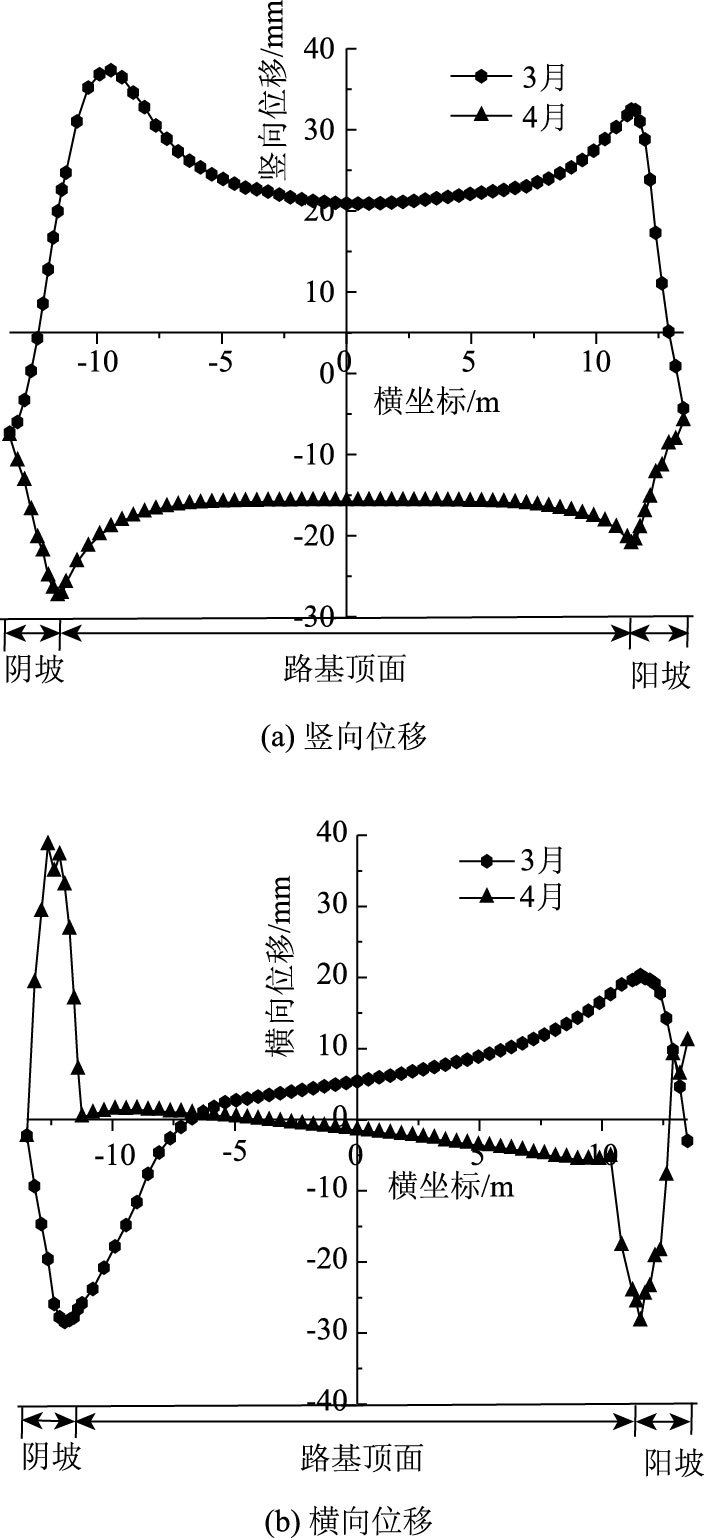
4月随着温度的持续上升,路基将逐渐融化。如图 6所示,从3月路基冻结状态到4月路基融化阶段,路基表面的竖向位移与横向位移变化很大。由图 6(a)可知,路基表面最大沉降发生在路基阴坡边坡顶部,路肩沉降也较大。这是由于温度场的不均匀分布导致水分的不均匀分布,最终引起路基浅层土体的不均匀沉降,这可能使路面产生较大附加应力,严重影响路面使用性能。阴坡处的竖向位移大于阳坡面的竖向位移,这是由于阴坡的温度较低,水分在此积聚较多,且范围较广,冻结深度也较阳坡大,而在融化过程中,边坡土体中的水分不能及时排除,导致土体模量急剧下降,使阴坡处竖向位移较大。
|
| 图 6 冻结至融化过程中路基顶面位移 Fig. 6 Deformations of subgrade top in freezing-thawing process |
| |
如图 6(b)所示,路基融化后,横向位移的正负极值点都出现在路基边坡处,阳坡出现负方向横向位移,阴坡出现正方向横向位移,这将会引起路基中部的沉陷,导致边坡向中部坍塌。这是因为土体含水量增大后,土体密度增大,由于重力作用产生弯矩作用而引起,使路基表面产生向路中心处的位移。由图 6(b)还可以知道,路基顶面靠近阴坡一侧及坡脚处均会产生相背离的横向位移,该处可能会产生较大的拉应力,在曲率较大处极易产生张拉破坏,即产生纵向裂缝,从而加速路基破坏。
4 结论本文基于第Ⅱ类与第Ⅲ类混合热边界条件,建立了伴有相变的非稳态温度场有限元模型,基于此,建立了路基位移场有限元模型,模拟了由阴阳坡温度差异所引起的路基变形发育过程,揭示了季节冻土地区公路路基破坏机理。
(1) 季节冻土地区路基的横断面变形与其下温度场的不对称分布状况密切相关,特别是在有地下水源的情况下,路基变形场受温度场影响较大,坡向不同而引起的阴阳坡温度差异是造成路基横向不均匀变形的主要原因。
(2) 在冻结过程中,路基顶面呈盆状隆起,路肩隆起较大,路面附加应力加大;坡脚处出现沉降,且坡脚处会产生较大的横向位移,可能导致路基边坡滑塌。在融化过程中,路基产生较大的不均匀变形,阴坡边坡顶部处沉降最大。在冻结和融化过程中,边坡及靠阴坡侧路基顶部均易产生张拉破坏。
(3) 结合数值模拟结果,阴阳坡可采取不同的设计与养护措施以减轻阴阳坡差异。在掌握季节冻土地区路基易发生破坏位置基础上,在路基变形观测现场试验中,路肩及边坡,特别是阴坡,可加设位移传感器,以高效而准确地掌握季节冻土地区路基实际变形规律。
(4) 路基型式、冻胀与融沉系数以及环境因素都会影响路基破坏形式,可基于多种因素开展数值模拟,使成果更具应用价值。同时行车荷载与路基内部水热耦合作用下的路基冻融变形,涉及了复杂的冻土动力学问题,也有待进一步研究。
| [1] | 王铁行. 多年冻土地区路基冻胀变形分析[J]. 中国公路学报, 2005, 18 (2) : 1-5 WANG Tie-hang. Analysis of Frost Heave on Subgrade in Permafrost Regions[J]. China Journal of Highway and Transport, 2005, 18 (2): 1-5 |
| [2] | 丑亚玲, 盛煜, 韦振明. 多年冻土区公路路基阴阳坡温度及变形差异分析[J]. 岩石力学与工程学报, 2009, 28 (9) : 1896-1903 CHOU Ya-ling, SHENG Yu, WEI Zhen-ming. Temperature and Deformation Differences between Southern and Northern Slopes of Highway Embankment on Permafrost[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28 (9): 1896-1903 |
| [3] | 田亚护, 房建宏, 沈宇鹏. 多年冻土地区宽幅公路路基稳定性模拟[J]. 中国公路学报, 2015, 28 (1) : 17-22 TIAN Ya-hu, FANG Jian-hong, SHEN Yu-peng. Simulation on Stability of Large-width Highway Embankment in Permafrost Regions[J]. China Journal of Highway and Transport, 2015, 28 (1): 17-22 |
| [4] | 杜兆成, 张喜发, 辛德刚, 等. 季节冻土区高速公路路基冻胀试验观测研究[J]. 公路, 2004 (1) : 139-145 DU Zhao-cheng, ZHANG Xi-fa, XIN De-gang, et al. Experiment Research on Subgrade Frost Heaving of Expressway in Seasonally Frozen Soil Region[J]. Highway, 2004 (1): 139-145 |
| [5] | EVANS G L, TRUEBE M A, HANEK G L. Monitoring Report of Frost Heave on Warm Lake Road[J]. Transportation Research Record, 2011, 2204 : 251-257 |
| [6] | 许健, 牛富俊, 牛永红, 等. 换填法抑制季节冻土区铁路路基冻胀效果分析[J]. 中国铁道科学, 2011, 32 (5) : 1-7 XU Jian, NIU Fu-jun, NIU Yong-hong, et al. Analysis on the Effect of Replacing-Soil Method on Inhibiting Frost Heave of Railway Roadbed in Seasonal Frozen Soil Region[J]. China Railway Science, 2011, 32 (5): 1-7 |
| [7] | 张玉芝, 杜彦良, 孙宝臣, 等. 季节性冻土地区高速铁路路基冻融变形规律研究[J]. 岩石力学与工程学报, 2014, 12 (33) : 12-2553 ZHANG Yu-zhi, DU Yan-liang, SUN Bao-chen, et al. Roadbed Deformation of High-speed Railway due to Freezing-thawing Process in Seasonally Frozen Regions[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 12 (33): 12-2553 |
| [8] | 毛雪松.多年冻土地区路基水热力场耦合效应研究[D].西安:长安大学, 2004. MAO Xue-song. Study on Coupling Effect of Moisture-heat-stress Fields in Permafrost Subgrade[D]. Xi'an:Chang'an University, 2004. |
| [9] | 胡和平, 杨诗秀. 土壤冻结时水热迁移规律的数值模拟[J]. 水利学报, 1992 (7) : 1-8 HU He-ping, YANG Shi-xiu. A Numerical Simulation for Heat and Moisture Transfer During Soil Freezing[J]. Journal of Hydraulic Engineering, 1992 (7): 1-8 |
| [10] | 关文章. 湿陷性黄土工程性能新篇[M]. 西安: 西安交通大学出版社, 1992. GUAN Wen-zhang. New Study on Engineering Performance of Soils[M]. Xi'an: Xi'an Jiaotong University Press, 1992. |
| [11] | 汪海年, 窦明健. 青藏高原多年冻土区路基温度场数值模拟[J]. 长安大学学报:自然科学版, 2006, 26 (4) : 11-15 WANG Hai-nian, DOU Ming-jian. Numerical Simulation of Thermal Field in Permafrost Embankments of Qindhai-Tibet Highway[J]. Journal of Chang an University:Natural Science Edition, 2006, 26 (4): 11-15 |
| [12] | 李辉, 黄晓明, 张久鹏, 等. 基于连续变温的沥青路面车辙模拟分析[J]. 东南大学学报:自然科学版, 2007, 37 (5) : 915-920 LI Hui, HUANG Xiao-ming, ZHANG Jiu-peng, et al. Simulation Analysis on Rutting of Asphalt Pavements Considering Consecutive Temperature Variation[J]. Journal of Southeast University:Natural Science Edition, 2007, 37 (5): 915-920 |
| [13] | 王铁行, 窦明健, 胡长顺. 多年冻土地区路基临界高度研究[J]. 土木工程学报, 2003, 36 (4) : 94-98 WANG Tie-hang, DOU Ming-jian, HU Chang-shun. Study on Critical Thickness of Subgrade in Permafrost Area[J]. China Civil Engineering Journal, 2003, 36 (4): 94-98 |
| [14] | 吴赣昌, 张淦生. 有效辐射计算对沥青路面温度场的影响[J]. 佛山大学学报:社会科学版, 1995, 13 (2) : 19-25 WU Gan-chang, ZHANG Gan-sheng. Calculation of Effective Radiation and its Influence on the Bituminous Pavement Temperature Field[J]. Journal of Foshan University:Social Science Edition, 1995, 13 (2): 19-25 |
| [15] | 付宏渊, 郭芳, 邵腊庚. 基于温度场的混合式基层沥青路面结构车辙数值模拟分析[J]. 公路交通科技, 2015, 32 (12) : 46-52 FU Hong-yuan, GUO Fang, SHAO La-geng. Numerical Analysis of Rutting in Composite Base Asphalt Pavement Structure Based on Temperature Field[J]. Journal of Highway and Transportation Research and Development, 2015, 32 (12): 46-52 |
| [16] | 宁波. 浅层地温能为住宅节能带来广阔前景[J]. 住宅产业, 2008 (4) : 52-54 NING Bo. Energy Saving and Its Broad Prospects for Shallow Geothermal Energy[J]. Housing Industry, 2008 (4): 52-54 |
| [17] | 侯曙光.多年冻土路基融沉机理及路面结构对策研究[D].南京:东南大学, 2005. HOU Shu-guang. Study on Mechanism of Subgrade Thawing Settlement and Countermeasure against Pavement Structure Distress in Permafrost Region[D]. Nanjing:Southeast University, 2005. |
| [18] | 国家气象局数据中心.地面气象资料三十年数据汇编[R].北京:国家气象局数据中心, 2008. Data Center of National Weather Service. Compilation of Meteorological Data for Thirty-years[R]. Beijing:Data Center of National Weather Service, 2008. |
| [19] | 汪海年.青藏高原多年冻土地区路基温度场研究[D].西安:长安大学, 2004. WANG Hai-nian. Study on Temperature Field of Permafrost Embankment in Qinghai-Tibet Plateau[D]. Xi'an:Chang'an University, 2004. |
| [20] | 徐学祖, 王家澄, 张立新. 冻土物理学[M]. 北京: 科学出版社, 2001. XU Xue-zu, WANG Jia-cheng, ZHANG Li-xin. Physics of Frozen Soil[M]. Beijing: Science Press, 2001. |
| [21] | AZMATCH T F, SEGO D C, ARENSON L U, et al. Tensile Strength and Stress-strain Behavior of Devon Silt under Frozen Fringe Conditions[J]. Cold Regions Science and Technology, 2011, 68 (1): 85-90 |
| [22] | 吴紫汪, 张家懿, 王雅卿, 等. 冻土融化下沉性的初步研究[M]. 北京: 科学出版社, 1981. WU Zi-wang, ZHANG Jia-yi, WANG Ya-qing, et al. Primary Research on Thaw Settlement Properties of Frozen Soil[M]. Beijing: Science Press, 1981. |
 2017, Vol. 34
2017, Vol. 34
