公路交通科技  2015, Vol. 31 Issue (4): 59-63,77

扩展功能

文章信息

张劲泉, 冷艳玲, 李万恒, 程寿山
ZHANG Jin-quan, LENG Yan-ling, LI Wan-heng, CHENG Shou-shan
中国公路桥梁承载能力评定规程的可靠性水准
Reliability Level of Load-bearing Capacity Evaluation Specification of Highway Bridges in China
公路交通科技, 2015, Vol. 31 (4): 59-63,77
Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (4): 59-63,77
10.3969/j.issn.1002-0268.2015.04.011

文章历史

收稿日期：2014-07-02
引用本文 0
张劲泉, 冷艳玲, 李万恒, 程寿山. 中国公路桥梁承载能力评定规程的可靠性水准[J]. 公路交通科技, 2015, Vol. 31 (4): 59-63,77.
ZHANG Jin-quan, LENG Yan-ling, LI Wan-heng, CHENG Shou-shan. Reliability Level of Load-bearing Capacity Evaluation Specification of Highway Bridges in China[J]. Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (4): 59-63,77.
中国公路桥梁承载能力评定规程的可靠性水准
张劲泉, 冷艳玲, 李万恒, 程寿山    
交通运输部公路科学研究院, 北京 100088
收稿日期:2014-07-02;
基金项目：交通运输部建设科技项目(2013318223040).
作者简介：张劲泉(1963-),男,江苏泰州人,研究员.
摘要：分析了我国公路桥梁承载能力评定规程的可靠性水准,明确了提高该规范可靠性水准的需求及方法;借鉴美国基于可靠性的规范的相关研究所采用的方法理论,推导出了计算规范隐含可靠度的公式,并采用该方法计算了我国现行公路桥梁设计规范的强度极限状态方程的隐含可靠度,计算的隐含可靠度值与规范规定的目标可靠度值较吻合;然后应用该方法,计算出了我国公路桥梁评定规范强度极限状态方程的隐含可靠度;最后,比较了中、美公路桥梁承载能力评定方法的可靠性水准、适用范围、评定基准期、目标可靠度、抗力模型及荷载模型,对我国公路桥梁承载能力评定规程的进一步完善有指导意义。另外,本文分析了美国统计桥梁历史失效概率的方法。
关键词： 桥梁工程     可靠性水准     校准     承载能力评定     荷载抗力因子    
Reliability Level of Load-bearing Capacity Evaluation Specification of Highway Bridges in China
ZHANG Jin-quan, LENG Yan-ling, LI Wan-heng, CHENG Shou-shan     
Research Institute of Highway, Ministry of Transport, Beijing 100088, China
Abstract:We analyzed the reliability level of current highway bridge load-bearing capacity evaluation code of China, specified the requirement and the methods to upgrade the reliability level of this code. Using the method and theory used in the related researches of American reliability-based code for reference, we derived a formula to calculate the implied reliability index of the current code, and calculated the implied reliability index of the strength limit state equation in the current Chinese highway bridge design code with this formula, which is complied with the target reliability index of the same code. Then, we calculated the implied reliability index of the strength limit state equation in the current load-bearing capacity evaluation code with this method. At last, we compared the reliability levels, scopes, time periods, target reliability indexes, resistance modes and load modes of the Chinese load-bearing capability code and American load rating code, which would serve as a guidance to upgrade the current highway bridge load-bearing capability code. We also analysed the procedures by which American codes defined the historical failure rates of highway bridges.
Key words: bridge engineering     reliability level     calibration     load-bearing capacity evaluation     load and resistance factor    
0 引言

我国公路桥梁承载能力评定方法[1]基于荷载抗力因子评定方法，方法中所涉及的各参数(如荷载、材料性能、构件几何参数等)均为随机变量，然而，由于该规程没有明确其目标可靠度，尚属于半经验性半可靠性的评定规程。本文分析了我国公路桥梁承载能力评定规程(以下简称“现评定规程”)的可靠性水准，明确了现评定规程的研究方向；校准了现评定规程隐含的可靠度指标，给出了计算桥梁历史失效概率的方法，得到了确定评定规范目标可靠度的主要依据；比较了中、美公路桥梁承载能力评定方法的可靠性水准、适用范围、评定基准期、目标可靠度、抗力模型及荷载模型。最后，基于上述研究，为我国公路桥梁承载能力评定规程的进一步完善提供了建议。

1 可靠性规范极限状态方程的可靠度

结构可靠度是指在规定时间内，规定条件下，结构完成预定功能的概率。可靠性规范的校准，首先要确定设计(或评定)的极限状态方程，然后确定设计(或评定)的极限状态方程的失效概率，即设计或评定的目标可靠度，最后根据目标可靠度校准荷载因子及抗力系数。

计算可靠指标的极限状态方程可表达为：

式中，G为安全储备；R为结构的抗力储备；S为荷载效应。G ≥0，表示结构安全；G<0，表示结构失效。

由于R，S均为变量，因此绝对安全，即失效概率为0是不可能实现的，故结构必然存在一定的失效概率。 可靠度β，是反映结构失效概率的一个指标，

式中，σ(G)为G的标准差；G为G的平均值,若R与S均服从正态分布，则G也为正态分布。β=3，对应的失效概率约为10-3；β=4.2，对应的失效概率约为10-5；β=4.2，对应的失效概率约为10-6。

2 现评定规程的可靠性水准

基于可靠性的设计、评定规范把影响结构可靠性的各项参数视为随机变量，以调查实测资料和试验数据为基础，运用数理统计的方法，分析各随机变量的统计分布规律，确定结构的失效概率(或可靠度)。设计、评定规范的根本目的则是确定设计、评定的最低安全水准，即可靠度。根据确定可靠度的方法，基于可靠度的设计、评定规范可分为4个水准[2]：

水准1：规范使用确定性设计(或评定)公式，其安全水准通过中心安全系数(即抗力与荷载效应的比值)，分项安全系数(即荷载分项系数、抗力因子)来体现，属于不完全可靠性规范。

水准2：规范规定了设计(或评定)的目标可靠度，以实际可靠度与目标可靠度的闭合度来评判设计(或评定)的优劣，即设计(或评定)的实际可靠度越接近目标可靠度，则设计(或评定)越好。美国现行AASHTO LRFD公路桥梁设计规范[3]及AASHTO LRFR公路桥梁荷载评定方法[4]属于水准2规范。

水准3：规范是完全可靠性规范，通过分析、量化结构在各种荷载情况下的失效概率，确定最优可靠度，作为设计(或评定)的目标可靠度并以设计(或评定)的实际可靠度与最优可靠度的闭合度来评判设计(或评定)的优劣。水准3规范与水准2 规范的差别在于，水准2 规范的目标可靠度是根据工程经验主观规定的，水准3的最优可靠度是基于量化结构在各种荷载情况下的失效概率计算出来的。

水准4：规范是可靠性规范的最高水准，以设计(或评定)的效用作为优化准则。可靠度的确定准则就是建立设计(或评定)的效用函数，即在提高可靠度所产生的成本与设计(或评定)失效产生的成本中找到一个可被接受的平衡点，这实际是个经济问题。目前，该方法实际应用较难实现，只能称之为理想准则[5]。

美国AASHTO公路桥梁荷载抗力因子设计规范及荷载评定规范都属于水准2 设计规范，该规范已经发展了20多年，目前在进行水准3规范的前期研究工作。另外在一些前沿研究中，一些关键结构使用了水准3或水准4设计规范。中国目前的桥梁承载能力评定规程是通过中心安全系数(即抗力与荷载效应的比值)，分项安全系数(即荷载分项系数、抗力因子)来体现评定的安全水准，属于可靠性规范的范畴。然而，由于没有统一规范的目标可靠度，从可靠性水准上来说，与美国同类规范还存在差距。因此，为了提高我国评定规范的水准，需要进行确定该规范的目标可靠度，并据此对各荷载系数及抗力因子进行可靠度校准。

3 评定规范目标可靠度的确定 3.1 规范目标可靠度的确定准则

欲提高现评定规范的可靠性水准，必须确定评定规范的目标可靠度。目标可靠度主要是采用校准法并结合工程经验加以确定的，即根据各变量的统计参数及概率分布，运用可靠度的计算方法，揭示现行规范隐含的可靠度，以此作为确定目标可靠度的主要依据。这种方法在总体上延承了以往规范的可靠度水平，同时也考虑了基于工程实际的调查统计资料，是比较现实和稳妥的，这也是国内外基于可靠性的设计、评定规范确定目标可靠度的常用方法[6, 7, 8]。基于上述理论，下文对现行评定规程的隐含可靠度进行了校准分析。

3.2 现评定规范强度极限状态方程的隐含可靠度的分析

现行评定规程的极限状态评定公式如下[1]：

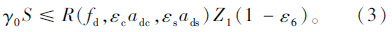
现行评定规程的形式与设计规范相似，均基于荷载抗力因子法。评定规程的荷载模型沿用了设计规范[7]的荷载模型，评定规程的抗力模型则在设计规范抗力模型的基础上，根据旧桥评定的特点，引入了承载能力校验系数、承载能力恶化系数、钢筋(及混凝土)截面折减系数，本文将上述指标统称为旧桥抗力折减系数。由于缺乏统计参数，尚未对旧桥抗力折减系数进行校准，从而无法确定现行判定规范的可靠度指标。

由于桥梁的荷载模型比较复杂，本文的重点是为了校准评定规程的旧桥抗力折减系数、计算评定规程的隐含可靠度，借鉴美国AASHTO公路桥梁荷载评定规范的抗力折减系数校准方法[9, 10]，推导评定规程可靠度与旧桥折减系数的关系。

为了计算方便，将式(3)简化为：

根据可靠度理论，由式(4)可推算出式(5)[10]：
分离变量R，S，分离变量常数取为0.55，得到，
即结构抗力≥荷载效应，由此得到，目标可靠度与抗力折减系数的关系如式(7)所示，
式中，Φ为旧桥抗力折减系数；β为可靠度指标；γ0为荷载系数；R，S分别为抗力R、荷载S的期望值；VR，VS为变异系数；δR，δS为偏差因子。

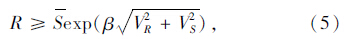
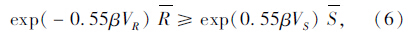
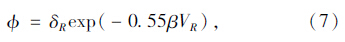
由于设计规范[7]有明确的目标可靠度，用式(7)来计算设计规范强度极限状态方程的计算可靠度，计算可靠度与目标可靠度进行比较，进而验证式(7)的适用性。

根据统一标准[6]，得到各种受力状态下混凝土构件的计算可靠度如表 1所示。表 1验证了式(7)的适应性。下文用式(7)计算现行评定规程[1]的计算可靠度，即隐含可靠度。

表 1 混凝土构件在不同受力状态下的设计计算可靠度与设计目标可靠度 Tab. 1 esign reliability indexes and design target reliability indexes for concrete components under different stresses
受力状态 偏差因子 变异系数 抗力模型中隐含
的抗力折减系数		 计算可
靠度		 目标可
靠度
轴心受力 1.374 3 0.154 6 0.87 5.4 4.7
轴心受拉 1.082 1 0.132 2 0.81 4.0 4.2
正截面受弯 1.226 2 0.141 4 0.89 4.1 4.2
斜截面受弯 1.671 7 0.288 3 0.80 4.7 4.7
大偏心受压 1.204 2 0.144 7 0.86 4.2 4.2
表选项

由于缺乏旧桥构件抗力的统计参数，故根据承载能力校验系数的评定标度，确定各项统计参数的上、下限，中间状态采用插值法近似得到。表 2以受弯构件为例，给出了旧混凝土构件的抗力统计参数及评定可靠度。

表 2 受弯构件的假定抗力统计参数及评定可靠度 Tab. 2 Assumed statistic parameters and evaluation reliability indexes for resistance of concrete components under flexural stress
评定标
度D		 承载能力校
验系数Z1		 假定偏
差因子		 假定变
异系数		 抗力模型中
隐含的抗力
折减系数		 计算可
靠度
1 1.15 1.23 0.10 1.02 3.29
2 1.10 1.17 0.125 0.98 2.77
3 1.00 1.12 0.15 0.89 2.79
4 0.90 1.06 0.175 0.80 2.91
5 0.80 1 0.2 0.71 3.09
表选项

本文确定抗力偏差因子的原则为：评定标度为1时，假定既有构件的抗力平均值等于设计构件的抗力平均值，故评定标度为1的旧构件的抗力偏差因子与对应的新构件的抗力偏差因子相等，对于正截面受弯构件，偏差因子则为1.226 2；而评定标度越高，构件的平均抗力越低，既有构件的名义抗力与设计构件的名义抗力相等，故相应的偏差因子越低。

本文确定抗力变异系数的原则为：根据美国的相关研究结论[9, 10]，评定标度越高，即技术状况越差的构件，抗力变异系数越高，通常情况下，抗力变异系数的变化范围为0.1~0.2。

按照上述方法，得到了混凝土构件各种受力状态下的评定可靠度，如表 3所示，现评定规程的隐含可靠度大于2.75。

表 3 混凝土构件各种受力状态下的评定可靠度 Tab. 3 Evaluation reliability indexes for concrete components under different stresses
评定标度
D1		受弯轴心受压轴心受拉偏心受压
Z1 β Z1 β Z1 β Z1 β
1 1.15 3.29 1.2 5.02 1.05 4.38 1.15 3.52
2 1.1 2.77 1.15 3.48 1.00 3.91 1.1 2.84
3 1 2.79 1.05 3.12 0.95 3.65 1 2.98
4 0.9 2.91 0.95 2.79 0.85 4.08 0.9 3.17
5 0.8 3.09 0.85 2.75 0.75 4.53 0.8 3.40
表选项
3.3 基于工程经验的目标可靠度

可靠性规范目标可靠度的确定不仅要延承现行规范的隐含可靠度，还要参考工程经验，即桥梁的历史失效概率(historic failure rate)。美国、英国[11]公路桥梁设计、评定规范在初步拟定目标可靠度时，主要是参考历史经验，即统计过去若干年内发生桥梁失效(failure)事件的概率。

要统计桥梁的历史失效概率，首先要明确失效的概念。美国80年代对桥梁失效模式进行过探索研究[12, 13, 14]，这些研究成果很有参考意义，遂在此加以阐述。

美国在确定桥梁失效模式时，进行了如下探讨：如果将失效模式定义为效用损失(utility loss)，即桥梁存在功能缺陷或老化，那么美国44％左右的桥梁都已经失效，因为美国44％的桥梁均存在结构缺陷或功能老化。另一方面，如果将桥梁垮塌定义为失效，美国1974—1984年内仅有2例钢筋混凝土桥梁坍塌事件的报道，这一失效概率显然也不合理。而据相关研究报告[12]，美国每年有5 000座桥梁拆除重建，对应的年失效概率为0.009，另一项调查[13]显示，过去10 a内关闭交通的桥梁共5 950座，对应的年失效概率为0.001。但需要注意的是，桥梁重建或封闭的原因不限于结构失效，文献[13]提到，过去10 a内，美国因活载过大而拆除重建的桥梁数量为596座，对应年失效概率10-4。考虑到大多数桥梁失效是由洪水、火灾、地震等极端事故造成的，这些极端事故毁坏了很多技术状况良好的桥梁，减去这一部分桥梁，则桥梁的年失效概率是在10-4至10-5之间。

建议统计中国过去10 a内因活载过大而拆除重建的桥梁数量，统计桥梁的历史失效概率，作为确定评定规范极限状态方程的失效概率，即目标可靠度的参考。

4 中、美公路桥梁承载能力评定方法比较

中、美桥梁承载能力评定规范的比较见表 4～表 7。首先，美国的荷载评定(load rating) 与中国承载能力评定的使用范围不同。美国规范的使用范围是针对所有技术等级的桥梁，其抗力折减系数的取值主要基于桥梁常规检查数据，即桥梁的技术状况等级，当荷载额定结果不理想时，才考虑采用实测数据；而中国规范是针对技术状况等级为四、五类的桥梁或其他有特许需求的桥梁，其抗力折减系数基于桥梁特殊检查数据，当作用效应与抗力效应的比值在1.0~1.2之间时，应根据规程的有关规定通过荷载试验评定承载能力。

表 4 中、美桥梁承载能力评定规范比较 Tab. 4 Comparison between Chinese and American codes for evaluating highway bridge load-bearing capacity
表选项

表 5 美国AASHTO LRFR状况因子的取值 Tab. 5 Values of condition factor for American AASHTO LRFR
构件的状态 好 一般 差
状态因子Φc 1.00 0.95 0.85
表选项

表 6 美国AASHTO LRFR系统因子的取值 Tab. 6 Values of system factor for American AASHTO LRFR
上部结构
类型		 梁/桁架/拱
构件之间是
焊接		 梁/桁架/拱
构件之间是
铆接		 桁架桥有多
个眼杆式
构件		 3片梁组成
的桥梁，梁
间距6 ft		 4片梁组成
的桥梁，梁
间距≤4 ft		 其他所有梁
式桥和板桥		 横梁间距大于
12 ft且纵梁
不连续		 横梁间有冗
余纵梁子系统
系统因子Φs 0.85 0.90 0.90 0.85 0.95 1.00 0.85 1.00
表选项

表 7 美国AASHTO LRFR 钢筋混凝土桥梁极限状态及荷载分项系数 Tab. 7 Limit states and corresponding load factors for reinforced concrete bridges for American AASHTO LRFR
表选项

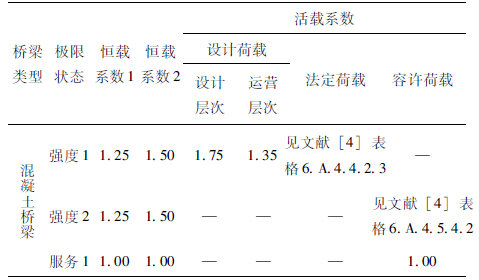
另外，目前大多数基于可靠度的规范(包括中国的设计、评估规范)是针对构件可靠性，而非系统可靠度。需要意识到的是，对于桥梁结构而言，某个构件的失效并不一定是整个结构系统的失效。美国LRFR评估规范引用系统因子(system factor)，将评估的构件可靠性层次提升到系统可靠性层次。构件到系统是研究的一个进行过程，故建议新规范也引用一个参数，反映桥梁结构的冗余度，将评估由构件层次进化到系统层次。

5 结论

我国桥梁承载能力评定规程是基于可靠性的评定规程，为了与美国、欧洲的评定规范接轨，提高其可靠性水准，需要研究其目标可靠度，并基于目标可靠度校准极限状态方程的荷载系数和抗力因子。目标可靠度的确定一方面要参考现行规范的隐含可靠度，另一方面要考虑桥梁的历史失效概率。本文提出了计算现规范隐含可靠度的方法，并根据旧桥构件的特征参数，估算出现行桥梁承载能力评定规程的隐含可靠度为2.75~5.02，并给出了统计桥梁历史失效概率的分析方法。

为了确定桥梁评定规范的目标可靠度，并对荷载因子和抗力系数进行校准，提高规范的可靠性水准，拟进行下述研究：

(1)开展文献调研，配合试验研究，统计旧桥构件在各种受力状态下的抗力统计参数,以便得到现评定规范的隐含可靠度；

(2)统计中国过去10 a内因活载过大而拆除重建的桥梁数量，统计桥梁的历史失效概率，作为确定评定规范目标可靠度的参考；

(3)校准承载能力检算系数、恶化系数；

(4)进行桥梁系统安全性和冗余度研究，并在此基础上，在极限方程中引入一个考虑冗余度的系统因子，将评定由构件层次提升到系统层次。

此外，本文系统比较了中国桥梁承载能力评定规程与美国AASHTO LRFR桥梁荷载鉴定规范，两国规范各有侧重，借鉴美国规范的优点，对下一步研究有参考意义。

参考文献
[1] JTG/T J21—2011,公路桥梁承载能力检测评定规程 [S]. JTG/T J21—2011, Specification for Inspection and Evaluation of Load-bearing Capacity of Highway Bridges[S].
[2] ANDRZEJ S N,KEVIN R C. Reliability of Structures [M]. Columbus:The McGraw-Hill Companies Inc.,2000.
[3] AASHTO. LRFD Bridge Design Specification[M]. 6th ed. Washington,D.C.:American Association of State Highway and Transportation Officials,2012.
[4] AASHTO. The Manual for Bridge Evaluation[M]. 2nd ed. Washington,D.C.:American Association of State Highway and Transportation Officials,2011.
[5] MOSES F. Calibration of Load Factors for LRFR Bridge Evaluation [M]. Washington,D.C.:Transportation Research Board,2000.
[6] GB/T 50283—1999,公路工程结构可靠度设计统一标准[S]. GB/T 50283—1999,Unified Standard for Reliability Design of Highway Engineering Structures[S].
[7] JTG D60—2004,公路桥涵设计通用规范[S]. JTG D60—2004,General Code for Design of Highway Bridges and Culverts[S].
[8] CHRISTOPHER D E. Reliability Based Resistance Model for Bridge Structural Systems[D]. Ann Arbor:The University of Michigan,2000.
[9] IMBSEN R A,LIU W D,SCHAMBE R A. Strengthen Reinforced Concrete Bridges[M]. Washington,D.C.:Transportation Research Board,1984.
[10] MOSES F,VERMA D. Load Capacity Evaluation of Existing Bridges[M]. Washington,D.C.:Transpor-tation Research Board,1987.
[11] DAS P C. Safety of Bridges[M]. London:Thomas Telford Publishing,1997.
[12] GALAMBOS C F. Bridge Safety [J]. Public Roads,1984,48(2):41-47.
[13] IMBSEN R A. Bridge Weight and Limit Posting Practice[M]. Washington,D.C.:Transportation Research Board,1984.
[14] AUGUSTI G,BARATTA A,CASCIATI F. Probabilistic Methods in Structural Engineering[M]. London:Chapman and Hall,1984.
[15] 逯一新,张喜刚,赵君黎,等.桥梁设计荷载与安全鉴定荷载的研究,XBKY-01[R]. 北京:中交公路规划设计院有限公司,2012. LU Yi-xin,ZHANG Xi-gang,ZHAO Jun-li,et al. Research on Design Vehicle Load and Safety Assessment Load of Bridges,XBKY-01[R]. Beijing:CCCC Highway Consultants Co., Ltd., 2012.
[16] JUNSIK E. Verification of Bridge Reliability Based on Field Test [D]. Ann Arbor:The University of Michigan,2001.
[17] ACI 318-11,Building Code Requirements for Structural Concrete and Commentary [S].
[18] TONY M,ALLEN A S,NOWAK R J. Bathurst,Calibration to Determine Load and Resistance Factors for Geotechnical and Structural Design[M]. Washington,D.C.:Transportation Research Board,2005.
[19] NOWAK A S,KASZYNSKA M. Target Safety Levels for Design and Evaluation of Bridges [J]. Transactions of Joining and Welding Research Institute,2003,32(1),189-196.
[20] NOWAK A S, PARK C H,CASAS J R. Reliability Analysis of Prestressed Concrete Bridge Girders:Comparison of Eurocode,Spanish Norma IAP and AASHTO LRFD [J]. Structural Safety,2001,23(4):331-344.