扩展功能
文章信息
- 张向东, 任昆
- ZHANG Xiang-dong, REN Kun
- 煤渣改良土的阻尼比影响因素试验研究
- Experimental Study on Influencing Factors of Damping Ratio of Cinder Improved Soil
- 公路交通科技, 2019, 36(10): 43-51
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(10): 43-51
- 10.3969/j.issn.1002-0268.2019.10.006
-
文章历史
- 收稿日期: 2018-01-02
2. 大连交通大学 土木工程学院, 辽宁 大连 116028
2. School of Civil Engineering, Dalian Jiaotong University, Dalian Liaoning 116028, China
阜新地区煤炭资源较为丰富,火力发电及冬季供暖会大量燃烧煤炭,煤渣作为煤炭燃烧后的产物,如处理不当将会给自然环境带来极大的污染。煤渣的主要化学成分为Al2O3和SiO2,与粉煤灰的化学成分相似,但在利用方面却远低于粉煤灰[1-2]。在路基工程中,对于工程性质不良的土体常使用水泥、石灰等材料进行化学改良。大量使用水泥、石灰势必增加工程成本,若能将部分煤渣作为路基填料将会产生巨大的环境效益和社会效益。
对于煤渣、矿渣等大宗固体废弃物,刘栋等[3-4]研究了以生活垃圾焚烧炉渣替代部分碎石对路面基层材料产生的影响。张互助等[5]对水泥煤渣稳定煤矸石基层的温缩性进行了研究,发现水泥煤渣稳定煤矸石基层的温缩系数较低,适合作为寒冷地区的路面基层。国外也有一些学者[6-7]使用炉渣作为混凝土骨料,并对炉渣混凝土的性能进行了研究。
路基结构主要承受的荷载来自上部的行车荷载,研究路基结构在动荷载作用下的动力特性,分析路基所用土体的弹性模量及阻尼比的变化规律十分必要,许多学者对此进行了大量的研究。
罗飞等[8]对青藏冻结黏土路基滞回曲线的形态特征进行了研究,通过不闭合程度、宽窄程度、倾斜程度、密集程度及曲线围成的面积对动载作用下青藏冻结黏土的反映进行了定量分析。黄斌等[9]通过归一化方法研究了不同的围压、频率、固结比条件下,动弹性模量及阻尼比的变化规律。严晗等[10]研究了冻融循环对粉砂土动弹性模量及阻尼比的影响,结果表明冻融循环对粉砂土动弹性模量及阻尼比的影响较大,但经过多次循环后影响基本趋于稳定。焦贵德等[11]研究了循环荷载作用下冻土滞回曲线的变化规律。罗飞等[12]研究了兰州黄土在分级加载条件下,围压、频率及温度对阻尼比的影响。Vinson[13]对不同围压及不同含水率下土体的阻尼比进行了研究,发现阻尼比随含水率和围压的变化不明显。Czajkowski等[14]对冻土的阻尼比进行了研究,结果表明冻土的阻尼比不受频率的影响。
目前,对于路基土阻尼比的研究主要分为两个方面。一是研究外界环境,如温度、水分的变化和围压、荷载的施加等对土体阻尼比产生的影响;二是研究更加精确的阻尼比计算方法,找出滞回曲线围成面积合理的计算方法,进行较为精确的阻尼比计算。但由于土形成的过程十分复杂,使得其具有极强的区域性,不同类型的土在经过改良后的效果也不尽相同。为研究煤渣土的动力特性,本研究对不同配合比、围压及频率下滞回曲线的特征进行分析,提出一种适用于求解开口及闭合状态滞回曲线面积的简化计算方法,据此分析改良土阻尼比的变化规律及影响因素,并根据修正的Hardin-Drnevich模型形式建立阻尼比随动应变增加的增长模型。
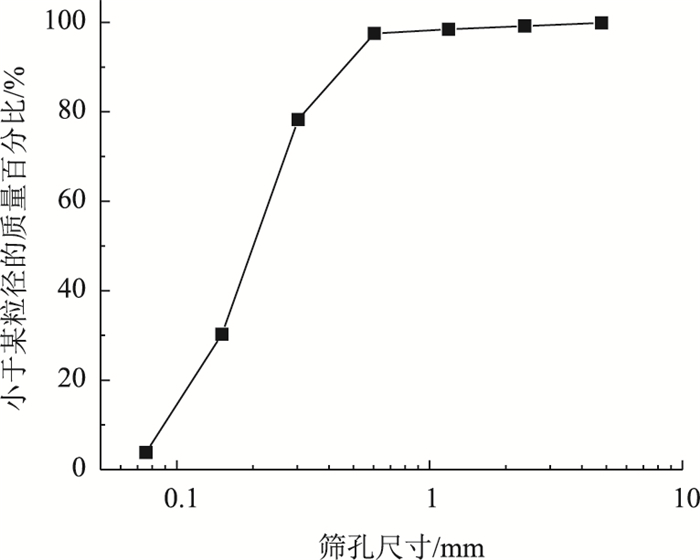
1 试验过程及阻尼比的确定 1.1 试验材料及制备试验中采用的土取自某施工现场,属于级配不良的细砂,其级配曲线如图 1所示。煤渣为某公司燃煤的废弃炉渣,经过破碎处理后取粒径小于2.36 mm的燃煤炉渣备用,其主要化学成分为Al2O3及SiO2,堆积密度为921 kg/m3。水泥选用42.5级普通硅酸盐水泥。
|
| 图 1 风积砂的级配曲线 Fig. 1 Gradation curve of aeolian sand |
| |
试验中各材料的质量配合比设计见表 1。将试验中使用的土样加水搅拌均匀,在ϕ39.1×80 mm的三瓣饱和器内分5层振捣压实。试样制备完成后,立即使用保鲜膜对试件进行包裹,放置在温度(20±2) ℃、湿度≥95%的标准养护环境下养护7 d,之后进行动力学试验。
| 组号 | 水泥 | 煤渣 | 风积砂 |
| 1 | 3 | 5 | 92 |
| 2 | 3 | 10 | 87 |
| 3 | 3 | 15 | 82 |
| 4 | 3 | 20 | 77 |
| 5 | 0 | 0 | 100 |
1.2 试验方法
试验采用英国GDS动态三轴测试系统进行,该设备围压控制系统控制压力范围为0~2 MPa,最大轴向荷载25 kN,最大轴向位移90 mm,荷载频率0.1~5 Hz,可以满足中低围压、高振次、多种频幅的试验要求。
路基作为道路结构层的主要作用是承受和传递行车荷载。加载幅值、频率以及围压条件均会对路基填土的阻尼比造成一定的影响。石峰、何海鹰等[15-16]通过现场实测得到路基顶面的动应力,发现行车荷载在经过路面结构层后其幅值会发生一定程度的衰减。正常行车荷载作用时,路床以下残余动应力幅值大致为10~40 kPa,在超载情况下动应力幅值最高可达80 kPa。本研究考虑一定的车辆超载情况,对应力幅值进行了小幅放大,取应力幅值为50 kPa。
为探究试验围压和加载频率对改良土阻尼比的影响,采用固结不排水的试验方法(CU试验)。围压分别为100,150,200,300 kPa,频率分别为0.5,1,3,5 Hz,加载次数为10 000次,采用正弦波的加载形式用以分析不同加载频率、不同围压下改良土阻尼比的变化规律。试验终止的条件为每小时变形小于0.1 mm或累积应变超过5%。前者认为变形已趋于稳定,后者认为试件已发生破坏。具体试验控制条件见表 2。
| 序号 | 煤渣含量/% | 围压/kPa | 频率/Hz |
| 1 | 0,5,10,15,20 | 100,150,200,300 | 1 |
| 2 | 15 | 100,150,200,300 | 0.5,1,3,5 |
| 3 | 0,5,10,15,20 | 100 | 0.5,1,3,5 |
1.3 阻尼比的确定
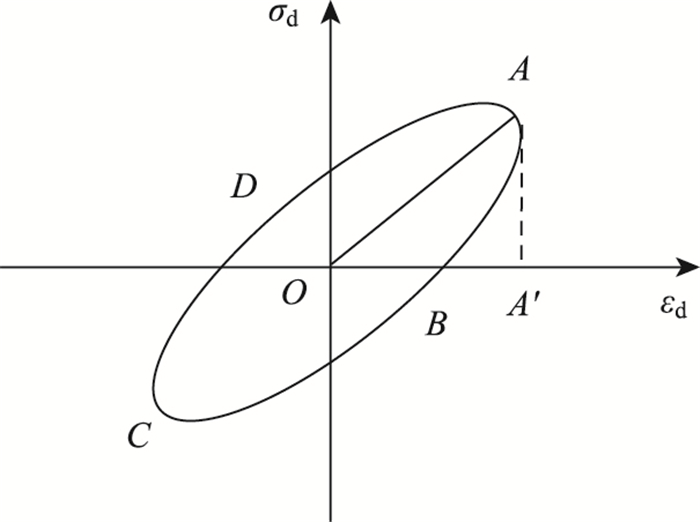
若将土体看作为一种黏弹性材料,则其动应力-应变曲线在1个荷载周期内将构成1个闭合的椭圆(见图 2),其阻尼比λ确定的方法为:
|
| 图 2 理想黏弹性土的滞回曲线示意图 Fig. 2 Hysteretic curve of perfect viscous elastic soil |
| |
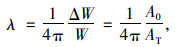
|
(1) |
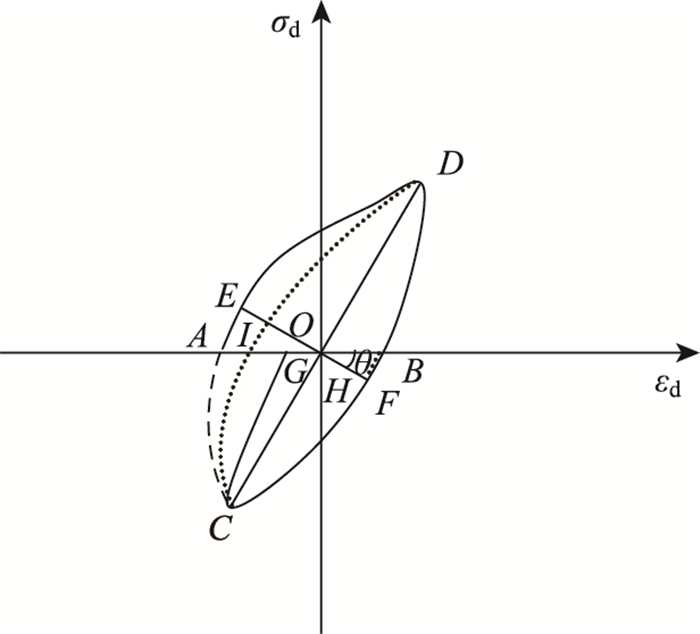
式中,ΔW为土体在荷载作用1个周期内所损耗的能量;W为在荷载作用1个周期内所贮存的总能量;A0为滞回曲线ABCDA围成的椭圆面积;AT为三角形OAA′的面积。然而煤渣改良土并不是理想的黏弹性体,其滞回曲线大多不是闭合的椭圆(图 3),即使曲线闭合也并不构成真椭圆。对于煤渣改良土的滞回曲线,在计算其面积时常见的方法有两种:一种为将试验所测得的试验点看作理想椭圆,进行拟合后再对面积进行求解。另一种为将所测的试验点以直线相连构成多个多边形,再将这些多边形的面积进行求和,以多边形面积之和代替滞回曲线椭圆的面积。但两种方法都存在一定的缺点,椭圆面积法所需数据量较少但计算获得的阻尼比误差较大;多边形面积累加法在采样频率较高时具有较高的计算精度但其所需数据点较多,计算量较大。为回避两种方法的缺点,本研究提出一种改进的椭圆面积法来进行改良土阻尼比的计算。
|
| 图 3 改良土的滞回曲线示意图 Fig. 3 Hysteretic curve of improved soil |
| |
对于这种不闭合的滞回曲线,可以通过以下方法近似求得其围成的面积。设滞回曲线与横轴的焦点为A,B,G,坐标原点为O,AG的中点为I,应力最大值与最小值对应的点为C,D。通过原点作与CD垂直的直线,与滞回曲线的交点为E和F,直线EF与横轴的夹角为θ,过点B作OF的垂线与OF的交点为H。
以椭圆面积法求解滞回曲线面积的难点主要在于椭圆短轴位置及长短的确定。以往常用的方法是将滞回曲线近似看作椭圆曲线,以CD作为长轴,EF作为短轴,其所围成的面积AE可以按照椭圆面积公式进行计算,即:
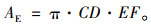
|
(2) |
但由于滞回曲线的不闭合的性质,导致OE的长度大于OF,使得所计算的面积比真正的滞回曲线围成的面积增大了面积ACG。
为减小上述计算方法带来的误差,本研究对椭圆面积的计算进行了修正,用直线OH来近似代替OF,椭圆短轴的长度可用式(3)确定:
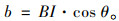
|
(3) |
当滞回曲线闭合时,A,I,G 3点重合,AG的长度趋于0,短轴的长度为:
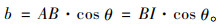
|
(4) |
滞回曲线所围成的面积AL可以用椭圆IDBC的面积来代替,使得计算结果更加准确:
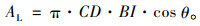
|
(5) |
阻尼比λ可以由式(6)进行计算:
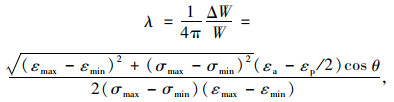
|
(6) |
式中,εmax,εmin,σmax,σmin分别为荷载作用1个周期内所对应的最大、最小应变及应力;εa为卸载过程中应力为0时所对应的应变;εp为1个周期荷载作用后不能恢复的塑性变形。
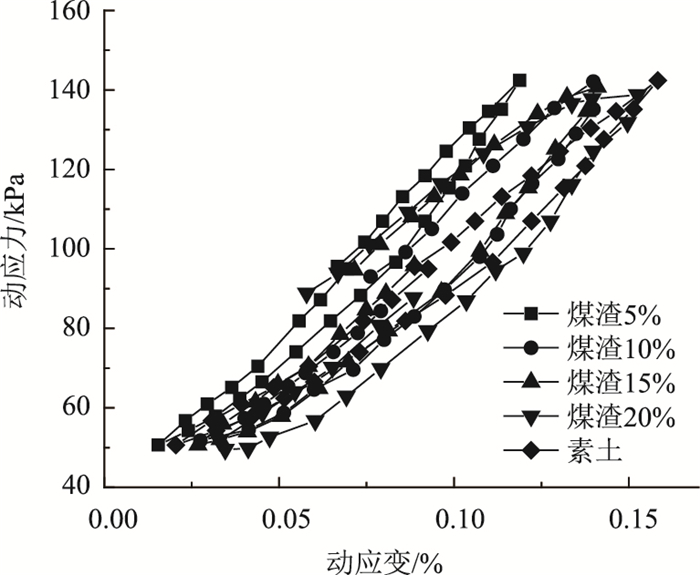
图 4为不同煤渣掺量时所获得的滞回曲线。为验证阻尼比计算方法的准确性,分别采用椭圆面积法、多边形面积累加法和改进的椭圆面积法对试验过程中的阻尼比进行计算。滞回曲线描述的准确性与荷载施加1个周期内所采集的数据点个数有关,采样频率越高所得出的滞回曲线越接近真实情况。在采样频率较高的情况下,各采样点之间可以采用直线代替曲线。所以在较高采样频率的情况下,可近似认为以多边形面积累加法所得到的阻尼比为精确值,其余方法与之进行比较可以得出各方法的优劣。
|
| 图 4 煤渣改良土的滞回曲线 Fig. 4 Hysteretic curves of cinder improved soil |
| |
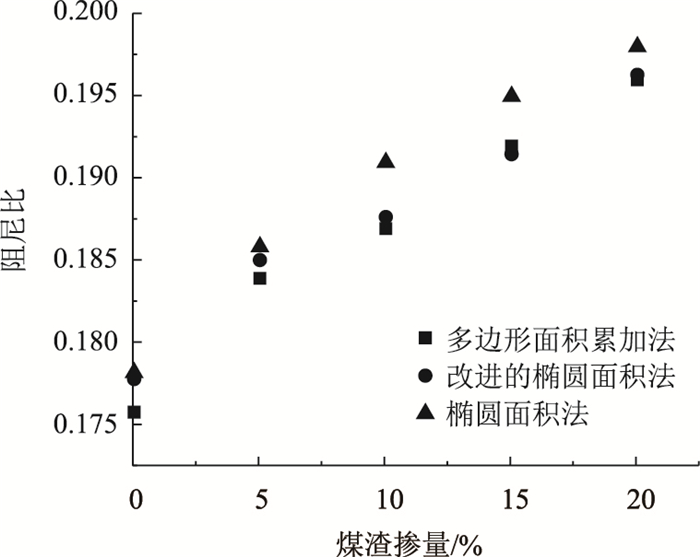
图 5为利用3种方法计算所得的阻尼比。可以看出,使用椭圆面积法所求得的阻尼比要大于多边形面积累加法和改进的椭圆面积法所得阻尼比。改进的椭圆面积法与多边形面积累加法所得阻尼比较为接近,具有一定的精度,且所需数据量、计算量较少。
|
| 图 5 改良土的阻尼比 Fig. 5 Damping ratios of improved soil |
| |
2 试验结果与分析 2.1 改良土的滞回曲线
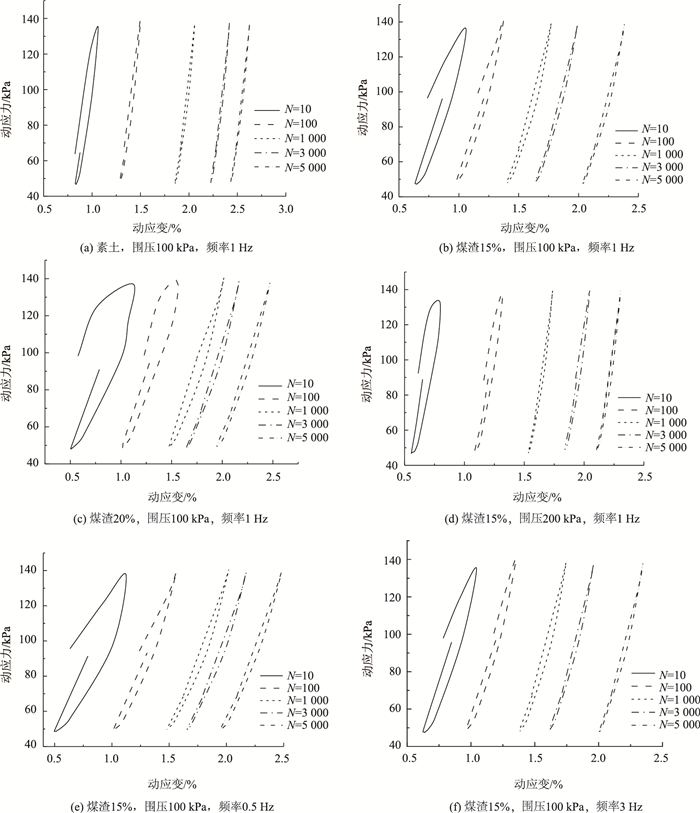
当煤渣掺量不同时,改良土在加载过程中滞回曲线的演化规律如图 6所示。由于篇幅限制,仅列出了部分数据。
|
| 图 6 改良土滞回曲线的演化 Fig. 6 Evolution of hysteresis curve of improved soil |
| |
由图 6可知,随着荷载作用次数的增加,各组改良土试样的滞回曲线均逐渐由开口型向闭合型过渡,滞回曲线所围成的面积也逐渐减小,当加载次数超过1 000次后,滞回曲线形状基本保持不变。这是因为改良土在动荷载的作用下结构变得紧密,导致改良土对振动能量吸收的能力逐渐减弱,表现出滞回曲线围成的面积随加载次数的增加而逐渐减小,最终趋于稳定。
当围压与加载频率一定时,改良土滞回曲线所围成的面积随煤渣掺量的增加而逐渐增加,曲线的不闭合程度逐渐增大。煤渣是一种疏松多孔的结构物,随煤渣掺量的增加,改良土内部的孔隙逐渐增多,对振动能量的吸收程度也逐渐增大,从而出现改良土滞回曲线围成的面积随煤渣掺量的增加而逐渐增大的现象。
当煤渣掺量及加载频率一定时,随着围压的增大,试样滞回曲线所围成的面积逐渐减小。当煤渣掺量与围压一定时,随频率的增加,改良土滞回曲线围成的面积逐渐减小,低频的作用较为明显。这是因为围压的增大使得土颗粒之间的联系更为紧密,试样变得更加致密,表现出对振动能量的吸收有所减弱,滞回曲线围成的面积逐渐减小。而加载频率主要体现在加卸载的速率上,频率越高加卸载的速度越快,土样的变形还未完全发生就已经开始了下一次加载,从而使得滞回曲线围成的面积随频率的增加而逐渐减小。
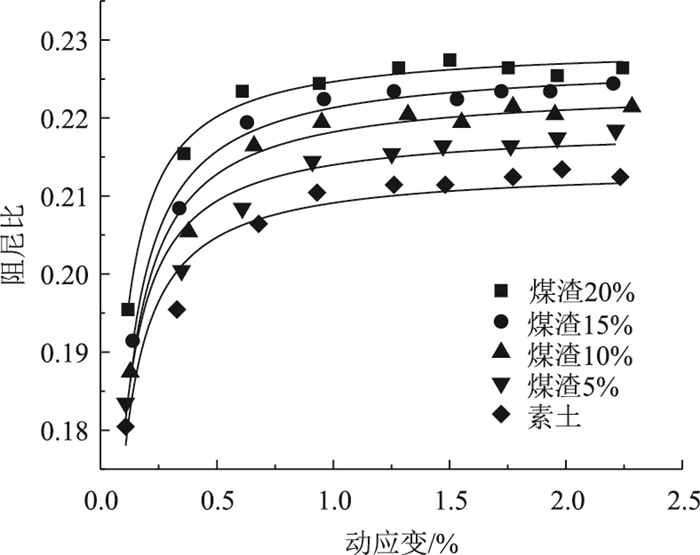
2.2 煤渣掺量的影响煤渣掺量不同时,加载过程中阻尼比与动应变的关系如图 7所示。
|
| 图 7 不同煤渣掺量下阻尼比与动应变的关系 Fig. 7 Relationships between damping ratio and dynamic strain with different cinder contents |
| |
图 7给出了围压为100 kPa、加载频率为1 Hz时阻尼比与动应变的关系。可以看出,各煤渣掺量下阻尼比均随着动应变的增加而逐渐增加,在荷载作用的初期,改良土的阻尼比增长迅速,当动应变超过0.5%时,阻尼比变化开始趋于平缓,呈现出收敛趋势。出现这种现象的原因是:循环荷载的作用使得改良土颗粒之间的距离逐渐减小,土颗粒之间的接触点开始增多,土体逐渐变得密实,对循环荷载的能量消耗逐渐降低,反映出阻尼比随动应变的增加而逐渐增大。当动应变继续增加时,土颗粒间的接触点达到极限,对振动产生的能量消耗趋于稳定[17],表现出阻尼比开始收敛并趋于稳定。
还可发现,阻尼比随着煤渣掺量的增加而逐渐增加,煤渣掺量的多少直接影响了改良土阻尼比的最大值。这是因为煤渣是一种疏松多孔的结构物,煤渣掺量的增加相当于增大了改良土的空隙率,动力波在穿过改良土时会引起土颗粒在空隙中不断振动,从而消耗了部分能量。随着其掺量的逐渐增大,改良土对动力波能量的吸收作用也逐渐增强,进而表现出最大阻尼比保持在较高水平。最大阻尼比与煤渣掺量之间大致呈线性关系,可以表达为:
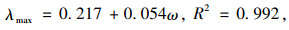
|
(7) |
式中,λmax为改良土的最大阻尼比;ω为煤渣掺量;R为回归系数。
可以看出二者线性回归精度较高,式(7)能够较好地反映出煤渣掺量与最大阻尼比之间的关系。
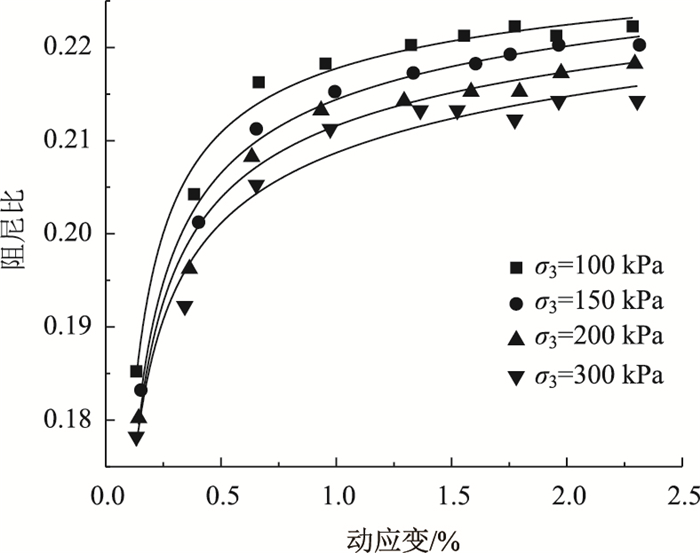
2.3 围压的影响加载频率为1 Hz、煤渣掺量为15%时,阻尼比与动应变的关系如图 8所示。
|
| 图 8 不同围压下阻尼比与动应变的关系 Fig. 8 Relationships between damping ratio and dynamic strain under different confining pressures |
| |
由图 8可知,在频率及煤渣掺量一定的情况下,改良土的阻尼比随着围压的提高而逐渐降低,这是因为在循环荷载作用时,改良土颗粒之间产生爬滚、剪碎的情况很难发生。改良土阻尼比变化的主要原因是荷载作用下所引起的土体体积变形,即:围压越大改良土的内部结构越紧密,抵抗变形的能力越强,对动力波能量的吸收越小,其阻尼比水平较低;反之围压降低时,改良土的内部结构松散,抵抗变形的能力越弱,在动力作用下土颗粒经过多次运动才能达到稳态,而这一过程消耗了较多的能量,其阻尼比水平较高。
不难发现,围压也对改良土最大阻尼比有所影响,随着围压的提高,改良土最大阻尼比逐渐增加,说明较大的围压对改良土结构的保护效果较好,使阻尼比保持在较低水平。二者之间的关系可以表示为:
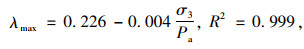
|
(8) |
式中,σ3为试验围压;Pa为大气压力。
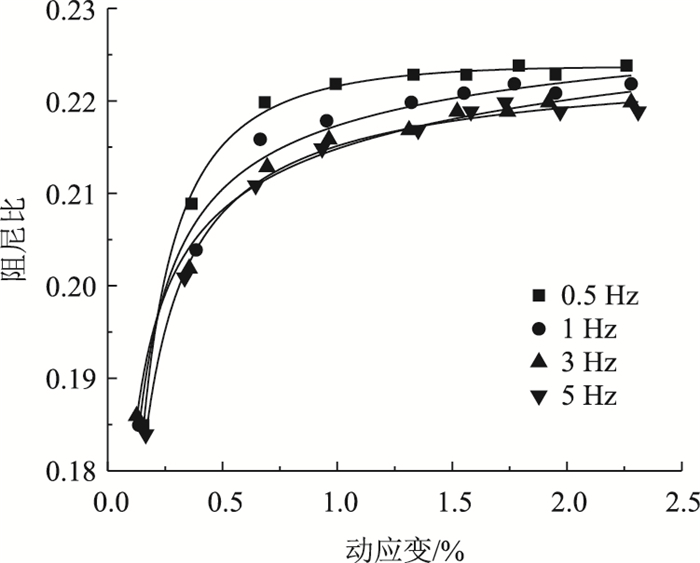
2.4 频率的影响当围压为100 kPa、煤渣掺量为15%时,阻尼比与动应变的关系如图 9所示。
|
| 图 9 不同频率下阻尼比与动应变的关系 Fig. 9 Relationships between damping ratio and dynamic strain at different frequencies |
| |
可以发现,加载频率的高低主要影响了阻尼比上升的速率,低频对改良土的影响较为突出,当频率为0.5 Hz时,阻尼比的上升较为迅速,最终阻尼比保持在一个较高的水平。随着频率的逐渐提高,这种影响开始逐渐减弱,阻尼比的上升速度开始降低。当加载频率由3 Hz提高到5 Hz时,频率对阻尼比的影响几乎消失,这两种条件下除阻尼比变化速率稍有区别外,最终所达到的阻尼比基本相同。这是因为荷载频率逐渐提高使得加载、卸载的速度增加,土体变形还没完全呈现加载过程就已经结束,随着频率的提高,对动力波能量的吸收逐渐减少,表现出较低的阻尼比水平。
2.5 阻尼比增长模型等效线性方法是土动力学中解决非线性复杂问题的一种有效方法,可以简化计算,而精准地描述阻尼比与动应变之间的关系[18-20]则是解决此类问题的关键。改良土的阻尼比受到煤渣掺量、围压及加载频率等多方面的影响,为研究改良土阻尼比的变化规律,本研究借助于修正Hardin-Drnevich模型[21]的形式对改良土阻尼比的变化规律进行分析,模型的具体表达式为:
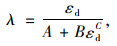
|
(9) |
式中,λ为阻尼比;εd为动应变;A,B,C为试验参数,当C=1时此模型退化为普通的Hardin-Drnevich模型。
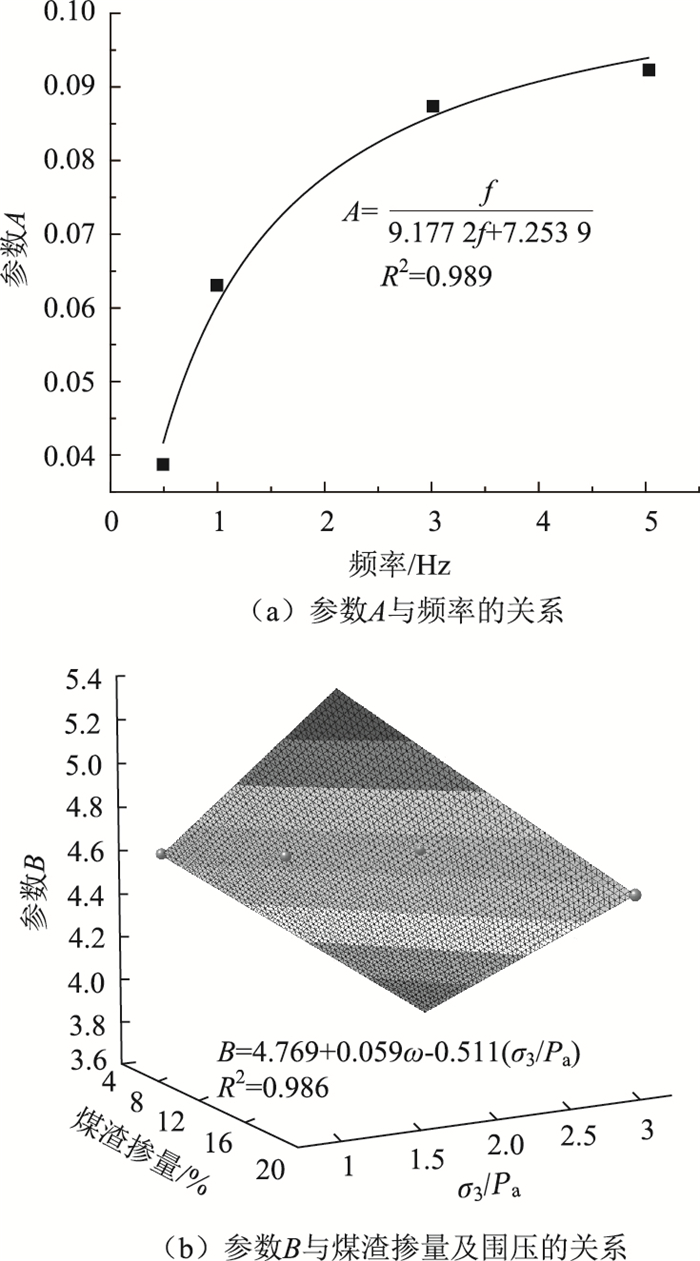
根据前几节中对阻尼比影响因素的分析可知,煤渣掺量及围压主要影响了改良土的最大阻尼比,双曲线模型的渐近线为1/B,可见参数B和煤渣掺量及围压之间存在着某种关系。而加载频率对阻尼比的影响更多反映在阻尼比的上升速率上,这与模型中代表双曲线初始斜率的参数A数学意义相近。据此对模型中参数A和B分别进行分析,其拟合情况如图 10所示。
|
| 图 10 模型参数 Fig. 10 Model parameters |
| |
可以看出,参数A,B分别具有一定的物理含义,且拟合效果较好。将参数A,B分别代入阻尼比的双曲线增长模型可得:
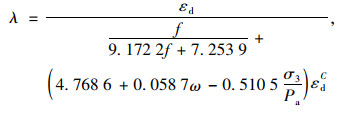
|
(10) |
式中f为加载频率。
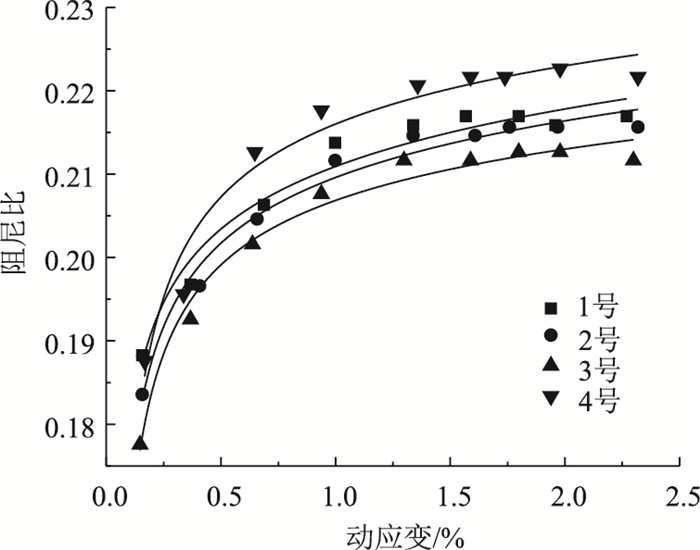
为验证模型的准确性,将试验数据代入进行验证,验证结果如表 3及图 11所示。
| 序号 | ω /% | σ3/kPa | f/Hz | R2 |
| 1 | 5 | 100 | 0.5 | 0.964 |
| 2 | 10 | 150 | 1 | 0.979 |
| 3 | 15 | 200 | 3 | 0.983 |
| 4 | 20 | 300 | 5 | 0.962 |
|
| 图 11 模型的验证 Fig. 11 Model verification |
| |
由表 3及图 11可见,以修正的Hardin-Drnevich模型建立的阻尼比增长模型能够较好地反映阻尼比在加载过程中的变化趋势,模型具有一定的精度,可以为类似工程提供参考。
3 结论本研究对不同煤渣掺量的改良土在不同围压及频率下进行了动三轴试验,得到以下结论:
(1) 通过对滞回曲线的分析,改进了原有的阻尼比计算方式,改进的椭圆面积法具有一定的精度,且所需数据量、计算量更少,可以作为阻尼比的一种简化计算方法。
(2) 煤渣掺量及围压主要影响改良土的最大阻尼比。随着煤渣掺量的增加,改良土的阻尼比逐渐增大,对振动能量的吸收逐渐提高。随着围压的增加,改良土的结构变得更加紧致,动力波更容易穿透土体进入到下一层,使得阻尼比逐渐降低。
(3) 频率主要影响阻尼比的增加速率,低频的影响较为突出,随着频率的提高,这种影响开始逐渐降低,当频率超过3 Hz后,频率对改良土的影响极弱,3 Hz和5 Hz的阻尼比变化曲线基本相同。
(4) 借助修正的Hardin-Drnevich模型,建立了阻尼比的增长模型,模型中的参数具有一定的物理意义,能较好地反映出阻尼比在加载过程中的变化趋势。
| [1] |
王红鑫, 周承京, 陈群. 煤渣掺量对灰渣混合料力学性质的影响[J]. 水电能源科学, 2015, 33(9): 113-116. WANG Hong-xin, ZHOU Cheng-jing, CHEN Qun. Impact of Coal Cinder Content on Mechanical Properties of Ash Residue Mixture[J]. Water Resources and Power, 2015, 33(9): 113-116. |
| [2] |
KURAMA H, KAYA M. Usage of Coal Combustion Bottom Ash in Concrete Mixture[J]. Construction and Building Materials, 2008, 22(9): 1922-1928. |
| [3] |
刘栋, 李立寒, 崔华杰. 水泥稳定炉渣碎石的强度性能[J]. 建筑材料学报, 2014, 17(3): 538-542. LIU Dong, LI Li-han, CUI Hua-jie. Strength Performance of Cement Stabilized Aggregate Containing Bottom Ash Aggregate (BAA)[J]. Journal of Building Material, 2014, 17(3): 538-542. |
| [4] |
刘栋, 李立寒, 崔华杰. 水泥稳定炉渣碎石基层路用性能[J]. 同济大学学报:自然科学版, 2015, 43(3): 405-409, 415. LIU Dong, LI Li-han, CUI Hua-jie. Pavement Performance of Cement Stabilized Municipal Solid Waste Incineration Bottom Ash Aggregate and Crushed Stones[J]. Journal of Tongji University:Natural Science Edition, 2015, 43(3): 405-409, 415. |
| [5] |
张互助, 程培峰, 邵洪杰, 等. 水泥煤渣稳定煤矸石基层材料温缩性能的试验研究[J]. 公路交通科技, 2007, 24(11): 29-32. ZHANG Hu-zhu, CHENG Pei-feng, SHAO Hong-jie, et al. Test Research on Temperature Shrinkage Performance of Cement and Cinder Stabilized Coal Gangue Base Course Materials[J]. Journal of Highway and Transportation Research and Development, 2007, 24(11): 29-32. |
| [6] |
PECQUEUR G, CRIGNON C, QUÉNÉE B. Behaviour of Cement-treated MSWI Bottom Ash[J]. Waste Management, 2001, 21(3): 229-233. |
| [7] |
MULLER U, RUBNER K. The Microstructure of Concrete Made with Municipal Waste Incinerator Bottom Ash as an Aggregate Component[J]. Cement and Concrete Research, 2006, 36(8): 1434-1443. |
| [8] |
罗飞, 赵淑萍, 马巍, 等. 青藏冻结黏土滞回曲线形态特征的定量研究[J]. 岩石力学与工程学报, 2013, 32(1): 208-215. LUO Fei, ZHAO Shu-ping, MA Wei, et al. Quantitative Research on Morphological Characteristics of Hysteretic Curves of Qinghai-Tibet Frozen Clay[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(1): 208-215. |
| [9] |
黄斌, 傅旭东, 张本蛟, 等. 动弹模量阻尼比测试技术与归一化特性研究[J]. 岩土工程学报, 2015, 37(4): 659-666. HUANG Bin, FU Xu-dong, ZHANG Ben-jiao, et al. Test Technology and Normalized Characteristics of Dynamic Elastic Modulus and Damping Ratio[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(4): 659-666. |
| [10] |
严晗, 王天亮, 刘建坤, 等. 反复冻融条件下粉砂土动力学参数试验研究[J]. 岩土力学, 2014, 35(3): 683-688. YAN Han, WANG Tian-liang, LIU Jian-kun, et al. Experimental Study of Dynamic Parameters of Silty Soil Subjected to Repeated Freeze-thaw[J]. Rock and Soil Mechanics, 2014, 35(3): 683-688. |
| [11] |
焦贵德, 赵淑萍, 马巍, 等. 循环荷载下冻土的滞回圈演化规律[J]. 岩土工程学报, 2013, 35(7): 1343-1349. JIAO Gui-de, ZHAO Shu-ping, MA Wei, et al. Evolution Laws of Hysteresis Loops of Frozen Soil under Cyclic Loading[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(7): 1343-1349. |
| [12] |
罗飞, 何依婷, 赵淑萍, 等. 分级加载下冻土阻尼比的试验研究[J]. 岩土力学, 2015, 36(11): 3143-3149. LUO Fei, HE Yi-ting, ZHAO Shu-ping, et al. Experimental Study of Damping Ratio of Frozen Soil under Stepwise Loading[J]. Rock and Soil Mechanics, 2015, 36(11): 3143-3149. |
| [13] |
VINSON T S. Response of Frozen Ground to Dynamic Loadings: Chapter 9 in Geotechnical Engineering in Cold Regions[M].[S. l.]: McGraw-Hill Book Company, Inc., 1978: 405-458.
|
| [14] |
CZAJKOWSKI R L, VINSON T S. Dynamic Properties of Frozen Silt under Cyclic Loading[J]. Journal of the Geotechnical Engineering Division, 1980, 106(9): 963-980. |
| [15] |
石峰, 刘建坤, 房建宏, 等. 季节性冻土地区公路路基动应力测试[J]. 中国公路学报, 2013, 26(5): 15-20. SHI Feng, LIU Jian-kun, FANG Jian-hong, et al. Subgrade Dynamic Stress Test on Highway in Seasonal Frozen Soil Area[J]. China Journal of Highway and Transport, 2013, 26(5): 15-20. |
| [16] |
何海鹰. 高速公路路基动力响应现场试验与数值分析[J]. 长沙理工大学学报:自然科学版, 2012, 9(2): 13-18. HE Hai-ying. The Field Test and Numerical Analysis of Expressway Subgrade Dynamic Response[J]. Journal of Changsha University of Science and Technology:Natural Science Edition, 2012, 9(2): 13-18. |
| [17] |
汪明元, 单治钢, 王亚军, 等. 应变控制下舟山岱山海相软土动弹性模量及阻尼比试验研究[J]. 岩石力学与工程学报, 2014, 33(7): 1503-1512. WANG Ming-yuan, SHAN Zhi-gang, WANG Ya-jun, et al. Dynamic Elastic Moduli and Damping Ratios of Marine Sediments at Zhoushan Daishan Based on Dynamic Triaxial Tests under Strain Control[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(7): 1503-1512. |
| [18] |
ZHONG X G, ZENG X, ROSE J G. Shear Modulus and Damping Ratio of Rubber-modified Asphalt Mixes and Unsaturated Subgrade Soils[J]. Journal of Materials in Civil Engineering, 2002, 14(6): 496-502. |
| [19] |
钱家欢, 殷宗泽. 土工原理与计算[M]. 北京: 中国水利水电出版社, 2000. QIAN Jia-huan, YIN Zong-ze. Geotechnical Principle and Calculation[M]. Beijing: China Water & Power Press, 2000. |
| [20] |
白冰. 土的动力特性及应用[M]. 北京: 中国建筑工业出版社, 2016. BAI Bing. Dynamic Characteristics of Soil and Its Application[M]. Beijing: China Architecture & Building Press, 2016. |
| [21] |
HARDIN B O, DRNEVICH V P. Shear Modulus and Damping in Soils[J]. Journal of the Soil Mechanics and Foundations Division, 1972, 98(7): 667-692. |
 2019, Vol. 36
2019, Vol. 36
