扩展功能
文章信息
- 孙川, 吴超仲, 褚端峰, 黄子超, 李必军
- SUN Chuan, WU Chao-zhong, CHU Duan-feng, HUANG Zi-chao, LI Bi-jun
- 基于SAX的车载数据时空语义编码及分析方法
- Space-time Semantic Coding for On-board Data and Analysis Method Based on SAX
- 公路交通科技, 2019, 36(8): 124-132
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(8): 124-132
- 10.3969/j.issn.1002-0268.2019.08.016
-
文章历史
- 收稿日期: 2017-03-14
2. 武汉大学 测绘遥感信息工程国家重点实验室, 湖北 武汉 430079;
3. 武汉理工大学 智能交通系统研究中心, 湖北 武汉 430063;
4. 交通运输部公路科学研究院, 北京 100088
2. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan Hubei 430079, China;
3. ITS Research Center, Wuhan University of Technology, Wuhan Hubei 430063, China;
4. Research Institute of Highway, Ministry of Transport, Beijing 100088, China
目前车载监控系统的各项功能及技术指标趋于成熟,实车试验因而得以顺利开展,同时收集了丰富的车载监控数据[1-2]。车载监控数据的类型与数量已经远达到了可以分析的技术要求,但是车载数据的编码分析手段却并未随着数据量的增加而有所突破,这就对其挖掘分析工作带来了一定的技术障碍[3-4]。一段12 h的驾驶数据容量即可高达到2 GB,传统的数据编码分析方法难以适应如此庞大的数据容量,因此当前研究人员更多的是从具有较高驾驶风险的重点事件(如变道、超车、避碰等)入手进行分析,这类高驾驶风险的重点事件时间区间往往较短,分析时长一般不超过30 s,这种短时区间重点驾驶事件通常难以捕捉定位,尤其是当需要调取车辆监控视频时显得尤为困难[5];另一方面,在某些需要分析长时区间的驾驶行为(如车队运输任务)时,虽然可以通过数据的统计分析整体把握,但是一些驾驶行为的细节部分(如急加减速)往往得不到直观可视化的呈现[6]。因此,车载监控数据的挖掘处理亟待引入一些新思路,突破原有的技术瓶颈。
时间序列是一组基于时间变化事件数据或序列值构成的集合,体现了数据属性值在时间轴上的随动特性,且时间序列数据通常体量大、维度高、更新频率快,目前广泛应用于汽车交通、通讯传播、气象监控、医疗卫生、股市金融等各个领域[7-10]。时间序列数据简化方法能够大幅度减少数据的容量,为短时区间驾驶行为的快速提取、长时区间驾驶行为的细节捕捉提供有力的技术保障。针对时间序列的分段处理已有较多方法,如分段累积近似法(Piecewise Aggregate Approximation, PAA)[11]、适应性分段常数近似法(Adaptive Piecewise Constant Approximation, APCA)[12]、分段线性表示法(Piecewise Linear Representation, PLR)[13]等。上述方法的核心思路均为捕捉并保留时间轴上具有明显变化的数据点,筛选掉未有明显变化特征的点,然后通过线段将保留的数据点进行连接。如此就在实现降低维度、压缩数据体量的同时,又能保留时间序列总体变化形态。近年来,有关学者对原有PAA方法进行补充改进,演化得出一种符号化聚合近似(Symbolic Aggregate Approximation, SAX)方法,在各个领域内的时间序列数据研究中广泛应用。因此本研究选定SAX方法将其运用于汽车交通领域内,针对车载时间序列数据进行分析与挖掘。
本研究将在其他领域(医疗、气象、经济等)较常使用的时间序列符号化思想借鉴到汽车交通领域,按照车载数据的特征对其进行时空语义编码,基于范例演示该方法的使用过程,最后通过实例分析,剖析利用车载数据时空语义编码分析车辆驾驶安全的方法。
1 符号化聚合近似(SAX)方法时间序列符号化表示是这些年所构建的一种对时间序列数据进行离散处理的理论方法,其核心思路是把以具体数值形式体现的时间序列串按照既定的变化规则进行编码,转化为以离散符号形式体现的符号序列串。时间序列符号化由于其离散化、非实数化的特征,在处理复杂时间序列数据领域逐渐成为研究焦点。在前人的研究基础上,Keogh构建了一种改进型符号化表示方法,即为符号化聚合近似(SAX),具体实现过程如下[14]。
(1) 对原始时间序列T=t1, …, tn进行正规化。即把原始时间序列转换成均值为0、标准方差为1的标准化时间序列,记为T′=t′1, …, t′n。
(2) 基于分段累积近似(PAA)方法将标准化后的时间序列T′=t′1, …, t′n进行降维。即把长度为n的标准化时间序列继续转换成一组长度为N(N < < n)的时间序列向量,记为T=t1, …, tN。
(3) 将降维后的t1, …, tN时间序列向量离散化,完成具体数值时间序列转化为符号化时间序列的目的。通常经过PAA方法处理后的序列值近似服从正态分布,即t1, …, tN满足正态分布,因此可将其划分成m个等概率区间。然后把每个概率区间用1个对应字符进行表示,共计m个字符数,最终完成原始时间序列数据转化成符号化时间序列a1, …, aN的目的。
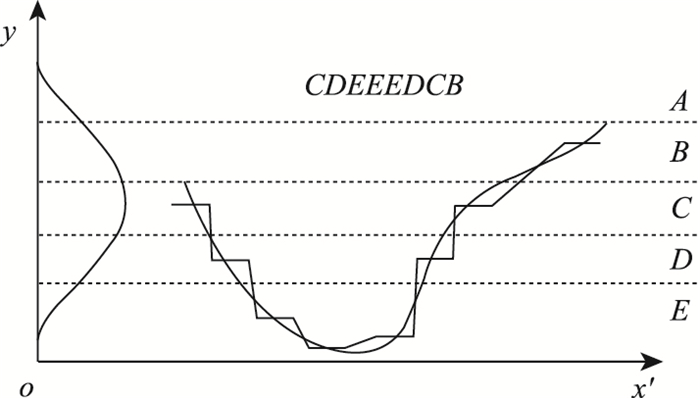
上述3个步骤如图 1所示,横坐标x′代表时间序列数据的样本点,纵坐标y代表经过标准化后时间序列样本点对应的数值。在该图中利用4条横虚线对时间序列进行了等概率划分,共计5个区间,并对每个区间分别赋予相应的字符A,B,C,D,E,该段原始时间序列数据经过符号化后为“CDEEEDCB”。
|
| 图 1 符号化聚合近似方法(SAX)示意图 Fig. 1 Schematic diagram of SAX method |
| |
通过上述步骤,成功地把长度为n的时间序列在不失主体形态特征的情况下转化为长度为N的字符序列,且共使用了m个字符完成整个符号化过程。SAX方法具有如下优势:
(1) 算法可操作性强,广泛适用于各类时间序列数据。
(2) 具有较强的降维能力(N<<n),大幅度降维对于时间序列数据的挖掘工作带来极大便利。
(3) 等概率划分原则能够有效保证各个符号序列的间距满足实际距离的下界标准,可以有效避免漏报现象的发生。
因此,SAX方法一方面保留了时间序列数据的主体信息,另一方面又实现了合理降维,为后续数据挖掘工作的展开提供了前期基础;另外,算法本身对数据质量并无较高要求,能够处理一定程度的噪声数据,分段过程在某种程度上也可理解为一种数据平滑处理;算法可视化能力强,具有较高的多分辨率特征等。因而,作为时间序列数据挖掘的前期处理方法,在较多的领域均有普遍应用,尤其是对车载监控数据挖掘具有很强的针对性。
2 基于SAX的车载数据语义编码方法 2.1 实车驾驶数据采集某研究中心基于某小型乘用车自行开发了车载一体化的信息采集系统(图 2)。实车驾驶试验线路位于湖北省中西部G70福银高速公路汉十段(限速120 km/h),30名驾驶人分成30组,每组试验于上午9点开始,限时当天完成,总共历时2个月。每组试验开始前事先调查第二天试验沿途区域的天气情况,尽量选择晴天、能见度良好的日期,避免在恶劣天气下进行。每组试验开始后,被试人员驾驶试验车从武汉理工大学余家头校区航海楼前出发,在市区行驶后抵达汉十高速路口收费站入口,然后驶入汉十高速沿十堰方向行驶,到达随州服务区后休息1 h,然后继续行驶,到达襄阳北收费站后开始折回,返回试验出发地点。本研究选取府河收费站至随州服务区的单程车辆驾驶数据作为实例分析的试验工况,该选取线路行驶里程约为300 km,数据所涉及的试验时长约为2~3 h。试验平台如图 3所示。

|
| 图 2 车辆试验平台 Fig. 2 Vehicle test platform |
| |

|
| 图 3 试验过程 Fig. 3 Experimental process |
| |
2.2 车载监控数据时空语义编码流程
按照SAX方法的3个步骤对拟截取的驾驶数据进行语义编码,图 4为基于SAX方法的驾驶数据时空语义编码流程。

|
| 图 4 基于SAX的驾驶数据时空语义编码流程 Fig. 4 Flowchart of space-time semantic coding for driving data based SAX |
| |
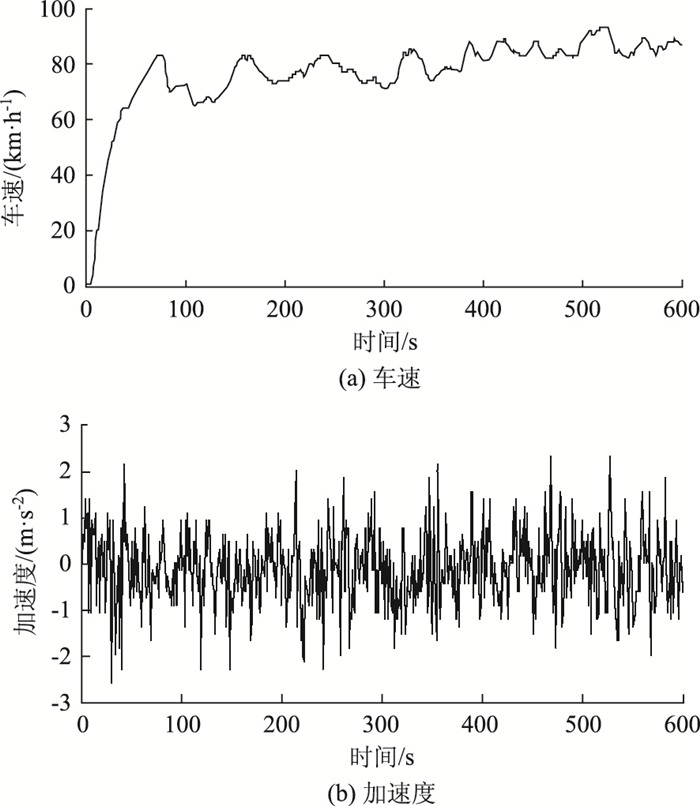
以驾驶行为分析最常用的2类数据(车速、纵向加速度)进行范例编码,通常通过这2类数据就能完成对车辆行驶安全性及驾驶风险辨识的常规分析,所截取的范例为其中1名驾驶人驾驶该试验车连续行驶10 min的一段驾驶数据(车速、加速度),行驶工况为车辆平稳地由匝道进入高速公路,并加速至巡航车速,稳定行驶于汉十高速,采集频率约为20 Hz,这里截取并保留整数秒的数据。图 5为所截取的原始驾驶时间序列数据。
|
| 图 5 原始驾驶时间序列数据 Fig. 5 Original time series driving data |
| |
由图 5可知,截取的10 min驾驶时间序列反映了车辆在高速公路上稳定加速至巡航状态的这一过程,车速变化区间约为[0, 100],单位为km/h,加速度变化区间约为[-2.5, 2.5],单位为m/s2。根据所截取的驾驶时间序列数据特征,所采用SAX方法的各个参数定义及取值如表 1所示,参数取值依据具体见下文所述,整个驾驶数据的时空语义编码过程可在MTALAB里编程实现。
| 参数 | 数字化注释 | 文字化注释 | 范例 | |
| 车速/(km·h-1) | 加速度/(m·s-2) | |||
| n | n | 原始时间序列长度 | nv=600 | na=600 |
| T | T=t1, …, tn | 原始时间序列 | Tv | Ta |
| T′ | T′=t′1, …,t′n | 标准化时间序列 | T′v | T′a |
| N | N<<n | 降维后时间序列长度 | Nv=100 | Na=50 |
| T | T=t1, …, tN | 降维后时间序列 | Tv | Ta |
| m | m | 划分的字符数(等概率) | mv=7 | ma=4 |
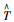 |
 |
离散化字符串 | 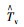 |
 |
2.3 驾驶时间序列数据正规化
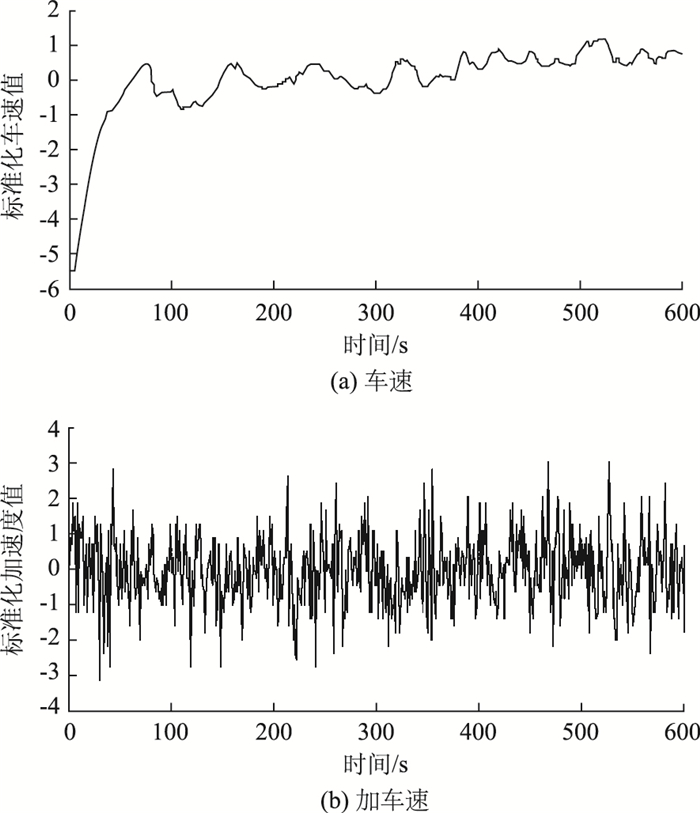
SAX方法第一步是将时间序列数据正规化,即将序列变换为均值为0,标准方差为1。这样做的目的是为了消除量纲影响和变量自身变异大小和数值大小的影响,即纵坐标无量纲化处理,方便后续将时间序列数据进行降维及等概率划分为若干区间,进而进行符号序列的标记编码。图 6为标准化后的驾驶时间序列数据。
|
| 图 6 标准化驾驶时间序列数据 Fig. 6 Standardizing time series driving data |
| |
由图 6可知,原始驾驶时间序列数据经过标准化处理后,变成均值为0、标准方差为1的序列,原始车速时间序列纵坐标区间由原始的[0, 100]变成标准化的[-6, 2],原始加速度时间序列数据也有相同变化。值得注意的是,其标准化过程并不会破坏时间序列数据本身的幅值及频率等,仅仅是数据同趋化及无量纲化处理,因此不会对后续数据语义编码工作造成影响。
2.4 驾驶时间序列数据降维处理SAX方法第二步是对标准化后的驾驶时间序列数据进行降维处理,通过合理的降维,进一步离散与符号化时间序列数据。截取的驾驶时间序列数据(速度、加速度)长度各为600个,每秒1个,共计10 min,即n=600。选定需要降至的维数N,对于速度、加速度时间序列数据需要分别进行时空语义编码。对于速度时间序列数据,根据其自身范围即车辆的行驶速度区间约为[0, 100],单位为km/h,可设定Nv为100(< 600)即可;对于纵向加速度时间序列数据,同样可以根据其数据特征设定相应参数,所截取的纵向加速的区间约为[-2.5, 2.5],单位为m/s2,可设定Na为50(< 600)。选定上述参数后,通过分段累积近似方法(PAA)就可完成对截取的速度时间序列数据、加速度时间序列数据标准化后的降维处理。图 7为降维后的驾驶时间序列数据。

|
| 图 7 降维后驾驶时间序列数据 Fig. 7 Dimensionality reduced time series driving data |
| |
由图 7可知,降维后的驾驶时间序列数据由原先的连续曲线变成了若干个分段折线段,用某个区间内分段折线段就可“代替”原先该区间内的曲线段,这样既保留了原先区间内数据的主要特征,又实现了降低维度的需要,从而可以避免由于维度过高带来的数据挖掘问题。下一步将针对分段折线段进行合理划分,即可完成时间序列数据的离散及符号化。
2.5 驾驶时间序列数据离散及符号化SAX方法第三步是在第二步数据降维的基础上,针对降维后的分段折线段进行数据离散化,然后对离散化后的数据按照语义特征(反映在速度、加速度上即为其值域)进行编码。采用SPSS 19.0统计软件对降维后的时间序列数据(速度及加速度)进行K-S检验,对于速度时间序列数据P值为0.283,对于加速度时间序列数据P值为0.316,均大于0.05,因此通过PAA方法降维后的驾驶时间序列数据近似服从正态分布。将其划分为m个等概率区间,划分区间的断点可以通过表 2查询得到。β1, β2, …, β8是划分断点,按照标准正态分布表可以计算其具体取值[14]。如当m取值为3时,被划分的3个空间概率均为1/3,通过查询标准正态分布表可得:Φ(0.43)=0.666 4,Φ(-0.43)=0.333 6,如此可得划分点的取值。进而采用相同符号对位于同一概率区间的时间序列值进行编码处理,得出对应的符号序列,完成驾驶时间序列数据的离散化及符号化。
| β | m | |||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| β1 | 0 | -0.43 | -0.67 | -0.84 | -0.97 | -1.07 | -1.15 | -1.22 |
| β2 | — | 0.43 | 0 | -0.25 | -0.43 | -0.57 | -0.67 | -0.76 |
| β3 | — | — | 0.67 | 0.25 | 0 | -0.18 | -0.32 | -0.43 |
| β4 | — | — | — | 0.84 | 0.43 | 0.18 | 0 | -0.14 |
| β5 | — | — | — | — | 0.97 | 0.57 | 0.43 | 0.14 |
| β6 | — | — | — | — | — | 1.07 | 0.67 | 0.43 |
| β7 | — | — | — | — | — | — | 1.15 | 0.76 |
| β8 | — | — | — | — | — | — | — | 1.22 |
划分字符数m需要在实际应用时根据场景情况合理设置,根据经验以及应用效果,一般不超过10个为佳。样本数据车速变化范围约为[30, 100],加速度变化范围约为[-2.5, 2.5],车速可按照其值域与10 km/h的商、加速度可按照其值域与1 m/s2的商作为参考进行划分较为合理,即ma=70/10=7,mv=5/1=5,选择7与5附近值均可。本研究最终定为ma=7,mv=4,即分别采用7个符号与4个符号来对车速、加速度进行符号化划分,这些符号为a, b, c, d, e, f, g。
同样,在MATLAB里进行等概率区间算法编程,并设置相应的符号化区间,这样就完成了基于SAX方法的驾驶时间序列数据语义编码。降维后的驾驶时间序列数据可以被等概率地划分为若干个区间,划分区间的确定可如前所述通过表 2确定。降维后的车速时间序列数据被等概率地划分为7个区间(a, b, c, d, e, f, g),加速度时间序列数据被等概率地划分为4个区间(a, b, c, d)。表 3为驾驶时间序列数据符号化区间取值。
| 车速/(km·h-1) | 加速度/(m·s-2) | |||
| 字符串 | 取值区间 | 字符串 | 取值区间 | |
| a | (0, 62] | a | (-2.5, -0.6] | |
| b | (62, 69] | b | (-0.6, 0] | |
| c | (69, 74] | c | (0, 0.67] | |
| d | (74, 80] | d | (0.67, 2.5] | |
| e | (80, 85] | — | — | |
| f | (85, 92] | — | — | |
| g | (92, 100] | — | — | |
对于处在相应划分区间的时间序列即可采用相对应的符号进行表示,这样就把原本维度很高、数据特征冗杂的时间序列语义编码成了直观可见的符号化序列,在降低数据维度的同时又保留了时间序列数据的主要特征,且数据存储容量由原先的48.74 MB下降至6.73 MB,降幅达到86.2%,这些对于后续关于驾驶行为安全性分析及风险辨识,尤其是长时间区间的驾驶行为均有重要作用。表 4为截取范例里某段驾驶数据的语义编码示例。
| 时间/s | 车速编码/(km·h-1) | 加速度编码/(m·s-2) | 纬度/(°) | 经度/(°) | 海拔/m | 航向角/(°) | ||
| 347 | c | 74 | c | 0.2 | 32.010 942 | 112.764 837 | 119 | 308.36 |
| 348 | d | 75 | c | 0.1 | 32.011 113 | 112.764 562 | 119 | 310.02 |
| 349 | d | 75 | c | 0.3 | 32.011 283 | 112.764 278 | 119 | 311.75 |
| 350 | d | 76 | b | 0 | 32.011 450 | 112.763 991 | 118 | 311.81 |
在完成上述3个步骤后,就实现了对驾驶数据的时空语义编码,整个编码过程的一个重要环节就是编码得到表 3,对于具体某段驾驶数据(见表 4),即可通过前面已经编码完成的表 3查询编码,同时也可以通过程序化编程批量完成全部驾驶数据的语义编码工作。
2.6 编码方法补充说明驾驶数据时空语义编码在实际操作使用时有以下几点需要补充解释:
(1) 驾驶数据的类型在实际编码过程中并不仅仅局限于范例中所提到的车速、纵向加速度,这里选择这两个量是考虑到通常通过这两类数据就可完成对车辆行驶安全性及驾驶风险辨识的常规分析。在实际编码时,可以根据分析内容的需要进行扩展,如增加经纬度、航向角、三轴加速度以及CAN数据(节气门开度、制动信号等)等的编码工作。
(2) 驾驶数据编码时需要确定各个参数的取值,参数取值并没有十分严格的规定,具体编码时可以根据数据类型特征灵活确定,但是依然要遵循一定原则。原始序列长度n可以选择较长时长,例如可选定一项8 h中长途运输任务。时间频率则可根据分析精度的需要灵活确定,对于速度、加速度参数1 Hz的频率基本可以满足常规分析,而对于方向盘转角参数可能需要10 Hz或更高的频率才能达到预期分析效果。降维后的时间序列长度N原则上应远小于原始序列长度n,具体取值可以将数据的值域范围作为参考。划分的字符数m可将数据值域与精度的商值作为参考依据。本研究为了构建简明并演示驾驶数据的语义编码方法,所采用的范例时间较短(10 min)。实际过程如上所述,可以选择较长的整个时间段,并不完全拘泥于范例。
(3) 驾驶数据的语义编码方法可以在MATLAB里完整实现,目前程序可以实现语义编码的所有步骤,只需要简单读取需要编码的驾驶数据就可快速完成数据的语义编码,并直接调用整理需要分析的符号化数据。
(4) 驾驶时空语义编码方法的核心本质是将数值化时间序列转化为符号化时间序列,为分析带来直观、便利的条件。从编码方法的3个步骤来看,编码方法本身具有很强的可靠性,关于结果有效性评价更多地可以从实际案例的应用效果中得出。
3 实例分析 3.1 试验工况实例选定的实车驾驶试验工况如前详述,驾驶人为所选定招募的30名驾驶人。本研究实例分析的驾驶数据截取线路为单程驾驶行驶工况,即从府河收费站单向至随州服务区行驶线路,行驶时间约为2.5 h。
3.2 驾驶数据语义编码结果在实例中,对30组(即30名驾驶人)驾驶数据重新进行整体编码,样本驾驶人(车辆)编号依次为1至30。编码数据类型为驾驶安全性分析里最常用的速度、加速度。每组原始驾驶数据长度N统一截取约为2.5 h时长数据,截取频率为1 Hz(整数秒时的数据字节),即N=9 190×30。降维后的驾驶数据长度按上文所述原则确定,这里取Nv=120,Na=100。划分的字符数同样按照上文所述原则确定,这里取mv=7,ma=7。
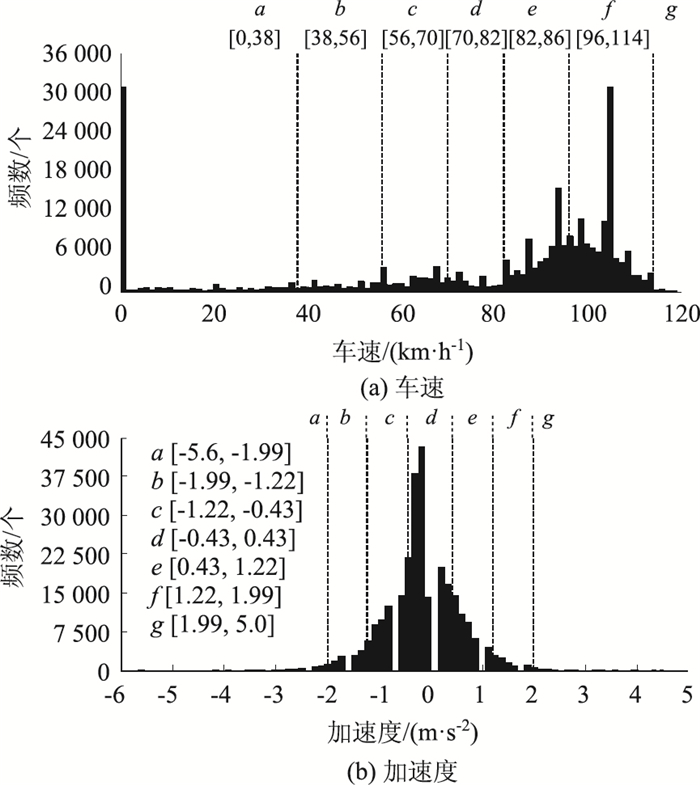
将30组驾驶数据进行统一整理后,按照所述SAX方法的3个步骤,将整理好的数据源导入MATLAB里进行语义编码计算,得到整体30组驾驶数据的全部编码序列。图 8为全部30组驾驶数据源统一编码后的区间及符号化统计分布图,方便直观地观察语义编码的总体结果。
|
| 图 8 案例试验工况数据时空语义编码结果分布 Fig. 8 Result of space-time semantic coding for data of test case |
| |
由图 8可知,案例试验工况中的驾驶数据按照所述的语义编码方法成功地进行了符号化划分。车速数据按照等概率区间被依次划分为7个字符,同理加速度数据被依次划分为7个字符。下面将简述符号化后的驾驶数据在驾驶行为安全性分析里的实际作用。
3.3 案例分析结果国内外车辆行驶工况特征研究表明,普通小型乘用车纵向加速度一般不超过0.5g[14],对纵向减速度也有相关研究将瞬时减速度大于0.4g作为一个危险事件的触发条件[15]。根据上文的加速度统计分布可知,加速度分布区间主要集中在(-0.4g, 0.5g)之间,在此区间外的加速度分布往往占有很小比例,这是由于车辆行驶时大部分时间段会处在稳定的、中低风险驾驶情景下[16]。同时,驾驶人由于自身驾驶风格,如具有愤怒驾驶、攻击性驾驶等特征,或者驾驶时为了紧急避险,均会出现急加速、急减速的情况,反映在车辆特征参数上即为出现较大的纵向加速度或减速度[17-18]。更进一步,如果在车速较高的情况下出现这种情况(急加速、急减速),那么有可能出现更高风险的驾驶场景,例如目标车辆前方出现紧急情况需要急减速,或者目标车辆为避险需要急加速等,此类情况定义为高风险驾驶事件,即车辆以较高车速行驶时出现了较大的加速度值(绝对值)的情况。准确地捕捉此类高风险驾驶事件对于分析车辆驾驶行为安全有着重要作用。
据上文驾驶数据语义编码结果的特征,在数据阈值上规定车速大于82 km/h且纵向加速度绝对值大于1.99 m/s2时,认为车辆正处在较高车速行驶状态下且进行了一个较急的加速或者制动,即发生了一个高风险驾驶事件。根据符号化的编码结果,这一事件可以通过字符串表示为ea, fa, ga, eg, fg, gg,这样,一个从直观定性及客观定量角度上比较复杂的高风险驾驶事件被符号化表示成了6个字符串,并且通过字符串的搜索可以快速划分30组驾驶试验工况里的高风险驾驶事件。结果表明,30组驾驶数据共产生了2 979个高风险驾驶事件,平均每组驾驶数据产生99.3个高风险驾驶事件,而且有5组(编号3,4,20,21,25)驾驶数据的高风险驾驶事件数量占到了总数的41%,即有1 518个。而有6组驾驶数据(编号1,8,14,17,27,29)只有少量各不超过50个高风险驾驶事件。这一结果为监控具有高驾驶风险的车辆和捕捉高风险驾驶事件提供了很重要的技术手段。
4 结论本研究主要研究了车载数据的时空语义编码方法,基于符号化聚合近似(SAX)的3个步骤对选定的一段范例数据依次进行了正规处理、降维处理、离散及符号化处理。经过语义编码后,以往维数很高、数据特征冗杂的驾驶时间序列数据合理地转换成了可读性强且易于搜索定位的符号化序列,在实现大幅降低数据维度的同时,又适时地保留了时间序列数据的主要特征。通过实例分析,演示了该方法在实际车辆驾驶安全性分析里的作用与优势。分析结果可为重点监控车辆高风险驾驶事件及有针对性地开展驾驶安全培训等方面提供一定的理论依据,同时也为今后一些特定驾驶场景的快速提取进行了技术储备。目前在车载数据语义编码过程里选取的数据类型为速度、加速度,虽然通过这两类数据就能保证车辆驾驶安全性分析的效果,但是在一些有特定需求的案例里,未来可以根据分析内容进行扩展并详述编码方法在海量样本数据中的应用过程与效果,以期得出更有针对性的结论。
| [1] |
姚振强, 王建, 胡永祥, 等. 基于RFID/GPRS/GPS/GIS的危险品物流智能监管系统[J]. 公路交通科技, 2013, 30(2): 147-152, 158. YAO Zhen-qiang, WANG Jian, HU Yong-xiang, et al. An Intelligent Supervision System for Hazardous Materials Logistics Based on RFID/GPRS/GPS/GIS[J]. Journal of Highway and Transportation Research and Development, 2013, 30(2): 147-152, 158. |
| [2] |
刘应吉, 曾诚, 王书举, 等. 基于卫星定位数据的驾驶行为安全与节能评价方法[J]. 公路交通科技, 2018, 35(1): 121-128, 158. LIU Ying-ji, ZENG Cheng, WANG Shu-ju, et al. An Evaluation Method of Safety and Energy-saving Driving Behavior Based on Satellite Positioning Data[J]. Journal of Highway and Transportation Research and Development, 2018, 35(1): 121-128, 158. |
| [3] |
GORDON T J, KOSTYNIUK L P, GREEN P E, et al. Analysis of Crash Rates and Surrogate Events Unified Approach[J]. Transportation Research Record, 2011, 2237: 1-9. |
| [4] |
吴金中, 范文姬, 杨富峰. 危险货物道路运输运单电子化管理研究[J]. 公路交通科技, 2015, 32(12): 12-18. WU Jin-zhong, FAN Wen-ji, YANG Fu-feng. Research on Electronic Waybill Management for Road Dangerous Goods Transport[J]. Journal of Highway and Transportation Research and Development, 2015, 32(12): 12-18. |
| [5] |
JOVANIS P, AGUERO-VALVERDE J, WU K F, et al. Analysis of Naturalistic Driving Event Data:Omitted-variable Bias and Multilevel Modeling Approaches[J]. Transportation Research Record, 2011, 2236: 49-57. |
| [6] |
DINGUS T A, NEALE V L, KLAUER S G, et al. The Development of a Naturalistic Data Collection System to Perform Critical Incident Analysis:An Investigation of Safety and Fatigue Issues in Long-haul Trucking[J]. Accident Analysis & Prevention, 2006, 38(6): 1127-1136. |
| [7] |
李海林, 郭崇慧. 基于云模型的时间序列分段聚合近似方法[J]. 控制与决策, 2011, 26(10): 1525-1529. LI Hai-lin, GUO Chong-hui. Piecewise Aggregate Approximation Method Based on Cloud Model for Time Series[J]. Control and Decision, 2011, 26(10): 1525-1529. |
| [8] |
弓晋丽, 彭贤武. 城市道路交通流时间序列模式相似性分析[J]. 公路交通科技, 2013, 30(11): 119-123. GONG Jin-li, PENG Xian-wu. Analysis of Similarity of Pattern of Traffic Flow Time Series on Urban Road[J]. Journal of Highway and Transportation Research and Development, 2013, 30(11): 119-123. |
| [9] |
桑夏夏, 李旭伟. 一种金融时间序列区域分割方法的研究[J]. 四川大学学报:自然科学版, 2018, 55(6): 1189-1196. SANG Xia-xia, LI Xu-wei. Research on the Region Based Segmentation Method of Financial Time Series[J]. Journal of Sichuan University:Natural Science Edition, 2018, 55(6): 1189-1196. |
| [10] |
蒋艳, 满晓玮, 赵丽颖, 等. 基于时间序列数据的北京市卫生筹资水平、构成趋势研究[J]. 中国卫生政策研究, 2018, 11(7): 1-6. JIANG Yan, MAN Xiao-wei, ZHAO Li-ying, et al. Analysis on the Level, Structures and Trend of Regional Health Expenditure in Beijing Based on Time Series[J]. Chinese Journal of Health Policy, 2018, 11(7): 1-6. |
| [11] |
GEORGOULAS G, KARVELIS P, STYLIOS C D, et al. Automatizing the Broken Bar Detection Process via Short Time Fourier Transform and Two-dimensional Piecewise Aggregate Approximation Representation[C]//Energy Conversion Congress and Exposition (ECCE). Pittsburgh: IEEE, 2014: 3104-3110.
|
| [12] |
DEREICH S, LI S. Multilevel Monte Carlo for Lévy-driven SDEs:Central Limit Theorems for Adaptive Euler Schemes[J]. The Annals of Applied Probability, 2016, 26(1): 136-185. |
| [13] |
LUO L, CHEN X. Integrating Piecewise Linear Representation and Weighted Support Vector Machine for Stock Trading Signal Prediction[J]. Applied Soft Computing, 2013, 13(2): 806-816. |
| [14] |
LIN J, KEOGH E, WEI L, et al. Experiencing SAX:A Novel Symbolic Representation of Time Series[J]. Data Mining and Knowledge Discovery, 2007, 15(2): 107-144. |
| [15] |
张建伟, 李孟良, 艾国和, 等. 车辆行驶工况与特征的研究[J]. 汽车工程, 2005, 27(2): 220-224. ZHANG Jian-wei, LI Meng-liang, AI Guo-he, et al. A Study on the Features of Existing Typical Vehicle Driving Cycles[J]. Automotive Engineering, 2005, 27(2): 220-224. |
| [16] |
JIANG Y B, GAO X N, HAN P. Application of Maximum Entropy Model in Distribution of Vehicle Speed[J]. Advanced Materials Research, 2014, 1079-1080: 942-945. |
| [17] |
雷虎.愤怒情绪下的汽车驾驶行为特征及其对交通安全的影响研究[D].武汉: 武汉理工大学, 2011. LEI Hu. Characteristics of Angry Driving Behaviors and Its Effects on Traffic Safety[D]. Wuhan: Wuhan University of Technology, 2011. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1880778 |
| [18] |
BERDOULAT E, VAVASSORI D, SASTRE M T M. Driving Anger, Emotional and Instrumental Aggressiveness, and Impulsiveness in the Prediction of Aggressive and Transgressive Driving[J]. Accident Analysis & Prevention, 2013, 50: 758-767. |
 2019, Vol. 36
2019, Vol. 36
