扩展功能
文章信息
- 赵庶旭, 屈睿涛, 王婧雯
- ZHAO Shu-xu, QU Rui-tao, WANG Jing-wen
- 基于改进的反距离权重插值的车辆轨迹重构方法
- A Vehicle Trajectory Reconstruction Method Based on Improved Inverse Distance Weighted Interpolation
- 公路交通科技, 2018, 35(10): 133-139
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(10): 133-139
- 10.3969/j.issn.1002-0268.2018.10.018
-
文章历史
- 收稿日期: 2018-01-03
2. 甘肃省教育厅, 教育考试院, 甘肃 兰州 730030
2. Education Examination Authority of Gansu Provincial Education Department, Lanzhou Gansu 730030, China
近年来,随着工业技术、全球定位技术、通信技术以及无线传感技术的不断发展,智能交通领域也有了很大进展,采用先进的技术我们可以获得大量的车辆轨迹数据。这些数据背后反映的本质就是我们所需要研究的内容。我们可以通过车辆轨迹数据分析车辆异常状态、交通事故重现等[1]。车辆轨迹重构可以全面、准确地再现城市路网交通的时空分布和交通流量的演化规律,从而提高例如速度、时间、排队等交通状态参数的估计预测精度和效率[2]。因此,对车辆轨迹数据缺失和异常进行重构对后期的数据处理具有重要的意义。
车辆轨迹重构的主要方法是插值法,已有一些研究提出了相关方法。文献[3]采用线性插值算法解决轨迹重构问题,但实际中车辆的运动轨迹很难保持直线;文献[4]通过单位四元数对曲线轨迹进行插值,但其计算比较复杂且只能针对特定曲线;文献[5]通过高次多项式对曲线轨迹进行插值,但高次多项式容易造成曲线波动且收敛性不好;文献[6]将三次多项式函数引入Hermite插值算法中来解决插值精度低的问题,但其需要斜率求解适应性差,因此很难应用于实际中。
在众多插值方法中,反距离权重因其插值原理易于理解、便于实现,且插值后能够保留原样点真值,从而得到了广泛的应用,但当分布点采集不均匀时,会严重影响插值精度。根据以上前人的研究成果,本研究提出了一种改进的反距离权重插值方法来解决车辆轨迹重构问题,引入自然邻近关系解决反距离权重插值方法对采样点要求苛刻的问题,通过对路网的重新构建得到新的车辆轨迹,有效地提高了轨迹重构的精度和速度,为基于车辆轨迹重构的相关研究提供了一定的基础。
1 车辆轨迹重构原理轨迹重构的原理是利用有效的插值算法与路网地图匹配相结合[7],对缺失或未知的轨迹段进行修复,从而恢复出完整的轨迹曲线。按插值点是否在已知的数据点内外可分为内插和外插,按具体的插值算法可以划分为线性插值法和非线性插值法。下面针对单个车辆的轨迹重构算法,对其重构的基本思想进行描述。
1.1 基本思想以时间-位置为例,假设有一条不完整的某车辆行驶轨迹,致使其不完整的原因是由于信号传输、故障等原因导致该车辆在[t1, t2]时间段内的轨迹数据丢失,其示意图如图 1所示。接下来,我们的工作就是寻找这些丢失的轨迹数据,轨迹重构的目的便是采用一定的插值方法对图中缺失的轨迹数据进行插补,最终使该车辆能够恢复完整的车辆运行路线轨迹。

|
| 图 1 车辆轨迹重构 Fig. 1 Vehicle trajectory reconstruction |
| |
假设车辆在[t1, t2]时间段内的速度和加速度值由于某种原因也存在丢失,此时,可采用局部多项式法对其进行拟合插值。假设车辆为周期性采样,采样周期为Δt。此时,选取t1前和t2后各k个已知的采样数据点,构造2k-1次多项式:

|
(1) |
式中,ai(i=0, 1, …, 2k-1)是待定系数; ti为缺失时间点。根据2k-1个数据点计算系数值,再计算缺失时间点的相应位置即可恢复车辆轨迹。当在时间段内的速度已知时,可得:

|
(2) |
式中,xp为需要求的位置;v(t)为已知的速度表达式; xl为i=l时的位置缺失值;tp为p时刻的缺失时间点。通过以上计算便可得出车辆缺失的轨迹数据点。
1.2 反距离权重插值方法反距离权重(inverse distance weighted, IDW)算法是1968年Shepare提出的基于Tobler定理提出的一种简单的插值方法[8]。其计算公式为[9]:

|
(3) |
式中,Z为待插值点要素估计值;Zi为控制点i的Z值;di为待插值点与第i个样本空间位置之间的欧式距离;n为估算中控制点数目;ρ为幂指数,一般为:ρ=2。
从式(3)中可以看出,反距离权重插值方法与待插值点及邻近范围内样本点之间的距离有关,其距离与待插值点的贡献度成反比[10]。当车辆轨迹数据点分布均匀时,该方法能够很好地实现轨迹重构。然而,在大多数情况下由于环境等因素的影响,车辆轨迹采样点分布不均,此时反距离权重插值方法就很难保证车辆轨迹重构的精度和速度。因此,针对此问题本研究提出了一种改进的反距离权重插值方法。
2 改进的反距离权重插值方法 2.1 基于3σ准则的粗差剔除方法车辆轨迹数据的获取途径主要是通过车载GPS装置,由于房屋、建筑物等的遮挡,势必会影响到车辆GPS数据的接收、更新实效性等问题。当车辆通过GPS等设备进行轨迹数据更新时,就会产生出一些测量值与其他测量值差异很大的情况,这种测量误差称为粗大误差。这些粗大误差对车辆轨迹的重构精度有很大的影响,且会导致重构后的车辆轨迹出现较大的偏差,因此,为避免这类问题的出现,在进行车辆轨迹重构前,必须要对一定的数据进行粗差剔除。考虑众多粗差剔除方法的优缺点,且3σ准则在各类数据处理中有较多的应用,已有较为成熟的实现方法,所以本研究采用基于3σ准则的粗差剔除方法。
其方法实现步骤为:
① 求出车辆轨迹数据的算术平均值


|
(4) |
式中N为车辆轨迹数据序列里包含的数据个数的数量。用算术平均值代表真值后计算得到的误差即为残余误差:

|
(5) |
根据Bessel公式可以得到标准偏差估计值为[11-12]:

|
(6) |
② 按照3σ准则剔除粗差值。
当某个轨迹数据残差满足|vi|≥3δ,此时便可以得出该数据含有粗大误差,应该剔除。
③ 将剔除含有粗大误差后的数据重新求
车辆轨迹粗差数据剔除具体算法流程图如图 2所示。

|
| 图 2 粗差剔除流程图 Fig. 2 Flowchart of gross error elimination |
| |
2.2 自适应反距离权重插值方法
通过以上分析,本研究针对传统的反距离权重插值方法提出一种改进的反距离权重插值方法-自适应反距离权重插值方法。自适应的反距离权重插值方法,通过建立自适应规则,自适应调整各子区域内的变化参数[13]。同时,在3σ准则剔除粗差的基础上通过对获取到的车辆轨迹数据构建初始Delaunay三角网(将车辆轨迹数据经过多次采集转换成网络形状),并采用逐点插值的方法得到局部调整后的新路网,并以待插点的一阶邻近点(剔除与插值点共点三角形的重复元素点)作为反距离权重插值参考点,使其自适应均匀地分布在待插值点的周围,然后进行反距离权重插值计算。其具体步骤如下:
步骤1:采用3σ准则对路网中车辆轨迹数据进行粗差剔除预处理。其处理流程如图 2所示。
步骤2:通过对预处理后的车辆轨迹数据点集合进行等距离划分建立初始Delaunay三角网(具有灵活方便、简单操作等优点,在此基础上,对于任何的插值点,只需要局部的更新和调整相应的三角网即可)。
步骤3:对初始路网逐点插值并与路网地图匹配相结合得到局部调整后的新路网。假设对原始车辆轨迹数据构建Delaunay三角网的插入点为p时,需要在已构建的网中一次遍历所有三角网,查找包含点p的三角形,并进行局部更新。本研究通过对每个网格中加入索引值来达到快速确定包含点p的三角形的目的。首先将路网划分成规格的单元格,如图 3所示,这样便可记录点p所在的单元格。通过以上分析进行查找插值点的自然邻近点作为参考点。

|
| 图 3 轨迹构建网格索引 Fig. 3 Trajectory construction grid index |
| |
步骤4:以待插点的一阶邻近点作为反距离权重插值参考点,使其自适应均匀地分布在待插值点周围。如图 4所示,中间点A的自然邻近点数目为8;中间点B的自然邻近点数目为9,不同的插值点,对应不同的参考点。

|
| 图 4 自适应选取自然邻近点 Fig. 4 Self-adaptive selection natural neighbors |
| |
步骤5:自适应选取自然邻近点后再进行反距离权重插值计算。由式(3)假设插值点p的坐标为(xp, yp),zp为需要估计的属性值,则邻域内的车辆轨迹点b为:

|
(7) |
式中,xi, yi为车辆轨迹坐标点;zi为观测值属性。且任何一点的属性值zp都为邻域内参考点的属性值加权平均得到[14-16]:

|
(8) |

|
(9) |
式中,λi为权重;r为权重系数,在实际插值中取r=2一般能得到较好效果[17]。整个方法的实现流程如图 5所示。

|
| 图 5 自适应反距离权重插值方法框图 Fig. 5 Block diagram of self-adaptive inverse distance weight interpolation method |
| |
自适应反距离权重插值方法通过逐点插值法局部调整得到新的车辆轨迹,以待插点的一阶邻近点作为反距离权重插值参考点。其具有以下优点:插值过程不需要指定参数点数目、具有自适应确定参考点的优点;一阶自然邻近点数避免了参考点过多,减少了计算量。
3 方法验证为验证本研究提出方法的优势,将传统的反距离权重插值方法与本研究提出的改进反距离权重插值方法进行对比,同时通过仿真数据和实际山东省淄博市的GPS数据验证,说明了本方法具有一定的应用价值。
3.1 基于仿真数据的实证分析首先,采用MATLAB仿真平台进行仿真,通过MATLAB产生类GPS数据作为车辆轨迹数据,其中,仿真时间为100 s;仿真距离为100 m;允许的最大仿真误差设置为10 m。图 6为车辆轨迹采样数据点的仿真结果,从图中可以看出轨迹数据点的分布存在较多粗差(GPS卫星数据点服从高斯分布)。

|
| 图 6 仿真车辆轨迹采样点 Fig. 6 Sampling points of simulation vehicle trajectory |
| |
图 7是本研究提出的3σ准则剔除粗差后的车辆轨迹点,从图中可以看出处理后的轨迹数据更加平滑。

|
| 图 7 预处理前后数据对比 Fig. 7 Comparison of data before and after preprocessing |
| |
通过MATLAB搭建反距离权重插值算法和改进的反距离权重插值算法,并将其应用于图 6的数据中,其结果如图 8和图 9所示,从图中可以看出改进的反距离权重插值效果明显优于反距离权重插值的效果。

|
| 图 8 反距离权重插值结果 Fig. 8 Result of inverse distance weight interpolation |
| |

|
| 图 9 改进的反距离权重插值结果 Fig. 9 Result of improved inverse distance weight interpolation |
| |
3.2 基于实际GPS数据的实证分析
为了进一步说明本研究提出方法的有效性,本研究在共同依托项目的课题交通时空数据可视化平台的基础上进行验证[18],将上节验证过的算法结合山东省淄博市出租车GPS轨迹数据与当地路网地图匹配为基础进行基于实际GPS数据的仿真,如图 10所示,为车辆轨迹数据点分布情况。

|
| 图 10 山东省淄博市出租车GPS轨迹数据 Fig. 10 Taxi GPS trajectory data of Zibo City, Shandong Province |
| |
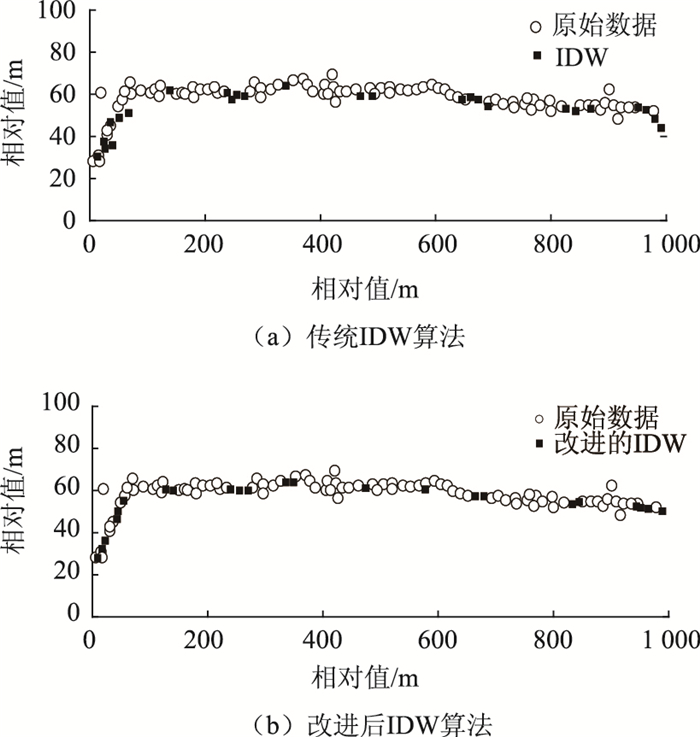
其中,选取主干道出租车的轨迹数据作为MATLAB仿真的数据来源,其中图 11为传统IDW算法和本研究提出的改进后IDW算法的计算结果对比图。从图中可以看出改进后的IDW算法在数据缺失处的插值效果更加接近真实的路线轨迹。
|
| 图 11 处理结果 Fig. 11 Process result |
| |
为了说明本研究提出方法的优越性,根据以上实际GPS数据,分别采用三次样条插值法、拉格朗日插值法、Hermite插值法以及IDW和本研究提出的改进的IDW对比,其处理后的误差结果如表 1所示。
| 插值重构方法 | 误差 |
| 三次样条插值 | 0.065 2 |
| 拉格朗日插值 | 0.084 5 |
| Hermite插值 | 0.058 6 |
| 反距离权重插值 | 0.040 2 |
| 改进的反距离权重插值 | 0.024 1 |
4 结论
针对传统的反距离权重插值方法存在的不足,本研究结合3σ准则方法和自然邻近关系,将其应用于反距离权重插值方法中,提出改进的IDW方法,最后通过MATLAB仿真、交通时空数据可视化平台的验证、真实车辆轨迹数据与路网地图匹配相结合验证了本研究提出的方法在插值精度方面明显优于传统的IDW方法,为未来车辆轨迹重构方法的研究提供一定的参考价值。今后的工作将着重以交通时空数据可视化平台上的动态插值及可视化方法为主要研究目标。
| [1] |
NAKAYAMA S. Lane Image Processing System for Vehicle: US5790403[P]. 1998-08-04.
|
| [2] |
JENELIUS E, KOUTSOPOULOS H N. Travel Time Estimation for Urban Road Networks Using Low Frequency Probe Vehicle Data[J]. Transportation Research Part B:Methodological, 2013, 53(4): 64-81. |
| [3] |
FRENTZOS E, GRATSIAS K, PELEKIS N, et al. Algorithms for Nearest Neighbor Search on Moving Object Trajectories[J]. Geoinformatica, 2007, 11(2): 159-193. |
| [4] |
XING Y, XU R, TAN J, et al. A Class of Generalized B-spline Quaternion Curves[J]. Applied Mathematics and Computation, 2015, 271: 288-300. |
| [5] |
BOGORNY V, RENSO C, AQUINO A R, et al. Constant:A Conceptual Data Model for Semantic Trajectories of Moving Objects[J]. Transactions in GIS, 2014, 18(1): 66-88. |
| [6] |
陈志军, 吴超仲, 吕能超, 等. 基于改进三次Hermite插值的车辆时空轨迹重构研究[J]. 交通信息与安全, 2013, 31(6): 43-46. CHEN Zhi-jun, WU Chao-zhong, LÜ Neng-chao, et al. Vehicle Trajectory Reconstruction Based on Improved Cubic Hermite Interpolation[J]. Journal of Transport Information and Safety, 2013, 31(6): 43-46. |
| [7] |
张健钦, 李明轩, 段颖超, 等. 一种改进的快速浮动车地图匹配方法[J]. 测绘通报, 2017(1): 87-92. ZHANG Jian-qin, LI Ming-xuan, DUAN Ying-chao, et al. An Improved Algorithm for Fast Map-matching of Floating Car[J]. Bulletin of Surveying and Mapping, 2017(1): 87-92. |
| [8] |
SHEPARD D. Geography and the Properties of Surfaces. A Two-dimensional Interpolation Function for Computer Mapping of Irregularly Spaced Data[C]//ACM'68 Proceedings of the 196823rd ACM National Conference. New York: ACM, 1968.
|
| [9] |
孔龙星, 汤晓安, 张俊达, 等. 顾及局部特性的自适应3D矢量场反距离权重插值法[J]. 系统工程与电子技术, 2016, 38(7): 1697-1702. KONG Long-Xing, TANG Xiao-an, ZHANG Jun-da, et al. Adaptive IDW Interpolation Method Involving Local Behavior for 3D Vector Field[J]. Systems Engineering and Electronics, 2016, 38(7): 1697-1702. |
| [10] |
DE MESNARD L. Pollution Models and Inverse Distance Weighting:Some Critical Remarks[J]. Computers & Geosciences, 2013, 52(1): 459-469. |
| [11] |
LI Y, WANG W, YA L, et al. Study of an Atomic Clock Steering Method Based on Least Square[C]//Frequency Control Symposium (FCS), 2014 IEEE International. Taipei: IEEE, 2014: 1-4.
|
| [12] |
MARTINI A, COCO D, SORCE A, et al. Gross Error Detection Based on Serial Elimination: Applications to an Industrial Gas Turbine[C]//ASME Turbo Expo 2014: Turbine Technical Conference and Exposition. Dusseldorf: American Society of Mechanical Engineers, 2014.
|
| [13] |
高鹏, 石为人, 周伟, 等. 基于图论模糊聚类的室内自适应RSSI定位算法[J]. 仪器仪表学报, 2013, 34(9): 1998-2004. GAO Peng, SHI Wei-ren, ZHOU Wei, et al. Indoor Adaptive RSSI Localization Algorithm Based on Graph Theory and Fuzzy Clustering in Wireless Sensor Networks[J]. Chinese Journal of Scientific Instrument, 2013, 34(9): 1998-2004. |
| [14] |
PIAH A R M, SAABAN A, ABD M A. Range Restricted Positivity-preserving Scattered Data Interpolation[J]. Journal of Fundamental and Applied Sciences, 2014, 2(1/2): 63-75. |
| [15] |
CUOMO S, GALLETTI A, GIUNTA G, et al. A Novel Triangle-based Method for Scattered Data Interpolation[J]. Applied Mathematical Sciences, 2014, 8(134): 6717-6724. |
| [16] |
PENG J, YU Y, ZHOU W, et al. Using Triangle-based Cubic Interpolation in Generation of Object-adaptive Fringe Pattern[J]. Optics and Lasers in Engineering, 2014, 52(1): 41-52. |
| [17] |
DECLERCQ F A N. Interpolation Methods for Scattered Sample Data:Accuracy, Spatial Patterns, Processing Time[J]. Cartography and Geographic Information Systems, 2006, 23(3): 128-144. |
| [18] |
张金秋, 赵庶旭, 屈睿涛. 基于点与热度的交通时空数据可视化[J]. 兰州交通大学学报, 2017, 36(3): 63-69, 75. ZHANG Jin-qiu, ZHAO Shu-xu, QU Rui-tao. Visualization of Traffic Spatio-Temporal Data Based on Point and Heatmap[J]. Journal of Lanzhou Jiaotong University, 2017, 36(3): 63-69, 75. |
 2018, Vol. 35
2018, Vol. 35
