2. 河南省自然资源科技创新中心(信息感知技术应用研究), 河南 郑州 450000
2. Henan Science and Technology Innovation Center of Natural Resources (Application Research of Information Perception Technology), Zhengzhou 450000, China
地质灾害易发性评价是在对以往地质灾害调查基础上,通过对其发育的地质环境条件分析和判断,总结有利于地质灾害发育的地质环境条件组合,推断相同条件下地质灾害发育的可能性 [1],为防灾减灾工作提供目标靶区. 常用的地质灾害易发性评价方法可分为定性评价、定量评价两种,具体包括专家打分法、层次分析法、信息量法、证据权法、确定性系数法、支持向量机、决策树、神经网络等. 这些方法经广泛应用和验证,取得了很好的效果 [2-4]. 但各方法均存在一定的缺陷,如人为因素影响大、无法比较不同指标间的相对重要性、偏离实际等. 而多方法、多模型的相互耦合,由于能相互验证、相互补充且评价精度和合理性更高,在近年来被广泛应用 [5-10].
传统确定性系数(Certainty Factor,CF)模型 [11]能客观反映指标内部不同分级对地质灾害易发性的影响值,解决多源数据类型的合并问题,但是忽略了不同指标间的差异性;而逻辑回归(Logistic Regression,LR)模型基于对大量数据的统计分析,能够较为精确地反映指标间的相对权重. 两种方法结合使用 [12],即CF-LR模型,由传统确定性系数模型提供地质灾害与评价指标关系的数据,经逻辑回归计算得到指标相对权重,能够大大提高评价的精度和合理性.
信阳市地质灾害数量多年保持在250~350处,尤其是南部山区的县区,地质灾害密度达3~6处/100 km2,是地质灾害多发市,地质灾害防治任务艰巨. 本研究通过以往地质灾害资料收集和分析,选取研究区内地质灾害影响指标,构建评价指标体系,基于ArcGIS平台,采用CF-LR模型,对地质灾害易发性进行评价,以期为信阳市防灾减灾、国土空间规划等工作提供参考.
1 研究区概况信阳市位于河南省东南部,豫皖鄂三省交界,地处中国地理南北分界线、气候分界线. 整体地势西南高、东北低,海拔高度19~1 570 m. 气候温暖湿润,年均气温6~15 ℃,年均降雨量1 000~1 400 mm. 受大别山造山运动和淮河冲积共同作用,地貌类型自南向北依次为低山、丘陵、岗地和平原,岩性由南部的混合岩、花岗岩,逐渐向北变化为泥岩、砂岩和第四系冲洪积层. 复杂的造山运动对区内岩土体挤压、抬升和错断,形成网格状构造格局,龟梅断裂、桐商断裂和定远-八里贩断裂等区域断层纵贯全区. 区内地质灾害主要为崩塌、滑坡,多受降雨诱发失稳.
2 研究方法 2.1 确定性系数模型确定性系数模型(CF)以确定性系数来表征地质灾害发育的可能性,主要通过衡量现状条件下地质灾害发育情况确定 [13]. 通过式(1)可以获得无量纲的CF值,其以比值形式将不同地质环境条件统一. 通常CF取值为[-1, 1],值越大表示地质灾害发生的确定性越大.
| $ C_{\mathrm{F}}= \begin{cases}\frac{P_{\mathrm{a}}-P_{\mathrm{s}}}{P_{\mathrm{a}}\left(1-P_{\mathrm{s}}\right)}, & P_{\mathrm{a}} \geqslant P_{\mathrm{s}} \\ \frac{P_{\mathrm{a}}-P_{\mathrm{s}}}{P_{\mathrm{s}}\left(1-P_{\mathrm{a}}\right)}, & P_{\mathrm{a}}<P_{\mathrm{s}}\end{cases} $ | (1) |
式中,CF-确定性系数,地质灾害发育的概率;Pa-地质灾害在地质环境条件a中发生的概率,通常用地质环境条件a中的地灾数量与地质环境条件a总面积的比值表示,其取值范围为[0, 1];Ps-地质灾害发育的概率,通常用地质灾害总数与研究区面积比值表示,同一研究区内为定值.
2.2 逻辑回归模型逻辑回归模型(LR)是探索众多数据特征关系的一种常用的统计方法,计算公式见式(2). 在地质灾害易发性评价中,地质灾害是否发生为因变量(0为否,1为是),各地质环境条件为自变量,通过自变量与因变量之间关系分析,得到不同自变量组合下的地质灾害发生概率.
| $ \left\{\begin{array}{l} Y=\beta_0+\beta_1 x_1+\beta_2 x_2+\cdots+\beta_n x_n \\ P=\frac{1}{1+\mathrm{e}^{-Y}} \end{array}\right. $ | (2) |
式中,P-地质灾害发生的概率;Y-地质灾害与地质环境条件的关系方程;β1,…,βn-逻辑回归系数,为各地质环境条件对地质灾害的作用强度;β0-常数,表示在不受任何因素影响条件下,地质灾害发生与不发生概率之比的对数值 [14];x1,x2,…,xn-各地质环境条件对应的CF值.
3 数据来源和评价指标 3.1 数据来源信阳市地质灾害数据主要来自2012~2021年各县区统计和公布的2022年地质灾害隐患点核查数据,共收集933处地质灾害点(见图 1),其中崩塌、滑坡地质灾害点914处,占比98%,其他为泥石流和地面塌陷. 由于泥石流和地面塌陷地质灾害占比小,且发育分布受单个因素控制明显,本次研究选取914处崩塌、滑坡作为研究对象.
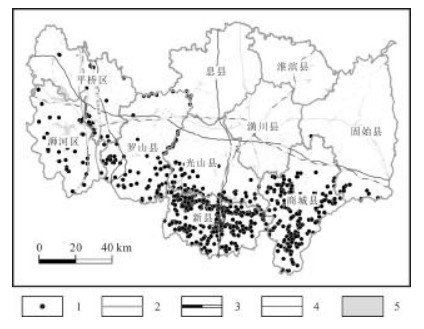
|
图 1 信阳市地质灾害分布图 Fig.1 Distribution map of geohazards in Xinyang City 1-地灾点(geohazard site);2-县区界线(boundary of county);3-铁路(railway);4-公路(highway);5-水库(reservoir) |
研究采用DEM数据为地理空间数据云平台获取的ASTER GDEM数据,夜间灯光数据源为2021年NPP/VIIRS年均夜光遥感数据,植被数据为Landsat8影像波段叠加计算得到的归一化植被指数(Normalized Differential Vegetation Index,NDVI),地质数据源为1 : 20万地质图.
3.2 评价指标的选择与分级影响地质灾害发育分布的因素十分复杂 [15],各因素的作用方式、强度在不同区域存在差异. 通过对研究区资料分析,选择坡度、坡向、地形曲率、到水系距离、到断层距离、夜间灯光指数和NDVI共7项指标进行地质灾害易发性评价. 地质灾害点在各指标图层中的分布见图 2-8.
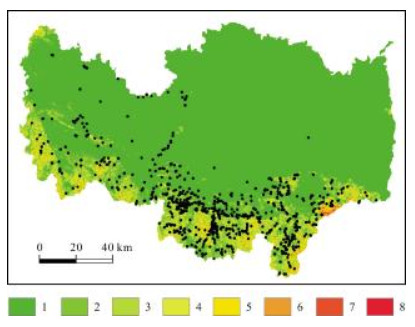
|
图 2 地质灾害点在坡度图层中的分布 Fig.2 Distribution of geohazard sites by slope gradient 1~8:≤5;5~10;10~15;15~20;20~25;25~30;30~35;>35 |
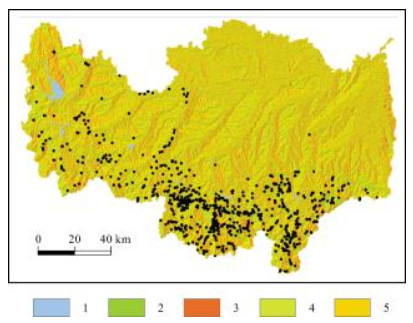
|
图 3 地质灾害点在坡向图层中的分布 Fig.3 Distribution of geohazard sites by slope aspect 1-平地、水域(flat ground,water area);2-北(northward);3-南(southward);4-东(eastward);5-西(westward) |
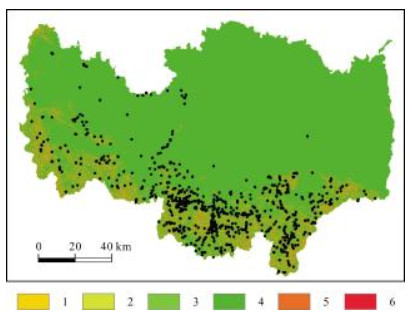
|
图 4 地质灾害点在地形曲率图层中的分布 Fig.4 Distribution of geohazard sites by terrain curvature 1~6:≤-0.5;-0.5~-0.2;-0.2~ -0.05;-0.05~ +0.05;0.05~0.2;>0.2 |
|
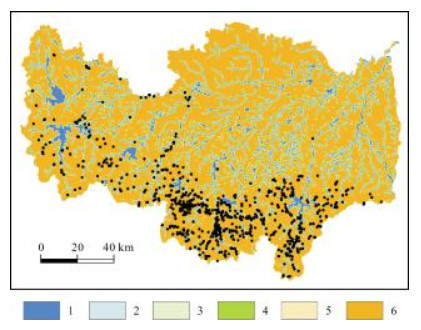
图 5 地质灾害点在到水系距离图层中的分布 Fig.5 Distribution of geohazard sites by distance to water system 1~6:≤100;100~200;200~300;300~400;400~500;>500 m |
|
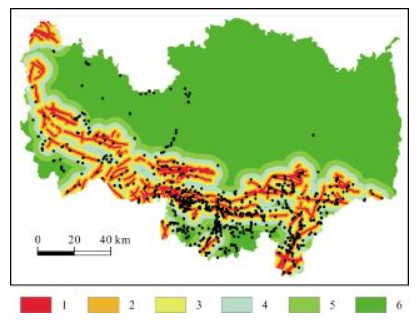
图 6 地质灾害点在到断层距离图层中的分布 Fig.6 Distribution of geohazard sites by distance to faults 1~6:≤0.5;0.5~1.5;1.5~3;3~5;5~8;>8 km |
|
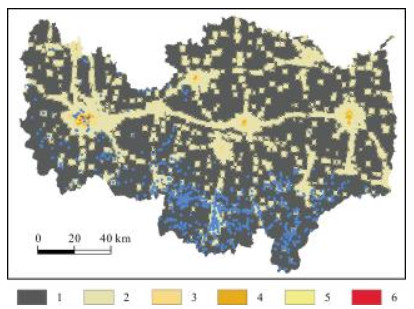
图 7 地质灾害点在夜间灯光指数图层中的分布 Fig.7 Distribution of geohazard sites by nighttime light index 1~6:0;0~10;10~20;20~30;30~40;>40 |
|
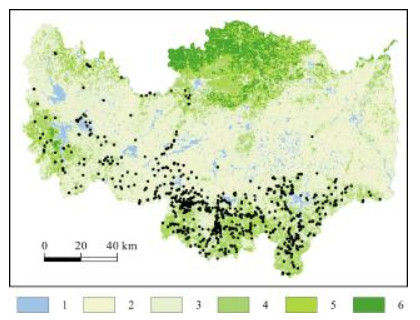
图 8 地质灾害点在NDVI图层中的分布 Fig.8 Distribution of geohazard sites by NDVI 1~6:≤-0.1;-0.1~0;0~0.1;0.1~0.2;0.2~0.3;>0.3 |
坡度:斜坡岩土体是在各种力相互作用下保持平衡的,其中坡度的大小直接影响重力沿斜坡向下的分力,是影响斜坡稳定性的重要因素. 坡度的大小还决定地质灾害发生的类型和破坏机制. 通过ArcGIS中坡度工具,基于DEM,提取得到地形坡度数据,并分类成8级:≤5°,5~10°,10~15°,15~20°,20~25°,25~30°,30~35°,>35°(图 2).
坡向:不同坡向在接受阳光照射、降雨等方面存在差异,从而间接影响植被覆盖、风化速率和人口分布等,进而影响地质灾害的发育分布. 通常在相同岩土体条件下,阳坡面接受了较多的阳光照射和降雨,岩石风化速率更快,坡表松散的覆盖层更厚,人类对地质环境条件的改造也更多. 将坡向数据分成东、西、南、北和平地共5个方向(图 3).
地形曲率:斜坡剖面形态影响了岩土体内的应力分布,凸型坡在坡体前缘形成应力集中,更容易发生失稳. 地形曲率是斜坡剖面形态的定量度量指标,正值表示凸型坡,负值表示凹型坡,曲率越接近0表示坡面越平坦. 研究区地形曲率为-0.84~0.45,将其分成6级:<-0.5,-0.5~ -0.2,-0.2~ -0.05,-0.05~+0.05,0.05~0.2,>0.2 (图 4).
到水系距离:河流对地质灾害的影响主要在于水流对河道两侧岸坡的侵蚀作用,不断增加的岸坡高度和坡度,为岩土体失稳提供了临空条件. 区内水系主要为淮河二级及以下支流,结合现场实际,将河流影响划分成6级:<100 m,100~200 m,200~300 m,300~400 m,400~500 m,>500 m (图 5).
到断层距离:断层破坏岩土体的完整性,控制地质灾害边缘,为雨水入渗提供通道. 一般到断层距离越近,岩土体结构面越发育,结构越破碎,地质灾害发育也越集中. 选择1 km间隔作断层缓冲区,研究区共分为6级:<0.5 km,0.5~1.5 km,1.5~3 km,3~5 km,5~8 km,>8 km (图 6).
夜间灯光指数:为人类活动的一种有效表征形势,对国民生产总值、人口数量有一定的指示意义. 研究区夜间灯光指数分布相对集中,其中大值主要分布在市区、县城、经济活跃乡镇以及重要道路周边,其余位置夜间灯光指数为小值. 将夜间灯光指数划分成6级:0,0~10,10~20,10~30,30~40,>40 (图 7).
NDVI:植被能减少雨水冲刷,减缓水流入渗,对自然斜坡具有一定保护作用,但植被的自重加载和根劈作用又破坏着坡体的稳定性. 研究区NDVI值在-0.56~+0.79之间,将其分成6级:水域(<-0.1)、裸地(-0.1~0)、荒地(0~0.1)、草地(0.1~0.2)、林地(0.2~0.3,>0.3)(图 8).
4 地质灾害易发性评价为保证各评价指标栅格单元的一致性,首先需要对各评价指标图层进行统一. 各评价指标图层按照100 m×100 m进行重采样,共计1 892 722个栅格单元.
4.1 计算评价指标的CF值根据914处地质灾害点在各指标分类级别中的分布数量和对应面积,利用CF模型,得到各分类级别对应的CF值,结果见表 1.
|
|
表 1 各评价指标确定性系数CF计算结果表 Table 1 Deterministic coefficient calculation results of each evaluation factor |
相关性过大的指标可导致计算结果偏离实际,为保证计算结果的合理性,需要对指标的独立性进行检验. 采用相关性分析法对7个指标的独立性进行检验,在SPSS 19.0中得到相关系数矩阵(见表 2). 表 2中x1、x2、x3、x4、x5、x6、x7分别代表坡度、坡向、地形曲率、到水系距离、到断层距离、夜间灯光指数、NDVI.
|
|
表 2 评价指标间的相关性系数矩阵 Table 2 Correlation coefficient matrix of evaluation indexes |
结果显示:评价指标之间的相关性系数绝对值最大为0.177,小于0.3,表明所选取的因子之间的相关性小,7个指标全部可纳入分析.
4.3 计算评价指标的权重采用LR模型计算回归系数,首先需要选择训练样本,确定训练样本集. 样本选择的合理与否直接影响计算结果的准确性. 本次计算采用随机选取的方式确定,其中地质灾害点随机选取总数的80%左右,非地质灾害点在地质灾害点200 m缓冲区以外的区域内随机生成. 共选取714处地质灾害点和714处非地质灾害点,形成包含1 428点的训练集. 通过点提取,确定各样本对应的评价指标分类,并替换成各CF值. 将CF值作为自变量,是否发生地质灾害作为因变量(0为否,1为是),导入SPSS软件进行逻辑回归,计算结果见表 3. 由结果可知,评价指标的显著性均小于0.05,回归系数有效,具有统计意义. 回归系数均为正数表示所有评价指标对模型均起正向作用.
|
|
表 3 逻辑回归结果汇总表 Table 3 Results of logistic regression |
将计算得到的各指标回归系数代入LR模型,可得逻辑回归方程,见式(3).
| $ \left\{\begin{aligned} Y= & -0.176+0.975 x_1+1.333 x_2+0.719 x_3+1.971 x_4 \\ & +1.759 x_5+1.253 x_6+0.847 x_7 \\ P= & \frac{1}{1+\mathrm{e}^{-Y}} \end{aligned}\right. $ | (3) |
式中:P-地质灾害发生的概率,值为[0, 1];x1、x2、x3、x4、x5、x6、x7-坡度、坡向、地形曲率、到水系距离、到断层距离、夜间灯光指数、NDVI各分类等级的CF值.
利用ArcGIS中栅格计算器将各指标图层的栅格值赋为对应的CF,通过加权叠加计算,得到栅格单元的地质灾害发生的概率P.
由计算可知,研究区发生地质灾害的概率P位于0.0043~0.9753之间.
5 评价结果及检验对得到的概率P栅格图按照等间距法确定地质灾害易发程度等级(见图 9),共分成4类:低易发区(<0.25)、中易发区(0.25~0. 5)、高易发区(0.5~0.75)、极高易发区(>0.75). 其面积及占比分别为10 337.73 km2(54.90%)、2 674.38 km2(14.20%)、3 673.03 km2 (19.51%)和2 145.30 km2 (11.39%).
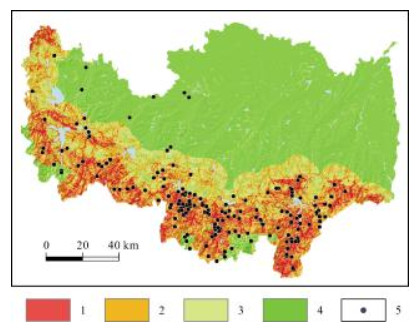
|
图 9 地质灾害易发程度区划与检验样本分布 Fig.9 Susceptibility zoning and distribution of geohazard test samples 1-极高易发区(extremely high-risk area);2-高易发区(high-risk area);3-中易发区(medium-risk area);4-低易发区(low-risk area);5-地灾点(geohazard site) |
从易发程度分区结果可知:信阳市地质灾害易发程度以低为主,分布在东北部,主要为淮河冲积平原,地势较为平坦,地层岩性为冲洪积粉土、粉砂,构造不发育;其次为中-高易发区,合计占比33.71%,分布在中部,呈带状展布,为丘陵地貌区;极高易发区主要分布在南部、西北部,沟道深切,地势起伏较大,岩性复杂多变,构造发育.
评价结果是否有效,通常进行两个方面的检验,即合理性检验和准确性检验.
5.1 合理性检验为保持评价模型的稳定性,减少检验样本选择中的人为影响,本研究选取未参与逻辑回归计算的200处地质灾害点进行合理性检验. 由检验结果(表 4)可知,随着地质灾害易发等级的提高,地质灾害在数量、密度上均呈增多的趋势,占总面积30.9%的极高、高易发区,分布了77.5%的检验点地质灾害,说明易发程度越高,越易发育地质灾害,区划结果是合理的.
|
|
表 4 地质灾害易发性评价合理性检验统计表 Table 4 Rationality test results of geohazard susceptibility evaluation |
ROC曲线 [16]是一种不受临界约束的结果评价方法,能有效地对评价结果的准确性进行检验 [17]. 其以假阳性率(未发生地质灾害的单元被正确预测的比例) 为横坐标,真阳性率(发生地质灾害的单元被正确预测的比例)为纵坐标绘制的曲线,用于描述敏感性和特异性之间的关系. 曲线下的面积为AUC (Area Under Curve)值,是衡量模型准确性指标 [18],取值区间为[0.5,1],值越大表示模型准确性越好.
将914处地质灾害点和714处随机生成的非地质灾害点全部作为样本,通过SPSS 19.0进行ROC曲线分析(图 10). 结果显示,本次评价AUC值为0.828,易发性评价结果准确性较高,表明CF-LR模型可以较为准确地对信阳市的地质灾害易发程度进行评价.
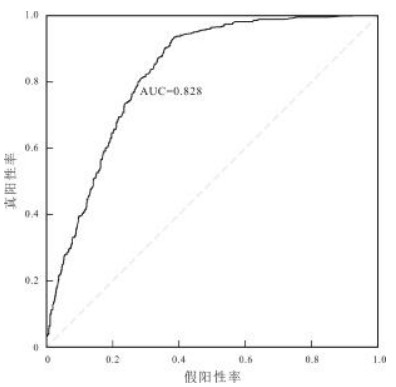
|
图 10 评价模型ROC曲线 Fig.10 ROC curve of evaluation model |
1) 在诸多前人研究中,指标体系的构建均根据经验人为选定,带有一定的主观性 [19]. 本研究在指标选取时,断层、岩性、高程等相关性较大,进行了取舍,存在一定的片面性.
2) 对地质灾害评价目前趋于风险评价,是在易发性、危险性、易损性基础上开展的 [20],将地质灾害发生概率、承载对象易损程度综合考虑,更客观、合理. 研究区的风险性将在其他论文中进行阐述.
7 结论1) 信阳市地质灾害易发性影响大小依次是:到水系距离>到断层距离>坡向>夜间灯光指数>坡度>NDVI>地形曲率.
2) 信阳市地质灾害易发性以低易发为主,面积10 337.73 km2,占比54.90%,主要分布在东北部淮河冲积平原区,地形起伏较小;极高易发区面积2 145.30 km2,占比11.39%,主要分布在南部、西北部,地势起伏较大,岩性复杂多变,结构破碎. 中-高易发区分布在中部,带状分布.
3) 将逻辑回归模型进行合理性检验,地质灾害易发程度越高,地质灾害分布则越多,评价结果较为合理. 用ROC曲线对模型的准确性进行检验,其AUC值为0.828,精度较高,说明CF-LR模型能够较为客观准确地对信阳市地质灾害进行评价.
| [1] |
田春山, 刘希林, 汪佳. 基于CF和Logistic回归模型的广东省地质灾害易发性评价[J]. 水文地质工程地质, 2016, 43(6): 154-161, 170. Tian C S, Liu X L, Wang J. Geohazard susceptibility assessment based on CF model and Logistic Regression models in Guangdong[J]. Hydrogeology & Engineering Geology, 2016, 43(6): 154-161, 170. |
| [2] |
吴常润, 赵冬梅, 刘澄静, 等. 基于GIS和信息量模型的陇川县滑坡易发性评价[J]. 西北地质, 2020, 53(2): 308-320. Wu C R, Zhao D M, Liu C J, et al. Landslide susceptibility assessment of Longchuan County based on GIS and information value model[J]. Northwestern Geology, 2020, 53(2): 308-320. |
| [3] |
王雷, 吴君平, 赵冰雪, 等. 基于GIS和信息量模型的安徽池州地质灾害易发性评价[J]. 中国地质灾害与防治学报, 2020, 31(3): 96-103. Wang L, Wu J P, Zhao B X, et al. Susceptibility assessment of geohazards in Chizhou City of Anhui Province based on GIS and informative model[J]. The Chinese Journal of Geological Hazard and Control, 2020, 31(3): 96-103. |
| [4] |
许冲, 戴福初, 姚鑫, 等. 基于GIS与确定性系数分析方法的汶川地震滑坡易发性评价[J]. 工程地质学报, 2010, 18(1): 15-26. Xu C, Dai F C, Yao X, et al. GIS platform and certainty factor analysis method based Wenchuan earthquake-induced landslide susceptibility evaluation[J]. Journal of Engineering Geology, 2010, 18(1): 15-26. DOI:10.3969/j.issn.1004-9665.2010.01.003 |
| [5] |
周天伦, 曾超, 范晨, 等. 基于快速聚类-信息量模型的汶川及周边两县滑坡易发性评价[J]. 中国地质灾害与防治学报, 2021, 32(5): 137-150. Zhou T L, Zeng C, Fan C, et al. Landslide susceptibility assessment based on K-means cluster information model in Wenchuan and two neighboring counties, China[J]. The Chinese Journal of Geological Hazard and Control, 2021, 32(5): 137-150. |
| [6] |
杨光, 徐佩华, 曹琛, 等. 基于确定性系数组合模型的区域滑坡敏感性评价[J]. 工程地质学报, 2019, 27(5): 1153-1163. Yang G, Xu P H, Cao C, et al. Assessment of regional landslide susceptibility based on combined model of certainty factor method[J]. Journal of Engineering Geology, 2019, 27(5): 1153-1163. |
| [7] |
付树林, 梁丽萍, 刘延国. 基于CF-Logistic模型的雅砻江新龙段地质灾害易发性评价[J]. 水土保持研究, 2021, 28(4): 404-410. Fu S L, Liang L P, Liu Y G. Assessment on geohazard susceptibility in Xinlong section of Yalong River based on CF-logistic model[J]. Research of Soil and Water Conservation, 2021, 28(4): 404-410. |
| [8] |
张钟远, 邓明国, 徐世光, 等. 镇康县滑坡易发性评价模型对比研究[J]. 岩石力学与工程学报, 2022, 41(1): 157-171. Zhang Z Y, Deng M G, Xu S G, et al. Comparison of landslide susceptibility assessment models in Zhenkang County, Yunnan Province, China[J]. Chinese Journal of Rock Mechanics and Engineering, 2022, 41(1): 157-171. |
| [9] |
武雪玲, 杨经宇, 牛瑞卿. 一种结合SMOTE和卷积神经网络的滑坡易发性评价方法[J]. 武汉大学学报(信息科学版), 2020, 45(8): 1223-1232. Wu X L, Yang J Y, Niu R Q. A landslide susceptibility assessment method using SMOTE and convolutional neural network[J]. Geomatics and Information Science of Wuhan University, 2020, 45(8): 1223-1232. |
| [10] |
朱进守, 邓辉, 苑泉, 等. 藏东高山峡谷地带地质灾害危险性评价——以西藏贡觉县为例[J]. 地质与资源, 2018, 27(3): 272-278. Zhu J S, Deng H, Yuan Q, et al. Risk assessment on the geohazards in alpine and gorge region of Eastern Tibet: A case study of Gonjo County[J]. Geology and Resources, 2018, 27(3): 272-278. DOI:10.3969/j.issn.1671-1947.2018.03.010 |
| [11] |
张玘恺, 凌斯祥, 李晓宁, 等. 九寨沟县滑坡灾害易发性快速评估模型对比研究[J]. 岩石力学与工程学报, 2020, 39(8): 1595-1610. Zhang Q K, Ling S X, Li X N, et al. Comparison of landslide susceptibility mapping rapid assessment models in Jiuzhaigou County, Sichuan Province, China[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(8): 1595-1610. |
| [12] |
覃乙根, 杨根兰, 江兴元, 等. 基于确定性系数模型与逻辑回归模型耦合的地质灾害易发性评价——以贵州省开阳县为例[J]. 科学技术与工程, 2020, 20(1): 96-103. Qin Y G, Yang G L, Jiang X Y, et al. Geohazard susceptibility assessment based on integrated certainty factor model and logistic regression model for Kaiyang, China[J]. Science Technology and Engineering, 2020, 20(1): 96-103. |
| [13] |
Shortliffe E H, Buchanan B G. A model of inexact reasoning in medicine[J]. Mathematical Biosciences, 1975, 23(3/4): 351-379. |
| [14] |
王进, 郭靖, 王卫东, 等. 权重线性组合与逻辑回归模型在滑坡易发性区划中的应用与比较[J]. 中南大学学报(自然科学版), 2012, 43(5): 1932-1939. Wang J, Guo J, Wang W D, et al. Application and comparison of weighted linear combination model and logistic regression model in landslide susceptibility mapping[J]. Journal of Central South University (Science and Technology), 2012, 43(5): 1932-1939. |
| [15] |
刘振辉. 天津市蓟县山区突发性地质灾害特征及其形成机理研究[D]. 北京: 中国地质大学, 2014. Liu Z H. Research on characteristics and formation mechanism of sudden geological disasters in Tianiin Jixian mountain area[D]. Beijing: China University of Geosciences, 2014. |
| [16] |
秦红富, 谈树成, 施旖奇, 等. 基于CF-LR组合模型的地质灾害易发性评价——以云南省宁洱哈尼族彝族自治县为例[J]. 人民长江, 2022, 53(7): 119-127. Qin H F, Tan S C, Shi Y Q, et al. Geological hazard susceptibility assessment based on CF&LR combined model: Case of Ning'er Hani and Yi Autonomous County, Yunnan Province[J]. Yangtze River, 2022, 53(7): 119-127. |
| [17] |
罗路广, 裴向军, 黄润秋, 等. GIS支持下CF与Logistic回归模型耦合的九寨沟景区滑坡易发性评价[J]. 工程地质学报, 2021, 29(2): 526-535. Luo L G, Pei X J, Huang R Q, et al. Landslide susceptibility assessment in Jiuzhaigou scenic area with GIS based on certainty factor and logistic regression model[J]. Journal of Engineering Geology, 2021, 29(2): 526-535. |
| [18] |
屠水云, 张钟远, 付弘流, 等. 基于CF与CF-LR模型的地质灾害易发性评价[J]. 中国地质灾害与防治学报, 2022, 33(2): 96-104. Tu S Y, Zhang Z Y, Fu H L, et al. Geological hazard susceptibility evaluation based on CF and CF-LR model[J]. The Chinese Journal of Geological Hazard and Control, 2022, 33(2): 96-104. |
| [19] |
黄敬军, 甘义群, 缪世贤, 等. 江苏省地质环境区划评价指标体系初步研究[J]. 中国地质, 2011, 38(6): 1599-1606. Huang J J, Gan Y Q, Miao S X, et al. A preliminary study of the evaluation index system for geo-environment regionalization in Jiangsu[J]. Geology in China, 2011, 38(6): 1599-1606. |
| [20] |
郭邦梅, 权开兄. 基于ArcGIS的青海隆务河流域灾害风险性评价[J]. 地质与资源, 2019, 28(3): 289-292. Guo B M, Quan K X. ArcGIS-based disaster risk assessment of Longwu river basin in Qinghai Province[J]. Geology and Resources, 2019, 28(3): 289-292. |
 2024, Vol. 33
2024, Vol. 33

