地-井瞬变电磁(TEM)法是井中瞬变电磁法中应用最广的一种装置形式, 其发送回线通常采用铺设于地面的边长由几百米到1000 m以上的矩形单匝绝缘不接地大回线, 供以脉冲电流产生激发电磁场, 切断场源后通过布设于钻孔中的探头接收地层中导电地质体由一次场激发而感应产生的二次场(轴向分量), 并研究分析二次场特征获取关于目标体的有用信息[1-3].
地-井TEM装置下, 作用于局部导体的一次场可近似看作指向某个方面的均匀场. 在其激励下, 局部导体中产生感应涡流. 一次场消失后, 涡流于早期分布于局部导体表面, 后因欧姆损耗逐渐衰变(中期), 最终分布状况处于稳定且按指数规律衰减(晚期)[1-5].
通过对局部导体的井中TEM响应进行数值及物理模拟研究, 总结模型参数的特征关系曲线, 可为实际工作中的定性、定量解释提供依据和理论基础. 这方面前人做了大量相关研究工作, 对简单形体(如球体、圆柱体等)TEM响应问题进行了详细阐述; 关于薄板状导体井中TEM响应的模拟计算, 加拿大多伦多大学Lamontagne等[1-2]采用求解薄板状体内本征电流场编制了计算程序模拟单板体响应, 此后研究人员在工作中采用了"本征电流"等模型(如澳大利亚Maxwell4. 0中TEMH程序, 设置若干个互不影响的本征电流环来等效薄板体的涡流)模拟计算板状导体下钻井中3个分量的正演; 此外, "等效涡流"模型利用位于薄板体中心部位的单个方形等效涡流环来模拟晚期TEM响应; 在研究走向较长的板状体时可用一对平行的无限长反向线电流进行等效. 资料解释方面, Eaton等[6]和West等[7]研究了导电围岩对二维、三维导体井中TEM响应的影响; Macnae等[8]阐述了导电背景中地-井TEM响应符号变化; Dyck等[9]分析总结了地-井TEM技术勘探中资料解释方法.
实际条件下, 局部导体(如矿床)往往由多个导体组合在一起, 观测到的结果是多个导体响应相叠加的异常, 其响应规律较为复杂. 本文通过建立等效数学模型对该问题进行研究.
1 等效涡流环计算方法在等效数学模型中, "等效涡流"法较为简单方便, 能计算组合体和导电围岩或覆盖层的响应情况, 其晚期计算结果与本征环流法计算结果相一致, 具有一定的适用性[2], 基本能满足模拟计算的需要.
设长、短边分别为b、a的薄板状导体在Tx回线产生的近于均匀的一次场激励下, 薄板体中心部位会产生一个长、短边分别为0. 7b、0. 7a的等效涡流环. Tx回线与等效涡流环之间的互感系数为M1, 等效涡流环与Rx回线之间的互感系数为M2. 通过电路原理分16次计算Tx各个边与等效涡流环各个边的互感系数[10-11], 例如Tx的某条边l1和等效涡流与其平行的某条边l2之间的互感系数由Neumann公式可得:
| $ \begin{align} & M=\frac{{{\mu }_{0}}}{4\pi }\int\limits_{0}^{{{l}_{1}}}{\int\limits_{0}^{{{l}_{2}}}{\frac{\text{d}{{l}_{1}}\cdot \text{d}{{l}_{2}}}{{{R}_{12}}}}} \\ & =\frac{{{\mu }_{0}}}{4\pi }\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{\int\limits_{{{x}^{\prime }}_{1}}^{{{x}^{\prime }}{{2}_{2}}}{\frac{\text{d}{{l}_{1}}\cdot \text{d}{{l}_{2}}}{\sqrt{{{\left( {{l}_{1}}+{{l}_{2}} \right)}^{2}}+\Delta {{Y}^{2}}+\Delta {{Z}^{2}}}}}} \\ \end{align} $ | (1) |
R12为dl1与dl2间距; l1两端的横坐标为x1、x2, l2两端的横坐标为x′1、x′2; ΔY和ΔZ分别为dl1与dl2纵向和垂向的距离, 因该式为两条同样走向平行线, 故ΔY和ΔZ的值固定; μ0为磁导率, 地层中一般取1. 256×10-6 H/m. 式(1)进一步推导[12-13]可得:
| $ \begin{aligned} M=& \frac{\mu_0}{4 \pi}\left[\left(x_2-x_1^{\prime}\right) \ln \left(x_2-x_1^{\prime}+\sqrt{\left(x_2-x_1^{\prime}\right)^2+\Delta Y^2+\Delta Z^2}\right)\right.\\ &\left.-\sqrt{\left(x_2-x_1^{\prime}\right)^2+\Delta Y^2+\Delta Z^2}\right] \\ &-\frac{\mu_0}{4 \pi}\left[\left(x_2-x_2^{\prime}\right) \ln \left(x_2-x_2^{\prime}+\sqrt{\left(x_2-x_2^{\prime}\right)^2+\Delta Y^2+\Delta Z^2}\right)\right.\\ &\left.-\sqrt{\left(x_2-x_2^{\prime}\right)^2+\Delta Y^2+\Delta Z^2}\right] \\ &+\frac{\mu_0}{4 \pi}\left[\left(x_1-x_2^{\prime}\right) \ln \left(x_1-x_2^{\prime}+\sqrt{\left(x_1-x_2^{\prime}\right)^2+\Delta Y^2+\Delta Z^2}\right)\right.\\ &\left.-\sqrt{\left(x_1-x_2^{\prime}\right)^2+\Delta Y^2+\Delta Z^2}\right] \\ &-\frac{\mu_0}{4 \pi}\left[\left(x_1-x_1^{\prime}\right) \ln \left(x_1-x_1^{\prime}+\sqrt{\left(x_1-x_1^{\prime}\right)^2+\Delta Y^2+\Delta Z^2}\right)\right.\\ &\left.-\sqrt{\left(x_1-x_1^{\prime}\right)^2+\Delta Y^2+\Delta Z^2}\right] \end{aligned} $ | (2) |
用类似解法可以取得另外各边之间的互感系数并相加即可求出Tx与等效涡流环的总互感系数; 再用同样的方法计算等效涡流环与Rx之间的互感系数.
| $ \mathit{\Phi}_1=I \cdot M_1 $ | (3) |
| $ \mathit{\Phi}_2=i_0 \cdot \mathrm{e}^{-t / \tau} \cdot M_2 $ | (4) |
Φ1为导体内产生的磁通量; Φ2为Rx接收二次场产生的磁通量; I为Tx所通电流; i0·e-t/τ为感应等效涡流. 式中感应电流的初始值以及时间常数的经验表达式分别为[2-3]:
| $ i_0=0.6 H_{1 \mathrm{n}} \cdot a \cdot f_1(b / a) $ | (5) |
| $ \tau=\mu_0 \cdot S \cdot a \cdot f_2(b / a) / 10 $ | (6) |
H1n(即H1·cosθ)[3]为作用于薄板体的一次场法向分量; H1为一次场; θ为薄板导体与Tx所在平面(一般即水平面)的夹角; S为纵向电导.
| $ V(t)=-\frac{\partial \mathit{\Phi}_2}{\partial t} $ | (7) |
用类似的算法, 可以再加上3块板体的响应值. 这4块板的大小、倾角、走向以及电性参数等可以任意改变或组合[2](经过试算对比, 当板状导体不多于4块时, 可以忽略板体之间的耦合关系, 进行直接计算, 依然保证足够精度).
2 多个薄板状导体的地-井TEM响应特征通过对"等效涡流环"方法和电路原理中互感耦合原理的理解, 推导了算法, 利用VC语言编写代码, 对其进行实现. 本文模型参数的选取参考了大量前人研究中的模拟参数[14-20]: 发送回线Tx统一选取400 m× 400 m单匝矩形回线, 中心位于原点(0, 0, 0), 电流强度1 A; 模型选取边长100 m的正方形薄板导体, 板体中心都位于原点正下方, 保证各板体与Tx的耦合, 纵向电导10 S; 钻孔为垂井, 位于Tx中心线(轴)上, 接收回线Rx为20 m × 20 m, 测量点距20 m; 测道选取在晚期, t1=0. 108 ms, t2=0. 17 ms, t3=0. 28 ms, t4=0. 44 ms. 本文中各个模型的相关参数均与上述相同, 保持模拟参数的一致性.
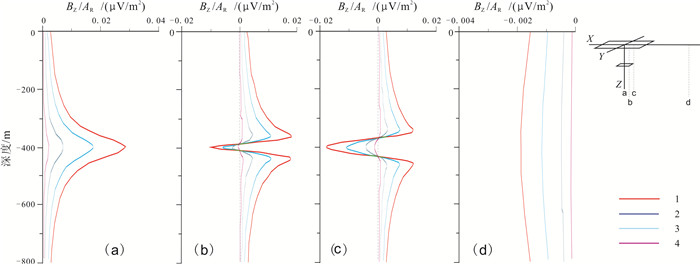
2.1 单板体地-井TEM的一般响应特征图 1为不同位置钻孔所观测的单个水平薄板导体TEM晚期异常响应曲线. 模型参数为: 边长100 m的正方形板体置于Tx中心下部, 中心坐标(0, 0, -400), 纵向电导10 S; 垂井中Rx为20 m× 20 m, 测量点距20 m; 4个测道分别为t1=0. 108 ms, t2=0. 17 ms, t3=0. 28 ms, t4=0. 44 ms. 图 1a为钻孔穿过板体中心, 接收异常响应始终为正; 图 1b为钻孔穿过板体边缘内侧, 图 1c为钻孔在板体外侧, 近板体处二次场方向与一次场反向, 响应异常中部为负, 两侧为正; 图 1d为钻孔离板体足够远, 异常为负.
|
图 1 不同钻孔接收水平单板体异常响应曲线 Fig.1 Surface-hole TEM response curves for single horizontal conductive plate in different boreholes 1—测道1响应时间, t1=0. 108 ms (response time of track No. 1); 2—测道2响应时间, t2=0. 170 ms (response time of track No. 2); 3—测道3响应时间, t3=0. 280 ms (response time of track No. 3); 4—测道4响应时间, t4=0. 440 ms (response time of track No. 4) |
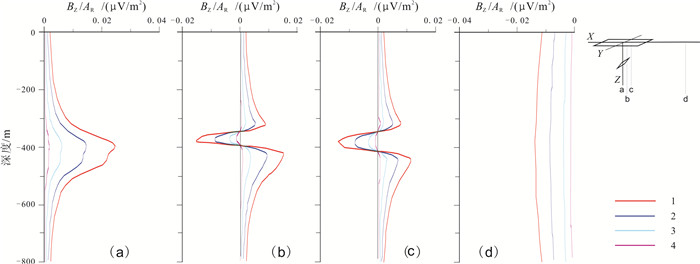
图 2为同样情况下薄板导体呈45°倾角, Rx分别在穿过中心、穿过边缘内侧、在边缘外侧、离板体足够远的钻孔中所接收的TEM晚期响应曲线.
|
图 2 不同钻孔接收倾斜单板体异常响应曲线 Fig.2 Surface-hole TEM response curves for single tilt conductive plate in different boreholes 1—测道1响应时间, t1=0. 108 ms (response time of track No. 1); 2—测道2响应时间, t2=0. 170 ms (response time of track No. 2); 3—测道3响应时间, t3=0. 280 ms (response time of track No. 3); 4—测道4响应时间, t4=0. 440 ms (response time of track No. 4) |
图 3为不同位置钻孔所观测的组合薄板导体TEM晚期异常响应曲线. 模型参数: 4块边长100 m的水平正方形薄板导体纵向罗列放置于Tx中心下部, 中心坐标分别为(0, 0, -355)、(0, 0, -385)、(0, 0, -415)、(0, 0, -445), 各板间距30 m, 纵向电导均为10 S; t1取0. 108 ms.

|
图 3 不同钻孔接收水平多板体纵向组合异常曲线 Fig.3 Surface-hole TEM response curves for vertical combination of multiple horizontal conductive plates in different boreholes 1—组合板响应(response for multiple conductive plates); 2—薄板1响应(response for No. 1 conductive plate); 3—薄板2响应(response for No. 2 conductive plate); 4—薄板3响应(response for No. 3 conductive plate); 5—薄板4响应(response for No. 4 conductive plate); 6—组合板响应幅值(response amplitude for multiple conductive plates) |
图 3a为顶端位于(0, 0, 0)点的钻孔所测得异常响应曲线, 钻孔穿过4个板体中心, 所接收到的二次场方向与一次场一致, 异常均为正, 组合板体的异常响应相当于4个同号(都为正)响应的叠加. 就该模型各板体来说, 位于上层的板体离Tx更近, 其产生的二次场响应幅值一定略大于下层板体, 故同号叠加产生的总响应曲线上部幅值稍大于下部.
图 3b为顶端位于(100, 0, 0)的钻孔所测异常响应曲线, 钻孔与板体水平距离50 m(距等效涡流65 m); 各单个板体的异常响应都出现了正负号差别(变号), 在二次场与一次场方向相反的深度段, 异常响应为负, 因各板体变号位置(过零点)的差异, 中间部分总响应相当于各板体正负(异号)响应叠加; 在各板体均为正异常的部分仍为正异常叠加.
虽然该板体组合的总异常响应曲线特征和单个板体异常响应特征相似, 但响应幅值(不考虑符号的响应大小)有很大不同. 单个水平板体的幅值是由中部极大值(板体与近板体位置的Rx耦合最佳)向两侧逐步减小, 而组合板体因各单板体变号位置(过零点)的差异, 在中段存在有的板为正异常、有的板为负异常的情况, 该情况下各个板体的正负响应相互叠加抵消使该井段的部分总响应幅值(位于响应极值的两侧)低于同号叠加的部分, 并因异号响应叠加抵消而在响应极值两侧各产生一个极小值, 造成异常幅值由中心极大值向两边过渡中出现两个低幅值段(谷), 整个幅值曲线近似侧立的"山"状, 如图 3b中的组合板响应幅值曲线所示.
图 3c为顶端坐标(150, 0, 0)钻孔所测异常响应曲线及响应幅值曲线, 可进一步看出各单体正负响应叠加抵消会产生较小幅值段和极小幅值的情况, 随负号响应部分逐渐变宽(Rx位置渐远), 极小值和较小值部分逐渐向两侧移动(因各单板变号位置移动), 且在一定观测范围内叠加抵消产生的极小幅值也渐渐减小; 同时, 各板体同为负响应的范围变宽, 负异常叠加.
图 3d为顶端位于足够远(630, 0, 0)的钻孔所得异常曲线, 在该距离接收的各单板响应皆为负, 组合体响应因各单体响应同号叠加也为负. 若使各板体在全井段观测的响应都为负, 需在足够远的距离观测, 异常响应幅值都较小, 曲线较平缓. 本文模型仅是以高阻介质作为背景的理论计算, 实际地-井TEM的"旁视"能力受各种因素制约达不到模型所示距离.
图 4为图 3模型的4个板体倾角为45°在过中心点, 顶端坐标(100, 0, 0)、(150, 0, 0), 离板体组合足够远的钻孔中所接收到的晚期异常响应曲线.

|
图 4 不同钻孔接收倾斜多板体纵向组合异常曲线 Fig.4 Surface-hole TEM response curves for vertical combination of multiple tilt conductive plates in different boreholes 1—组合板响应(response for multiple conductive plates); 2—薄板1响应(response for No. 1 conductive plate); 3—薄板2响应(response for No. 2 conductive plate); 4—薄板3响应(response for No. 3 conductive plate); 5—薄板4响应(response for No. 4 conductive plate); 6—组合板响应幅值(response amplitude for multiple conductive plates) |
距多板体组合较近的钻孔所接收的异常响应曲线, 因各板体间距、观测距离、板体数量、板体大小等影响, 会出现各单体特征、相邻板体叠加特征等特殊情况, 其响应特征规律的普遍性较差, 故未作讨论.
3 通过组合体地-井TEM异常响应分辨各单板体地面大定回线源装置TEM剖面法分辨组合体中各参数相近的单板体异常特征, 需板体间距p大于等于其埋深h的3倍[2]. 本文讨论地-井TEM观测下, 大小及电性参数相近的板状体在板体组合总响应上的分辨问题, 其中制约因素很多, 笔者就钻孔位于各单板体等效涡流环以外的情况分析两个条件: 单体可分辨的最大观测距离和最小板体间距.
图 5为板体间距相同的组合体在不同钻孔观测的TEM晚期异常响应曲线. 模型参数: 两块边长100 m的水平正方形板体纵向罗列置于Tx中心下部, 中心坐标分别为(0, 0, -350)、(0, 0, -450), p=100 m; 其余模拟条件与上文模型相同.

|
图 5 由不同钻孔观测水平板组合异常响应分辨单个板体 Fig.5 Distinction of single plates by responses of multiple horizontal conductive plates in different boreholes 1—组合板响应(response for multiple conductive plates); 2—薄板2响应(response for No. 2 conductive plate); 3—薄板1响应(response for No. 1 conductive plate) |
图 5a和5b分别为顶端坐标(50, 0, 0)和(70, 0, 0)的钻孔所测得异常响应曲线. Rx等效边到板体内等效涡流环的水平距离d分别为5 m和25 m; 钻孔观测距离增大, 组合体异常响应幅值减小; 因变号位置差异, 中部两板体正负异常响应叠加抵消, 两侧同号响应叠加; 总响应曲线中各单体负响应峰值位置的异常特征明显, 可分辨单个板体的响应特征.
图 5c为顶端坐标(90, 0, 0)的钻孔所测得响应曲线. 两个单板响应的变号位置接近, 同为负异常响应的部分同号叠加; 单板负异常峰值因两板体异号响应叠加抵消幅值减小, 低于同负号响应叠加后的幅值, 从总响应曲线中无法分辨单个板体.
可知, 当p值确定, 观测距离越大, 从板体组合异常响应上分辨单体特征的情况越差; 仅当钻孔距组合体小于一定距离(单体可分辨的最大观测距离)时, 可从接收的总响应中分辨出单体特征. 图 5的参数条件下, d≤25 m可分辨出单体异常特征. 需说明的是, 模型参数改变, 具体计算结果会略有差别, 但结论一致.
图 6为板体间距不同的组合体在相同钻孔观测的TEM晚期异常响应曲线. 模型参数: 两块边长100 m水平正方板体纵向罗列置于Tx中心下部, 使板体间距p分别为100、80、60 m; 钻孔穿过各板体边缘, 顶端坐标(50, 0, 0); d=5 m, 其余模拟条件与上文模型相同.

|
图 6 由固定钻孔观测水平板组合异常响应分辨单个板体 Fig.6 Distinction of single plates by responses of multiple horizontal conductive plates in the same borehole 1—组合板响应(response for multiple conductive plates); 2—薄板2响应(response for No. 2 conductive plate); 3—薄板1响应(response for No. 1 conductive plate) |
图 6a为两个薄板深度分别为350 m、450 m, 板体边缘钻孔接收的响应曲线. 因变号位置差异, 中部两板体正负异常叠加抵消, 但各单板体负异常峰值仍明显, 可从总响应中分辨单个板体的响应特征. 图 6b中两单板深度分别为360 m、440 m, 可分辨单板特征.
图 6c为两单板深度分别为370 m、430 m, 板体边缘钻孔接收的响应曲线. 两个板体响应的变号位置接近, 有的同为负异常响应的部分, 同号叠加; 单板的负异常峰值部分因两单板异号响应叠加抵消而幅值减小, 使总响应仅有单个负异常峰值, 无法分辨中单个板体.
由上可知, p值越大, 组合板体异常响应上分辨单体的情况越好; 当p小于一定距离(单体可分辨的最小间距), 即使离组合体足够近的钻孔, 也不能从接收的总响应中分辨出单体特征. 图 6的参数条件下, 板体组合中单体最小可分辨间距约71 m. 通过计算多个模型, 发现p值作为组合体响应中单板特征可分辨的条件, 是有下限的, 即钻孔位于贴近板体涡流环边缘能分辨组合中单体的情况下各板体最小间距, 同参数条件下, 若p小于该值, 则板体涡流环外任何位置钻孔接收的响应都不能分辨出单体特征.
4 结语通过等效涡流环和电路原理求取板状体TEM响应的方法原理, 对地-井观测方式下多板体组合的晚期TEM异常响应情况进行了数值模拟, 取得了如下成果和结论:
1) 总结了纵向排布下多板体组合在不同位置钻孔观测得到异常响应的特征规律, 并结合单板体的响应特征进行了分析, 重点分析了多个板体异号响应叠加抵消产生的幅值减小情况;
2) 通过多板体响应叠加形成总异常响应, 分析其特征规律, 认识到地-井TEM在对组合体的观测中, 除异常响应曲线以外, 不考虑正负号的响应幅值曲线也可以提供组合体相关信息, 作为对组合体进行推断的依据;
3) 对比地面大定回线源TEM剖面法对板体组合中单体进行分辨的条件, 分析了在某些条件下, 通过多个平行板体纵向组合产生的地-井TEM总异常响应对其中单个组成部分进行分辨的情况.
笔者仅考虑了最简单条件下多板组合的静态响应特征和规律, 参数选择较为单一, 文中部分图件曲线在不影响基本特征的前提下做了圆滑处理; 组合导体的响应特征规律复杂, 其中还存在很多不足和问题, 如良导电性覆盖层和低阻围岩影响、随深度变化的信噪比、异常响应的衰减以及早期和中期的异常响应特征规律等问题, 都有待进一步研究分析.
| [1] |
蒋邦远. 实用近区磁源瞬变电磁法勘探[M]. 北京: 地质出版社, 1998: 199-237. Jiang B Y. Practical near-field magnetic source transient electromagnetic exploration[M]. Beijing: Geological Publishing House, 1998: 199-237. |
| [2] |
牛之琏. 时间域电磁法原理[M]. 长沙: 中南大学出版社, 2007: 249-267. Niu Z L. Principle of time domain electromagnetic method[M]. Changsha: Central South University Press, 2007: 249-267. |
| [3] |
Buselli G, Lee S K. Modelling of drill-hole TEM responses from multiple targets covered by a conductive overburden[J]. Exploration Geophysics, 1996, 27(2/3): 141-153. |
| [4] |
Singh N P, Mogi T. Electromagnetic response of a large circular loop source on a layered earth: A new computation method[J]. Pure and Applied Geophysics, 2005, 162(1): 181-200. DOI:10.1007/s00024-004-2586-2 |
| [5] |
Richards D J. CRAE's approach to downhole TEM at Broken Hill[J]. Exploration Geophysics, 1987, 18(3): 279-284. DOI:10.1071/EG987279 |
| [6] |
Eaton P A, Hohmann G W. The influence of a conductive host on two- dimensional borehole transient electromagnetic responses[J]. Geophysics, 1984, 49(7): 861-869. DOI:10.1190/1.1441732 |
| [7] |
West R C, Ward S H. The borehole transient electromagnetic response of a three-dimensional fracture zone in a conductive half-space[J]. Geophysics, 1988, 53(11): 1469-1478. DOI:10.1190/1.1442427 |
| [8] |
Macnae J, Staltari G. Classification of sign changes in Borehole TEM decays[J]. Exploration Geophysics, 1987, 18(3): 331-339. DOI:10.1071/EG987331 |
| [9] |
Dyck A V, West G F. The role of simple computer models in interpretations of wide-band, drill-hole electromagnetic surveys in mineral exploration[J]. Geophysics, 1984, 49(7): 957-980. DOI:10.1190/1.1441741 |
| [10] |
Telford W M, Geldart L P, Sheriff R E. Applied geophysics[M]. Cambridge: Cambridge University Press, 1990: 353.
|
| [11] |
Paul C R. Inductance: Loop and partial[M]. Hoboken: John Wiley and Sons Ltd, 2010: 196-206.
|
| [12] |
Dwight H B. Tables of integrals and other mathematical data[M]. 4th ed. New York: MacMillan, 1964: 45.
|
| [13] |
Jeffrey A. Handbook of mathematical formulas and integrals[M]. San Diego: Academic Press, 1995: 178.
|
| [14] |
Vella L. Taking downhole EM underground, at hill 50 decline, mount magnet, Western Australia[J]. Exploration Geophysics, 1997, 28(1/2): 141-146. |
| [15] |
Zhang Z, Xiao J. Inversions of surface and borehole data from large- loop transient electromagnetic system over a 1-D earth[J]. Geophysics, 2001, 66(4): 1090-1096. DOI:10.1190/1.1487056 |
| [16] |
Aziz A A, Strack K, Hanstein T. Surface-to-borehole TEM for reservoir monitoring[C]//SEG Technical Program Expanded Abstracts 2011. Society of Exploration Geophysicists, 2011: 1882-1886.
|
| [17] |
李建慧, 刘树才, 焦险峰, 等. 地-井瞬变电磁法三维正演研究[J]. 石油地球物理勘探, 2015, 50(3): 556-564. Li J H, Liu S C, Jiao X F, et al. Three-dimensional forward modeling for surface-borehole transient electromagnetic method[J]. Oil Geophysical Prospecting, 2015, 50(3): 556-564. |
| [18] |
杨海燕, 岳建华, 徐正玉, 等. 覆盖层影响下典型地-井模型瞬变电磁法正演[J]. 吉林大学学报(地球科学版), 2016, 46(5): 1527-1537. Yang H Y, Yue J H, Xu Z Y, et al. Transient electromagnetic method modeling in ground-borehole model with overburden influence[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(5): 1527-1537. |
| [19] |
Paggi J, Macklin D. Discovery of the Eureka volcanogenic massive sulphide lens using downhole electromagnetics[J]. Exploration Geophysics, 2016, 47(3): 248-257. DOI:10.1071/EG15096 |
| [20] |
Kolaj M, Smith R. Robust conductance estimates from spatial and temporal derivatives of borehole electromagnetic data[J]. Geophysics, 2014, 79(3): E115-E123. DOI:10.1190/geo2013-0387.1 |
 2022, Vol. 31
2022, Vol. 31

