石油天然气勘探开发工作是一个循序渐进的过程,对油气藏的认识也逐步深入.为了实现石油公司油气田的科学有序、经济有效的勘探开发以及战略部署,储量评估工作贯穿于各个勘探开发阶段[1].现行的储量计算规范《石油天然气储量计算规范DZ/T 0217-2005》指出,已查明为统一油(气)水界面的油(气)水系统一般划为一个计算单元(即油层组),含油(气)高度很大时也可细分为亚油层组或小层.在油田开发早期,受油藏地质认识的局限,往往纵向上以具有独立的油气水系统的油层组为基本计算单元,对油层组或砂层组内的层内非均质性考虑不足.随着油田精细研究和开发的需要,进行更精细的储量评估愈加迫切,精细储量评估过程中最重要的一环就是对油藏纵向单元划分.在以往有关储量计算方面的研究成果中,对油藏纵向细分计算单元方法及其合理性、纵向细分计算单元对储量参数影响及储量计算精度方面的论述甚少,也没有引起足够重视.随着油田精细研究和开发的需要增加,进行更精细的储量评估愈加迫切,精细储量评估过程中最重要的一环就是对油藏纵向单元的划分.中国油田大多数属于陆相沉积,其中三角洲相沉积是陆相沉积的重要组成部分,而三角洲沉积一般形成隔夹层较稳定分布的薄互层储层.本文针对隔夹层较稳定分布的多层构造油藏(包括层状构造油藏和岩性-构造油藏),探讨储量精细计算过程中,具有统一油气水系统的油藏,在纵向单元划分前后各储量参数之间的差异及其变化规律,为精细的储量研究中如何纵向细分单元提供技术指导.
1 多层构造油藏地质特征多层构造油藏在中国以陆相沉积为主的各大油田中均有分布,以盆地边缘的三角洲储层形成的多层构造油藏最为典型.三角洲储层一般横向上连片分布,纵向上多期砂体叠置.湖盆基准面的相对变化控制着三角洲砂体的充填样式、层序演化及每个层序内部组成单元的形成和发育[2-5].在湖盆基准面相对下降期,随着湖平面下降,湖盆范围缩小,沉积物向湖区进积,以进积型三角洲沉积为主,该时期形成的砂层组总体上表现为反韵律;在湖盆基准面相对上升期,随着湖平面上升,湖盆范围扩大,沉积物向滨岸退积,以退积型三角洲沉积为主,该时期形成的砂层组总体上表现为正韵律[6].同时,受物源远近的影响,形成不同类型的三角洲沉积.一般辫状河三角洲沉积以水下分流河道砂体为主,横向砂体厚度变化较大;正常三角洲沉积以河口坝砂体为主,横向分布稳定.
2 石油地质储量计算方法目前,国内外在石油地质储量评价过程中用到的计算方法主要有:类比法(即经验法)、概率统计法、单井控制法、容积法、物质平衡法、产量递减法、水驱特征曲线法、数模法.究竟选用哪种方法比较合适,主要取决于该油田所处的勘探开发阶段、圈闭类型、储层类型及流体类型[7-13](表 1).容积法适用的油藏类型广泛,对不同圈闭类型、储集类型和驱动方式的油藏均可使用,在油田的各个勘探开发阶段也均适用,是目前国内储量计算中使用最广泛的一种方法,也是现行石油天然气储量计算规范中推荐的计算方法[14-15].
|
|
表 1 不同储量计算方法统计表 Table 1 Various calculation methods for reserves |
在现行的储量规范和实际工作中,容积法计算石油地质储量往往将一个具有独立的油气水系统的油层组或者砂层组作为一个计算单元,因为它能够有效地反映出当前油藏内部宏观油气分布状况[16-18],但是随着工作的进一步深入,为进一步了解储层及流体分布特征,在开发中计算商业储量时会细分到小层.针对单元细分前后的变化,本文以具有代表性的多层构造油藏为例,分析容积法计算储量过程中,纵向细分计算单元前后各储量参数的变化规律及对储量计算结果的影响.
3 细分单元前后各储量参数对比分析从容积法储量计算公式[14]分析,影响石油地质储量计算的5个参数包括含油面积、平均有效厚度、平均有效孔隙度、平均油层原始含油饱和度、体积系数.而反映油藏中流体性质的体积系数,一般通过原油高压物性数据求得,数据点较少,故同一油藏纵向细分单元前后该参数一般为同一数,在下面的参数对比中也就不予考虑.因此,本文重点剖析其他4个参数在纵向单元细分前后对储量评估的影响.
3.1 含油面积含油面积为含油气构造中含油边界以内的垂直投影面的面积.含油面积一般结合流体界面、断层,在相应的顶面构造图上圈定.含油面积的圈定是影响储量最关键的一步,它不仅直接影响含油面积,同时也影响其他参数的加权结果[19].一方面,随着油田逐步进入中高含水阶段,油水分布日趋复杂,剩余油分布呈现高度分散局部富集的特征,对于大段合采的油层,受储层的纵向韵律变化,造成纵向水驱不均,目前以油组为单元的储量计算不能满足定量评估剩余油分布状况;另一方面,目前随着储层构型研究的深入,三角洲储层的研究尺度已经达到单成因砂体级别,对剩余油的挖潜也已达到单成因砂体级别.因此在储层精细研究的基础上,按照小层进一步细分计算单元是很有必要的.由于油层组内部纵向上储层分布相对连续,隔夹层厚度不大,一般细分后的各单元实钻流体界面仍基本一致,故油层组内细分后的各单元仍采用该油层组统一的流体界面.因此,细分单元后各单元的叠合含油面积与以油层组圈定的含油面积一致(如图 1).
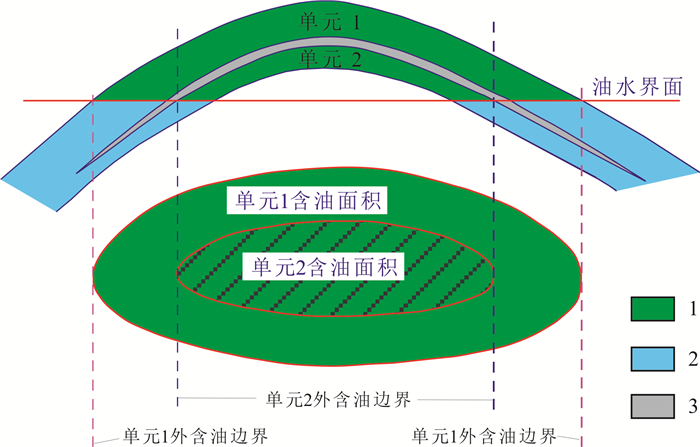
|
图 1 含油面积圈定示意图 Fig.1 Sketch of oil-bearing area delineation (据文献[20]) 1-油层(oil layer);2-水层(water layer);3-隔夹层(interlayer) (From Reference [20]) |
油层有效厚度指达到储量起算标准的含油层系中具有产油能力的那部分储层厚度.容积法计算储量中,单元有效厚度一般采用等值线面积权衡法.在有效厚度等值线的勾绘过程中主要参考井点油层有效厚度值均匀插值及储层沉积展布特征约束等值线趋势勾绘各单元有效厚度等值线[21].因此,单元细分前后有效厚度的变化主要与砂体的展布特征有关,包括沉积类型,地层剥蚀等.
1)储层横向沉积变化的差异:若某油藏细分后,各单元在含油面积范围内无储层尖灭(图 2a).如等值线间隔无限小,细分单元后各单元平面上同一位置的厚度值累加与该点处以油层组为单元的厚度值相等.但是,在等值线勾绘和取值过程中,一般视储层有效厚度分布情况以1~5 m为间隔勾绘等值线.在纵向细分后的有效厚度图中受等值线疏密的影响,可能不能体现细分单元前的最大等值线,导致细分单元后各单元的平均有效厚度加权得到的油层组平均有效厚度较以油层组为单元直接得到的加权平均值小.以某油藏为例,根据现行规范的要求,最大有效厚度等值线不能超过现有井的最大有效厚度,在有效厚度的面积加权过程中,每个厚度最大的等值线内的有效厚度采用该等值线处厚度与该等值线内井点最大值的平均值.在以油层组为单元的有效厚度图中可以得到8 m线区域,在细分单元后各单元的有效厚度图中该区域累加小于8 m线(如图 2a中4 m线内取4.75 m,2 m线内取2.25 m).但由于厚度最大的等值线控制的面积很小,纵向细分单元后有效厚度变化极小.但是储层横向沉积变化频繁,如辫状河(三角洲)沉积砂体,纵向细分单元对平均有效厚度影响变成上述变化的累加,此时有效厚度有一定减小.
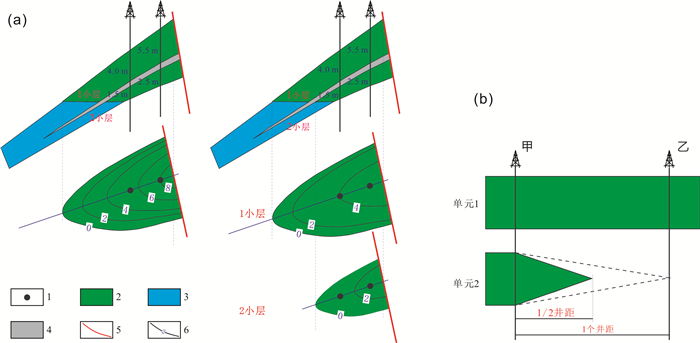
|
图 2 平均有效厚度取值示意图 Fig.2 Sketch of average effective thickness valuing 1-钻遇井(oil well);2-油层(oil layer);3-水层(water layer);4-隔夹层(interlayer);5-断层(fault);6-有效厚度等值线(effective thickness contour);b-据文献[16](from reference [16]) |
2)储层尖灭时的差异:若某油藏细分后可分为2个计算单元(图 2b),单元2在含油面积范围内存在较大范围的岩性或物性尖灭,包括储层相变、地层尖灭等.根据岩性油气藏储量计算细则的有关要求,当相邻井的砂体相变为泥岩或虽然砂体存在但转变为渗透性变差的非储层(干层)时,取从油井到邻井距离的1/2~1/3处划岩性含油边界[22].在实际应用中,当2小层从油井到邻井为砂岩相变为泥岩时,自油井外推取1/3井距划岩性含油边界;当2小层从油井到邻井转变为渗透性变差的非储层时,自油井外推取1/2井距划岩性含油边界.因此,细分单元后,单元2作为一个独立计算单元时,考虑到以井距1/2或1/3处圈定有效储层尖灭线,故油层的有效厚度0线位于甲井外推1/2或1/3井距处;而当单元1与单元2合并成一个单元时,考虑到均匀插值,单元2油层的有效厚度0线则位于乙井点处. 图 2b中虚线所圈定的范围即为两种算法之间的差值.因此在该类型油藏纵向细分单元后有效厚度也将变小,变化大小与单元2在该油藏含油面积内的尖灭范围、尖灭处油层有效厚度及井距成正相关.因此该类型油藏,若细分后的某单元在该油藏含油面积内尖灭范围较大、尖灭处油层有效厚度及井距也较大,单元细分后有效厚度将有一定的变小.
3.3 平均有效孔隙度有效孔隙度是指有效厚度段内单位地下岩石所有具有连通性的孔隙空间体积与岩石体积的比值.在容积法计算储量中,先用厚度权衡法计算单井平均孔隙度再用岩石体积权衡法计算得到单元平均有效孔隙度.为便于分析和理论推导,本文在分析平均有效孔隙度和平均饱和度中,以某具有2个小层的油藏为例(图 3).该油藏具有2个小层,1小层含油面积范围内分布较稳定,2小层在油田北东部储层尖灭.同时,该油藏井网分布较均匀.因此在下面的论证过程中,我们选取甲乙两井及其井控储量进行分析,甲、乙井分别控制的含油面积近似相等,同时可认为该油藏是若干个甲乙井控范围在三维空间的拼叠.考虑以下3种类型:类型一,甲、乙井均处于过渡带内,且2小层均为水层;类型二,甲、乙井均处于纯油区内,且储层在两井之间稳定分布;类型三,甲、乙井均处于纯油区内,但乙井的2小层不发育储层.
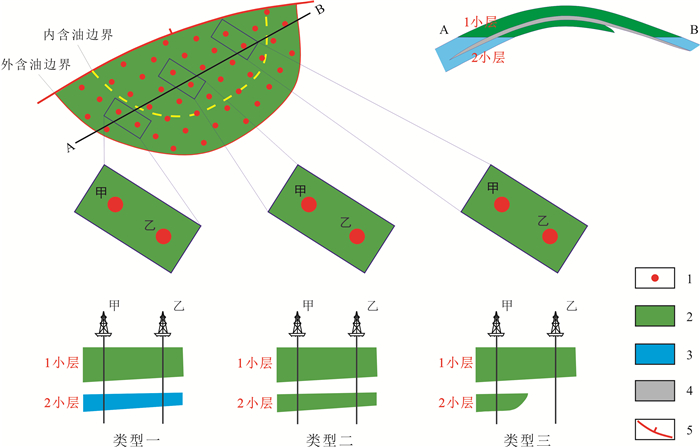
|
图 3 不同储层模式示意图 Fig.3 Sketch of different reservoir models 1-已钻井(drilled well);2-油层(oil layer);3-水层(water layer);4-隔夹层(interlayer);5-边界断层(boundary fault) |
纵向以油层组为单元计算单元平均有效孔隙度:
| $ {\phi _1} = \frac{1}{2} \times \left( {\frac{{{\phi _{\rm{a}}} \times a + {\phi _{\rm{b}}} \times b}}{{a + b}} + \frac{{{\phi _{\rm{c}}} \times c + {\phi _{\rm{d}}} \times d}}{{c + d}}} \right) $ | (1) |
纵向以小层为单元计算各单元平均孔隙度,再用含油面积加权得到油层组孔隙度:
| $ {\phi _2} = \frac{{\frac{{{\phi _{\rm{a}}} + {\phi _{\rm{c}}}}}{2} \times {h_1} \times {s_1} + \frac{{{\phi _{\rm{b}}} + {\phi _{\rm{d}}}}}{2} \times {h_2} \times {s_2}}}{{{h_1} \times {s_1} + {h_2} \times {s_2}}} $ | (2) |
式(1)(2)中:a、b分别为甲井钻遇1、2小层的有效厚度,c、d分别为乙井钻遇1、2小层的有效厚度;ϕa、ϕb分别为甲井钻遇1、2小层的平均有效孔隙度,ϕc、ϕd分别为乙井钻遇1、2小层的平均有效孔隙度;h1为1小层平均有效厚度,h2为2小层平均有效厚度,s1为1小层井控含油面积,s2为2小层井控含油面积,s为以油层组为单元时井控含油面积.
按照储层的展布特征和流体分布,分以下3种情况分析两种方法计算得到的ϕ1与ϕ2之差.
类型一:有b=d=0;ϕb=ϕd=0.取h1=(a+c)/2;h2=0(考虑对比的可计算性,本文在平均有效孔隙度和平均饱和度的对比中,取井点平均值等效为面积权衡的平均有效厚度);s1=s,s2=0.则有
| $ {\phi _1} = \frac{{{\phi _{\rm{a}}} + {\phi _{\rm{c}}}}}{2} $ | (3) |
| $ {\phi _2} = \frac{{\frac{{{\phi _{\rm{a}}} + {\phi _{\rm{c}}}}}{2} \times {h_1} \times {s_1} + \frac{{{\phi _{\rm{b}}} + {\phi _{\rm{d}}}}}{2} \times {h_2} \times {s_2}}}{{{h_1} \times {s_1} + {h_2} \times {s_2}}} = \frac{{{\phi _{\rm{a}}} + {\phi _{\rm{c}}}}}{2} $ | (4) |
此时,ϕ1=ϕ2,故,纵向细分单元后,孔隙度不变.
类型二:取h1=(a+c)/2,h2=(b+d)/2,s1=s2=s.则有
| $ {{\phi _2} = \frac{1}{2} \times \frac{{\left( {{\phi _{\rm{a}}} \times {\phi _{\rm{c}}}} \right)(a + c) + \left( {{\phi _{\rm{b}}} \times {\phi _{\rm{d}}}} \right)(b + d)}}{{a + b + c + d}}} $ | (5) |
| $ {{\phi _1} - {\phi _2} = \frac{1}{2} \times \frac{{(ad - bc)\left[ {(c + d)\left( {{\phi _{\rm{a}}} - {\phi _{\rm{b}}}} \right) + (a + b)\left( {{\phi _{\rm{d}}} - {\phi _{\rm{c}}}} \right)} \right]}}{{(a + b + c + d)(a + b)(c + d)}}} $ | (6) |
ϕ1与ϕ2之差的分子为两个多项式乘积,多项式一为不同井不同小层有效厚度交叉相乘之差;多项式二为井点的油层组有效厚度与另一井的小层平均孔隙度之差交叉相乘之和.考虑到多层构造油藏储层的空间展布特征,ϕ1-ϕ2在0值附近波动.规模油藏中往往包含多个这样的井控区域,故用误差的观点分析,在该条件下,两种方法得到的孔隙度基本无差别.
类型三:取h1=(a+c)/2;h2=b;d=0;ϕd=0;s1=s;取s2=μs,当2小层从油井到邻井为砂岩相变为泥岩时(即储层岩性尖灭),自油井外推取1/3井距划岩性含油边界,取μ=1/3;当2小层从油井到邻井转变为渗透性变差的非储层时(即储层物性尖灭),自油井外推取1/2井距划岩性含油边界,取μ=1/2.则有
| $ {{\phi _1} = \frac{{{\phi _{\rm{a}}} \times a + {\phi _{\rm{b}}} \times b + {\phi _{\rm{e}}} \times (a + b)}}{{2(a + b)}}} $ | (7) |
| $ {{\phi _2} = \frac{1}{2} \times \frac{{\left( {{\phi _{\rm{a}}} + {\phi _{\rm{c}}}} \right)(a + c) + 4{\phi _{\rm{b}}}b\mu }}{{a + b + 2b\mu }}} $ | (8) |
| $ \begin{array}{l} {\phi _1} - {\phi _2} = \frac{1}{2} \times \\ \;\;\;\;\;\;\frac{{b\left[ {(2a\mu + 2b\mu )\left( {{\phi _{\rm{c}}} - {\phi _{\rm{b}}}} \right) - (a + c - 2q\mu )\left( {{\phi _{\rm{a}}} - {\phi _{\rm{b}}}} \right)} \right]}}{{(a + 2b\mu + c)(a + b)}} \end{array} $ | (9) |
在1小层储层分布稳定的条件下,一般a≈c,则a+b>c;ϕc≈ϕa,则ϕc-ϕb≈ϕa-ϕb.设f=ϕc-ϕb≈ϕa-ϕb,则
| $ {\phi _1} - {\phi _2} \approx \frac{1}{2} \times \frac{{b\left( {4a\mu + 2b\mu - a - c} \right)f}}{{(a + 2b\mu + c)(a + b)}} $ | (10) |
当μ=1/2时:
| $ {\phi _1} - {\phi _2} \approx \frac{1}{2} \times \frac{{b\left( {a + b - c} \right)f}}{{\left( {a + b + c} \right)\left( {b + c} \right)}} $ | (11) |
此时,一般有a+b>c.故孔隙度变化只与f有关,即与油层组内储层韵律性有关.若储层总体为正韵律,一般有f<0,故ϕ1-ϕ2<0,即纵向细分单元后,孔隙度变大;若储层总体为反韵律,有f>0,则ϕ1-ϕ2>0,即纵向细分单元后,孔隙度变小.因此,在包含两个小层的油藏中,其中一个小层有储层物性尖灭,若该小层物性较另一小层好,纵向细分单元后,孔隙度变大;反之则孔隙度变小.变化大小与有物性尖灭的单元的有效厚度大小及两个小层的孔隙度差异成正相关.
当μ=1/3时:
| $ \begin{array}{l} {\phi _1} - {\phi _2} \approx \frac{1}{2} \times \frac{{b({\rm{a}} + 2b - 3c)f}}{{(3a + 2b + 3c)(b + c)}}\\ \;\;\;\;\;\;\;\;\;\; \approx \frac{{b(b - c)f}}{{(3a + 2b + 3c)(b + c)}} \end{array} $ | (12) |
此时,孔隙度变化复杂,不仅与1、2小层孔隙度差异有关,也与有效厚度差异有关.分以下2类4种情况:1)2小层有效厚度较1小层大,若2小层孔隙度较1小层小,则ϕ1>ϕ2,因此细分单元后,孔隙度变小;若2小层孔隙度较1小层大,则ϕ1<ϕ2,因此细分单元后,孔隙度变大. 2)2小层有效厚度较1小层小,若2小层孔隙度较1小层大,则ϕ1>ϕ2,因此细分单元后,孔隙度变小;若2小层孔隙度较1小层小,则ϕ1<ϕ2,因此细分单元后,孔隙度变大.
综合以上3种不同类型考虑:1)当各小层在全区分布稳定的条件下,纵向细分单元前后孔隙无变化. 2)纵向细分单元后,某单元存在较大范围的储层物性尖灭时,若其平均孔隙度较其他单元高,孔隙度变大;若其平均孔隙度较其他单元低,孔隙度变小;变化大小与有储层尖灭的单元在含油面积范围内的尖灭范围、该单元有效厚度及该单元与其他单元的孔隙度差异呈正相关. 3)纵向细分单元后,某单元存在较大范围的储层岩性尖灭时,孔隙度变化规律复杂,不仅与细分单元后各单元的孔隙度差异有关,也与有效厚度差异有关.在无地层尖灭的三角洲储层中,不管是以水下分流河道沉积为主的辫状河三角洲沉积还是以河口坝为主的正常三角洲沉积储层中,一般都遵循展布范围大,水体能量相对较强,砂体厚度大,物性也相对较好的规律.正常三角洲沉积一般以物性尖灭为主,因此,细分单元后孔隙度变小;辫状河三角洲沉积一般以岩性尖灭为主,因此,细分单元后孔隙度变大.
3.4 平均油层原始含油饱和度原始含油饱和度指尚未投入开采油层的有效孔隙中含油体积和岩石总有效孔隙体积之比,以百分数表示.在容积法计算储量中,先用厚度、孔隙度权衡计算单井平均含油饱和度,再用孔隙体积权衡法计算得到单元平均含油饱和度.纵向以油层组为单元计算单元平均含油饱和度:
| $ {S_1} = \frac{1}{2}\left( {\frac{{{\phi _{\rm{a}}} \times a \times {S_{\rm{a}}} + {\phi _{\rm{b}}} \times b \times {S_{\rm{b}}}}}{{{\phi _{\rm{a}}} \times a + {\phi _{\rm{b}}} \times b}} + \frac{{{\phi _{\rm{c}}} \times c \times {S_{\rm{c}}} + {\phi _{\rm{d}}} \times d \times {S_{\rm{d}}}}}{{{\phi _{\rm{c}}} \times c + {\phi _{\rm{d}}} \times d}}} \right) $ | (13) |
纵向以小层为单元计算各单元平均含油饱和度再用单元体积加权得到油层组平均含油饱和度:
| $ {S_2} = \frac{{\frac{{{\phi _{\rm{a}}} + {\phi _{\rm{c}}}}}{2} \times {h_1} \times {s_1} \times \frac{{{S_{\rm{a}}} + {S_{\rm{c}}}}}{2} + \frac{{{\phi _{\rm{b}}} + {\phi _{\rm{d}}}}}{2} \times {h_2} \times {s_2} \times \frac{{{S_{\rm{b}}} + {S_{\rm{d}}}}}{2}}}{{\frac{{{\phi _{\rm{a}}} + {\phi _{\rm{c}}}}}{2} \times {h_1} \times {s_1} + \frac{{{\phi _{\rm{b}}} + {\phi _{\rm{d}}}}}{2} \times {h_2} \times {s_2}}} $ | (14) |
式(13)(14)中,Sa、Sb分别为甲井钻遇1、2小层的含油饱和度,Sc、Sd分别为乙井钻遇1、2小层的含油饱和度.按照储层的展布特征和流体分布分以下3种情况分析两种方法计算得到的S1与S2之差.
类型一:由于h1=(a+c)/2,h2=0,s1=s,s2=0,则有
| $ {S_1} = {S_2} = \frac{{{S_{\rm{a}}} + {S_{\rm{c}}}}}{2} $ | (15) |
即在该条件下,纵向细分单元对饱和度无影响.
类型二:由于h1=(a+c)/2,h2=(b+d)/2,s1=s2.则有
| $ {S_2} = \frac{1}{2}\frac{{\left( {{\phi _{\rm{a}}} + {\phi _{\rm{c}}}} \right)(a + c)\left( {{S_{\rm{a}}} + {S_{\rm{c}}}} \right) + \left( {{\phi _{\rm{b}}} + {\phi _{\rm{d}}}} \right)(b + d)\left( {{S_{\rm{b}}} + {S_{\rm{d}}}} \right)}}{{\left( {{\phi _{\rm{a}}} + {\phi _{\rm{c}}}} \right)(a + c) + \left( {{\phi _{\rm{b}}} + {\phi _{\rm{d}}}} \right)(b + d)}} $ | (16) |
S1与S2之差与该情况下ϕ1与ϕ2之差类似,因此S1-S2在0值附近波动.规模油藏中往往包含多个这样的井控区域,故用误差的观点分析,在该条件下,两种方法得到的含油饱和度基本无差别.
类型三:由于h1=(a+c)/2,h2=b,d=0,ϕd=0,s1=s,s2=μs.当2小层存在储层岩性尖灭时,μ=1/3;当2小层存在储层物性尖灭时,取μ=1/2.则有
| $ {S_1} = \frac{1}{2}\left( {\frac{{{\phi _{\rm{a}}} \times a \times {S_{\rm{a}}} + {\phi _{\rm{b}}} \times b \times {S_{\rm{b}}}}}{{{\phi _{\rm{a}}} \times a + {\phi _{\rm{b}}} \times b}} + {S_{\rm{c}}}} \right) $ | (17) |
| $ {S_2} = \frac{1}{2}{\rm{ \times }}\frac{{\left( {{\phi _{\rm{a}}} + {\phi _{\rm{c}}}} \right)(a + c)\left( {{S_{\rm{a}}} + {S_{\rm{c}}}} \right) + 8{\phi _{\rm{b}}}b\mu {S_{\rm{b}}}}}{{\left( {{\phi _{\rm{a}}} + {\phi _{\rm{c}}}} \right)(a + c) + 4{\phi _{\rm{b}}}b\mu }} $ | (18) |
| $ \begin{array}{l} {S_1} - {S_2} = \frac{{2\phi _{\rm{b}}^2{b^2}\left( {{S_{\rm{c}}} - {S_{\rm{b}}}} \right) + {\phi _{\rm{a}}}{\phi _{\rm{b}}}ab\left( {2{S_{\rm{c}}} + {S_{\rm{a}}} - 3{S_{\rm{b}}}} \right) - \left( {{\phi _{\rm{a}}}{\phi _{\rm{b}}}bc + {\phi _{\rm{b}}}{\phi _{\rm{c}}}ab + {\phi _{\rm{b}}}{\phi _{\rm{c}}}bc} \right)\left( {{S_{\rm{a}}} - {S_{\rm{b}}}} \right)}}{{2\left( {{\phi _{\rm{a}}}a + {\phi _{\rm{b}}}b} \right)\left( {{\phi _{\rm{a}}}a + {\phi _{\rm{a}}}c + {\phi _{\rm{c}}}a + {\phi _{\rm{c}}}c + 4{\phi _{\rm{b}}}b\mu } \right)}}\\ = \frac{{4\phi _{\rm{b}}^2{b^2}\mu \left( {{S_{\rm{c}}} - {S_{\rm{b}}}} \right) + 4{\phi _{\rm{a}}}{\phi _{\rm{b}}}ab\mu \left( {{S_{\rm{a}}} + {S_{\rm{c}}} - 2{S_{\rm{b}}}} \right) - \left( {{\phi _{\rm{a}}}{\phi _{\rm{b}}}bc + {\phi _{\rm{b}}}{\phi _{\rm{c}}}ab + {\phi _{\rm{b}}}{\phi _{\rm{b}}}bc + {\phi _{\rm{a}}}{\phi _{\rm{b}}}bc} \right)\left( {{S_{\rm{a}}} - {S_{\rm{b}}}} \right)}}{{2\left( {{\phi _{\rm{a}}}a + {\phi _{\rm{b}}}b} \right)\left( {{\phi _{\rm{a}}}a + {\phi _{\rm{c}}}c + {\phi _c}a + {\phi _c}c + 4{\phi _{\rm{b}}}b\mu} \right)}} \end{array} $ | (19) |
在1小层储层分布稳定的条件下,一般有Sa≈Sc,a≈c,ϕa≈ϕc.取r=ϕaϕbab≈ϕaϕbbc≈ϕbϕcbc≈ϕbϕcab,取m=Sc-Sb≈Sa-Sb,则
| $ {S_1} - {S_2} \approx \frac{{4\phi _{\rm{b}}^2{b^2}\mu m + 4rm(2\mu - 1)}}{{2\left( {{\phi _{\rm{a}}}a + {\phi _{\rm{b}}}b} \right)\left( {{\phi _{\rm{a}}}a + {\phi _{\rm{a}}}c + {\phi _{\rm{c}}}a + {\phi _c}c + 4{\phi _{\rm{b}}}b\mu } \right)}} $ | (20) |
当μ=1/2时:
| $ {S_1} - {S_2} \approx \frac{{2\phi _{\rm{b}}^2{b^2}m}}{{2\left( {{\phi _{\rm{a}}}a + {\phi _{\rm{b}}}b} \right)\left( {{\phi _{\rm{a}}}a + {\phi _{\rm{a}}}c + {\phi _{\rm{c}}}a + {\phi _c}c + 4{\phi _{\rm{b}}}b} \right)}} $ | (21) |
此时,饱和度变化只与m有关,即与1、2小层饱和度差异有关.因此(S1-S2)主要与(Sc-Sb)有关,2小层含油饱和度较1小层低时,则m>0,S1>S2,因此细分单元后,饱和度变小;2小层含油饱和度较1小层高时,则m<0,S1<S2,因此细分单元后,饱和度变大.变化大小与有储层物性尖灭的单元的有效厚度、孔隙度及两小层饱和度差异呈正相关.
当μ=1/3时:
| $ {S_1} - {S_2} \approx \frac{{2\phi _{\rm{b}}{b}\left( {{S_{\rm{a}}} - {S_{\rm{b}}}} \right)\left( {{\phi _{\rm{b}}}b - {\phi _{\rm{a}}}a} \right)}}{{3\left( {{\phi _{\rm{a}}}a + {\phi _{\rm{b}}}b} \right)\left( {{\phi _{\rm{a}}}a + {\phi _{\rm{a}}}c + {\phi _{\rm{c}}}a + {\phi _c}c + 2{\phi _{\rm{b}}}b} \right)}} $ | (22) |
此时,饱和度变化规律复杂.不仅与1、2小层饱和度差异有关,同时与储层的有效储集能力差异有关(本文中统一将有效厚度和对应孔隙度的乘积定义为储层的有效储集能力).分以下2类4种情况:1)2小层有效储集能力较1小层好时,若2小层含油饱和度较1小层低,则S1>S2,因此细分单元后,饱和度变小;若2小层含油饱和度较1小层高,则S1<S2,因此细分单元后,饱和度变大. 2)2小层有效储集能力较1小层差时,若2小层含油饱和度较1小层低,则S1<S2,因此细分单元后,饱和度变大;若2小层含油饱和度较1小层高,则S1>S2,因此细分单元后,饱和度变小.
综合以上3种类型考虑:纵向细分单元后对饱和度影响不大,仅在储层较大范围的尖灭,且细分后的两个单元间饱和度差异较大时,饱和度有一定变化.纵向细分单元后,若某单元存在较大范围的储层物性尖灭时,且该单元平均含油饱和度较其他单元高,纵向细分单元后的饱和度变大,反之则饱和度变小,且变化大小与该单元在含油面积范围内的尖灭范围、有效厚度、孔隙度及该单元与其他单元饱和度差异呈正相关.若某单元有较大范围储层岩性尖灭时,饱和度变化规律复杂,不仅与细分单元后各单元的饱和度差异有关,同时与储层的有效储集能力差异有关.根据前人的研究,含油饱和度随含油高度增加、孔隙结构变好而增大[23-24],纯油层段的高部位含油饱和度较低部位高,河口坝储层的含油饱和度较远沙坝-席状砂储层高.因此,对于进积型正常三角洲储层,纵向细分单元后,下部单元存在储层物性尖灭,纵向细分单元后的饱和度变小.对于进积型辫状河三角洲储层,纵向细分单元后,下部单元存在储层岩性尖灭,纵向细分单元后的饱和度变大.
4 各参数变化规律及应用实例分析本文为了方便计算,以均匀井网条件下的两口井为例,对纵向细分单元前后各储量参数的变化规律进行了探讨,实际油藏中是包含几十个,甚至成百上千个这样的小的井块在三维空间上的拼叠,它们的变化规律是这些小井块的累加,因此,以上规律仍然是适用的.在以上分析的基础上,并结合含油面积范围内储层尖灭情况,将辫状河三角洲和正常三角洲储层的多层构造油藏纵向细分单元前后储量参数变化规律总结于表 2.
|
|
表 2 不同类型多层构造油藏纵向细分单元储量参数变化表 Table 2 Reserve parameter variation of vertical subdivision units in different types of multilayer structural reservoir |
以锦州9-3油田多层构造油藏A、B为例,A油藏发育正常三角洲沉积储层,按小层纵向细分后可分为上下两个单元,下部单元在含油面积范围内出现大范围的物性变化造成的储层尖灭,且其物性和含油饱和度均较上部单元低.按纵向是否细分单元两种方案计算储量如表 3.按小层纵向细分单元后以面积或者体积加权后得到以油层组为单元的参数,含油面积无变化,有效厚度、平均孔隙度和含油饱和度均不同程度变小,总储量数变小. B油藏发育辫状河三角洲沉积储层,按小层纵向细分后可分为上下两个单元,下部单元在含油面积范围内出现大范围的岩性变化造成的储层尖灭,且其物性和含油饱和度均较上部单元低.按纵向是否细分单元两种方案计算储量如表 3.按小层纵向细分单元后以面积或者体积加权后得到以油层组为单元的参数,含油面积无变化,有效厚度略有变小,平均孔隙度和含油饱和度变大,总储量数较纵向细分单元前略有变大.该计算结果验证了本文理论推导的正确性,可为同类油田的精细储量研究提供技术支撑.
|
|
表 3 锦州9-3油田A、B油藏储量计算表 Table 3 Reserve calculation of A and B reservoirs in JZ9-3 oilfield |
计算单元划分是储量计算中的关键一环,其划分是否合理,对储量计算结果的准确性和适用性至关重要.为确保储量精细研究过程中各单元的参数选取合理,应尽量减少油层组内部储层非均质性对储量评价的影响[25].根据储量计算规范,将油层组内不同岩性、储集特征进一步细分计算单元.根据本文的理论研究,同时考虑工作实际情况,对纵向细分计算单元的原则做进一步优化.
1)在储层的横向展布特征和纵向分布规律认识清楚的基础上,纵向细分计算单元主要考虑油层组内部各小层的储层横向展布和隔夹层展布,尤其是对于在含油面积范围内存在较大范围尖灭的小层一定要单独划分计算单元.
2)可将物性和储层展布特征相似的邻近小层合并为一个单元进行计算,在此尺度下计算的储量和以小层为单元计算的储量基本无差异.
6 结论1)以上研究对不同类型(储层展布、物性变化、流体分布)的多层构造油藏纵向细分单元前后储量参数(容积法)变化规律进行了系统分析,为同类油田的精细储量研究提供了技术支撑.
2)对于多层构造油藏,纵向细分单元后,含油面积无变化.若含油面积范围内无储层尖灭,仅辫状河三角洲沉积储层的油藏纵向细分单元后有效厚度变小,而其他储量参数无变化.若含油面积范围内储层尖灭,一般情况下,正常三角洲沉积储层的油藏纵向细分单元后各参数均变小,但退积型正常三角洲沉积储层油藏的含油饱和度可能变大;辫状河三角洲沉积储层的油藏纵向细分单元后有效厚度变小,有效孔隙度和含油饱和度变大,但退积型辫状河三角洲沉积储层的油藏含油饱和度可能变小.
3)纵向细分单元后,由于各储量参数变化的方向性,储量计算结果也存在规律变化.无储层尖灭的正常三角洲沉积储层的油藏,一般储量基本无变化;无储层尖灭的辫状河三角洲沉积储层的油藏和有储层尖灭的正常三角洲沉积储层的油藏一般储量变小;有储层尖灭的辫状河三角洲沉积储层的油藏储量可能变大.因此,对于多层岩性-构造油藏,为了更准确表征储量分布情况,应根据储层展布特征和物性差异,进一步细分计算单元.
4)纵向细分计算单元时应以油藏内部各小层砂体横向展布和物性差异及隔夹层为地质依据,也可将不同微相类型控制下的具有相似物性特征的邻近小层合并为一个单元进行计算.
| [1] |
赵文智, 高瑞祺, 胡素云, 等. 对我国油气储量规范修订工作的思考[J]. 新疆石油地质, 2005, 26(2): 221-225. |
| [2] |
朱筱敏, 董艳蕾, 杨俊生, 等. 辽东湾地区古近系层序地层格架与沉积体系分布[J]. 中国科学(D辑:地球科学), 2008(S1): 1-10. |
| [3] |
樊太亮. 层序地层体制中的陆相储层发育规律[J]. 地学前缘, 2000, 7(4): 315-321. |
| [4] |
邓宏文, 王洪亮, 翟爱军, 等. 中国陆源碎屑盆地层序地层与储层展布[J]. 石油与天然气地质, 1999, 20(2): 108-114. |
| [5] |
刘忠保, 吕奇奇, 罗顺社, 等.进、退积型辫状河三角洲沉积模拟实验研究[C]//第十三届全国古地理学及沉积学学术会议.北京: 中国矿物岩石地球化学学会岩相古地理专业委员会, 2014.
|
| [6] |
符勇, 黄礼, 白玉彬, 等. 靖边油田L区块长6油层组沉积特征[J]. 地质与资源, 2019, 28(1): 49-56. |
| [7] |
薛艳霞, 廖新武, 霍春亮, 等. 海上河流相储层应用地质模型计算储量的不确定性分析[J]. 油气藏评价与开发, 2018, 8(4): 1-5, 10. |
| [8] |
刘吉余, 隋新光, 于润涛, 等. 地质储量精细计算方法研究[J]. 海洋地质动态, 2003, 19(9): 31-34. |
| [9] |
陈元千, 郝明强, 李飞. 油气资源量评估方法的对比与评论[J]. 断块油气田, 2013, 20(4): 447-453. |
| [10] |
张玲, 魏萍, 肖席珍. SEC储量评估特点及影响因素[J]. 石油与天然气地质, 2011, 32(2): 293-301. |
| [11] |
李定军. 概率统计法在储量估算中的应用[J]. 断块油气田, 2014, 21(5): 615-618. |
| [12] |
张雪峰, 罗安湘, 惠潇, 等. 基于层区带刻度区地质特点的资源评价方法适用性分析[J]. 地质科技情报, 2016, 35(4): 59-65. |
| [13] |
李伟, 鲁雪松, 柳少波, 等. 随机模拟在油气资源评价中的应用[J]. 断块油气田, 2013, 20(4): 443-446. |
| [14] |
中华人民共和国国土资源部. DZ/T 0217-2005石油天然气储量计算规范[S].北京: 中国标准出版社, 2005.
|
| [15] |
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. GB/T 19492-2004石油天然气资源/储量分类[S].北京: 中国标准出版社, 2004.
|
| [16] |
赵文智, 毕海滨. 论储量评估中的单元划分[J]. 石油与天然气地质, 2007, 28(3): 309-314. |
| [17] |
金之钧, 张金川. 油气资源评价方法的基本原则[J]. 石油学报, 2002, 23(1): 19-23. |
| [18] |
毕海滨, 查全衡, 王永卓. 提高储量评估水平的三大地质要素[J]. 石油学报, 2004, 25(1): 25-29. |
| [19] |
周永炳, 刘国志, 俞静. 大庆低渗透油藏探明储量面积圈定的几点认识[J]. 岩性油气藏, 2007, 19(4): 111-115. |
| [20] |
杨通佑, 范尚炯, 陈元千, 等. 石油及天然气储量计算方法[M]. 北京: 石油工业出版社, 1990.
|
| [21] |
黄文华, 郭瑞, 周伯玉, 等. 准噶尔盆地风城地区油砂矿勘探评价[J]. 新疆石油地质, 2017, 38(2): 144-148. |
| [22] |
中国石油天然气总公司. SY/T 5782-1993砂岩透镜体岩性油藏储量计算细则[S].北京: 石油工业出版社, 1994.
|
| [23] |
欧阳健, 王贵文, 吴继余, 等. 测井地质分析与油气层定量评价[M]. 北京: 石油工业出版社, 1999.
|
| [24] |
欧阳健. 油藏中饱和度-电阻率分布规律研究——深入分析低电阻油层基本成因[J]. 石油勘探与开发, 2002, 29(3): 44-47. |
| [25] |
陈清华, 杨超, 王秀玲, 等. 基于储层构成单元的油气储量计算方法[J]. 西安石油大学学报(自然科学版), 2008, 23(2): 32-34. |
 2020, Vol. 29
2020, Vol. 29

