20世纪40年代,塞尔维亚的科学家米卢廷·米兰科维奇(Milutin Milanković)提出的米兰科维奇旋回理论,即地球自转和围绕太阳公转时由于其他行星对它的引力摄动作用导致的地球轨道3个参数(岁差、斜率和偏心率)具有万年到百万年尺度的周期性变化,从而驱动了地球表面接受的太阳辐射量沿纬度和季节分配上的周期性的波动,导致了地球的气候也在万年到百万年时间尺度上发生有规律的变化[1~4]。米兰科维奇旋回理论在近40年的古气候研究中获得了普遍的认可和广泛的应用(从Hays等1976年的Science论文算起)[1],成为了古气候研究从定性描述到定量研究的里程碑。那么,除了普遍被认可的米兰科维奇旋回理论是地球气候系统在万年到百万年时间尺度上发生变化的主要驱动机制[5],近年来有关太阳活动的研究被越来越多的学者所关注,被认为是地球气候在年际-百年-千年尺度上发生变化的可能的主要驱动因素[6~13]。
太阳辐射是驱动地球表层气候系统发生变化的主要外部驱动力,到达地表的太阳辐射量的变化直接驱动了地表各种过程发生变化[9]。近30多年来的监测数据表明,地表接受的太阳总辐射量(Total Solar Irradiance,简称TSI)与太阳活动的黑子数(sunspot number,简称SSN)之间呈现出明显的正相关关系[14~16]。太阳活动虽然包括发生在太阳表面如黑子、光斑、谱斑、耀斑以及日珥和日冕等一切扰动现象,但是在目前的研究中一般以太阳黑子数的变化来指示太阳活动的变化。研究表明[10, 16],太阳黑子的活动直接影响了地表接受的太阳辐射量的变化,进而驱动了地球气候系统的变化。
太阳亮度的变化具有显著的约11 a的周期,这已经被1978年以来由多个太空辐射计直接观测到的太阳辐射量的变化所证实,当太阳黑子数增加即太阳活动增强时,地表接受的太阳总的辐射量增加,从最近的第22、23和24这3个太阳活动周期看,从最小值到最大值太阳辐射增加约为0.1 % [9]。这个约11 a的太阳活动周期早在1843年就被Schwabe发现[8],因而也被称为“Schwabe cycle”,Ineson等[17]和Thiéblemont等[18]证实约11 a的太阳活动周期驱动了北半球和北大西洋气候的变化。此外,在年际尺度上的太阳活动周期还有22 a的太阳磁极性反转的周期也称为“Hale cycle”也是稳定存在的[19~21]。在百年尺度上的太阳活动周期主要有约88 a格莱斯堡周期“Gleissberg Cycle”[22~23],研究表明这个周期在频谱图上呈现双峰型且具有50~80 a和90~140 a两个周期范围[24~26],以及约210 a双世纪周期又称Suess(或de Vries)周期,也在宇宙成因的14 C记录中被发现[27~28]。千年尺度的太阳活动周期还有约1000 a的Eddy周期和约2300 a(或2200~2400 a)被称为“Hallstatt cycle”即哈尔斯塔周期也在地质记录中被发现与气候事件具有明显的联系[8, 25, 27]。Usoskin等[29]利用重建的太阳黑子数序列获得了太阳活动Hallstatt周期;Steinhiber等[13]利用宇宙成因核素重建了过去9400年的太阳活动(太阳总辐射量TSI)数据序列,小波分析能量谱表现出约210 a的Suess周期、约1000 a的Eddy周期及约350 a、500 a和710 a等一些其他周期;Peristykh和Damon[25]通过分析国际年代矫正工作组(International Calibration(IntCal)1998年校正得到的过去14000年的反映大气中宇宙成因的14 C浓度随时间变化的数据序列,即INTCAL98曲线,从频谱图中识别出了约2300 a、208 a、104 a、88 a、44.9 a以及150 a和61 a的太阳活动周期;Braun等[7]认为前人在北大西洋发现的约1470 a的D-O气候变化事件信号可能也是由于太阳活动周期所驱动的,通过模拟发现约1470 a的气候变化信号是约87 a和210 a的太阳活动周期的叠加信号。
目前,米兰科维奇旋回理论用来解释轨道尺度的气候变化的驱动机制问题已经获得了普遍认可[1, 2, 4],但是太阳活动周期与不同尺度的气候变化之间的驱动机制还仍然很不明确,地球气候系统在年际-百年甚至千年的亚轨道尺度上变化的驱动机制问题一直存在着诸多争议。本文试图从不同太阳活动周期与气候指标中识别出来的周期旋回之间的相互关系,以及不同时间尺度的太阳活动周期之间的调制和耦合关系的角度来解释亚轨道尺度上的气候变化的驱动机制问题。
2 材料和方法 2.1 太阳黑子的观测及其重建数据本文用于研究的300多年(1700~2018年)的太阳黑子数(Sunspots number也称为Wolf numbers,SSN)数据是从http://sidc.oma.be/silso/datafiles网站上下载获得的,近1000年的太阳黑子数序列是从太阳活动指数(Extended time series of Solar Activity Indices,简称ESAI)http://www.gao.spb.ru/databaseesai网站的数据库上下载获得的,此数据是在分析了已有的1750~2002年观测太阳黑子数的非平稳频率-振幅结构,通过模拟重建了1090~2002年以及0~11400 a B.P.的太阳黑子数变化序列[30]。
2.2 石笋数据石笋是研究气候环境变化的重要载体,它记录了不同时间尺度的气候变化信息[31~37],包括米兰科维奇旋回、气候突变事件甚至年际尺度的气候变化。从石笋中提取的氧同位素δ18O数据序列被认为是可以指示季风和降水强度变化信号的古气候替代指标[38~43]。对于年际-百年尺度的气候变化指标,本文选取南美洲巴西Pau d'Alho洞(15°12′ S,56°49′ W) ALHO6石笋δ18O数据[44],ALHO6石笋全长240 mm,层序连续性好,其定年结果基于12个U-Th和年层计数相结合的方法,时间跨度从约491.7~1860.3 A.D.,平均时间分辨率为1.15年,本文选取ALHO6石笋数据的1000~1860 A.D.进行分析。石笋所处位置属于南美热带季风(South American Monsoon System,简称SAMS)气候区,石笋δ18O数据反映的是南美地区降水量的变化,当δ18O正偏时,指示降水减少,SAMS强度减弱,当石笋δ18O负偏时,指示降水增加,SAMS强度增强。对于百年-千年尺度的气候变化指标,本文选取贵州董哥洞(DA)石笋(25°17′N,108°5′E,海拔688 m)δ18O数据[45]。DA石笋长度为962.5 mm,层序连续性好,其定年结果由45个230 Th值共同确定,230Th年龄误差小于50年,从距今约9000年到2002年,共测得2124个δ18O测量值,平均时间分辨率为4.5年,生长速率大约每年约100 μm。DA石笋位于中亚热带的东亚季风和西南季风交汇区,冬季表现为干-冷的气候特征;夏季受热带辐合带北移的影响该地区降水量增大,表现为暖-湿的气候特征,研究表明,该石笋记录的气候信息与南美ALHO6石笋类似,δ18O偏负意味着季风降水增强,δ18O偏正意味季风降水强度减弱。高分辨率的石笋是研究全新世气候变化特征的重要载体,也是揭示气候变化-太阳活动之间关系的重要依据。
2.3 树轮数据本文选取美国加利福尼亚州白山山脉(37°27′N,118°10′ W,海拔3200 m)的布兰科西部地区5 km2范围内的7棵古狐尾松[46]。由于该区寒冷干燥的气候条件,狐尾松(Pinus longaeva)的生长季节短且生长非常缓慢,平均每100年长高不到2.5 cm。据标准树轮年代定年[46],该数据序列记录从1085~2005年,时间分辨率为1年,共测得921个树轮δ13C值。研究结果表明[46],从α-纤维素组分测得的稳定碳同位素比率对过去大气降水变化的信号敏感,当δ13C负偏时指示该地区降水增加,当δ13C正偏时指示该地区降水减少,这与石笋δ18O指示的降水量的变化一致。
2.4 太阳总辐射量变化数据本文选取全新世太阳总辐射量变化(Total Solar Irradiance,简称ΔTSI)数据是从Steinhilber等[13]利用冰岛和南极冰芯中的记录的10 Be数据以及全球树轮中记录的14 C数据,重建的全新世太阳总辐照量变化曲线,时间范围- 57.5~9312.5 a B.P. (0为1950 A.D.),时间分辨率是5年。太阳总辐射量变化与太阳黑子数变化一样,都是反应太阳活动的重要指标,当太阳总辐射值高时指示太阳活动强烈,当太阳总辐射值低时指示太阳活动较弱[16]。
2.5 研究方法本文采用多窗口谱(Multi-taper Method,简称MTM)频谱分析方法对时间数据序列进行从时间域到频率域的转换,以获取时间序列中存在的不同旋回周期。进行频谱分析前,对数据序列进行线性插值处理使非等间距的数据转化为频谱分析需要的等间距的数据序列。在频谱分析的基础上,利用高斯(Gaussian)带通滤波(band-pass filtering)的方法,提取出数据序列中有用的周期信号,同时滤除与旋回周期无关的“噪音”信号,然后将提取出来的旋回周期信号再与原始数据序列叠置在一起,观察旋回的变化并识别出主要的天文周期旋回[47]。
同时,本文还采用了Morlet小波分析方法,利用连续小波变换(Continue Wavelet Transform,简称CWT)分析获得不同指标存在的长/短周期,在现代气候研究和分析中得到了广泛应用[48~49]。功率谱分析表明[48],气候振荡和太阳活动具有复杂的时频结构和多周期尺度特征。交叉小波变换(Cross Wavelet Transform,简称XWT)是一种新的多信号分析技术[48],将小波变换与交叉谱分析结合来分析两组等采样间隔的时间序列,可以同时展示多尺度下两组序列在时间域和频率域中的相互关系,用来分析不同气候指标之间的相互影响的时延相关特征和时频位相关系;小波相干谱(Wavelet Coherence,简称WTC)可以用来说明两组时间序列在时间域和空间域的局部密切程度[48]。
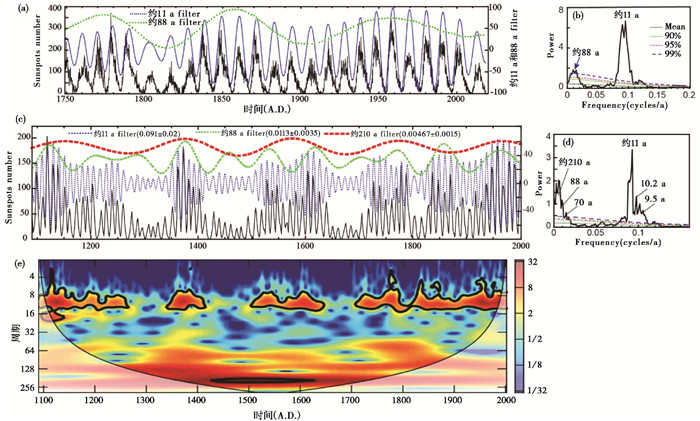
3 结果分析 3.1 年际-百年尺度的太阳活动周期特征分析从观测的太阳黑子数据序列(1749~2018年)及其频谱分析图上可以看出,太阳活动即太阳黑子数的变化存在着明显的约11 a和约88 a的周期变化信号(图 1a和1b),重建的太阳黑子数据序列中存在着约11 a、88 a和210 a的周期变化信号(图 1c和1d),从小波分析图上可以看出,整个数据序列都存在着明显的约11 a的变化周期,并且时强时弱,约88 a(60~130 a)的周期也稳定存在的,但是能量不是很强,约210 a的周期稳定存在,尤其是在1270~1700年这一段时间(图 1e)。从图 1a和1c可以看出,约11 a和88 a的周期存在着某种调制关系,约88 a的周期旋回基本上是随着约11 a太阳黑子数振幅变化而变化的周期。
|
图 1 实际观测的太阳黑子数(1749~2018年)及重建的太阳黑子数序列及其周期滤波、频谱和小波分析图 (a)和(b)为实测太阳黑子序列及其约11 a和88 a周期滤波和频谱分析图;(c)、(d)和(e)分别为重建太阳黑子序列及其约11 a、88 a和200 a周期滤波和频谱及小波分析图 Fig. 1 Actual observed sunspot number(1749~2018)and reconstructed sunspot number variations and its main cycle filtering, spectra and wavelet analysis. (a)The observed sunspot number variation series with about 11 a and 88 a filtered output and its power spectrum (b); (c)The reconstructed sunspot number variations series with ca. 11 a, 88 a and 210 a filtered output and its power spectrum (d); (e)Wavelet analysis of the reconstructed sunspot number in (c) |
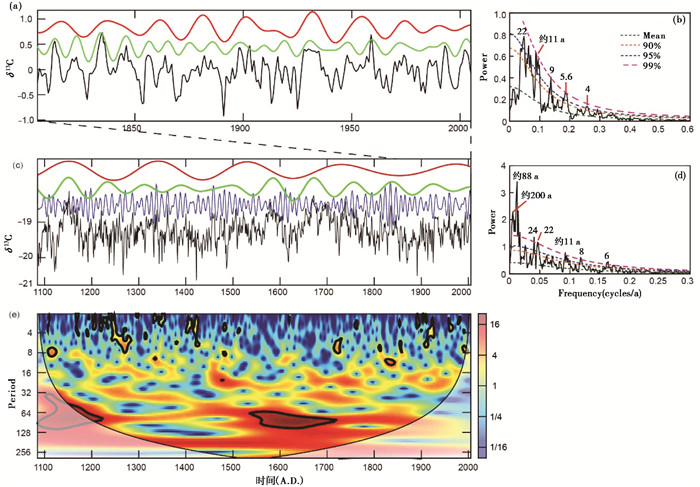
通过对Bale等[46]建立的美国加州白山狐尾松树轮δ13C(1085~2005年)数据序列以及放大的1800~2005年数据段的频谱分析,发现δ13C序列存在着明显的约11 a、22 a、88 a和200 a的周期变化(图 2a、2b、2c和2d),以及约4 a和5~6 a的短周期。约88 a周期变化范围较大,在50~140 a之间波动,约88 a的周期在1085~1300年和1500~1900年时间段稳定存在(图 2e)。约11 a、22 a、88 a和200 a的周期与太阳黑子的Schwabe、Hale、Gleissberg和Suess活动周期一致,说明白山狐尾松树木的生长明显受到多个太阳活动周期的影响,这指示了这些太阳活动周期影响了该地区的降水,从而被狐尾松树轮记录下来了这些气候变化信息。
|
图 2 美国加州白山狐尾松树轮δ13C时间序列及其周期滤波和频谱及小波分析图 (a)和(c)分别为1800~2005年和1085~2005年的δ13C数据去除35 %的加权平均值后的剩余值序列(数据来源于Bale等[46])及其它们的滤波曲线(b)和频谱图(d),滤波曲线和带宽分别为(a)约22 a红色(0.045±0.02),约11 a绿色(0.09±0.03);(c)约200 a红色(0.005±0.001),约88 a绿色(0.0113±0.003),约11 a蓝色(0.09±0.03);(e)1085~2005年的δ13C数据(c)的小波分析图 Fig. 2 The δ13C time series from the bristlecone pine tree-ring in California(USA)and its main cycle filtering, spectra and wavelet analysis. (a)Theδ13C residual series after subtracted the 35 % weighted average 1800~2005 A.D. with about 11 a(green, passband:0.09±0.03)and 22 a(red, passband:0.045±0.02)filter and its power spectrum of (b); (c)The δ13C residual series after subtracted the 35 % weighted average 1085~2005 A.D. with about 11 a(blue), 88 a(green)and 200 a(red)filter and its power spectrum of (d), original data from Bale, et al. [46]; (e)Wavelet analysis of the δ13C series in (c) |
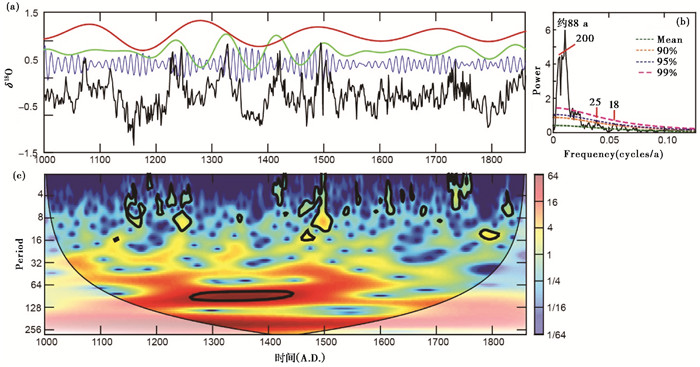
通过对Novello等[44]建立的南美洲巴西Pau d'Alho洞ALHO6石笋δ18O(1000~1860年)序列进行频谱分析,发现δ18O序列存在着明显的约20 a、88 a和200 a周期变化信号(图 3a和3b),从小波变换分析图上也可以看出,约88 a周期变化范围较大,在60~140 a之间波动,约88 a周期在1150~1600年时间段信号非常强,而约200 a的周期信号在整个数据序列都非常稳定地存在(图 3c),这指示了南美夏季风的周期性变化信号与太阳活动周期的Gleissberg和Suess周期一致,说明该地区降水量的变化可能主要受到这两个太阳活动周期的驱动。
|
图 3 巴西ALHO6石笋δ18O时间序列及其周期滤波和频谱及小波分析图 (a)ALHO6石笋δ18O变化序列(数据来源于Novello等[44],原始数据去除35 %加权平均值后的剩余值序列)及其约200 a红色、88 a绿色和11 a蓝色滤波曲线,其中心频率及带宽分别为0.005±0.001、0.0113±0.004和0.091±0.02;(b)ALHO6石笋δ18O序列的能量频谱分析图;(c)小波变换分析图 Fig. 3 The δ18O time series from the ALHO6 stalagmite in Brazil and its main cycle filtering, spectrum and wavelet analysis. (a)The δ18O residual series after subtracted the 35 % weighted average with about 11 a(blue, passband:0.091±0.02), 88 a(green, passband:0.0113±0.004), and 200 a(red, passband:0.005±0.001)filter and its power spectrum on the right (b), the original data from Novello, et al. [44]; (c)Wavelet analysis of the series in (a) |
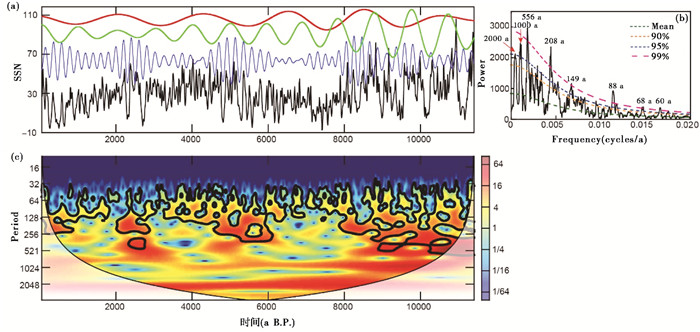
通过对Solanki等[30]重建的过去11000年的太阳黑子数据序列进行频谱分析,发现该序列存在较强的约88 a、208 a、556 a和约1000 a的旋回周期,以及明显的60 a、68 a、149 a和约2000 a的周期(图 4a和4b),其中,约88 a、208 a、1000 a和2000 a是Gleissberg、Suess、Eddy和Hallstatt太阳活动周期,而60 a、68 a和149 a可能是约88 a的Gleissberg周期,而约2000 a周期基本上是约208 a旋回振幅的变化周期(图 4a)。从图 4a可以看到约1000 a在3500~11405 a B.P.的时间段都较为稳定的存在,约2000 a的周期旋回在整个时间序列中都稳定的存在,而约88 a和208 a的信号在能量频谱图上虽然非常强(图 4b),但是在小波分析图上可以看出是时强时弱,而约556 a的信号虽然在能量功率谱上最强,但是在小波分析图上只在8000 a B.P.年以前非常强(图 4c)。对于这个500 a左右的周期信号,一方面可能是由于重建时用到的数据的年代精度问题造成的,另一方面,也可能是实际存在的太阳活动周期信号,但迄今为止还没有被命名。
|
图 4 重建的近1.2万年太阳黑子数时间序列及其主要周期滤波和频谱及小波分析图 (a)太阳黑子数变化序列(数据来源于Solanki等[30])及其约2000 a红色、约1000 a绿色和208 a蓝色滤波曲线,其中心频率及带宽分别为0.0005±0.00015、0.001±0.0002和0.0048±0.0008;(b)太阳黑子数变化序列的能量频谱分析图;(c)小波变换分析图 Fig. 4 The reconstructed ca.12 ka-long sunspot number variations series with its main cycles filtering, spectrum and wavelet analysis. (a)The sunspot series with about 208 a(blue), 1000 a(green)and 2000 a(red)filtered output(passband:0.0048±0.0008, 0.001±0.0002 and 0.0005±0.00015 respectively)and its power spectrum (b), the original data from Solanki, et al. [30]; (c)wavelet analysis of the series in (a) |
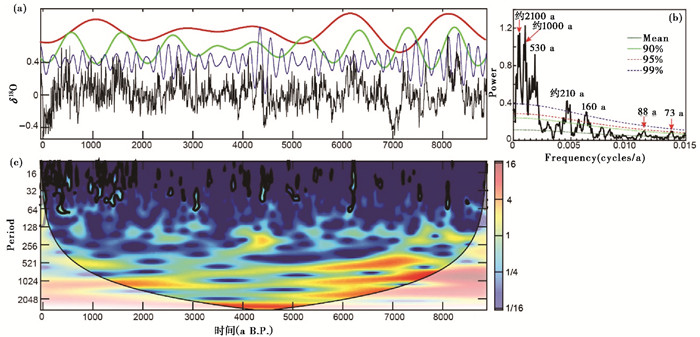
利用Wang等[45]建立的贵州董哥洞DA石笋δ18O数据序列进行频谱分析,发现δ18O序列中存在较强的约210 a、530 a、1000 a和2100 a的旋回周期,以及明显的约88 a、73 a和160 a的周期(图 5a和5b),其中,约88 a、210 a、1000 a和2100 a是Gleissberg、Suess、Eddy和Hallstatt太阳活动周期,约73 a和160 a的周期可能分别是Gleissberg和Suess周期,约530 a的周期与重建的太阳黑子序列中的约556 a的周期接近。从小波变换分析图上观察到约1000 a周期除了在3000~5000 a B.P.之间信号较弱外,其余时期都较强,而约2100 a的周期则一直稳定地存在(图 5c)。从上述分析的结果可以推断,该区域的季风强度和降水主要受约210 a、1000 a和2100 a这3个太阳活动周期的驱动和影响。
|
图 5 贵州董哥洞DA石笋δ18O数据序列及其周期滤波和频谱及小波分析图 (a)DA石笋δ18O变化序列(数据来源于Wang等[45],原始数据去除35 %加权平均值后的剩余值序列)及其约2000 a(红色)、1000 a(绿色)和210 a(蓝色)滤波曲线,其中心频率及带宽分别为0.0005±0.00015、0.001±0.00025和0.0048±0.0015);(b)DA石笋δ18O序列的能量频谱分析图;(c)小波变换分析图 Fig. 5 The δ18O time series from the DA stalagmite in Guizhou, China and its main cycle filtering, spectrum and wavelet analysis. (a)The δ18O residual series after subtracted the 35 % weighted average with about 210 a(blue), 1000 a(green)and 2000 a(red)filtered output(passband:0.0048±0.0015, 0.001±0.00025 and 0.0005±0.00015 respectively)and its power spectrum on the right (b), the original data from Wang, et al.[45]; (c)Wavelet analysis of the series in (a) |
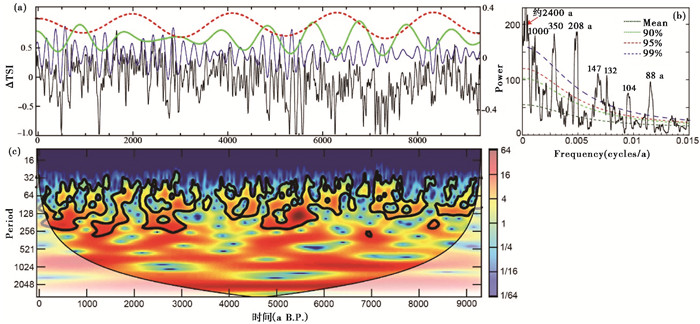
Steinhilber等[13]重建得到的近9400年太阳总辐射量(ΔTSI)的变化序列的频谱分析,发现存在较强的约88 a、104 a、132 a、147 a、208 a、350 a、1000 a和2400 a的旋回周期(图 6a和6b),从图 6c上也可以看出,约1000 a和2400 a在整个序列中都稳定存在,约88 a和208 a两个旋回虽然在频谱图上非常强,但是在小波分析图上表现为时强时弱(图 6c)。约104 a的周期可能是208 a周期的谐波,但也可能与132 a和147 a这两个周期一起都属于Gleissberg周期。太阳活动的百年-千年尺度的Gleissberg、Suess、Eddy和Hallstatt周期稳定存在于ΔTSI变化序列中,这说明,利用冰芯和树轮中记录的指示地表接受的太阳辐射量变化的10 Be和14 C数据重建的太阳总辐射量ΔTSI变化序列,可以用来作为太阳活动的替代指标。频谱图 6b上显示的非常强的约350 a的周期,一方面可能是由于重建时测年精度的误差造成,但也不排除是可能存在的太阳活动周期,尽管还没有被命名。
|
图 6 重建的近万年太阳总辐射量ΔTSI数据变化序列及其主要周期滤波和频谱及小波分析图 (a)Steinhilber等[13]重建的近万年太阳总辐射变化量ΔTSI时间序列及其约2400 a(红色虚线)、1000 a(绿色)和208 a(蓝色)滤波曲线,其中心频率及带宽分别为0.00048±0.00015、0.001±0.00025和0.0048±0.0015;(b)太阳总辐射量ΔTSI数据变化序列的能量频谱分析图;(c)小波变换分析图 Fig. 6 The reconstructed ΔTSI series and its main cycle filtering, spectrum and wavelet analysis. (a)The ΔTSI series with about 208 a(blue), 1000 a(green)and 2400 a(red dash line)filtered output(passband:0.0048±0.0015, 0.001±0.00025 and 0.00048±0.00015 respectively)and its power spectrum on the right (b), the original data from Steinhilber et al. [13]; (c)Wavelet analysis of the series in (a) |
通过对树轮、石笋与太阳黑子数和太阳总辐射量变化做小波交叉谱(XWT)和相干谱(WTC)分析(图 7),发现美国加州白山狐尾松δ13C[46]和太阳黑子数的约11 a、88 a和200 a周期之间存在相关性,表现为约11 a和88 a高能量带的箭头大致指向左下方,说明Schwabe周期和Gleissberg周期在太阳黑子数序列中发生的时间要早于狐尾松δ13C数据序列中约3/ 8个周期(分别约为4年和33年左右);而约200 a周期的高能量区的箭头指向垂直向下,这意味着太阳黑子数发生变化的早于加州白山狐尾松δ13C数据序列发生变化约1/ 4个周期即约50年的时间(图 7a和7b)。南美洲巴西ALHO6石笋δ18O数据[34]和太阳黑子数(1090~2002年)的小波交叉谱和小波相干谱分析,其中,约11 a周期之间相关性不明显,可能原因是巴西ALHO6石笋δ18O数据本身约11 a周期不明显,但二者约88 a(约64~150 a)周期具有一定的相关性,表现为高能量区的箭头几乎水平向左,说明太阳黑子数的约88 a周期早于ALHO6石笋δ18O变化约1/ 2个周期即40多年;同时发现二者约200 a周期具有一定的相关性,表现为约200 a周期的高能量区的箭头指向左下方,这意味着太阳黑子数发生变化的约200 a周期早于巴西ALHO6石笋δ18O数据序列变化约3/ 8个周期(图 7c和7d)。

|
图 7 树轮δ13C和石笋δ18O与太阳黑子数(SSN),以及SSN和ΔTSI与董哥洞石笋δ18O之间的小波交叉谱和相干谱分析图 (a)和(b)分别为美国白山狐尾松δ13C和太阳黑子数的小波交叉谱(XWT)和相干谱(WTC)分析图[46];(c)和(d)分别为南美巴西ALHO6石笋δ18O与太阳黑子数的XWT和WTC分析图[44];(e)和(f)分别为董哥洞DA石笋δ18O与ΔTSI的XWT和WTC分析图[45];(g)和(h)分别为董哥洞DA石笋δ18O与太阳黑子数的XWT和WTC分析图[45] Fig. 7 Cross Wavelet Transform(XWT)and Wavelet coherence(WTC)spectra analysis between tree-ring δ13C and stalagmite δ18O and sunspot number(SSN), and between SSN and ΔTSI and DA stalagmite δ18O. (a)and (b) are the XWT and WTC between the δ13C time series from the bristlecone pine tree-ring in California(USA)and SSN[46]; (c)and (d) are XWT and WTC between the δ18O series from the ALHO6 stalagmite in Brazil and SSN[44]; (e)and (f) are XWT and WTC between the δ18O series from the DA stalagmite in Guizhou, China and ΔTSI[45]; (g)and (h) are XWT and WTC between the δ18O series from the DA stalagmite in Guizhou, China and SSN[45] |
通过对Wang等[45]建立的贵州董哥洞DA石笋δ18O序列和Steinhiber等[13]重建的太阳总辐射量ΔTSI变化序列做小波交叉谱和小波相干谱分析,发现二者在约88 a、200 a、500 a、和1000 a周期上都都存在相关性,虽然时频变化复杂,但是不同周期黑色箭头的指向大致水平向左,指示了太阳总辐射量发生变化的(约88 a、200 a、500 a和1000 a)周期早于董哥洞DA石笋δ18O发生变化约1/ 2个周期;而约2000 a周期在3000~6000 a B.P.指向近乎垂直向下,指示了在该时间段太阳总辐射量发生变化的约2000 a的周期早于董哥洞DA石笋δ18O发生变化约1/ 4个周期(图 7e和7f)。通过对Solanki等[30]重建的太阳黑子数序列与董哥洞DA石笋δ18O序列做小波交叉谱和小波相干谱分析,发现二者在约88 a(50~150 a)、500 a、1000 a和2000 a周期上都都存在相关性,不同周期黑色箭头的指向大致水平向左,指示了太阳黑子数变化先于董哥洞DA石笋δ18O变化1/ 2个周期。而约200 a周期的高能量区在2000~3000 a B.P.箭头指向左,在8000~9000 a B.P.箭头指向上,这指示在8000~9000 a B.P.时期,太阳黑子数变化早于董哥洞DA石笋δ18O变化约3/ 4个周期,之后又变为早于它约1/ 2个周期(图 7g和7h)。
上述小波的交叉和相干谱综合分析结果表明,太阳活动即太阳黑子数发生变化和太阳总辐射量的变化周期普遍要早于气候指标发生变化的周期约1/ 4个甚至3/ 4个周期,北美的狐尾松树轮的碳同位素数据以及南美石笋的氧同位素记录与太阳黑子数的交叉谱图上(图 7a和7c)都显示出在约88 a和210 a的周期高能量区的箭头几乎水平向左,太阳活动周期都是早于树轮和石笋记录的气候变化半个周期的,这指示了太阳活动周期驱动的气候变化周期不受研究材料所在纬度的影响。而太阳黑子数和太阳总辐射量的变化周期几乎同时发生变化,不存在滞后性,这指示了太阳黑子的活动直接驱动了地表接受的太阳辐射量的变化(几乎无滞后),而地表接受的太阳辐射量的变化又进一步驱动了地球气候系统的变化(存在滞后)。由于不同时间尺度的太阳活动周期的相互叠加效应,再加上地球本身是一个复杂的系统,不同圈层之间的相互作用,以及大气环流和大洋环流的耦合及反馈作用,使得我们研究的材料中记录的古气候变化信息不仅仅是来自于太阳活动,同时还夹杂着很多其他信号,因而在研究中要充分考虑这些因素。
米兰科维奇理论在解释万年-百万年长时间尺度的气候变化的驱动机制方面已经获得普遍认可,即地球轨道参数包括约2万年的岁差、约4万年斜率、约10万年和40万年左右的偏心率的周期性变化导致地表接受的太阳日照量的周期性变化,进而驱动了地球气候系统的周期性变化[1~4]。但是,地球气候在年际-百年甚至千年尺度上的变化规律及其驱动机制问题,还一直存在争议[7, 17~18, 25]。通过本研究,发现气候变化的替代性指标的变化周期与太阳活动的替代性指标的变化周期具有一定的相关性,即目前发现的太阳活动的几个主要周期包括约11 a的Schwabe周期、约22 a的Hale磁周期、约88 a的Gleissberg周期、约210 a的Suess周期、约1000 a的Eddy周期和约2400 a的Hallstatt周期都在石笋和树轮的古气候替代指标中发现且稳定存在,据此可推断在年际-千年尺度上的太阳活动周期与地球气候系统的变化之间存在着某种关联性,这指示了不同尺度的太阳活动周期驱动了地球气候的变化,因而使得这些古气候替代指标序列记录了这些周期变化的信号。
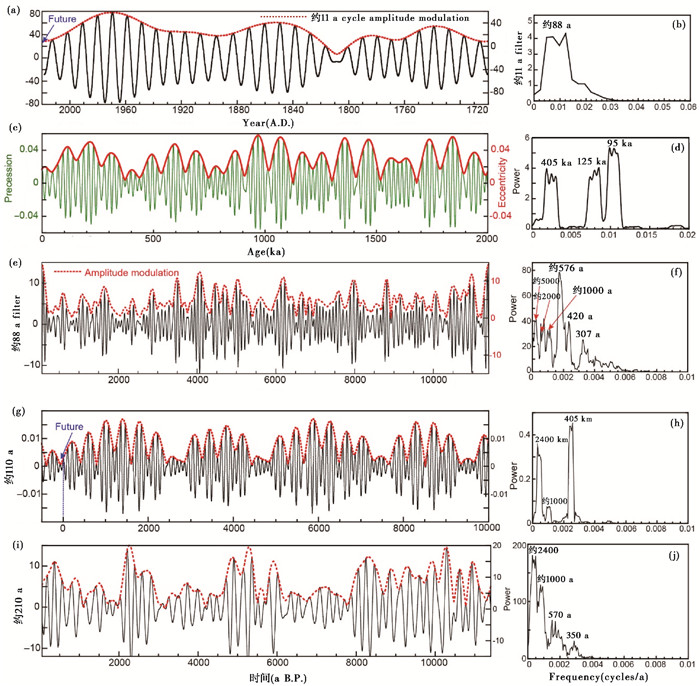
不同时间尺度的地球古气候替代指标变化周期是受到了多个不同太阳活动周期的共同作用和影响,不同时间尺度的太阳活动周期之间到底是如何相互作用的,到目前为止,其驱动机制仍然是一个未解之谜。通过对实际观测的太阳黑子序列中存在的约11 a太阳活动周期进行振幅调制分析(图 8a),发现约11 a的太阳黑子的活动周期的振幅变化信号的频谱图中显示出88 a左右的周期(图 8b),这指示了约11 a的太阳黑子的活动周期的变化是受约88 a的Gleissberg周期调制的,这与米拉科维奇旋回理论中的岁差和偏心率的调制关系类似,偏心率调控岁差周期旋回的振幅变化(图 8c),偏心率通过调制岁差周期旋回的振幅变化来改变地表接收到的太阳辐射的变化,从而导致冰期和间冰期旋回的发生,2万年左右的岁差周期的振幅调制周期即偏心率旋回具有约10万年(95 ka和125 ka)和40.5万年的周期变化(图 8d)。在岁差周期的振幅低值处即偏心率的低值时期,地表接受的日照量要比岁差周期高振幅时期少很多,这一时期一般是地球上的冰期,而岁差周期的振幅高值处,一般是地球上的间冰期。对11000多年来重建的太阳黑子数变化序列进行约88 a的滤波,其振幅调制信号的频谱图显示出非常强的约576 a周期信号,以及明显的307 a、420 a、1000 a、2000 a以及5000 a的周期信号(图 8e和8f),据此推断,约576 a的周期很可能是88 a的Gleissberg周期的振幅调制信号,这与Peristykh和Damon[25]认为的约210 a的Suess周期是约88 a的Gleissberg周期的振幅调制周期明显不同。通过对其进行约210 a的滤波,其振幅调制信号的频谱图显示出非常强的约1000 a和2400 a的周期信号,以及明显的350 a和570 a的周期信号(图 8i和8j),据此推断约1000 a和2400 a的周期可能是210 a的Suess周期的振幅调制信号,570 a的周期可能也是210 a的Suess周期的振幅调制信号,这与约100 ka的短偏心率周期滤波曲线的振幅调制周期信号极为相似,其具有405 ka、约1000 ka和2400 ka的周期(图 8g和8h)。据此我们可以推论,570 a、1000 a和2400 a左右的周期信号可能是约88 a和210 a的太阳活动周期的共同振幅调制周期。
|
图 8 实测和重建的太阳黑子数序列的太阳黑子周期旋回的振幅调制关系与米兰科维奇理论中的岁差与偏心率之间的调制关系对比图 (a)实际观测的太阳黑子数(1700~2018年,数据来源于http://sidc.oma.be/silso/datafiles)的约11 a和88 a周期旋回的调制关系,利用Taner带通滤波(0.076~0.106)获取约11 a的太阳黑子的周期滤波序列(黑色)及其振幅变化序列(红色虚线);(b)为(a)图中约11 a周期的振幅变化信号的频谱图;(c)米兰科维奇理论中的岁差和偏心率周期旋回的振幅调制关系,图中展示的是Laskar2004理论曲线(0~2 Ma)的岁差和偏心率曲线[2];(d)为0~2 Ma理论偏心率数据序列的频谱图;(e)重建的约11400年的太阳黑子数序列[30]中约88 a太阳黑子周期旋回的振幅调制关系,利用Taner带通滤波(0.0073~0.0153)获取的约88 a太阳黑子周期的滤波曲线(黑色)及其振幅变化序列(红色);(f)为(e)中的88 a周期变化的振幅调制信号(红色虚线)的频谱图;(g)米兰科维奇理论中的短偏心率周期约100 ka与长偏心率405 ka旋回的振幅调制关系,图中展示的是Laskar2004理论曲线[2](未来0.5 Ma及过去10 Ma)的短偏心率曲线滤波曲线(带通滤波:0.007~0.012)及其振幅振幅变化曲线即405 ka旋回;(h)为图(g)中的振幅变化信号的频谱图;(i)重建的约11400年的太阳黑子数序列[30]中约210 a太阳黑子周期旋回的振幅调制关系,利用Taner带通滤波(0.00276~0.0676)获取的约210 a太阳黑子周期的滤波曲线(黑色)及其振幅变化序列(红色);(j)为(i)中的210 a周期变化的振幅调制信号(红色虚线)的频谱图 Fig. 8 The amplitude modulation relationship between the measured and reconstructed sunspot number variation cycle compared with the modulation relationship between the precession and eccentricity cycles in the Milankovitch's theory. (a)The modulation relationship between the 11 a and 88 a solar cycles of the actual observed sunspot number(1700~2018 A.D., data download from http://sidc.oma.be/silso/datafiles), use Taner bandpass filtering(0.076~0.106)to obtain about 11 a sunspots cycle filter(black)and its amplitude variation sequence(red), and (b) is the spectrum of the amplitude variation signal of the 11 a period in (a). (c)The amplitude modulation relationship between precession and eccentricity cycle in the Milankovitch's theory, shows the precession and eccentricity curves of the theory curve(0~2 Ma)of the Laskar 2004[2] and its power spectrum (d). (e)The 88 a filter(0.0073~0.0153)from the reconstructed about 11400 a SSN[30] with its amplitude modulation variation curve(red)and its power spectrum (f). (g)The ca.100-ka filter(0.007~0.012)from Laskar 2004 eccentricity curve[2] with its amplitude modulation variation curve(405-ka long eccentricity cycle, red)and its power spectrum (h). (i)The ca.210 a filter(0.00276~0.0676)(red)from the reconstructed 11400 a SSN[30] with its amplitude modulation variation curve and its power spectrum (j) |
目前我们的地球正处于太阳活动的振幅低值处,即约11 a左右的太阳黑子的活动减弱,地球正经历着约88 a周期的低值时期(图 8a),轨道尺度的天文旋回理论的偏心率的长周期也是在未来2万年左右达到最低值(图 8g),这将对缓解地球近年来的全球变暖趋势提供有力的证据,根据太阳活动的年际-百年尺度的周期推测,未来几年地球处于一个变冷的趋势。
致谢: 非常感谢南京大学鹿化煜教授和匿名审稿专家以及编辑部杨美芳老师对稿件提出的建设性修改意见。
| [1] |
Hinnov L A. Cyclostratigraphy and its revolutionizing applications in the Earth and Planetary sciences[J]. Geological Society of America Bulletin, 2013, 125(11-12): 1703-1734. DOI:10.1130/B30934.1 |
| [2] |
Laskar J, Robutel P, Joutel F, et al. A long-term numerical solution for the insolation quantities of the Earth[J]. Astronomy and Astrophysics, 2004, 428(1): 261-285. DOI:10.1051/0004-6361:20041335 |
| [3] |
Laskar J, Fienga A, Gastineau M, et al. La2010:A new orbital solution for the long-term motion of the Earth[J]. Astronomy and Astrophysics, 2011, 532(2): 784-785. |
| [4] |
Milankovitch M M. Canon of Insolation and the Ice-age Problem (Beograd: Koniglich Serbische Akademie, 1941) English Translation by the Israel Program for Scientific Translations. Washington D C: Published for the US Department of Commerce and the National Science Foundation, 1969: 1-633.
|
| [5] |
吴怀春, 房强, 张世红, 等. 新生代米兰科维奇旋回与天文地质年代表[J]. 第四纪研究, 2016, 36(5): 1055-1074. Wu Huaichun, Fang Qiang, Zhang Shihong, et al. Cenozoic Milankovitch cycles and astronomical time scale[J]. Quaternary Sciences, 2016, 36(5): 1055-1074. |
| [6] |
Adolphi F, Muscheler R, Svensson A, et al. Persistent link between solar activity and Greenland climate during the Last Glacial Maximum[J]. Nature Geoscience, 2014, 7(9): 662-666. DOI:10.1038/ngeo2225 |
| [7] |
Braun H, Christl M, Rahmstorf S, et al. Possible solar origin of the 1, 470-year glacial climate cycle demonstrated in a coupled model[J]. Nature, 2005, 438(7065): 208-211. DOI:10.1038/nature04121 |
| [8] |
Eddy J A. Climate and the changing sun[J]. Climatic Change, 1977, 1(2): 173-190. DOI:10.1007/BF01884410 |
| [9] |
Gray L J, Beer J, Geller M, et al. Solar influence on climate[J]. Reviews of Geophysics, 2010, 48(4): 1032-1047. |
| [10] |
Lean J L. Cycles and trends in solar irradiance and climate[J]. Wiley Interdisciplinary Reviews Climate Change, 2010, 1(1): 111-122. DOI:10.1002/wcc.18 |
| [11] |
Sloan T, Wolfendale A W. Cosmic rays, solar activity and the climate[J]. Environmental Research Letters, 2013, 8(4): 575-591. |
| [12] |
Stefan E, Bas V G. The effects of changing solar activity on climate:Contributions from palaeoclimatological studies[J]. Journal of Space Weather and Space Climate, 2012, 2(2): 555-638. |
| [13] |
Steinhilber F, Abreu J A, Beer J, et al. 9, 400 years of cosmic radiation and solar activity from ice cores and tree rings[J]. Proceedings of the National Academy of Sciences of the United States of America, 2012, 109(16): 5967-5971. DOI:10.1073/pnas.1118965109 |
| [14] |
Lean J L. Estimating solar irradiance since 850 CE[J]. Earth and Space Science, 2018, 5(4): 133-149. DOI:10.1002/ess2.v5.4 |
| [15] |
Kopp G, Lean J L. A new, lower value of total solar irradiance:Evidence and climate significance[J]. Geophysical Research Letters, 2011, 38(1): 541-551. |
| [16] |
Solanki S K, Krivova N A, Haigh J D. Solar irradiance variability and climate[J]. Annual Review of Astronomy and Astrophysics, 2013, 51(3-4): 311-351. |
| [17] |
Ineson S, Scaife A A, Knight J R, et al. Solar forcing of winter climate variability in the Northern Hemisphere[J]. Nature Geoscience, 2011, 4(11): 753-757. DOI:10.1038/ngeo1282 |
| [18] |
Thiéblemont R, Matthes K, Omrani N E, et al. Solar forcing synchronizes decadal North Atlantic climate variability[J]. Nature Communications, 2015, 22: 8268. |
| [19] |
Cliver E W. The extended cycle of solar activity and the Sun's 22-year magnetic cycle[M]//Balogh A, Hudson H, Petrovay K, et al. The Solar Activity Cycle. New York: Springer, 2015: 169-189.
|
| [20] |
Mursula K, Usoskin I G, Kovaltsov G A. Persistent 22-year cycle in sunspot activity:Evidence for a relic solar magnetic field[J]. Solar Physics, 2001, 198(1): 51-56. DOI:10.1023/A:1005218414790 |
| [21] |
Petrie G J D, Petrovay K, Schatten K. Solar polar fields and the 22-year activity cycle: Observations and models[M]//Balogh A, Hudson H, Petrovay K, et al. The Solar Activity Cycle. New York: Springer, 2015: 325-357.
|
| [22] |
Gleissberg W. The eighty-year sunspot cycle[J]. Journal of the British Astronomical Association, 1958, 68: 148-152. |
| [23] |
Gleissberg W. The eighty-year solar cycle in auroral frequency numbers[J]. Journal of the British Astronomical Association, 1965, 75: 227-231. |
| [24] |
Ma L H. Gleissberg cycle of solar activity over the last 7000 years[J]. New Astronomy, 2009, 14(1): 1-3. DOI:10.1016/j.newast.2008.04.001 |
| [25] |
Peristykh A N, Damon P E. Persistence of the Gleissberg 88-year solar cycle over the last~12, 000 years:Evidence from cosmogenic isotopes[J]. Journal of Geophysical Research, 2003, 108(A1): 1003. DOI:10.1029/2002JA009390 |
| [26] |
Ogurtsov M G, Nagovitsyn Y A, Kocharov G E, et al. Long-period cycles of the Sun's activity recorded in direct solar data and proxies[J]. Solar Physics, 2002, 211(1): 371-394. |
| [27] |
Damon P E, Sonett C P. Solar and terrestrial components of the atmospheric C-14 variation spectrum[M]//Sonett C P, Giampapa M S, Matthews M S. The Sun in Time. Tucson: University of Arizona Press, 1991: 360-388.
|
| [28] |
Suess H E. The radiocarbon record in tree rings of the last 8000 years[J]. Radiocarbon, 1980, 22: 200-209. DOI:10.1017/S0033822200009462 |
| [29] |
Usoskin I G, Gallet Y, Lopes F, et al. Solar activity during the Holocene:The Hallstatt cycle and its consequence for grand minima and maxima[J]. Astronomy and Astrophysics, 2016, 587: A150. DOI:10.1051/0004-6361/201527295 |
| [30] |
Solanki S K, Usoskin I G, Kromer B, et al. Unusual activity of the Sun during recent decades compared to the previous 11, 000 years[J]. Nature, 2004, 18(9): 4225-4237. |
| [31] |
Wang Y J, Cheng H, Edwards R L, et al. A high-resolution absolute-dated Late Pleistocene monsoon record from Hulu cave, China[J]. Science, 2001, 294(5550): 2345-2348. DOI:10.1126/science.1064618 |
| [32] |
Yuan D X, Cheng H, Edwards R L, et al. Timing, duration, and transitions of the last interglacial Asian monsoon[J]. Science, 2004, 304(5670): 575-578. DOI:10.1126/science.1091220 |
| [33] |
Wang Y J, Cheng H, Edwards R L, et al. Millennial and orbital scale changes in the East Asian monsoon over the past 224000 years[J]. Nature, 2008, 451(7182): 1090-1093. DOI:10.1038/nature06692 |
| [34] |
王权, 汪永进, 刘殿兵, 等. DO3事件的湖北神农架高分辨率年纹层石笋记录[J]. 第四纪研究, 2017, 37(1): 108-117. Wang Quan, Wang Yongjin, Liu Dianbing, et al. The DO3 event in Asian monsoon climates evidenced by an annually laminated stalagmite from Qingtian cave, Mt. Shennongjia[J]. Quaternary Sciences, 2017, 37(1): 108-117. |
| [35] |
胡超涌, 汪颖钊, 刘浴辉, 等. 9.6-6.0 ka B.P.阿曼降水重建及其与中国南方降水的对比[J]. 第四纪研究, 2016, 36(3): 581-586. Hu Chaoyong, Wang Yingzhao, Liu Yuhui, et al. Rainfall reconstruction from Oman during 9.6-6.0 ka B.P. and its comparison with that from Southwest China[J]. Quaternary Sciences, 2016, 36(3): 581-586. |
| [36] |
Couchoud I, Genty D, Hoffmann D, et al. Millennial-scale climate variability during the last interglacial recorded in a speleothem from south-western France[J]. Quaternary Science Reviews, 2009, 28(27-28): 3263-3274. DOI:10.1016/j.quascirev.2009.08.014 |
| [37] |
Rossi C, Mertz-Kraus R, Osete M L. Paleoclimate variability during the Blake geomagnetic excursion(MIS 5d) deduced from a speleothem record[J]. Quaternary Science Reviews, 2014, 102: 166-180. DOI:10.1016/j.quascirev.2014.08.007 |
| [38] |
Cai Y J, Cheng H, An Z S, et al. Large variations of oxygen isotopes in precipitation over south-central Tibet during marine isotope stage 5[J]. Geology, 2010, 38(3): 243-246. DOI:10.1130/G30306.1 |
| [39] |
Meyer M C, Spøtl C, Mangini A. The demise of the last interglacial recorded in isotopically dated speleothems from the Alps[J]. Quaternary Science Reviews, 2008, 27(5-6): 476-496. DOI:10.1016/j.quascirev.2007.11.005 |
| [40] |
Regattieri E, Zanchetta G, Drysdale R N, et al. A continuous stable isotope record from the penultimate glacial maximum to the last interglacial(159-121 ka) from Tana Che Urla Cave (Apuan Alps, Central Italy)[J]. Quaternary Research, 2014, 82(2): 450-461. DOI:10.1016/j.yqres.2014.05.005 |
| [41] |
蒋文静, 赵侃, 陈仕涛, 等. 小冰期十年际尺度亚洲季风变化的四川黑竹沟洞石笋记录[J]. 第四纪研究, 2017, 37(1): 118-129. Jiang Wenjing, Zhao Kan, Chen Shitao, et al. Decadal climate oscillations during the Little Ice Age of stalagmite record from Heizhugou cave, Sichuan[J]. Quaternary Sciences, 2017, 37(1): 118-129. |
| [42] |
孙喜利, 杨勋林, 史志超, 等. 石笋记录的西南地区MIS 4阶段夏季风的演化[J]. 第四纪研究, 2017, 37(6): 1370-1380. Sun Xili, Yang Xunlin, Shi Zhichao, et al. The evolution of summer monsoon in Southwest China during MIS 4 as revealed by stalagmite δ18O record[J]. Quaternary Sciences, 2017, 37(6): 1370-1380. |
| [43] |
董进国, 赵侃, 沈川洲, 等. 黄土高原石笋记录的DO25季风增强事件[J]. 第四纪研究, 2016, 36(6): 1502-1509. Dong Jinguo, Zhao Kan, Shen Chuan-Chou, et al. Strong East Asian summer monsoon during the do 25 event recorded by an absolute-dated stalagmite from Dragon cave, Northern China[J]. Quaternary Sciences, 2016, 36(6): 1502-1509. |
| [44] |
Novello V F, Vuille M, Cruz F W, et al. Centennial-scale solar forcing of the South American monsoon system recorded in stalagmites[J]. Scientific Reports, 2016, 6: 1-8. DOI:10.1038/s41598-016-0001-8 |
| [45] |
Wang Y J, Cheng H, Edwards R L, et al. The Holocene Asian monsoon:Links to solar changes and North Atlantic climate[J]. Science, 2005, 308(5723): 854-857. DOI:10.1126/science.1106296 |
| [46] |
Bale R J, Iain R, Salzer M W, et al. An annually resolved bristlecone pine carbon isotope chronology for the last millennium[J]. Quaternary Research, 2011, 76(1): 22-29. DOI:10.1016/j.yqres.2011.05.004 |
| [47] |
黄春菊. 旋回地层学和天文年代学及其在中生代的研究现状[J]. 地学前缘, 2014, 21(2): 48-66. Huang Chunju. The current status of cyclostratigraphy and astrochronology in the Mesozoic[J]. Earth Science Frontiers, 2014, 21(2): 48-66. |
| [48] |
周长志, 张珂, 张海平, 等. 基于小波分析的太阳活动周期性研究[J]. 现代测绘, 2017, 40(1): 32-35. Zhou Changzhi, Zhang Ke, Zhang Haiping, et al. The periodic variations of solar activity by wavelet analysis[J]. Modern Surveying and Mapping, 2017, 40(1): 32-35. DOI:10.3969/j.issn.1672-4097.2017.01.008 |
| [49] |
张志平, 黄伟, 陈建徽, 等. 全新世东亚夏季风演化的多尺度周期变化及其可能机制探讨[J]. 第四纪研究, 2017, 37(3): 498-509. Zhang Zhiping, Huang Wei, Chen Jianhui, et al. Multi-time scale analysis of East Asian summer monsoon and its possible mechanism during Holocene[J]. Quaternary Sciences, 2017, 37(3): 498-509. |
Abstract
In recent years, more and more scientists have paid more attention to the research on solar activity. There are interannual-century or even millennium scale climate cycles found in the high-resolution paleoclimate proxies data series extracted from the ice cores, stalagmites, tree rings and lake sediments. There are some correlations between the climate changes signals and the solar cycles at the different time scales, however, its physical drive mechanism is still an unsolved mystery. In this study we collected the actual observed and reconstructed data sequences of sunspots data series, and the tree-ring δ13C from the bristlecone pine tree-ring in California(USA) and stalagmite δ18O from the ALHO6 stalagmite of Pau d'Alho cave in Brazil and Dongge cave stalagmite in Guizhou of China reflecting monsoon and precipitation intensity, through spectrum analysis, cross spectrum of wavelet transform, coherent spectrum analysis and amplitude modulation. It was found that the periodic signals of climate change recorded in stalagmites and tree rings are significantly correlated with the interannual-millennial scale cycle of solar activity, and that there is a relationship between these periodic signals recorded in the climate proxies and the solar cycles. The lag of 1/4 to 3/4 cycle, according to which it is inferred that the changes in the Earth's surface climate system in interannual-Millennium scale are driven by the solar cycles. In addition, it is found that the period of about 88 a is the amplitude modulation period signal of the sunspot activity cycle of about 11 a, while the climate change signals of ca. 500 a, 1000 a and 2000 a are the solar activity cycle ca. 88 a and 210 a amplitude modulation period signals, indicate that the Earth's climate is not only driven by such an eccentricity-modulated precession cycle, but also by the ca. 88 a modulation of the 11 a solar activity cycle amplitude, as well as ca. 500 a modulation ca. 88 a period amplitude variation, ca. 1000 a and 2000 a period modulation ca. 210 a period amplitude changes. We found that the Earth is currently in a low amplitude of about 88 a period. The Earth may experience a cooling trend in the next few years, combined with the trend of long eccentricity, which provides an important scientific basis for predicting the short-term and long-term trends for the future global climate change. 2018, Vol.38
2018, Vol.38
