2. 武汉地震科学仪器研究院有限公司,湖北省咸宁市青龙路11号,437099;
3. 辽宁省地震局,沈阳市黄河北大街44号,110031
DSQ水管倾斜仪是一种经典的地形变观测仪器,在全国多个地震台站大量布置,期望获取较干净的固体潮曲线。在实际应用中,DSQ水管倾斜仪会遭受异常天气和人类活动的影响,导致固体潮曲线含有噪声,需要进行降噪处理[1-5]。
常见的仪器信号去噪模型有卡尔曼滤波、小波去噪、低通FIR滤波、Savitzky-Golay滤波等方法,拥有一定的去噪或光滑作用,但往往存在重构误差较大或信噪比不高的情形,具有一定的模型缺陷。完备集合经验模态分解(complementary ensemble empirical mode decomposition,CEEMD)是在集合经验模态分解(ensemble emperial mode decomposition,EEMD)和经验模态分解(empirical mode decomposition,EMD)基础上进行改进的新型信号分解技术[6-8]。与EEMD的区别是,CEEMD通过引入一对性质相反的白噪声来进行经验模态分解,而不是在原始信号中加入随机的白噪声,可以在一定程度上压制引入白噪声带来的重构误差。
为改善传统去噪模型效果,本文提出一种基于主成分分析[9-10](principal component analysis,PCA)优化CEEMD的DSQ水管倾斜仪信号去噪模型CEEMD-PCA。该模型综合考虑相关系数、分布熵、MSE、R2、SSE、RMSE、MAE、MAPE等8个指标对筛选IMF分量的影响力,利用PCA进行IMF特征指标矩阵的多维压缩,构建IMF分量质量综合评价函数,根据函数值的排名结果完成原始含噪信号的线性重构。最后,设计仿真信号实验和DSQ水管倾斜仪实测信号去噪实验验证本文CEEMD-PCA模型的去噪性能。
1 信号去噪模型 1.1 主成分分析PCA求解主成分的一般步骤如下[9-10]:1)标准化处理初始特征矩阵,得到X′(x′1, x′2, …, x′p),从而消除数据量纲和数量级不同的影响,并计算相关系数矩阵R。2)根据特征方程|R-λI|=0,计算得到相关系数矩阵R的p个特征根,用λi(i=1, 2, …, p)表示。将特征根按照值的大小降序排列,得到相关系数矩阵R与特征根λi相对应的特征向量ui。3)计算得到第i个主成分的方差贡献率为
为验证CEEMD-PCA去噪模型的有效性,选用相关系数、分布熵、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、判定系数(R2)、均方根误差(RMSE)、均方误差(MSE)、误差平方和(SSE)等8个指标作为去噪结果的准确性及一致性评价标准。
1.3 PCA-CEEMD去噪模型CEEMD-PCA去噪模型的信号处理流程(图 1)分为以下几步:1)首先对DSQ水管倾斜仪信号进行CEEMD处理,得到若干个IMF分量;2)分别计算这些IMF分量的相关系数、分布熵、MSE、R2、SSE、RMSE、MAE、MAPE,组建IMF特征指标矩阵;3)对IMF特征矩阵进行主成分分析,依次进行标准化、相关性分析、特征分析与主成分贡献率计算、得分估计,得到全部IMF分量的排名结果;4)将排名靠后的半数IMF分量进行线性重构,即可得到DSQ水管倾斜仪去噪后数据。
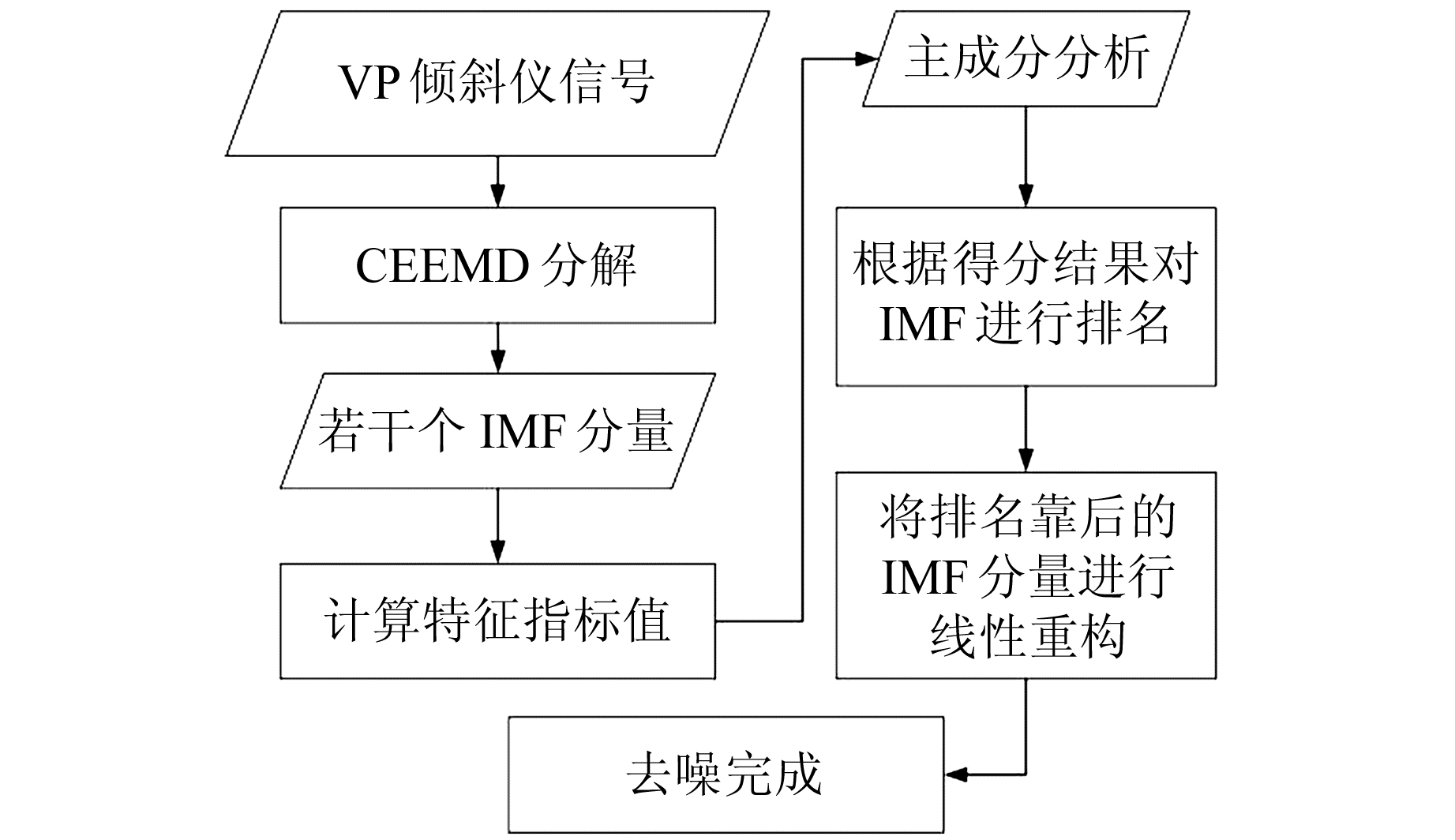
|
图 1 CEEMD-PCA模型去噪流程 Fig. 1 CEEMD-PCA model denoising process |
为测试CEEMD-PCA去噪模型的效果,设计一个仿真含噪信号的去噪实验和一个DSQ水管倾斜仪信号的去噪实验,融合相关系数、分布熵、MSE、R2、SSE、RMSE、MAE、MAPE等多个指标评价CEEMD分解的IMF分量的质量,然后利用相关系数、信噪比、MSE等3个指标评价去噪效果,最后与多个经典去噪模型结果进行对比。
算法参数为:仿真含噪信号信噪比为12 dB,纯净信号为y=sin(2πt)+cos(t)+sin(5πt);CEEMD分解的噪声标准差比、平均次数分别为0.15和20。
2.1 仿真信号的去噪实验与分析基于MATLAB 2023a设计一个仿真信号的去噪实验,根据复合正余弦函数生成纯净信号和加噪信号,得到实验所需数据(图 2)。
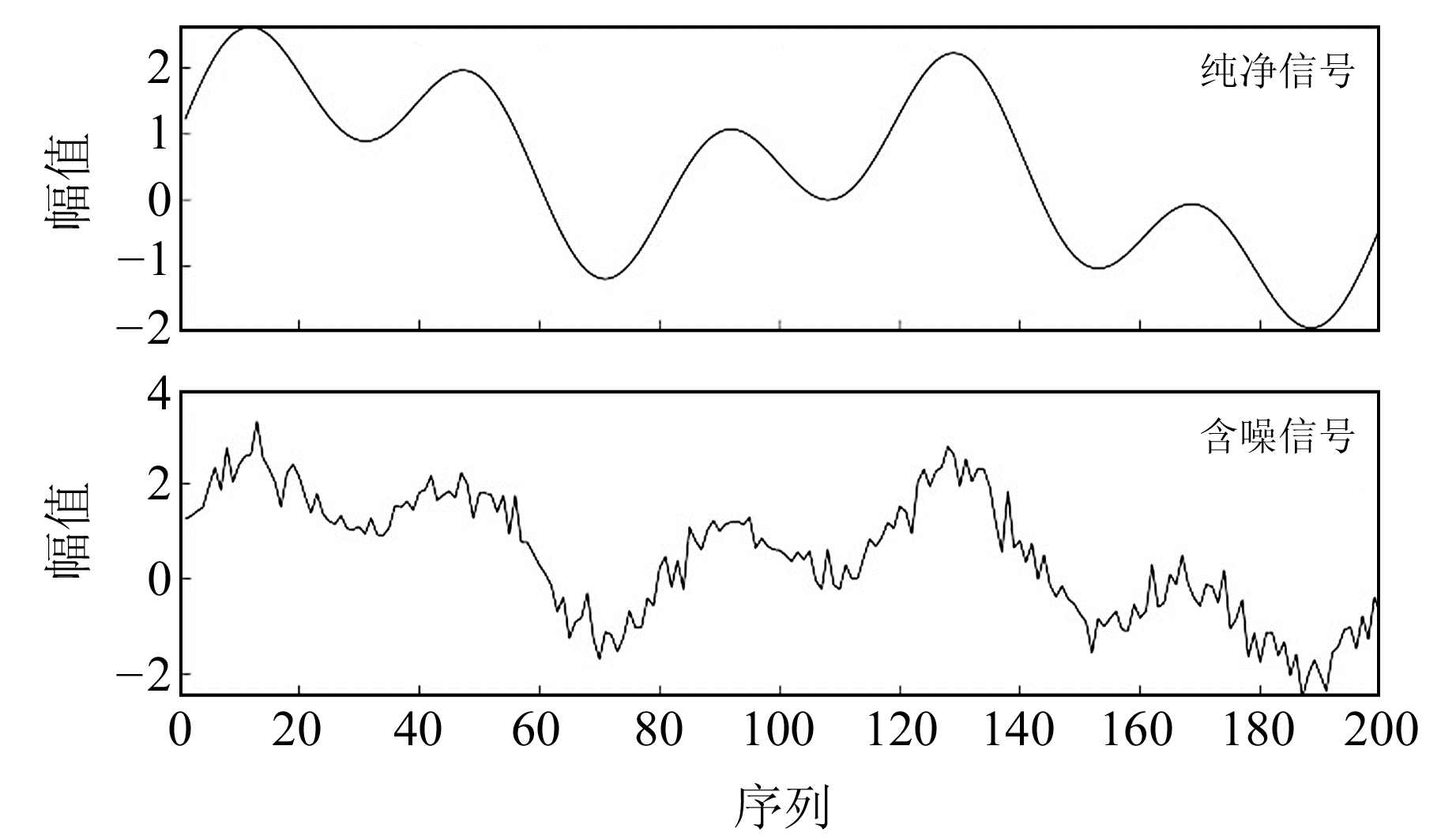
|
图 2 仿真纯净信号与加噪波形 Fig. 2 Simulation of pure signals and noise-added waveforms |
图 3为仿真含噪信号的CEEMD分解结果。由图 3可知,含噪信号被CEEMD分解成了7个IMF分量,其中IMF1~IMF2存在较频繁的波形振荡且幅值相对较小,基本可断定为需要剔除掉的噪声成分;IMF4~IMF7的曲线较为光滑,与原波形特征相差较大,属于CEEMD分解得到的主要幅值成分,包含了原始信号的大部分能量;同时发现,IMF3、IMF5与原始信号曲线的整体趋势极为相似,只在部分峰值附近存在幅值大小上的差异,仍然含有少量噪声。
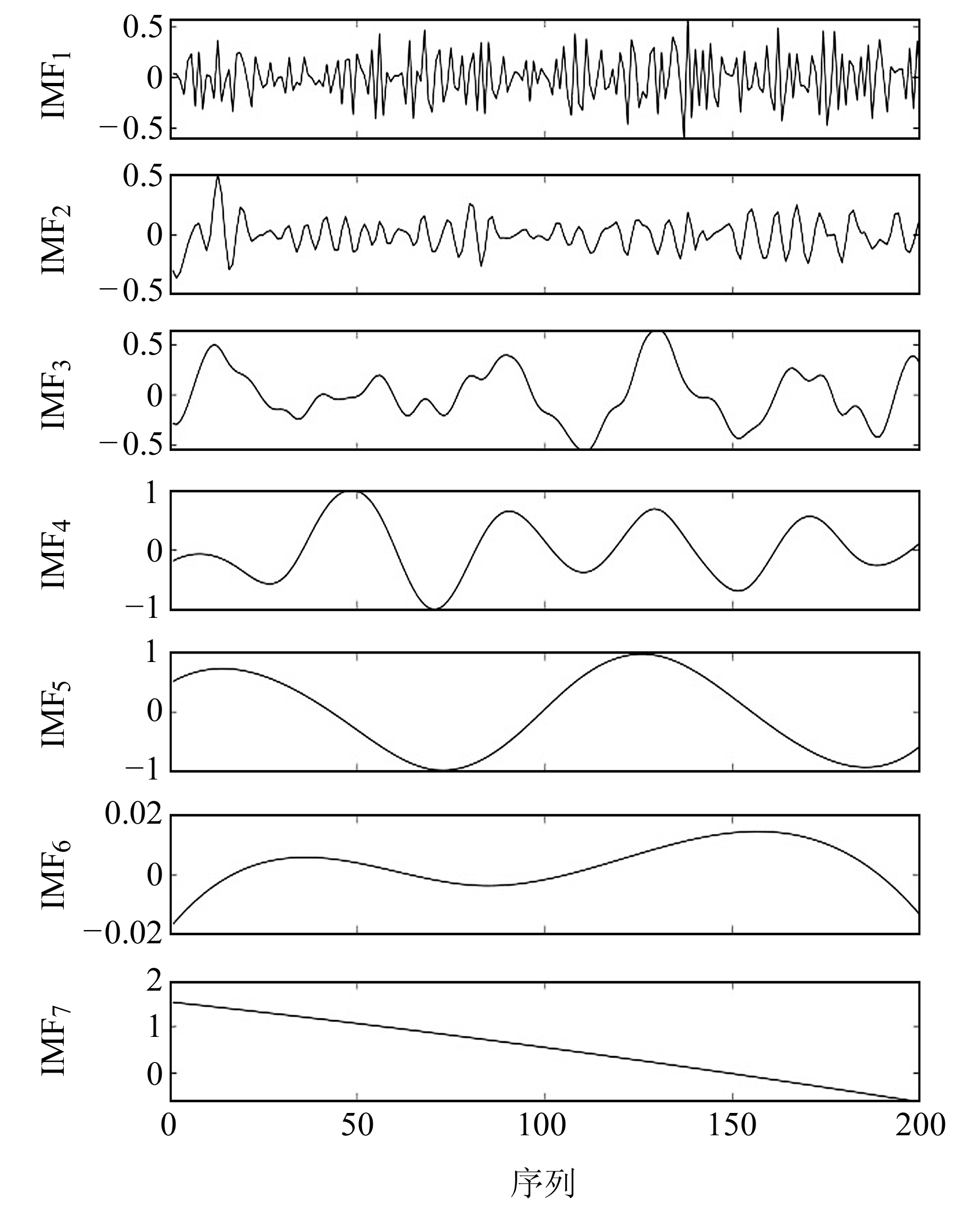
|
图 3 仿真含噪信号的CEEMD分解结果 Fig. 3 Results of CEEMD decomposition of simulated signals |
表 1为原始含噪信号经过CEEMD分解后各个IMF分量的特征值。可以看出,IMF3、IMF4、IMF5、IMF7的指标值与其他IMF分量差异较大,其相关系数、分布熵、R2、MAPE较大,表示该IMF与原始信号形态相似,可能是有效成分,其MSE、SSE、RMSE、MAE较小,表示该IMF分量越接近初始信号的幅值能量,需要尽可能保留。
|
|
表 1 CEEMD分解后各IMF的特征值 Tab. 1 Eigenvalues of each IMF after CEEMD decomposition |
原始含噪信号的IMF特征矩阵经过标准化、相关性分析、特征分析与贡献率计算、主成分得分、综合评价函数计算等步骤,可得到主成分分析结果(表 2~4)。
|
|
表 2 各IMF标准化特征向量的相关系数 Tab. 2 Correlation coefficient of each IMF normalized eigenvector |
|
|
表 3 各参数的特征值、特征向量及贡献率 Tab. 3 Eigenvalues, feigenvectors and contribution rates of each parameter |
|
|
表 4 PCA综合评价函数值与排名 Tab. 4 Composite evaluation function values and rankings of PCA |
由表 2~4可知:1)部分指标之间的相关性较高,如MSE与RMSE高度正相关,相关系数与MSE高度负相关,R2与SSE高度负相关;2)主成分1在全部主成分中的贡献率达到86.640 6 %,可直接代表全部IMF指标参与后续分析;3)PCA综合评价函数值排名结果为IMF6>IMF2>IMF1>IMF3>IMF4>IMF5>IMF7,由于该函数表征IMF与原信号的误差大小以及含噪程度,故取最后4位IMF分量参与线性重构信号,得到的去噪结果如图 4。
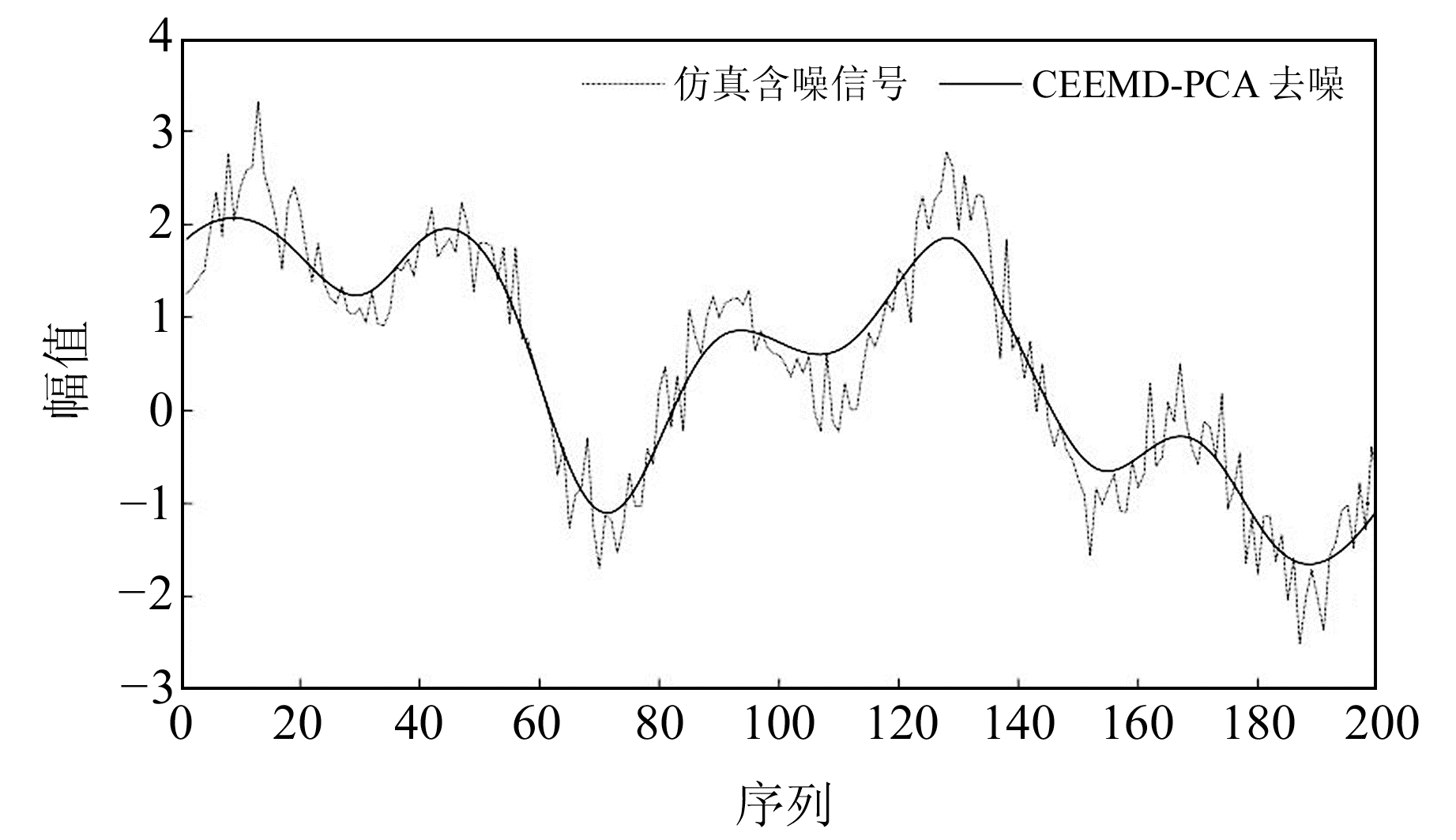
|
图 4 基于CEEMD-PCA模型的仿真信号去噪结果 Fig. 4 Simulated signal denoising results based on CEEMD-PCA model |
由图 4可知,CEEMD-PCA模型的去噪结果较光滑,保留了原始含噪信号的主要成分,重构误差较小,是一种可取的去噪模型,其相关系数、MSE、信噪比分别为0.972 2、0.087 3、12.957 4 dB。
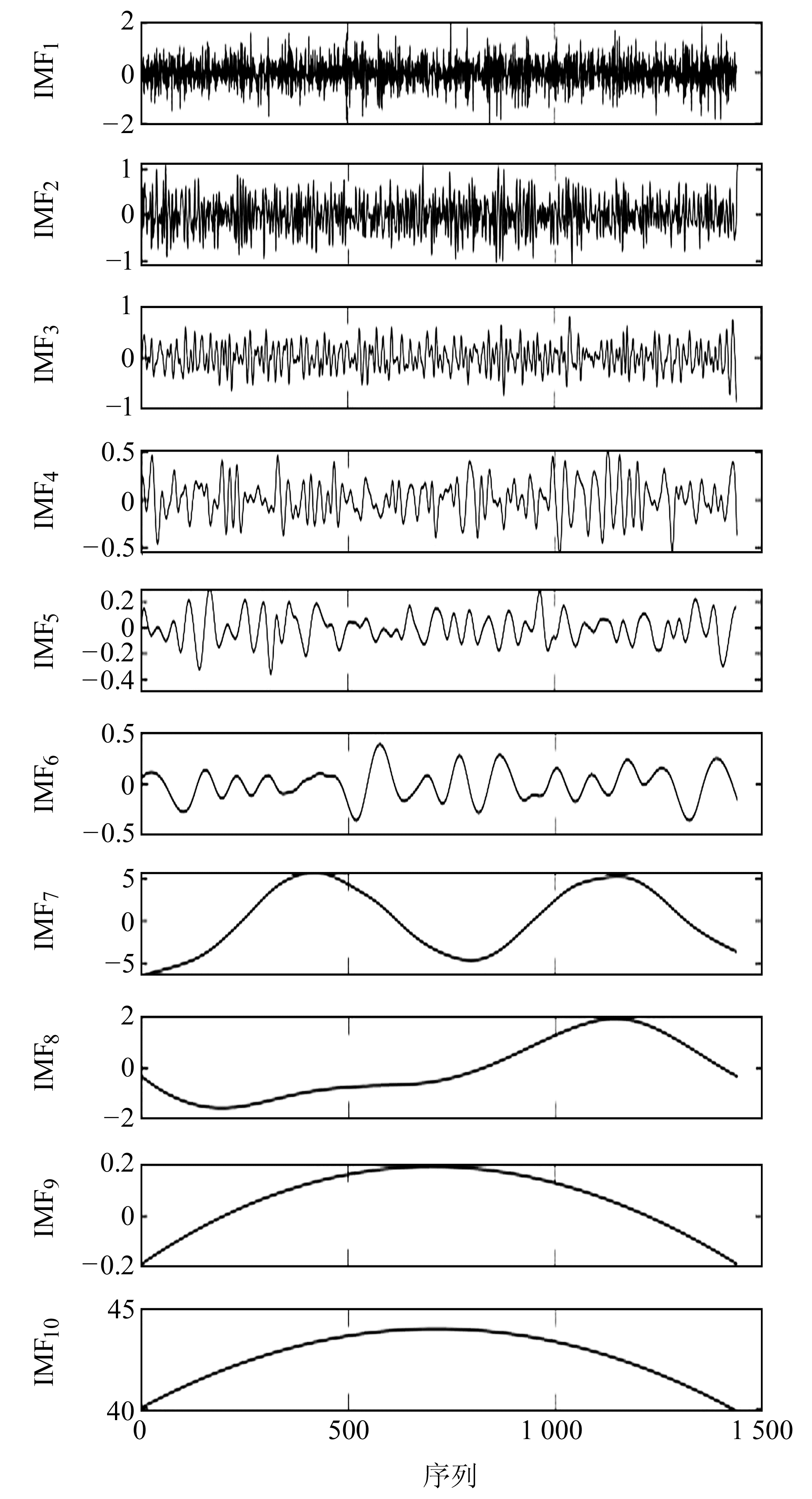
2.2 DSQ水管倾斜仪实测信号的去噪实验与分析使用武汉地震科学仪器研究院生产的DSQ水管倾斜仪数据进行去噪实验,仪器布设在武汉地震中心站九峰山山洞内。单条信号去噪实验数据时间为2022-05-02,多条去噪实验数据时间为2022-05-11~20,每条信号长度固定为1 440,反映每日每分钟采样情况。首先,使用一条典型信号进行CEEMD-PCA去噪分析,得到表 6~9和图 5~6;然后,针对多条DSQ水管倾斜仪信号进行多轮CEEMD-PCA去噪分析,多轮实验结果如表 10和图 7所示。
|
图 5 DSQ水管倾斜仪信号经过CEEMD分解结果 Fig. 5 Results of CEEMD decomposition of DSQ water tube tiltmeter signals |
|
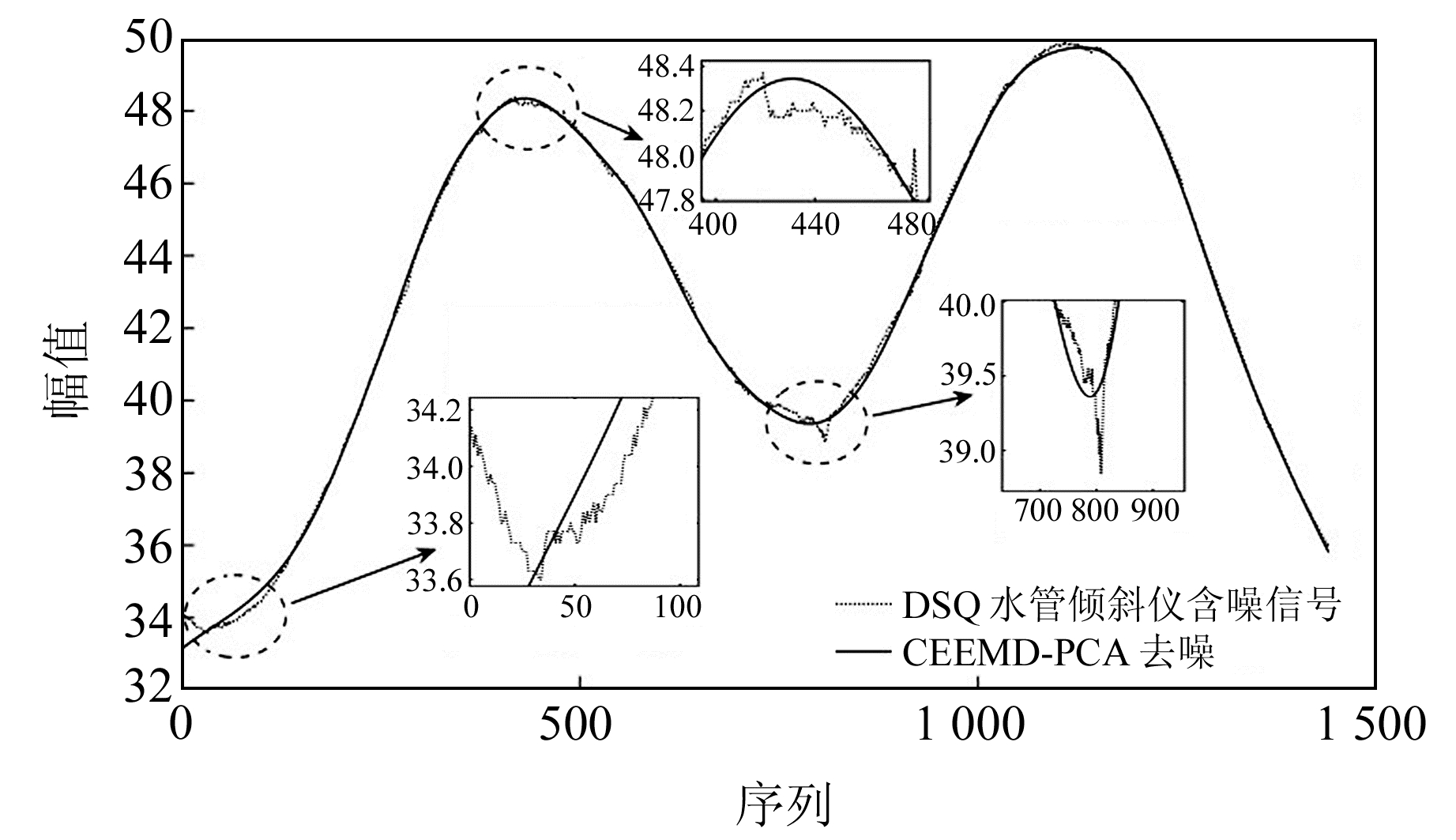
图 6 DSQ水管倾斜仪信号的CEEMD-PCA去噪结果 Fig. 6 CEEMD-PCA denoising results of DSQ water tube tiltmeter signals |
|
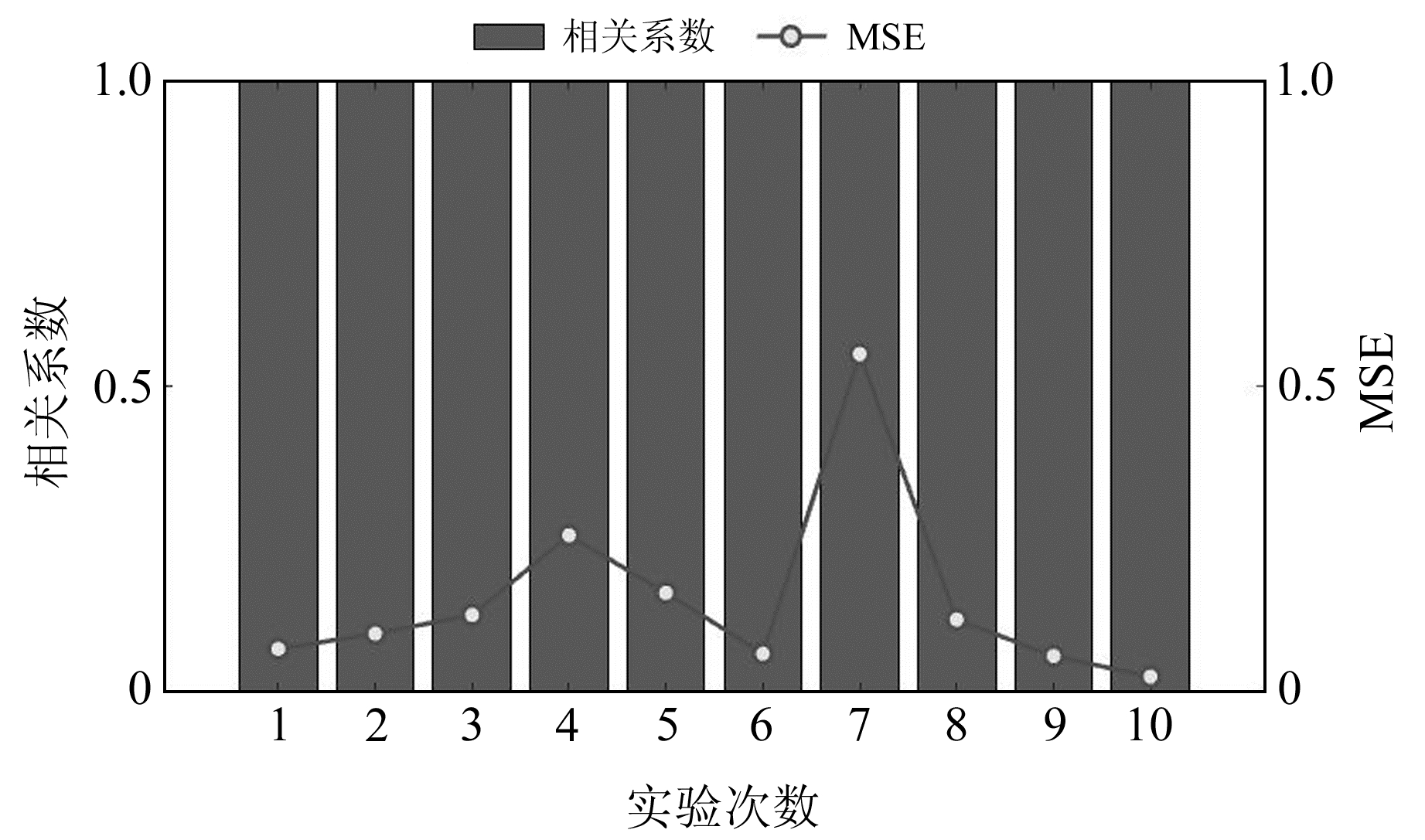
图 7 10条DSQ水管倾斜仪信号的CEEMD-PCA模型去噪结果 Fig. 7 Denoising results for 10 DSQ water tube tiltmeter signals using CEEMD-PCA model |
图 5为DSQ水管倾斜仪信号经过CEEMD分解得到的多条IMF结果。由图 5、6可以看出,IMF10涵盖了初始信号的主要能量,幅值较大;IMF1~IMF6含有不同程度的噪声且幅值极小;IMF7~IMF10波形较为光滑,不存在零点附近快速振荡的现象,幅值整体较大;IMF7与初始波形较为相似,两者的相关系数值也最大,达到0.943 0(表 5)。此外,CEEMD分解得到的每个IMF分量可表征信号在不同频率下的局部特征,其按照高频到低频的顺序依次排列,除了用来鉴别噪声成分,还可以作为输入向量进行山洞环境噪声分析或形变异常识别等研究。表 5为DSQ水管倾斜仪信号经过CEEMD分解后的各IMF的特征值。可以看出,IMF10与其他IMF分量的特征值存在较大差异,特别是在表征误差程度的MSE、SSE、R2等方面。
|
|
表 5 CEEMD分解后各IMF的特征值 Tab. 5 Eigenvalues of each IMF after CEEMD decomposition |
由表 5~8可知:1)部分IMF特征指标之间的相关性较高,如分布熵与相关系数高度正相关,R2与MSE高度负相关,MSE与RMSE高度正相关;2)主成分1在全部主成分中的贡献率达到78.526 2 %,认定为已包含样本数据的大部分信息,可直接代表全部IMF特征指标参与后续分析,而主成分3~8的贡献率均在1%以下,在实际应用中可以直接省略;3)由表 8可知,PCA综合评价函数值排名结果为IMF5>IMF4>IMF3>IMF1>IMF2>IMF6>IMF9>IMF8>IMF7>IMF10,由于IMF特征参数多为反映各IMF与原始含噪信号间的误差情况,PCA函数值越大代表该IMF分量误差越大以及含噪程度越高,故取最后4位IMF分量参与线性重构信号,即IMF9、IMF8、IMF7、IMF10,得到的去噪结果如图 6所示。从图 6看出,去噪后的曲线整体极为光滑,有较好的重构效果,并从3个局部放大图像可以看出,CEEMD-PCA模型能有效光滑局部含噪数据,剔除大量毛刺数据。
|
|
表 6 各IMF标准化特征向量的相关系数 Tab. 6 Correlation coefficient of each IMF normalized eigenvectors |
|
|
表 7 各参数的特征值、特征向量及贡献率 Tab. 7 Eigenvalues, eigenvectors and contribution rates of each parameter |
|
|
表 8 PCA综合评价函数值与排名 Tab. 8 Composite evaluation function values and rankings of PCA |
为了测算CEEMD-PCA模型在DSQ水管倾斜仪信号处理中的有效性,引入卡尔曼滤波、70阶低通FIR滤波作为比对模型,评价指标为相关系数、MSE、信噪比,结果如表 9所示。可以看出,CEEMD-PCA模型的去噪效果最好,其相关系数值、MSE、信噪比分别为0.999 6、0.020 6、49.573 5 dB,均为3种模型中的最优值,证明其重构过程损失极小,能有效地找到随机噪声位置并精准剔除。
|
|
表 9 不同模型的DSQ水管倾斜仪信号去噪效果对比 Tab. 9 Comparison of denoising effect of DSQ water tube tiltmeter signals for different denoising models |
2022-05的10条DSQ水管倾斜仪信号去噪结果如图 7和表 10所示。CEEMD-PCA模型去噪效果的评价指标采用相关系数和MSE,图 7中的柱状图表征相关系数值,折线图表征MSE值。由图 7和表 10可知,DSQ水管倾斜仪信号去噪后的MSE值几乎都低于0.5,误差相对极小,且10条信号去噪前后的相关系数值都大于0.99,证明了该模型去噪的有效性和可靠性。
|
|
表 10 10条DSQ水管倾斜仪信号的去噪结果统计 Tab. 10 Statistics of denoising results of 10 DSQ water tube tiltmeter signals |
本文提出一种结合CEEMD和PCA的DSQ水管倾斜仪信号去噪模型CEEMD-PCA,该模型融合多种评价指标来构建一种全新的PCA主成分得分指标,可以更精确地识别出噪声IMF成分和有效IMF成分,重构误差较小,没有显著失真现象,在仪器信号去噪领域有一定的应用推广价值。
| [1] |
胡玮, 冯雪东, 石伟, 等. 乌加河地震台DSQ水管倾斜仪观测的小波及阈值去噪分析[J]. 防灾减灾学报, 2022, 38(4): 51-58 (Hu Wei, Feng Xuedong, Shi Wei, et al. Analysis on Wavelet Transform and Threshold Denoising of DSQ Water-Tube Tiltmeter at Wujiahe Seismic Station[J]. Journal of Disaster Prevention and Reduction, 2022, 38(4): 51-58)
(  0) 0) |
| [2] |
余尚江, 成万里, 曲翠兰, 等. 信阳地震台DSQ型水管仪异常特征分析[J]. 防灾减灾学报, 2015, 31(4): 60-65 (Yu Shangjiang, Cheng Wanli, Qu Cuilan, et al. The Analysis of Abnormal Characteristics about Model DSQ Water Tube Tiltmeter of Xinyang Seismostation[J]. Journal of Disaster Prevention and Reduction, 2015, 31(4): 60-65)
(  0) 0) |
| [3] |
余尚江, 成万里, 卢亚, 等. 道路建设对DSQ水管倾斜仪影响分析[J]. 地震地磁观测与研究, 2016, 37(3): 67-71 (Yu Shangjiang, Cheng Wanli, Lu Ya, et al. The Study of Road Construction Effect on the DSQ Water Tube Tiltmeter[J]. Seismological and Geomagnetic Observation and Research, 2016, 37(3): 67-71)
(  0) 0) |
| [4] |
卢亚. 信阳地震台DSQ水管倾斜仪干扰因素分析[J]. 地下水, 2020, 42(4): 124-125 (Lu Ya. Analysis of Interference Factors of DSQ Water Pipe Tiltmeter at Xinyang Seismic Station[J]. Ground Water, 2020, 42(4): 124-125)
(  0) 0) |
| [5] |
史春伟, 罗词建, 张晨蕾, 等. 乾陵地震台DSQ型水管倾斜仪观测数据常见干扰分析[J]. 地震地磁观测与研究, 2022, 43(2): 153-159 (Shi Chunwei, Luo Cijian, Zhang Chenlei, et al. Interference Analysis of DSQ Water-Tube Tiltmeter at Qianling Seismic Station[J]. Seismological and Geomagnetic Observation and Research, 2022, 43(2): 153-159)
(  0) 0) |
| [6] |
马愈昭, 刘逵, 张岩峰, 等. CEEMD结合改进小波阈值的激光雷达信号去噪算法[J]. 系统工程与电子技术, 2023, 45(1): 93-100 (Ma Yuzhao, Liu Kui, Zhang Yanfeng, et al. Laser Radar Signal Denoising Algorithm Based on CEEMD Combined with Improved Wavelet Threshold[J]. Systems Engineering and Electronics, 2023, 45(1): 93-100)
(  0) 0) |
| [7] |
梁沛, 杨志强, 杨兵, 等. 顾及GNSS坐标时间序列中季节信号的CEEMD降噪方法[J]. 大地测量与地球动力学, 2022, 42(10): 1010-1014 (Liang Pei, Yang Zhiqiang, Yang Bing, et al. CEEMD Denoising Method with Seasonal Signals in GNSS Coordinate Time Series[J]. Journal of Geodesy and Geodynamics, 2022, 42(10): 1010-1014)
(  0) 0) |
| [8] |
王民顿, 尚俊娜. 基于CEEMD和改进小波阈值法的钢架结构沉降数据去噪方法[J]. 大地测量与地球动力学, 2022, 42(11): 1191-1195 (Wang Mindun, Shang Junna. Denoising Method of Steel Frame Structure Settlement Data Based on CEEMD and Improved Wavelet Threshold Method[J]. Journal of Geodesy and Geodynamics, 2022, 42(11): 1191-1195)
(  0) 0) |
| [9] |
符永海, 李帆, 高建军, 等. 稳健主成分分析在地震资料异常值噪声压制中的应用[J]. 现代地质, 2023, 37(1): 114-120 (Fu Yonghai, Li Fan, Gao Jianjun, et al. Application of Robust Principal Component Analysis in Seismic Data Erratic Noise Suppression[J]. Geoscience, 2023, 37(1): 114-120)
(  0) 0) |
| [10] |
李军辉, 何康, 王燚坤, 等. 基于主成分方法分析2013年甘肃岷县漳县6.6级地震前地磁日变化异常[J]. 地震, 2022, 42(1): 122-132 (Li Junhui, He Kang, Wang Yikun, et al. Principal Component Analysis of Geomagnetic Daily Variation before the 2013 Minxian-Zhangxian MS6.6 Earthquake, Gansu, China[J]. Earthquake, 2022, 42(1): 122-132)
(  0) 0) |
2. Wuhan Institute of Seismic Scientific Instruments Co Ltd, 11 Qinglong Road, Xianning 437099, China;
3. Liaoning Earthquake Agency, 44 North-Huanghe Street, Shenyang 110031, China
 2024, Vol. 44
2024, Vol. 44

