2. 北京白家疃地球科学国家野外科学观测研究站,北京市白家疃路,100095;
3. 中国地震局第一监测中心,天津市耐火路7号,300180
地球内部物质迁移和地壳变形过程引起的地表重力场和电磁场的时空变化信号在大地震深部孕育环境变化研究中发挥着关键作用。探究这些变化的规律和物理机制有助于深入理解地球系统的动力学过程,同时可根据这些物理规律来推断潜在的地球系统灾变现象。近年来,光纤技术、量子技术、高稳定激光技术和低温超导技术等新兴技术的发展,极大提升了地球物理核心传感器检测地球深部微弱信号的能力。这些新技术的引入,为科学家们重新审视经典的断层破裂、大地震孕育模型与假说以及精确监测地震深部潜在风险源的状态变化与运动过程提供了更有效的时变物理过程监测方法。
陆地时变重力测量技术是以高精度绝对重力的重复观测为基准,通过相对重力组网联测扩展其空间分辨率,实现对μGal级重力场时变信号的监测。经过40多年的发展,该技术在测网建设、数据处理和模型解释方面逐步形成体系,为应用不同时空尺度微重力变化研究地学问题带来新的机遇与挑战。20世纪70年代,根据海城和唐山地震前观测到的重力场变化现象,陈运泰等[1]提出“地下物质迁移”假说。随后,根据在京津唐张地区的重力组网观测结果,顾功叙等[2]认为,地壳内部多个深度内的流体物质运动对局部重力场变化有显著影响,并与地震孕育密切相关。然而,当时相对重力观测仪器的观测精度不够,缺少绝对重力基准约束,且测网覆盖有限,导致对“地下物质迁移”假说的验证面临巨大的挑战,在陆地上获取具有一定时空分辨能力的高精度时变重力数据一直是制约重力学方法研究大地震孕育物理机制的“卡脖子”难题。
自20世纪70年代开始,我国科学家通过不断尝试在地震活动带进行时变重力测量,推动了“中国地壳运动观测网络”、“中国大陆构造环境监测网络”等项目的建设。我国已经建成一个覆盖全国的时变重力监测网络[3]。该监测网络包含约100个绝对重力点和4 000个相对重力测点[3]。这些点位每年都会进行定期复测,通过绝对和相对重力联测,获取不同时空尺度的重力观测数值,旨在建立高质量的时空一体化陆地时变重力观测网。
现今中国大陆重力观测系统的规模和数据产出量已经位居世界首位,为深入探索中国大陆的地球动力学过程提供了重要的科学基础。然而,尽管在重力观测方面取得显著进展,高精度时变重力观测技术体系仍有待完善,尤其是缺乏适用于复杂重力观测系统的专有数据处理算法,导致高质量的时变重力场模型产品相对稀缺。因此,针对中国大陆重力监测系统,我们需要着手研制有特色的时变重力数据处理和建模算法。具体而言,亟需建立适应复杂观测系统的处理算法,进而能够有效处理多源重力观测数据并生成高精度的场源模型产品。为实现这一目标,我们还需要开发成套的软件工具,以高效地解算模型产品。这些工作对于提高重力监测网络的模型产品质量至关重要,同时也将为深入开展科学研究、理解大震孕育过程提供必要的技术支持。
1 陆地重力观测系统重力学是一门基于观测的地球科学,它不仅能揭示静态的地球内部结构,同时反映了地球系统内外部物质质量迁移与重分布的动态过程[4-6]。重力观测方式包括卫星重力观测、航空重力观测、船载重力观测和陆地(地表)重力观测(图 1, http://www.iag-ggos.org/)。在这众多方法中,陆地(地表)重力观测是一种利用绝对或相对重力仪在固定点及移动路径上开展连续或间断的重力测量的方式,其观测精度高,可以监测μGal级重力场信号。陆地时变重力观测技术不仅在地震监测领域有显著应用,而且在经济建设和国家安全等领域也具有重要的应用价值,这些领域包括力值溯源、油田注采、二氧化碳地质封存、水资源变化、地震与火山监测以及国防军事等。本节首先介绍陆地时变重力观测的概念、特征与重力仪的分类,随后概述中国大陆高精度重力观测系统的建设和发展,最后分析该系统存在的问题,并提出优化建议。
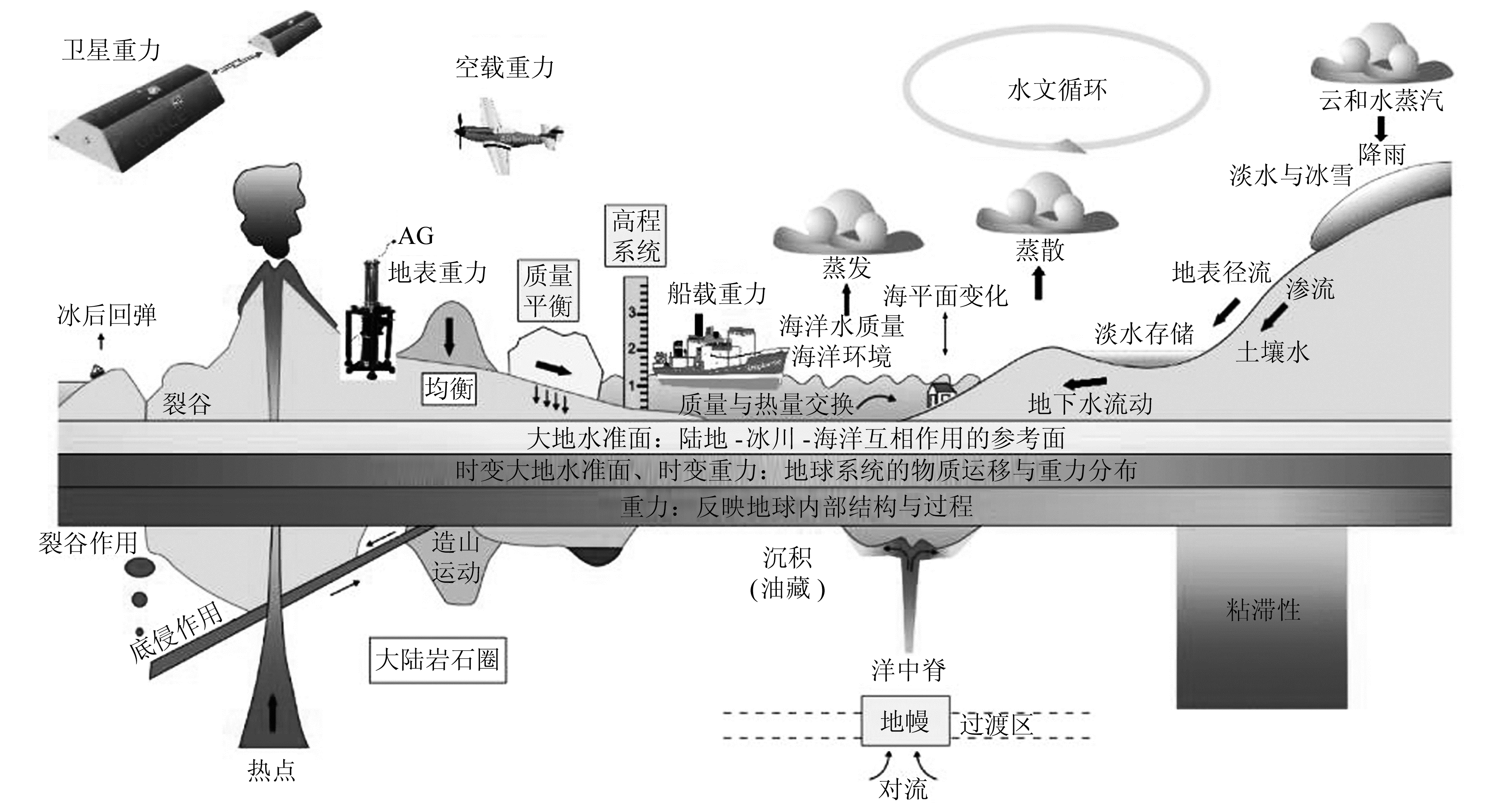
|
图 1 地球系统中的质量迁移过程和重力观测手段类型示意图 Fig. 1 Mass migration processes in the earth system and schematic of gravity observation methods |
地球重力场的时空变化反映地球内部和表层的物质运动,而陆地时变重力测量是观测这种变化的有效手段。其测量原理是基于重力仪在地球表面测量重力加速度或重力差值,以获得重力场的变化信息[7-8]。作为核心观测装备,重力仪的性能和技术水平直接关系到重力测量的精度和效率[5]。图 2展示了主要的地表重力观测仪器。根据测量原理,这些重力仪可以分为绝对重力仪(图 2(a)~(c))和相对重力仪(图 2(d)~(i))两大类。绝对重力仪直接测量物体在地球重力场中的自由落体加速度,具有精度高和稳定性高的特点,但观测效率低、设备成本高;相对重力仪测量不同位置之间的重力差值,具有效率高和设备价格低的特点,但受环境因素影响大,需定期用绝对重力仪进行校准。绝对重力仪(AG)和相对重力仪中的超导重力仪(SG)主导着大地观测站和基本参考站的重力测量。根据仪器结构,重力仪又可以分为弹簧型重力仪、落体型重力仪、超导型重力仪[9-10]。其中,弹簧型重力仪是最为常见的类型,具有结构简单、成本低廉、操作方便等优点。超导重力仪(SG)作为一种基于超导材料的技术,由于内置的超导小球质量非常小(几g到几十g),其灵敏度较高,观测精度可达到0.1 μGal量级。并且由于其低频性(低于1 mHz)使其在观测长周期地震频段方面具有独特优势,更容易捕获地球深部信号[9, 11]。特别是在需要连续观测的情况下,超导重力仪展现出卓越性能,被认为是首选的重力仪。近年来,量子型重力仪作为新式落体型重力仪的代表发展迅速,具有高精度、高稳定性、无物理磨损、可连续观测等优点[12]。相对于传统的绝对重力仪,量子重力仪为时变重力场观测提供了更多可能性[13],尤其为连续监测地震和火山活动提供了更加可行的新手段[14]。

|
(a)FG5-X绝对重力仪;(b)A10绝对重力仪;(c)AQG量子绝对重力仪;(d)LaCoste Romberg G型(LCR-G)相对重力仪;(e)gPhone相对重力仪;(f)CG-5相对重力仪;(g)CG-6相对重力仪;(h)iGrav型超导相对重力仪;(i)Burris相对重力仪 图 2 陆地重力观测的主要仪器装备 Fig. 2 Primary instruments for land gravity observation |
总体而言,这些先进的重力观测装备在地球物理学研究中扮演着不可或缺的角色,为科学家们提供高精度的重力数据,有助于深入理解地球内部结构和地球重力场的时空微变化。同时在选择观测设备与技术时,需要全面权衡不同技术的优劣,包括精度、稳定性、成本等。尽管重力模型的应用可能涉及数学复杂性,高精度重力仪仍然是确保数据质量和科学研究可靠性不可或缺的工具。为推动重力观测技术的发展,我们需要进一步提高其精度和适应性,以更好地满足复杂地球科学研究的需求。
1.2 中国大陆高精度重力观测网中国大陆高精度重力观测网是一个覆盖中国大陆主要构造活动区域的重力监测体系,它包括绝对重力基准网、相对重力联测网和连续重力台网3个部分。根据重力观测区域的不同,该系统又分为两个部分:重点监视区和一般监视区。重点监视区包括华北地震带、青藏高原、南北地震带和东南沿海地震带等区域,而其他地区则属于一般监视区。该观测系统是在“中国地壳运动网络工程”、“陆态网络”[15]、“中国地震科学台阵”等一系列国家级地震科学项目的支持下建设和完善的。该重力监测网的设计目标是通过相对重力联测网提高空间分辨率,通过连续重力台网提高时间分辨率,并利用绝对重力基准网的观测为相对重力联测和连续重力观测提供时空基准服务。目前,该系统在中国大陆主要活动构造区已实现百km空间尺度的μGal级重力信号的监测能力[16],并在地震监测、地壳垂直形变、水文变化特征、重力基准建立等研究领域广泛应用。
1.3 问题与建议中国大陆重力监测网是获取强震地球物理场前兆的重要基础设施,其现代化监测能力对提高潜在强震风险源状态判定和强震预测能力至关重要。尽管经过多年的建设和发展,该网络已覆盖中国大陆的地震活动构造,实现多手段、多频次的组合观测,并完成由模拟到数字化再到网络化的升级转型,但仍面临一些挑战和问题:
1) 重力网各种监测手段之间缺乏有机融合。不同监测手段之间缺乏同址观测的相互验证,导致观测到的信号往往是多种场源响应的叠加,难以区分真实异常和干扰噪声。
2) 缺乏针对潜在地震风险源区的靶向监测能力。由于地球的不可入性,直接观测深入地壳内场源的能力受到限制。目前的观测系统设计和台阵式观测难以实现从监测地表的时变重力场到监控地壳介质源的转变。
3) 高精度绝对观测基准的控制能力不足。尽管现阶段已经具有一定数量的绝对重力仪器设备,但观测规模有限,已经成为未来重力发展的瓶颈。
本世纪初以美国GRACE卫星为代表的时变重力观测系统,为300 km以上尺度的时变重力信号研究提供了新的可能性。要进一步提高重力场的时空分辨率,发展陆地重力观测系统是有效途径之一。回顾中国大陆多年来的重力观测系统建设经验,需要在提高陆地重力观测数据质量、减小观测系统和场源不确定性方面继续进行多方面的优化:
1) 从单一重力方法向多手段综合观测转变。利用多分量、小型化、一体式传感器技术,实现多种地球物理手段的同址、同步观测,大幅减少“虚假”异常信号的出现。同时,通过多观测数据融合、模型同化等技术,实现多手段地球物理观测的有机结合与相互验证。
2) 从地表重力测量向提高地壳内部风险源的靶向监控转变。通过改进的观测系统设计和台阵式观测,研制可变“焦距”的陆域重力观测台阵系统,实现从监测地表的时变重力场到监控地壳深部介质源的转变。
3) 从相对观测向绝对观测转变。通过扩大绝对重力仪器设备的数量和覆盖范围,提高绝对基准的控制能力,保障时变重力研究的可靠性和有效性。
2 时变重力技术与模型产品如§1.1所述,陆地重力观测系统的核心在于重力仪器,其观测数据的质量直接决定了重力场模型的可靠性和准确性。为保证重力仪器的性能符合标准,通常需要按照国家标准和技术规范进行严格的检验和校准。在实际的重力观测过程中,仪器类型的多样性和观测本身的不确定性较大,如何有效地消除或减小这些不确定性对数据处理的干扰仍然是一个亟待解决的难题。为了解决这个难题,国际上已经开发了多种处理重力数据的软件产品,如gravnet[17]、Tsoft[18]、GSadjust[19]、pyGrav[20]、GraProcess[21]以及gTOOLS[22]等。这些软件采用不同方法处理重力数据,生成静态或动态的重力场模型。然而实际上,时变重力观测数据的处理流程不仅要生成重力场图像,还应包括对场源信号的解释和对未来趋势的推测。总体上分为6个处理阶段:观测、平差、建模、反演、模拟和预测(图 3)。这6个阶段涵盖了时变重力数据处理的基础步骤和数据应用拓展步骤。基础步骤通过时变重力数据认识场源属性,包括产出L0级原始数据、L1级点值数据和L2级模型数据。应用步骤在基础步骤基础上进行重力时变反演、构建场源模型,并利用物理和概率模型对场源变化进行预测。应用步骤产出L3级场源解、L4级模拟数据和L5级推估模型。在地震趋势判断和预报业务中,通过将L5级重力场推估模型与观测结果进行对比,能够确定重力变化的异常信号,为强震危险源判定和预报提供科学指导。

|
图 3 陆地时变重力数据和产品处理流程 Fig. 3 Processing workflow for terrestrial time-variable gravity data and products |
通过时变重力场观测到模型驱动的变化预测,再通过实际测量与预测结果对比校正模型参数,实现“预测-校正”的模型数据同化闭环过程,为认识地球系统非潮汐时变重力场变化规律和物理机制提供技术支撑。图 3所示的基础步骤和应用步骤同等重要,只有保证整个产品链条上的技术都达到高水平、高质量,才能有效支撑应用步骤的实施,并提高预测结果的可信度和准确度,为物理地震预报提供可靠的数据支撑。
2.1 时变重力观测观测是获取时变重力信息的基础,主要包括卫星重力观测和陆地重力观测。卫星重力观测是利用人造卫星在轨道上对地球重力场进行测量的方法。目前,主要由GRACE、GRACE-FO、GOCE等卫星承担这一任务。卫星重力观测的优势在于能够覆盖全球范围,获取大尺度的时变重力信号。其动态重力测量已经探测到巨大地震的同震和震后效应信息,例如2004年苏门答腊-安达曼MW9.1地震[23]和2010年智利MW8.8地震[24]等。然而,GRACE数据的劣势在于分辨率低(约300 km),又具有一定的平滑作用[6],无法监测8级以下地震的影响[25-26]。
陆地重力观测则是利用不同类型的重力仪在地表或地下对重力场进行定点或流动测量。其优势在于能够获取高精度的时变重力信号,通常可以实现μGal级精度水平,在重复测量情况下,精度可达3 μGal[6, 27]。这种高精度的测量方式更有利于探测地壳深部质量的动态变化[28]。在时变重力数据的获取过程中,按观测方式可分为定点(台站)连续观测型和流动定期复测型。定点(台站)型观测是指在固定台站设置重力仪(常用仪器为gPhone和GWR,见图 2(e)和(h))进行连续重力观测。GWR是目前最精密的重力仪,观测精度优于0.05 μGal,达到秒级采样[9]。这种观测方式具有较高的时间分辨率(通常为1 s)和较高的观测精度(μGal级),适用于反映重力场的短期变化,如潮汐、地震、火山等[10]。然而,由于建站成本高且台站数量有限,这种观测方式不利于获取区域性重力变化信息。流动重力定期复测过程中,常见的代表仪器有FG5型(观测精度2 μGal)和A10型绝对重力仪(观测精度10 μGal)(图 2(a)、(b)),以及LaCoste Romberg G、CG5、CG6、Burris型相对重力仪(图 2(d)、(f)、(g)和(i))。这种观测方式具有设站灵活、空间分辨率高的优势,适用于反映重力场的动态变化,但存在观测精度较低(10 μGal级)、时间采样间隔长(半年至多年)的不足[29]。因此,有必要对多源时变重力数据进行融合处理,实现对时变重力信号全方位、高效率和高分辨率的观测目标。随着各类陆地重力测量的快速发展,形成一种混合(微)地表流动重力测量手段[30-31]。该手段利用绝对重力测量以确保获得具有统一起算基准的绝对重力变化,并借助流动重力高空间分辨率和连续重力观测高时间分辨率的独特优势,显著提升了重力测量的时空分辨率。除了混合重力观测外,文献[32]提出阵列式场地微重力观测系统,联合运用物理、几何和水文3种观测方式,以降低地下场源微重力信号分离的不确定性。文献[33]通过使用地下和地上多台重力仪观测,即“垂直重力仪阵列”,减少环境重力效应,从而检测与地震现象相关的地下深处质量再分配引起的重力变化。
2.2 时变重力平差平差是处理和优化相对重力观测数据的核心,旨在消除重力测量中的闭合差,提高数据的精度和可靠性。陆地时变重力网平差中,常用的方法包括最小二乘方法和拟稳平差方法。最小二乘方法作为一种经典的重力平差方法,已广泛应用于处理局部和区域混合重力网数据[34]。而拟稳平差法则通过权重约束来优化观测结果,有效减少异常观测的影响[35]。相较于最小二乘法,拟稳平差法更适于处理高原地区的重力数据[35]。近年来,贝叶斯重力平差模型作为一种新的平差方法受到关注。该模型基于贝叶斯理论构建,将仪器漂移率方差作为超参数,并利用ABIC贝叶斯信息准则来求解超参数的最优值,从而解决区域重力测量中重力仪非线性漂移的问题[36]。此外,王林海等[37]提出改进的贝叶斯重力平差模型,引入格值系数作为新的超参数进行求解。贝叶斯重力平差模型已被广泛验证和采用[38-40]。该模型的引入不仅解决了多仪器协同观测中的平差问题,还为仪器漂移和格值系数误差的处理提供了先进的解决途径。目前,贝叶斯重力网平差模型算法代码已集成到GEOIST开源软件平台的模块中,可以通过网址https://cea2020.gitee.io/geoistdoc下载获取。
2.3 时变重力建模建模是将时变重力数据转换为时变重力场模型的过程,主要采用球谐函数模型和网格模型两种形式。球谐函数模型适用于表达全球尺度的时变重力场,但受到截断误差的影响。实际陆地时变重力测量由于受地理和环境等因素制约,导致重力场变化无法实现全球覆盖,而且重力测点空间分布不均匀,不适于采用经典的球谐方法进行重力场建模[41]。网格模型是将时变重力场离散为网格点值,采用一组网格点坐标和变化值来描述时变重力场的局部或区域特征。构建局部重力场模型的常用方法包括最小曲率法、反距离加权法、克里格方法、多面函数法和最小二乘配置法[42]等。杨锦玲等[16]基于3种建模方法(最小曲率法、克里格方法和最小二乘配置法)对华南区域进行重力场重建,认为最小二乘配置法的建模效果最优。阮明明等[43]认为,最小二乘配置法更适用于局部高精度重力场建模问题。传统建模方法对于静态局部重力场建模效果显著,而对于含有时间尺度噪声干扰的时变重力信号往往无法引入有效的模型约束。因此,采用适合局部陆地时变重力场的建模方法来构建高信噪比时变重力模型成为当前陆地时变重力数据处理的关键问题。陈石等[44]和韩建成等[41, 45]将Slepian局部谱分析方法[46-47]引入到地面时变重力场建模中,成功恢复了华北地区和川滇地区的120阶时变重力场模型,并将这些模型与卫星重力估计结果进行对比分析,得出与经典球谐函数具有等价意义的重力场建模结果。目前,在国家地震科技创新工程“透明地壳”计划的支持下,时变重力场模型已实现可持续更新,并推出了更精细的华北地区150阶时变重力场模型[48](www.esdc.ac.cn/class/40)。
2.4 时变重力反演重力反演是指利用重力场数据提取密度分布信息或特殊密度体结构的过程。经典的重力位场反演方法同样适用于时变重力场的反演[49]。不同之处在于,时变重力反演需要对多个离散时间节点上的观测重力信号进行反演和参数优化[40],以获得时变场源的动态特征。在进行重力场反演时,首先需要根据地质背景或其他目标特征,选择合适的反演模型,如点源、线源、面源或块体模型等,以参数化形式表示出来;其次,要根据具体的反演目标和数据特征来选择合适的反演方法;最后,建立目标函数并求解最优参数。由于反演问题往往存在多解性和不确定性,因此在反演过程中通常需要引入正则化项来约束参数空间,最常用的正则化方法是洪基洛夫(Tikhonov)正则化[50]。然而,正则化方法也不能完全消除反演结果的多解性和不确定性[51],因为正则化参数的选择往往依赖于先验信息和主观判断,缺乏统一的标准和准则。近年来,基于贝叶斯原理的概率性反演方法受到广泛关注,它通过贝叶斯公式进行反演可以更好地结合观测数据和先验信息,利用马尔可夫链蒙特卡洛方法(MCMC)进行抽样来探索参数空间,从而实现对参数不确定性的量化[52]。经验贝叶斯方法还可以引入ABIC准则来解决先验参数选择的主观性问题[53]。贝叶斯方法在时变重力场源反演中有着广泛的应用[40, 54-56]。
2.5 时变重力模拟时变重力模拟是通过数值方法建立数值模型,对时变重力场或时变质量分布与其产生源或影响因素之间的关系进行数学描述或物理解释。目前常用的模拟方法主要是基于有限元或有限差分等方法建立数值模型。以文献[57]的研究为例,通过基于有限元的数值模拟实验评估高压地壳流体侵入6~10 km深度所引起的重力变化,构建多场耦合的非潮汐重力场源模型,为研究地壳内部物质(流体)运移引起的地表重力变化提供理论依据。该研究发现,高压流体入侵导致流体密度增加,并在10 a内产生正向的重力变化。流体压力是影响流体密度变化的关键因素,而温度则影响较小。随着流体压力的衰减,相应的重力变化速度也会从快(大于3 μGal/a)到慢。流体运移产生的重力变化与邻近流体源处的岩石孔隙率和渗透率、流体盐度和规模、初始温度呈正相关,与入侵深度呈负相关。时变重力模拟的研究为监测地壳流体运动提供了一种方法,尤其是通过高精度的时变重力观测。
2.6 时变重力预测时变重力预测是根据已有的观测数据和模型,运用贝叶斯数据同化等手段,推断未来时变重力场的变化趋势和规律的技术,可应用于地震、火山等灾害的预测,相关预测研究内容将在下一节详细介绍。
本文提出一种创新的处理方案,即“观测-平差-建模-反演-模拟-预测”链条式处理方案。为了更详细地提炼这一方案,表 1列举了部分近年来更具创新性的链条式方案,包括“原位观测-点值平差-球谐建模-重力反演-场源模拟-同化预测”,并详细展示各个层级数据处理和场源模型构建技术的目标、处理技术及用途。链条式处理方案的技术思路主要是通过综合利用时变重力数据产品和场源模型产品,采用“以场求源、场源结合”的策略,以及利用多个震例数据进行深入研究。然而,目前尚缺乏成熟的技术手段来实现大范围的时变微重力观测。对于陆地时变重力而言,目前存在两个难点:一是如何精确求解时变微重力场,二是如何揭示重力场微小短期变化的物理机制。此外,影响重力场源变化的因素包括地壳变形、孔隙流体压力扩散、地震断裂活动等多种因素,这也增加了深入研究其内在机理的难度。
|
|
表 1 部分陆地时变重力数据处理及场源模型构建技术 Tab. 1 Techniques for processing partial terrestrial time-variable gravity data and constructing field source models |
综合而言,通过深入研究陆地时变重力技术方法与模型,将有望突破目前的技术限制,为更全面、准确地理解地球动态过程提供有力支持。这不仅需要在实际观测中不断创新,也需要在理论方法上取得重要突破,以推动陆地时变重力领域的可持续发展。
3 陆地时变重力观测的应用和进展时变重力场是由多种场源综合作用的结果,其中包括固体潮、海洋潮汐、大气压强、水文变化、地震、火山活动等[5-6]。这些场源信号在频带和量级上存在显著差异。图 4展示了非潮汐时变重力场信号的时频分布。观察发现,与地壳内部变形相关的时变信号主要集中在低频段,其量级通常在10 μGal或更小。为了捕获这种微小量级的时变重力信号,必须借助高精度的重力仪器。陆地时变重力观测具有观测仪器精度高、对近场源敏感性强、采样率高和观测点可重复性强等优势[6]。

|
图 4 与地面重力变化相关的地球内外部信号时频特征图(修自参考文献[5]) Fig. 4 Time-frequency characteristics of earth's internal and external signals associated with ground gravity changes(adapted from reference[5]) |
地震作为地球内部应力不断积累和释放的产物,通常发生在断层等薄弱部位。地震发生时,地壳介质由于变形而引起密度变化,从而导致重力场的改变[8, 59, 61]。通过反复进行重力测量,可以获得局部重力场的动态变化,从而反演出断层的活动参数[62]。分析陆地时变重力场的空间分布和时间演化,可以揭示地壳垂直位移运动[11, 33, 63-64]。
时变重力观测还可以被用来监测地震。目前已利用地表重力观测手段多次监测到大地震前后的微重力异常变化,如2008年汶川MS8.0地震[65]、2013年芦山MS7.0地震[56]、2015年尼泊尔MW7.8地震[62]、2016年门源MS6.4地震[66]和2022年门源MS6.9地震[55]。为解释重力观测结果,众多学者探讨与地震相关的重力场变化物理机制,提出各种理论模型,如质量迁移、膨胀扩容、联合膨胀、断层位错、密度变化、闭锁剪力、震质中/源等模型[67]。基于“震质中和震质源”的概念,Wang等[56]利用密度均匀变化的圆盘模型模拟孕震区的等效质量变化,提取2013年芦山MS7.0地震前后高精度的时变重力信号,并结合小震时空分布特征、流体观测结果(He同位素,甲烷等)以及壳幔速度模型等多种地球物理和地球化学观测手段,首次构建融合多学科研究结果的震前深部物质迁移的场源模型,揭示深部流体对大震孕育的关键性作用。
在地震预测方面,祝意青等[3]根据中国大陆构造特征和强震活动规律,发现时变重力在不同时间尺度下具有时空分布不均匀以及重力分区的现象,强震倾向于发生在沿活动构造块体边界且重力变化正、负异常区过渡的高梯度带上,以及重力变化等值线的拐弯处。同时,部分震区由于构造活动断裂带产生强烈的差异运动,构造变形出现了很强的非连续性,容易发生急剧的重力变化。这些时空变化重力观测特征可作为地震中期预测的有效指标,反映强震重点监视区与防御区的地壳介质物性变化[68]。目前已经在一些中强以上的地震预测和评估中取得成功案例,如2008年于田7.3级地震[69]、2008年汶川8.0级地震[70]、2013年芦山7.0级地震[71]、2016年门源6.4级地震[72]、2017年九寨沟7.0级地震[73]、2022年门源6.9级地震[74]。这些案例充分展示了陆地时变重力观测系统在地震预测和灾害评估中的重要价值。
3.2 火山活动与岩浆运动火山活动一般伴随着岩浆的升降运动,在火山区周围地区引起明显的重力场变化[75]。由于岩浆作用和活火山地下结构的几何形状都异常复杂,准确地确定火山活动的机制并非易事[76]。通过重复和连续的时变重力测量,可以有效解决这类问题。可根据重力变化反映的深部质量运移[77-79],从而监测火山体内部的岩浆运动和压力变化[80-81]。随着技术的不断进步,时变重力测量在火山大地测量中的应用已经取得显著进展,并成功实施于全球数10座火山[77, 79, 82]。除了监测火山活动,陆地时变重力测量还可以深入研究火山体内部的岩浆运动和迁移的动力学过程,如垂直入侵[83-84]或岩浆横向流出[85-86],从而有助于建立新的地球动力学模型。
3.3 水资源监测与管理水循环过程会导致水的质量在不同储存层之间的转移,从而使重力场发生变化。通过连续或重复的重力测量,可以监测地下水变化,并建立和评估水文地质模型,应用于监测与水循环相关的参数,如含水层储量[87-88]、土壤湿度[89]、降雨量或积雪[90-91]等。通过观测陆地时变重力场,可以反演出陆地水储量的时空变化特征与趋势,尤其是在估计给水度(specific yield,SY)[92-94]方面具有优势,为水资源状况的评估、地下水资源管理和环境保护提供科学依据。
3.4 油气资源勘探等工业领域时变重力测量技术是本世纪初发展起来的一种新型油气资源勘探手段。其可以有效监测油气藏开发过程中的质量转移和压力变化,为油气藏评价、管理和优化提供有力的数据支持[94-95]。此外,陆地时变重力测量还可以揭示油气藏的潜在地质风险和环境影响,如地面沉降、裂缝扩展、二氧化碳泄漏等[96]。在众多工业领域中,陆地时变重力测量已经成功应用于地热开发[97-99]、油气库的含水层监测[87, 100-101]、石油生产[102]、二氧化碳封存[103-104]等方面,典型应用案例包括荷兰格罗宁根油田[105]和美国阿拉斯加普拉德霍湾油田[101, 106-107]。
在实际应用中,陆地时变重力测量技术在可行性分析[94, 108]、布设方案[87, 100]、噪声估计[109]、储层压实影响分析、数据处理[87]、反演计算[27]和分辨率分析[87]等方面也取得长足进步。同时,地表重力观测技术在其他领域也有着重要的科学价值,例如城市地表下沉[110]、利用超导重力数据探测地球内部微弱动力学信号[58]、评估影响引力波探测器的牛顿噪声[111-112]等。因此,无论是理论技术还是应用,陆地时变重力测量技术都有着广阔的发展前景。
4 结语本文系统综述了陆地时变重力的基本概念、观测方法、数据处理和技术方法、模型产品和应用领域等方面的研究进展。相较于卫星重力、航空重力等观测方式,陆地时变重力具有不可替代的优势,同时也面临着机遇和挑战。为提升场源监测能力,以实现对深部地壳介质变化的准确、连续和物理一致的描述,未来新一代陆地时变重力观测系统的设计和布局需兼顾当前重力观测技术前沿趋势和工程可操作性。
4.1 从全覆盖到重点加强在现有的全国重力监测网络基础上,应围绕中国地震科学实验场,选择具备较佳观测条件的场地,加强重点区域观测。通过综合应用多技术和多变量数据,分离不同深部场源引起的重力变化信号,建立对深部介质物性变化的监测能力,以获取更准确的信号,可用于研究地震引起的重力变化,特别是震前重力扰动。同时,聚焦潜在的发震构造位置和深部介质场源信号,为研究深地壳介质变形和可靠地震前兆提供重要的基础观测资料。
4.2 从单一手段到多手段综合地球物理阵列观测由于重力时间变化量级小,场源因素更加复杂,局部降雨、地下水开采、地表形变都可能引起不同程度的重力变化。为了排除这些潜在的场源因素,获得深部介质变化的重力信号,必须依靠多手段综合观测。如图 5所示,通过综合应用形变场(GNSS与InSAR)、重力场、电磁场和地震波场的地球物理参数,可以监测断层闭锁状态、提取视密度和视电阻率变化以及地震学成像异常结果等,进而反演分析地下介质物性,揭示其与地震活动的内在联系。未来陆地时变重力观测系统应整合多种观测手段,构建多手段综合地球物理阵列观测系统。这样的综合观测能够从不同角度和尺度反映地球内部的物理性质和动态变化,推动地球物理观测从单一走向交叉、从单点走向阵列、从静态走向动态,提高信噪比、提高精度,量化不确定性,获得可靠性更高的深部时变微重力信号,进一步拓展研究对象、深化研究内容、加强跨学科交叉融合,实现对地球动态过程的深入理解和有效预测。
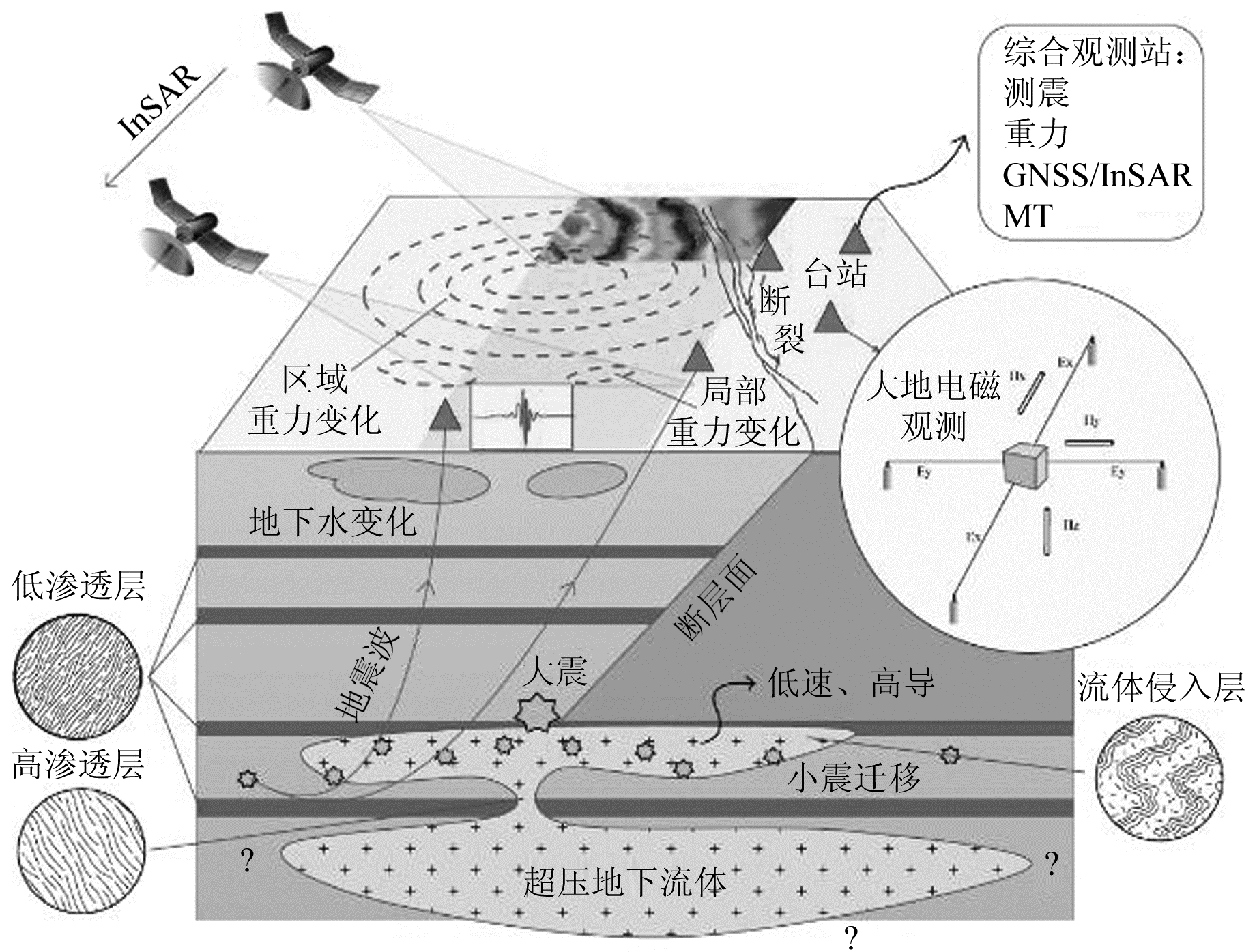
|
图 5 监测深部物质迁移的多手段综合地球物理观测阵列设想 Fig. 5 Conceptualization of a multi-method integrated geophysical monitoring array for deep-seated material migration |
深部地壳介质的场源特征需要通过反演来研究,而反演问题从数学上看属于不适定问题。解决不适定问题的关键在于改进观测系统,从地表的平面观测到近地空、陆地、井下的立体观测,可以提高场源监测能力。因此,构建空、地、井一体化的高精度重力观测系统,是提高场源观测能力以及改进台网监测能力的有效方法。
综上所述,陆地时变重力学是一项具有广泛应用前景和科学价值的地球物理研究方向,可为地球内部和外部的多种物理过程提供重要的信息和途径。随着重力仪精度和稳定性的提高、观测网络的建设和完善、技术方法的拓展和升级以及高分辨率和高精度陆地时变重力模型产品的不断产出,陆地时变重力观测系统的应用将会更加深入和广泛。
| [1] |
Chen Y T, Gu H D, Lu Z X. Variations of Gravity before and after the Haicheng Earthquake, 1975, and the Tangshan Earthquake, 1976[J]. Physics of the Earth and Planetary Interiors, 1979, 18(4): 330-338 DOI:10.1016/0031-9201(79)90070-0
(  0) 0) |
| [2] |
顾功叙, 刘克人, 郑金涵, 等. 中国京津唐张地区时间上连续的重力变化与地震的孕育和发生[J]. 科学通报, 1997, 42(18): 1919-1930 (Gu Gongxu, Liu Keren, Zheng Jinhan, et al. Time-Continuous Gravity Change and Earthquake Preparation and Occurrence in Tangzhang Area of Beijing, Tianjin and China[J]. Chinese Science Bulletin, 1997, 42(18): 1919-1930 DOI:10.3321/j.issn:0023-074X.1997.18.003)
(  0) 0) |
| [3] |
祝意青, 张勇, 张国庆, 等. 21世纪以来青藏高原大震前重力变化[J]. 科学通报, 2020, 65(7): 622-632 (Zhu Yiqing, Zhang Yong, Zhang Guoqing, et al. Gravity Variations Preceding the Large Earthquakes in the Qinghai-Tibet Plateau from 21st Century[J]. Chinese Science Bulletin, 2020, 65(7): 622-632)
(  0) 0) |
| [4] |
李建成. 地球重力场逼近理论与中国2000似大地水准面的确定[M]. 武汉: 武汉大学出版社, 2003 (Li Jiancheng. Approximation Theory of Earth Gravity Field and Determination of China 2000 Quasi-Geoid[M]. Wuhan: Wuhan University Press, 2003)
(  0) 0) |
| [5] |
Crossley D, Hinderer J, Riccardi U. The Measurement of Surface Gravity[J]. Reports on Progress in Physics Physical Society(Great Britain), 2013, 76(4)
(  0) 0) |
| [6] |
Van Camp M, de Viron O, Watlet A, et al. Geophysics from Terrestrial Time-Variable Gravity Measurements[J]. Reviews of Geophysics, 2017, 55(4): 938-992 DOI:10.1002/2017RG000566
(  0) 0) |
| [7] |
申重阳, 祝意青, 胡敏章, 等. 中国大陆重力场时变监测与强震预测[J]. 中国地震, 2020, 36(4): 729-743 (Shen Chongyang, Zhu Yiqing, Hu Minzhang, et al. Time-Varying Gravity Field Monitoring and Strong Earthquake Prediction on the Chinese Mainland[J]. Earthquake Research in China, 2020, 36(4): 729-743)
(  0) 0) |
| [8] |
祝意青, 张勇, 杨雄, 等. 时变重力在地震研究方面的进展与展望[J]. 地球与行星物理论评, 2022, 53(3): 278-291 (Zhu Yiqing, Zhang Yong, Yang Xiong, et al. Progress of Time-Varying Gravity in Seismic Research[J]. Reviews of Geophysics and Planetary Physics, 2022, 53(3): 278-291)
(  0) 0) |
| [9] |
Hinderer J, Crossley D, Warburton R. Superconducting Gravimetry, Treatise on Geophysics[J]. Geodesy, 2015, 3: 65-122
(  0) 0) |
| [10] |
Debs J E, Hardman K S, Altin P A, et al. From Apples to Atoms: Measuring Gravity with Ultra Cold Atomic Test Masses[J]. Preview, 2013, 2013(164): 30-33 DOI:10.1071/PVv2013n164p30
(  0) 0) |
| [11] |
Van Camp M, de Viron O, Scherneck H G, et al. Repeated Absolute Gravity Measurements for Monitoring Slow Intraplate Vertical Deformation in Western Europe[J]. Journal of Geophysical Research, 2011, 116(B8)
(  0) 0) |
| [12] |
Ménoret V, Vermeulen P, Le Moigne N, et al. Gravity Measurements below 10-9g with a Transportable Absolute Quantum Gravimeter[J]. Scientific Reports, 2018, 8(1)
(  0) 0) |
| [13] |
Stray B, Lamb A, Kaushik A, et al. Quantum Sensing for Gravity Cartography[J]. Nature, 2022, 602(7898): 590-594 DOI:10.1038/s41586-021-04315-3
(  0) 0) |
| [14] |
Carbone D, Antoni-Micollier L, Hammond G, et al. The NEWTON-g Gravity Imager: Toward New Paradigms for Terrain Gravimetry[J]. Frontiers in Earth Science, 2020(8)
(  0) 0) |
| [15] |
甘卫军, 李强, 张锐, 等. 中国大陆构造环境监测网络的建设与应用[J]. 工程研究-跨学科视野中的工程, 2012, 4(4): 324-331 (Gan Weijun, Li Qiang, Zhang Rui, et al. Construction and Application of Tectonic and Environmental Observation Network of China's Mainland[J]. Journal of Engineering Studies, 2012, 4(4): 324-331)
(  0) 0) |
| [16] |
杨锦玲, 陈石, 李红蕾, 等. 华南地区时变重力场建模实验和异常分析[J]. 地震, 2021, 41(1): 141-152 (Yang Jinling, Chen Shi, Li Honglei, et al. Modeling Experiment and Anomaly Analysis of Time-Varying Gravity Field in South China[J]. Earthquake, 2021, 41(1): 141-152)
(  0) 0) |
| [17] |
Hwang C, Wang C G, Lee L H. Adjustment of Relative Gravity Measurements Using Weighted and Datum-Free Constraints[J]. Computers and Geosciences, 2002, 28(9): 1005-1015 DOI:10.1016/S0098-3004(02)00005-5
(  0) 0) |
| [18] |
Van Camp M, Vauterin P. Tsoft: Graphical and Interactive Software for the Analysis of Time Series and Earth Tides[J]. Computers and Geosciences, 2005, 31(5): 631-640 DOI:10.1016/j.cageo.2004.11.015
(  0) 0) |
| [19] |
Kennedy J K. GS Adjust V1.0[Z]. USGS, 2021
(  0) 0) |
| [20] |
Hector B, Hinderer J. PyGrav, a Python-Based Program for Handling and Processing Relative Gravity Data[J]. Computers and Geosciences, 2016, 91
(  0) 0) |
| [21] |
Cattin R, Mazzotti S, Baratin L M. GravProcess: An Easy-to-Use MATLAB Software to Process Campaign Gravity Data and Evaluate the Associated Uncertainties[J]. Computers and Geosciences, 2015, 81: 20-27 DOI:10.1016/j.cageo.2015.04.005
(  0) 0) |
| [22] |
Battaglia M, Calahorrano-Di Patre A, Flinders A F. GTOOLS, an Open-Source MATLAB Program for Processing High Precision, Relative Gravity Data for Time-Lapse Gravity Monitoring[J]. Computers and Geosciences, 2022, 160
(  0) 0) |
| [23] |
Han S C, Shum C K, Bevis M, et al. Crustal Dilatation Observed by GRACE after the 2004 Sumatra-Andaman Earthquake[J]. Science, 2006, 313(5787): 658-662 DOI:10.1126/science.1128661
(  0) 0) |
| [24] |
Chao B F, Liau J R. Gravity Changes Due to Large Earthquakes Detected in GRACE Satellite Data via Empirical Orthogonal Function Analysis[J]. Journal of Geophysical Research: Solid Earth, 2019, 124(3): 3024-3035 DOI:10.1029/2018JB016862
(  0) 0) |
| [25] |
De Viron O, Panet I, Mikhailov V, et al. Retrieving Earthquake Signature in Grace Gravity Solutions[J]. Geophysical Journal International, 2008, 174(1): 14-20 DOI:10.1111/j.1365-246X.2008.03807.x
(  0) 0) |
| [26] |
Han S C, Sauber J, Pollitz F. Postseismic Gravity Change after the 2006-2007 Great Earthquake Doublet and Constraints on the Asthenosphere Structure in the Central Kuril Islands[J]. Geophysical Research Letters, 2016, 43(7): 3169-3177 DOI:10.1002/2016GL068167
(  0) 0) |
| [27] |
Krahenbuhl R. A, Li Y. Time-Lapse Gravity: A Numerical Demonstration Using Robust Inversion and Joint Interpretation of 4D Surface and Borehole Data[J]. Geophysics, 2012, 77(2): G33-G43 DOI:10.1190/geo2010-0412.1
(  0) 0) |
| [28] |
Zhang G, Zhu Y, Zhang T, et al. Crustal Deformations in the Northeastern Tibetan Plateau Revealed by Multiple Geodetic Datasets[J]. Pure and Applied Geophysics, 2022, 180(2): 703-714
(  0) 0) |
| [29] |
韩建成, 陈石, 李红蕾, 等. 陆地高精度重力观测数据的应用研究进展[J]. 地球与行星物理论评, 2022, 53(1): 17-34 (Han Jiancheng, Chen Shi, Li Honglei, et al. The Recent Progress Using High-Precision Terrestrial Gravity Measurements[J]. Reviews of Geophysics and Planetary Physics, 2022, 53(1): 17-34)
(  0) 0) |
| [30] |
Hinderer J, Hector B, Mémin A, et al. Hybrid Gravimetry as a Tool to Monitor Surface and Underground Mass Changes[C]. International Symposium on Earth and Environmental Sciences for Future Generations, Cham, 2016
(  0) 0) |
| [31] |
Portier N, Hinderer J, Riccardi U, et al. Hybrid Gravimetry Monitoring of Soultz-Sous-Forêts and Rittershoffen Geothermal Sites(Alsace, France)[J]. Geothermics, 2018, 76: 201-219 DOI:10.1016/j.geothermics.2018.07.008
(  0) 0) |
| [32] |
陈石, 龚立卓, 徐伟民, 等. 深部场源变化微重力观测系统设计与模型研究[J]. 大地测量与地球动力学, 2018, 38(1): 1-4 (Chen Shi, Gong Lizhuo, Xu Weimin, et al. Study on Time-Lapse Microgravity Observation System for Detecting the Crustal Deep Mass Changes[J]. Journal of Geodesy and Geodynamics, 2018, 38(1): 1-4)
(  0) 0) |
| [33] |
Tanaka T, Honda R. Vertical Gravimeter Array Observations and Their Performance in Groundwater-Level Monitoring[J]. Earth and Space Science, 2018, 5(3): 62-74 DOI:10.1002/2017EA000311
(  0) 0) |
| [34] |
Kennedy J R, Ferré T P A. Accounting for Time- and Space-Varying Changes in the Gravity Field to Improve the Network Adjustment of Relative-Gravity Data[J]. Geophysical Journal International, 2016, 204(2): 892-906 DOI:10.1093/gji/ggv493
(  0) 0) |
| [35] |
Wu Q, Liu S, Wang B, et al. Data Processing of Gravity Base Network in Plateau Area: The Case of Qinghai Province, China[J]. Remote Sensing, 2022, 14(5)
(  0) 0) |
| [36] |
Wang L, Chen S, Zhuang J, et al. Simultaneous Calibration of Instrument Scale Factor and Drift Rate in Network Adjustment for Continental-Scale Gravity Survey Campaign[J]. Geophysical Journal International, 2022, 228(3): 1541-1555
(  0) 0) |
| [37] |
王林海, 陈石, 庄建仓, 等. 精密重力测量中相对重力仪格值系数的贝叶斯估计方法[J]. 测绘学报, 2020, 49(12): 1543-1553 (Wang Linhai, Chen Shi, Zhuang Jiancang, et al. Bayesian Estimation of the Scale Factor of Relative Gravimeter in Precise Gravity Survey[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(12): 1543-1553)
(  0) 0) |
| [38] |
Yang J L, Chen S, Zhang B, et al. Gravity Observations and Apparent Density Changes before the 2017 Jiuzhaigou MS7.0 Earthquake and Their Precursory Significance[J]. Entropy, 2021, 23(12)
(  0) 0) |
| [39] |
杨锦玲, 陈石, 王林海, 等. 华南陆地时变重力观测数据质量评估[J]. 测绘学报, 2021, 50(3): 333-342 (Yang Jinling, Chen Shi, Wang Linhai, et al. Data Quality Assessment of Time-Varying Terrestrial Gravity Observation in South China[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(3): 333-342)
(  0) 0) |
| [40] |
张贝, 陈石, 李红蕾, 等. 时变重力场球面模型反演算法和模拟实验[J]. 地震, 2021, 41(1): 13-24 (Zhang Bei, Chen Shi, Li Honglei, et al. Time-Varying Gravity Inversion Using Spherical Model and Synthetic Test[J]. Earthquake, 2021, 41(1): 13-24 DOI:10.3969/j.issn.1003-3246.2021.01.003)
(  0) 0) |
| [41] |
韩建成, 陈石, 卢红艳, 等. 基于Slepian方法和地面重力观测确定时变重力场模型: 以2011—2013年华北地区数据为例[J]. 地球物理学报, 2021, 64(5): 1542-1557 (Han Jiancheng, Chen Shi, Lu Hongyan, et al. Time-Variable Gravity Field Determination Using Slepian Functions and Terrestrial Measurements: A Case Study in North China with Data from 2011 to 2013[J]. Chinese Journal of Geophysics, 2021, 64(5): 1542-1557)
(  0) 0) |
| [42] |
Moritz H. Least-Squares Collocation[J]. Reviews of Geophysics, 1978, 16(3): 421-430 DOI:10.1029/RG016i003p00421
(  0) 0) |
| [43] |
阮明明, 陈石, 韩建成. 用最小二乘配置法构建局部重力场模型[J]. 地震学报, 2020, 42(1): 53-65 (Ruan Mingming, Chen Shi, Han Jiancheng. Regional Gravity Field Model Constructed by the Least Squares Collocation[J]. Acta Seismologica Sinica, 2020, 42(1): 53-65)
(  0) 0) |
| [44] |
陈石, 徐伟民, 王谦身. 应用Slepian局部谱方法解算中国大陆重力场球谐模型[J]. 测绘学报, 2017, 46(8): 952-960 (Chen Shi, Xu Weimin, Wang Qianshen. The Spherical Harmonic Model of Gravity Field in China's Mainland by Slepian Local Spectrum Method[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(8): 952-960)
(  0) 0) |
| [45] |
Han J, Chen S, Chen Z, et al. Determination of the Degree 120 Time-Variable Gravity Field in the Sichuan-Yunnan Region Using Slepian Functions and Terrestrial Measurements[J]. Earthquake Science, 2021, 34(3): 211-221 DOI:10.29382/eqs-2021-0029
(  0) 0) |
| [46] |
Simons F J, Dahlen F A. Spherical Slepian Functions and the Polar Gap in Geodesy[J]. Geophysical Journal International, 2006a, 166(3): 1039-1061 DOI:10.1111/j.1365-246X.2006.03065.x
(  0) 0) |
| [47] |
Simons F J, Dahlen F A, Wieczorek M A. Spatiospectral Concentration on a Sphere[J]. SIAM Review, 2006b, 48(3): 504-536 DOI:10.1137/S0036144504445765
(  0) 0) |
| [48] |
Han J C, Chen S, Lu H Y, et al. A High-Resolution Time-Variable Terrestrial Gravity Field Model of Continental North China[J]. Communications Earth and Environment, 2024, 44(5)
(  0) 0) |
| [49] |
Li Y G, Oldenburg D W. 3-D inversion of gravity data[J]. Geophysics, 1998, 63(1): 109-119 DOI:10.1190/1.1444302
(  0) 0) |
| [50] |
Calvetti D, Somersalo E. Inverse Problems: From Regularization to Bayesian Inference[J]. WIREs Computational Statistics, 2018, 10(3)
(  0) 0) |
| [51] |
Muñoz G, Rath V. Beyond Smooth Inversion: The Use of Nullspace Projection for the Exploration of Non-Uniqueness in MT[J]. Geophysical Journal International, 2006, 164(2): 301-311 DOI:10.1111/j.1365-246X.2005.02825.x
(  0) 0) |
| [52] |
Li Y, Chen S, Li H, et al. Bayesian Estimation of Parameters and Uncertainty of a 3-D Dipping Fault Using Gravity Anomalies[J]. Geophysical Journal International, 2023, 235(3): 2482-2498 DOI:10.1093/gji/ggad379
(  0) 0) |
| [53] |
Li H, Chen S, Zhang B, et al. Bayesian Inversion for Modelling 3-D Density Structures in the Eastern Margin of Bayan Har Block and Its Tectonic Implications[J]. Geophysical Journal International, 2024, 236(2): 872-887
(  0) 0) |
| [54] |
Yang J, Chen S, Zhang B, et al. Gravity Observations and Apparent Density Changes before the 2017 Jiuzhaigou MS7.0 Earthquake and Their Precursory Significance[J]. Entropy, 2021, 23(12)
(  0) 0) |
| [55] |
Jia L, Chen S, Wang L, et al. Gravity Yearly Transient Change Around the Epicenter of 2022 MS6.9 Menyuan Earthquake, China and Seismotectonic Implications[J]. Tectonophysics, 2023, 846
(  0) 0) |
| [56] |
Wang L, Chen S, Zhuang J, et al. Gravity Field Changes Reveal Deep Mass Transfer before and after the 2013 Lushan Earthquake[J]. Communications Earth and Environment, 2023, 4(1)
(  0) 0) |
| [57] |
Liu X, Chen S, Xing H. Gravity Changes Caused by Crustal Fluids Invasion: A perspective from Finite Element Modeling[J]. Tectonophysics, 2022, 833
(  0) 0) |
| [58] |
孙和平, 徐建桥, 崔小明. 重力场的地球动力学与内部结构应用研究进展[J]. 测绘学报, 2017, 46(10): 1290-1299 (Sun Heping, Xu Jianqiao, Cui Xiaoming. Research Progress of the Gravity Field Application in Earth's Geodynamics and Interior Structure[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1290-1299 DOI:10.11947/j.AGCS.2017.20170298)
(  0) 0) |
| [59] |
付广裕. 中国地震重力研究现状及其面临的挑战[J]. 武汉大学学报: 信息科学版, 2023, 48(6): 858-869 (Fu Guangyu. Status and Challenges of Chinese Gravity Observation for Seismic Events[J]. Geomatics and Information Science of Wuhan University, 2023, 48(6): 858-869)
(  0) 0) |
| [60] |
Chen S, Zhuang J, Li X, et al. Bayesian Approach for Network Adjustment for Gravity Survey Campaign: Methodology and Model test[J]. Journal of Geodesy, 2018, 93(5): 681-700
(  0) 0) |
| [61] |
Chen S, Liu M, Xing L L, et al. Gravity Increase before the 2015 MW7.8 Nepal Earthquake[J]. Geophysical Research Letters, 2016, 43(1): 111-117 DOI:10.1002/2015GL066595
(  0) 0) |
| [62] |
申重阳, 李辉, 王琪, 等. 滇西重力断层运动时间分布特征的初步研究[J]. 大地测量与地球动力学, 2002, 22(2): 68-74 (Shen Chongyang, Li Hui, Wang Qi, et al. Preliminary Study on Characteristics of Time Distribution of Fault Movement by Gravity Data in Western Yunnan[J]. Journal of Geodesy and Geodynamics, 2002, 22(2): 68-74 DOI:10.3969/j.issn.1671-5942.2002.02.013)
(  0) 0) |
| [63] |
Sun W K, Wang Q, Li H, et al. Gravity and GPS Measurements Reveal Mass Loss beneath the Tibetan Plateau: Geodetic Evidence of Increasing Crustal Thickness[J]. Geophysical Research Letters, 2009, 36(2)
(  0) 0) |
| [64] |
邢乐林, 王林海, 胡敏章, 等. 时变重力测量确定青藏高原地壳隆升与增厚速率[J]. 武汉大学学报: 信息科学版, 2017, 42(5): 569-574 (Xing Lelin, Wang Linhai, Hu Minzhang, et al. Determination of Crust Uplifting and Thickening of Qinghai-Tibetan Plateau from Time-Variable Gravity Measurements[J]. Geomatics and Information Science of Wuhan University, 2017, 42(5): 569-574)
(  0) 0) |
| [65] |
Zhang Y, Chen S, Xing L L, et al. Gravity Changes before and after the 2008 Mw 7.9 Wenchuan Earthquake at Pixian Absolute Gravity Station in more than a Decade[J]. Pure and Applied Geophysics, 2020, 177(1): 121-133 DOI:10.1007/s00024-019-02356-4
(  0) 0) |
| [66] |
Xuan S B, Jin S G, Chen Y, et al. Insight into the Preparation of the 2016 MS6.4 Menyuan Earthquake from Terrestrial Gravimetry-Derived Crustal Density Changes[J]. Scientific Reports, 2019, 9(1)
(  0) 0) |
| [67] |
杨锦玲. 陆地时变微重力数据处理与场源模型解释[D]. 北京: 中国地震局地球物理研究所, 2022 (Yang Jinling. Terrestrial Time-Varying Microgravity Data Processing and Field Source Model Interpretation[D]. Beijing: Institute of Geophysics, CEA, 2022)
(  0) 0) |
| [68] |
刘代芹, 玄松柏, 陈石, 等. 基于高精度时变微重力方法研究呼图壁储气库地下介质密度变化特征[J]. 地震地质, 2022, 44(2): 414-427 (Liu Daiqin, Xuan Songbai, Chen Shi, et al. Study on the Density Variation Characteristics of Underground Medium in Hutubi Gas Storage Based on High-Precision Time-Varying Microgravity Method[J]. Seismology and Geology, 2022, 44(2): 414-427 DOI:10.3969/j.issn.0253-4967.2022.02.009)
(  0) 0) |
| [69] |
申重阳, 李辉, 孙少安, 等. 2008年于田MS7.3地震前重力场动态变化特征分析[J]. 大地测量与地球动力学, 2010, 30(4): 1-7 (Shen Chongyang, Li Hui, Sun Shaoan, et al. Characteristic Analysis of Dynamic Gravity Change before Yutian MS7.3 Earthquake, 2008[J]. Journal of Geodesy and Geodynamics, 2010, 30(4): 1-7 DOI:10.3969/j.issn.1671-5942.2010.04.001)
(  0) 0) |
| [70] |
祝意青, 徐云马, 吕弋培, 等. 龙门山断裂带重力变化与汶川8.0级地震关系研究[J]. 地球物理学报, 2009, 52(10): 2538-2546 (Zhu Yiqing, Xu Yunma, Lü Yipei, et al. Relations between Gravity Variation of Longmenshan Fault Zone and Wenchuan MS8.0 Earthquake[J]. Chinese Journal of Geophysics, 2009, 52(10): 2538-2546 DOI:10.3969/j.issn.0001-5733.2009.10.012)
(  0) 0) |
| [71] |
祝意青, 闻学泽, 孙和平, 等. 2013年四川芦山MS7.0地震前的重力变化[J]. 地球物理学报, 2013, 56(6): 1887-1894 (Zhu Yiqing, Wen Xueze, Sun Heping, et al. Gravity Changes before the Lushan, Sichuan, MS7.0 Earthquake of 2013[J]. Chinese Journal of Geophysics, 2013, 56(6): 1887-1894)
(  0) 0) |
| [72] |
祝意青, 李铁明, 郝明, 等. 2016年青海门源MS6.4地震前重力变化[J]. 地球物理学报, 2016, 59(10): 3744-3752 (Zhu Yiqing, Li Tieming, Hao Ming, et al. Gravity Changes before the Menyuan, Qinghai MS6.4 Earthquake of 2016[J]. Chinese Journal of Geophysics, 2016, 59(10): 3744-3752 DOI:10.6038/cjg20161019)
(  0) 0) |
| [73] |
祝意青, 梁伟锋, 赵云峰, 等. 2017年四川九寨沟MS7.0地震前区域重力场变化[J]. 地球物理学报, 2017, 60(10): 4124-4131 (Zhu Yiqing, Liang Weifeng, Zhao Yunfeng, et al. Gravity Changes before the Jiuzhaigou, Sichuan, MS7.0 Earthquake of 2017[J]. Chinese Journal of Geophysics, 2017, 60(10): 4124-4131 DOI:10.6038/cjg20171037)
(  0) 0) |
| [74] |
赵云峰, 祝意青, 隗寿春, 等. 2022年1月8日青海门源MS6.9地震前重力场动态变化[J]. 地球物理学报, 2023, 66(6): 2337-2351 (Zhao Yunfeng, Zhu Yiqing, Wei Shouchun, et al. Dynamic Gravity Changes before the Menyuan, Qinghai MS6.9 Earthquake on January 8, 2022[J]. Chinese Journal of Geophysics, 2023, 66(6): 2337-2351)
(  0) 0) |
| [75] |
Rymer H, Brown G. Gravity Changes as a Precursor to Volcanic Eruption at Poás Volcano, Costa Rica[J]. Nature, 1989, 342: 902-905 DOI:10.1038/342902a0
(  0) 0) |
| [76] |
Carbone D, Poland M P, Diament M, et al. The Added Value of Time-Variable Microgravimetry to the Understanding of how Volcanoes Work[J]. Earth Science Reviews, 2017, 169: 146-179 DOI:10.1016/j.earscirev.2017.04.014
(  0) 0) |
| [77] |
Dzurisin D. A Comprehensive Approach to Monitoring Volcano Deformation as a Window on the Eruption Cycle[J]. Reviews of Geophysics, 2003, 41(1)
(  0) 0) |
| [78] |
Battaglia M, Gottsmann J, Carbone D, et al. 4D Volcano Gravimetry[J]. Geophysics, 2008, 73(6)
(  0) 0) |
| [79] |
Gottsmann J, De Angelis S, Fournier N, et al. On the Geophysical Fingerprint of Vulcanian Explosions[J]. Earth and Planetary Science Letters, 2011, 306(1-2): 98-104 DOI:10.1016/j.epsl.2011.03.035
(  0) 0) |
| [80] |
Hemmings B, Gottsmann J, Whitaker F, et al. Investigating Hydrological Contributions to Volcano Monitoring Signals: A Time-Lapse Gravity Example[J]. Geophysical Journal International, 2016, 207(1): 259-273 DOI:10.1093/gji/ggw266
(  0) 0) |
| [81] |
Vigouroux N, Williams-Jones G, Chadwick W, et al. 4D Gravity Changes Associated with the 2005 Eruption of Sierra Negra Volcano, Galápagos[J]. Geophysics, 2008, 73(6)
(  0) 0) |
| [82] |
Gudmundsson A. Magma Chambers Modeled as Cavities Explain the Formation of Rift Zone Central Volcanoes and Their Eruption and Intrusion Statistics[J]. Journal of Geophysical Research: Solid Earth, 1998, 103(B4): 7401-7412 DOI:10.1029/97JB03747
(  0) 0) |
| [83] |
Wright T J, Sigmundsson F, Pagli C, et al. Geophysical Constraints on the Dynamics of Spreading Centres from Rifting Episodes on Land[J]. Nature Geoscience, 2012, 5(4): 242-250 DOI:10.1038/ngeo1428
(  0) 0) |
| [84] |
Sigmundsson F, Hooper A, Hreinsdóttir S, et al. Segmented Lateral Dyke Growth in a Rifting Event at Bárðarbunga Volcanic System, Iceland[J]. Nature, 2015, 517(7533): 191-195 DOI:10.1038/nature14111
(  0) 0) |
| [85] |
Gudmundsson M T, Jónsdóttir K, Hooper A, et al. Gradual Caldera Collapse at Bárdarbunga Volcano, Iceland, Regulated by Lateral Magma Outflow[J]. Science, 2016, 353(6296)
(  0) 0) |
| [86] |
Pool D R, Eychaner J H. Measurements of Aquifer-Storage Change and Specific Yield Using Gravity Surveys[J]. Groundwater, 1995, 33(3): 425-432 DOI:10.1111/j.1745-6584.1995.tb00299.x
(  0) 0) |
| [87] |
Davis K, Li Y G, Batzle M. Time-Lapse Gravity Monitoring: A Systematic 4D Approach with Application to Aquifer Storage and Recovery[J]. Geophysics, 2008, 73(6)
(  0) 0) |
| [88] |
Kazama T, Tamura Y, Asari K, et al. Gravity Changes Associated with Variations in Local Land-Water Distributions: Observations and Hydrological Modeling at Isawa Fan, Northern Japan[J]. Earth, Planets and Space, 2012, 64(4): 309-331 DOI:10.5047/eps.2011.11.003
(  0) 0) |
| [89] |
Imanishi Y, Kokubo K, Tatehata H. Effect of Underground Water on Gravity Observation at Matsushiro, Japan[J]. Journal of Geodynamics, 2006, 41(1-3): 221-226 DOI:10.1016/j.jog.2005.08.031
(  0) 0) |
| [90] |
Voigt C, Schulz K, Koch F, et al. Technical Note: Introduction of a Superconducting Gravimeter as Novel Hydrological Sensor for the Alpine Research Catchment Zugspitze[J]. Hydrology and Earth System Sciences, 2021, 25(9): 5047-5064 DOI:10.5194/hess-25-5047-2021
(  0) 0) |
| [91] |
Gehman C L, Harry D L, Sanford W E, et al. Estimating Specific Yield and Storage Change in an Unconfined Aquifer Using Temporal Gravity Surveys[J]. Water Resources Research, 2009, 45(4)
(  0) 0) |
| [92] |
Chen K H, Hwang C, Chang L C, et al. Measuring Aquifer Specific Yields with Absolute Gravimetry: Result in the Choushui River Alluvial Fan and Mingchu Basin, Central Taiwan[J]. Water Resources Research, 2020, 56(9)
(  0) 0) |
| [93] |
Robertson A J, Kennedy J R, Wildermuth L M, et al. Determining Seasonal Recharge, Storage Changes, and Specific Yield Using Repeat Microgravity and Water-Level Measurements in the Mesilla Basin Alluvial Aquifer, New Mexico, 2016-2018[J]. Journal of Applied Geophysics, 2023, 209
(  0) 0) |
| [94] |
Krahenbuhl R A, Li Y G, Davis T. Understanding the Applications and Limitations of Time-Lapse Gravity for Reservoir Monitoring[J]. The Leading Edge, 2011, 30(9): 1060-1068 DOI:10.1190/1.3640530
(  0) 0) |
| [95] |
Jacob T, Rohmer J, Manceau J C. Using Surface and Borehole Time-Lapse Gravity to Monitor CO2 in Saline Aquifers: A Numerical Feasibility Study[J]. Greenhouse Gases: Science and Technology, 2016, 6(1): 34-54 DOI:10.1002/ghg.1532
(  0) 0) |
| [96] |
Appriou D, Bonneville A, Zhou Q L, et al. Time-Lapse Gravity Monitoring of CO2 Migration Based on Numerical Modeling of a Faulted Storage Complex[J]. International Journal of Greenhouse Gas Control, 2020, 95
(  0) 0) |
| [97] |
Allis R G. Analysis of Exploitation-Induced Gravity Changes at Wairakei Geothermal Field[J]. Geophysics, 1986, 51(8): 1647 DOI:10.1190/1.1442214
(  0) 0) |
| [98] |
Nordquist G, Protacio J A P, Acuña J A. Precision Gravity Monitoring of the Bulalo Geothermal Field, Philippines: Independent Checks and Constraints on Numerical Simulation[J]. Geothermics, 2004, 33(1): 37-56
(  0) 0) |
| [99] |
Nishijima J, Umeda C, Fujimitsu Y, et al. Repeat Absolute and Relative Gravity Measurements for Geothermal Reservoir Monitoring in the Ogiri Geothermal Field, Southern Kyushu, Japan[J]. IOP Conference Series: Earth and Environmental Science, 2016, 42
(  0) 0) |
| [100] |
Ferguson J F, Chen T, Brady J, et al. The 4D Microgravity Method for Waterflood Surveillance: Part Ⅱ-Gravity Measurements for the Prudhoe Bay Reservoir, Alaska[J]. Geophysics, 2007, 72(2)
(  0) 0) |
| [101] |
Fores B, Champollion C, Le Moigne N, et al. Assessing the Precision of the iGrav Superconducting Gravimeter for Hydrological Models and Karstic Hydrological Process Identification[J]. Geophysical Journal International, 2017, 208(1): 269-280 DOI:10.1093/gji/ggw396
(  0) 0) |
| [102] |
Eiken O, Stenvold T, Zumberge M, et al. Gravimetric Monitoring of Gas Production from the Troll Field[J]. Geophysics, 2008, 73(6)
(  0) 0) |
| [103] |
Alnes H, Eiken O, Nooner S, et al. Results from Sleipner Gravity Monitoring: Updated Density and Temperature Distribution of the CO2 Plume[J]. Energy Procedia, 2011(4): 5504-5511
(  0) 0) |
| [104] |
Young W M, Lumley D. Feasibility Analysis for Time-Lapse Seafloor Gravity Monitoring of Producing Gas Fields in the Northern Carnarvon Basin, Offshore Australia[J]. Geophysics, 2015, 80(2)
(  0) 0) |
| [105] |
Van Gelderen M, Haagmans R, Bilker M. Gravity Changes and Natural Gas Extraction in Groningen[J]. Geophysical Prospecting, 1999, 47(6): 979-993 DOI:10.1046/j.1365-2478.1999.00159.x
(  0) 0) |
| [106] |
Ferguson J F, Klopping F J, Chen T Y, et al. The 4D Microgravity Method for Waterflood Surveillance: Part 3-4D Absolute Microgravity Surveys at Prudhoe Bay, Alaska[J]. Geophysics, 2008, 73(6)
(  0) 0) |
| [107] |
Brady J L, Hare J L, Ferguson J F, et al. Results of the World's First 4D Microgravity Surveillance of a Waterflood-Prudhoe Bay, Alaska[J]. SPE Reservoir Evaluation and Engineering, 2008, 11(5): 824-831 DOI:10.2118/101762-PA
(  0) 0) |
| [108] |
Hare J L, Ferguson J F, Aiken C L V, et al. The 4-D Microgravity Method for Waterflood Surveillance: A Model Study for the Prudhoe Bay Reservoir, Alaska[J]. Geophysics, 1999, 64(1)
(  0) 0) |
| [109] |
Glegola M, Ditmar P, Bierkens M F P, et al. Estimation of the Time-Lapse Gravity Errors Due to Water Table and Soil Moisture Variations[A]//Society of Exploration Geophysicists. SEG Technical Program Expanded Abstracts[M]. 2009
(  0) 0) |
| [110] |
陈晓东, 李航, 邓明莉, 等. 用重力测量技术观测城市地表下沉的实验研究[J]. 地球物理学报, 2020, 63(8): 2882-2892 (Chen Xiaodong, Li Hang, Deng Mingli, et al. Experimental Study of the Surface Subsidence in the City Using Gravity Observing Techniques[J]. Chinese Journal of Geophysics, 2020, 63(8): 2882-2892)
(  0) 0) |
| [111] |
Coughlin M, Mukund N, Harms J, et al. Towards a First Design of a Newtonian-Noise Cancellation System for Advanced LIGO[J]. Classical and Quantum Gravity, 2016, 33(24)
(  0) 0) |
| [112] |
Harms J, Venkateswara K. Newtonian-Noise Cancellation in Large-Scale Interferometric GW Detectors Using Seismic Tiltmeters[J]. Classical and Quantum Gravity, 2016, 33(23)
(  0) 0) |
2. Beijing Baijiatuan Earth Sciences National Observation and Research Station, Baijiatuan Road, Beijing 100095, China;
3. The First Monitoring and Application Center, CEA, 7 Naihuo Road, Tianjin 300180, China
 2024, Vol. 44
2024, Vol. 44


