2. 南京水利科学研究院,南京市广州路223号,210029;
3. 水利部水库大坝安全重点实验室,南京市虎踞关34号,210024
为保障大坝长期运行安全,一般在不同结构位置安装不同类型的传感器来量化大坝环境因素与结构之间的响应[1]。但传感器易受干扰,导致数据含有噪声,影响大坝变形预测模型的精度[2]。因此,降噪预处理是提升预测精度的关键[3]。主流的降噪过程主要分为序列分解[4]和序列降噪2个部分。变分模态分解(variational mode decomposition, VMD)及其改进方法已被证明是有效的分解方法[5-6]。序列分解后主要进行强制降噪和阈值降噪,但强制降噪易丢失高频信息,阈值降噪可能导致降噪不完全[7]。
KSVD(K-singular value decomposition)字典学习是对确立的训练样本进行训练,通过样本学习得到一个能够具有训练样本丰富特征信息的超完备字典D,使原始监测序列表现得更加稀疏化[8],并利用序列的稀疏化表示来实现更精确的序列重构和降噪[9-11]。KSVD字典稀疏降噪算法适用于包含噪声的监测序列,可以有效地消除大部分随机噪声,但在特殊情况下,如在序列的波峰和波谷仍会残留一些较明显的毛刺[12-13]。
针对这些问题,本文提出一种结合VMD和KSVD字典学习的降噪算法。首先将监测序列进行自适应变分模态分解,然后将分解后的IMF分量和残差分量分别采用KSVD字典学习进行降噪处理,使原始监测序列平滑的同时充分保留大坝的特征信息。经工程案例验证,该算法预测模型精度较传统方法更高。
1 方法原理 1.1 基于可解释因子的大坝安全监测统计模型原理根据现有的大坝安全监测理论[14]和工程经验,大坝变形效应主要与水压(δH)、温度(δT)和时效(δθ)等因素有关。由于大坝内部结构温度趋于稳定,故选择具有周期性的谐波函数来模拟温度分量。本文使用水位-周期温度-时间(hydrostatic-seasonal-time,HST)统计模型来预测大坝的变形:
| $ \delta=\delta_H+\delta_T+\delta_\theta $ | (1) |
| $ \left\{\begin{array}{l} \delta_H=\sum\limits_{i=1}^3\left(a_i H^i\right) \\ \delta_T=\sum\limits_{i=1}^2\left[b_{1 i} \sin \frac{2 \pi i t}{365}+b_{2 i} \cos \frac{2 \pi i t}{365}\right] \\ \delta_\theta=c_1 \theta+c_2 \ln (\theta) \end{array}\right. $ | (2) |
式中,ai、b1i、b2i、c1和c2为线性回归系数,H为河段上游水深,t为当前监测日期到初始监测日期的累计天数,
实际的大坝变形监测序列降噪需要对原始的监测序列进行多尺度和多频率的分析,针对VMD的分解效果与分解层数K和二次惩罚系数α的相关性较大,容易造成序列过分解或欠分解,导致无法直接人工进行自适应设置的问题,本文采用鲸鱼优化算法(whale optimization algorithm, WOA)对VMD的分解层数K和二次惩罚系数α进行设计优化。
WOA具有精度高、收敛速度快、鲁棒性强等优点[15-16],其灵感来源于对海洋中座头鲸鲸群狩猎行为的模拟。具体优化过程主要分为包围捕食、气泡网攻击和搜索猎物3个阶段。算法中,At的数值直接决定鲸鱼是进行包围捕食还是搜索猎物,一定程度上影响算法的收敛能力[17]。
通过计算原始监测序列经过VMD分解得到的每个IMF分量的局部包络熵,可以定量分析序列的复杂程度和规律特性,把局部包络熵的极小值确立为WOA的适应度函数。优化后的VMD能通过自适应分解得到若干个监测子序列,进而充分提取原始监测序列的有效信息。包络熵的计算公式为:
| $ \left\{\begin{array}{l} p_{i j}=\frac{a_i(j)}{\sum\limits_{j=1}^N a_i(j)} \\ E_i=-\sum\limits_{j=1}^N p_{i j} \lg p_{i j} \end{array}\right. $ | (3) |
式中,i为分解层数,ai(j)为分解后的子监测序列IMF分量的包络信号。
1.3 KSVD字典构造训练目前确定超完备字典D主要有2种方式:1)给定确立的小波字典、DCT(离散余弦)字典等;2)将样本序列进行初始化处理。KSVD字典学习主要分为稀疏编码和字典更新2个阶段,算法原理如下。
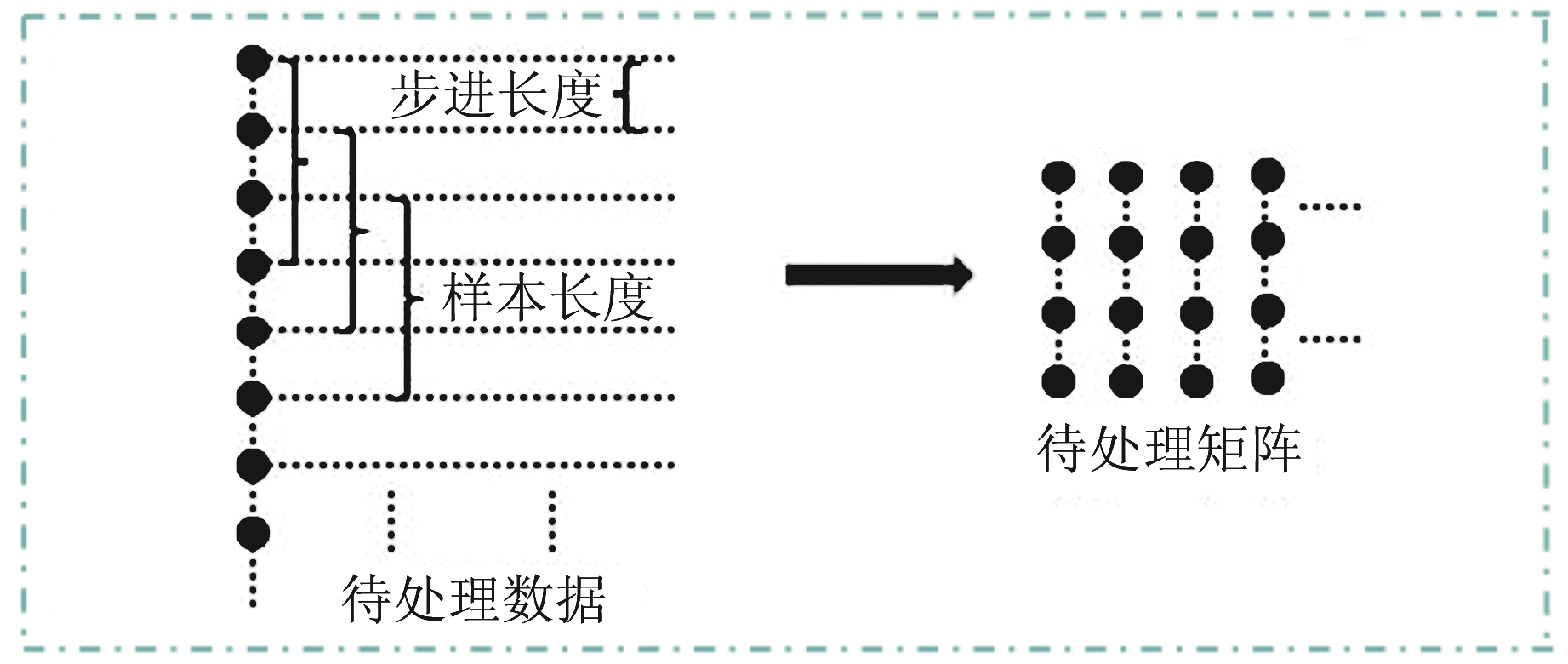
1) 稀疏编码阶段。将变形监测序列经过初始化得到超完备字典D,根据设定的步进长度和样本长度构建训练矩阵,如图 1所示。通过正交匹配追踪算法(orthogonal matching pursuit, OMP),求解待处理矩阵中每个数据样本yi对应的稀疏向量xi, 从而得到稀疏系数矩阵X=[x1, x2, x3, …, xN]。
|
图 1 待处理矩阵的构建 Fig. 1 Construction of the matrix to be processed |
2) 字典更新阶段。固定稀疏系数矩阵X,对确定的超完备字典D中的原子逐列计算更新,目标函数设立为:
| $ \begin{gathered} \|\boldsymbol{Y}-\boldsymbol{D} \boldsymbol{X}\|_F^2=\left\|\left(\boldsymbol{Y}-\sum\nolimits_{j \neq k} \boldsymbol{d}_j \boldsymbol{x}_j^{\mathrm{T}}\right)\right\|_F^2= \\ \left\|\boldsymbol{E}_k-\boldsymbol{d}_k \boldsymbol{x}_k^{\mathrm{T}}\right\|{ }_F^2 \end{gathered} $ | (4) |
式中,Y为原监测序列数值,dj为超完备字典D的第j列,xjT为稀疏系数矩阵X的第j行,Ek为除dk原子以外所有原子造成的误差。
3) 不断更新j,当OMP算法达到设定阈值时停止迭代更新,输出重构的已处理矩阵,按图 2所示还原得到重构后的变形监测序列。

|
图 2 已处理矩阵的还原 Fig. 2 Restoration of the processed matrix |
建立VMD和KSVD字典学习相结合的大坝变形监测序列降噪模型(简称VMD-KSVD),该模型保留了VMD分解后的高频分量和残差分量,使降噪处理后的监测序列具有丰富的有效信息。计算流程如图 3所示,具体步骤如下:

|
图 3 VMD和KSVD结合的大坝监测序列降噪模型 Fig. 3 Noise reduction model of dam monitoring sequence combined with VMD and KSVD |
1) 初始化鲸鱼种群数量,确立最大迭代次数,设置VMD的分解层数和二次惩罚系数的取值范围[N, M],选择局部包络熵的最小值作为WOA的适应度函数。
2) 基于步骤1)得到的[K, α],使用VMD对原监测序列X(t)进行分解,得到K个子序列分量IMF1, IMF2, …, IMFK和残差分量res。
3) 根据设立的步进长度和样本长度,将子序列分量和残差分量转化为二维矩阵进行KSVD字典学习,把已处理矩阵进行还原,得到降噪后的子序列分量IMF′1, IMF′2, …, IMF′K和残差分量res′。
4) 将降噪后的子序列分量和残差分量进行叠加,得到降噪后的监测序列Y(t)。
3 实验分析选取中国新疆开都河流域某混凝土面板沙砾石坝的监测资料作为实验对象,该水库大坝高约110 m,坝顶长337.6 m,坝底最大宽度约400 m,调节库容为0.724亿m3。
选取大坝侧面用于监测面板垂直接缝变形的单向测缝计J03、J12测点和用于监测混凝土面板应变的三向应变计S3-1-1、S3-6-3测点作为模型验证对象。选择监测时段为2015-05-01~2020-05-01,监测频率为1次/d的监测序列作为数据集。图 4为大坝上游水位历史曲线,图 5为4个测点的历史曲线。将2015-05-01~2019-06-08的监测序列作为样本训练集,剩余监测序列作为样本测试集。为实现实时预测,对样本训练集进行重构降噪处理,并将样本测试集作为原始的监测序列来进行预测比较和结果验证。

|
图 4 上游水位历史曲线 Fig. 4 Historical curve of upstream water level |

|
图 5 测点变形曲线 Fig. 5 Deformation curve of measurement point |
使用均方根误差RMSE、平滑度r和归一化互相关NCC作为降噪量化指标:
| $ \text { RMSE }=\sqrt{\frac{\sum\limits_{i=1}^n\left(x_i-y_i\right)^2}{n}} $ | (5) |
| $ r=\frac{\sum\limits_{t=1}^{n-1}[y(t+1)-y(t)]^2}{\sum\limits_{t=1}^{n-1}[x(t+1)-x(t)]^2} $ | (6) |
| $ \mathrm{NCC}=\frac{\sum\limits_{i=1}^n x_i \cdot y_i}{\sqrt{\left(\sum\limits_{i=1}^n x_i^2\right) \cdot\left(\sum\limits_{i=1}^n y_i^2\right)}} $ | (7) |
式中,xi为原始监测序列值,yi为降噪后序列值,n为样本量。
3.2 VMD-KSVD的降噪结果将自适应VMD应用于J03测点监测序列的训练集,对于WOA初始搜索参数的设立,种群个数设为50,最大迭代次数设为60,K值设为[6, 11],二次惩罚系数设为[500, 3 500]。J03训练集的分解结果和使用KSVD降噪的结果如图 6所示。可以看出,经过KSVD降噪后的子序列和残差序列与分解得到的序列趋势一致。为充分考虑监测序列中的有效信息,将降噪后的子序列和残差序列进行叠加得到最后的降噪序列。

|
图 6 J03训练集的分解和降噪 Fig. 6 Decomposition and noise reduction of the J03 training set |
为了验证本文数据重构降噪算法能从大坝的变形监测序列中提取丰富的有效信息,分别使用奇异谱分析(singular spectrum analysis, SSA)降噪算法、VMD降噪算法和KSVD稀疏重构算法进行比较分析(图 7、表 1)。考虑到单从指标层面对降噪效果进行分析,容易出现降噪过度或降噪不完全的现象,因此本文还使用同步挤压小波变换时频图进一步分析,如图 8所示。从时频图可以看出,各算法降噪后的监测序列的时频脊线均处于低频,反映出大坝变形监测数据频率分布稳定的特征。

|
图 7 J03测点降噪模型效果对比 Fig. 7 Comparison of the effects of the noise reduction model at J03 measurement point |
|
|
表 1 不同降噪模型的指标分析 Tab. 1 Indicators of different noise reduction models |

|
图 8 J03测点同步挤压小波变换时频图 Fig. 8 Time-frequency diagram of synchronous extrusion wavelet transform at J03 measurement point |
从表 1和图 8(图中色调变化代表序列中的能量密度,颜色越亮表示该时间点和频率点的序列信号能量越高)可以看出,与其他方法相比,SSA和VMD-KSVD在RMSE方面取得了优异的效果,但SSA在NCC和r方面不如VMD-KSVD。并且从时频图可以看出,VMD-KSVD对高频扰动噪声的抑制效果优于SSA,时频特征信息表现更清晰,侧面说明SSA容易出现降噪不完全的现象。VMD方法虽保持较好的RMSE,但其平滑程度较差,并且VMD很少保留序列的高频特征信息,容易出现降噪过度的现象。KSVD和VMD-KSVD都减少了高频噪声对监测序列有效信息的干扰,但从时频图可以看出,后者能够更清晰地表征大坝的详细特征,对高频噪声的抑制效果更优,并且其3个定量指标的表现均更好。
3.4 不同预测方法结果比较本文通过重构真实监测序列来提高预测精度,因此选择大坝预测中常用的极致梯度提升(extreme gradient boosting, XGBoost)和多元线性回归(mixed logistic regression, MLR)机器学习模型来进行比较。依据§1.1理论考虑水位、温度、时效等因素对大坝变形预测的影响。为精准量化模型的预测性能,选取平均绝对百分比误差MAPE、均方误差MSE、平均绝对误差MAE、可决系数R2、相关系数R作为评价标准。考虑到当实测数值为0时无法计算MAPE值,将实测数值最大值的绝对值作为归一化辅助指标,分别对实测数值和预测数值进行归一化,把实测数值和监测数值归一化后的残差绝对值的平均值记为归一化平均绝对百分比误差nMAPE:
| $ \left\{\begin{array}{l} A^{\prime}(t)=A(t) /|A(t)|_{\max } \\ F^{\prime}(t)=F(t) /|A(t)|_{\max } \\ \mathrm{nMAPE}=\frac{1}{T} \sum\limits_{t=1}^T\left|A^{\prime}(t)-F^{\prime}(t)\right| \end{array}\right. $ | (8) |
式中,A(t)为实测数值,F(t)为预测数值,A′(t)为归一化实测数值,F′(t)为归一化预测数值,|A(t)|max为实测数值中绝对值最大值。
以J12和S3-1-1测点为例,分别使用XGBoost和MLR预测模型计算经本文方法、不降噪、SSA、VMD、KSVD处理的监测序列,结果如图 9、10所示。由精度雷达图不难看出,本文方法的nMAPE、MSE、MAE较小,同时R和R2也较大,且对噪声含量多的数据也有较好的预测效果。

|
图 9 测点J12预测模型对比 Fig. 9 Comparison of J12 measurement point prediction models |

|
图 10 测点S3-1-1预测模型对比 Fig. 10 Comparison of S3-1-1 measurement point prediction models |
考虑到传统的MLR模型对噪声的敏感性较差,导致降噪后的监测序列的预测精度提升不如XGBoost模型明显,因此,本文重点研究XGBoost模型预测结果的残差箱线图,如图 11所示。从XGBoost模型预测的残差箱线图来看,本文算法的残差中位数最接近0值,残差分布比其他方法更集中、稳定性更好。同时,从MLR模型预测的残差箱线图来看,本文算法与不进行降噪处理的残差中位数仅有较小幅度趋向0值,进一步说明传统回归模型MLR对噪声序列并不敏感,预测效果较差。从降噪角度看,降噪确实能够提高大坝变形的预测精度,即使对于对噪声不敏感的MLR预测模型,降噪后的监测序列也能提高预测的精度。

|
图 11 测点预测模型对比和残差箱线 Fig. 11 Comparison of measurement point prediction models and residual box plots |
从表 2的统计结果可以看出: 1)MLR模型的预测效果不如XGBoost模型,但本文方法在使用2种预测模型时预测精度均有提升。2)本文方法的R2和R相较于其他方法更接近于1,同时其nMAPE,MSE,MAE更小;使用XGBoost预测模型时,本文方法的nMAPE比未进行降噪处理的监测序列提升19%左右,MSE提升28%左右,MAE提升18%左右。
|
|
表 2 各降噪算法在不同测试集上的性能对比 Tab. 2 Comparison of the performance of each noise reduction method on different test sets |
1) 自适应变分模态分解在进行信噪分离时,不仅可以使重构序列与原始序列之间的残差变小,为后续降噪和预测提供有效帮助,而且可以对高频分量和残差分量进行重构保留,提取监测序列中更多的有效信息。
2) 在大坝建模预测中,对训练集的监测序列进行降噪处理可以显著提高预测精度。实验表明,本文方法相比SSA、VMD、KSVD方法具有更好的预测效果,并展现出较强的泛化能力,特别是在复杂情况下,本文降噪处理方法适用性更强。
3) 对于含有噪声的大坝原始监测序列,不同的机器学习模型的预测精度存在差异,集成学习模型XGBoost较传统的回归模型MLR能更有效地识别噪声,从而在预测精度方面表现更好。
| [1] |
Yi L T, Ding Y L, Hou J L, et al. Structural Health Monitoring Data Cleaning Based on Bayesian Robust Tensor Learning[J]. Structural Health Monitoring, 2023, 22(4): 2169-2192 DOI:10.1177/14759217221117238
(  0) 0) |
| [2] |
Ren Q B, Li M C, Kong R, et al. A Hybrid Approach for Interval Prediction of Concrete Dam Displacements under Uncertain Conditions[J]. Engineering with Computers, 2023, 39(2): 1285-1303 DOI:10.1007/s00366-021-01515-3
(  0) 0) |
| [3] |
鲁铁定, 陶蕊, 贺小星, 等. 顾及噪声影响的GNSS高程序列预测Prophet方法[J]. 国防科技大学学报, 2023, 45(2): 121-130 (Lu Tieding, Tao Rui, He Xiaoxing, et al. Prophet Method of GNSS Vertical Time Series Prediction Considering the Influence of Noise[J]. Journal of National University of Defense Technology, 2023, 45(2): 121-130)
(  0) 0) |
| [4] |
肖浩逸, 何晓霞, 梁佳佳, 等. 一种基于模态分解和机器学习的锂电池寿命预测方法[J]. 储能科学与技术, 2022, 11(12): 3999-4009 (Xiao Haoyi, He Xiaoxia, Liang Jiajia, et al. A Lithium Battery Life-Prediction Method Based on Mode Decomposition and Machine Learning[J]. Energy Storage Science and Technology, 2022, 11(12): 3999-4009)
(  0) 0) |
| [5] |
肖烈禧, 张玉, 周辉, 等. 基于IAOA-VMD-LSTM的超短期风电功率预测[J]. 太阳能学报, 2023, 44(11): 239-246 (Xiao Liexi, Zhang Yu, Zhou Hui, et al. Ultra Short Trem Wind Power Prediction Based on IAOA-VMD-LSTM[J]. Acta Energiae Solaris Sinica, 2023, 44(11): 239-246)
(  0) 0) |
| [6] |
Feng G R, Wei H R, Qi T Y, et al. A Transient Electromagnetic Signal Denoising Method Based on an Improved Variational Mode Decomposition Algorithm[J]. Measurement, 2021, 184
(  0) 0) |
| [7] |
Li H L, Shi J H, Li L J, et al. Novel Wavelet Threshold Denoising Method to Highlight the First Break of Noisy Microseismic Recordings[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60
(  0) 0) |
| [8] |
桂团福, 邓居智, 李广, 等. 数学形态学和K-SVD字典学习在大地电磁数据去噪中的应用[J]. 中国有色金属学报, 2021, 31(12): 3713-3729 (Gui Tuanfu, Deng Juzhi, Li Guang, et al. De-Noising Magnetotelluric Data Based on Mathematical Morphology and K-SVD Dictionary Learning[J]. The Chinese Journal of Nonferrous Metals, 2021, 31(12): 3713-3729)
(  0) 0) |
| [9] |
Li W, Liu F, Jiao L C, et al. A Group Matching Pursuit for Image Reconstruction[J]. Image Communication, 2016, 49: 47-62
(  0) 0) |
| [10] |
杨敬娜, 冯贺平, 朱霄珣, 等. 基于AP-KSVD-OMP重构算法的电机轴承故障诊断[J]. 机械设计与研究, 2022, 38(5): 130-133 (Yang Jingna, Feng Heping, Zhu Xiaoxun, et al. Bearing Fault Diagnosis Based on AP-KSVD-OMP Reconstruction Algorithm[J]. Machine Design and Research, 2022, 38(5): 130-133)
(  0) 0) |
| [11] |
朱会杰, 王新晴, 芮挺, 等. 改进的匹配追踪在方波信号滤波中的应用[J]. 解放军理工大学学报: 自然科学版, 2015, 16(4): 305-309 (Zhu Huijie, Wang Xinqing, Rui Ting, et al. Implication of Improved Matching Pursuit in De-Noising for Square Wave[J]. Journal of PLA University of Science and Technology: Natural Science Edition, 2015, 16(4): 305-309)
(  0) 0) |
| [12] |
甘振业, 陈浩, 杨鸿武. 结合EEMD与K-SVD字典训练的语音增强算法[J]. 清华大学学报: 自然科学版, 2017, 57(3): 286-292 (Gan Zhenye, Chen Hao, Yang Hongwu. Speech Enhancement Algorithm that Combines EEMD and K-SVD Dictionary Training[J]. Journal of Tsinghua University: Science and Technology, 2017, 57(3): 286-292)
(  0) 0) |
| [13] |
封常青, 李予国, 吴云具, 等. 利用K-SVD字典学习算法压制海洋大地电磁噪声[J]. 地球物理学报, 2022, 65(5): 1853-1865 (Feng Changqing, Li Yuguo, Wu Yunju, et al. A Noise Suppression Method of Marine Magnetotelluric Data Using K-SVD Dictionary Learning[J]. Chinese Journal of Geophysics, 2022, 65(5): 1853-1865)
(  0) 0) |
| [14] |
吴中如. 水工建筑物安全监控理论及其应用[M]. 北京: 高等教育出版社, 2003 (Wu Zhongru. Safety Monitoring Theoryand Its Application of Hydraulic Structures[M]. Beijing: Higher Education Press, 2003)
(  0) 0) |
| [15] |
柴岩, 朱玉, 任生. 多策略协同的改进鲸鱼优化算法[J]. 计算机工程与科学, 2023, 45(7): 1308-1319 (Chai Yan, Zhu Yu, Ren Sheng. An Improved Whale Optimization Algorithm Based on Multi-Strategy Coordination[J]. Computer Engineering and Science, 2023, 45(7): 1308-1319)
(  0) 0) |
| [16] |
许德刚, 王再庆, 郭奕欣, 等. 鲸鱼优化算法研究综述[J]. 计算机应用研究, 2023, 40(2): 328-336 (Xu Degang, Wang Zaiqing, Guo Yixin, et al. Review of Whale Optimization Algorithm[J]. Application Research of Computers, 2023, 40(2): 328-336)
(  0) 0) |
| [17] |
王浩然, 钮新强, 徐利福, 等. 基于奇异谱分析和改进WOA-BP的大坝变形预测模型[J]. 水力发电学报, 2023, 42(11): 136-145 (Wang Haoran, Niu Xinqiang, Xu Lifu, et al. Dam Deformation Prediction Model Based on Singular Spectrum Analysis and Improved Whale Optimization Algorithm-Optimized BP Neural Network[J]. Journal of Hydroelectric Engineering, 2023, 42(11): 136-145)
(  0) 0) |
2. Nanjing Hydraulic Research Institute, 223 Guangzhou Road, Nanjing 210029, China;
3. Key Laboratory of Reservoir Dam Safety, MWR, 34 Hujuguan, Nanjing 210024, China
 2024, Vol. 44
2024, Vol. 44


