2. 西南石油大学油气藏地质及开发工程国家重点实验室, 成都市新都大道8号, 610500;
3. 西南石油大学油气空间信息工程研究所, 成都市新都大道8号, 610500;
4. 武汉大学测绘遥感信息工程国家重点实验室, 武汉市珞喻路129号, 430079
长期的石油开采是造成油田地表沉降的决定性因素[1]。持续的地表沉降会对开采设施或建(构)筑物造成破坏,并可能诱发小型地震,危害油田安全生产[2]。及时获取石油开采区最新的地表形变与储层参数信息,对维护油田生产安全至关重要。辽河油田是我国最大的稠油和高凝油生产基地。随着开采技术的发展以及开采力度的增加,地下石油资源不断减少,地表沉降持续发生,对地表建筑物、地下管道、石油开采设施等造成一定影响。同时,由于辽河油田位于沿海地区,地表发生持续性沉降会增加海平面上升及风暴潮灾害等气候变化的风险性[3]。以往研究表明,该区域地表沉降较为严重[4-5]。因此,对该区域地表形变进行持续监测并获取最新的形变与油层参数信息具有实际意义。
时序InSAR具有全天候、全天时、低成本、高精度等优点,同时可有效抑制时空失相干和大气相位延迟,得到mm级形变,在地表形变监测中得到广泛应用。油田地表区域性形变是地下储层状态变化的直观表现。结合InSAR监测结果,通过地球物理反演可较好地获取油田储层参数信息,进而实时掌握油田储层参数变化,可为油田开采计划的制定及实施提供参考资料。目前国内外对辽河油田地表形变监测及储层参数进行反演的研究较少,且使用的反演模型均为常规的Okada和Mogi模型。同时,目前研究所获取的该区域形变仅截止到2021年,无法满足最新形变及储层参数信息的获取需求。
本文利用StaMPS-SBAS[6]技术获取研究区最新的地表形变信息,并基于InSAR监测结果,使用贝叶斯反演方法进行储层几何参数反演,探讨Okada、Mogi、复合位错模型(CDM)在油田储层参数反演中的精度,为后续学者对储层参数反演模型的选择提供参考。
1 研究区概况及数据源研究区地处辽河平原,构造上属辽河盆地西部凹陷西斜坡中段,属暖温带大陆性半湿润季风气候。该区为辽河油田核心产区,区内分布有大量开采井及附属设施。本文采用2021-01-08~2023-06-27的62景Sentinel-1升轨数据及2019-02-16~2021-12-14的83景Sentinel-1降轨数据进行数据处理(该区域内降轨存档数据仅到2021-12),哨兵数据升降轨覆盖范围如图 1所示。另外,获取精密定轨星历数据(POD)用于精化Sentinel-1轨道参数,同时获取ALOS world 3D 30 m分辨率数字表面模型(DSM)数据用于去除差分干涉处理中的地形相位。

|
图 1 研究区地理位置与SAR影像覆盖范围 Fig. 1 Geographical location of the study area and SAR image coverage |
本文采用StaMPS-SBAS方法进行SAR数据处理,提取地表形变速率及时间序列。在储层参数反演方面,主要采用Okada模型、Mogi模型和CDM模型开展储层几何参数反演。关于StaMPS-SBAS方法和Okada模型、Mogi模型的应用研究较多[5-8],本文不再赘述。
2.1 复合位错模型(CDM)Nikkhoo等[9]基于弹性半空间理论与矩形位错模型提出一种新的几何源模型,即复合位错模型(CDM),由3个矩形位错(rectangular dislocations, RD)模型组成。与Mogi和Okada等模型相比,CDM模型理论基础更为完备,且可描述具有一般形状和不规则形状的压力源,因此在压力源形状描述上具有一定优势。该模型采用2个坐标系,即原点位于CDM质心的笛卡尔坐标系(x, y, z)以及原点位于地球表面的XYZ坐标系(正X轴、正Y轴和正Z轴分别指向东、北和上)。本文使用X、Y、Z坐标系作为参考系来定义CDM和X、Y、Z坐标系的方向和位置。将CDM移动到其最终空间位置的平移向量为(X0, Y0, -depth),其中X0、Y0和depth分别为CDM质心在X、Y、Z坐标系中的东坐标、北坐标以及深度。此外,CDM在空间中有3个方向,可用ωX、ωY、ωZ表示。由于CDM模型由3个RD组合而成,具有3个半轴,一般用(a, b, c)表示。组成CDM的RD具有相同的均匀张开量。因此,CDM模型共有10个参数,包括CDM质心位置(X0, Y0, -d)、CDM旋转角(ωX, ωY, ωZ)、CDM三个半轴(a, b, c)和一个张开量(open)。
在几何源模型参数反演中,为便于表达,往往将地表形变与模型参数间的关系用如下格林函数表达:
| $ d=G(m)+e $ | (1) |
式中,d表示地表形变量;m表示待估的几何参数;G为格林函数,由一系列地球物理学和地质力学关系式决定,具有高度非线性特征;e为残差。
2.2 参数反演流程传统反演方法的目标仅是获取一组最优的源参数[10],如加权最小二乘最佳拟合算法,通过解决优化问题使测量和模拟表面位移之间的加权拟合最小化。常用的直接搜索方法(模拟退火[11]和遗传算法[12]无法充分和适当地描述与源参数估计相关的不确定性。贝叶斯方法在反演时允许表征源参数的后验概率密度函数,该函数能说明数据中的不确定性[10]。贝叶斯框架可表示为:
| $ p(m \mid d)=\frac{p(d \mid m) p(m)}{p(d)} $ | (2) |
式中,p(m|d)为模型参数m的后验概率密度函数,表示在考虑先验信息的情况下,m能解释数据d的概率;p(d|m)为似然函数,表示已知观测数据d的似然函数;p(m)表示m的先验概率密度函数;p(d)为一个与m无关的归一化常量,在反演时可以将其看作常数。当误差是均值为0的多维高斯分布时,似然函数可表示为:
| $ \begin{gathered} p(d \mid m)=(2 \pi)^{-N / 2}\left|\boldsymbol{\varSigma}_d\right|^{-\frac{1}{2}} \times \\ \exp \left[-\frac{1}{2}\left(d-G_m\right)^{\mathrm{T}} \boldsymbol{\varSigma}_d^{-1}\left(d-G_m\right)\right] \end{gathered} $ | (3) |
式中,d为观测数据,Gm为模拟数据,N为数据点总数;
|
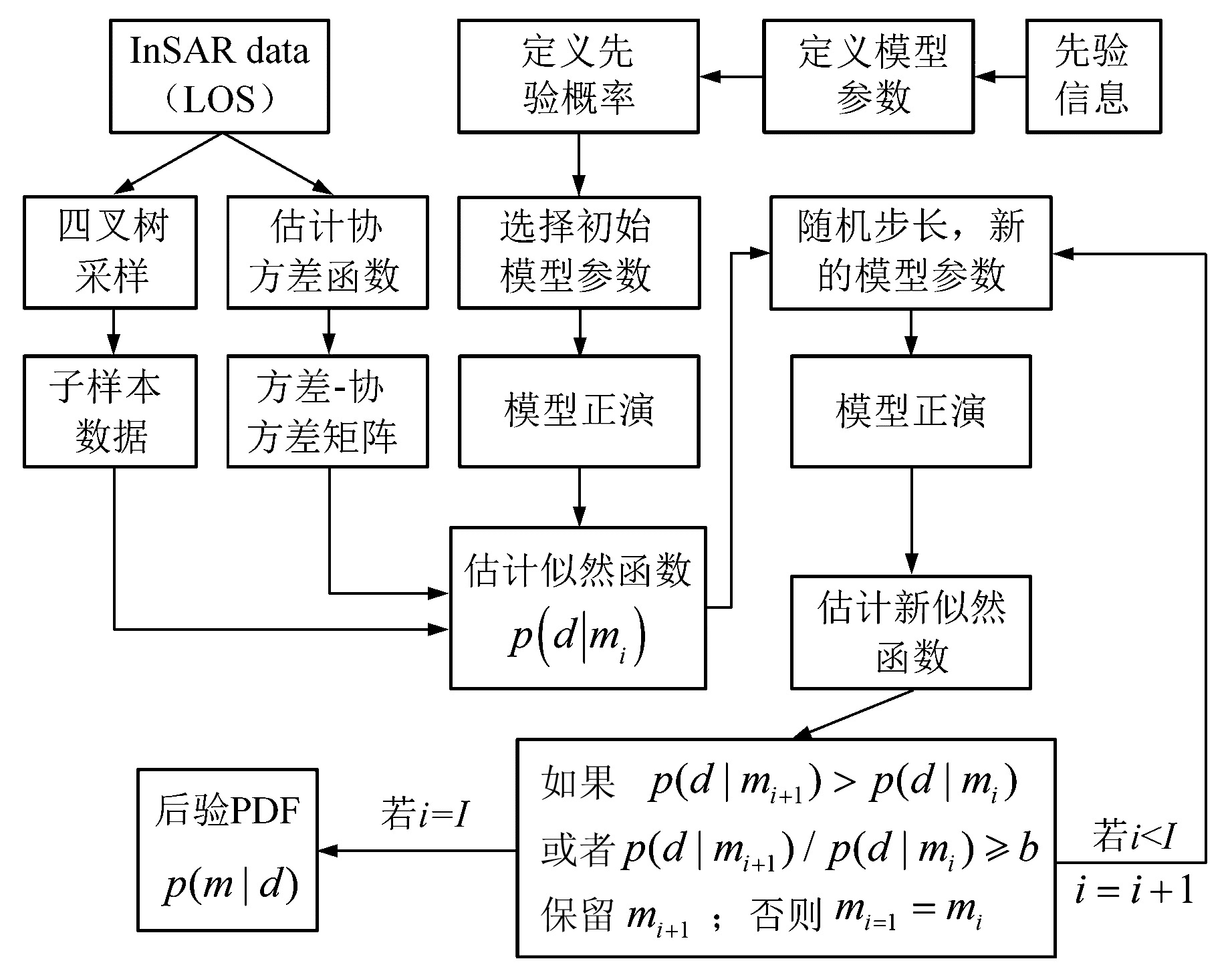
图 2 贝叶斯反演流程 Fig. 2 Flow chart of the Bayesian inversion |
StaMPS-SBAS技术通过低通以及自适应滤波去除噪声相位以及空间不相关误差相位,估计每个初始候选像素点的相位稳定性指标,并选择最终的缓慢失相干滤波相位点;然后通过三维相位解缠方法获取解缠相位。图 3为StaMPS-SBAS方法获得的研究区雷达视线向(LOS)地表形变速率,底图使用天地图光学影像。

|
图 3 研究区形变速率 Fig. 3 The deformation rate of the study area |
由图 3可知,研究区存在3个明显的沉降形变区域(图 3(a)中黑色方框)。本研究共探测到246 487个升轨和159 177个降轨SDFP点,LOS向形变速率分别为-165.84~54.52 mm/a和-176.87~62.69 mm/a。由图可知,87.13%升轨SDFP点的形变速率在-20~20 mm/a之间,68.33%降轨SDFP点的形变速率在-20~20 mm/a之间,表明该研究区大部分地区地表形变相对稳定。升降轨形变速率存在一定差异,可能与轨道入射角不同和监测时间跨度不同有关。值得注意的是,从图 3(b)可以看出,存档数据的可用性导致降轨数据未能完全覆盖锦州采油厂范围,且降轨数据时间跨度的现势性较弱。因此,本研究采用升轨监测结果进行后续分析。
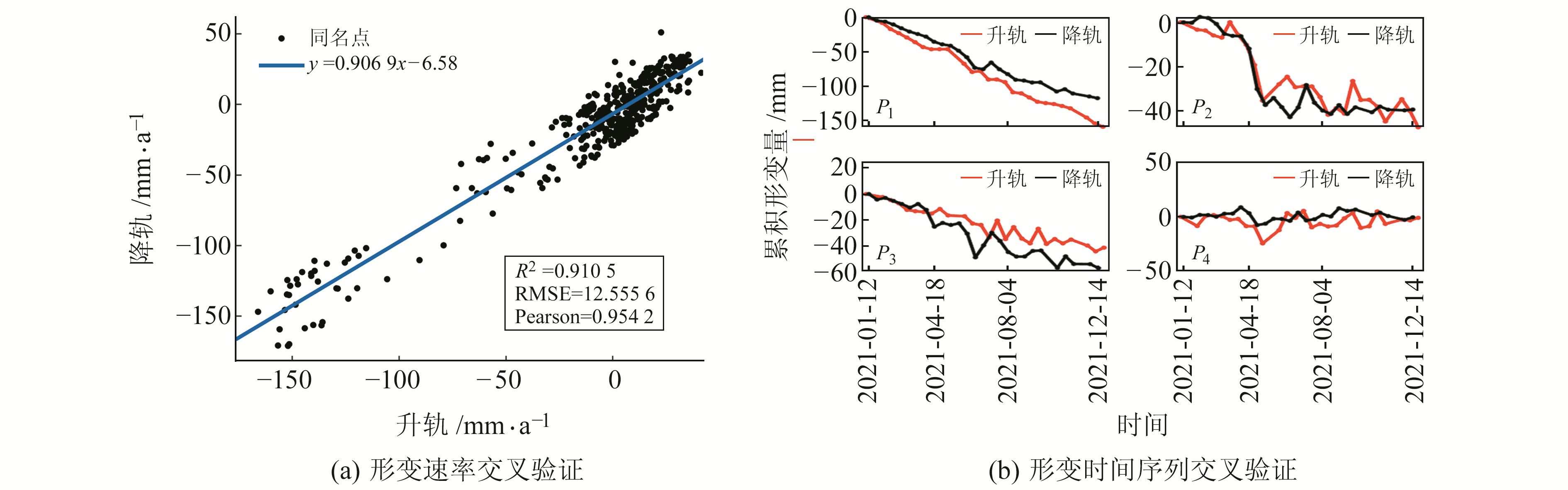
3.1.2 地表形变结果精度评估利用升降轨数据同名点对StaMPS-SBAS方法获取的地表形变监测结果进行验证,分别对同名点重叠时段(2021年)内的年形变速率及沉降时间序列进行分析,结果如图 4所示。图 4(a)为随机选取500个同名点的形变速率散点图,通过相关性分析得出升轨与降轨形变速率之间的相关性为0.954 2,R2=0.910 5。图 4(b)为3个主要形变区域和1个非形变区域的同名点时间序列形变(点位见图 3(b)),由图可知,不同形变区域的升轨和降轨结果在时间上呈现出相似的趋势。上述分析表明,本文获取的地表形变结果较为可靠。需要说明的是,升降轨时序形变的差异可能是由于沉降漏斗区存在相对明显的水平形变[13]。
|
图 4 升降轨同名点形变交叉验证 Fig. 4 Cross validation of deformation of ascending and descending homonymous points |
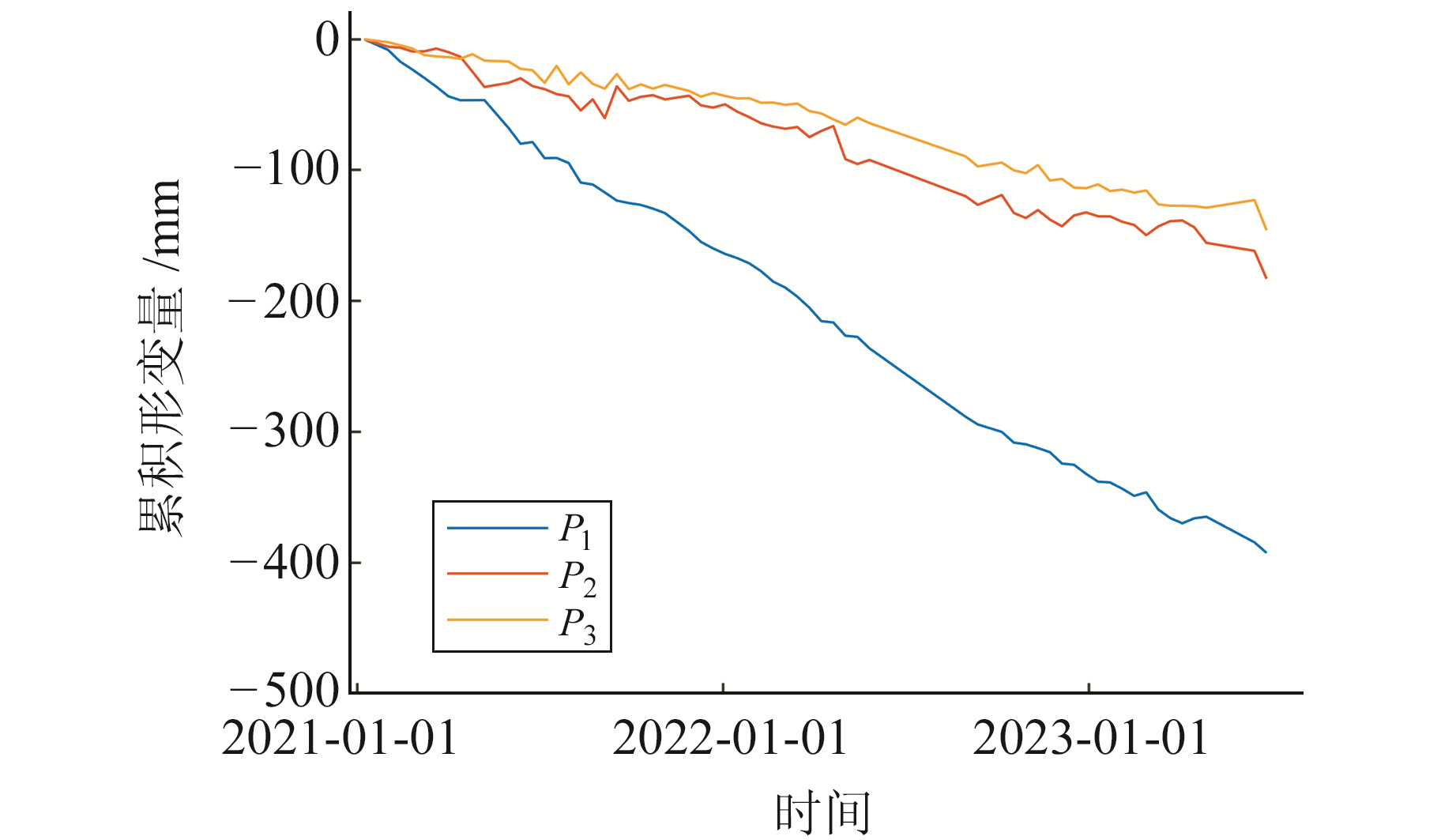
为更好地了解3个沉降漏斗在时间序列上的位移特征以及分析沉降漏斗的长期演变,提取 图 3(a)中A~C区域P1~P3特征点的形变时间序列,结果如图 5所示。P1~P3分别为3个漏斗区域形变最大点,LOS向累积形变量分别为-392.4 mm、-182.9 mm和-145.9 mm。由图 5可知,3个特征点均表现出较为稳定的持续性沉降,其中P1点整体呈线性形变趋势,波动较小。相比之下,P2和P3点也呈线性趋势,但波动较大,这可能与油气开采在局部时间内的增减产程度有关。但整体而言,3个特征点均呈现出线性趋势。
|
图 5 特征点累积形变量 Fig. 5 Cumulative deformation of feature points |
为进一步分析形变演化趋势,采用多项式模型对升轨形变时间序列结果进行拟合。拟合所用的多项式模型为
|
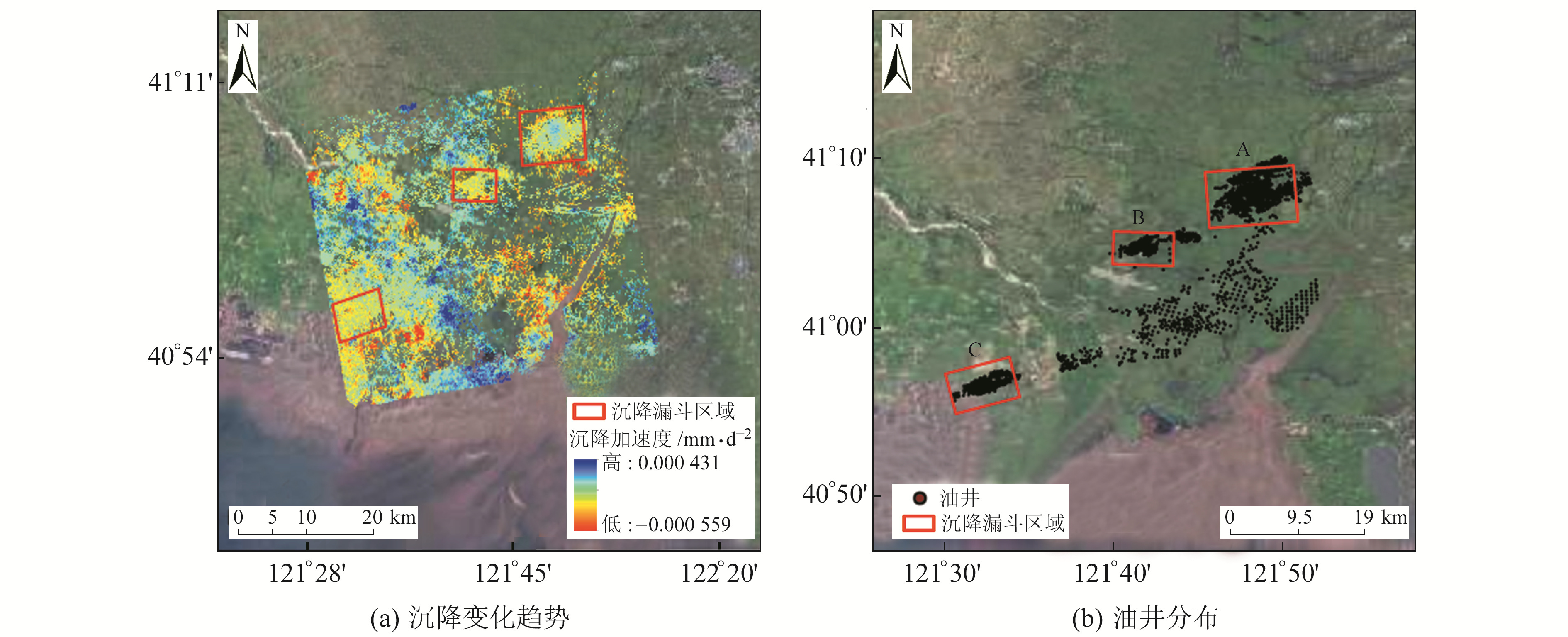
图 6 沉降变化趋势及油井分布 Fig. 6 Trend of subsidence changes and well distribution |
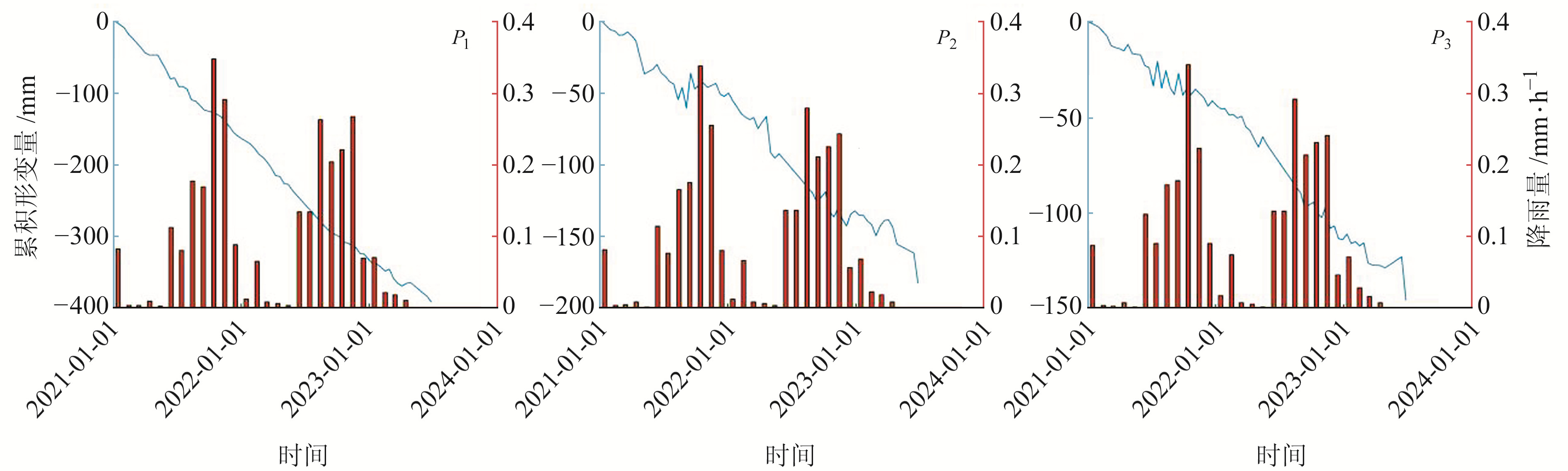
结合光学影像及油井分布(图 6(b))可知,研究区地表形变与油井分布具有良好的一致性,3个沉降漏斗均位于采油厂范围内。随着油气的开采,油层孔隙所承受的压力不断增大,导致油层被不断压实而产生地表沉降。研究表明[5,14],下辽河区域高沉降速率由油气开采所致。张静等[14]研究认为,区域内地下水开采是诱发沉降的另一个重要因素。由于缺少研究区的地下水资料,因此仅能根据以往的研究进行分析。由张静等[14]的分析可知,曙四联沉降区及龙王村沉降区均位于馆陶组地下水位降落漏斗中,这2个沉降区分别对应本文的曙光采油厂区域(A)和欢喜岭采油厂区域(B)。沉降区大致范围未发生变化,因此可以认为地下水开采与地表沉降存在一定的关系。由于地下水位会受降雨影响,即降雨会对浅层地下水(如第四系地下水)形成补充,因此地表形变亦可能受降雨影响。图 7为3个特征点的形变时间序列曲线以及月度降雨均值数据。
由图 7可知,3个特征点在降雨较多的时间段内累积形变曲线波动较大,且沉降呈现轻微变缓趋势,表明降雨对研究区地表形变具有一定影响。相关资料表明,研究区第四系地下水水位埋深0.5~3 m,且存在于冲海积、海积粉砂、粉细砂、细砂、砂砾石孔隙中[15]。由于埋深较浅,降雨可通过影响第四系地下水而导致地表沉降出现波动。同时,石油开采是研究区大沉降漏斗出现的决定性因素。因此需要说明的是,强降雨除了通过补充地下水影响地表形变过程外,还可以通过影响油气开采进程来影响地表形变过程。
|
图 7 特征点形变时间序列与降雨数据 Fig. 7 Deformation time series and rainfall data of feature points |
辽河油田沉降是由石油、天然气持续性开采引起的长时间地表形变,因此,对油气储层参数的确定极为重要。本文以获取的升轨LOS向形变速率作为观测量,采用§2.1所描述的复合位错模型对曙光采油厂沉降漏斗区地下储层参数进行反演,并与Okada和Mogi模型反演结果进行对比,探讨不同模型的适用性。在具体反演时,设定泊松比v=0.25。3种模型反演结果见表 1。
|
|
表 1 不同模型储层参数反演结果 Tab. 1 Inversion results of reservoir parameters with different models |
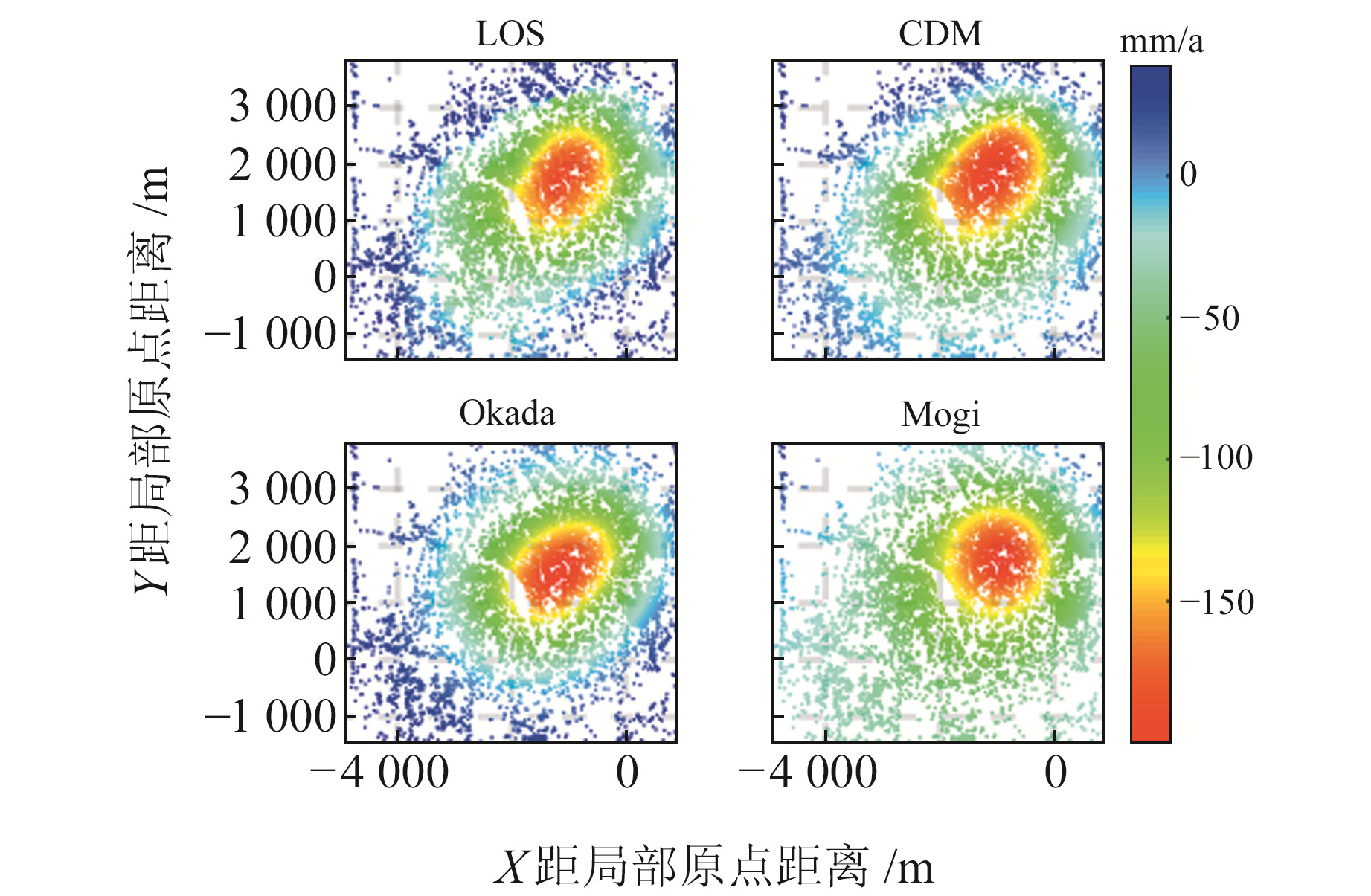
为评估模型反演精度,使用模型参数正演地表形变,结果如图 8所示。从模拟的漏斗形状来看,CDM模型与Okada模型能较好地匹配观测所得漏斗形状,而Mogi模型差异较为明显,这主要与各模型所表征的几何源特征有关。经资料调查可知,曙光油田深度为1 600 m左右[5],CDM模型反演深度为1 665.21 m,其绝对误差为-65.21 m;Mogi模型反演深度为1 765.81 m,绝对误差为-165.81 m;Okada模型反演深度为1 832.51 m,绝对误差为-232.51 m。从反演结果可知,CDM模型最为接近,Okada模型偏差最大,Mogi模型居中。为定量评估3个模型的反演效果,分别计算3个模型正演所得形变与观测值之间的R2、RMSE和Pearson相关系数,结果如表 2所示。由表 2可知,CDM模型模拟的地表形变在相关性、R2、RMSE上相对其他两个模型具有更好的可靠性。
|
图 8 形变模拟结果 Fig. 8 Simulated deformations |
|
|
表 2 不同模型精度对比 Tab. 2 Accuracy comparison of different models |
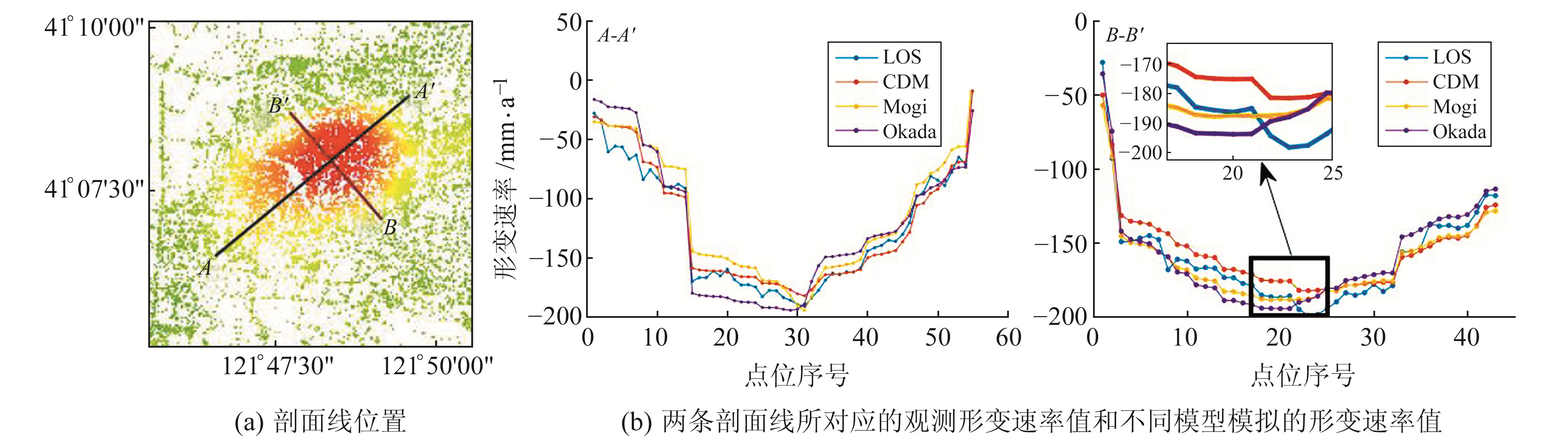
为判断沉降中心区域的模拟效果,绘制漏斗中心剖面线,结果如图 9所示。由图 9可见,模拟漏斗剖面线与观测漏斗剖面线具有较高的相似性。为更直观地定量评估模型模拟形变剖面与观测值剖面之间的关系,使用Kendall相关系数进行分析,结果见表 3。由表可知,对于剖面线A-A′,CDM模型相关系数最大,其次为Mogi模型,Okada模型相关系数最小;对于剖面线B-B′,Mogi模型相关系数最大,其次为CDM模型,Okada模型相关系数最小。尽管B-B′剖面线中Mogi模型相关系数最大,但从局部放大图可以看出,其在蓝色实线(观测值)形变速率最大处与黄色实线(Mogi模拟值)趋势不一致,而橙色实线(CDM模拟值)与蓝色实线形变趋势较为相似,因此认为CDM模型在沉降中心的模拟精度高于Okada模型和Mogi模型。
|
图 9 模拟结果与观测结果形变速率剖面 Fig. 9 Deformation rate profiles of simulated and observed results |
|
|
表 3 不同模型模拟形变剖面与观测形变剖面的相关系数 Tab. 3 The correlation coefficient between observed deformation profiles and simulated deformation profiles with different models |
分别对CDM模型、Okada模型和Mogi模型的残差结果进行统计,如图 10所示。可以看出,CDM模型残差为-45.7~43.3 mm/a,残差标准差为9.6 mm/a,均值为1.2 mm/a,且残差主要集中在0值附近,呈现出正态分布特点;Okada模型残差为-50.2~42.4 mm/a,残差标准差为11.4 mm/a,均值为1.0 mm/a,残差大部分分布在0值附近,呈现不标准的正态分布;Mogi模型残差为-52.8~69.0 mm/a,标准差为16.7 mm/a,均值为-4.0 mm/a,残差主要集中在±15 mm/a附近,且出现2个较为明显的峰值。上述分析表明,CDM模型模拟形变与观测值更为接近,反映出在该区域CDM模型反演精度高于Okada与Mogi模型。

|
图 10 不同模型残差及直方图 Fig. 10 Residuals and histograms of different models |
综合上述分析可知,CDM模型反演精度高于Okada和Mogi模型,且其模拟的漏斗形状较好,说明CDM模型更适用于本文研究区内油田的储层参数反演,这为了解油田地下流体开采所导致的地表沉降与储层之间的联系提供了一定的基础和参考。
4.2 历史反演结果对比分析通过文献检索与分析,获得已发表的辽河油田曙光采油厂储层几何参数反演结果(表 4)。由于龚志强等[4]未明确给出储层深度,因此仅与其他3个研究结果进行对比分析[5,7,16]。同时,由于不同模型的参数个数和类型不一致,本文仅对每种模型都涉及的储层深度进行对比分析。由表 4可知,本文反演深度与杨崇等[5]使用Mogi模型的反演结果较为接近,与Sun等[7]使用Okada模型和李春进等[16]使用双Okada以及双Mogi模型的反演结果相差较大。本文除使用Okada和Mogi模型外,首次使用CDM模型对辽河油田曙光采油厂储层参数进行反演。对于不同反演结果的差异,其可能与选择的模型及源数量有关。从InSAR地表形变监测时间段来看,本文使用2021-01~2023-06地表形变速率结果进行反演,而其他研究使用2007~2011年地表形变速率进行反演。不同时间段地表形变速率存在一定差异,这可能是导致反演结果不同的另一个原因。值得指出的是,沈阳地质矿产研究所公布的曙光采油厂储层深度约为1.6 km[5],该数值与本文CDM模型反演结果非常接近。这表明本文研究结果具有较好的可靠性,且CDM模型在该区域储层参数反演中具有最优的效果。
|
|
表 4 曙光油田不同反演结果 Tab. 4 Different inversion results of Shuguang Oilfield |
上述基于地球物理学模型的地下参数反演均为解析计算,通过建立地下应力应变与地表形变的解析关系,在预先设定的解空间中遍历最优的待估参数值。这种解析方法给出的是经验性最优解,对于不同的观测值以及初始值较为敏感。在对不同区域或不同现象进行研究时,必须根据测区具体情况进行参数配置,并选取最优的反演模型,而不能统一采用某一种模型。
5 结语1) 辽河油田核心产区在监测时段内时序InSAR升轨形变速率为-165.84~54.82 mm/a,降轨形变速率为-176.87~62.69 mm/a,沉降区主要分布在曙光采油厂、欢喜岭采油厂、锦州采油厂。石油开采是研究区地表沉降的主要影响因素,地下水开采及降雨对形变亦有影响。曙光采油厂沉降漏斗中心沉降呈现一定的减速趋势,漏斗外围则出现明显的加速趋势。欢喜岭采油厂漏斗中心呈现微弱加速趋势,而锦州采油厂在3 a内存在较大的沉降加速趋势。
2) 通过对CDM模型、Mogi模型及Okada模型反演结果进行综合分析,并结合模型相关系数、R2及RMSE等评价指标,结果表明在曙光采油厂区域CDM模型相对Mogi和Okada模型反演精度更高。CDM模型反演的曙光采油厂储层深度为1 665.21 m,这与官方公布的数据较为一致。对比分析表明,不同的模型、几何源数量以及不同InSAR结果均可能造成反演结果存在差异。在采用解析方法开展地球物理参数反演时,需要根据不同区域和对象的具体情况选择适当的模型和参数初始值、参数搜索区间等关键信息。
| [1] |
Khakim M Y N, Tsuji T, Matsuoka T. Geomechanical Modeling for InSAR-Derived Surface Deformation at Steam-Injection Oil Sand Fields[J]. Journal of Petroleum Science and Engineering, 2012, 96-97: 152-161 DOI:10.1016/j.petrol.2012.08.003
(  0) 0) |
| [2] |
Bayramov E, Buchroithner M, Kada M, et al. Quantitative Assessment of Vertical and Horizontal Deformations Derived by 3D and 2D Decompositions of InSAR Line-of-Sight Measurements to Supplement Industry Surveillance Programs in the Tengiz Oilfield(Kazakhstan)[J]. Remote Sensing, 2021, 13(13)
(  0) 0) |
| [3] |
孙岐发, 田辉, 张扩. 下辽河平原地区历史地面沉降情况研究[J]. 地质与资源, 2014, 23(5): 450-452 (Sun Qifa, Tian Hui, Zhang Kuo. Study on the History of Land Subsidence in Lower Liaohe River Plain[J]. Geology and Resources, 2014, 23(5): 450-452)
(  0) 0) |
| [4] |
龚志强, 唐伟, 蒋金豹, 等. 基于时序InSAR技术的辽河三角洲油田地面沉降监测与建模[J]. 武汉大学学报: 信息科学版 (Gong Zhiqiang, Tang Wei, Jiang Jinbao, et al. Monitoring and Modeling of Land Subsidence in Liaohe Delta Oilfield Based on Time Series InSAR Technology[J]. Geomatics and Information Science of Wuhan University)
(  0) 0) |
| [5] |
杨崇, 刘国祥, 于冰, 等. 基于InSAR形变的辽河油田曙光采油厂储层参数反演[J]. 国土资源遥感, 2020, 32(1): 209-215 (Yang Chong, Liu Guoxiang, Yu Bing, et al. Inversion of Reservoir Parameters in Shuguang Oil Production Plant of the Liaohe Oilfield Based on InSAR Deformation[J]. Remote Sensing for Land and Resources, 2020, 32(1): 209-215)
(  0) 0) |
| [6] |
Hooper A, Zebker H, Segall P, et al. A New Method for Measuring Deformation on Volcanoes and other Natural Terrains Using InSAR Persistent Scatterers[J]. Geophysical Research Letters, 2004, 31(23)
(  0) 0) |
| [7] |
Sun H, Zhang Q, Zhao C Y, et al. Monitoring Land Subsidence in the Southern Part of the Lower Liaohe Plain, China with a Multi-Track PS-InSAR Technique[J]. Remote Sensing of Environment, 2017, 188: 73-84 DOI:10.1016/j.rse.2016.10.037
(  0) 0) |
| [8] |
Hu J Y, Wu W H, Motagh M, et al. FIM-Based DSInSAR Method for Mapping and Monitoring of Reservoir Bank Landslides: An Application along the Lancang River in China[J]. Landslides, 2023, 20(11): 2 479-2 495 DOI:10.1007/s10346-023-02097-5
(  0) 0) |
| [9] |
Nikkhoo M, Walter T R, Lundgren P R, et al. Compound Dislocation Models(CDMS) for Volcano Deformation Analyses[J]. Geophysical Journal International, 2017, 208(2): 877-894 DOI:10.1093/gji/ggw427
(  0) 0) |
| [10] |
Bagnardi M, Hooper A. Inversion of Surface Deformation Data for Rapid Estimates of Source Parameters and Uncertainties: A Bayesian Approach[J]. Geochemistry, Geophysics, Geosystems, 2018, 19(7): 2 194-2 211 DOI:10.1029/2018GC007585
(  0) 0) |
| [11] |
卜璞, 李朝奎, 杨文涛, 等. D-InSAR与最优化算法的采空区几何参数反演[J]. 测绘科学, 2021, 46(5): 143-152 (Bu Pu, Li Chaokui, Yang Wentao, et al. Inversion of Goaf Geometric Parameters Based on D-InSAR and Optimization Algorithm[J]. Science of Surveying and Mapping, 2021, 46(5): 143-152)
(  0) 0) |
| [12] |
Currenti G, Del Negro C, Nunnari G. Inverse Modelling of Volcanomagnetic Fields Using a Genetic Algorithm Technique[J]. Geophysical Journal International, 2005, 163(1): 403-418 DOI:10.1111/j.1365-246X.2005.02730.x
(  0) 0) |
| [13] |
Yang C S, Zhang D X, Zhao C Y, et al. Ground Deformation Revealed by Sentinel-1 MSBAS-InSAR Time-Series over Karamay Oilfield, China[J]. Remote Sensing, 2019, 11(17)
(  0) 0) |
| [14] |
张静, 冯东向, 綦巍, 等. 基于SBAS-InSAR技术的盘锦地区地面沉降监测[J]. 工程地质学报, 2018, 26(4): 999-1 007 (Zhang Jing, Feng Dongxiang, Qi Wei, et al. Monitoring Land Subsidence in Panjin Region with SBAS-InSAR Method[J]. Journal of Engineering Geology, 2018, 26(4): 999-1 007)
(  0) 0) |
| [15] |
薛晓丹. 盘锦地区地下水水位模拟预报与水资源合理利用研究[D]. 长春: 吉林大学, 2005 (Xue Xiaodan. The Research on the Simulation with Prediction of the Groundwater Level and the Rational Utilization of the Water Resource in Panjin Area[D]. Changchun: Jilin University, 2005)
(  0) 0) |
| [16] |
李春进, 杨崇, 七珂珂, 等. 利用地表沉降信息反演油田储层参数[J]. 测绘地理信息, 2022, 47(3): 56-60 (Li Chunjin, Yang Chong, Qi Keke, et al. Inversion of Oilfield's Reservoir Parameters by Surface Subsidence Information[J]. Journal of Geomatics, 2022, 47(3): 56-60)
(  0) 0) |
2. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Southwest Petroleum University, 8 Xindu Road, Chengdu 610500, China;
3. Institute of Petroleum and Natural Gas Spatial Information Engineering, Southwest Petroleum University, 8 Xindu Road, Chengdu 610500, China;
4. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2024, Vol. 44
2024, Vol. 44

