2. 湘潭大学数学与计算科学学院,湖南省湘潭市北二环,411105
钟差是影响卫星服务质量的关键因素,即使是微小的时钟偏差也会导致显著的测距误差,因此,有必要对卫星钟差进行准确的预报。目前,二次多项式(quadratic polynomial, QP)和灰色模型(grey model, GM)是常用的钟差预报方法,但它们存在局限性,如误差随时间增长[1-2]和对非线性序列处理不足[3]。为了解决这些问题,研究者采用机器学习算法,如径向基函数(radial basis function, RBF)神经网络[4]、小波神经网络(wavelet neural networks, WNN)[5]、长短期记忆神经网络(long short-term memory neural networks, LSTM)[6]和TS模糊神经网络模型[7],取得了一定成果。然而,这些模型可能存在内存消耗大、运算时间长和预报结果不稳定等问题,且它们都是对模型自身的研究,未考虑钟差数据本身的特性。
本文的研究重点在于探索钟差数据的建模策略,并构建新的预报模型。考虑到钟差信号的非线性和非平稳性,本文采用奇异谱分析(SSA)对数据进行预处理,提取趋势项和残差项,以提高预报的准确性。结合自适应模糊神经网络(ANFIS),本文提出SSA-ANFIS模型,用于卫星钟差的预报,并与其他模型进行精度和稳定性的对比分析。
1 SSA-ANFIS卫星钟差预报模型 1.1 SSA原理SSA是一种全局分析法,基于相空间重构,通过奇异值分解得到原始序列的各种成分(趋势项、周期项或噪声项等)[8],其详细推导过程可参考文献[9]。由于卫星在太空中运行会受到光照、转动、温度等影响,卫星钟差序列呈现较强的非线性与非平稳特性,且包含趋势分量、多个周期分量和噪声分量[10]。而本文采用卫星频率数据,且为了提高计算速度,其周期分量可以融合在趋势分量中进行统一考虑,因此只需分解趋势信号和噪声信号。
目前,SSA方法的使用效果主要依赖于滞后窗口的大小。如果窗口长度太大,可能会使分解得到的分量产生混叠;如果窗口长度太小,可能分解不出想要的信号[11]。为此,Khan等[12]提出一种基于统计检验的窗长选择数学方法,为SSA的应用提供了更好的依据。本文研究重点不在于窗口长度的选择,而在于验证SSA方法在卫星钟差预报中的有效性。因此,通过实验来确定窗口长度,以保证所得到的分解信号准确无误。
1.2 ANFIS钟差预报模型自模糊系统与神经网络出现以来,涌现出大量相关模型[13]。在这些模型中,ANFIS模型由于自身的优势而被广泛运用于各种实际问题中[14-15]。ANFIS模型是一种基于TS模型的自适应能力很强的模糊推理系统[16],模型网络结构及具体公式可参考文献[17]。
本文结合卫星钟差的特点以及实验结果,从以下几个方面构造合适的网络结构。
1) 输入数据的个数。选取卫星钟差值的个数作为输入数据的个数。输入数据的个数会影响模型的运行速度,数量太少会使模型无法充分获得数据之间的信息,太多则会降低模型运行速度。目前并没有有效的方法确定输入数据的个数,因此本文通过参考文献[18]和下文实验1比较不同输入个数的效果,最终确定单次输入6个历元的卫星钟差。
2) 隶属函数的选择。由于输入量为卫星钟差或一次差值,相邻历元间不会发生突变,所以将其归一化到[0, 1]之间。计算的隶属度值对输入值的变化仍然会比较敏感,鉴于钟差数据具有高度的非线性和非平稳特性,选取钟型函数中高斯分布函数作为隶属函数[18]。
3) 学习算法的选择。通过下文实验1对比BP算法和混合学习算法的实验效果,虽然混合学习算法的运行速度比BP算法稍慢,但其效果更好,因此,本文使用混合学习算法。
4) 聚类算法的选择。聚类算法可以有效划分输入空间,减小模糊规则的数目。通过下文实验1得出,模糊C均值聚类算法效果更好,因此,本文选择其作为聚类算法。
5) 输出。由于卫星钟差预报只预报下一时刻的钟差值,所以输出变量数目为1,满足ANFIS要求单变量输出的要求。同时,针对钟差预报以连续6个历元预测后1个钟差的特点,本文采用滚动预报的方式进行钟差预报,即利用当前历元的数据和前5个历元的数据构成新的6个输入数据,进行反复迭代,预测未来一段时间的卫星钟差。
综上所述,本文构造的网络结构中,输入个数设为6,输出设为1,确定隶属度函数的个数为3,误差步长设为0.001,最大训练进化次数为500,学习算法采用混合学习算法,聚类算法采用模糊C均值聚类。
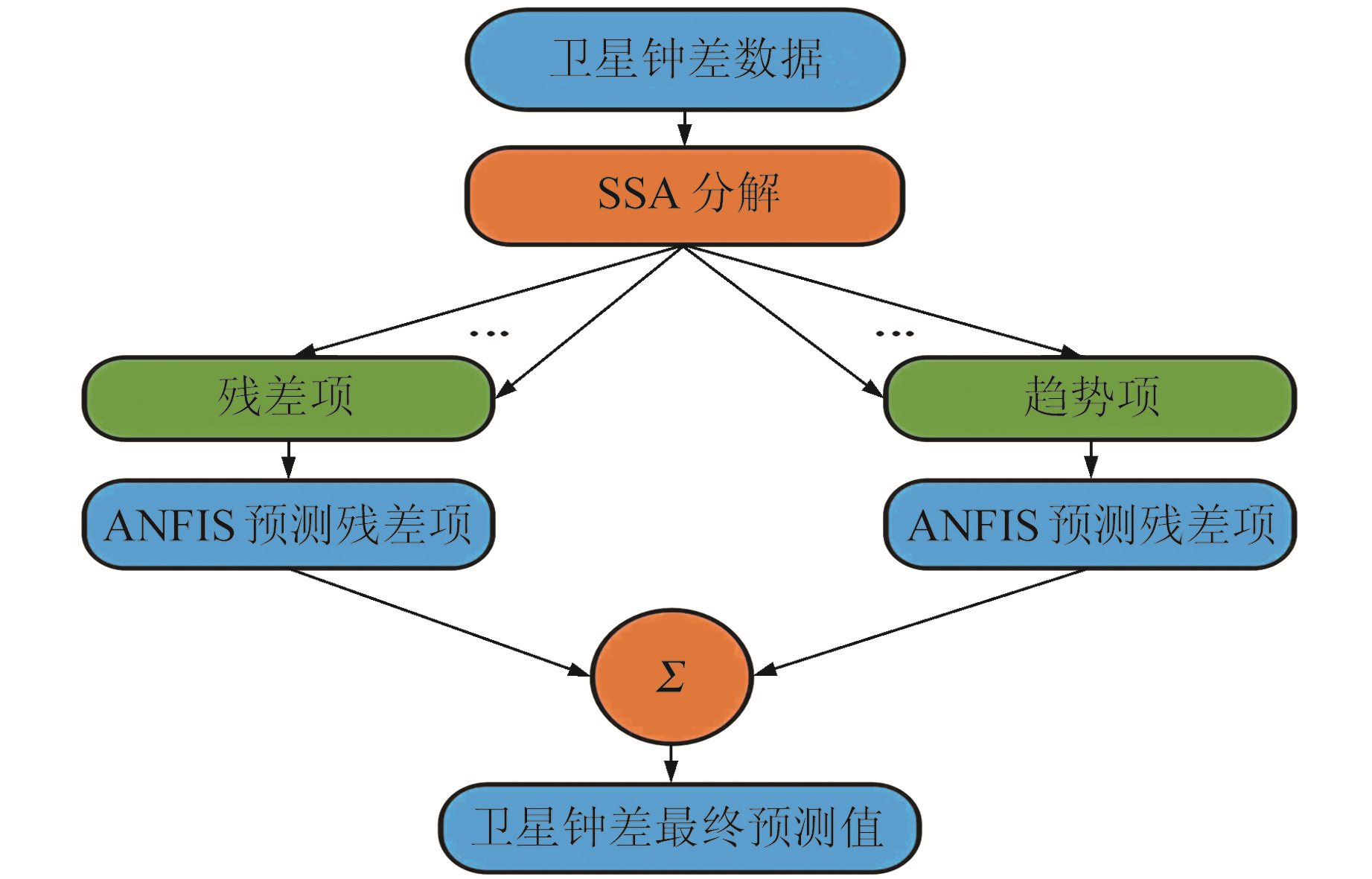
1.3 SSA-ANFIS组合模型图 2为SSA-ANFIS模型的预报流程,具体步骤如下:
|
图 1 SSA-ANFIS模型钟差预报流程 Fig. 1 Process of SCB prediction base on SSA-ANFIS model |

|
图 2 4颗卫星对比结果 Fig. 2 Comparison results of four satellites |
1) 使用卫星钟差相位数据作为模型的初始数据,再将其转为频率数据,并利用中位数方法对频率数据进行预处理,检测并剔除粗差,对剔除粗差的历元使用线性插值方法补齐。
2) 对经过预处理的钟差数据进行历元间作差,得到一次差数据,即模型所需建模数据序列。
3) 使用SSA方法对一次差数据进行分解,得到一系列分量,根据奇异值的大小,叠加不同奇异值所代表的分量,重构为趋势项与残差项。
4) 对网络模型输入进行模糊化,得到一个[0, 1]区间的隶属度;再将各隶属度相乘,并对结果进行归一化处理;然后对归一化后的数据进行加权求和,得到每条输入对应的输出;最后对每条输出求和,得到最终的钟差预报值。
5) 采用滚动预报的方式对趋势项和残差项进行预报,最后将2项分量预报值叠加,并进行反差分处理,得到最终的钟差预报序列。
2 实验及分析使用武汉大学IGS数据中心提供的事后精密钟差数据验证本文模型的有效性,时间为2022-09-24~30,采样间隔为30 s。本文只针对BDS-3卫星进行实验,因此使用C19~C46号BDS-3卫星,并以当天前12 h的数据为训练数据,后12 h的数据为测试数据。表 1为BDS-3卫星原子钟类型。实验前,先使用中位数方法对原始钟差数据进行粗差探测并剔除,其中的粗差阈值采用4倍中位数,然后用线性插值方法将剔除的数据恢复。选取均方根误差RMSE和极差RE作为评价模型精度和稳定性的指标。
|
|
表 1 BDS-3卫星原子钟类型 Tab. 1 Atomic clock types of BDS-3 satellites |
为了评估输入历元个数以及其他参数对ANFIS模型预报精度的影响,以2022-07-25的钟差数据作为实验数据,选取4颗BDS-3卫星(C21、C23、C26、C28)作为实验对象,从输入历元个数、学习算法、聚类算法等方面进行实验。同时,使用当天前12 h的数据进行建模,预测后12 h的钟差数据。实验只改变单一变量,同时保证其他变量不变。表 2为4颗卫星在不同输入个数时的12 h预报结果(包括其平均值和计算时间),表 3为不同聚类算法下的12 h预报结果,表 4为不同学习算法的12 h预报结果。
|
|
表 2 不同输入个数时的12 h预报结果 Tab. 2 12 h prediction results with different input numbers |
|
|
表 3 不同聚类算法的12 h预报结果 Tab. 3 12 h prediction results with different clustering algorithms |
|
|
表 4 不同学习算法的12 h预报结果 Tab. 4 12 h prediction results with different learning algorithms |
由表 2可见,随着输入个数的增加,其预测精度大体呈现先增加再降低的趋势,而模型训练和预测所需要的计算资源和计算时间却在不断增加。综合考虑预测精度和计算时间,认为输入个数为6是比较合适的。由表 3可见,模糊C均值聚类的预测精度和计算时间均优于减法聚类。由表 4可见,混合算法的预测精度较高,但耗时较长。考虑到计算时间之间的差距并没有预测精度的差距大,本文选择精度较高的混合算法。
2.2 实验2为验证分解层数和建模时长对模型的影响,以经过处理的一次差数据为实验数据,选取4颗BDS-3卫星(C21、C23、C26、C28)作为实验对象,分别使用SSA-ANFIS模型和ANFIS模型进行预报,并对建模时长为3 h、6 h、12 h、15 h、18 h、24 h的数据进行建模,预测后12 h的数据。本次实验选择的分解层数为3、6、9、12、15、18、21、24。限于篇幅,只给出9层、18层以及3 h、6 h、12 h的预测效果图。
图 2为4颗卫星SSA方法9层、18层以及3 h、6 h、12 h的结果,表 5为ANFIS模型和SSA-ANFIS模型的12 h预报结果统计值,表 6为不同分解层数下的12 h预报结果平均统计值,表 7为不同建模时长下的12 h预报结果平均统计值。
|
|
表 5 不同分解层数和不同建模时长下的12 h预报结果 Tab. 5 12 h prediction results with different decomposition layers and different modeling time |
|
|
表 6 不同分解层数下的12 h预报结果平均统计值 Tab. 6 Average statistical values of 12 h prediction results with different decomposition layers |
|
|
表 7 不同数据量下的12 h预报结果平均统计值 Tab. 7 Average statistical values of 12 h prediction results with different modeling time |
由图 2和表 5看出,不同建模时长对ANFIS模型的影响较大。建模时长为12 h时,4颗卫星普遍具备较好的预测效果,能够不同程度地改善预报结果,最大预报误差为0.557 ns;建模时长为6 h时,仅C28卫星具有较好预测效果,最大预报误差为1.324 ns;建模时长为3 h时,C23和C26卫星预测效果较好,最大预报误差为1.451 ns。
由表 6、7(单位ns)可见,分解层数从3层增加至24层时,模型预测精度先提高后降低,且9~18层间能取得较好的效果;建模时长对预测精度的影响也呈现相同的趋势,在12 h以后能取得较好的效果。虽然增加建模时长可以有效提升卫星钟差预测精度,但其计算时间也会增加,因此后续实验均以12 h作为建模时长。
对比分析4颗卫星的预报结果发现,SSA-ANFIS模型的预测精度受到分解层数以及建模时长的影响。9~18层分解都能有效增加SSA-ANFIS模型的预报精度,且存在随层数增加,精度提高或降低的趋势。比如,对于C21和C23卫星,9层分解能够取得最好的预测效果;而对于C26和C28卫星,18层分解能够取得最好的预测效果,这表明对于钟差而言,星钟类型的不同会导致同样的分解层数产生不同的效果。
另外,对于C28卫星,使用6 h数据量进行预测时,SSA-ANFIS模型的预测精度无法得到提高。这是因为此时ANFIS模型已经达到最优,进行多层分解也无法提高精度。
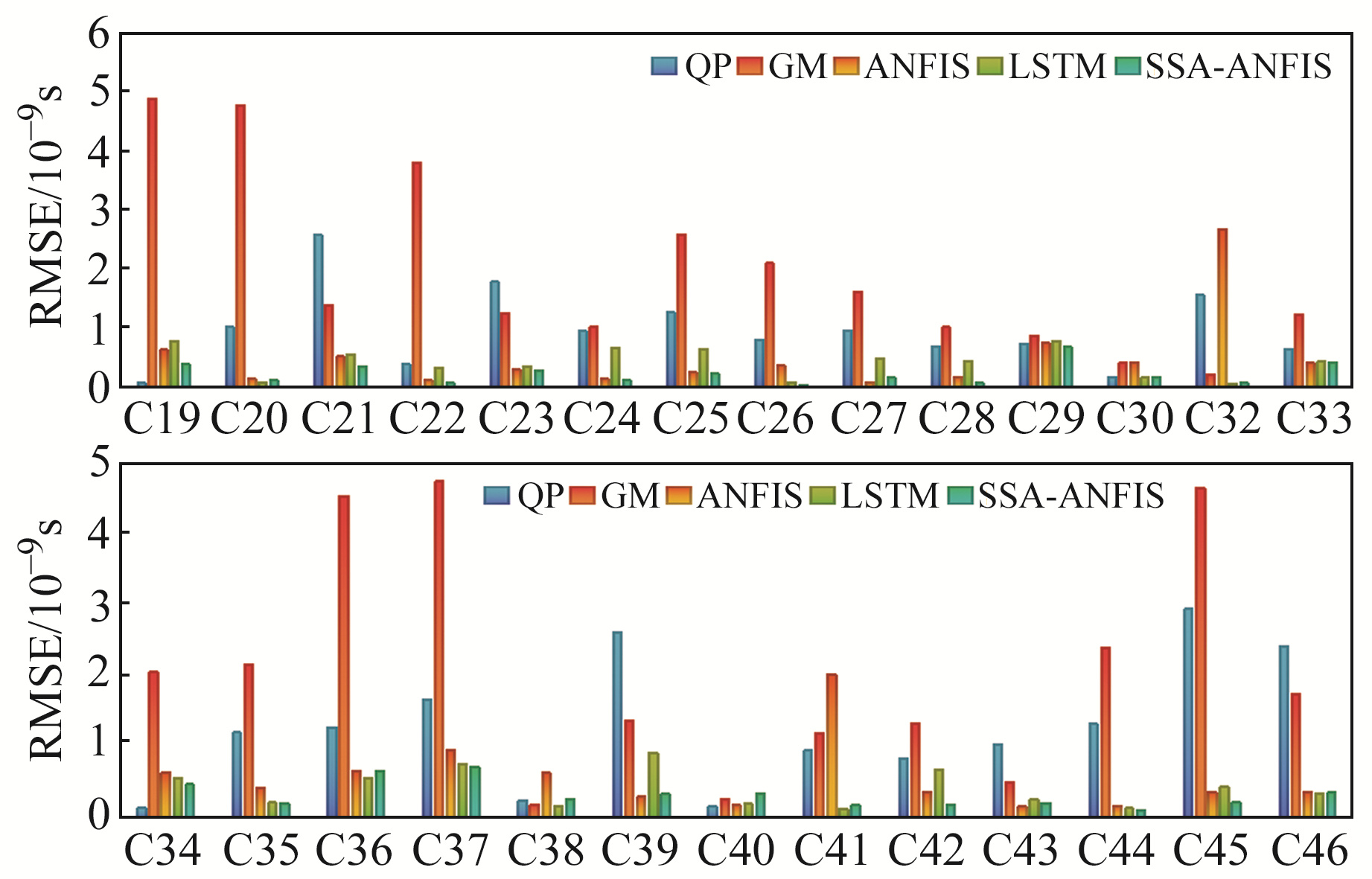
2.3 实验3为验证SSA-ANFIS模型在进行钟差预报时的优势,基于2022-09-30的钟差数据,对C19~C46卫星分别采用GM(1, 1)、QP、LSTM、ANFIS和SSA-ANFIS模型进行预报实验,其中GM(1, 1)和QP模型使用经过预处理的原始数据,LSTM模型、ANFIS模型以及SSA-ANFIS模型使用经过预处理的钟差一次差数据。所有模型均使用12 h的数据(共1 440个历元)进行建模,预测未来12 h的钟差数据。图 3为C26和C28卫星采用不同模型的预报残差结果图,图 4为所有卫星的预报结果。

|
图 3 C26和C28卫星短期预报残差结果 Fig. 3 Residual results of short-term prediction of C26 and C28 satellites |
|
图 4 C19~C46卫星12 h预报结果 Fig. 4 12 h prediction resultsof C19 to C46 satellites |
由图 3、4可见,5种模型均存在误差随时间增加而累积的现象,但3种神经网络模型的表现优于2种传统模型。
在预报精度方面,GM(1, 1)模型性能最差,其次为QP模型,仅达到ns级;ANFIS和LSTM模型效果较好,虽然在某些卫星上出现ANFIS模型优于LSTM模型的情况,但整体而言,LSTM模型性能更好;SSA-ANFIS模型在绝大部分卫星上都表现出最优效果。
由图 4还可以得出,搭载氢钟的卫星的预测精度普遍高于搭载铷钟的卫星,从侧面说明氢钟的性能比铷钟优越,所产生的卫星钟差数据质量更好。
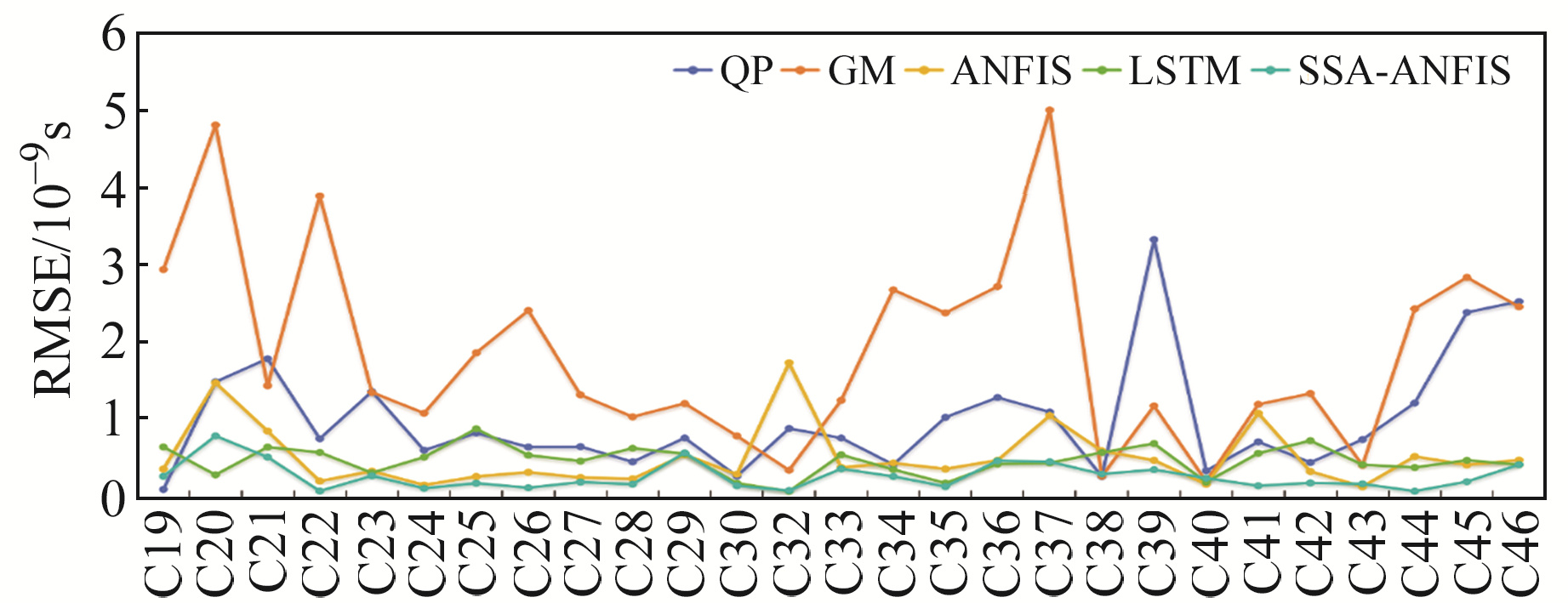
2.4 实验4为进一步验证SSA-ANFIS模型的有效性,基于实验3,将实验数据扩展至2022-09-24~30的连续7 d的钟差数据,以当天前12 h的数据为建模数据,分别采用5种模型预报3 h、6 h、12 h的卫星钟差,连续预报7 d,并求出平均值。图 5为C19~C46卫星12 h预报结果平均值,表 8(单位ns)为5种模型的3 h、6 h、12 h预报时长的RMSE和RE平均值。
|
图 5 C19~C46卫星12 h预报结果 Fig. 5 12 h prediction results of C19 to C46 satellites |
|
|
表 8 5种模型预报结果平均值 Tab. 8 Average values of prediction results of the 5 models |
由图 5和表 8可以看出,SSA-ANFIS模型的预测精度最高,其7 d的3 h、6 h和12 h预报误差均值分别为0.066 ns、0.112 ns和0.293 ns,相比LSTM模型提高25.7%~40.7%,相比ANFIS模型提高39.4%~45.7%;其稳定度相比LSTM模型提高19.5%~33.2%,相比ANFIS模型提高31.5%~34.5%。这是由于SSA方法能有效分解出钟差序列中的趋势项和随机项,并利用模型分别进行预测,充分考虑了钟差序列不同成分之间的干扰所引起的误差。而QP模型和GM(1, 1)模型预报精度较差,这是因为QP模型适合线性较强的数据,但卫星钟差受轨道、辐射等因素的影响会出现很强的非线性特征;GM(1, 1)模型则是因为要根据不同的卫星情况来建模,否则会产生较大误差。
随着预报时长的增加,QP和GM(1, 1)模型预报精度迅速下降;LSTM和ANFIS模型缓慢下降,具有误差累积效应;SSA-ANFIS模型虽然精度也在降低,但降低幅度小于其他模型。说明组合模型能有效降低误差累积的问题,提高模型的有效期。
从星钟类型来看,仍然是搭载氢钟的卫星预报效果优于搭载铷钟的卫星。
3 结语本文提出一种新的卫星钟差预测模型SSA-ANFIS,并对其进行有效性实验,为BDS-3钟差预测提供新的思路和方法。实验结果表明,相比于传统的QP、GM(1, 1)模型和单一的ANFIS、LSTM模型,SSA-ANFIS模型具有更好的预测效果和稳定性,具体结论如下:
1) 本文首先构建了ANIFS模型,与QP和GM(1, 1)模型相比,ANIFS模型能够更好地预测卫星钟差,但比LSTM模型略差。此外,建模时长对预测结果有显著的影响,适当增加建模时长可以提高预测精度,但计算成本也随之增加。因此综合考虑,选择12 h作为建模时长具有更好的效果。
2) 本文提出的SSA-ANFIS模型能够有效改善单一ANFIS模型的预测精度和稳定性。这是因为单一ANFIS模型难以考虑卫星钟差序列中各种成分之间的干扰,而SSA-ANFIS模型可以将其分解成趋势项和残差项,并分别进行预测,从而充分利用钟差序列中的信息。
3) 通过实验确定不同卫星需要的SSA分解层数,发现9~18层基本能满足所有卫星的需求,得到较好的预测结果。
4) 单一模型存在误差随时间增加而累积的问题,而SSA-ANFIS模型在控制误差累积方面表现更好,并且预测精度和稳定性都得到不同程度的提高。
5) 对于BDS-3卫星来说,氢钟的性能要优于铷钟。
6) 虽然SSA方法并不能在所有情况下都提高预测精度,但对于单一模型难以达到最优的情况,SSA是一种有效的改善方法。
| [1] |
Jonsson P, Eklundh L. Seasonality Extraction by Function Fitting to Time-Series of Satellite Sensor Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(8): 1 824-1 832 DOI:10.1109/TGRS.2002.802519
(  0) 0) |
| [2] |
Kosaka M. Evaluation Method of Polynomial Models' Prediction Performance for Random Clock Error[J]. Journal of Guidance, Control, and Dynamics, 1987, 10(6): 523-527 DOI:10.2514/3.20251
(  0) 0) |
| [3] |
Yuan H B, Wang Z M, Dong S W, et al. Dynamic Grey-Autoregressive Model of an Atomic Clock[J]. Metrologia, 2008, 45(6)
(  0) 0) |
| [4] |
王国成, 柳林涛, 徐爱功, 等. 径向基函数神经网络在GPS卫星钟差预报中的应用[J]. 测绘学报, 2014, 43(8): 803-807 (Wang Guocheng, Liu Lintao, Xu Aigong, et al. The Application of Radial Basis Function Neural Network in the GPS Satellite Clock Bias Prediction[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(8): 803-807)
(  0) 0) |
| [5] |
Wang Y P, Lu Z P, Qu Y Y, et al. Improving Prediction Performance of GPS Satellite Clock Bias Based on Wavelet Neural Network[J]. GPS Solutions, 2017, 21(2): 523-534 DOI:10.1007/s10291-016-0543-z
(  0) 0) |
| [6] |
He S F, Liu J L, Zhu X W, et al. Research on Modeling and Predicting of BDS-3 Satellite Clock Bias Using the LSTM Neural Network Model[J]. GPS Solutions, 2023, 27(3): 108 DOI:10.1007/s10291-023-01451-3
(  0) 0) |
| [7] |
蔡成林, 于洪刚, 韦照川, 等. 基于Takagi-Sugeno模糊神经网络模型的卫星钟差预报方法[J]. 天文学报, 2017, 58(3): 113-126 (Cai Chenglin, Yu Honggang, Wei Zhaochuan, et al. The Satellite Clock Bias Prediction Method Based on Takagi-Sugeno Fuzzy Neural Network[J]. Acta Astronomica Sinica, 2017, 58(3): 113-126)
(  0) 0) |
| [8] |
Golyandina N, Zhigljavsky A. Singular Spectrum Analysis for Time Series[M]. Heidelberg: Springer, 2013
(  0) 0) |
| [9] |
Golyandina N. Particularities and Commonalities of Singular Spectrum Analysis as a Method of Time Series Analysis and Signal Processing[J]. WIREs Computational Statistics, 2020, 12(4)
(  0) 0) |
| [10] |
丁慧敏, 王文贯, 李浩军. BDS-3卫星钟差模型化特性分析[J]. 大地测量与地球动力学, 2023, 43(2): 153-157 (Ding Huimin, Wang Wenguan, Li Haojun. Analysis of the Modeling Characteristics of BDS-3 Satellite Clock Offset[J]. Journal of Geodesy and Geodynamics, 2023, 43(2): 153-157)
(  0) 0) |
| [11] |
Chen Q, Dam T, Sneeuw N, et al. Singular Spectrum Analysis for Modeling Seasonal Signals from GPS Time Series[J]. Journal of Geodynamics, 2013, 72: 25-35 DOI:10.1016/j.jog.2013.05.005
(  0) 0) |
| [12] |
Khan M A R, Poskitt D S. Moment Tests for Window Length Selection in Singular Spectrum Analysis of Short-and Long-Memory Processes[J]. Journal of Time Series Analysis, 2013, 34(2): 141-155 DOI:10.1111/j.1467-9892.2012.00820.x
(  0) 0) |
| [13] |
Vieira J, Dias F M, Mota A. Neuro-Fuzzy Systems: A Survey[J]. Wseas Transactions on Systems, 2004, 3(2): 414-419
(  0) 0) |
| [14] |
Kar S, Das S, Ghosh P K. Applications of Neuro Fuzzy Systems: A Brief Review and Future Outline[J]. Applied Soft Computing, 2014, 15: 243-259 DOI:10.1016/j.asoc.2013.10.014
(  0) 0) |
| [15] |
Viharos Z J, Kis K B. Survey on Neuro-Fuzzy Systems and Their Applications in Technical Diagnostics and Measurement[J]. Measurement, 2015, 67: 126-136 DOI:10.1016/j.measurement.2015.02.001
(  0) 0) |
| [16] |
Jang J S R. ANFIS: Adaptive-Network-Based Fuzzy Inference System[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1993, 23(3): 665-685 DOI:10.1109/21.256541
(  0) 0) |
| [17] |
Karaboga D, Kaya E. Adaptive Network Based Fuzzy Inference System(ANFIS) Training Approaches: A Comprehensive Survey[J]. Artificial Intelligence Review, 2019, 52(4): 2 263-2 293 DOI:10.1007/s10462-017-9610-2
(  0) 0) |
| [18] |
王旭, 柴洪洲, 王昶. 卫星钟差预报的T-S模糊神经网络法[J]. 测绘学报, 2020, 49(5): 580-588 (Wang Xu, Chai Hongzhou, Wang Chang. T-S Fuzzy Neural Network to Predict Satellite Clock Bias[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(5): 580-588)
(  0) 0) |
2. School of Mathematics and Computational Science, Xiangtan University, North-Erhuan, , Xiangtan 411105, China
 2024, Vol. 44
2024, Vol. 44


