2023-08-06 02:33山东省德州市平原县发生M5.5地震,震中位置为116.34°E、37.16°N,震源深度10 km。本次地震发生于华北地区河北平原带与郯庐断裂带2个活动地块边界带中间区域[1],属于地震活动较弱区域[2],震中附近70 km范围内历史上无5级以上地震发生。
华北地区是我国地震灾害多发区,历史地震资料较为完备。很多学者对该区域地震活动进行了期幕分段研究[3],普遍认同华北地区在1998-01-10张北M6.2地震后进入地震活动平静幕[4],至2023-12时长已超过平静幕平均时长,因此华北地区震情走向成为关注重点。同时,张北地震后华北地区5、6级地震活动同步骤减,2000年以来仅发生3次5级地震,而本次山东平原地震为此时段震级最大地震,其对该区域震情发展的影响值得关注。
本文引入因子分析方法,通过对平原地震序列的各类地震活动性参数进行降维综合,从复杂多样的数据中提取所需特征,以研究平原地震区域中小震变化对华北地区地震活动性的影响。
1 地震活动性参数计算地震活动性是指一定区域、时期内地震的活动特性,包括时空分布和频度、强度变化等。地震活动性参数通常是根据地震观测目录计算得到,用以研究地震基本参数的关系和变化特征及其反映的地震活动趋势等[5]。地震预测研究中常用的地震活动性参数数量众多,有与地下介质特征相关的,如反映G-R关系拟合及与偏离信息相关的b值、η值、Mf值和反映介质稳定程度的响应比Y等,与地震活动强度相关的频度N、能量E、断层总面积Σt、地震活动因子A值、平均能量偏离度A(b)值、序列衰减系数P(b)值等,与空间分布相关的空间集中度C值、地震演化指数YH值等,反映时间分布特征的地震危险度D值、算法复杂性AC值、缺震M,反映固体潮的调制作用的Rm值等[6]。
本文以平原M5.5地震震中为中心,周边200 km为半径,选取1970年以来ML2.0~4.9地震序列目录(最小完整性震级计算所得),以窗长1 a、步长1个月计算16种常用的地震活动性参数(A值、AC值、A(b)值、b值、C值、D值、P(b)值、能量E、频度N、调制比Rm、响应比Y、YH值、Mf值、η值、缺震M、断层总面积Σt[7]),如图 1所示。参数中多个曲线特征表明,区域地震活动性分为2个明显不同的阶段,最为明显的是与地震活动强度相关的N、Σt、E、Ab值、P(b)值,其他参数中除与地下介质关系密切的参数b值、η值、Mf值外,均有不同程度的时间阶段性变化,这与华北地区的地震活动特征相符。

|
图 1 平原地震区域地震活动性参数变化 Fig. 1 Time variations of the seismic activity parameters in the Pingyuan earthquake area |
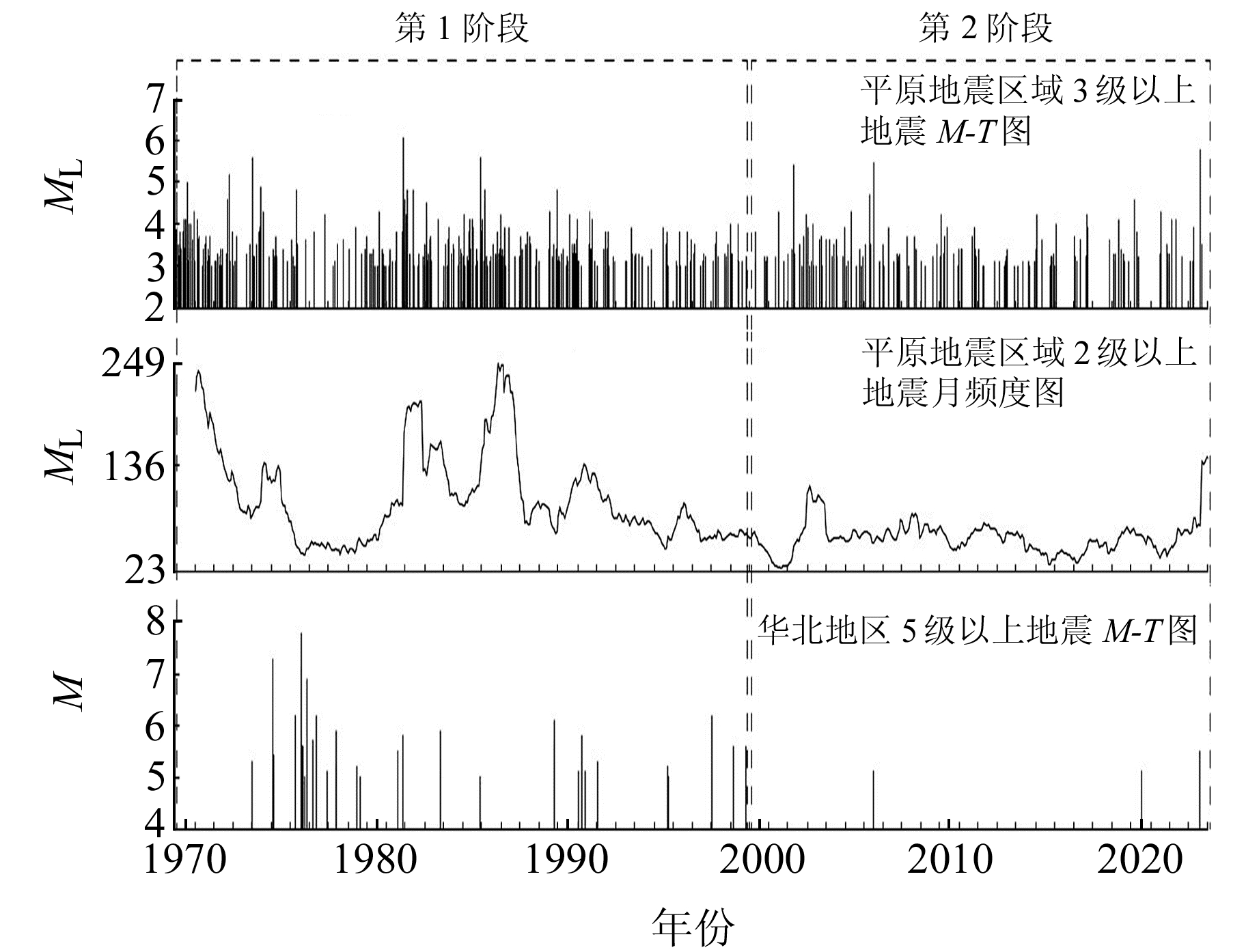
如图 2所示,1970年以来华北地区(110°~123°E,34°~42°N)5级以上地震序列活动有2个明显不同的阶段:第1阶段为1970~1999年,强震频发、地震活跃,共发生5级以上地震53次,其中6级以上地震9次,7级以上地震3次;第2阶段为2000年至今,地震活动水平较第1阶段显著降低,仅发生3次5级以上地震,最大地震为本次山东平原M5.5地震。这2个阶段的变化与华北地区1998年张北地震后进入平静幕的特征基本相符。平原地震区域的中小地震活动也呈现2个阶段的同步变化:第1阶段区域3级以上地震频发,2级以上地震频度均值约为101次/月;第2阶段区域3级以上地震活动明显减少,2级以上地震频度均值水平下降至约57次/月。平原地震发生在华北地区中心地带,其地震活动与华北强震活动存在明显的相关性,说明平原区域地震序列特征变化可在一定程度上反映华北地区整体地震的活动性特征。
|
图 2 平原地震区域地震活动与华北地区中强震活动 Fig. 2 The seismic activities in the Pingyuan earthquake area and the moderate-strong seismic activities in north China |
因子分析是在解决以多种方法判断同一问题时,针对事件复杂性高、分析结果不一致等问题的一种综合方法,也是一种有效的降维方法[8]。地震预测研究使用的地震活动性参数众多,分析难度大,且实际工作中常出现判断不一致的问题。因此,本文引入因子分析方法获取综合指数,以降低地震活动性特征分析的复杂性[9]。
因子分析的基本模型是:假设变量为x1,x2,…,xp,数据因子为f1,f2,…,fm,因子分析模型则表示为:
| $ \left\{\begin{array}{l} x_1=a_{11} f_1+a_{12} f_2+\cdots+a_{1 m} f_m+\varepsilon_1 \\ x_2=a_{21} f_1+a_{22} f_2+\cdots+a_{2 m} f_m+\varepsilon_2 \\ \cdots \\ x_p=a_{p 1} f_1+a_{p 2} f_2+\cdots+a_{p m} f_m+\varepsilon_p \end{array}\right. $ | (1) |
式中,a为相关系数,ε为特殊因子。本文利用因子分析方法对选取的地震序列计算得出的地震活动性参数进行综合分析。
1) 标准化数据:
| $ \begin{gathered} x_{i j}^{\prime}=\left(x_{i j}-\bar{x}_i\right) / \sigma_i, \\ i=1, 2, \cdots, p, j=1, 2, \cdots, n \end{gathered} $ | (2) |
式中,p为原始因子数,n为样本总数,σi为第i个指标的标准差。
2) 计算相关系数矩阵R=(aij)p×n,其中,
| $ a_{i j}=\frac{1}{n} \sum\limits_{k=1}^n\left(x_{i k}-\bar{x}_i\right)\left(x_{i k}-\bar{x}_i\right) / \sigma_i \sigma_j $ | (3) |
3) 计算特征方程|R-λI|=0中特征根λi及特征向量u1,u2,…,up。其中,I为单位矩阵,λ是特征值。
4) 计算贡献率,并确定因子中包含的信息:
| $ E_m=\sum\limits_{k=1}^m \lambda_k / \sum\limits_{k=1}^p \lambda_k $ | (4) |
5) 得到载荷矩阵A=(aij)p×m。因子分析中可根据需求对载荷矩阵A进行旋转,通常是正交矩阵右乘旋转。
6) 选取适合的新因子,计算综合指数为:
| $ W=E_i f_i $ | (5) |
针对平原地震区域的小震序列,选取图 1中常用的16种地震活动性参数进行相关性分析,结果如表 1(单位%)所示。地震活动性参数之间均存在一定的相关性,反映特征类似的参数相关性达70%以上,符合因子分析中研究样本冗余度特征的要求。在进一步的特征检验中,数据KMO检验统计量为0.816,说明数据之间的重叠度较高;Bartlett’s球型检验中,地震活动性参数之间的相伴概率P值小于设定的显著性水平0.05,独立性假设不成立。综上可知,平原地震区域的地震活动性参数符合因子分析方法对数据的要求。
|
|
表 1 16种地震活动性参数相关性分析 Tab. 1 Correlation analysis of 16 seismic activity parameters |
按照因子分析方法对原始的地震活动性参数进行重析,得到16个新因子。新因子是原始地震活动性参数经线性变换和旋转得到的反映原始参数公共信息的公因子,表 2为新产生的公因子的特征值与信息贡献情况。可以看出,重析后特征值大于1的前4个因子已经包含原16个地震活动性参数中超过80%的信息量,变换后公因子中同类信息更为集中。
|
|
表 2 新因子特征信息 Tab. 2 The characteristics of new factors |
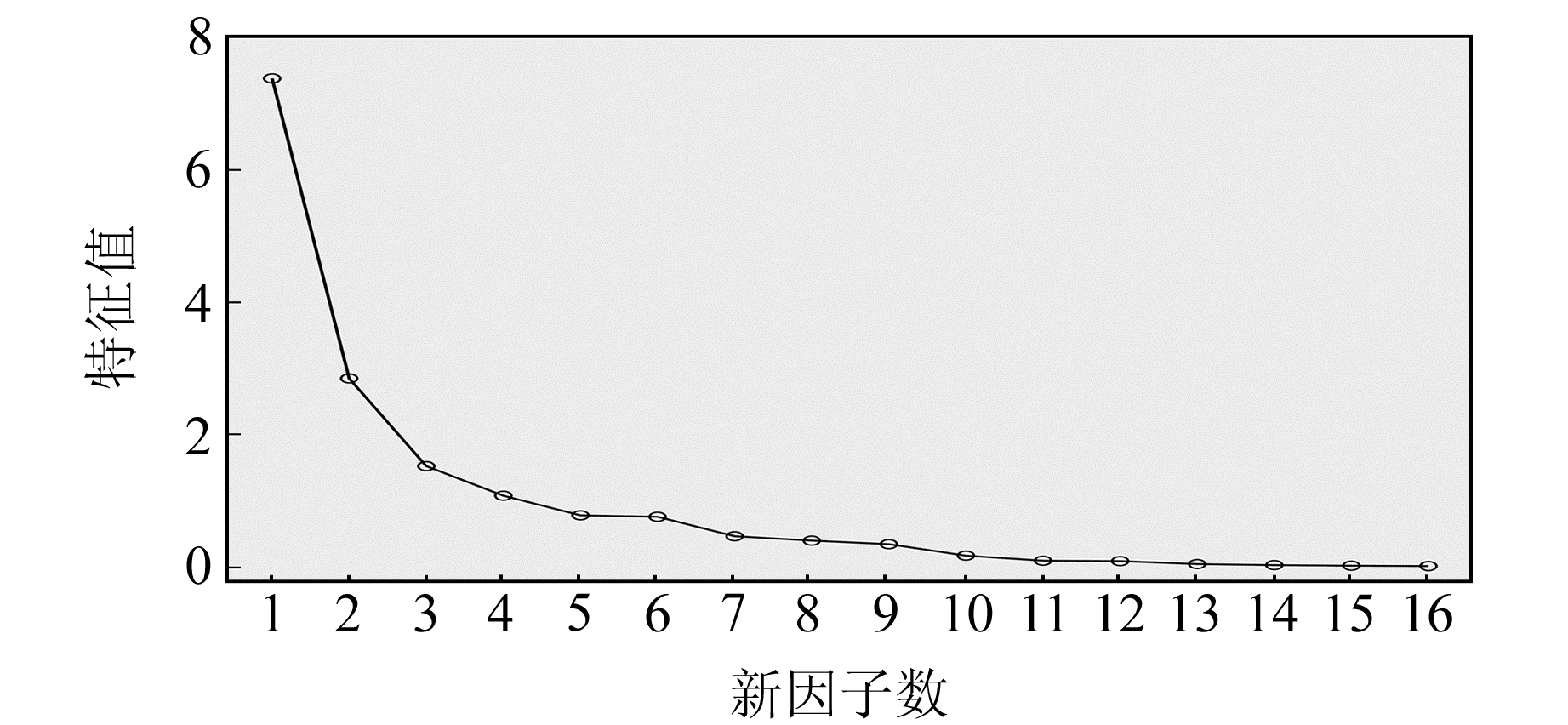
同时,应用碎石检验法[10]将平原地震区域地震活动性参数的特征值随因子数量的变化情况展示为碎石图。由图 3可见,随着因子数量的增多,特征值变化由陡峭变得平稳,而后变化不大,直观说明因子数增加不与信息量增加呈线性关系,特征值下降到1以下时更多因子的增加对整体趋势影响不大。
|
图 3 新因子碎石图 Fig. 3 Scree plot of the new factors |
在地震活动性分析中,同时分析16个参数的特征是极其复杂的,因此引入因子分析方法,将多参数中的信息旋转变化后集中于少量几个新产生的公因子中,通过分析几个代表性公因子或几个公因子的综合指数的变化,代替多参数的复杂分析。
本文选取前4个新因子(信息贡献率E累积80.14%)作为综合指数的计算基础因子,得到一个包含大部分有用信息的W参量。综合指数W中完全包含前4个新公因子的信息,同时舍弃了后12个信息含量少的公因子(包含不到20%信息量),后者之间的相关度低,所含信息偶然性强,对总体趋势的分析不具有决定性。
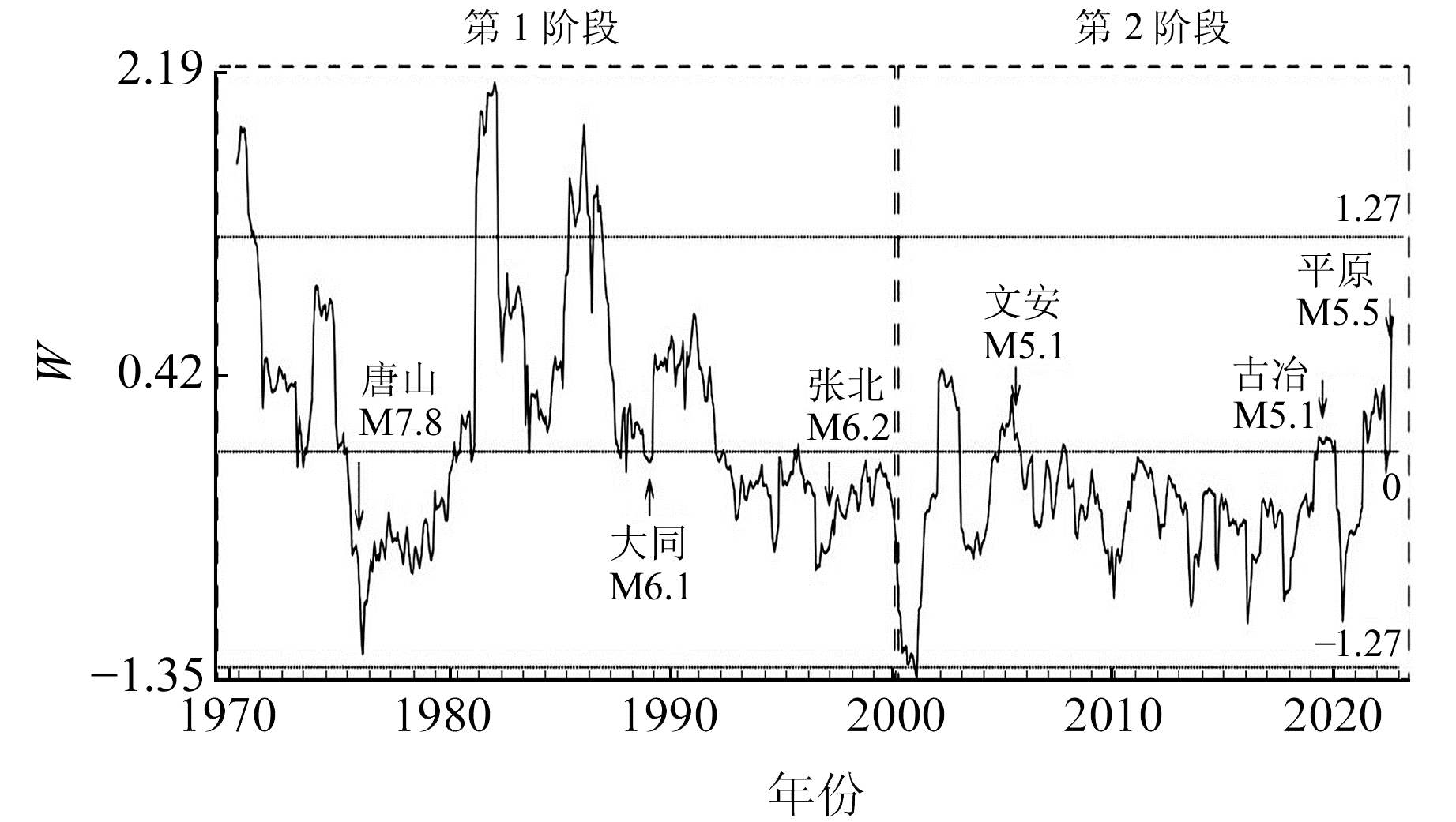
计算得到平原地震区域中小震序列的综合指数W随时间的变化曲线,如图 4所示,W的变化特征总体分为2个阶段:第1阶段为1970~1999年,综合指数W的变化幅度较大,出现多次超过2倍均方差的高值;第2阶段为2000年至今,综合指数W的变化幅度明显降低,大部分时间在平均线以下波动。这种阶段性特征与区域地震活动水平降低相关,1998年张北地震后华北地区进入平静幕,区内发生的最大地震为本次山东平原M5.5地震。
|
图 4 综合指数W随时间变化曲线 Fig. 4 Time variation of comprehensive factor W |
从震例特征分析,第1阶段华北地区6级地震发生前1~2 a,综合指数W均有不同程度的快速下降,其中变化最为剧烈的是1976年唐山M7.8地震,其次为1998年张北M6.2地震,而同一时段内周边5级地震前综合指数W值变化特征并不显著。第2阶段内平原地震周边500 km内无6级以上地震发生,5级以上地震发生3次,其中2006年河北文安M5.1地震和2020年唐山古冶M5.1地震均发生在综合指数W的相对高值区,而本次平原M5.5地震发生在综合指数W上升过程中,且平原地震前W值有数月小幅度降低。平原地震发生前后综合指数W的变化特征与第1阶段6、7级强震有一定相似性,但变化程度较小。
目前,综合指数W值上升至第2阶段的最高值,W值的阈值活动范围反映了区域地震活动水平,说明平原地震发生后区域整体的地震危险性有一定的抬升,但其活动幅度与6、7级地震活跃的第1阶段相比不高,说明危险程度未达到前一阶段的水平,后续应持续关注其变化。
4 平原地震区域单因子分析因子分析方法除综合多参数信息外,通过旋转特征值生成新因子的过程中,原始因子所含信息也按不同的方式重新组合。新因子分解了每个原始地震活动性参数的信息内容,将同质性高的归为一类,单因子指数是综合指数的不同特征的分解,其解释性更强。
表 3为本文计算综合指数时选取的4个公因子的信息含量表,表中给出不同单因子的信息来源及包含的每种原始地震活动性参数信息的含量。单一公因子中信息的同质性较强,其中单因子W1包含的信息主要来源于与地震强度和分布有关的地震活动性参数;单因子W2与b值、Mf值、A(b)值、P(b)值相关性大,一定程度上反映地下介质特征;单因子W3是地下介质特征和地震演化的综合表象;单因子W4则受调制地震和响应比影响更大。
|
|
表 3 单因子信息含量 Tab. 3 Values of the information content of single factors |
4种单因子参量随时间变化的曲线如图 5所示。单因子W1与综合指数W的特征几乎一致,原因是综合指数W中包含地震活动强度、能量的信息更多,起主导作用,与W1的重叠度高。而W1的变化阈值区间比综合指数W更大,说明W1中表现的地震强度信息更纯粹。

|
图 5 4种单因子随时间变化曲线 Fig. 5 Time variations of the 4 single factors |
单因子W2中贡献值最大的是b值等与地下介质相关的信息。由图 5可见,唐山地震前2 a单因子W2存在较长时段的低值异常,之后2018年出现过短暂的低值。2018年至今W2的阈值变化范围明显缩小,目前已接近1970年以来的最低值,如未来继续长时段保持低值,则说明区域地下介质发生变化,地震危险性将增强。
单因子W3也与地下介质相关,同时受地震演化特征的影响较大,其值在2009~2015年曾出现长时段的低值异常,推测与2008年汶川M8.0地震和2011年日本M9.0地震相关。W3所表现出的介质信息与区域外部受力特征相关性较大,而W2则更多反映区域内部介质特征的变化。
相对前3种单因子,W4中包含的信息量有一定程度的降低,主要受调制地震与响应比特征的影响,唐山地震前W4有显著升高,文安地震前则出现快速降低,张北地震、古冶地震和本次平原地震均无明显特征变化。
综合4种单因子参数特征可知,平原地震区域地震活动性水平正在升高,且区域地下介质有一定的变化,地震危险性有所增强。平原地震区域与华北地区地震活动性有明显的相关性,说明华北地区地震活动危险性也有增强趋势。
华北地区构造活动主要受太平洋板块俯冲作用的影响,同时印度板块向北的推挤作用力在大陆内部传递,使大陆西侧块体有明显的东向侧向运动,对华北地区也有一定的影响[11]。2008年汶川M8.0地震和2011年日本M9.0地震对华北地区地震活动影响明显,这在单因子W3的变化中有所反映。近几年日本区域和中国西部地区无特大地震事件发生,而W2时间序列可反映出区域内部介质有一定的变化,推测华北地区目前地震活动性增强。
5 结语山东平原M5.5地震震中位于华北中心地带,是华北地区地震活动较弱区域的一次显著地震活动。弱震区地震增强,说明周边地震应力有增强趋势。对平原地震区域中小震序列的地震活动性参数进行因子分析发现,综合指数W的变化存在2个阶段:以1998年张北M6.2地震为分界,此前的第1阶段(1970~1999年)指数W变化强烈,在强震发生前均有快速下降特征;而第2阶段(2000年至今) 整体活动水平较第1阶段显著下降,与1998年张北地震后华北地区进入地震平静幕相关。目前,平原地震区域的综合指数W值上升至第2阶段的最高值,且单因子分析表明,区域内部介质存在一定的变化。如综合指数W的变化阈值区间持续增大,预示未来华北地区可能开启新的活跃幕,应对区域序列变化进行持续跟踪。
| [1] |
朱红彬, 邢成起, 李红, 等. 华北构造区主要地震带分段与强震活动[J]. 地震学报, 2010, 32(6): 705-717 (Zhu Hongbin, Xing Chengqi, Li Hong, et al. Segmentation of Main Seismic Belts and Strong Earthquakes in North China Tectonic Region[J]. Acta Seismologica Sinica, 2010, 32(6): 705-717)
(  0) 0) |
| [2] |
廖武林, 张丽芬, 李井冈, 等. 弱震区弱活动断裂的地震危险性评价: 以丹江断裂为例[J]. 大地测量与地球动力学, 2017, 37(11): 1 131-1 135 (Liao Wulin, Zhang Lifen, Li Jinggang, et al. Assessment of Seismic Risk of Weakly Active Faults in Weak Seismic Background Region: Taking Danjiang Fault as an Example[J]. Journal of Geodesy and Geodynamics, 2017, 37(11): 1 131-1 135)
(  0) 0) |
| [3] |
薛艳, 姜祥华, 刘桂萍. 华北地区强震活动状态研究[J]. 地震, 2020, 40(2): 1-17 (Xue Yan, Jiang Xianghua, Liu Guiping. Active State and Trend on Strong Earthquakes in North China[J]. Earthquake, 2020, 40(2): 1-17)
(  0) 0) |
| [4] |
尹晓菲, 张国民, 邵志刚, 等. 华北地区强震活动特点研究[J]. 地震, 2020, 40(1): 11-33 (Yin Xiaofei, Zhang Guomin, Shao Zhigang, et al. Research on Activity Characteristics of Strong Earthquakes in North China[J]. Earthquake, 2020, 40(1): 11-33)
(  0) 0) |
| [5] |
易桂喜, 闻学泽. 多地震活动性参数在断裂带现今活动习性与地震危险性评价中的应用与问题[J]. 地震地质, 2007, 29(2): 254-271 (Yi Guixi, Wen Xueze. The Application and Limitation of Multiple Seismicity Parameters to Assessing Current Faulting Behavior and Seismic Potential of Active Fault Zones[J]. Seismology and Geology, 2007, 29(2): 254-271 DOI:10.3969/j.issn.0253-4967.2007.02.005)
(  0) 0) |
| [6] |
吕悦军, 陆远忠. 用算法复杂性分析时间序列[J]. 中国地震, 1993, 9(3): 229-234 (Lü Yuejun, Lu Yuanzhong. Characterization of Time Sequence by Algorithmic Complexity[J]. Earthquake Research In China, 1993, 9(3): 229-234)
(  0) 0) |
| [7] |
国家地震局预测预防司. 测震学分析预报方法[M]. 北京: 地震出版社, 1997 (Prediction and Prevention Department of the National Earthquake Administration. Seismic Analysis and Prediction Methods[M]. Beijing: Seismological Press, 1997)
(  0) 0) |
| [8] |
王炜, 林命週, 赵利飞, 等. 地震活动参数约简的因子分析方法[J]. 西北地震学报, 2006, 28(4): 303-308 (Wang Wei, Lin Mingzhou, Zhao Lifei, et al. Factor Analysis Method for Reducing Seismicity Parameters[J]. Northwestern Seismological Journal, 2006, 28(4): 303-308)
(  0) 0) |
| [9] |
王岩, 李彤霞, 钱蕊, 等. 主成分分析法在2013年灯塔MS5.1地震预测中的应用[J]. 地震地磁观测与研究, 2017, 38(5): 44-48 (Wang Yan, Li Tongxia, Qian Rui, et al. Prediction Study of Dengta MS5.1 Earthquake in 2013 Based on Principal Component Analysis[J]. Seismological and Geomagnetic Observation and Research, 2017, 38(5): 44-48)
(  0) 0) |
| [10] |
Cattell R B. The Scree Test for the Number of Factors[J]. Multivariate Behavioral Research, 1966, 1(2): 245-276 DOI:10.1207/s15327906mbr0102_10
(  0) 0) |
| [11] |
刘泽民, 倪红玉, 张炳, 等. 板块边界构造应力场的反演及其对华北地震的影响研究[J]. 地震, 2014, 34(1): 87-96 (Liu Zemin, Ni Hongyu, Zhang Bing, et al. Inversion of Plate Boundary Tectonic Stress Field and Its Effect on Earthquakes in North China[J]. Earthquake, 2014, 34(1): 87-96)
(  0) 0) |
 2024, Vol. 44
2024, Vol. 44

