2. 湖北工业大学土木建筑与环境学院,武汉市南李路28号,430068
地震动参数在地震危险性评估中至关重要,它受震源特性、传播路径及场地条件等多种因素的影响。鉴于地震活动的非线性特征,建立地震动参数与其他地震学变量之间的直接联系颇具挑战。在地震活动频繁且具备丰富强震观测数据的区域,一般使用非线性回归技术构建地震动预测方程[1-2]。然而,对于涉及多个异常值的高维地震数据分析,传统回归方法往往效果不佳。相比之下,基于人工智能的机器学习技术能够通过自适应学习从数据中提取特定模式,为处理非线性问题提供优化方案。如Ahmad等[3]用神经网络方法预测欧洲大陆的地震动峰值加速度;Giacinto等[4]使用基于神经网络方法的统计模式识别算法建立地震动风险评价模型;游姗等[5]基于自适应神经模糊推理方法提出一种竖向地震动参数预测技术。但这些方法难以提供显式预测公式,在工程实践中可能带来不便。
基于以上研究,本文尝试基于美国太平洋地震工程研究中心(PEER)的NGA数据库,利用遗传编程技术,给出一套地震动峰值加速度、峰值速度和峰值位移的预测方程。首先,建立地震动参数与震级、断层距、断层机制以及30 m内的场地剪切波速度等关键地震学参数的关联,并以此为基础给出地震动参数的显式预测公式;然后,通过信度检验和模型比对,确认研究方法的有效性和研究结果的准确性。
1 遗传编程技术本文将遗传编程技术用于建立地震动参数预测方程,通过对数据表达式的自动识别给出预测方程的显式公式。遗传编程是一种有效的函数建模方法,其优势主要在于函数结构的灵活性,其常采用的树形结构可以通过对所描述问题进行层次化来解决传统方法中难以确定函数结构的问题[6]。该方法的优点在于不需要给出具体的函数形式即可获得所拟合函数的表达式,同时在初始群体足够大且交叉和变异概率设置合理的情况下,确保模型不会陷入局部最优。
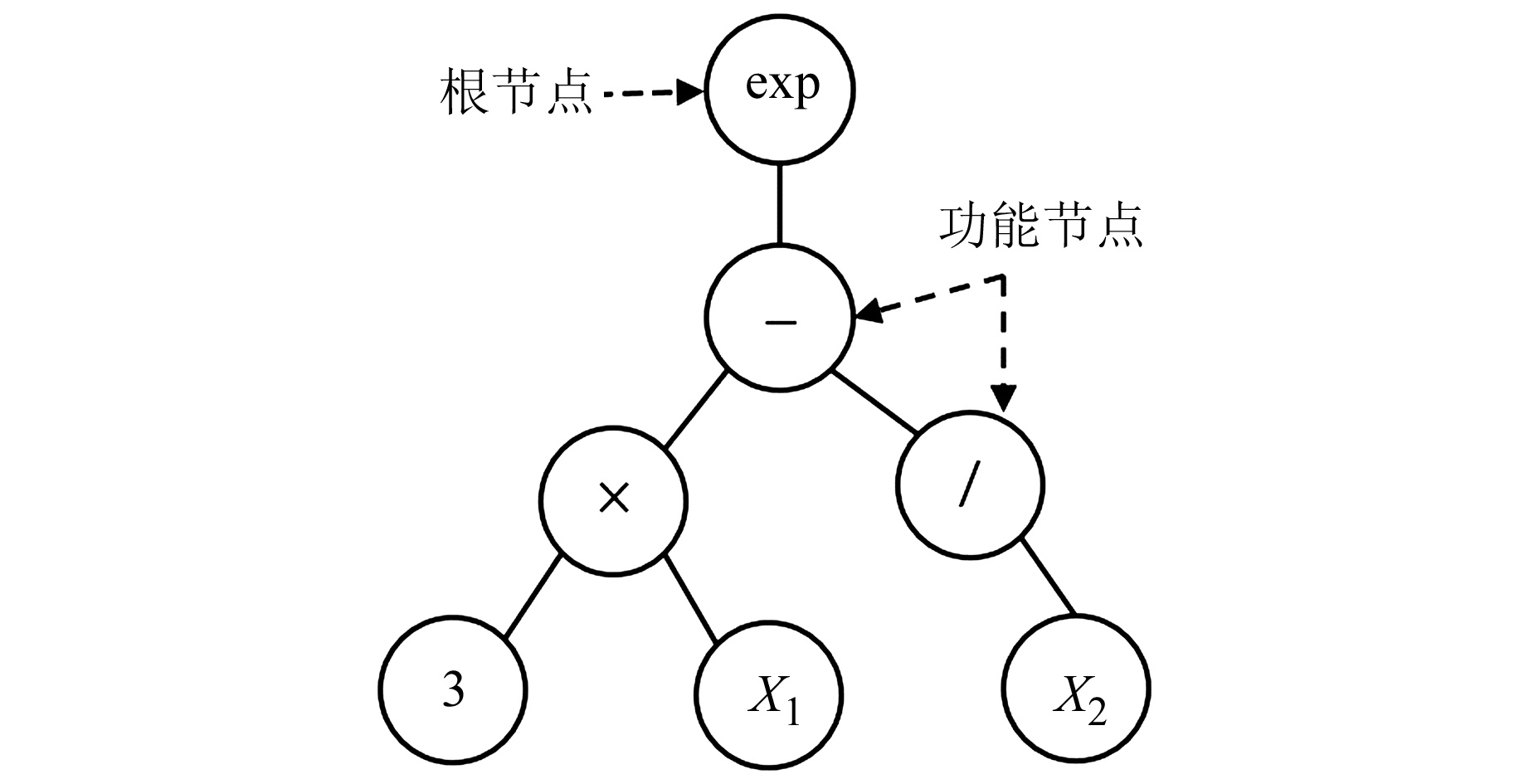
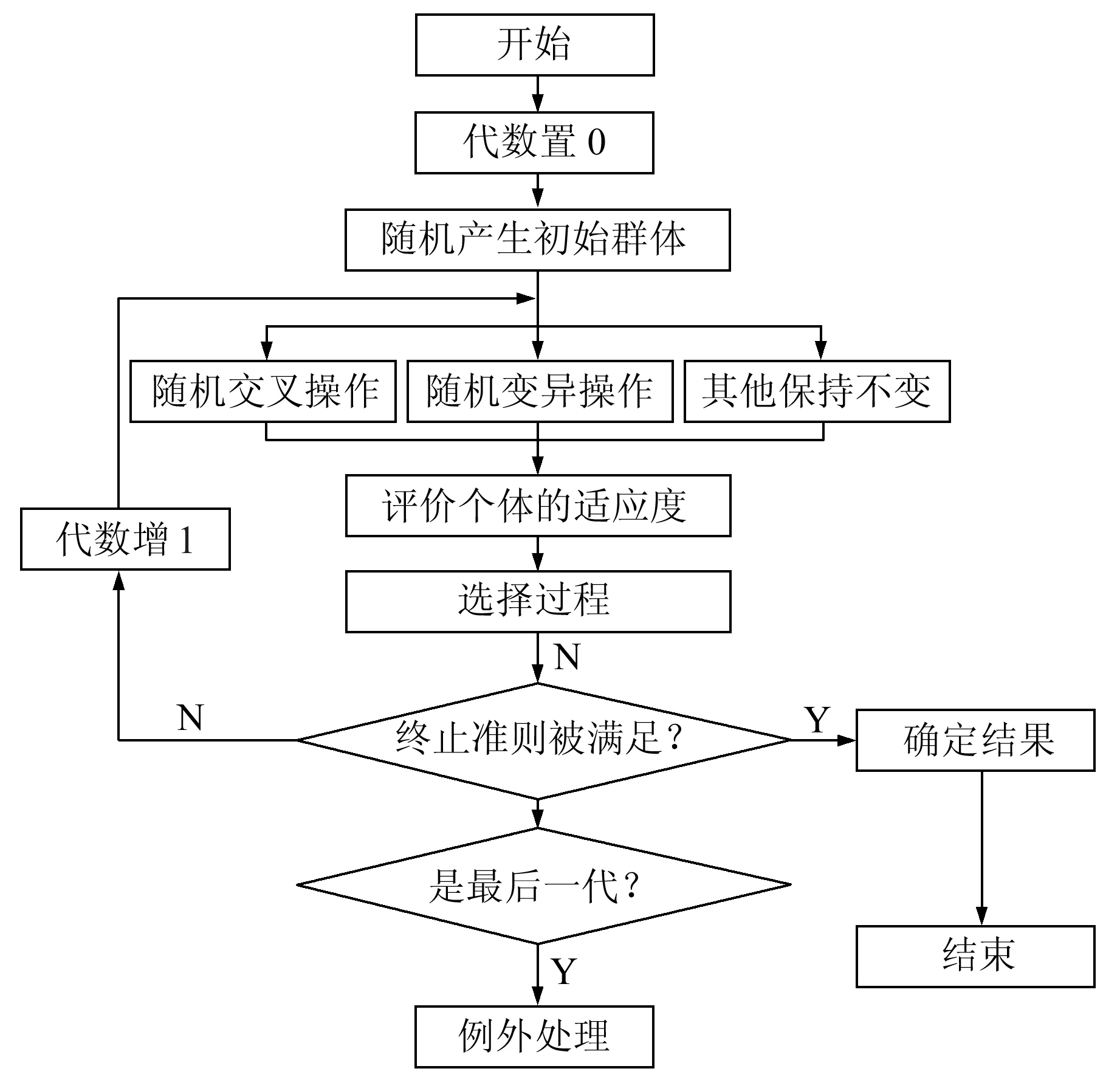
遗传编程的基本思想是,随机产生一个适合给定环境的初始群体,即问题的搜索空间。与遗传算法类似,构成群体的个体都有一个适应度值,依据达尔文适者生存原则,用遗传算子处理得到的高适应度个体去产生下一代的群体。如此一直进化,给定问题的解或近似解将在某一代出现。图 1和表 1给出了遗传编程的简单树形解决方案[7]及其基本参数,其算法流程如图 2所示。
|
图 1 遗传编程的树形示意图 Fig. 1 Tree schematic of the genetic programming |
|
|
表 1 遗传编程基本参数 Tab. 1 Basic parameters of genetic programming |
|
图 2 遗传编程流程 Fig. 2 Genetic programming flowchart |
地震动参数在结构抗震设计中起着至关重要的作用。从地震工程学的角度,地震动参数可以分为幅值、频谱和持时3类。地震动预测方程通常根据有效的决策变量(如震级、断层距、场地条件、震源特征和传播路径)来估算这些参数。对地震动参数影响较大的因素主要有震源效应、路径效应和场地效应[8]。震源条件通常与发震断层类型有关,场地条件通常使用场地30 m内剪切波速度替代。本文尝试使用遗传编程技术来获得地震动参数的预测方程,地震动峰值加速度PGA、峰值速度PGV和峰值位移PGD的计算公式为:
| $ \ln \mathrm{PGA}, \ln \mathrm{PGV}, \ln \mathrm{PGD}=f\left(M_W, \ln R, V_{\mathrm{S} 30}, \lambda\right) $ | (1) |
式中,MW为矩震级,R为断层距,VS30为场地30 m内的剪切波速度,λ为表征震源机制的参数,在走滑、正断和逆断机制下的取值分别为0.25、-1和1[9]。
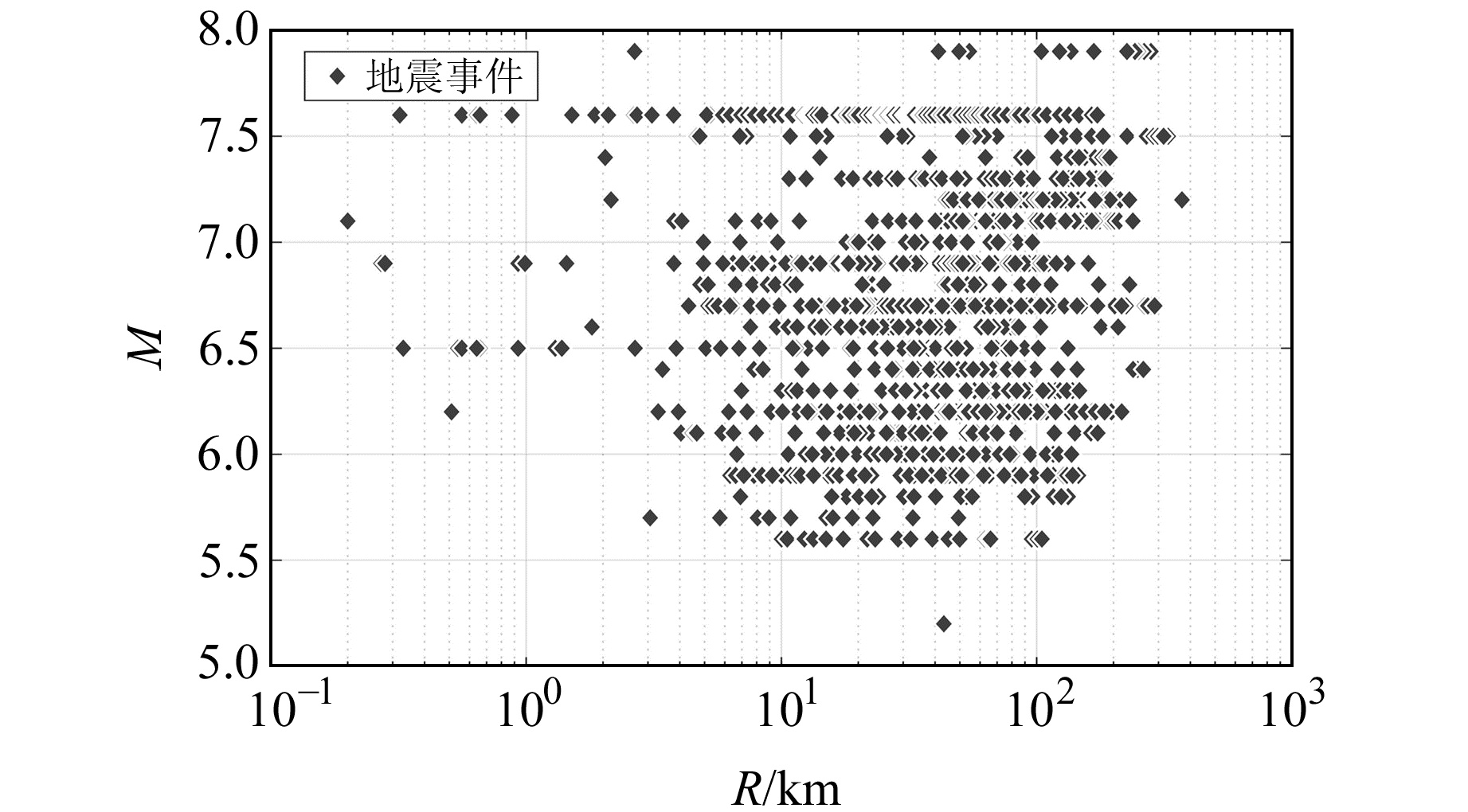
2.1 强地震动数据基于NGA数据库,采用Boore-Atkinson数据集[10],获得2 815条地震观测波形记录,其中训练数据集包含2 393个观测波形,测试数据集包含422个形波。尝试使用遗传编程方法将最合适的函数与地震动观测结果相匹配,建立地震动加速度反应谱的显式预测方程。
|
图 3 NGA地震事件集的断层距与震级 Fig. 3 Fault distance and magnitude for the NGA seismic events set |
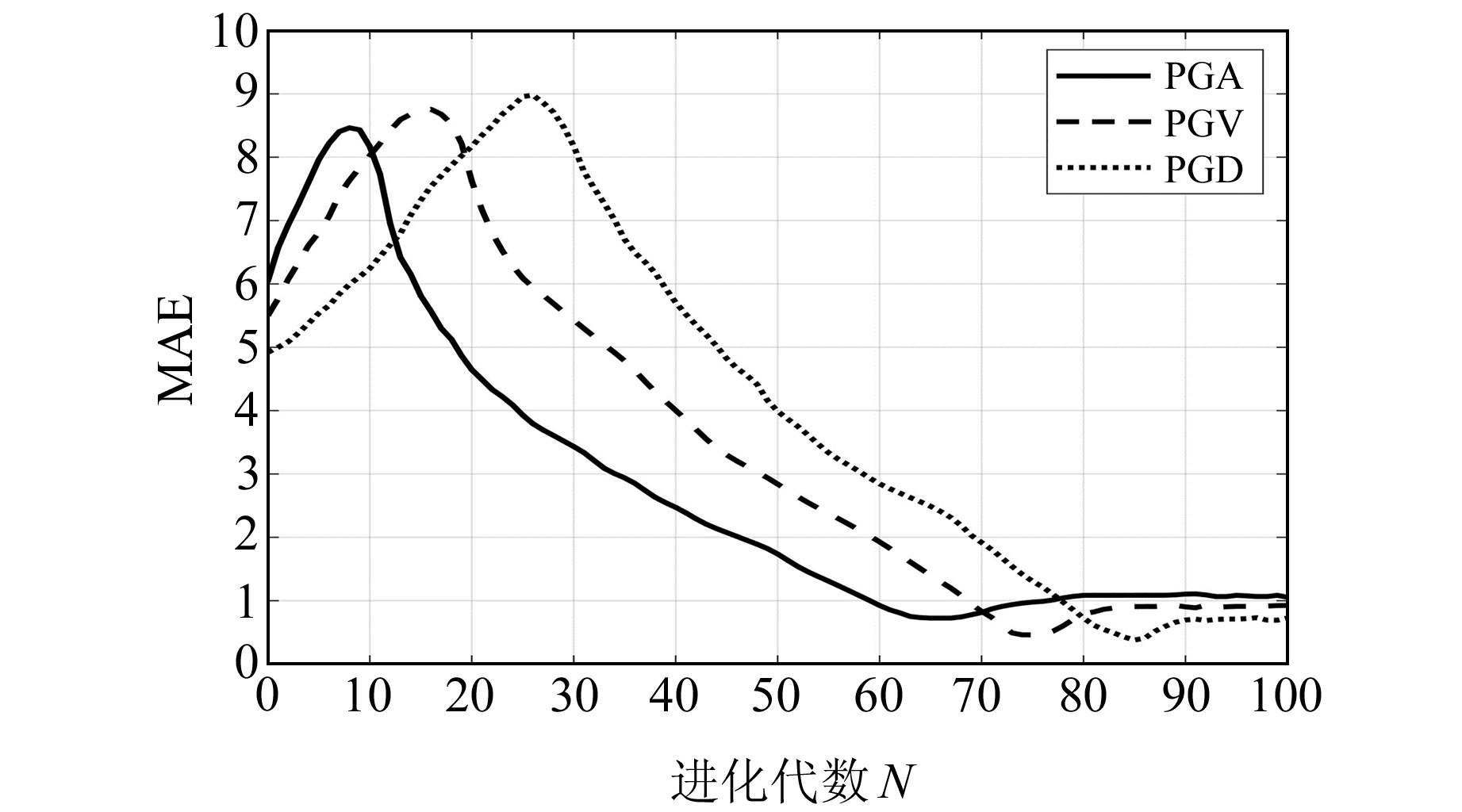
基于MATLAB环境下的Gptips工具箱[11-12],使用遗传编程方法得到3类地震动参数的显式预测方程。图 4给出了训练数据集下不同进化代数时3类地震动参数预测模型最佳个体的平均绝对误差MAE的收敛情况。
|
图 4 最佳个体平均绝对误差的进化收敛情况 Fig. 4 Evolutionary convergence of the mean absolute error of the best individual |
由图 4可见,随着进化代数的增加,3类地震动参数预测模型最佳个体的平均绝对误差在整体上呈现出快速增加而后收敛走平的特点。其中,PGA、PGV和PGD分别在进化代数N为65、74和86时取得最小MAE,分别约为0.751、0.472和0.377,其显式地震动预测方程如式(2)~(4)。表 2进一步给出3类地震动对应的地震动预测方程的参数取值。从图 4还可以看出,PGA在较小的进化代数时取得全局最优,而PGV、PGD则需要更多的进化代数,其数学表达式也呈现出更加复杂的形式:
| $ \begin{gathered} \operatorname{lnPGA}= \\ C_1-\ln R+C_2(\ln R)^2+C_3 M_W \ln R+\frac{C_4}{V_{\mathrm{S} 30}}+\frac{(\ln R)^3}{V_{\mathrm{S} 30}}+\frac{C_5}{C_6-V_{\mathrm{S} 30}+C_7 V_{\mathrm{S} 30} \lambda+\frac{V_{\mathrm{S} 30}}{M_{\mathrm{W}}+C_8}} \end{gathered} $ | (2) |
| $ \begin{aligned} & \ln \mathrm{PGV}=M_W-\ln R- \\ & \frac{C_1}{\left(C_2+\frac{\ln R\left[C_5 \ln R+C_6 M_W+M_W\left(\ln R+C_7\right)\left(C_5 \ln R-M_W+C_8\right)+M_W \ln R \lambda\right]}{C_3 M_W \lambda-V_{\mathrm{S} 30}+C_4}\right)} \\ & \end{aligned} $ | (3) |
| $ \begin{gathered} \ln \mathrm{PGD}=C_2+M_W+ \\ \frac{C_1\left(M_W-\ln R\right)}{C_3+\frac{\ln R}{C_2+\ln R+M_W^2 / \ln R}+\frac{M_W \ln R\left(M_W+C_7\right)\left(C_6 M_{\mathrm{W}}+C_8 \ln R\right)}{C_4-(\ln R)^2-\lambda+V_{\mathrm{S} 30}+C_4 M_W\left(M_W+C_5\right)}} \end{gathered} $ | (4) |
|
|
表 2 地震动参数预测方程的显式参数 Tab. 2 Explicit parameters of prediction equations for ground motion parameters |
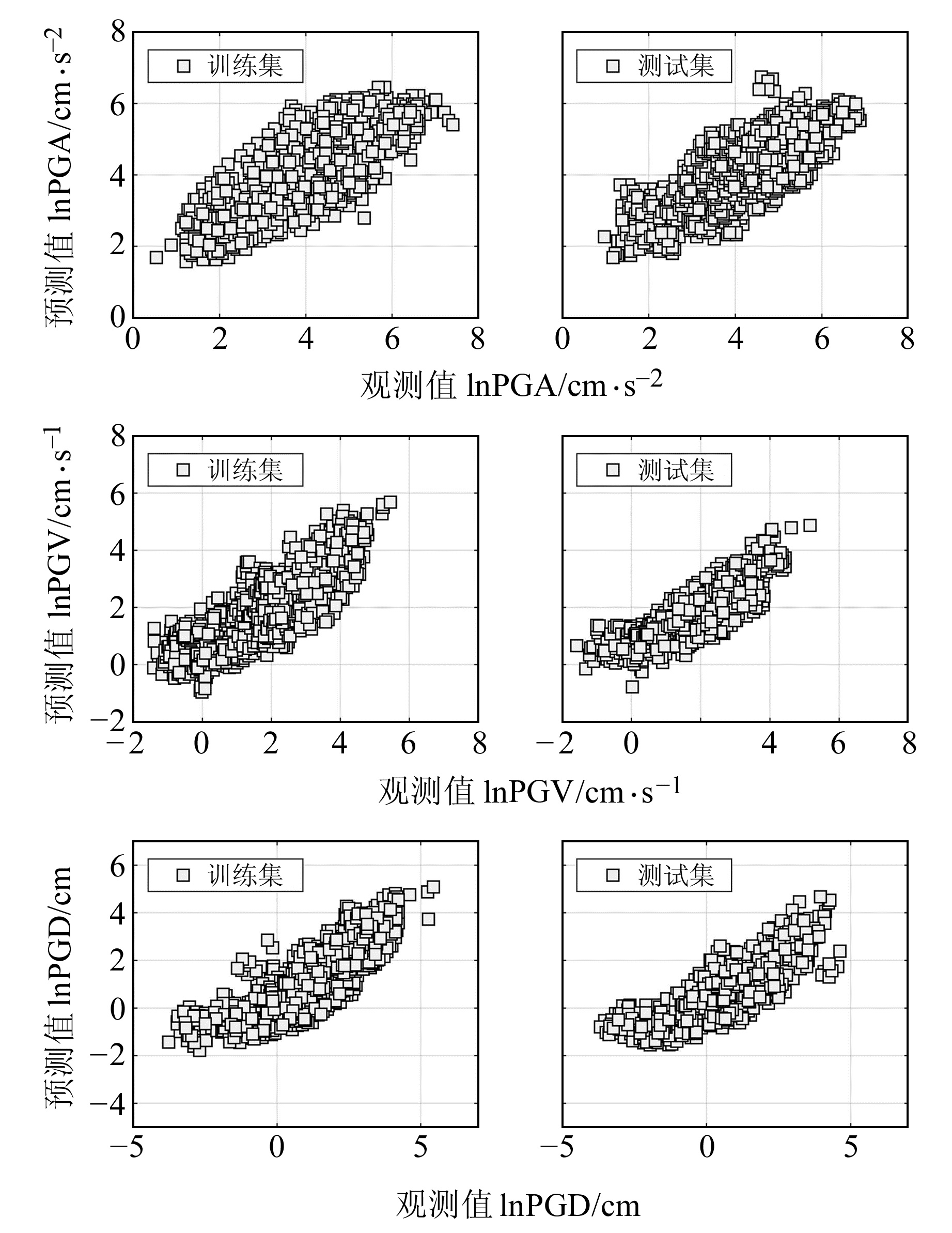
在获得地震动参数显式预测公式后,进一步开展信度检验工作,PGA、PGV和PGD的观测值与预测值在训练集和测试集下的分布情况如图 5所示。以此为基础,使用均方根误差(RMSE)、平均绝对误差(MAE)和相关系数(r)对模型的准确性进行评价。其中,RMSE重点检测预测值与实际观测值之间的距离;MAE计算残差平均值,而不考虑其方向;r评估真实观测数据与预测数据之间的相关性。值得注意的是,为了方便信度检验和误差分析,在建立RMSE和MAE两类评价函数的过程中,对其进行无量纲化处理,以表征被评价对象相对于总体某一对比标准的相对地位:
| $ \mathrm{RMSE}=\sqrt{\frac{1}{n} \sum\limits_{j=1}^n\left(y_j-Y_j\right)^2} $ | (5) |
| $ \text { MAE }=\frac{1}{n} \sum\limits_{j=1}^n\left|y_j-Y_j\right| $ | (6) |
| $ r=\frac{\sum\limits_{j=1}^n\left(y_j-\bar{y}\right)\left(Y_j-\bar{Y}\right)}{\sqrt{\frac{1}{n} \sum\limits_{j=1}^n\left(y_j-\bar{y}\right)^2\left(Y_j-\bar{Y}\right)^2}} $ | (7) |
式中,n为数据点总数,yj为第j个观测值,Yj为第j个预测值。
表 3给出了训练集和测试集下的3类地震动参数的信度检验结果。由表 3和图 5可见,PGA、PGV、PGD在训练集、测试集下的相关系数分别为0.856、0.847、0.836和0.843、0.831、0.812,PGA、PGV和PGD的相关系数逐渐减小,说明模型对PGA具有最强的预测效果,PGV次之,PGD则相对最弱。同时可见,模型对训练集的拟合效果小幅优于测试集,但测试集和训练集下的r值均大于0.8,说明模型获得的地震动预测值与实际观测值具有较好的相关性[13]。
|
|
表 3 训练集和测试集下地震动参数的信度检验结果 Tab. 3 Confidence test results of ground motion parameters under training and test sets |
|
图 5 PGA、PGV和PGD的观测值与预测值分布 Fig. 5 Distribution of observed and predicted values of PGA, PGV and PGD |
PGA、PGV和PGD在训练集和测试集下的RMSE分别为0.589、0.735、0.852和0.614、0.782、0.882;MAE分别为0.377、0.472、0.751和0.542、0.624、0.821。RMSE和MAE均呈现出训练集表现优于测试集的特征。PGA、PGV、PGD预测方程的RMSE和MAE逐步增大,说明基于遗传编程技术获得的地震动预测方程对地震动高频分量(PGA)的预测效果优于地震动低频长周期分量(PGD)。但总体而言,预测值与观测值之间的相关性大于0.8,且误差值较小,说明地震动预测模型具有较好的预测能力和泛化性能[13]。
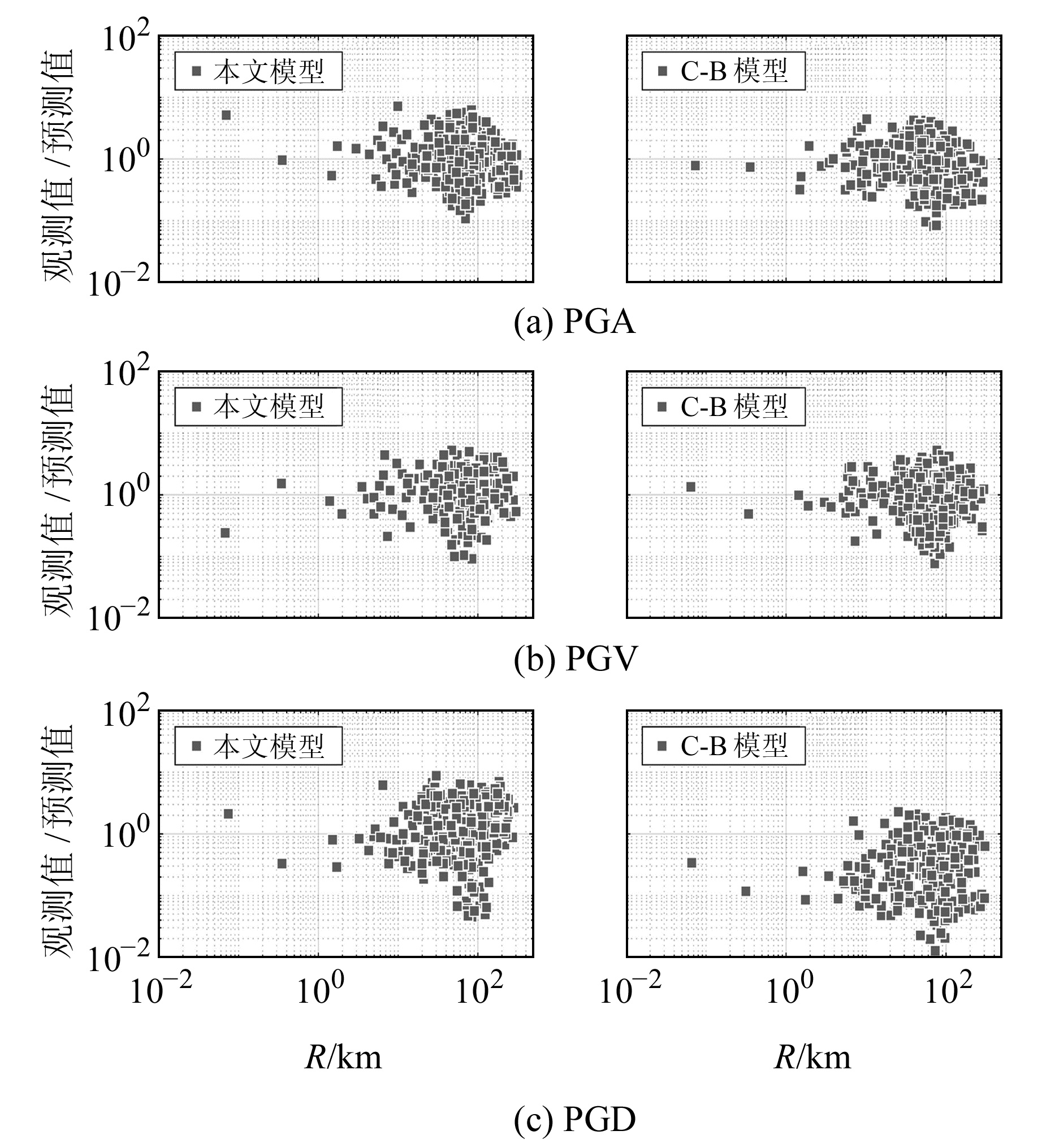
3.2 模型对比为探讨本文提出的地震动预测模型与现有地震动衰减关系之间的差异,将本文模型与Campbell等[9]基于NGA数据库提出的PGA、PGV和PGD经验模型(简称C-B模型)进行对比。表 4和图 6给出了两种模型观测值与预测值的残差分布和不确定性分析结果。可以看出,本文提出的PGA和PGV预测模型的RMSE和MAE均略小于C-B模型的结果,说明本文模型对PGA和PGV的预测能力略优于C-B模型。
|
|
表 4 两种模型的残差对比结果 Tab. 4 Comparison results of residuals of the two models |
|
图 6 两种地震动预测模型的残差分布 Fig. 6 Residuals distribution of two ground motion prediction models |
对于表征地震动长周期分量的地震动峰值位移而言,其残差分布呈现出与短周期分量较大的差异性。由图 6可见,本文模型获得的PGD观测值与预测值之比整体位于1附近,而C-B模型则明显位于1之下,说明后者获得的预测值明显偏大。本文PGD预测模型的RMSE和MAE分别为5.47及1.64,显著小于C-B模型的45.98和4.61,说明本文模型对于PGD的预测效果更好。
需要指出的是,基于遗传编程方法建立的显式函数结构与C-B模型相比更为复杂,但总体而言,经过信度检验和模型对比之后,基于遗传编程方法获得的显式地震动参数预测方程可以较好地反映震级、断层距、震源机制以及场地条件对PGA、PGV和PGD的影响,其输入参数具有较为明确的物理意义。
3.3 敏感性分析为评估不同预测变量对地震动参数预测结果的影响,利用Gandomi等[14]提出的遗传编程参数敏感性分析方法,计算得到残差最小的40个表达式中各类预测变量的出现频率,如表 5所示。
|
|
表 5 最佳地震动预测模型组中预测变量的出现频率 Tab. 5 Frequency of occurrence of predictor variables in the set of best ground motion prediction models |
由表 5可见,震级M和断层距R出现在最佳地震动预测模型组中,表明这两个预测变量会对地震动参数的PGA、PGV和PGD产生重要影响。场地剪切波速在PGA、PGV和PGD最佳模型组中的出现频率分别为0.575、0.650和0.700,与场地软硬对于远场长周期分量的影响作用更大的认识一致。需要注意的是,虽然表征震源机制的参数的出现频率较低,但不能据此简单地认为震源机制的影响较小,尤其是对断层距R≤15 km范围内的近场地震动,需展开进一步研究。
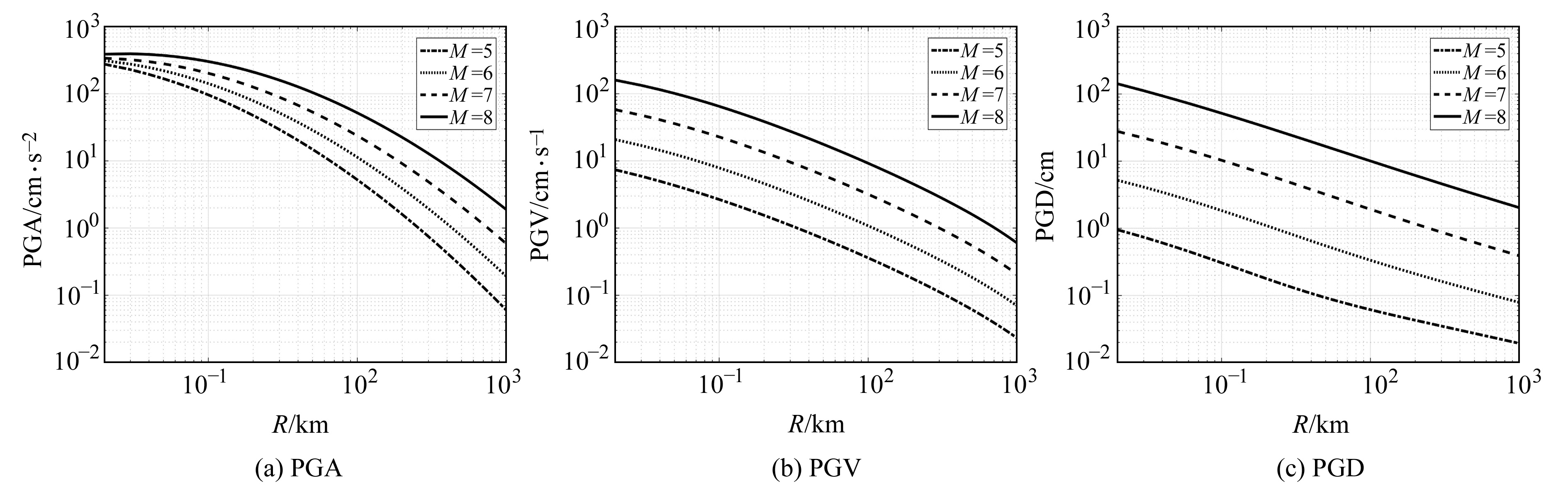
4 地震动衰减特征分析在上述信度检验与模型对比的基础上,对基于遗传编程技术获得的地震动预测模型的衰减特征进行分析。按照地震工程实际,给出M5.0以上破坏性地震作用下基岩场地(VS=700 m/s)处PGA、PGV和PGD随震级M和断层距R的衰减情况,如图 7所示。
|
图 7 基岩场地条件下地震动PGA、PGV和PGD的衰减情况 Fig. 7 PGA, PGV and PGD attenuation of ground motion under the condition of bedrock |
由图 7可见,近断层区域内,随着地震动PGA的增大,震级的增大呈现出大震近场震级饱和的特征。但随着震级的增大和距离的减小,PGV和PGD的增大速度慢于PGA,并未出现明显的过饱和现象。同时可见,PGA的近场衰减速度明显小于远场,而PGV和PGD则在近场和远场呈现出对数坐标下的线性衰减特征。与长周期地震动分量相比,上述特征说明高频分量在远场处具有更快的衰减速度,符合地震工程学的认识[15]。
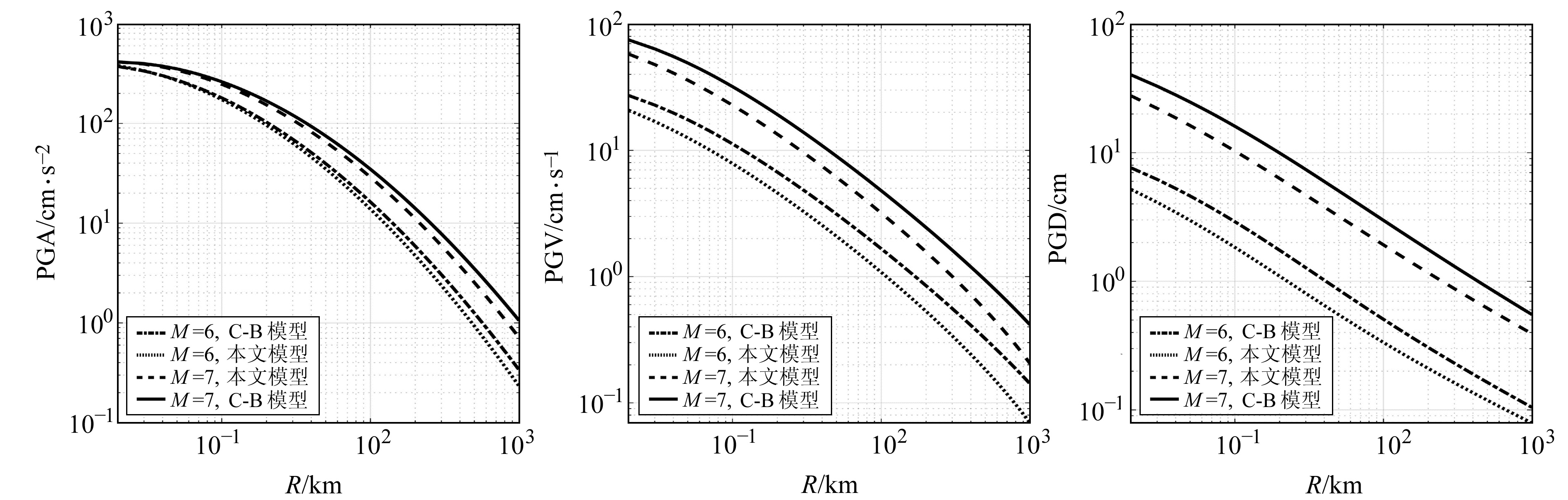
为进一步探讨本文模型与C-B模型的地震动衰减特征的差异,选择训练数据集中震级分布最集中的M=6和M=7,给出其随断层距R增大的计算结果,如图 8所示。从图 8可以看出,C-B模型的衰减关系预测结果与本文结果相比整体偏大,PGA一致性相对较好,而PGV和PGD则更倾向于安全保守。可见,基于遗传编程方法获得的地震动预测方程在保证较高预测精度的同时具备较好的经济性。
|
图 8 C-B模型与本文模型衰减关系的对比 Fig. 8 Comparison of attenuation relationship between C-B model and model in this paper |
为进一步研究本文地震动参数的场地放大效应,以基岩场地(VS30=1 000 m/s)处的地震动参数为基准,计算不同VS30条件下的3类地震动参数的放大系数,如图 9所示。
|
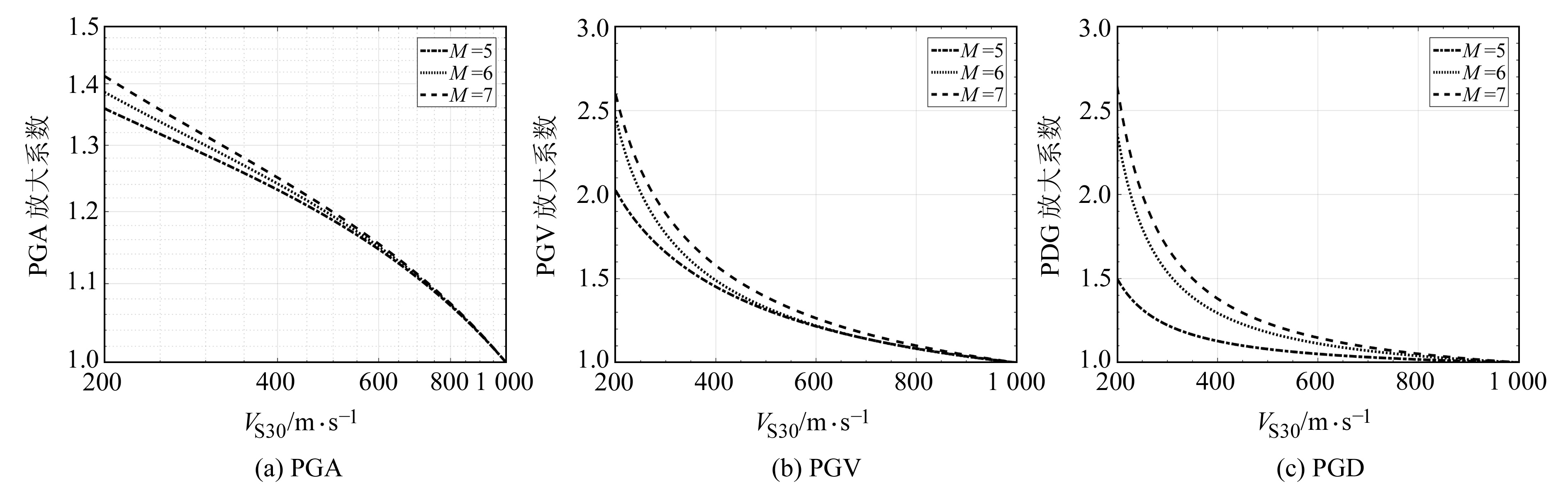
图 9 R=25 km时PGA、PGV和PGD的场地放大效应 Fig. 9 Site amplification effect of PGA, PGV and PGD at R=25 km |
从图 9可以发现,在200 m/s < VS30 < 1 000 m/s范围内,随着场地剪切波速的减小,所有震级条件下的放大系数均呈现出不断增大的趋势。PGA、PGV和PGD的最大放大系数约为1.42、2.53和2.64,且均在VS30=200 m/s处取得极大值,说明软土场地对于长周期地震动分量的放大效应高于高频地震动分量。同时可以发现,随着震级的增大,相同剪切波速条件下PGA、PGV和PGD的场地放大系数均有所增加,但是震级条件的变化对3类地震动参数的影响作用具有较为显著的差别。就放大系数的极值而言,PGA、PGV和PGD的取值范围分别为[1.36, 1.42]、[2.00, 2.53]和[1.49, 2.64],PGD放大系数的分布较前二者更加离散,说明震级变化对长周期地震动的场地效应的放大效应的复杂性具有更加显著的作用[16]。此外,需要指出的是,本文使用遗传编程技术获得的地震动预测方程未能在200 m/s以下的淤泥质软土场地条件下观测到显著的软土减震效应[15]。其原因可能为所用NGA强地震动数据集包含的淤泥质软土场地波形数量不足,说明基于遗传编程技术获得地震动预测方程的方法对于输入数据具有较高的依赖性,值得进一步探讨。
5 结语本研究利用遗传编程技术,基于NGA数据库给出一套地震动峰值加速度、峰值速度和峰值位移的预测方程。将3类地震动参数与关键地震学参数相关联,包括震级、断层距、断层机制以及30 m内的场地剪切波速度,在给出其显式预测公式的基础上,通过信度检验及模型对比,对研究方法的有效性进行确认。主要结论如下:
1) 与Campbell-Bozorgnia衰减关系相比,基于遗传编程技术的PGA与PGV预测效果略优,PGD预测模型的RMSE和MAE分别为5.47和1.64,显著小于Campbell-Bozorgnia模型的45.98和4.61,说明本文模型对长周期地震动分量的预测效果更佳,可以应用于实际地震工程。
2) 基于遗传编程技术的地震动参数预测方程获得的地震动衰减特征具备震级效应、场地放大效应和PGA的近场大震饱和效应特征,但尚未反映出足够的软土减震效应特征,可能与所用训练数据集中淤泥质粘土场地的地震观测波形数据较少有关。这种对训练数据依赖所带来的不确定性值得进一步研究。
| [1] |
俞言祥, 李山有, 肖亮. 为新区划图编制所建立的地震动衰减关系[J]. 震灾防御技术, 2013, 8(1): 24-33 (Yu Yanxiang, Li Shanyou, Xiao Liang. Development of Ground Motion Attenuation Relations for the New Seismic Hazard Map of China[J]. Technology for Earthquake Disaster Prevention, 2013, 8(1): 24-33)
(  0) 0) |
| [2] |
汪素云, 俞言祥, 高阿甲, 等. 中国分区地震动衰减关系的确定[J]. 中国地震, 2000, 16(2): 99-106 (Wang Suyun, Yu Yanxiang, Gao Ajia, et al. Development of Attenuation Relations for Ground Motion in China[J]. Earthquake Research in China, 2000, 16(2): 99-106)
(  0) 0) |
| [3] |
Ahmad I, El Naggar M H, Khan A N. Neural Network Based Attenuation of Strong Motion Peaks in Europe[J]. Journal of Earthquake Engineering, 2008, 12(5): 663-680 DOI:10.1080/13632460701758570
(  0) 0) |
| [4] |
Giacinto G, Paolucci R, Roli F. Application of Neural Networks and Statistical Pattern Recognition Algorithms to Earthquake Risk Evaluation[J]. Pattern Recognition Letters, 1997, 18(11-13): 1 353-1 362 DOI:10.1016/S0167-8655(97)00088-3
(  0) 0) |
| [5] |
游姗, 胡其志, 张洁, 等. 基于自适应神经模糊推理的竖向地震动参数预测模型[J]. 大地测量与地球动力学, 2023, 43(5): 517-522 (You Shan, Hu Qizhi, Zhang Jie, et al. A Method Based on Adaptive Neuro Fuzzy Inference System to Predict Vertical Ground Motion Parameters[J]. Journal of Geodesy and Geodynamics, 2023, 43(5): 517-522)
(  0) 0) |
| [6] |
于鹏, 王京. 数据插值技术对基于遗传编程算法符号回归的影响研究[J]. 江西师范大学学报: 自然科学版, 2014, 38(3): 286-289 (Yu Peng, Wang Jing. The Research of the Influence of Data Interpolating Technology on Symbolic Regression Based on Genetic Programming[J]. Journal of Jiangxi Normal University: Natural Science Edition, 2014, 38(3): 286-289)
(  0) 0) |
| [7] |
金金宝, 吴萍. 遗传编程在符号回归中的应用[J]. 计算机与数字工程, 2009, 37(5): 13-16 (Jin Jinbao, Wu Ping. Genetic Programming and Its Applications in the Symbolic Regression[J]. Computer and Digital Engineering, 2009, 37(5): 13-16)
(  0) 0) |
| [8] |
刘启方, 袁一凡, 金星, 等. 近断层地震动的基本特征[J]. 地震工程与工程振动, 2006, 26(1): 1-10 (Liu Qifang, Yuan Yifan, Jin Xing, et al. Basic Characteristics of Near-Fault Ground Motion[J]. Earthquake Engineering and Engineering Vibration, 2006, 26(1): 1-10)
(  0) 0) |
| [9] |
Campbell K W, Bozorgnia Y. Campbell-Bozorgnia NGA Ground Motion Relations for the Geometric Mean Horizontal Component of Peak and Spectral Ground Motion Parameters[R]. Pacific Engineering Research Center, University of California, Berkeley, 2007
(  0) 0) |
| [10] |
Boore D M, Atkinson G M. Boore-Atkinson NGA Ground Motion Relations for the Geometric Mean Horizontal Component of Peak and Spectral Ground Motion Parameters[R]. Pacific Engineering Research Center, University of California, Berkeley, 2007
(  0) 0) |
| [11] |
Baykasoǧlu A, Güllü H, Çanakçı H, et al. Prediction of Compressive and Tensile Strength of Limestone via Genetic Programming[J]. Expert Systems with Applications, 2008, 35(1-2): 111-123 DOI:10.1016/j.eswa.2007.06.006
(  0) 0) |
| [12] |
Alavi A H, Gandomi A H, Modaresnezhad M, et al. New Ground-Motion Prediction Equations Using Multi Expression Programing[J]. Journal of Earthquake Engineering, 2011, 15(4): 511-536 DOI:10.1080/13632469.2010.526752
(  0) 0) |
| [13] |
Pan Y, Jiang J C, Wang R, et al. A Novel QSPR Model for Prediction of Lower Flammability Limits of Organic Compounds Based on Support Vector Machine[J]. Journal of Hazardous Materials, 2009, 168(2-3): 962-969 DOI:10.1016/j.jhazmat.2009.02.122
(  0) 0) |
| [14] |
Gandomi A H, Alavi A H, Sahab M G. New Formulation for Compressive Strength of CFRP Confined Concrete Cylinders Using Linear Genetic Programming[J]. Materials and Structures, 2010, 43(7): 963-983 DOI:10.1617/s11527-009-9559-y
(  0) 0) |
| [15] |
薄景山, 李秀领, 李山有. 场地条件对地震动影响研究的若干进展[J]. 世界地震工程, 2003, 19(2): 11-15 (Bo Jingshan, Li Xiuling, Li Shanyou. Some Progress of Study on the Effect of Site Conditions on Ground Motion[J]. World Information on Earthquake Engineering, 2003, 19(2): 11-15)
(  0) 0) |
| [16] |
李小军, 彭青. 不同类别场地地震动参数的计算分析[J]. 地震工程与工程振动, 2001, 21(1): 29-36 (Li Xiaojun, Peng Qing. Calculation and Analysis of Earthquake Ground Motion Parameters for Different Site Categories[J]. Earthquake Engineering and Engineering Vibration, 2001, 21(1): 29-36)
(  0) 0) |
2. School of Civil Engineering Architecture and Environment, Hubei University of Technology, 28 Nanli Road, Wuhan 430068, China
 2024, Vol. 44
2024, Vol. 44


