地下水温度异常观测是地震短临预测预报的重要方法之一[1-4]。随着中国地下流体监测站网的完善,对地震水温观测仪器的示值误差、稳定性等计量性能的要求正在逐步提高。测温仪的测量准确度取决于多种因素,热迟滞性和漏热效应是其不确定度的重要来源[5-8],仪器漂移(短期稳定性)是评价其性能的关键计量技术指标。热迟滞性与传感器元件类型、制造工艺、电路设计等有关,可反映测温仪经历不同温度路径后的示值与参考值的差异水平,在实际观测中表现为升温或降温后对相同水温的测量偏差。本文热迟滞性指将传感器置于温度范围上限或下限前后,中点处的热循环特性,即在升温或降温循环过程中,温度范围中点处测量的2次示值误差之差;漏热效应指因传感器无法完全浸没于恒温槽导热介质而引起的示值损失;仪器漂移指由于测温仪计量特性改变引起的示值在一段时间内的连续或增量变化,通常以日变化幅度表示。
根据感温元件类型,地震行业使用的测温仪可分为3类,即石英晶体型、铂电阻型和热敏电阻型,目前国内外已开展相关类型感温元件温度计的热迟滞性和漏热效应研究,但对仪器漂移的研究较少[5, 8-21]。为全面评价测温仪的测量性能,本文查明在不同国际标准方法下3种感温元件类型测温仪的热迟滞性差异,并对局浸法校准的最小浸没深度和漏热效应进行分析,评估热迟滞性和漏热效应对测量不确定度的贡献,明确仪器漂移变化特征。
1 实验材料、测量系统与方法 1.1 实验材料实验仪器为4台地震监测常用测温仪,其中2台为石英晶体型(编号QZ-1、QZ-2),1台为铂电阻型(编号PT,感温元件为Pt1000型薄膜铂电阻),1台为热敏电阻型(编号NTC,感温元件为负温度系数热敏电阻)。测温仪是一种显示式测量仪器,其输出量值为温度,单位℃。各类测温仪的外形结构相似,均由数据采集器、温度传感器和电缆组成(图 1)。

|
图 1 测量系统结构示意图 Fig. 1 Schematic diagram of measurement system structure |
测温仪传感器呈圆柱状,具有一定重量以便投放至足够深度,保护壳可承受不小于10 MPa的静水压力,感温元件一般位于传感器中下部。不同类型仪器的测量范围、最大允许误差、分辨力和仪器漂移指标相同,分别为0~100 ℃、±0.05 ℃、0.000 1 ℃和不大于0.001 ℃/24 h。QZ-1测温仪传感器长度为590 mm,大于常见的恒温槽工作区深度,通常采用局浸方式校准。
1.2 测量系统实验测量系统由一等标准铂电阻温度计(SPRT)、电测仪器和3台恒温槽组成。其中,SPRT为参考标准,测量范围为0~419.527 ℃,校准结果的最大扩展不确定度为0.004 2 ℃(锌凝固点),自热效应0.001 6 ℃;电测仪器为1595A型测温电桥,分辨力为0.000 01 ℃,精确度为0.000 05 ℃;3台恒温槽的组合造温范围为-60~300 ℃,温场均匀性为0.006 ℃,波动度为0.006 ℃/10 min,工作区深度为50 cm,使用无水乙醇、蒸馏水和二甲基硅油作为导热介质。
1.3 热迟滞性实验方法实验参照国际电工委员会(IEC)最新发布的IEC 60751: 2022[22]和美国材料与试验协会(ASTM)最新发布的ASTM E644-11(2019)[23]国际标准,采用比较法开展研究。对于IEC标准,测量过程中的温度暴露顺序为温度范围下限-中点-上限-中点(升温循环),ASTM标准则与之相反,为温度范围上限-中点-下限-中点(降温循环)。
实验在3个温度范围内进行,分别为0~100 ℃、0~70 ℃和0~50 ℃,每个范围分别进行4次升温和降温循环,取4次循环中点处示值误差之差的平均值作为热迟滞性测量结果。为消除导热介质差异对结果的影响,前后2次区间中点的示值误差测量均在蒸馏水环境中进行。
1.4 漏热效应实验方法以QZ-1为实验对象,利用比较法在均匀分布于测量范围内(包括温度上、下限)的11个点位处测量各浸没深度(2~40 cm, 步进深度为2 cm, 共20个深度点)的示值误差,其中0 ℃、10~70 ℃和80~100 ℃的导热介质分别为无水乙醇、蒸馏水和二甲基硅油。
1.5 仪器漂移实验方法实验在30 ℃测量点处进行,以720 h(30 d)为时间间隔进行2次示值误差测量,并以首次和末次测量结果之差绝对值的日平均值(单位℃/24 h) 作为仪器漂移测量结果。实验期间测温仪连续运行。
2 讨论 2.1 热迟滞性特征3类测温仪的热迟滞性均表现出随测量点温度下降而减小的趋势(表 1,单位℃),且在降温循环(ASTM标准)中更为明显(图 2),该现象与朱蕾[13]和张恒等[14]对工业铂电阻温度计热迟滞性的研究结果一致。4台仪器热迟滞性绝对值的最大值均出现在50 ℃测量点,分别为0.005 2 ℃、0.001 3 ℃、0.025 5 ℃和0.011 2 ℃,其中PT测温仪的热迟滞性绝对值降幅最大,50 ℃与35 ℃测量点的差值分别为0.021 ℃(升温循环,IEC)和0.015 6 ℃(降温循环,ASTM),其他3台仪器的差值较小。结果表明,石英晶体型和热敏电阻型感温元件的热迟滞性与铂电阻感温元件具有相同的温度区间变化特征,测温仪在温度范围中点的热迟滞性可作为测量不确定度的来源之一。
|
|
表 1 测温仪热迟滞性测量结果 Tab. 1 Measurement results of thermal hysteresis of thermometers |

|
图 2 不同感温元件类型测温仪热迟滞性测量结果 Fig. 2 Measurement results of thermal hysteresis of thermometers with different temperature sensing elements |
在各测量温度点,石英晶体型测温仪的热迟滞性绝对值均小于铂电阻型和热敏电阻型(图 2)。在50 ℃测量点,PT测量结果的绝对值最大,分别为0.025 5 ℃(升温循环,IEC)和0.017 ℃(降温循环,ASTM);在35 ℃和25 ℃测量点,NTC热迟滞性的绝对值高于其他3台测温仪。张恒等[14]研究表明,薄膜型铂电阻温度计在-50~150 ℃区间中点(50 ℃测量点)的热迟滞性分别为0.014 2 ℃(升温循环,IEC)和0.020 5 ℃(降温循环,ASTM),与本文实验结果接近,说明热迟滞性可能为感温元件的固有属性[5]。
在IEC和ASTM标准方法中,石英晶体型测温仪与铂电阻型及热敏电阻型测温仪热迟滞性的符号相反(图 2、3),即QZ-1和QZ-2置于温度范围上限和下限之前的中点示值误差小于置于温度范围上限和下限之后,PT和NTC的热迟滞性行为与之相反。另外,石英晶体型测温仪的升温循环(IEC标准)测量结果略小于降温循环(ASTM标准),而铂电阻型及热敏电阻型测温仪的升温循环(IEC标准)测量结果略大于降温循环(ASTM标准)。由图 3可知,2种标准方法的热迟滞性表现出较好的关于x轴对称特征。

|
图 3 不同标准方法热迟滞性测量结果 Fig. 3 Measurement results of thermal hysteresis by different standard methods |
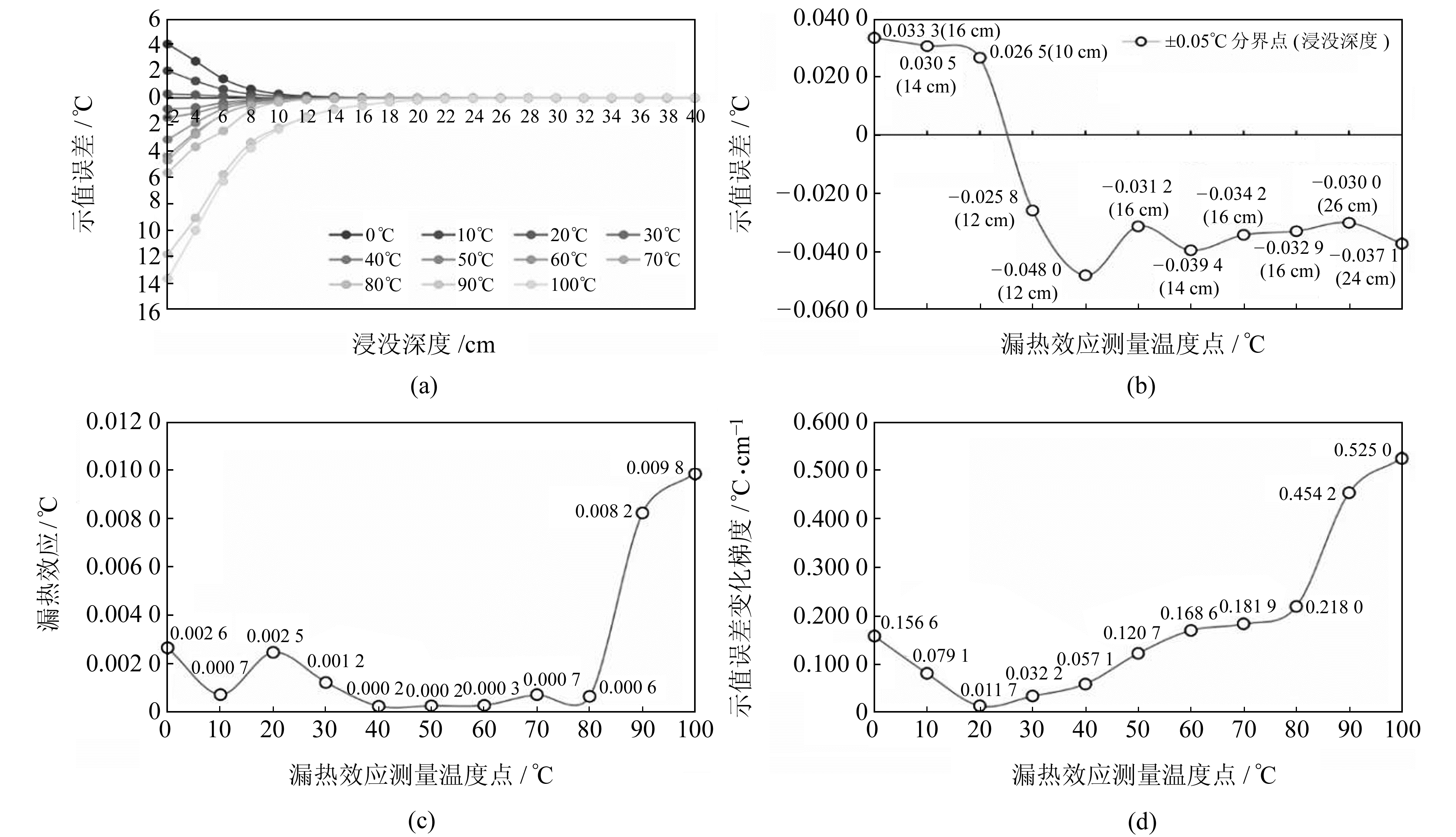
QZ-1在各浸没深度的示值误差见图 4(a),最大允许误差分界点(±0.05 ℃)对应的浸没深度见图 4(b)。在0~20 ℃范围内,分界点对应的浸没深度在10~16 cm之间,且随温度升高逐渐减小,分界点示值误差均为正值;在30~100 ℃范围内,分界点对应的浸没深度在12~26 cm之间,且随温度升高逐渐增大,分界点示值误差均为负值。总体而言,测温仪感温元件在各测量点的最小浸没深度,即分界点对应的深度,随温度升高而增大,最大值为26 cm(90 ℃测量点)。
|
图 4 QZ-1仪器漏热效应特征曲线 Fig. 4 Characteristic curves of heat leakage effect of QZ-1 instrument |
测温仪在各测量点30 cm以下深度的示值误差变化较小,幅度在0.000 2 ~0.009 8 ℃之间(图 4(a))。因此,在采用局浸法校准时,为减小漏热效应对结果的影响,测温仪感温元件的浸没深度应不小于30 cm,在假设恒温槽温场始终均匀的情况下,可将30 cm与40 cm处示值误差之差视为QZ-1漏热效应的估计值。漏热效应具有随温度升高逐渐增大的趋势(图 4(c)),最大值约为0.01 ℃(100 ℃测量点)。另外,在30 cm深度以上,示值误差变化梯度随温度升高总体呈上升的趋势(图 4(d))。
分界点示值误差符号的差异与环境温度有关。实验过程中室温约为23.5 ℃,受纵向热辐射引起的温度传导影响,0~20 ℃范围内测温仪在分界点处的测量温度高于SPRT示值;30~100 ℃范围内,因存在漏热效应,测温仪在分界点处的测量温度低于SPRT示值。Hocenski等[18]对铂电阻型工业温度计的研究结果也显示,当导热介质温度高于环境温度时,热交换导致最小浸没深度随温度升高逐渐增大。显然,当测量点温度低于环境温度时,漏热效应表现为吸热,反之则为放热。值得注意的是,在网运行的测温仪传感器投放井深通常在100 m以上,因此由不完全浸没引起的漏热效应仅存在于实验室校准过程中。
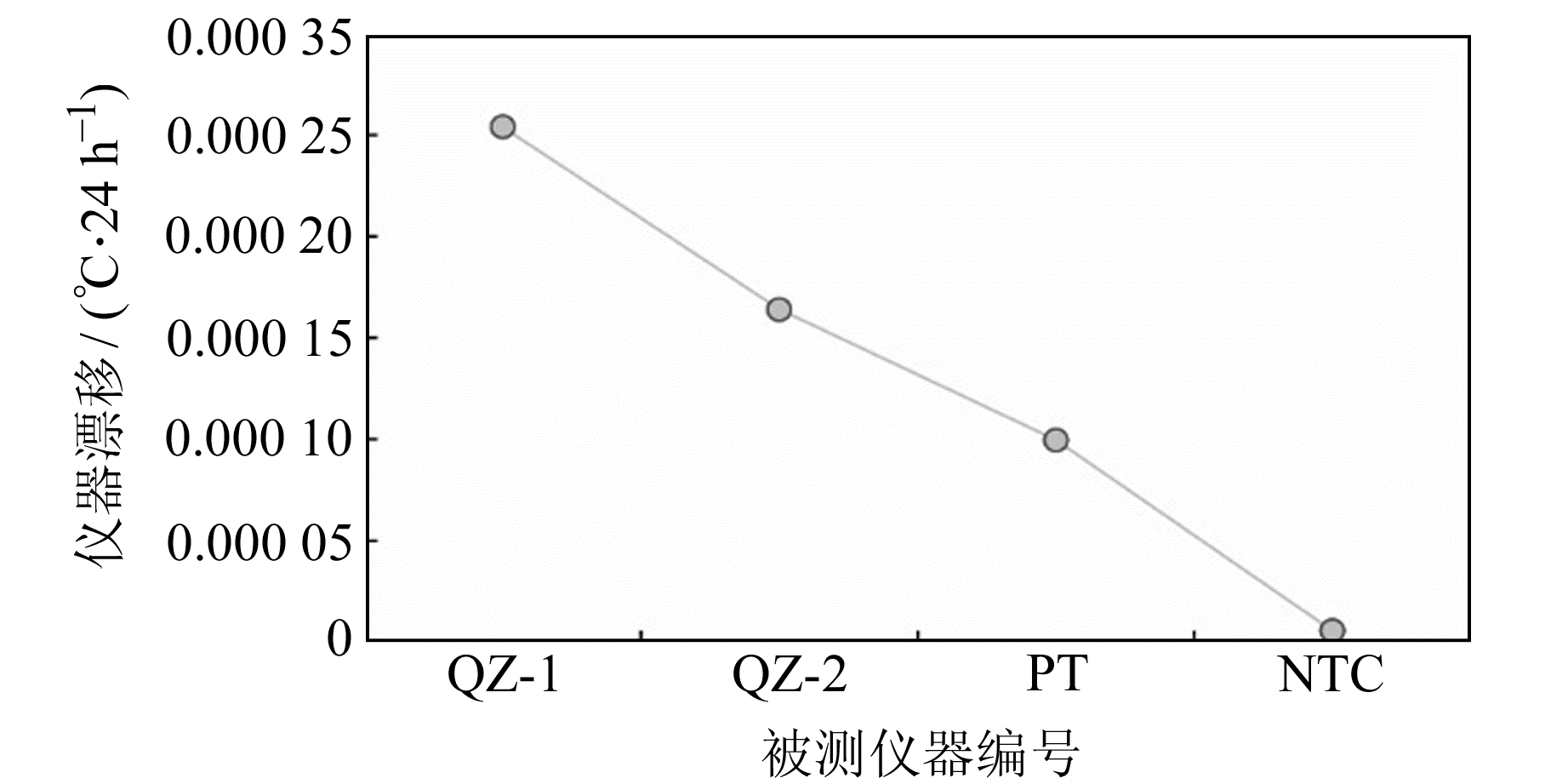
2.3 仪器漂移特征不同类型测温仪的漂移测量结果接近(表 2(单位℃)、图 5),其中石英晶体型测温仪略高于铂电阻型和热敏电阻型测温仪,但均满足DB/T 32.2-2008地震行业标准[24]规定的技术要求,即不大于0.001 0 ℃/24 h。热敏电阻型测温仪的仪器漂移最小,与石英晶体型测温仪的最大差值仅为0.000 3 ℃/24 h。
|
|
表 2 测温仪仪器漂移测量结果 Tab. 2 Measurement results of instrument drift of thermometers |
|
图 5 测温仪仪器漂移测量结果对比 Fig. 5 Comparison of instrument drift measurement results of thermometers |
以QZ-1在30 ℃测量点的示值误差为例,使用GUM法[25]对其测量不确定度进行评定。测量模型为:
| $ \Delta t_i=\bar{t}_i-\bar{T}_i $ | (1) |
式中,ti和Ti分别为测温仪和SPRT在第i个校准点的示值算数平均值(单位℃);Δti为测温仪在第i个校准点的示值误差(单位℃)。显然,测量不确定度来源于两部分,即被测仪器和测量系统。被测仪器引入的分量包括测量重复性、热迟滞性及漏热效应,灵敏系数c为1;测量系统引入的分量包括恒温槽均匀性和波动性、SPRT校准不确定度和自热效应、电测仪器分辨力和精确度,灵敏系数c为-1。
测量重复性分量属A类评定,可通过在重复条件下10次测量结果的标准偏差计算获得;其他分量属B类评定,除由上级计量机构提供的SPRT校准不确定(包含因子k=2)外,均按均匀分布处理,即k=
|
|
表 3 测温仪30 ℃校准结果的测量不确定度分量 Tab. 3 The measurement uncertainty components of calibration results of thermometers at 30 ℃ |
|
|
表 4 测温仪30 ℃校准结果的扩展不确定度 Tab. 4 The expanded uncertainty of calibration results of thermometers at 30 ℃ |
测温仪热迟滞性是一种复杂现象[5]。对于石英晶体型测温仪,热迟滞性的成因机制包括感温元件应变变化、石英晶体变化、杂质重新分布、振荡器电路迟滞和热梯度等[16];对于铂电阻型测温仪,热迟滞性是由铂薄膜或铂丝与衬底或支撑结构膨胀系数不同引起的应力变化所致[5, 8, 10];对于热敏电阻型测温仪,热迟滞性可能与感温元件的热机械性质有关[26]。测温仪的仪器漂移特征则主要受器件老化引起的参数变化影响[27],且该现象普遍存在[24]。
根据中国地震局中国地下流体监测站网规划(2023-2030),2030年地震地下水温度观测精度将提高至0.01 ℃,即最大允许误差为±0.01 ℃,显然目前测温仪校准结果的扩展不确定度无法满足规划需求。除降低测量重复性分量外,减小被测仪器的热迟滞性和漏热效应将成为提高测量准确度的关键课题之一。本质上,测量重复性和热迟滞性均为仪器稳定性的具体表现。前人研究表明[8],绕线结构允许铂丝在温度循环中自由膨胀和收缩,因此与薄膜型相比,铂丝与基底结合时会表现出更少的热迟滞性。未来可改用铂丝型铂电阻为感温元件,以提高测温仪的稳定性,另外可通过改进石英晶体谐振器频率-温度模型等方式对热迟滞性进行修正[17]。优化感温元件和电路设计、改善传感器封装工艺、提升制造水平等对降低测温仪热迟滞性同样十分重要,也对优化仪器漂移特性具有一定的借鉴意义。
在漏热效应方面,可通过使用满足全浸法校准条件的大深度恒温槽,同时在传感器露出部分增加必要的保温装置,并对露出部分的温度进行修正等,消除或减小由漏热效应引起的示值损失,从而避免或降低不确定度分量的引入,提高测量准确度。
3 结语本文对比石英晶体型、铂电阻型和热敏电阻型测温仪在0~100 ℃、0~70 ℃和0~50 ℃温度范围内的热迟滞性,明确局浸法校准的最小浸没深度和漏热效应,查明仪器漂移特征。在此基础上,分析热迟滞性和漏热效应对测量不确定度的贡献,并提出改进建议。具体结论如下:
1) 测温仪热迟滞性随测量点温度降低而减小,最大值为0.025 5 ℃(铂电阻型,50 ℃测量点)。在相同温度点,铂电阻型和热敏电阻型测温仪的热迟滞性高于石英晶体型,且前两者温度中点的示值误差符号与后者相反。升温循环(IEC标准)和降温循环(ASTM标准)的测量结果基本一致。
2) 测温仪感温元件的最小浸没深度总体随测量温度的升高而增大,漏热效应最大值约为0.01 ℃(100 ℃测量点)。采用局浸法校准时,感温元件浸没深度应不小于30 cm,最大允许误差分界点(±0.05 ℃)示值误差符号的差异与环境温度有关。
3) 3类测温仪的仪器漂移测量结果接近,符合地震行业标准的技术要求,即不大于0.001 ℃/24 h,测量结果极差仅为0.000 3 ℃/24 h。
4) 石英晶体型测温仪的测量准确度最佳。QZ-1和QZ-2校准结果的扩展不确定度分别为0.013 ℃和0.011 ℃,热迟滞性和漏热效应对其最大贡献率仅约为15.4%;铂电阻型和热敏电阻型测温仪校准结果的扩展不确定度(热迟滞性的贡献率)为0.028 ℃(约60.7%)和0.017 ℃(约35.3%)。
5) 测温仪热迟滞性成因复杂,未来可通过优化感温元件和电路设计、改善传感器封装工艺、提升制造水平等方法提高测量准确度和稳定性,这对优化仪器漂移特性也具有一定的借鉴意义。另外,使用大深度恒温槽、在传感器露出部分增加保温装置或修正公式等,可避免或降低漏热效应引入不确定度分量。
| [1] |
车用太, 刘成龙, 鱼金子. 地下流体观测环境的评估指标——干扰度[J]. 地震, 2005, 25(3): 63-68 (Che Yongtai, Liu Chenglong, Yu Jinzi. Interference Degree—An Index for Assessing the Observation Conditions of Subsurface Fluids[J]. Earthquake, 2005, 25(3): 63-68)
(  0) 0) |
| [2] |
刘耀炜. 我国地震地下流体科学40年探索历程回顾[J]. 中国地震, 2006, 22(3): 222-235 (Liu Yaowei. Review of the Research Progress on the Seismological Science of Underground Fluid in China during Last 40 Years[J]. Earthquake Research in China, 2006, 22(3): 222-235)
(  0) 0) |
| [3] |
汪集暘. 地热学及其应用[M]. 北京: 科学出版社, 2015 (Wang Jiyang. Geothermics and Its Applications[M]. Beijing: Science Press, 2015)
(  0) 0) |
| [4] |
王广才, 车用太, 刘成龙, 等. 我国地震地下流体观测的现状和趋势[J]. 水文地质工程地质, 2003, 30(6): 89-96 (Wang Guangcai, Che Yongtai, Liu Chenglong, et al. Subsurface Fluids Observation for Earthquake Study and Prediction in China[J]. Hydrogeology and Engineering Geology, 2003, 30(6): 89-96)
(  0) 0) |
| [5] |
Žužek V, Batagelj V, Bojkovski J. Determination of PRT Hysteresis in the Temperature Range from -50 ℃ to 300 ℃[J]. International Journal of Thermophysics, 2010, 31(8-9): 1 771-1 778 DOI:10.1007/s10765-010-0823-8
(  0) 0) |
| [6] |
Ross-Pinnock D, Maropoulos P G. Review of Industrial Temperature Measurement Technologies and Research Priorities for the Thermal Characterisation of the Factories of the Future[J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2016, 230(5): 793-806 DOI:10.1177/0954405414567929
(  0) 0) |
| [7] |
Tistomo A S, Larassati D, Achmadi A, et al. Estimation of Uncertainty in the Calibration of Industrial Platinum Resistance Thermometers(IPRT) Using Monte Carlo Method[J]. MAPAN, 2017, 32(4): 273-278 DOI:10.1007/s12647-017-0222-8
(  0) 0) |
| [8] |
Rusby R L, Machin D. Hysteresis and Instability in Some IPRT Sensors within Temperature Ranges Extending from -196 ℃ to 150 ℃[J]. International Journal of Thermophysics, 2017, 38(8)
(  0) 0) |
| [9] |
White D R, Jongenelen C L, Saunders P. The Hysteresis Characteristics of Some Industrial PRTs[J]. International Journal of Thermophysics, 2010, 31(8-9): 1 676-1 684 DOI:10.1007/s10765-010-0821-x
(  0) 0) |
| [10] |
Gam K S, Yang I, Kim Y G. Thermal Hysteresis in Thin-Film Platinum Resistance Thermometers[J]. International Journal of Thermophysics, 2011, 32(11-12): 2 388-2 396 DOI:10.1007/s10765-011-1041-8
(  0) 0) |
| [11] |
Hahtela O, Heinonen M, Kajastie H, et al. Calibration of Industrial Platinum Resistance Thermometers up to 700 ℃[J]. International Journal of Thermophysics, 2014, 35(3-4): 668-680 DOI:10.1007/s10765-014-1588-2
(  0) 0) |
| [12] |
Moiseeva N P. The Thermal Hysteresis of a Standard Platinum Resistance Thermometer[J]. Measurement Techniques, 2015, 58(4): 426-430 DOI:10.1007/s11018-015-0729-8
(  0) 0) |
| [13] |
朱蕾. -80~300 ℃铂电阻温度计在0 ℃的热迟滞性研究[J]. 计量技术, 2018(5): 26-28 (Zhu Lei. Study on Thermal Hysteresis of -80~300 ℃ Platinum Resistance Thermometer at 0 ℃[J]. Measurement Technique, 2018(5): 26-28)
(  0) 0) |
| [14] |
张恒, 曾凡超, 文昌俊, 等. 一种高精度薄膜铂电阻温度计测量迟滞性的研究[J]. 计量学报, 2019, 40(6): 1 025-1 029 (Zhang Heng, Zeng Fanchao, Wen Changjun, et al. Research on Hysteresis of the High-Precision Thin-Film Platinum Tesistance Thermometers[J]. Acta Metrologica Sinica, 2019, 40(6): 1 025-1 029)
(  0) 0) |
| [15] |
Geel J L W A, Bosma R, Wensveen J, et al. Thermistors Used in Climatic Chamber at High Temperature and Humidity[J]. International Journal of Thermophysics, 2015, 36(2-3): 569-576 DOI:10.1007/s10765-014-1753-7
(  0) 0) |
| [16] |
Kusters J A, Vig J R. Hysteresis in Quartz Resonators—A Review[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 1991, 38(3): 281-290 DOI:10.1109/58.79613
(  0) 0) |
| [17] |
Deng X G, Wang S B, Huang X R, et al. Modified Modeling Method of Quartz Crystal Resonator Frequency-Temperature Characteristic with Considering Thermal Hysteresis[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2021, 68(3): 890-898 DOI:10.1109/TUFFC.2020.3014887
(  0) 0) |
| [18] |
Hocenski Z, Cvitas L. Computer Based Method for Determining of Response Time and Immersion Depth of Industrial Thermometers[C]. SICE Annual Conference, Takamatsu, 2007
(  0) 0) |
| [19] |
金志军, 王池, 冯磊. 热能表温度传感器浸没深度影响的实验研究[J]. 计量学报, 2008, 29(5): 469-471 (Jin Zhijun, Wang Chi, Feng Lei. Experimental Study on Immersion Depth of Pairing Thermometer of Heat Meter[J]. Acta Metrologica Sinica, 2008, 29(5): 469-471)
(  0) 0) |
| [20] |
车用太, 鱼金子. 井水温度观测中有待解决的若干基本问题[J]. 中国地震, 2013, 29(3): 306-315 (Che Yongtai, Yu Jinzi. Some Basic Problems in Well Water Temperature Observation[J]. Earthquake Research in China, 2013, 29(3): 306-315)
(  0) 0) |
| [21] |
邱永平. 高精度温度计在水温观测中的仪器稳定性分析[J]. 中国地震, 2018, 34(4): 828-836 (Qiu Yongping. Stability Analysis of High Precision Thermometer in Water Temperature Observation[J]. Earthquake Research in China, 2018, 34(4): 828-836)
(  0) 0) |
| [22] |
International Electrotechnical Commission. IEC 60751: 2022 Industrial Platinum Resistance Thermometers and Platinum Temperature Sensors[S]. 2022
(  0) 0) |
| [23] |
American Society of Testing Materials. ASTM E644-11(2019) Standard Test Methods for Testing Industrial Resistance Thermometers[S]. 2019
(  0) 0) |
| [24] |
中国地震局. DB/T 32.2—2008地震观测仪器进网技术要求: 地下流体观测仪第2部分: 测温仪[S]. 北京: 地震出版社, 2008 (China Earthquake Administration. DB/T 32.2—2008 Technical Requirements of Instruments in Network for Earthquake Monitoring—Underground Fluid Observation Instruments—Part 2: Temperature Indicator[S]. Beijing: Seismological Press, 2008)
(  0) 0) |
| [25] |
国家质量监督检验检疫总局. JJF 1059.1—2012测量不确定度评定与表示[S]. 北京: 中国质检出版社, 2013 (General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. JJF 1059.1—2012 Evaluation and Expression of Uncertainty in Measurement[S]. Beijing: Quality Inspection Press of China, 2013)
(  0) 0) |
| [26] |
Balam A, Cen-Puc M, May-Pat A, et al. Influence of Polymer Matrix on the Sensing Capabilities of Carbon Nanotube Polymeric Thermistors[J]. Smart Materials and Structures, 2020, 29(1)
(  0) 0) |
| [27] |
何案华, 邓卫平, 李国佑. 青海地热台网温度漂移问题初步分析[J]. 大地测量与地球动力学, 2017, 37(10): 1 083-1 086 (He Anhua, Deng Weiping, Li Guoyou. Analyses of Temperature Drift in Qinghai Geothermal Network[J]. Journal of Geodesy and Geodynamics, 2017, 37(10): 1 083-1 086)
(  0) 0) |
 2024, Vol. 44
2024, Vol. 44


