2. 地理信息工程国家重点实验室,西安市雁塔路中段1号,710054;
3. 西安测绘研究所,西安市雁塔路中段1号,710054
水下潜器使用的导航技术现阶段主要为惯性导航系统(inertial navigation system,INS),但是惯性导航系统只能保证短时间内的精确导航,其漂移误差会随时间增长而逐渐累积。重力匹配导航具有无源自主性和隐蔽性等特点,因此,可以采用重力匹配导航来辅助惯性导航系统修正累积漂移误差[1-2]。在重力辅助惯性导航过程中,导航精度不仅受重力匹配导航算法的影响,而且与重力匹配区的适配性息息相关[3]。适配性在一定程度上受重力场特征分布的影响,变化越剧烈、特征越明显的重力匹配区的适配性更好,可使匹配导航的精度更高。
国内外众多学者提出多种决策方法来分析重力匹配区的适配性问题。Xiong等[4]提出一种基于主成分分析法和层次分析法的重力梯度匹配区选择准则,通过提取重力梯度特征参数,在主成分分析法与层次分析法基础上,建立PA模型并融合多个特征参数,得到重力梯度匹配区的选择准则。李钊伟等[5]基于主成分分析法和加权平均原则,提出一种新的主成分加权平均归一化方法并计算总体特征参数,从而划分适配区与非适配区。马越原等[6]通过信息熵整合多种特征参数,将其与单一特征参数方法进行对比,证明基于特征参数信息熵方法的优越性。Zong等[7]基于主成分分析理论和PSO-BP神经网络,提出基于PPBA的匹配区分类方法,并采用TERCOM算法验证PPBA方法的可行性。Li等[8]提出一种基于矢量特征的重力适配区选择方法,利用不规则三角网建立重力异常矢量图,结合矢量模型中提取的特征参数得到综合特征参数,进而筛选重力适配区。肖云等[9]基于多属性决策理论,对多个特征参数进行加权规范化处理,得到总决策参数来划分适配区。
在评价重力匹配区适配性过程中,重力特征参数种类多种多样,仅用单个特征参数对重力匹配导航区的适配性进行评价可能会导致结果不全面,故采用基于信息熵的单特征分析准则与基于多属性决策的多特征分析准则进行对比分析。信息熵是以单个特征参数作为研究目标,来衡量其包含信息的丰富程度,可反映该特征参数所包含信息的无序度和随机性[10]。多属性决策是在综合多个特征参数基础上,将多种特征参数所包含的信息进行融合,来提供最优方案或对多个方案进行排序的决策方法[11]。为分析这两种方法结果的全面性,区分其对适配区评价的优劣,本文选取某局部海域的重力异常值作为重力底图进行比较实验,分别使用两种方法对重力匹配导航局部区域适配性进行分析与评价,通过TERCOM算法对单特征准则和多特征准则两种评价方式进行验证对比。
1 重力特征参数重力特征参数是用来评价匹配区适配性的一种综合指标。本文新增重力特征丰度与累加梯度均值2种新的特征参数,另选重力标准差、相关系数、粗糙度和坡度4种传统特征参数,将这6种特征参数用于评价匹配区的适配程度。
为此,定义某区域经纬度跨度m×n的重力网格图重力异常值集合Z={g(i, j)},其中g表示该区域的重力异常值,(i, j)为区域内的一组坐标,
1) 重力标准差σ。标准差σ作为一种数值分布统计参数,可用于评价重力场数据序列的离散程度,计算公式为:
| $ \left\{\begin{array}{l} \sigma=\sqrt{\frac{1}{m n-1} \sum\limits_{i=1}^m \sum\limits_{j=1}^n[g(i, j)-\bar{g}]^2} \\ \bar{g}=\frac{1}{m n} \sum\limits_{i=1}^m \sum\limits_{j=1}^n g(i, j) \end{array}\right. $ | (1) |
式中,g为该区域的重力异常平均值。
2) 重力相关系数R。重力相关系数R表示区域内相邻网格点重力异常值的线性相关程度。由于方向不同,重力相关系数分为x向相关系数和y向相关系数,计算公式为:
| $ \left\{\begin{array}{l} R=\left(R_x+R_y\right) / 2 \\ R_x=\frac{1}{n(m-1) \sigma^2} \\ \quad\sum\limits_{i - 1}^{m - 1} {\sum\limits_{j = 1}^n {} } -\bar{g}][g(i+1, j)-\bar{g}] \\ R_y=\frac{1}{m(n-1) \sigma^2} \\ \quad\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^{n - 1} {} }[g(i, j)-\bar{g}][g(i, j+1)-\bar{g}] \end{array}\right. $ | (2) |
式中,Rx为x方向相关系数,Ry为y方向相关系数。
3) 重力粗糙度r。重力粗糙度r用于描述重力趋势面的光滑程度,分为x向粗糙度和y向粗糙度,计算公式为:
| $ \left\{\begin{array}{l} r=\left(r_x+r_y\right) / 2 \\ r_x=\frac{1}{n(m-1)} \sum\limits_{i = 1}^{m - 1}\sum\limits_{j = 1}^{n}|g(i, j)-g(i+1, j)| \\ r_y=\frac{1}{m(n-1)} \sum\limits_{i = 1}^{m}\sum\limits_{j = 1}^{n - 1}|g(i, j)-g(i, j+1)| \end{array}\right. $ | (3) |
式中,rx为x方向粗糙度,ry为y方向粗糙度。
4) 重力坡度S。重力坡度S可表示为过重力趋势面上一点的法线方向与垂直方向的夹角,在不同方向上分为x向坡度和y向坡度,计算公式为:
| $ \left\{\begin{array}{l} S=\sqrt{S_x^2+S_y^2} \\ S_x=[g(i+1, j+1)+g(i, j+1)+ \\ \quad g(i-1, j+1)-g(i+1, j-1)- \\ \quad g(i, j-1)-g(i-1, j-1)] / 6 \\ S_y=[g(i+1, j+1)+g(i+1, j)+ \\ \quad g(i+1, j-1)-g(i-1, j+1)- \\ \quad g(i-1, j)-g(i-1, j-1)] / 6 \end{array}\right. $ | (4) |
式中,Sx为x方向坡度,Sy为y方向坡度。
5) 重力特征丰度Ag。重力特征丰度Ag可以反映重力场特征变化的丰富程度。当重力特征丰度数值较大时,表明相邻网格采样点间的变化较整个重力场的变化更大。计算公式为:
| $ A_g=\frac{\sqrt{r_x^2+r_y^2}}{\sigma} $ | (5) |
6) 累加梯度均值T。累加梯度均值T可用来描述局部区域重力信息量,累加梯度数值越大,表明重力场包含的信息量越大。计算公式为:
| $ \left\{\begin{array}{l} T=\frac{1}{(m-2)(n-2)} \\ \quad\sum\limits_{i = 2}^{m - 1}\sum\limits_{j = 2}^{n - 1} \sqrt{T_x(i, j)^2+T_y(i, j)^2} \\ T_x(i, j)=g(i+1, j)-g(i, j) \\ T_y(i, j)=g(i, j+1)-g(i, j) \end{array}\right. $ | (6) |
式中,Tx(i, j)、Ty(i, j)分别表示在(i, j)处x方向和y方向梯度值。
2 适配性分析准则重力适配区选择的关键在于采用合理的适配性分析准则。为更好地分析重力场局部区域的适配性问题,在上述6种重力特征参数基础上,采用单特征和多特征2种分析准则对重力匹配导航局部区域适配性进行对比分析。
2.1 基于信息熵的单特征分析准则单特征分析准则是基于信息熵来衡量重力匹配导航区域适配性的方法。信息熵用于表示信息量的多少,信息量较多的局部重力场更适合进行重力匹配导航,计算公式如下:
| $ H=-\sum\limits_i p\left(x_i\right) \log _a p\left(x_i\right) $ | (7) |
式中,H为信息量;p(xi)为事件xi发生的概率;底数a=2,单位为比特(bit)。
通过上述6种特征参数可知,以重力坡度为例,重力坡度S分为x向坡度Sx和y向坡度Sy。将x和y向坡度通过信息熵进行单特征分析,x向坡度Sx发生的概率为x向坡度与重力坡度之比,即p(Sx)=Sx/S;同理,y向坡度Sy发生的概率为p(Sy)=Sy/S。在信息熵的定义下,x和y向坡度的信息熵为:
| $ H_{i j}=-\left[p\left(S_x\right) \log _a p\left(S_x\right)+p\left(S_y\right) \log _a p\left(S_y\right)\right] $ | (8) |
多特征分析准则的核心为多属性决策理论。多属性决策是在考虑多个属性参数的情况下,评估选择出最优备选方案或进行方案排序的决策方法。将上述6种重力特征参数结合成联合决策集,按照各个参数的不同属性筛选出正相关和负相关两类指标,并将6种参数进行联合决策,综合评价总决策属性。
1) 设立关联矩阵X。假定待匹配区共有M个,每个待匹配区共有N个重力特征参数,则关联矩阵维度为M×N,其矩阵结构如下:
| $ \boldsymbol{X}=\left[\begin{array}{cccc} x_{11} & x_{12} & \cdots & x_{1 n} \\ x_{21} & x_{22} & \cdots & x_{2 n} \\ \vdots & \vdots & \ddots & \vdots \\ x_{m 1} & x_{m 2} & \cdots & x_{m m} \end{array}\right]=\left[x_{m n}\right]_{M \times N} $ | (9) |
式中,元素xmn(m= 1, 2, …, M, n= 1, 2, …, N)为待匹配区m中第n个重力特征参数。
2) 特征参数归一化。对各个重力特征参数进行归一化处理,使其变为无量纲参数。
根据各重力特征参数的属性,将其分为正、负相关两类,归一化处理流程为:
| $ \left\{\begin{array}{l} v_{m n}^{+}=\frac{x_{m n}-\min x_{n m}}{\max x_{m n}-\min x_{m m}} \\ v_{m n}^{-}=\frac{\max x_{n m}-x_{n m}}{\max x_{n m}-\min x_{m m}} \end{array}\right. $ | (10) |
式中,maxxmn和minxmn为关联矩阵X中第n列参数的最大值与最小值。
归一化后的关联矩阵V可表示为:
| $ \boldsymbol{V}=\left[\begin{array}{cccc} v_{11} & v_{12} & \cdots & v_{1 n} \\ v_{21} & v_{22} & \cdots & v_{2 n} \\ \vdots & \vdots & \ddots & \vdots \\ v_{m 1} & v_{m 2} & \cdots & v_{m n} \end{array}\right]=\left[v_{m n}\right]_{M \times N} $ | (11) |
式中,vmn为归一化后的重力特征参数值。
3) 对参数进行配权。第n个参数的熵值en计算公式为:
| $ \left\{\begin{array}{l} e_n=-\log _a(M)^{-1} \sum\limits_{m = 1}^{M} p_{m m} \log _a p_{m n} \\ p_{m n}=\frac{v_{m n}}{\sum\limits_{m = 1}^{M} v_{m n}} \end{array}\right. $ | (12) |
式中,底数a一般取2。
利用熵值en分配权重ωn:
| $ \omega_n=\frac{1-e_n}{\sum\limits_{n = 1}^{N}\left(1-e_n\right)} $ | (13) |
4) 定权归一化决策矩阵Y。令归一化后的关联矩阵V中参数vmn与相应的权重ωmn相乘,得到定权归一化决策矩阵Y,其矩阵结构如下:
| $ \boldsymbol{Y}=\left[\begin{array}{cccc} y_{11} & y_{12} & \cdots & y_{1 n} \\ y_{21} & y_{22} & \cdots & y_{2 n} \\ \vdots & \vdots & \ddots & \vdots \\ y_{m 1} & y_{m 2} & \cdots & y_{m n} \end{array}\right]=\left[y_{m n}\right]_{M \times N} $ | (14) |
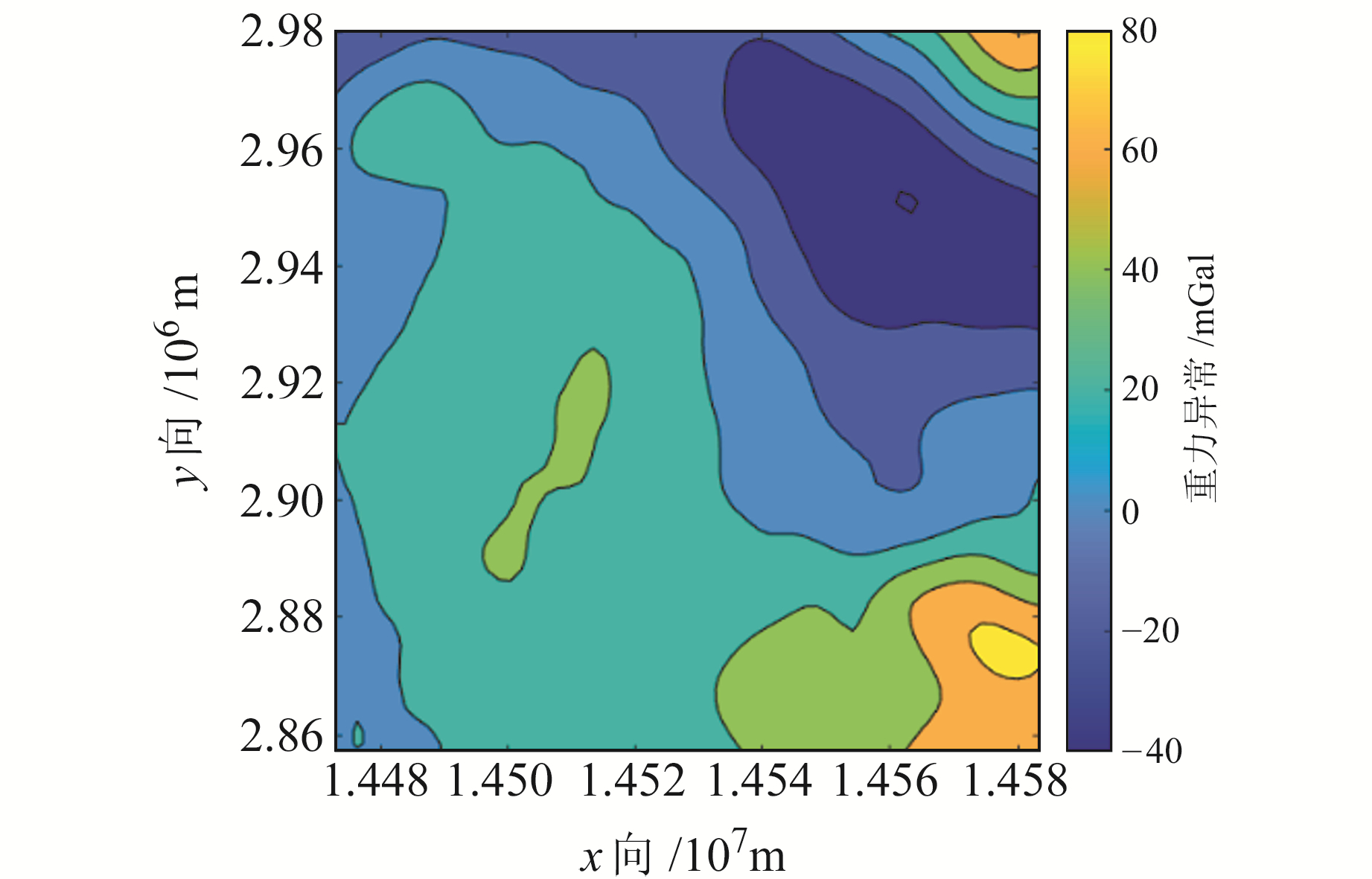
为验证单特征分析准则与多特征分析准则对重力匹配导航适配性的优劣,选取某局部海域的重力异常数据为基准图(图 1),重力异常分辨率为1′×1′。图 2为6种特征参数在实验海域的二维等值线图,分辨率为1′×1′。
|
图 1 重力异常基准图 Fig. 1 Reference map of gravity anomalies |

|
图 2 实验海域二维等值线图 Fig. 2 Two-dimensional contour map of experimental sea area |
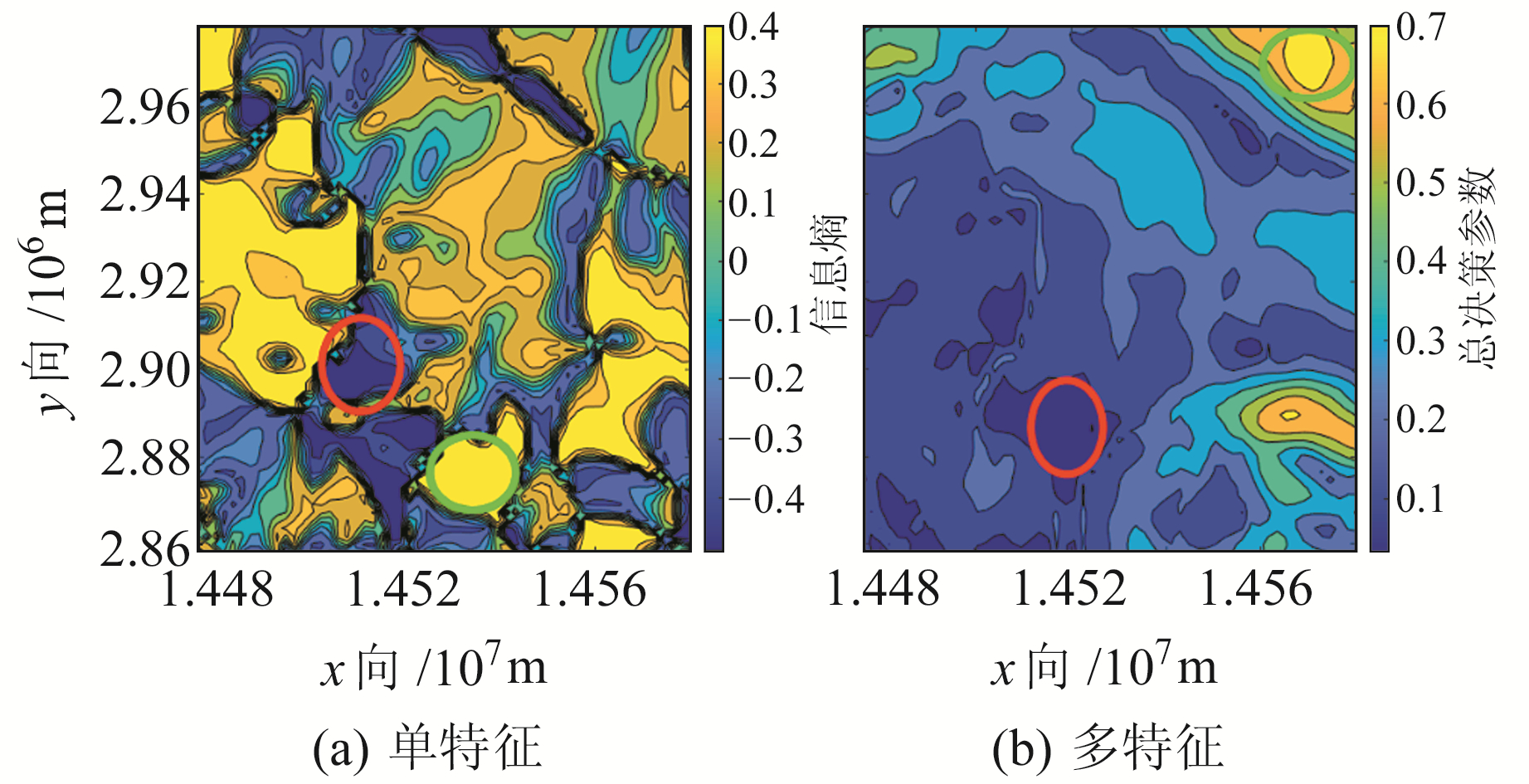
根据上述6种特征参数进行基于信息熵的单特征分析准则评价与基于多属性决策的多特征分析准则评价,图 3为以重力坡度为例得到的单特征分析结果以及结合6种特征参数采用多属性决策得到的多特征分析结果。
|
图 3 单特征及多特征分析准则结果 Fig. 3 Results of single feature and multi feature analysis criteria |
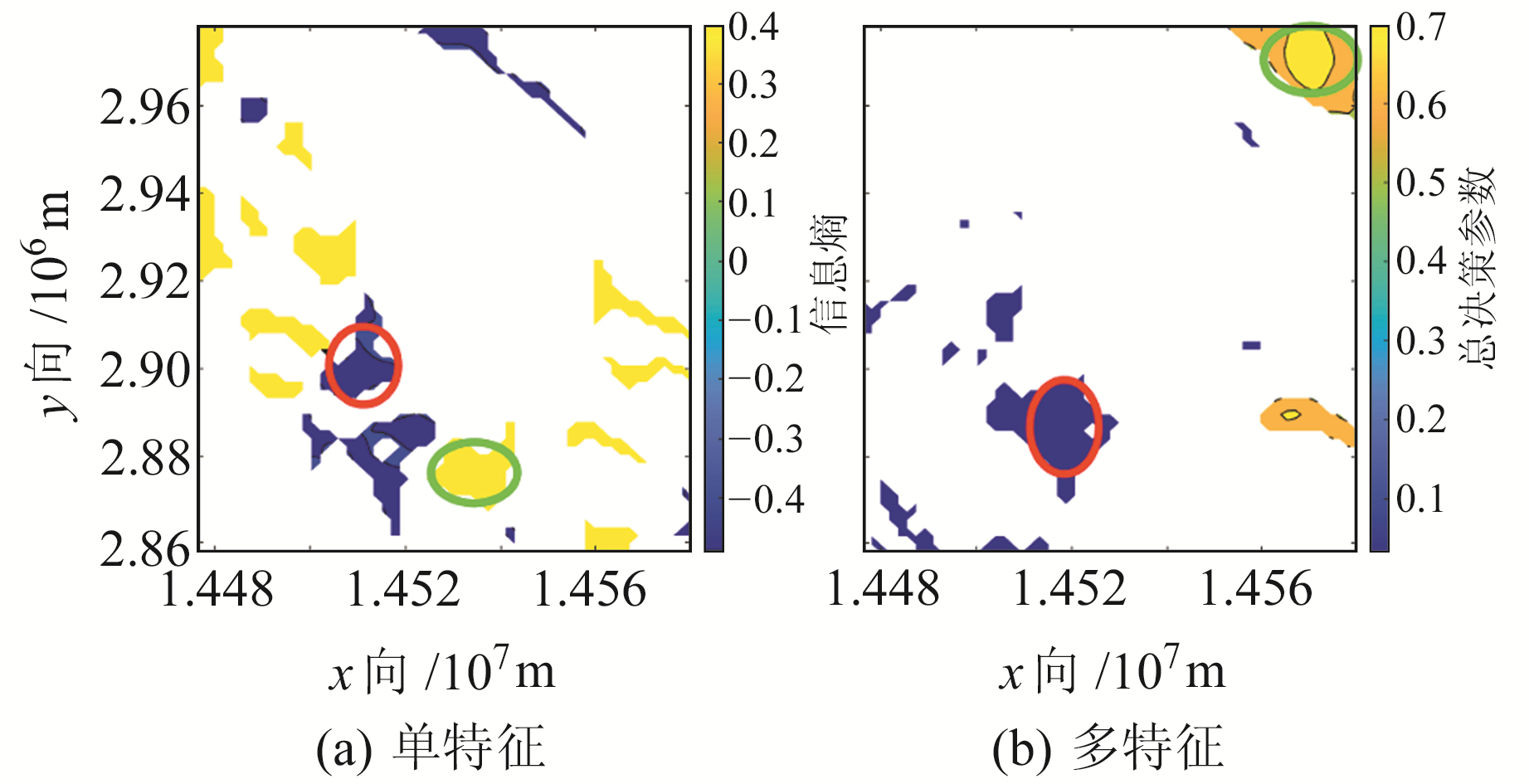
通过大量实验选定单特征分析和多特征分析结果图阈值,设置单特征分析准则阈值1为-0.33,阈值2为0.45;多特征分析准则阈值3为0.10,阈值4为0.58。筛选所得黄色和深黄色区域为适配区,蓝色和深蓝色区域为非适配区,结果如图 4所示。实验区选择为图 4中面积较大且分布均匀的区域,即图中椭圆区域,其中绿色椭圆代表验证分析的适配区,红色椭圆代表非适配区。
|
图 4 单特征和多特征分析准则筛选结果 Fig. 4 Filter results of single feature and multi feature analysis criteria |
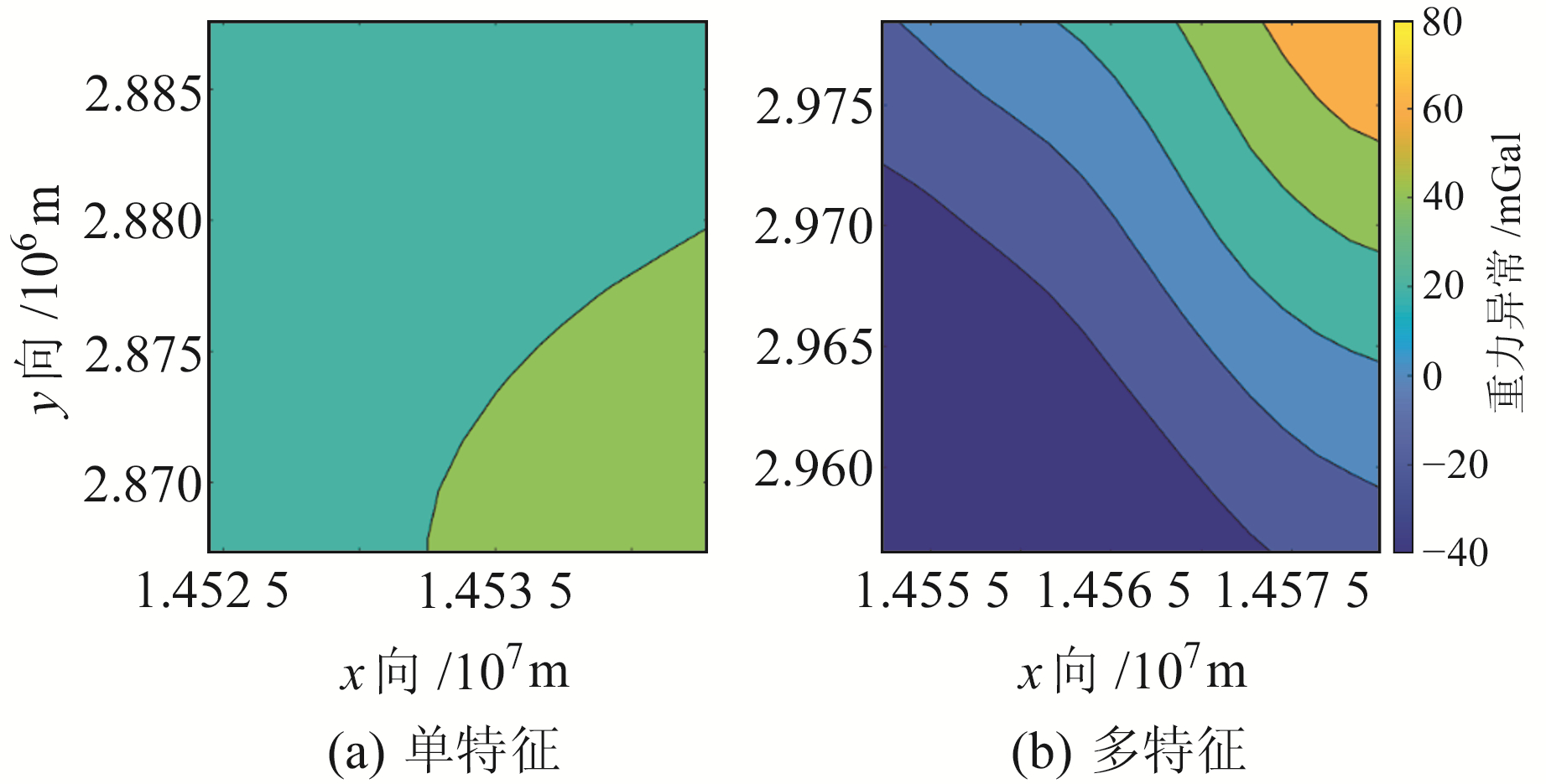
单特征与多特征分析准则适配区重力异常结果如图 5所示。单特征分析准则适配区重力异常统计信息如下:最大值为52.70 mGal,最小值为28.30 mGal,最大重力异常差异为24.40 mGal,平均值为35.09 mGal。多特征分析准则适配区重力异常统计信息如下:最大值为69.50 mGal,最小值为-38.80 mGal,最大重力异常差异为108.30 mGal,平均值为-4.80 mGal。
|
图 5 适配区重力异常 Fig. 5 Gravity anomalies in adaptive area |
为避免航线对匹配精度的影响,在单特征和多特征2种方法所选适配区内设计相同航线并采用TERCOM算法对其进行实验验证。其中,潜器惯性导航系统参数设置为:陀螺仪常值漂移0.003°/h,陀螺仪随机漂移

|
图 6 单特征和多特征适配区轨迹 Fig. 6 Trajectory of single feature and multi feature in adaptive area |
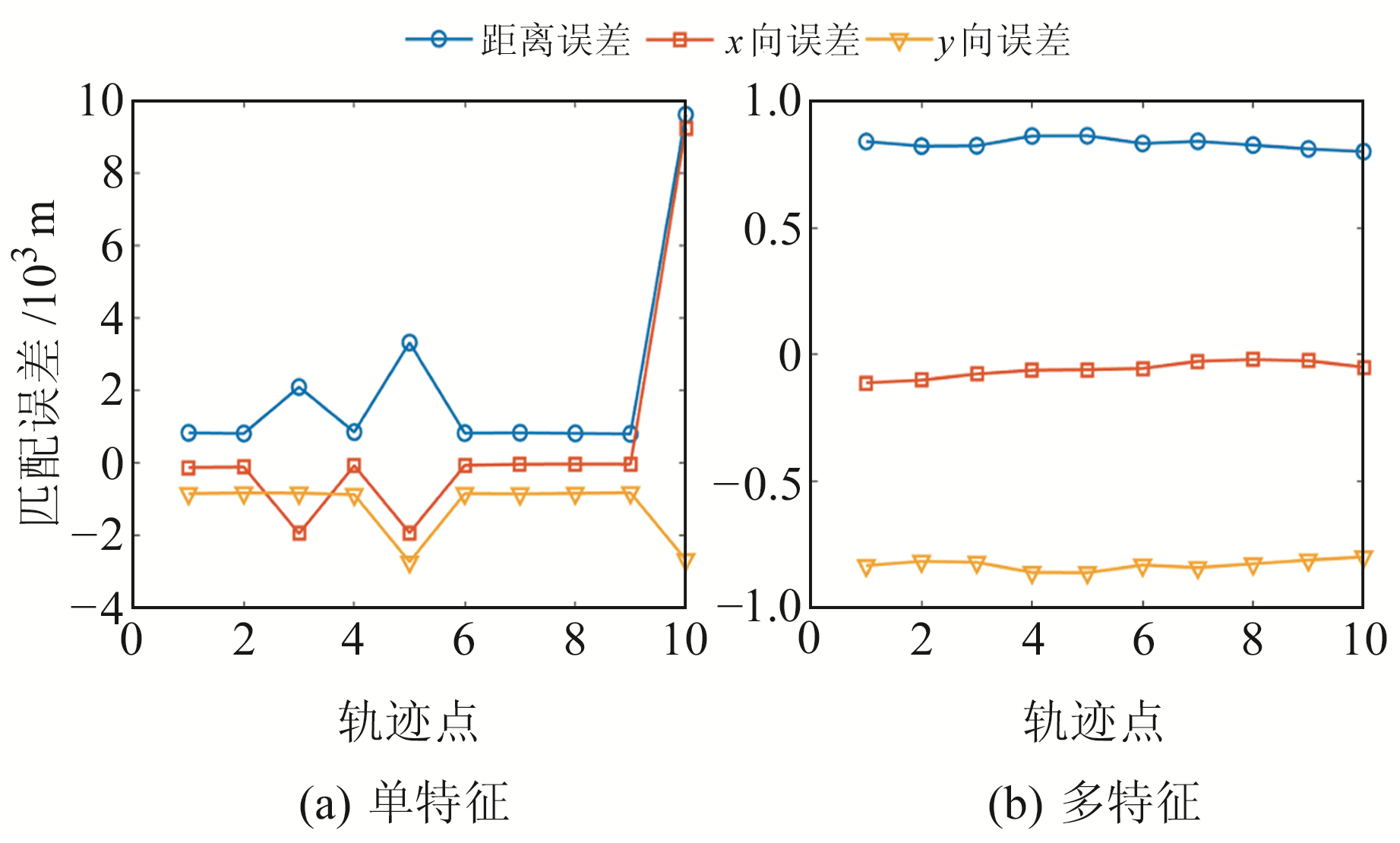
由图 6可知,相较于单特征分析准则,多特征分析准则适配区的匹配轨迹更优,误匹配率更低,能更好地评价区域的适配性。为使对比分析更科学严谨,对上述2个轨迹图的x向误差、y向误差、距离误差进行统计(图 7)。
|
图 7 单特征和多特征适配区轨迹误差 Fig. 7 Trajectory error of single feature and multi feature in adaptive area |
由图 7可知,单特征适配区中轨迹点3、5和10出现明显的误匹配情况,而多特征适配区则无明显的误匹配点,且误差基本稳定在1 km以内。为直观地体现单特征和多特征分析适配区的匹配误差,对3种误差进行统计分析,结果如表 1所示。
|
|
表 1 单特征与多特征适配区误差对比 Tab. 1 Error comparison between single feature and multi feature in adaptive area |
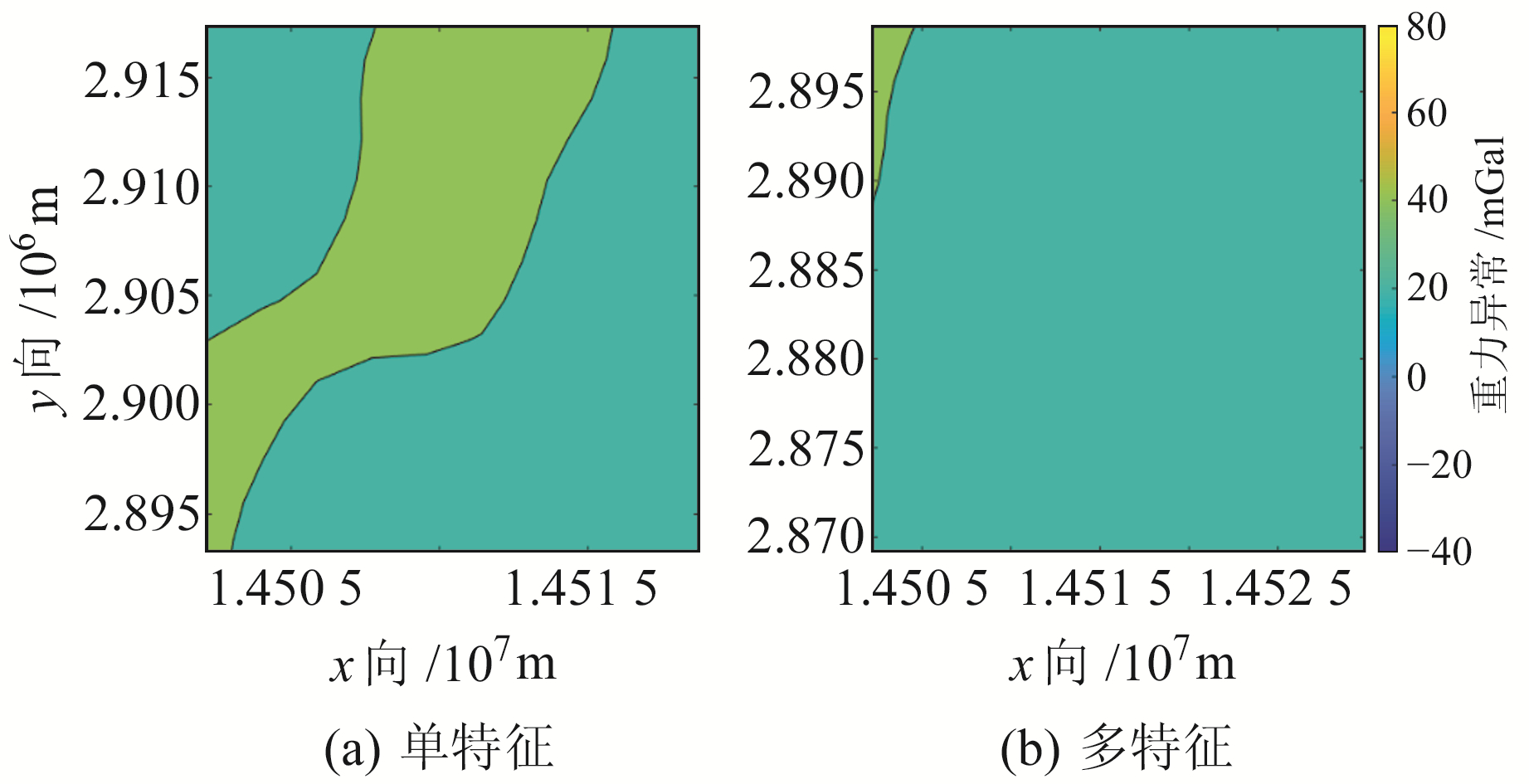
对单特征与多特征分析准则在非适配区的适配性进行验证分析,非适配区重力异常如图 8所示。单特征分析准则非适配区重力异常统计信息如下:最大值为41.70 mGal,最小值34.40 mGal,最大重力异常差异为7.30 mGal,平均值为38.78 mGal。多特征分析准则非适配区重力异常统计信息如下:最大值为40.80 mGal,最小值为27.30 mGal,最大重力异常差异为13.50 mGal,平均值为33.48 mGal。
|
图 8 非适配区重力异常 Fig. 8 Gravity anomalies in non-adaptive area |
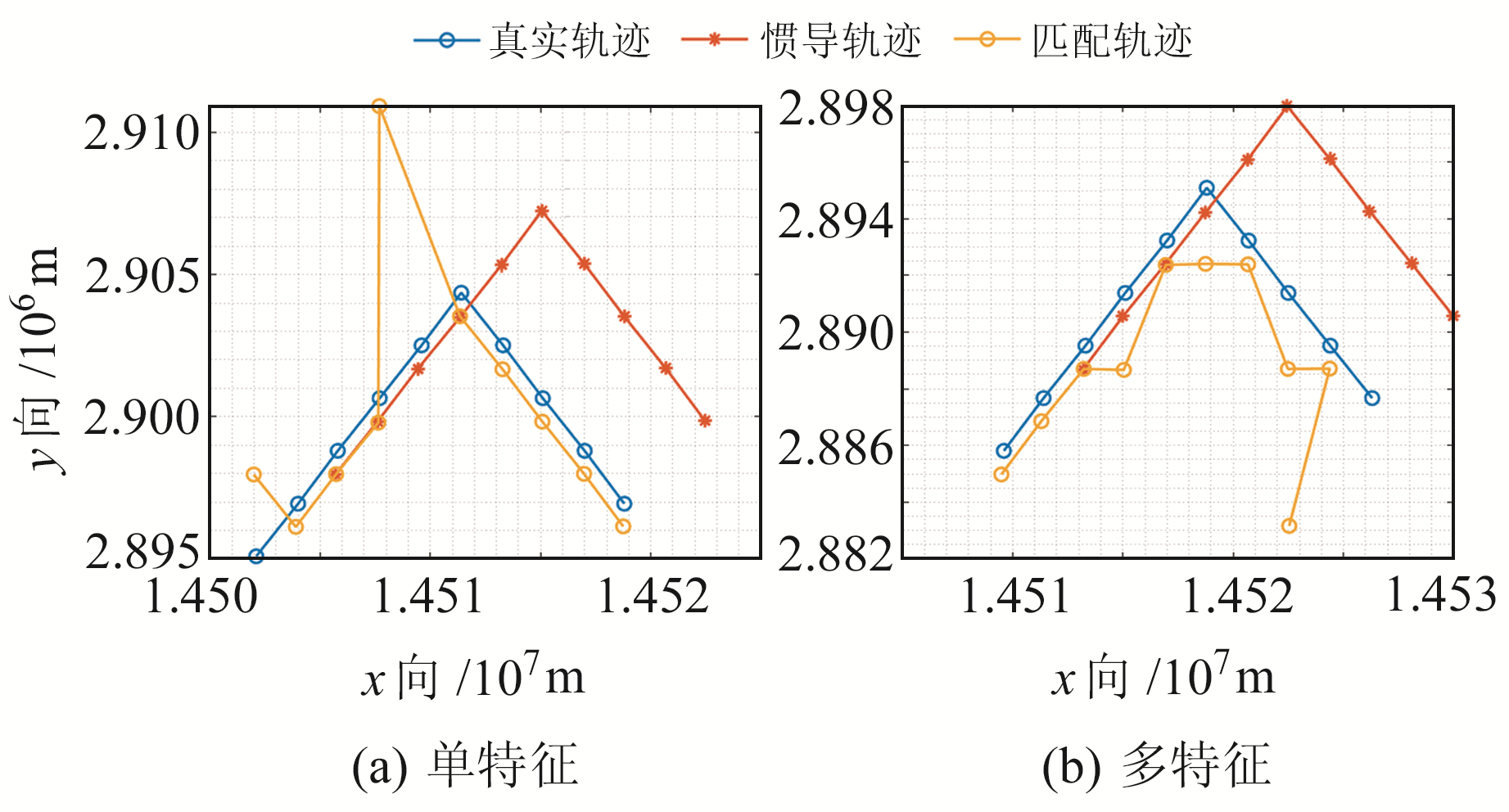
为避免航线对匹配精度的影响,在单特征和多特征2种方法所选非适配区内设计相同航线对其进行实验验证。其中,潜器惯性导航系统的参数设置与适配区仿真轨迹参数一致。单特征分析非适配区的真实轨迹起始坐标为x=145 021 00 m、y=289 509 0 m;多特征分析非适配区的真实轨迹起始坐标为x=145 096 00 m、y=288 581 0 m。真实轨迹如图 9所示。
|
图 9 单特征和多特征非适配区轨迹 Fig. 9 Trajectory of single feature and multi feature in non-adaptive area |
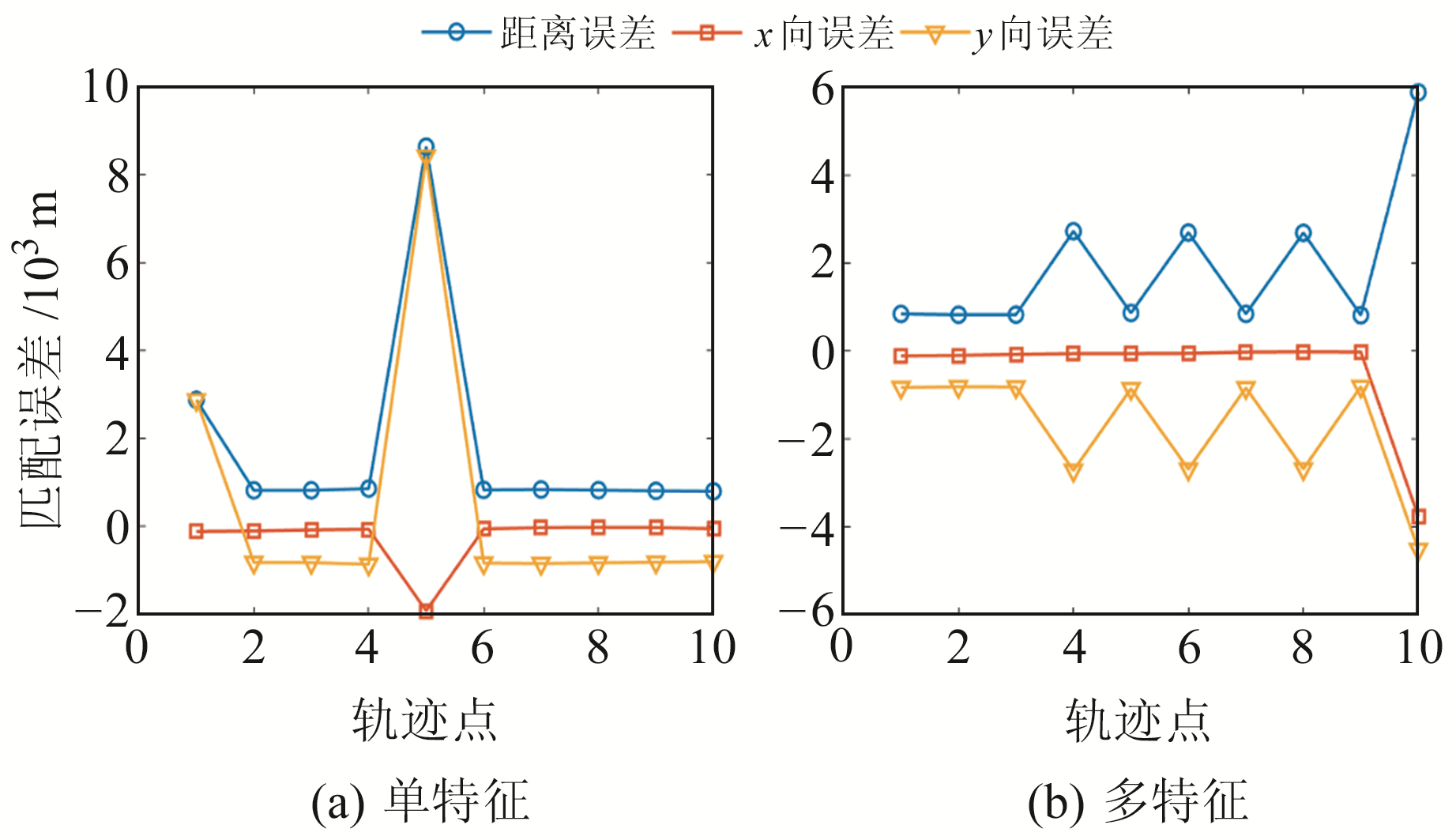
对于非适配区的非适配性来说,轨迹点的误匹配率越高,表明区域的非适配性越高,该区域不宜进行重力匹配导航。由图 9可知,多特征非适配区误匹配率约为40%,而单特征非适配区误匹配率约为20%,多特征非适配区误匹配率明显大于单特征非适配区误匹配率,表明多特征分析准则筛选的区域更能体现其非适配性。图 10为上述2个轨迹图的x向误差、y向误差和距离误差。
|
图 10 单特征和多特征非适配区轨迹误差 Fig. 10 Trajectory error of single feature and multi feature in non-adaptive area |
从图 10可以看出,单特征适配区中轨迹点1和5出现误匹配情况,而多特征适配区中有4个轨迹点出现误匹配情况,多特征分析准则更能反映区域非适配性。表 2为单特征分析和多特征分析非适配区的匹配误差。
|
|
表 2 单特征与多特征非适配区误差对比 Tab. 2 Error comparison between single feature and multi feature in non-adaptive area |
综上分析可知,在适配区验证方面,通过单特征与多特征分析准则的适配区重力异常统计信息可以看出,多特征准则所选适配区最大重力异常差异值为108.30 mGal,单特征准则所选适配区最大重力异常差异值仅为24.40 mGal,多特征准则筛选的适配区最大重力异常差异值远大于单特征所选适配区。由TERCOM算法实验验证的匹配轨迹点可知,多特征准则匹配轨迹点的误匹配率基本为0,且误差基本稳定在1 km以内,而单特征准则误匹配率约为30%,其轨迹误差均值在1 km以上,表明多特征准则所选区域更加适合匹配。从单特征和多特征适配区的误差来看,多特征适配区的RMS值远小于单特征适配区,说明多特征准则所选区域导航误差较小。在非适配区验证方面,两种准则在非适配区的最大重力异常差异值和标准差都较为接近,区域重力异常值离散度较小;TERCOM算法匹配轨迹点的误匹配率相差较大,多特征准则出现频率约为40%,而单特征准则出现频率仅为20%;多特征非适配区的轨迹误差相较于单特征非适配区更大。作为筛选非适配区的准则,在其所筛选区域开展重力匹配导航应出现大量误匹配情况,故多特征准则在筛选非适配区方面相较于单特征准则更为准确。
综上可知,多特征准则在适配区和非适配区筛选方面更加准确合理,能更好地评价分析重力匹配导航区的适配性问题。
4 结语本文对比分析基于信息熵的单特征分析准则与基于多属性决策的多特征分析准则两种重力匹配适配区划分方式。实验结果表明,在适配区匹配验证方面,多特征准则匹配轨迹基本无误匹配点,且误差基本稳定在1 km以内,而单特征准则误匹配率和轨迹误差较大,故多特征分析准则所选适配区相较于单特征分析准则更适合进行匹配导航;在非适配区匹配验证方面,多特征匹配区的轨迹点误匹配率高于单特征匹配区,且多特征匹配区的轨迹误差约为单特征匹配区的2倍,表明其筛选的区域不宜进行匹配导航。综上可知,单特征分析准则无法明显区分适配区与非适配区,而多特征分析准则可以准确有效地评价重力匹配导航区的适配性。
| [1] |
李姗姗. 水下重力辅助惯性导航的理论与方法研究[D]. 郑州: 信息工程大学, 2010 (Li Shanshan. Research on the Theory and Method of Underwater Gravity-Aided Inertial Navigation[D]. Zhengzhou: Information Engineering University, 2010)
(  0) 0) |
| [2] |
Bishop G C. Gravitational Field Maps and Navigational Errors[J]. IEEE Journal of Oceanic Engineering, 2002, 27(3): 726-737 DOI:10.1109/JOE.2002.1040954
(  0) 0) |
| [3] |
李婷, 张金生, 王仕成, 等. 基于改进地磁熵的地磁适配区选择准则[J]. 大地测量与地球动力学, 2014, 34(5): 151-155 (Li Ting, Zhang Jinsheng, Wang Shicheng, et al. Study on Selection of Geomagnetic Suitable Matching Area Based on Improved Geomagnetic Entropy[J]. Journal of Geodesy and Geodynamics, 2014, 34(5): 151-155)
(  0) 0) |
| [4] |
Xiong L, Li K H, Tang J Q, et al. Research on Matching Area Selection Criteria for Gravity Gradient Navigation Based on Principal Component Analysis and Analytic Hierarchy Process[C]. Ninth International Symposium on Multispectral Image Processing and Pattern Recognition(MIPPR2015), Enshi, 2015
(  0) 0) |
| [5] |
李钊伟, 郑伟, 房静, 等. 基于新型主成分加权平均归一化法优选水下重力匹配导航适配区[J]. 地球物理学报, 2019, 62(9): 3 269-3 278 (Li Zhaowei, Zheng Wei, Fang Jing, et al. Optimizing Suitability Area of Underwater Gravity Matching Navigation Based on a New Principal Component Weighted Average Normalization Method[J]. Chinese Journal of Geophysics, 2019, 62(9): 3 269-3 278)
(  0) 0) |
| [6] |
马越原, 欧阳永忠, 黄谟涛, 等. 基于重力场特征参数信息熵的适配区选择方法[J]. 中国惯性技术学报, 2016, 24(6): 763-768 (Ma Yueyuan, Ouyang Yongzhong, Huang Motao, et al. Selection Method for Gravity-Field Matchable Area Based on Information Entropy of Characteristic Parameters[J]. Journal of Chinese Inertial Technology, 2016, 24(6): 763-768)
(  0) 0) |
| [7] |
Zong J W, Bian S F, Tong Y D, et al. Classification of Gravity Matching Areas Using PSO-BP Neural Networks Based on PCA and Satellite Altimetry Data over the Western Pacific[J]. Sensors, 2022, 22(24)
(  0) 0) |
| [8] |
Li Y T, Wang C L, Zhang J, et al. Selection Method of the Matching Area of Underwater Gravity-Aided Inertial Navigation Based on Vector Characteristics[C]. 39th Chinese Control Conference(CCC), Shenyang, 2020
(  0) 0) |
| [9] |
肖云, 张锦柏, 曹杰, 等. 多属性决策理论的重力匹配导航适配性分析[J]. 武汉大学学报: 信息科学版, 2023, 48(7): 10 89-1 099 (Xiao Yun, Zhang Jinbai, Cao Jie, et al. Suitability Analysis of Gravity Matching Navigation Based on Multiple Attribute Decision Making Theory[J]. Geomatics and Information Science of Wuhan University, 2023, 48(7): 10 89-1 099)
(  0) 0) |
| [10] |
周薇, 李筱菁. 基于信息熵理论的综合评价方法[J]. 科学技术与工程, 2010, 10(23): 5 839-5 843 (Zhou Wei, Li Xiaojing. A Comprehensive Evaluation Method Based on Information Entropy[J]. Science Technology and Engineering, 2010, 10(23): 5 839-5 843)
(  0) 0) |
| [11] |
申滨, 刘笑笑, 黄晓舸. 基于多属性决策模型的雾计算用户关联算法[J]. 北京邮电大学学报, 2021, 44(4): 68-74 (Shen Bin, Liu Xiaoxiao, Huang Xiaoge. User Association Algorithm for Fog Computing Based on Multiple Attribute Decision Making Model[J]. Journal of Beijing University of Posts and Telecommunications, 2021, 44(4): 68-74)
(  0) 0) |
2. State Key Laboratory of Geo-Information Engineering, 1 Mid-Yanta Road, Xi'an 710054, China;
3. Xi'an Institute of Surveying and Mapping, 1 Mid-Yanta Road, Xi'an 710054, China
 2024, Vol. 44
2024, Vol. 44


