2. 湖南科技大学测绘遥感信息工程湖南省重点实验室,湖南省湘潭市桃园路,411201;
3. 湖南科技大学地球科学与空间信息工程学院,湖南省湘潭市桃园路,411201
卫星与传感器技术的发展为大地测量提供了更为丰富和高效的观测手段,但受观测条件以及观测环境限制,在PolInSAR(polarimetric interferometric synthetic aperture radar)地表参数反演、GNSS空间环境参数反演以及地球重力场反演等大地测量反演中常会出现病态问题[1-3],严重影响物理参数反演的可靠性,须采用合理的病态问题解算方法,提高物理参数反演精度。正则化方法与TSVD方法是目前最为常用的病态问题解算方法,可有效改善病态模型参数的反演精度与稳定性。其中,正则化方法在最小二乘基础上增加稳定泛函约束,并通过正则化参数调节泛函约束作用,从而改善参数估计的稳定性[4-5];TSVD方法则利用奇异值分解技术,将影响参数估值方差的小奇异值截掉,进而改善参数估值精度[6]。
正则化方法与TSVD解算方式的不同导致两种方法的解算精度与适用场景有所不同。在实际应用中,应选择最为合适的解算方法以提高模型参数的反演质量。然而,由于病态性对参数估值方差的严重影响,通过常规精度分析方法难以确定两种解算方法的优劣[7]。文献[7-8]从均方误差角度对两种方法的解算过程进行分析,尽管两种方法处理病态问题的方式不同,但在均方误差意义下,二者均是通过引入少量偏差,大幅降低方差,从而使均方误差下降。因此,通过分析均方误差的下降量可以确定出更优的解算方案。然而,均方误差的计算需要模型参数真值,在实际应用中参数真值是未知的,均方误差也难以准确计算。针对此问题,本文提出一种解算精度相对比较分析方法,通过计算均方误差相对变化量,避免计算过程中引入参数真值,实现病态问题解算方法的参数估值误差比较分析,进而确定更优的解算方法,提高模型参数估值精度。
1 基于相对均方误差的病态问题解算精度比较分析方法均方误差可反映模型参数估值相对于真值的离散程度,是评价模型参数估计质量的重要指标。病态模型参数估值的均方误差可表示为[8]:
| $\begin{aligned} & M=E\left[(\hat{\boldsymbol{X}}-E(\hat{\boldsymbol{X}}))^{\mathrm{T}}(\hat{\boldsymbol{X}}-E(\hat{\boldsymbol{X}}))\right]+ \\ & (E(\hat{\boldsymbol{X}})-\widetilde{\boldsymbol{X}})^{\mathrm{T}}(E(\hat{\boldsymbol{X}})-\tilde{\boldsymbol{X}})=T+\boldsymbol{b}^{\mathrm{T}} \boldsymbol{b} \end{aligned} $ | (1) |
式中,M表示均方误差,E表示数学期望运算,
参数估值方差的计算无需参数真值,可由两种方法的方差计算式计算得到。其中,正则化方法的方差计算式可表示为:
| $ T_r=\sigma_0^2\left(\sum\limits_{i=1}^n \frac{\gamma_i^2}{\left(\gamma_i^2+\alpha\right)^2}\right) $ | (2) |
式中,n表示未知模型参数的个数;σ02为单位权方差,可由仪器观测精度得到,或利用多余观测估计得到,具体可表示为:
| $ \hat{\sigma}_0^2=\frac{\boldsymbol{V}^{\mathrm{T}} \boldsymbol{V}}{m-n} $ | (3) |
式中, V表示观测值残差,考虑到正则化方法与TSVD方法存在偏差,观测值残差主要采用最小二乘无偏估计获得;m表示观测值个数。
TSVD方法的方差计算式可表示为:
| $T_t=\sigma_0^2\left(\sum\limits_{i=1}^t \frac{1}{\gamma_i^2}\right) $ | (4) |
在计算得到参数估值方差后,若能获得偏差则可有效计算出均方误差,进而分析不同方法的病态问题解算精度。偏差计算需要模型参数真值,而在实际应用中无法获得真值。鉴于此,考虑采用相对均方误差,避免真值的引入。由均方误差公式可得2次估计的相对均方根误差为:
| $ \begin{aligned} \boldsymbol{k}=\boldsymbol{R}_1-\boldsymbol{R}_0 & =E\left(\hat{\boldsymbol{X}}_1-\widetilde{\boldsymbol{X}}\right)- \\ E\left(\hat{\boldsymbol{X}}_0-\widetilde{\boldsymbol{X}}\right) & =E\left(\hat{\boldsymbol{X}}_1-\hat{\boldsymbol{X}}_0\right) \end{aligned} $ | (5) |
式中,k表示均方根误差相对变化量,R1表示病态问题解算方法的均方根误差,R0表示最小二乘估计均方根误差。由式(5)可知,相对均方根误差不受参数真值影响,为模型参数估值变化量的数学期望值,仅与模型参数的2次估值有关。考虑到各模型参数估值均为平差后的平均值,因此,相对均方根误差向量可近似为:
| $ \boldsymbol{k}=\left|\hat{\boldsymbol{X}}_1-\hat{\boldsymbol{X}}_0\right| $ | (6) |
由此可得到2次估计的均方根误差变化量近似为:
| $ r=\left(\sum\limits_{i=1}^n\left|\hat{\boldsymbol{X}}_1^i-\hat{\boldsymbol{X}}_0^i\right|\right) $ | (7) |
式中,r表示均方根误差变化量。上式表明,均方根误差变化量可近似为模型参数估值变化量。鉴于均方根误差由标准差和偏差2个部分组成,因此,均方根误差变化量应包含标准差变化量和偏差变化量2个部分。
在各方法的方差可准确计算的情况下,标准差变化量可由方差变化量取平方根计算得到,则正则化估值与TSVD估值的标准差变化量可表示为:
| $ \left\{\begin{array}{l} s_r=\sqrt{T_0-T_r} \\ s_t=\sqrt{T_0-T_t} \end{array}\right. $ | (8) |
式中, sr表示正则化估值的标准差变化量,st表示TSVD估值的标准差变化量,T0表示最小二乘估计方差。由两种方法的标准差变化量结合式(1)可得:
| $ \left\{\begin{array}{l} p_r=r_r-s_r \\ p_t=r_t-s_t \end{array}\right. $ | (9) |
式中,pr表示正则化法的偏差近似变化量,pt表示TSVD法的偏差近似变化量,rr表示正则化法的均方根误差变化量,rt表示TSVD法的均方根误差变化量。
正则化方法与TSVD方法降低均方根误差主要是通过引入偏差促使标准差下降来实现。因此,标准差下降量与偏差引入量的差值大小决定了两种方法解算的优劣。在绝对偏差无法有效计算的情况下,通过比较正则化方法与TSVD方法相对于同一最小二乘算法的标准差相对下降量与偏差相对引入量的差值,即可比较均方根误差相对下降量大小,进而判定两种方法的解算优劣。两种方法的均方根误差相对下降量可表示为:
| $ \left\{\begin{array}{l} z_r=s_r-p_r \\ z_t=s_t-p_t \end{array}\right. $ | (10) |
式中,zr与zt分别表示正则化方法与TSVD方法的均方根误差相对下降量。均方根误差相对下降量越大,则解算结果越优,由此即可确定精度更高的病态问题解算方法。
2 实验分析 2.1 空间坐标测量反演实验空间距离交会是大地测量中动态定位的常用测量手段,但在部分偏僻区域,受交会观测几何条件限制,交会测量的坐标解算常常出现病态问题,导致坐标解算精度较低,须采用病态问题解算方法以提高坐标参数估计精度。为验证本文分析方法的有效性,采用文献[10]中空间距离交会算例进行实验分析。算例中包含2个未知点,坐标设计真值为(0,0,0)与(7,10,-5)。分别采用正则化方法与TSVD方法进行解算,在参数真值未知的情况下,采用本文方法对比分析两种方法的估值结果,其中正则化参数与截断参数的选择以及均方根误差相对下降量情况见表 1。
|
|
表 1 均方根误差相对变化 Tab. 1 Relative changes of root mean square error |
由表 1可知,采用不同方法确定正则化参数与截断参数时,均方根误差相对下降量也有所不同,表明在不同正则化参数与截断参数情况下,正则化法与TSVD法的解算精度存在差异。由均方根误差相对下降量大小可知,采用最小MSE法确定正则化参数的正则化法的均方根误差相对下降量最大,其模型参数解算结果最优;其次为采用L曲线法确定截断参数的TSVD法和采用L曲线法确定正则化参数的正则化法;最后则为采用最小MSE法确定截断参数的TSVD法。为验证本文比较方法的有效性,利用坐标参数的设计真值计算各方法的坐标参数估值误差,结果见表 2(单位m)。
|
|
表 2 不同方法的模型参数估计 Tab. 2 Model parameters estimation using different methods |
由表 2可知,最小二乘估计受模型病态性影响,参数估值误差较大,难以得到参数的可靠估值,而采用正则化方法与TSVD方法进行解算均可有效降低参数估值误差。由各方法估值误差大小可知,采用最小MSE法确定正则化参数的正则化法的模型参数估值误差最小,表明参数估计结果最优;其次为采用L曲线法确定截断参数的TSVD法和采用L曲线法确定正则化参数的正则化法;最后则为采用最小MSE法确定截断参数的TSVD法。这与本文提出的比较分析方法的分析结果一致,从而验证了本文方法的可行性与有效性。
2.2 PolInSAR植被高测量反演实验PolInSAR技术具备良好的穿透测量能力,可有效实现大范围植被覆盖区结构参数的测量反演。采用PolInSAR技术测量反演植被高参数时,受干涉相干机制及模型过度参数化影响,植被高参数反演常存在病态问题,严重影响植被高参数的反演精度,因此,有必要选择合理有效的病态模型解算方法,以改善植被高参数的反演精度[1]。为验证本文算法分析选择病态问题解算方法的有效性,分别采用正则化方法与TSVD方法进行解算,并对比分析两种方法的植被高反演结果,确定最佳反演方法。正则化参数与截断参数的选择以及均方根误差相对下降量情况见表 3。
|
|
表 3 均方根误差相对变化 Tab. 3 Relative changes of root mean square error |
由表 3可知,采用正则化方法与TSVD方法解算后,均方根误差相对下降量较大,其原因主要为设计矩阵中存在一个极小奇异值,导致常规解算参数的估值方差较大。在奇异值被正则化方法与TSVD方法有效处理后,方差得到大幅改善,均方根误差也实现大幅下降。由均方根误差相对下降量大小可知,采用最小MSE法确定截断参数的TSVD方法的均方根误差相对下降量最大,表明相比于其他方法,其均方根误差最小,参数估计结果最优;其次为采用最小MSE法确定正则化参数的正则化方法和采用L曲线法确定正则化参数的正则化方法;最后则为采用L曲线法确定截断参数的TSVD方法。图 1为各方法的解算结果,其中图 1(f)为采用LiDAR技术获取的植被高参数,由于LiDAR技术反演的植被高精度远高于PolInSAR技术,因此LiDAR反演结果常作为真值验证分析PolInSAR反演结果的可靠性。但LiDAR技术易受雨雪、云雾等天气状况影响,导致部分区域反演结果缺失,因此只有在反演成功的区域可作为植被高参数真值对比分析各方法PolInSAR植被高反演精度。
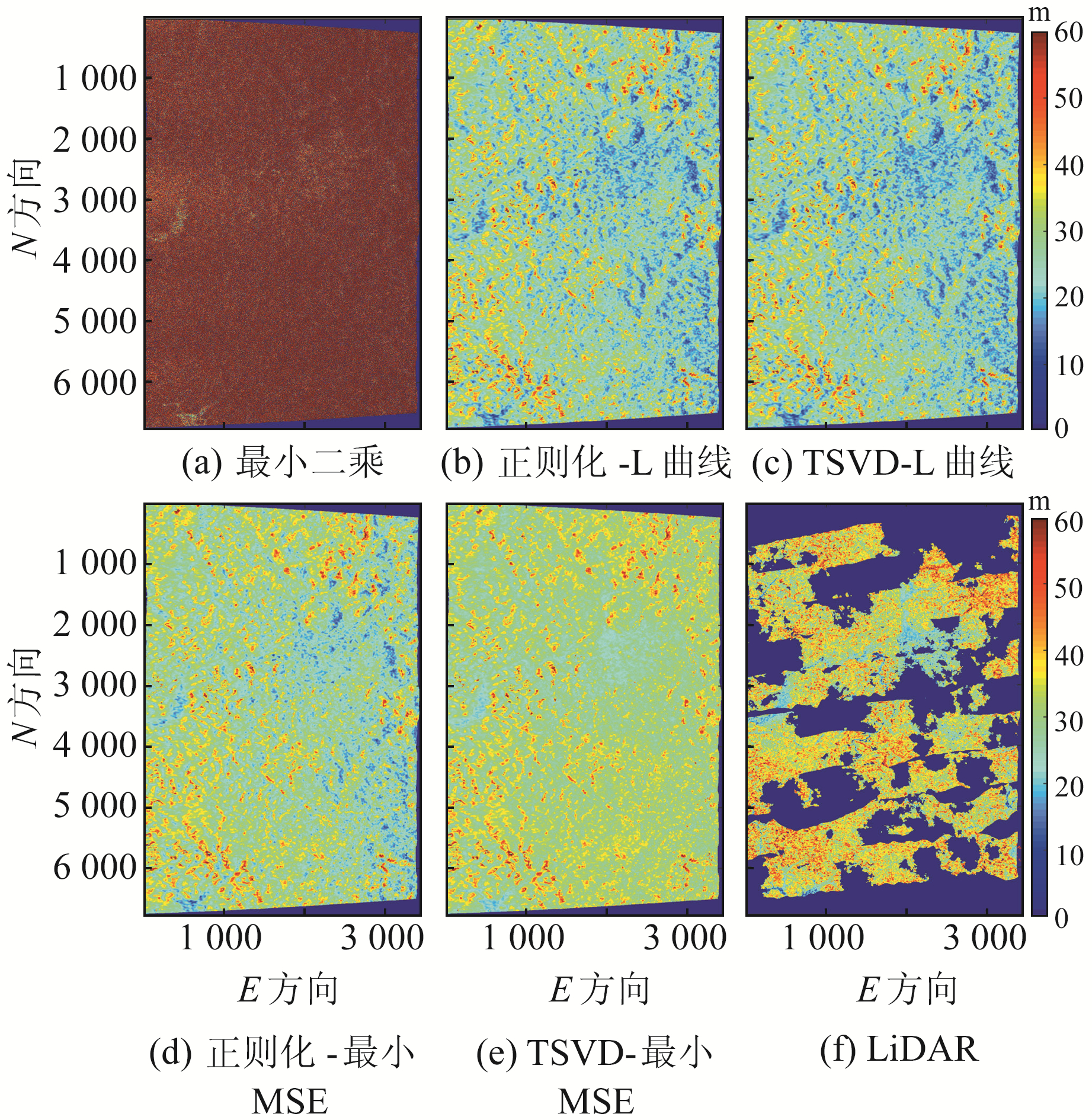
|
图 1 不同方法的植被高反演结果 Fig. 1 Vegetation inversion results of each methods |
图 1(a)常规最小二乘方法的植被高估计结果与LiDAR反演结果存在巨大差异,表明最小二乘方法受病态问题影响较大,已无法得到植被高参数的有效估值。图 1(e)为采用最小MSE法确定截断参数的TSVD方法的植被高参数估计结果,相比于其他方法,其植被高估值最接近于LiDAR估值,估计结果最优;其次为图 1(d)采用最小MSE法确定正则化参数的正则化法;图 1(b)采用L曲线法确定正则化参数的正则化法与图 1(c)采用L曲线法确定截断参数的TSVD方法的反演结果相近。为进一步分析各方法的反演精度,基于LiDAR植被高反演结果,均匀选取1 170块样地,统计分析各方法的反演误差,结果如图 2所示。

|
图 2 不同方法的植被高反演误差统计 Fig. 2 Statistics of vegetation inversion errors of each methods |
由图 2可知,图 2(a)最小二乘估计的植被高参数估值的均方根误差较大,已基本为无效估计。从4种病态问题解算方法的均方根误差可知,图 2(e)采用最小MSE法确定截断参数的TSVD方法的均方根误差最小,植被高参数估计结果最优;其次为图 2(d)采用最小MSE法确定正则化参数的正则化法和图 2(b)采用L曲线法确定正则化参数的正则化法;最后则为图 2(c)采用L曲线法确定截断参数的TSVD方法。这与本文提出的病态问题解算精度相对比较分析方法的分析结果一致,进一步验证了该方法的可行性与有效性。
3 结语病态问题会严重影响大地测量模型参数反演的可靠性与稳定性,选择合理的病态问题解算方法有助于改善模型参数的反演精度。针对病态问题解算方法的参数估值精度比较分析问题,本文提出一种基于均方误差相对变化的病态模型参数估计结果比较分析方法,可有效实现病态问题解算方法的精度比较与优选。通过理论和实验分析得到以下结论:
1) 利用正则化方法与TSVD方法相对于最小二乘方法的模型参数估值变化量可近似估算出均方根误差的相对变化量。
2) 基于病态问题解算中偏差增加与标准差下降的相对关系可确定出均方根误差相对下降量,依据相对下降量大小可比较分析病态问题的解算精度。
3) 空间坐标测量实验与PolInSAR植被高反演实验结果表明,相对均方误差比较分析方法可有效实现病态问题解算方法的精度比较与优选。
| [1] |
林东方, 朱建军, 李志伟, 等. 顾及地表散射贡献与多基线参数线性相关性的PolInSAR植被高反演方法[J]. 测绘学报, 2023, 52(1): 51-60 (Lin Dongfang, Zhu Jianjun, Li Zhiwei, et al. A Multi-Baseline PolInSAR Forest Height Inversion Method Taking into Account the Ground Scattering Effects and Parametric Linear[J]. Acta Geodaetica et Cartographica Sinica, 2023, 52(1): 51-60)
(  0) 0) |
| [2] |
Wang L Y, Sun L X, Xu G Y. An Improved Bayesian von Karman Regularization Method for the Joint Inversion of GNSS and InSAR Data[J]. Journal of Surveying Engineering, 2023, 149(1)
(  0) 0) |
| [3] |
Mu D P, Yan H M, Feng W, et al. GRACE Leakage Error Correction with Regularization Technique: Case Studies in Greenland and Antarctica[J]. Geophysical Journal International, 2017, 208(3): 1 775-1 786
(  0) 0) |
| [4] |
Wang L Y, Gu W W. A-Optimal Design Method to Determine the Regularization Parameter of Coseismic Slip Distribution Inversion[J]. Geophysical Journal International, 2020, 221(1): 440-450 DOI:10.1093/gji/ggaa030
(  0) 0) |
| [5] |
邓伟, 宋迎春, 谢雪梅. 基于GCV的迭代Tikhonov正则化在测绘中的应用[J]. 大地测量与地球动力学, 2023, 43(6): 587-592 (Deng Wei, Song Yingchun, Xie Xuemei. Application of Iterative Tikhonov Regularization Based on GCV in Surveying and Mapping[J]. Journal of Geodesy and Geodynamics, 2023, 43(6): 587-592)
(  0) 0) |
| [6] |
Hanson R J. A Numerical Method for Solving Fredholm Integral Equations of the First Kind Using Singular Values[J]. SIAM Journal on Numerical Analysis, 1971, 8(3): 616-622 DOI:10.1137/0708058
(  0) 0) |
| [7] |
林东方, 姚宜斌, 郑敦勇, 等. 利用TSVD参数估值变化特性确定算法截断参数[J]. 测绘学报, 2022, 51(8): 1 787-1 796 (Lin Dongfang, Yao Yibin, Zheng Dunyong, et al. Determination of Truncation Parameter Based on the Differences of TSVD Parameter Estimates for Ill-Posed Problems in Geodesy[J]. Acta Geodaetica et Cartographica Sinica, 2022, 51(8): 1 787-1 796)
(  0) 0) |
| [8] |
徐天河, 杨元喜. 均方误差意义下正则化解优于最小二乘解的条件[J]. 武汉大学学报: 信息科学版, 2004, 29(3): 223-226 (Xu Tianhe, Yang Yuanxi. Condition of Regularization Solution Superior to LS Solution Based on MSE Principle[J]. Geomatics and Information Science of Wuhan University, 2004, 29(3): 223-226)
(  0) 0) |
| [9] |
Lin D F, Zhu J J, Li C K, et al. Bias Reduction Method for Parameter Inversion of Ill-Posed Surveying Model[J]. Journal of Surveying Engineering, 2020, 146(3)
(  0) 0) |
| [10] |
归庆明, 张建军, 郭建锋. 压缩型抗差估计[J]. 测绘学报, 2000, 29(3): 224-228 (Gui Qingming, Zhang Jianjun, Guo Jianfeng. Shrunken Type-Robust Estimation[J]. Acta Geodaetica et Cartographic Sinica, 2000, 29(3): 224-228)
(  0) 0) |
2. Hunan Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Hunan University of Science and Technology, Taoyuan Road, Xiangtan 411201, China;
3. School of Earth Sciences and Spatial Information Engineering, Hunan University of Science and Technology, Taoyuan Road, Xiangtan 411201, China
 2024, Vol. 44
2024, Vol. 44


