2024, Vol. 44
表1(Table 1)
2. 安徽理工大学矿区环境与灾害协同监测煤炭行业工程研究中心，安徽省淮南市泰丰大街168号，232001;
3. 安徽理工大学矿山采动灾害空天地协同监测与预警安徽普通高校重点实验室，安徽省淮南市泰丰大街168号，232001
GNSS是进行导航定位和遥感的重要工具，也被用于GNSS气象学领域[1-2]。然而，GNSS观测结果易受误差影响，其中对流层延迟是主要来源之一[3]。对流层延迟主要通过ZTD模型进行计算，包括依赖实测气象参数的模型[4-5]和经验模型[6-14]。前者需要实测气象参数来确定大气中水汽含量对导航定位的影响，但在实际情况下，有时无法获取稳定的气象参数。后者仅基于大量经验数据来确定不同影响因素和经验ZTD之间的映射关系，无需实测气象参数，但模拟季节或日变化时存在局限性，尤其是模拟ZTD快速变化。
为了提高预测精度，本文利用机器学习方法[15-17]建立欧洲地区ZTD优化模型(MGPT3)，并与GPT3和UNB3m模型进行精度对比。研究成果对于提高经验ZTD模型精度、区域ZTD建模和短时段内GNSS水汽反演等方面具有重要意义。
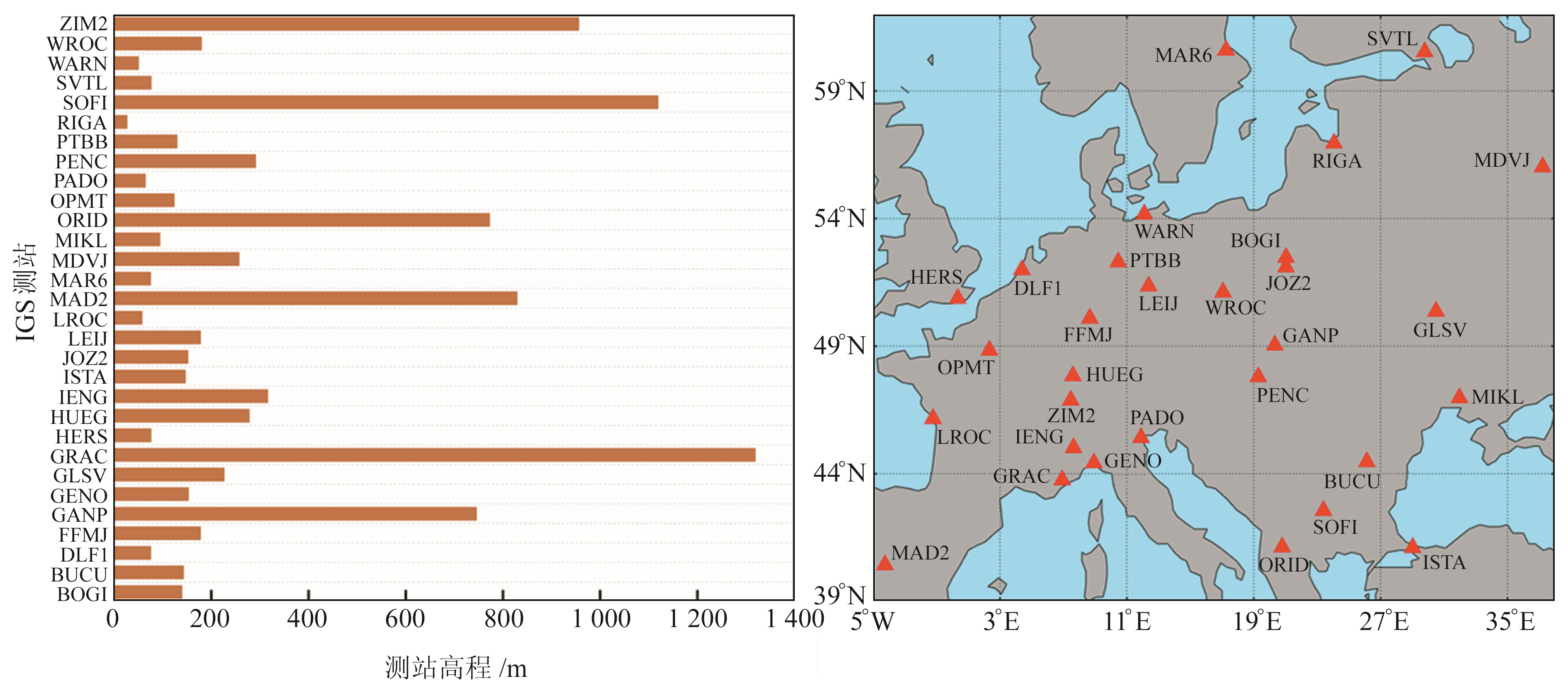
1 数据来源及处理欧洲地区(38°~62°N，5°W~38°E)地形较为平坦，具有漫长海岸线，以温带气候为主，受海洋影响全年温和多雨。该地区ZTD受地理和气候条件影响表现出较大的可变性，这为ZTD建模工作带来挑战。选取欧洲地区30个IGS站点2020年doy1~366的RINEX观测数据，利用GAMIT软件对其进行解算处理，得到时间分辨率为2 h的ZTD解算数据GNSS_ZTD，并将其作为真值[18]。使用GPT3和UNB3m模型进行精度对比分析，将欧洲地区30个IGS站点的经纬度、大地高等时空信息输入模型中进行计算，得到相应的GPT3_ZTD和UNB3m_ZTD值。图 1为30个站点的空间分布以及海拔情况。随机选择80%的站点数据作为训练样本，剩余20%用于测试。为了降低数据量级并提高神经网络模型的训练速度，对站点数据进行归一化处理，并在获得结果后进行反归一化处理，以还原为原始数据的量级。
|
图 1 IGS测站高程与位置 Fig. 1 Elevation and location of IGS stations |
GNSS_ZTD与GPT3_ZTD之间的残差dZTD具有明显的时空变化特征[19]。本文研究重点是对dZTD进行建模，并将其作为输出值，从而更好地描述除季节变化外的ZTD变化，特别是ZTD的波动变化。本研究构建一个区域ZTD模型，将纬度、经度、大地高、年积日、每日小时数和Mean_dZTD(测站点的年平均dZTD)作为输入参数。机器学习模型的预测结果可能存在过多异常值，为了减小异常值的影响，使用Mean_dZTD作为输入，并拟合dZTD与Mean_dZTD、三维坐标和时间之间的关系，可使输出的预测结果在一定程度上受到Mean_dZTD约束，异常值不会出现过大的情况。另外，本文使用GPT3模型来表示ZTD的季节性变化。通过机器学习方法，可以将自变量与因变量之间的关系表示为：
| dZTD PSo-BP =φ(B,L,H, doy , hod, Mean_dZTD ) | (1) |
式中，φ(·)为机器学习模型，doy为年积日，hod为每日小时数(0~23 h), dZTD为GNSS_ZTD与GPT3_ZTD之间的残差，Mean_dZTD为测站点的年平均dZTD。
2.1 粒子群优化算法基本原理粒子群优化算法(particle swarm optimization, PSO)是一种基于群体智能的优化算法，其灵感来源于鸟类群体活动的行为规律。PSO的适应度函数为神经网络的输出误差，可表示为：
| fi=1nn∑q=1(yiq−xiq)2 | (2) |
式中，n为训练集样本个数；yiq和xiq分别为训练样本q在第i个粒子的位置所决定的权值和阈值。粒子速度和位置更新公式可表示为：
| \boldsymbol{V}_{i d}^t=\omega \mathbf{V}_{i d}^{t-1}+C_1 \text { random }(0, 1)\left(\boldsymbol{P}_{i d}-\boldsymbol{X}_{i d}^{t-1}\right)+ \\ C_2 \text { random }(0, 1)\left(\boldsymbol{P}_{g d}-\boldsymbol{X}_{i d}^{t-1}\right) | (3) |
| \begin{gathered} \boldsymbol{X}_{i d}^t=\boldsymbol{X}_{i d}^{t-1}+\mathbf{V}_{i d}^{t-1} \end{gathered} | (4) |
式中，i为粒子群中第i个粒子；Vid为第i个粒子的速度；Xid为第i个粒子的位置；Pid为第i个粒子搜索到的最优位置；Pgd为整个粒子群搜索到的最优位置；ω为惯性权重；C1和C2为加速常数，也称学习因子；random(0, 1)为在(0, 1)范围内变化的随机函数。
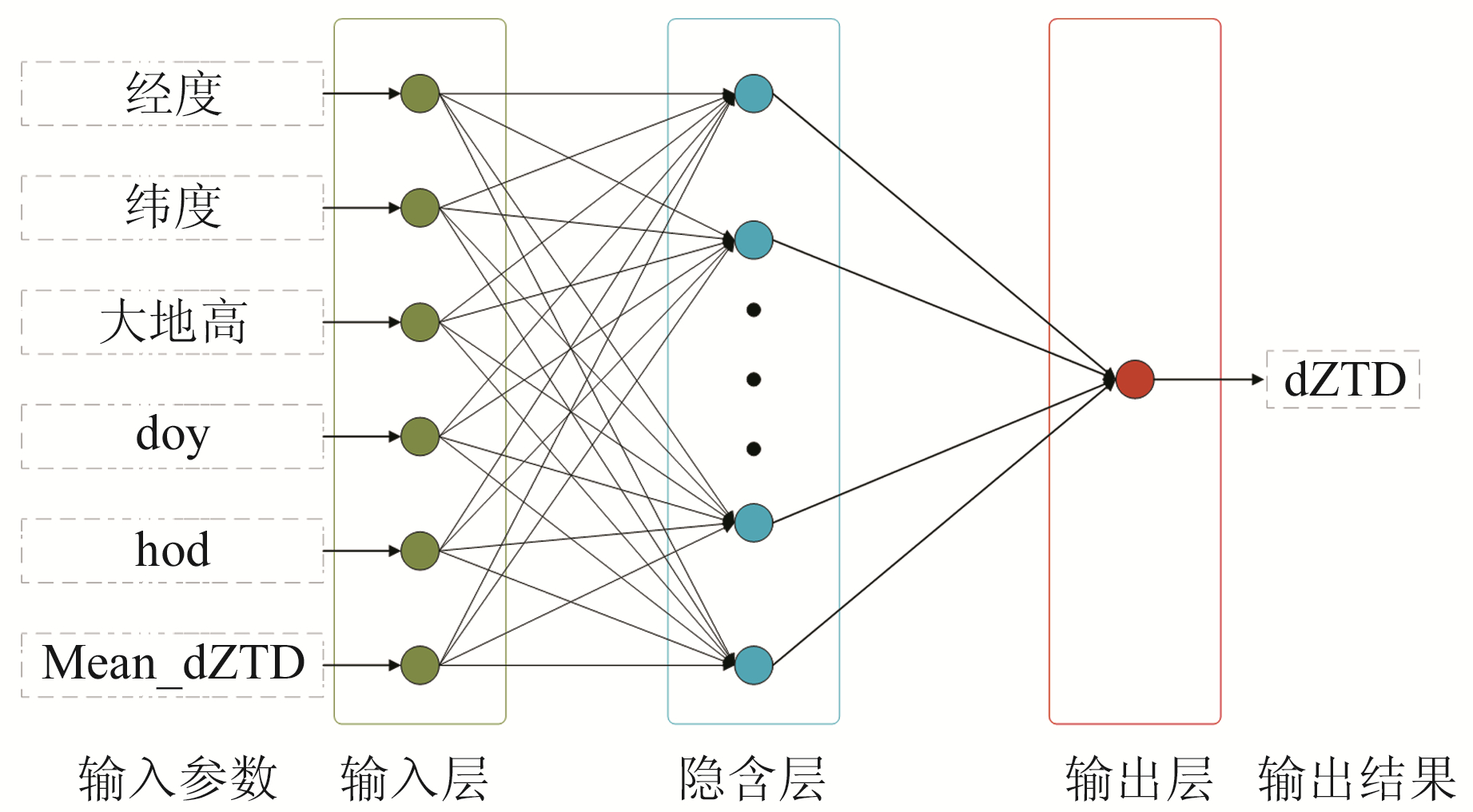
2.2 BPNN基本原理反向传播神经网络(back propagation neural network, BPNN)是一种按误差逆向传播算法训练的多层前馈神经网络，其通过不断调整神经元之间的连接权重和阈值来最小化误差函数，从而对数据进行拟合和分类。BPNN结构包括输入层、输出层和若干个隐含层，每个隐含层包含多个神经元，其模型结构如图 2所示：
| \begin{gathered} u=\boldsymbol{X}_n \boldsymbol{W}_{n m}^1+Y_m \end{gathered} | (5) |
| L_m(u)=y | (6) |
|
图 2 BPNN结构 Fig. 2 BPNN structure |
式中，Xi为神经网络的输入向量，n为输入层节点数，i∈(1, n)；Wnm1为输入层和第1层隐含层之间的权值阵列，n为输入层中第n个神经元，m为隐含层中第m个神经元；Ym为隐含层中第m个神经元的阈值参数；Lm为隐含层中第m个神经元的激活函数。
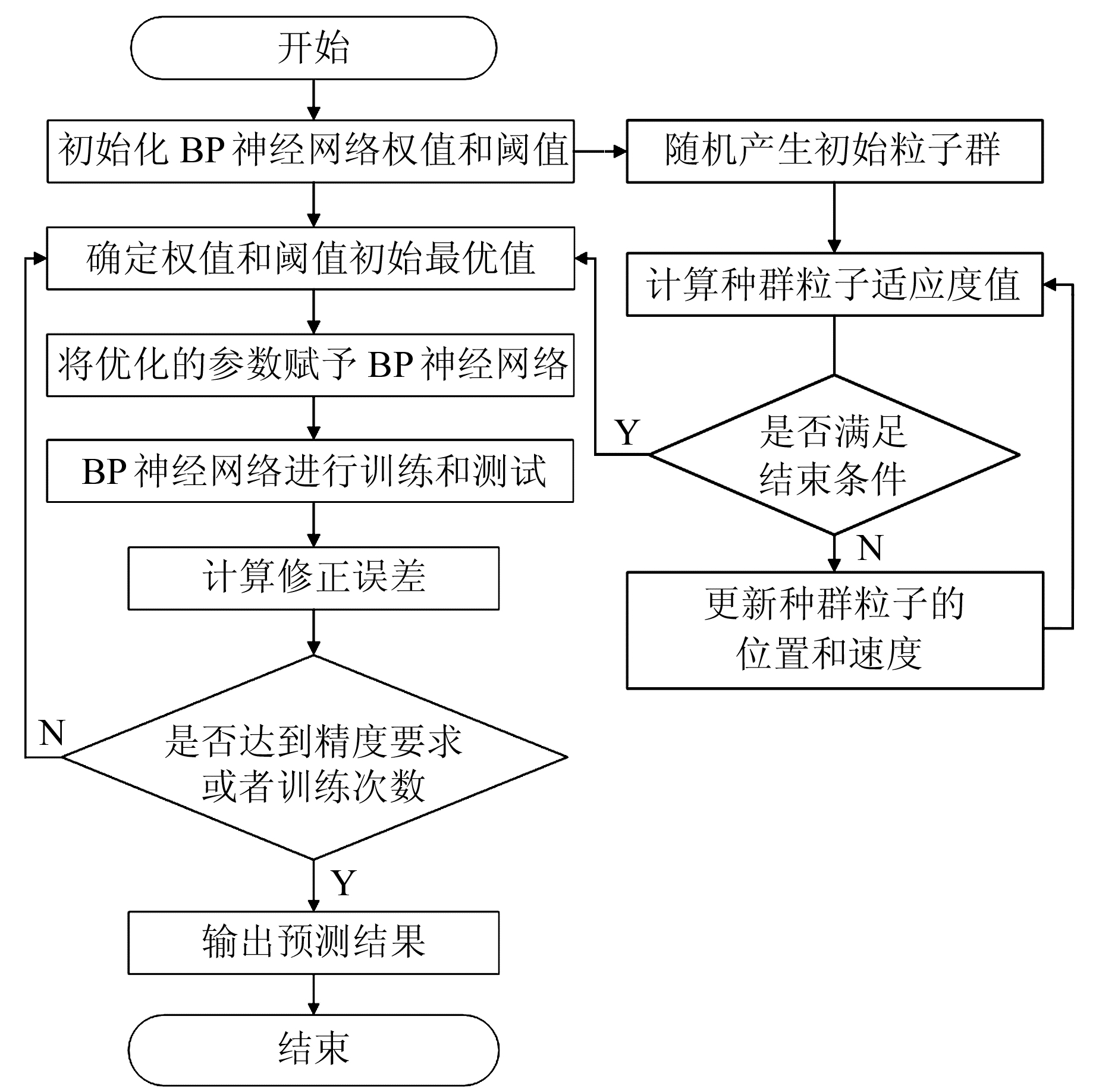
2.3 PSO-BPNNPSO-BPNN是一种结合PSO和BPNN的优化算法。相比于传统的BPNN，PSO-BPNN在数据预测优化方面具有强大的全局搜索能力，可有效避免陷入局部最优解的问题，提高网络的优化性能。PSO-BPNN流程图如图 3所示。
|
图 3 PSO-BPNN算法流程 Fig. 3 The flowchart of PSO-BPNN |
以欧洲地区6个站点作为实验点，其位置信息见表 1。以实验点2020年GNSS_ZTD作为参考，估算测试精度，各模型的bias、RMSE和MAE见表 2。通过对建模过程中的训练精度和测试精度进行比较，可以有效揭示模型的过拟合问题。MGPT3模型的bias、RMSE和MAE分别为-4.68 mm、16.34 mm和14.73 mm，与测试精度相差不大，表明模型不存在明显的过拟合问题。MGPT3模型的bias、RMSE和MAE的平均值分别为-5.13 mm、18.49 mm、15.60 mm，相比于UNB3m和GPT3模型，精度分别提升72.6%、55.0%、42.8%和33.6%、47.7%、32.5%。MGPT3模型表现出较好的拟合性能和精度。
|
表 1 实验点位置信息 Tab. 1 Location information of experimental sites |
|
|
表 2 3种模型的拟合精度 Tab. 2 Fitting accuracy of the three models |
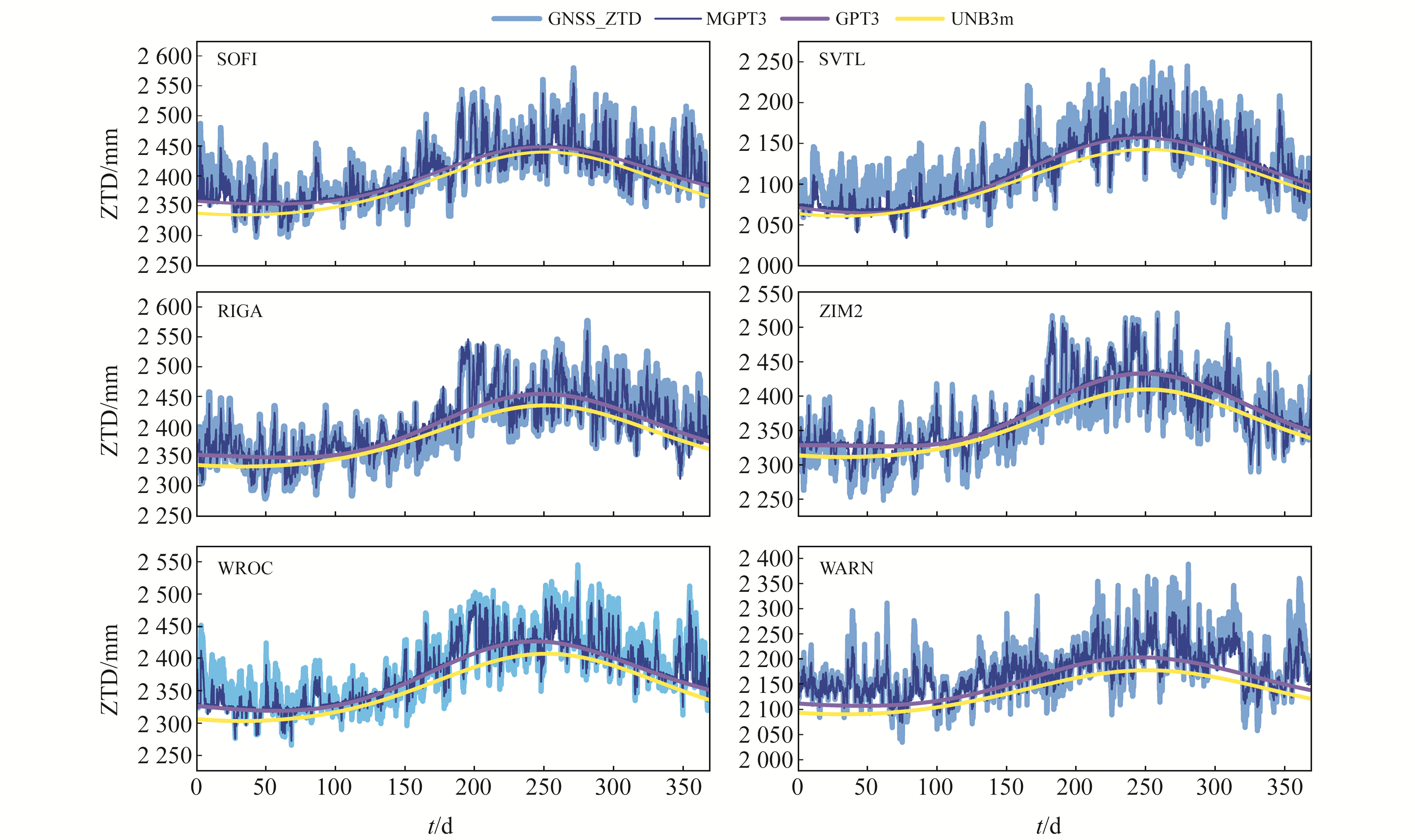
时间是影响ZTD变化的重要因素。多项研究表明，ZTD存在显著的季节变化特征。为验证不同预测模型的准确性，选择上述6个实验点的数据，比较不同模型的ZTD时间序列，结果如图 4所示。可以看出，6个站点的GNSS_ZTD呈现出明显的年际变化特征。GPT3_ZTD和UNB3m_ZTD具有相似且相对平滑的曲线特征，在短时间内无峰值。MGPT3模型能够更好地捕捉除年周期等季节变化以外的ZTD快速变化。这是因为基于PSO-BPNN建模的MGPT3模型能够有效捕捉ZTD的快速变化，证明了PSO-BPNN鲁棒非线性拟合的优越性和建模方法的正确性。表 3为6个站点的ZTD估计精度。
|
图 4 不同模型的ZTD和GNSS _ZTD时间序列 Fig. 4 ZTD and GNSS-ZTD time series of different models |
|
|
表 3 6个站点的ZTD估计精度 Tab. 3 ZTD prediction accuracy of six sites |
纬度和测站周围的建模站点密度也是影响ZTD精度的重要因素。6个站点的预测精度大致相当，其中SOFI和ZIM2站点的精度相对较高。这是因为这2个站点的高度大于其他站点，海拔较高，大气压力较低，水汽含量也相对较低，因此ZTD精度较高。相比之下，ZIM2站点的精度略高于SOFI站点，其原因为ZIM2测站周围的建模站点较密集，而SOFI测站周围的建模站点较少。SVTL和WARN站点的精度较低，这是由于这2个测站周围的建模站点较少。
站点与海洋的距离也会影响ZTD精度，从图 1和表 3可以看出，靠近海洋的站点如SVTL、RIGA和WARN精度相对较差，而内陆站点(SOFI、ZIM2和WROC)精度较高。值得一提的是，在受到海洋水汽干扰的情况下，MGPT3模型精度仍然较高。
从表 3还可以看出，MGPT3模型的各个指标均优于其他2种传统的经验ZTD模型，且UNB3m模型精度最差。这是因为UNB系列模型是基于北美地区的气象参数，其在欧洲地区的适用性较差。
4 结语本文通过引入PSO和BPNN，构建基于时空信息的MGPT3模型，用于欧洲地区的ZTD建模。相较于传统方法，MGPT3模型无需进行平面插值和高程校正等操作，从而降低了计算成本。测试结果表明，MGPT3模型具有优秀的拟合性能和高精度。此外，该模型能够更准确地捕捉ZTD的快速变化。本研究构建的MGPT3模型结构简单，对于提高经验ZTD模型精度、区域ZTD建模和短时段内GNSS水汽反演等具有重要意义。
| [1] |
黄聪, 郭杭. 基于GPT3模型的ZTD及PWV反演精度分析[J]. 大地测量与地球动力学, 2022, 42(5): 489-493 (Huang Cong, Guo Hang. Accuracy Analysis of ZTD and Precipitable Water Vapor Inversion Based on GPT3 Model[J]. Journal of Geodesy and Geodynamics, 2022, 42(5): 489-493)
(  1) |
| [2] |
刘江涛, 刘双童, 叶正真, 等. 一种区域精密天顶对流层延迟组合预报模型[J]. 大地测量与地球动力学, 2022, 42(9): 951-956 (Liu Jiangtao, Liu Shuangtong, Ye Zhengzhen, et al. A Regional Precise Zenith Tropospheric Delay Combined Prediction Model[J]. Journal of Geodesy and Geodynamics, 2022, 42(9): 951-956)
( 1) |
| [3] |
李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2016 (Li Zhenghang, Huang Jinsong. GPS Surveying and Data Processing[M]. Wuhan: Wuhan University Press, 2016)
( 1) |
| [4] |
Hopfield H S. Tropospheric Effect on Electromagnetically Measured Range: Prediction from Surface Weather Data[J]. Radio Science, 1971, 6(3): 357-367 DOI:10.1029/RS006i003p00357
( 1) |
| [5] |
Saastamoinen J. Introduction to Practical Computation of Astronomical Refraction[J]. Bulletin Géodésique, 1972, 106(1): 383-397 DOI:10.1007/BF02522047
( 1) |
| [6] |
Leandro R, Santos M, Langley R B. UNB Neutral Atmosphere Models: Development and Performance[C]. Proceedings of ION NTM, Monterey, 2006
( 1) |
| [7] |
Collins J P, Langley R B. A Tropospheric Delay Model for the User of the Wide Area Augmentation System[R]. Fredericton: University of New Brunswick, 1996
( 0) |
| [8] |
Penna N, Dodson A, Chen W. Assessment of EGNOS Tropospheric Correction Model[J]. The Journal of Navigation, 2001, 54(1): 37-55 DOI:10.1017/S0373463300001107
( 0) |
| [9] |
Böhm J, Heinkelmann R, Schuh H. Short Note: A Global Model of Pressure and Temperature for Geodetic Applications[J]. Journal of Geodesy, 2007, 81(10): 679-683 DOI:10.1007/s00190-007-0135-3
( 0) |
| [10] |
Lagler K, Schindelegger M, Böhm J, et al. GPT2: Empirical Slant Delay Model for Radio Space Geodetic Techniques[J]. Geophysical Research Letters, 2013, 40(6): 1 069-1 073 DOI:10.1002/grl.50288
( 0) |
| [11] |
Böhm J, Möller G, Schindelegger M, et al. Development of an Improved Empirical Model for Slant Delays in the Troposphere(GPT2w)[J]. GPS Solutions, 2015, 19(3): 433-441 DOI:10.1007/s10291-014-0403-7
( 0) |
| [12] |
Landskron D, Böhm J. VMF3/GPT3: Refined Discrete and Empirical Troposphere Mapping Functions[J]. Journal of Geodesy, 2018, 92(4): 349-360 DOI:10.1007/s00190-017-1066-2
( 0) |
| [13] |
李薇, 袁运斌, 欧吉坤, 等. 全球对流层天顶延迟模型IGGtrop的建立与分析[J]. 科学通报, 2012, 57(15): 1 317-1 325 (Li Wei, Yuan Yunbin, Ou Jikun, et al. A New Global Zenith Tropospheric Delay Model IGGtrop for GNSS Applications[J]. Chinese Science Bulletin, 2012, 57(15): 1 317-1 325)
( 0) |
| [14] |
姚宜斌, 何畅勇, 张豹, 等. 一种新的全球对流层天顶延迟模型GZTD[J]. 地球物理学报, 2013, 56(7): 2 218-2 227 (Yao Yibin, He Changyong, Zhang Bao, et al. A New Global Zenith Tropospheric Delay Model GZTD[J]. Chinese Journal of Geophysics, 2013, 56(7): 2 218-2 227)
( 1) |
| [15] |
杨旭, 何祥祥, 王媛媛, 等. 一种基于机器学习算法的区域/单站ZTD组合预测模型[J]. 全球定位系统, 2022, 47(1): 98-102 (Yang Xu, He Xiangxiang, Wang Yuanyuan, et al. A Regional/Single Station ZTD Combined Forecasting Model Based on Machine Learning Algorithm[J]. GNSS World of China, 2022, 47(1): 98-102)
( 1) |
| [16] |
郭骐嘉, 姚宜斌, 周永江. 融合GNSS气象参数的PM2.5随机森林预测模型[J]. 测绘科学, 2021, 46(4): 37-42 (Guo Qijia, Yao Yibin, Zhou Yongjiang. PM2.5 Random Forest Prediction Model Incorporating GNSS Meteorological Parameters[J]. Science of Surveying and Mapping, 2021, 46(4): 37-42)
( 0) |
| [17] |
肖恭伟, 欧吉坤, 刘国林, 等. 基于改进的BP神经网络构建区域精密对流层延迟模型[J]. 地球物理学报, 2018, 61(8): 3 139-3 148 (Xiao Gongwei, Ou Jikun, Liu Guolin, et al. Construction of a Regional Precise Tropospheric Delay Model Based on Improved BP Neural Network[J]. Chinese Journal of Geophysics, 2018, 61(8): 3 139-3 148)
( 1) |
| [18] |
钟储汉, 李新瑞, 张双成, 等. GAMIT/TrackRT用于滑坡实时GNSS监测研究[J]. 测绘科学, 2022, 47(12): 57-65 (Zhong Chuhan, Li Xinrui, Zhang Shuangcheng, et al. GAMIT/TrackRT Used in Landslide Real-Time GNSS Monitoring[J]. Science of Surveying and Mapping, 2022, 47(12): 57-65)
( 1) |
| [19] |
Li T, Wang L, Chen R Z, et al. Refining the Empirical Global Pressure and Temperature Model with the ERA5 Reanalysis and Radiosonde Data[J]. Journal of Geodesy, 2021, 95(3)
( 1) |
2. Coal Industry Engineering Research Center of Ming Area Environmental and Disaster Cooperative Monitoring, Anhui University of Science and Technology, 168 Taifeng Street, Huainan 232001, China;
3. Key Laboratory of Aviation-Aerospace-Ground Cooperative Monitoring and Early Warning of Coal Mining-Induced Disasters of Anhui Higher Education Institutes, Anhui University of Science and Technology, 168 Taifeng Street, Huainan 232001, China