2. 东华理工大学自然资源部环鄱阳湖区域矿山环境监测与治理重点实验室,南昌市广兰大道418号,330013;
3. 中国矿业大学环境与测绘学院,江苏省徐州市大学路1号,221116
地球自转参数(ERP)包含极移和日长变化,可反映地球各圈层的整体运动状况,也是天球坐标框架和地球坐标框架相互转换的必要参数[1]。受限于复杂的数据处理过程,ERP观测结果存在延迟,导致用户无法实时获取高精度ERP产品,只能依赖于预报产品[2]。极移作为ERP重要组成部分,许多学者采用多种模型对其展开预报研究,常用的预报模型包括LS+AR组合模型[3]、灰色系统理论[4]、LS+AR+Kalman滤波组合预报模型[5]、奇异谱分析[6]、人工神经网络[7]等,这些模型采用的基础数据主要来源于国际地球自转和参考系服务组织(IERS)发布的最终解ERP产品。该产品由多种现代大地测量观测数据综合解算得到,时间分辨率为1 d。尽管诸如IGS等国际组织定期发布分辨率为6 h的极移解算产品,但该类产品仅由GPS或GNSS数据解算得到,相对于IERS发布的最终产品解算精度较差。
采用插值函数对数据进行拟合及内插,是获取时间序列插值数据的有效途径之一,且利用高分辨率数据有望提高模型的拟合及预报精度。通过对比部分常用的插值方法,本文采用径向基函数对目前公开发布且精度较高的IERS 20 C04 EOP产品的极移观测数据进行插值,获取内插分辨率为6 h的极移参数,并基于LS+AR预报模型,分别对相同时段内插值与未进行插值的数据进行500组跨度为1~7 d的预报实验,验证本文方法的有效性。
1 径向基函数插值法径向基函数插值法在输入空间中以中心为基准进行局部逼近,可更好地捕捉数据集中的局部变化特征,具有计算简单、节点配置灵活、计算工作量小、内插精度较高等优点。本文采用的径向基函数插值模型如下[8]。
给定n个不同的点x1,x2,…,xn,其对应函数值f(x1),f(x2),…,f(xn)已知,取定径向基函数φ,构建响应面模型,即寻找具有如下形式的函数:
| $s_n(\boldsymbol{x})=\sum\limits_{i=1}^n \lambda_i \varphi\left(\left\|\boldsymbol{x}-x_i\right\|\right)+\boldsymbol{b}^{\mathrm{T}} \boldsymbol{x}+a $ | (1) |
式中,f为一个确定性的连续函数,x ∈Rd, ‖x -xi‖表示x与中心点xi之间的欧氏距离,λi∈R,i=1,2,…,n,b ∈Rd,a∈R,φ为径向基函数。
插值计算步骤如下:1)定义径向基函数。选择合适的径向基函数作为插值的基础函数,常用的径向基函数有高斯函数、多孔径函数等[9],本文选用高斯径向基函数进行插值。2)选择插值节点。根据已知函数值的节点,确定插值节点的位置。3)计算权重系数。根据插值节点与待估节点之间的距离,计算径向基函数的权重系数。4)插值计算。根据权重系数和径向基函数值进行插值计算,得到待估节点的函数值。
2 实验分析LS+AR模型[2]是一种包含常数项、线性趋势项及周期项的预报模型,插值函数获取的内插数据相对平滑,符合该模型的主要特征。本文基于LS+AR模型,以1 a为解算模型参数的基础数据量,共进行500组间隔为1 d、预报跨度为1~7 d的预报实验。实验数据来源于IERS中心发布的2021-01-01~2022-05-22期间IERS 20 C04版极移产品(https://datacenter.iers.org/data/latestVersion/EOP_20_C04_one_file_1962-now.txt)。本文在前期实验中分别采用径向基函数、三次样条函数[10]、拉格朗日函数[11]3种插值方法,对实验数据进行分辨率为6 h的内插计算。实验结果中基于拉格朗日函数插值数据的预报效果存在过拟合,导致其预报结果存在较大误差。因此,下文仅列出2种插值方案的预报结果,并采用平均绝对误差(MAE)及绝对误差(AE)[2]作为精度指标,具体预报方案如表 1所示。
|
|
表 1 预报方案 Tab. 1 The prediction scheme |
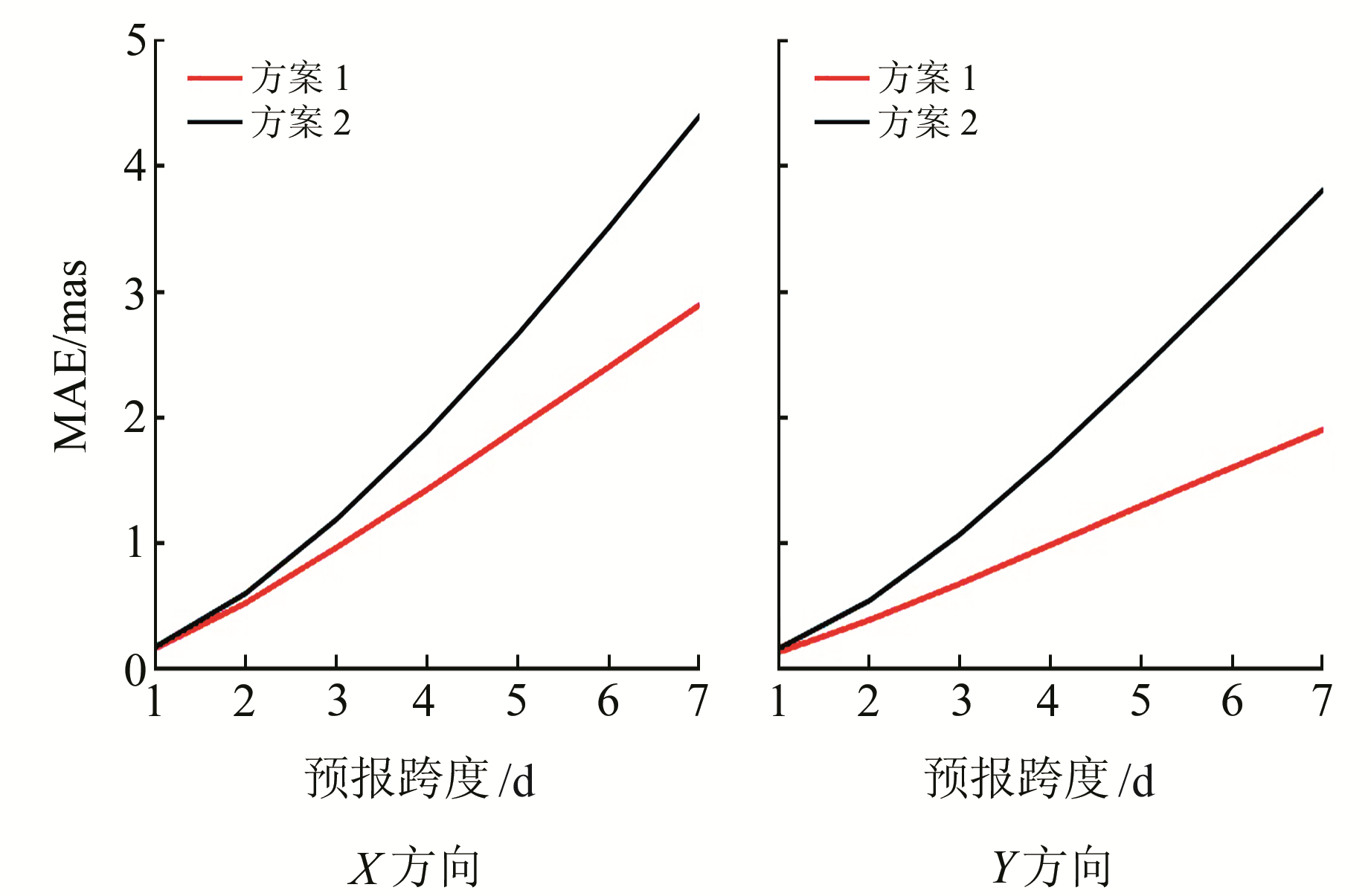
表 2为2种不同插值方法与未进行插值的预报精度统计,可以看出,基于三次样条函数的插值结果与另外两种方法差别较大。此外,由图 1可知,相较于未进行插值的实验方案,基于径向基函数的插值预报精度显著提升,在X和Y方向,方案1相较于方案2预报精度平均提升22.4%和38.4%。
|
|
表 2 不同预报方案MAE统计 Tab. 2 MAE statistical results of different prediction schemes |
|
图 1 不同方案预报结果MAE值 Fig. 1 MAE values of prediction results of different schemes |
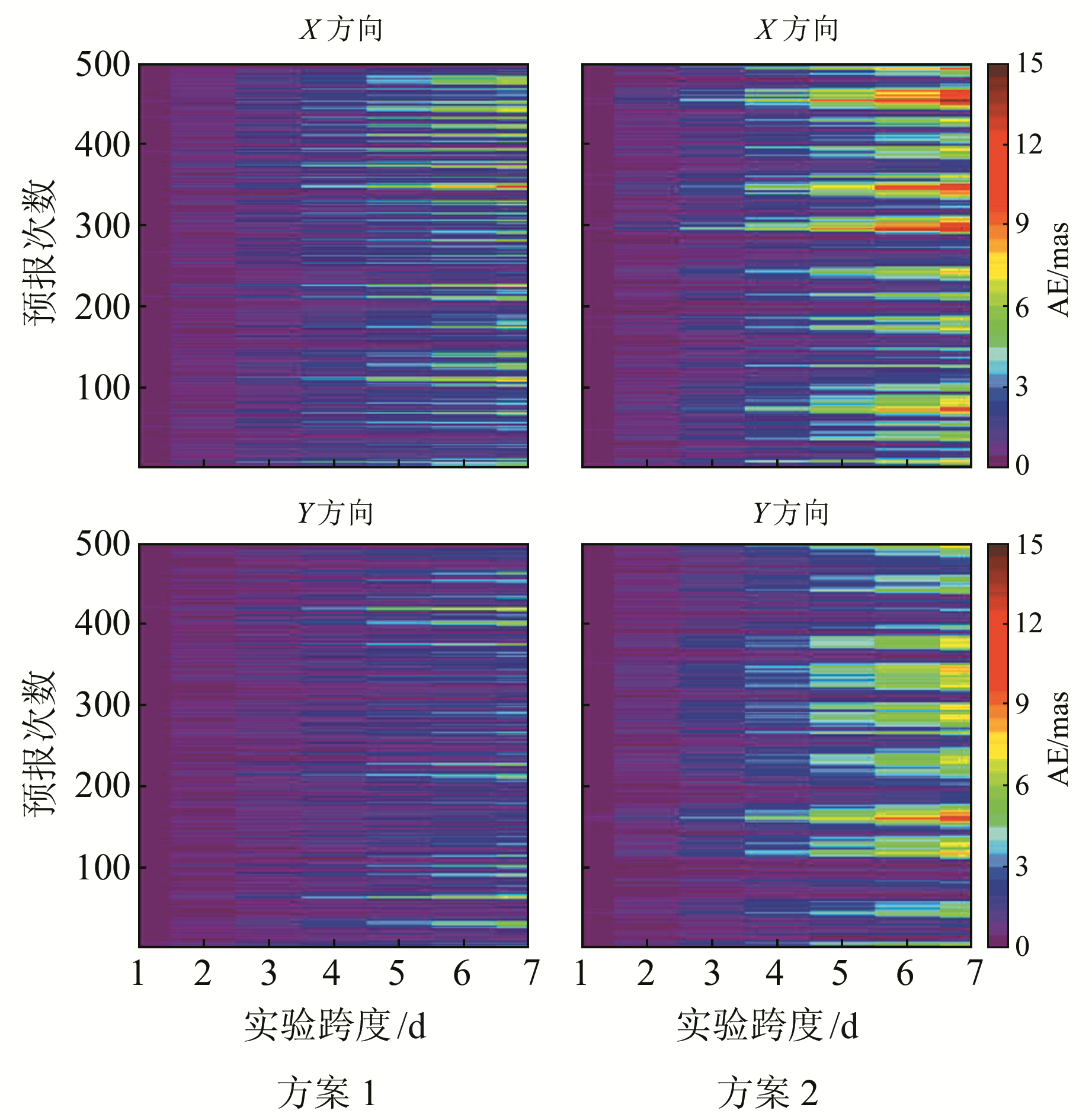
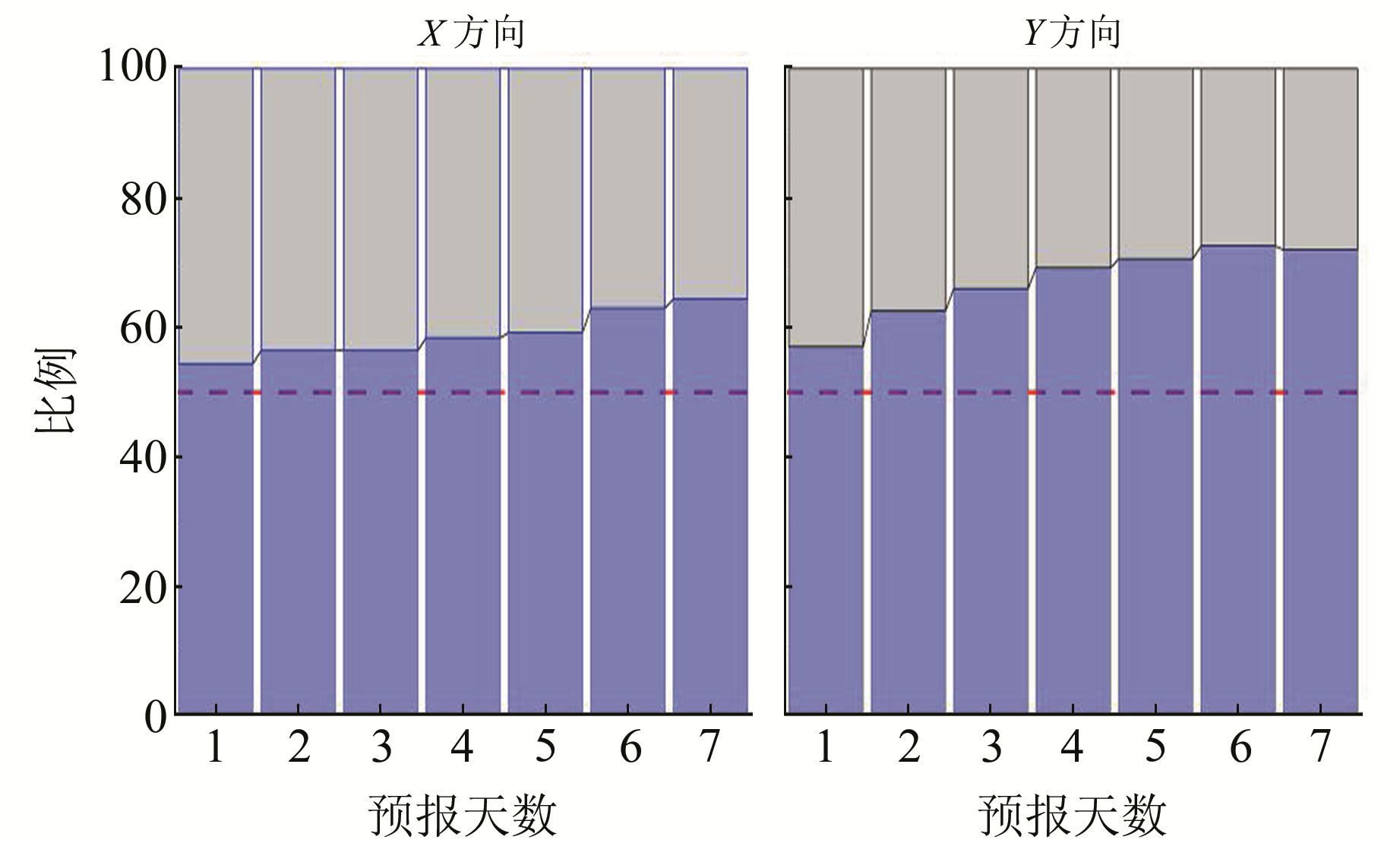
由图 2可知,方案1预报结果与官方发布的最终产品更为接近,尤其是5~7 d预报跨度。图 3为方案1相对于方案2的预报优劣占比结果,当预报值与最终产品差值的绝对值更小则判定该预报结果更优。图中每列代表第n天的500次实验,蓝色表示方案1优于方案2,灰色表示方案2优于方案1。
|
图 2 不同方案预报结果AE值 Fig. 2 AE values of prediction results of different schemes |
|
图 3 预报结果优劣占比 Fig. 3 Proportion of better and worseprediction results |
随着预报跨度的增加,无论是在X或Y方向,方案1优于方案2的占比始终高于50%,且在Y方向上方案1优于方案2的占比平均达67.5%。
3 结语本文采用径向基函数插值方法对IERS发布的极移参数产品进行内插,获得6 h分辨率的极移数据;基于LS+AR模型及相同时段数据,对比分析采用1 d分辨率及6 h分辨率数据的预报结果,共进行500组跨度为1~7 d的超短期预报实验。结果表明,采用相同预报模型时,相较于采用1 d分辨率数据的预报结果,基于6 h分辨率数据的预报精度在极移X和Y方向上分别平均提升22.4%和38.4%。
| [1] |
Wu F, Liu Z P, Deng K Z, et al. A Polar Motion Prediction Method Considering the Polar Coordinates[J]. Advances in Space Research, 2021, 68(3): 1 318-1 328 DOI:10.1016/j.asr.2021.03.020
(  0) 0) |
| [2] |
吴飞. 几种改进的地球自转参数预报方法[D]. 徐州: 中国矿业大学, 2019 (Wu Fei. Several Improved Methods for Prediction of Earth Rotation Parameters[D]. Xuzhou: China University of Mining and Technology, 2019)
(  0) 0) |
| [3] |
Wu F, Deng K Z, Chang G B, et al. The Application of a Combination of Weighted Least-Squares and Autoregressive Methods in Predictions of Polar Motion Parameters[J]. Acta Geodaetica et Geophysica, 2018, 53(2): 247-257 DOI:10.1007/s40328-018-0214-3
(  0) 0) |
| [4] |
孙张振. 高精度地球自转参数预报的理论与算法研究[D]. 西安: 长安大学, 2013 (Sun Zhangzhen. Research on the Theories and Algorithms of Earth Rotation Parameters Prediction[D]. Xi'an: Chang'an University, 2013)
(  0) 0) |
| [5] |
Xu X Q, Zhou Y H, Liao X H. Short-Term Earth Orientation Parameters Predictions by Combination of the Least-Squares, AR Model and Kalman Filter[J]. Journal of Geodynamics, 2012, 62: 83-86 DOI:10.1016/j.jog.2011.12.001
(  0) 0) |
| [6] |
Jin X, Liu X, Guo J Y, et al. Analysis and Prediction of Polar Motion Using MSSA Method[J]. Earth, Planets and Space, 2021, 73(1)
(  0) 0) |
| [7] |
Jin X, Guo J Y, Shen Y, et al. Application of Singular Spectrum Analysis and Multilayer Perceptron in the Mid-Long-Term Polar Motion Prediction[J]. Advances in Space Research, 2021, 68(9): 3 562-3 573 DOI:10.1016/j.asr.2021.06.039
(  0) 0) |
| [8] |
齐静. 径向基函数插值若干问题研究[D]. 重庆: 重庆师范大学, 2016 (Qi Jing. Research for Some Problems of the Radial Basis Function Interpolation[D]. Chongqing: Chongqing Normal University, 2016)
(  0) 0) |
| [9] |
Regis R G, Shoemaker C A. Improved Strategies for Radial Basis Function Methods for Global Optimization[J]. Journal of Global Optimization, 2007, 37(1): 113-135
(  0) 0) |
| [10] |
陶婷. 三次样条插值函数稳定性分析及其应用[D]. 成都: 成都理工大学, 2021 (Tao Ting. Stability Analysis and Application of Cubic Spline Interpolation Function[D]. Chengdu: Chengdu University of Technology, 2021)
(  0) 0) |
| [11] |
王建敏, 李特. 北斗三号卫星位置插值研究[J]. 测绘通报, 2021(12): 50-53 (Wang Jianmin, Li Te. Research on Position Interpolation of BDS-3 Satellite[J]. Bulletin of Surveying and Mapping, 2021(12): 50-53)
(  0) 0) |
2. Key Laboratory of Mine Environmental Monitoring and Improving around Poyang Lake, MNR, East China University of Technology, 418 Guanglan Road, Nanchang 330013, China;
3. School of Environment and Spatial Informatics, China University of Mining and Technology, 1 Daxue Road, Xuzhou 221116, China
 2024, Vol. 44
2024, Vol. 44

