2. 中国科学院大学地球与行星科学学院,北京市玉泉路19号甲,100049;
3. 中国科学院精密测量科学与技术创新研究院武汉大地测量国家野外科学观测研究站,武汉市徐东大街340号,430077
SLR可以精确测量地球与卫星的距离,在卫星精密定轨与检核、激光链路时间传递、板块运动监测、地球自转测定、地球重力场研究、空间碎片监测等领域至关重要[1-4]。SLR与多普勒无线电定轨定位系统(Doppler orbitography and radiopositioning integrated by satellite, DORIS)、全球卫星导航系统(global navigation satellite system, GNSS)、甚长基线干涉测量(very long baseline interferometry, VLBI)一起参与构建和维持国际地球参考框架(international terrestrial reference frame, ITRF)。相较于其他3种大地测量技术,SLR对地心位置和尺度因子足够敏感,可实现ITRF尺度因子精度小于0.7 ppb[5]。
SLR各台站的观测精度和观测数据量差异较大,选择合适的测站权重对SLR卫星定轨极为重要。原始测站定权[6]主要是基于观测值的标准差,但该方法只代表观测值的内符合情况,无法完全反映SLR测站的坐标精度、系统偏差、标校精度等。Soto等[7]提出将模糊聚类算法应用于精密定轨,该算法采用马氏距离进行测站分类,顾及各个质量因素之间的相关性,使LAGEOS-1卫星的定轨精度提升5%~20%。邵璠等[8]将一种改进的模糊聚类方法应用于LAGEOS-1卫星定轨,定轨精度平均提高3.7 mm,该方法对不同类别台站赋予不同的标准差,将其与测站隶属度乘积之和的倒数作为测站权重,但未顾及聚类中心之间相关性的影响,同时分类数据采用上海天文台的SLR质量报告,未考虑其他机构的数据。赵春梅等[9]使用FCM算法对SLR测站进行分级并应用于GNSS星座的轨道检核,结果表明,Ⅰ级测站数据的校轨残差均值的绝对值和标准差总体小于Ⅱ、Ⅲ级测站。本研究着重开展基于全球所有分析机构的质量报告进行测站分类与定权,提出更加合理的定权方案,并以LAGEOS-2卫星展开精密定轨实验,分析FCM定权和原始测站定权对定轨精度的影响。
目前国际上有5个机构评估SLR台站质量并定期上传到ILRS中,分别为德国大地测量研究所(DGFI)、日本一桥大学(Hitotsubashi University)、美国地球系统技术联合中心(JCET)、俄罗斯太空任务控制中心(MCC)以及中国科学院上海天文台(SHAO)[10-11]。其中,DGFI在2018年第一季度之后数据缺失,在此不予考虑。因此,本文以其他4个机构的质量报告为基础,分别进行原始测站定权和FCM定权,对比2种定权方法对定轨精度的影响。
1 测站聚类原理与方法 1.1 SLR测站聚类指标SLR测站质量评价准则包括3个方面,分别为数据数量、数据质量以及运行协议遵守情况[9]。针对数据数量,ILRS分析机构会统计SLR台站对各种卫星的观测圈数及生成的标准点数量。数据质量分为两部分,一部分指生成标准点数据的精度和合格率,另一部分为SLR台站的技术指标,包括测站短期稳定性和长期稳定性。运行协议遵守情况则指SLR台站运行方面,如数据提交时间、设备运行和维护情况以及标准点格式等。
ILRS定期发布全球SLR台站的观测质量和测距稳定性报告(ilrs.gsfc.nasa.gov/network/system_performance)。观测质量报告包含过去1 a测站的卫星观测圈数和生成的标准点数量、总观测时间、系统单次测量校准误差、卫星单次观测精度等信息。测距稳定性报告包含各分析机构基于快速精密定轨得到的SLR测站LAGEOS卫星标准点RMS值、测站长期稳定性、测站短期稳定性及标准点合格率4项指标。本文以LAGEOS卫星标准点数量、标准点RMS值以及测站短期稳定性3个因素作为分类指标。
1.2 模糊聚类定权原理FCM模糊聚类算法[12]是一种代表性的软聚类方法,其思想是通过优化目标函数得到每个样本相对于每个类别的隶属度,进而实现对样本数据的自动分类。目前,以FCM为代表的模糊逻辑方法已广泛应用于地学研究中[13-15]。
本文FCM算法基于马氏距离进行聚类,与欧式距离相比,马氏距离考虑到各种特性之间的相关性,修正了欧氏距离中各个维度尺度不一致且相关的问题[16]。利用该算法对SLR台站进行分类的步骤如下:
1) 样本数据标准化。由于标准点数量与标准点RMS值和测站短期稳定性单位不同,且量级相差巨大,若不进行标准化处理则会出现“大数吃小数”的情况。本文使用最小-最大缩放方法对数据进行标准化,假设有N个测站x,每个测站均为多属性样本(包括标准点数量、短期稳定性和标准点RMS值),标准化方法如下:
| $ \left\{\begin{array}{l} x_i^*=\frac{x_i-\min (X)}{\max (X)-\min (X)} \\ \forall i=1, 2, \cdots, N \end{array}\right. $ | (1) |
2) 指定SLR测站的聚类数目c、收敛标准ε,并初始化SLR测站对每个聚类中心的隶属度uij,其中隶属度应满足以下约束条件:
| $ \left\{\begin{array}{l} u_{i j}=[0, 1] \\ \sum\limits_{j=1}^c u_{i j}=1 \end{array}\right. $ | (2) |
3) 根据初始化的隶属度矩阵,计算聚类中心C和各测站与聚类中心的距离dij,然后进行迭代,更新隶属度矩阵和聚类中心,具体步骤可[8]。
4) 判断是否停止迭代:
| $ \left|C_j^{(t)}-C_j^{(t-1)}\right|<\varepsilon $ | (3) |
若未达到收敛标准,则重复步骤3);若达到收敛标准,则输出权重结果。权重计算方法为:
| $ \begin{aligned} Q_i & =\sum\limits_{j=1}^c u_{i j}\left\|C_j\right\| \\ P_i & =Q_i^{-1} \end{aligned} $ | (4) |
式中,
为验证本文定权方法相较于原始测站定权的优劣,分别将两种方法应用于LAGEOS-2卫星精密定轨,分析卫星轨道精度状况。
2.1 LAGEOS-2卫星定轨策略及观测数据分析采用动力学方法对2021年LAGEOS-2卫星标准点数据进行精密定轨,表 1为LAGEOS-2卫星精密定轨策略。
|
|
表 1 LAGEOS-2卫星精密定轨策略 Tab. 1 Precise orbit determination strategies for LAGEOS-2 satellite |
定轨过程中使用的力学模型包括地球中心引力、太阳辐射压、N体摄动、地球辐射压、固体潮、海潮、相对论扰动和经验R、T、N摄动。针对参考框架的各项改正,参照IERS 2010规范进行处理。对于测量模型,采用Mendes-Pavlis模型进行大气折射改正。质心改正与激光入射角、地面测站分布等因素有关,因此对不同测站使用不同的质心校正。对于估计参数,分别每3 d估计1次切向和法向经验力系数以及类阻力系数,太阳辐射压系数固定为1.13[5]。
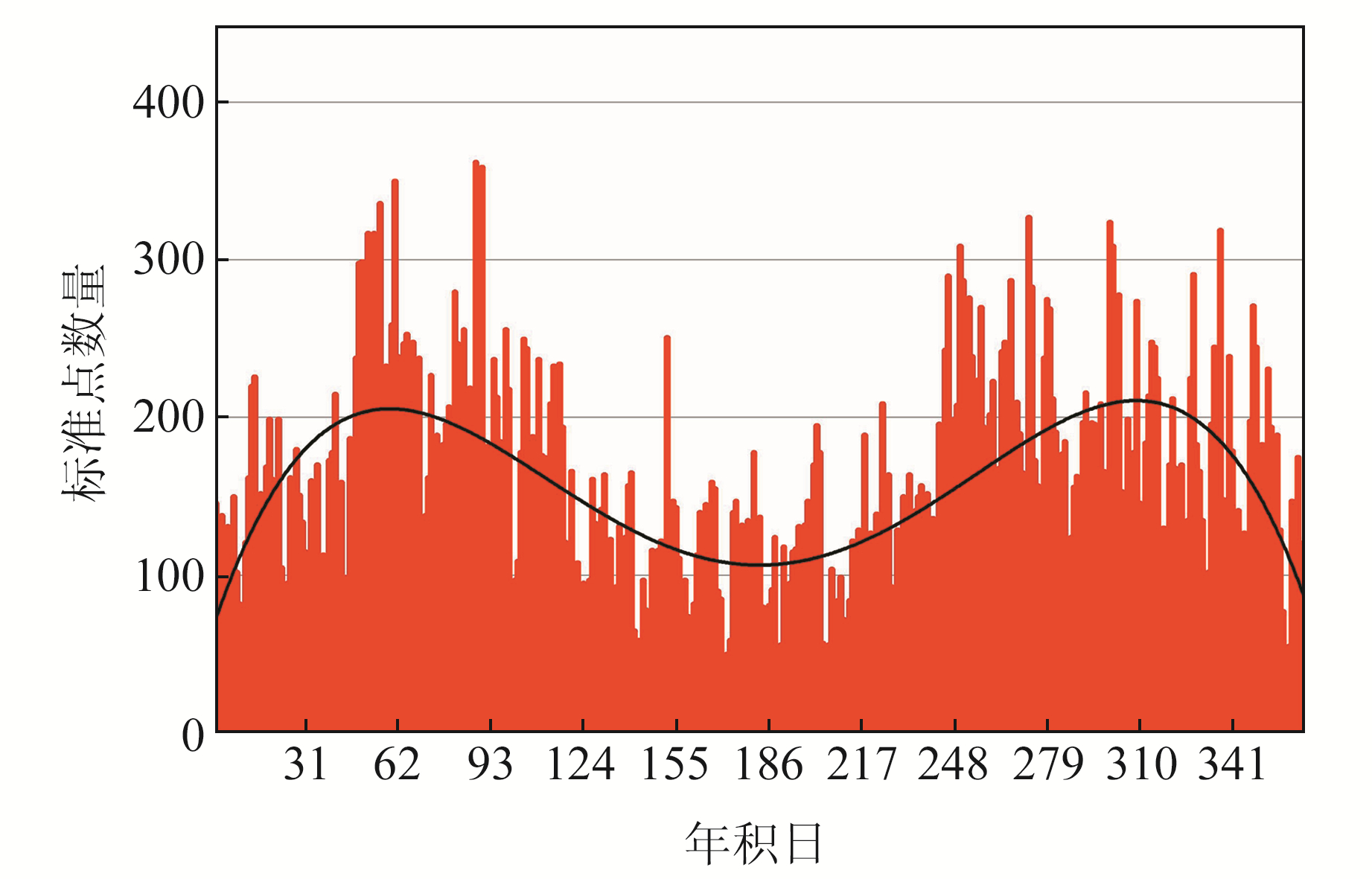
本文观测数据来自ILRS EDC数据中心(ftp://edc.dgfi.tum.de/)所存档的全球SLR台站的标准点数据。图 1为LAGEOS-2卫星观测值情况,2021年每日平均观测量为158个,在05-03(doy123)观测量最少,仅为30个,03-29(doy88)观测量最多,达到362个。图 1中曲线为多项式拟合曲线,从趋势可以看出,SLR观测具有一定的季节性特征,夏季观测值明显低于其他季节。
|
图 1 2021年LAGEOS-2卫星每日观测值数量 Fig. 1 Number of daily observations of LAGEOS-2 satellite in 2021 |
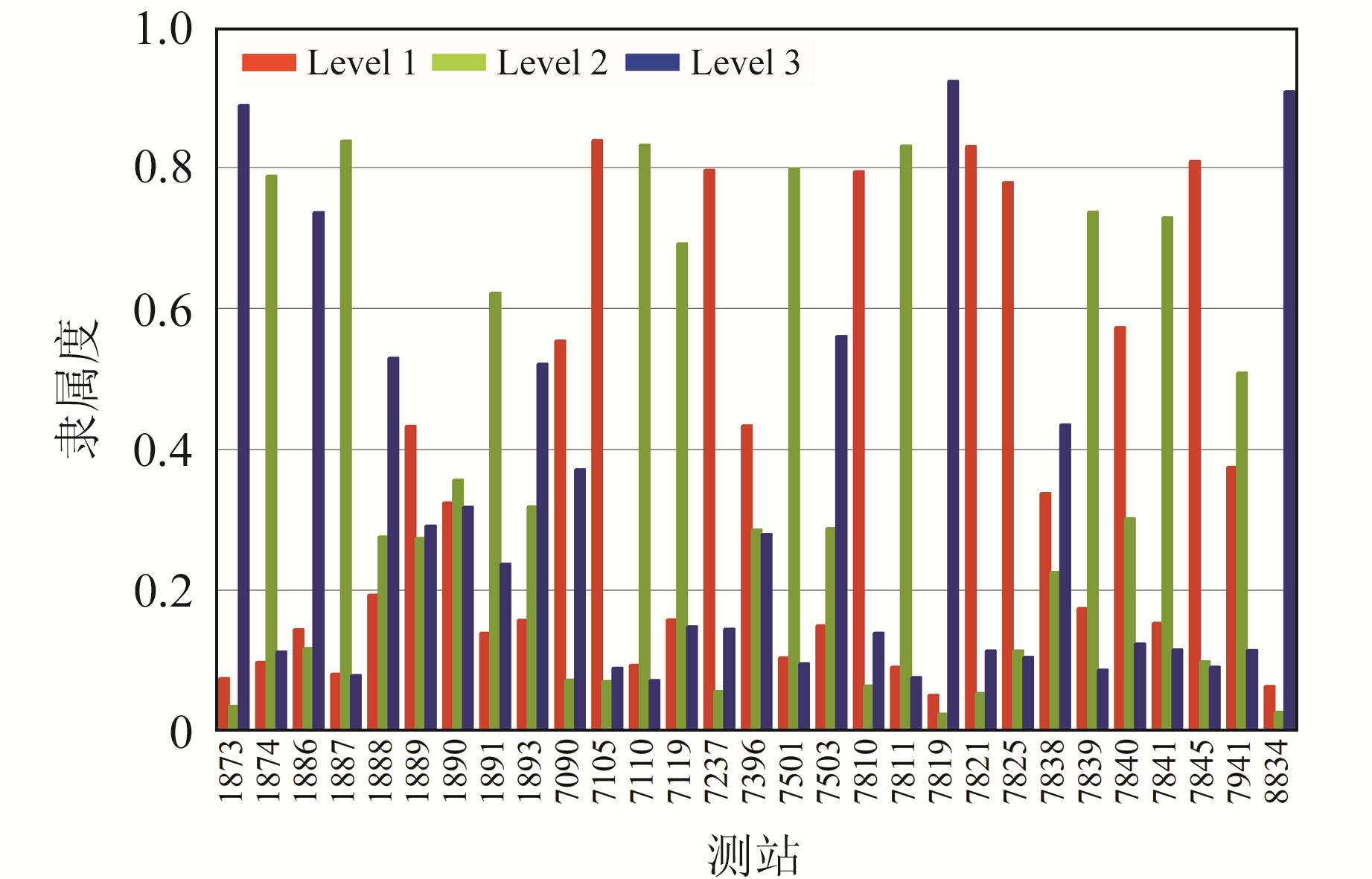
利用§1.2中方法每季度对测站进行1次分类与定权。从图 2可以看出,SLR台站可分为3类(Level 1、Level 2、Level 3),其中Level 1离原点较近,表示该类测站观测值数量较多,LAGEOS卫星标准点RMS值较小,测站短期稳定性也较小,性能较好,Level 2、Level 3则依次次之。根据测站对各聚类中心的隶属度大小划归不同类别。图 3为2021年第四季度根据MCC发布的质量数据进行分类的测站隶属度情况,以1873测站为例,该测站对各类别的隶属度分别为0.075、0.036和0.889,显然该测站属于Level 3。测站权重即为3个聚类中心距坐标原点的距离与该测站对3个聚类中心隶属度乘积之和的倒数。

|
图 2 根据MCC机构2021年第四季度质量报告的测站分类结果 Fig. 2 Classification results of stations of MCC quality report in the fourth quarter of 2021 |
|
图 3 MCC机构2021年第四季度各测站对各类别的隶属度情况 Fig. 3 The membership of each station for each level of MCC in the fourth quarter of 2021 |
表 2为根据4个分析机构2021年第四季度发布的质量报告进行分类的结果,对于大多数测站而言,根据4个分析机构数据进行分类的结果一致,区别仅在于隶属度有所不同。而对于1874、1889等10个测站,由于不同机构发布的质量报告如LAGEOS卫星标准点RMS值、测站短期稳定性差异较大,分类情况有所不同。在4个机构中,JCET和MCC对全球SLR测站的质量监测较为全面,而Hitotsubashi University及SHAO对部分测站的质量监测存在不足,如1873、1891、7503以及7819测站,这些测站的短期稳定性均存在缺失,无法进行分类。
|
|
表 2 2021年第四季度测站分类结果 Tab. 2 Classification results of stations in the fourth quarter of 2021 |
为验证4家机构发布的质量报告对卫星定轨的影响,本文以各分析机构提供的LAGEOS卫星标准点RMS值作为原始测站权重,分别采用原始测站定权和FCM定权方法进行LAGEOS-2卫星定轨,定轨弧长为7 d,时间为2021-01-01~12-31,共计52个定轨弧段。参考轨道采用ILRS发布的ILRSA产品,并从观测资料残差、参考轨道比较两个方面分析定轨精度。
表 3(单位cm)为原始测站定权与FCM定权方法的轨道精度情况,可以看出,FCM定权的有效观测值数量和外符合精度相较于原始测站定权有明显提高,分别提升461~1 591个有效观测值和0.11~0.45 cm定轨精度。在原始测站定权中,根据SHAO发布的质量报告进行定权的外符合精度较差,这是因为上海天文台(SHAO)所解算的LAGEOS卫星标准点RMS值与其他机构有所差异,精度可能有所欠缺,因此轨道外符合精度较低,而FCM定权方法考虑到多种因素,其定轨精度具有一定提高。在4个分析机构中,JCET无论是在外符合精度还是有效观测值数量方面,均表现最好,其三维方向RMS值为4.94 cm。而在FCM定权中,4个机构的定轨结果相差不大,三维RMS值在4.83~4.86 cm之间。在O-C残差方面,原始测站定权的残差RMS值比FCM定权小,但这并不意味着原始测站定权的轨道内符合精度更高,相较于FCM定权,原始测站定权方法剔除了更多的观测数据,这也会降低轨道残差。另外,从内符合精度来看,本文结论与文献[8]结果在同一水平,但文献[8]并未就外符合精度进行分析。在此,本文与ILRSA产品进行比对,给出LAGEOS-2卫星的外符合精度情况。
|
|
表 3 不同定权方法的卫星定轨结果 Tab. 3 POD results with different weighting methods |
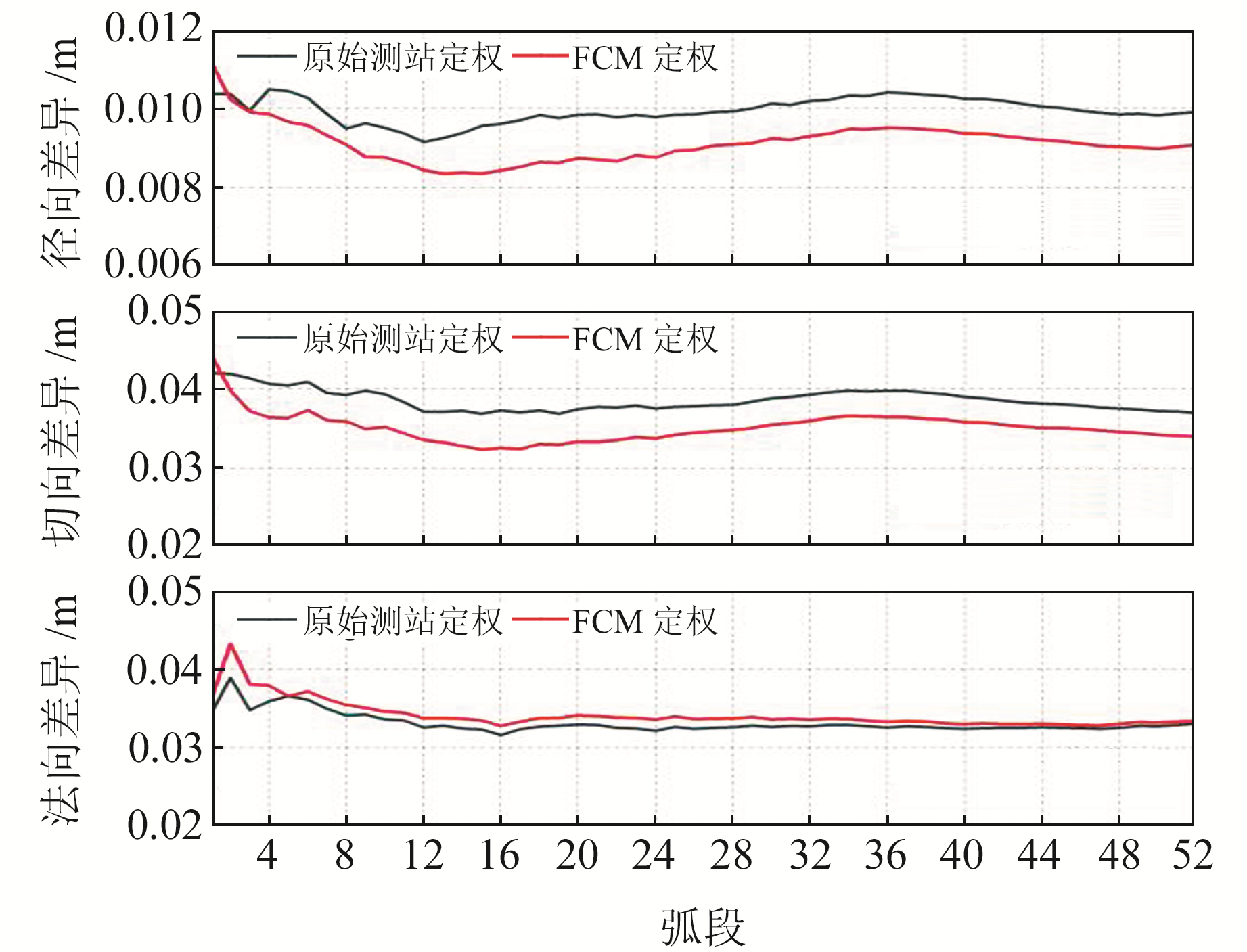
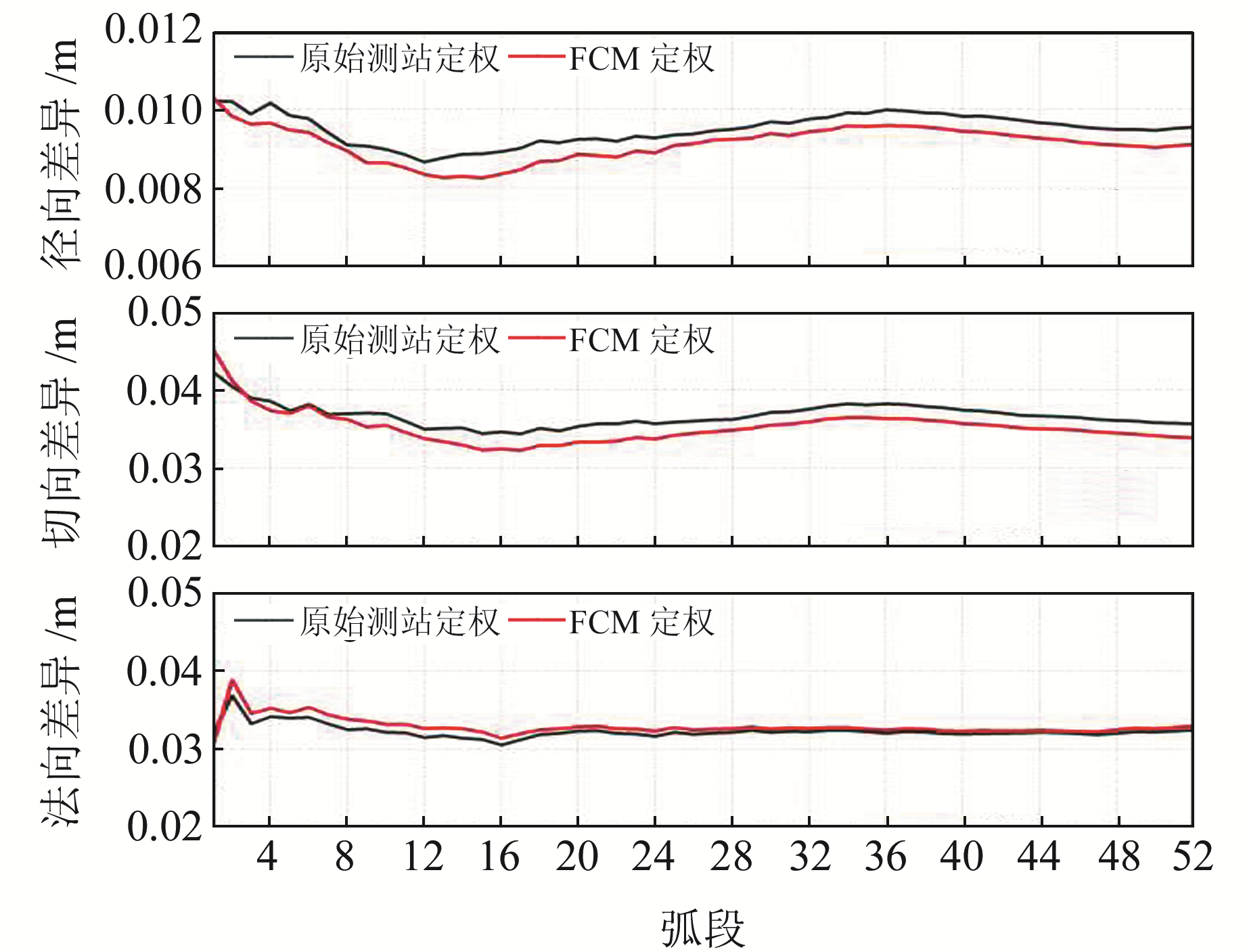
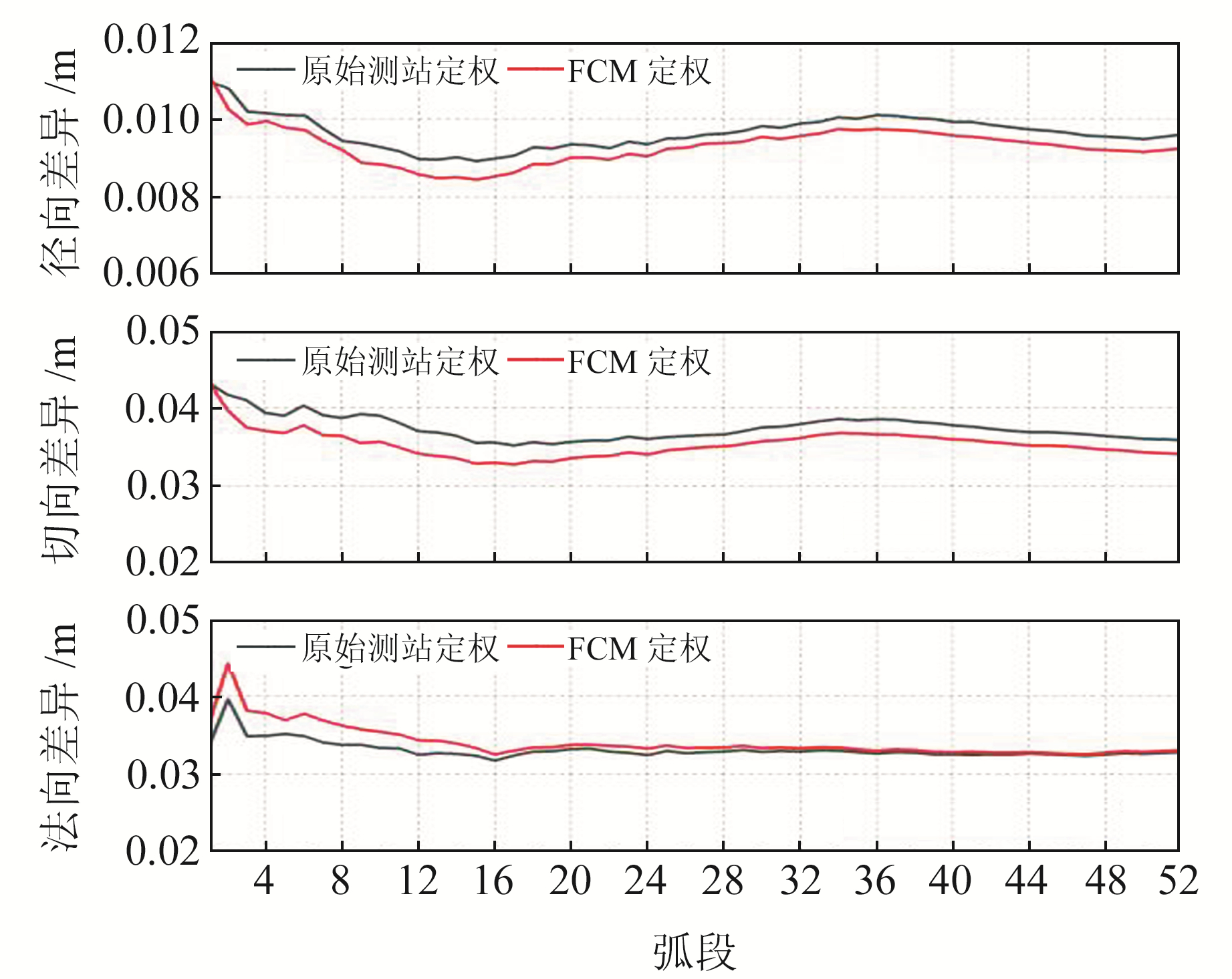
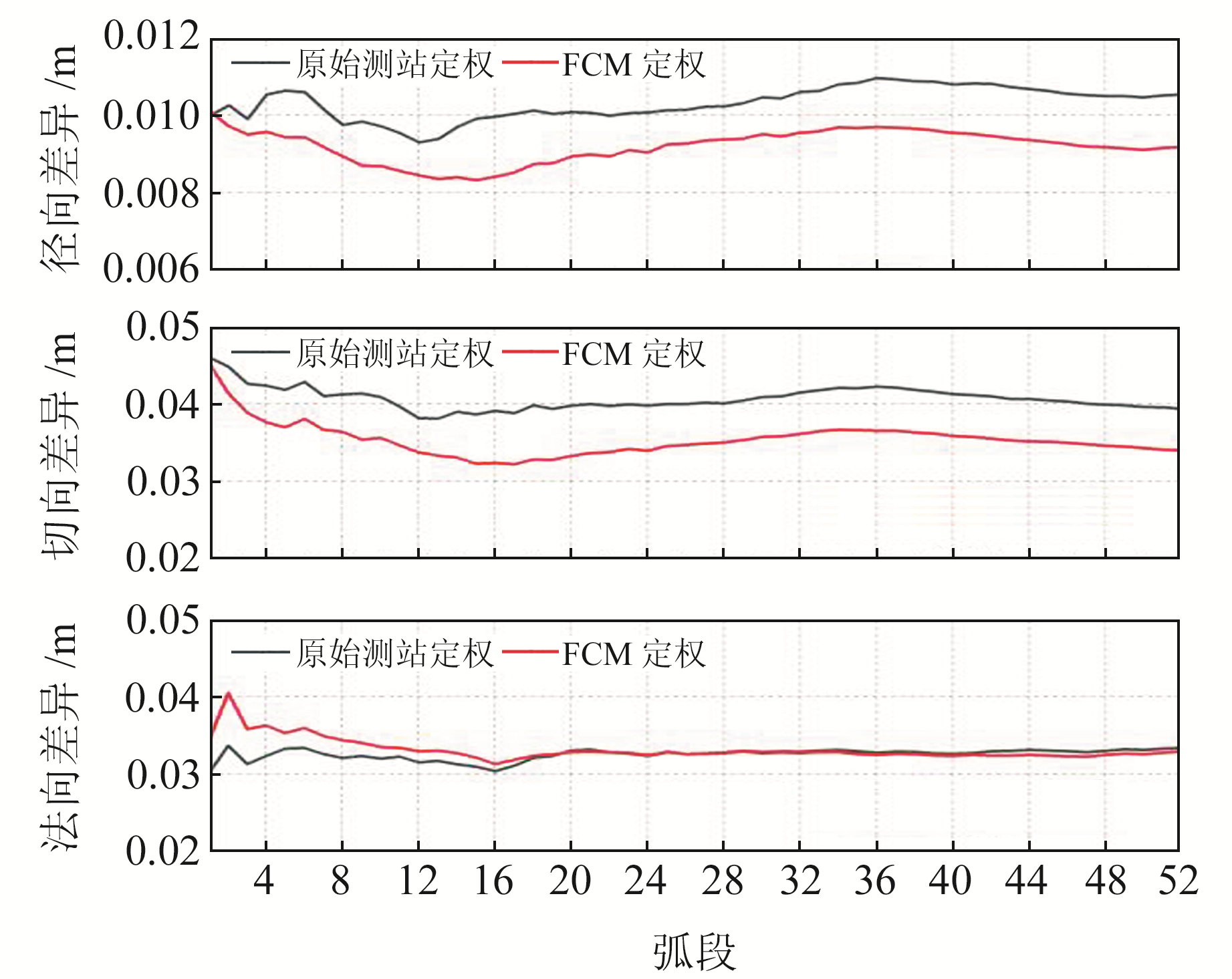
图 4~7为采用两种定权方法进行定轨的外符合精度情况,可以看出,相较于原始测站定权,FCM定权方法对轨道精度的提高主要体现在径向和切向,法向则差距很小。同时,通过误差序列分析发现,FCM定权方法并未改变误差序列的变化趋势,只是降低整体偏差。这说明FCM定权方法并未在力学模型及参数估计上影响定轨结果,而是优化了观测值的权重分配,也从侧面表现出该方法的合理性与正确性。
|
图 4 根据Hitotsubashi University质量报告采用不同定权方法的定轨误差 Fig. 4 Orbit determination error with different weighting methods according to Hitotsubashi University quality report |
|
图 5 根据JCET质量报告采用不同定权方法的定轨误差 Fig. 5 Orbit determination error with different weighting methods according to JCET quality report |
|
图 6 根据MCC质量报告采用不同定权方法的定轨误差 Fig. 6 Orbit determination error with different weighting methods according to MCC quality report |
|
图 7 根据SHAO质量报告采用不同定权方法的定轨误差 Fig. 7 Orbit determination error with different weighting methods according to SHAO quality report |
本文利用原始测站定权和FCM定权对2021年LAGEOS-2卫星进行精密定轨,分析2种方法对卫星轨道精度的影响,得到以下结论:
1) 分析原始测站定权与FCM定权对LAGEOS-2卫星精密定轨的影响,结果表明,FCM定权可将定轨精度和有效观测值数量分别提高2%~8%和1%~3%。
2) 通过分析ILRS四个机构的质量报告对测站定权的影响发现,基于JCET质量报告进行测站定权的效果更好。
本文FCM定权相较原始测站定权更加符合SLR台站的观测水平,可降低对观测值筛选的要求,从而增加有效观测值数量,对定轨精度有一定提升。
| [1] |
Guillemot P, Gasc K, Petitbon I, et al. Time Transfer by Laser Link: The T2L2 Experiment on Jason 2[C]. IEEE International Frequency Control Symposium and Exposition, Miami, 2006
(  0) 0) |
| [2] |
Sośnica K, Bury G, Zajdel R, et al. Estimating Global Geodetic Parameters Using SLR Observations to Galileo, GLONASS, Beidou, GPS, and QZSS[J]. Earth, Planets and Space, 2019, 71
(  0) 0) |
| [3] |
Steindorfer M A, Kirchner G, Koidl F, et al. Daylight Space Debris Laser Ranging[J]. Nature Communications, 2020, 11(1)
(  0) 0) |
| [4] |
严奉轩, 郭唐永, 王培源, 等. SLR应用展望——伽利略计划和非合作目标跟踪[J]. 大地测量与地球动力学, 2006, 26(3): 118-121 (Yan Fengxuan, Guo Tangyong, Wang Peiyuan, et al. Prospect of Application of SLR——On Galileo Plan and Debris Tracking[J]. Journal of Geodesy and Geodynamics, 2006, 26(3): 118-121 DOI:10.3969/j.issn.1671-5942.2006.03.022)
(  0) 0) |
| [5] |
Appleby G, Rodríguez J, Altamimi Z. Assessment of the Accuracy of Global Geodetic Satellite Laser Ranging Observations and Estimated Impact on ITRF Scale: Estimation of Systematic Errors in LAGEOS Observations 1993-2014[J]. Journal of Geodesy, 2016, 90(12): 1 371-1 388 DOI:10.1007/s00190-016-0929-2
(  0) 0) |
| [6] |
秦显平, 杨元喜. 抗差方差分量估计在卫星定轨中的应用[J]. 大地测量与地球动力学, 2003, 23(4): 40-43 (Qin Xianping, Yang Yuanxi. Applications of Robust Variance Component Estimation to Satellite Orbit Determination[J]. Journal of Geodesy and Geodynamics, 2003, 23(4): 40-43 DOI:10.3969/j.issn.1671-5942.2003.04.008)
(  0) 0) |
| [7] |
Soto J, Aguiar M I V, Flores-Sintas A. A Fuzzy Clustering Application to Precise Orbit Determination[J]. Journal of Computational and Applied Mathematics, 2007, 204(1): 137-143 DOI:10.1016/j.cam.2006.04.050
(  0) 0) |
| [8] |
邵璠, 王小亚, 何冰, 等. 模糊聚类定权法对SLR定轨精度的影响[J]. 测绘学报, 2019, 48(10): 1 236-1 243 (Shao Fan, Wang Xiaoya, He Bing, et al. Effect Analysis of the Weighting Scheme with Modified FCM Clustering Algorithm on Precision of SLR Orbit Determination[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(10): 1 236-1 243 DOI:10.11947/j.AGCS.2019.20180373)
(  0) 0) |
| [9] |
赵春梅, 王磊, 何正斌. 卫星激光测距站分级与GNSS卫星轨道精度校核[J]. 测绘学报, 2023, 52(3): 357-366 (Zhao Chunmei, Wang Lei, He Zhengbin. Satellite Laser Ranging Station Classification for GNSS Satellite Orbit Accuracy Validation[J]. Acta Geodaetica et Cartographica Sinica, 2023, 52(3): 357-366)
(  0) 0) |
| [10] |
Pearlman M R, Noll C E, Pavlis E C, et al. The ILRS: Approaching 20 Years and Planning for the Future[J]. Journal of Geodesy, 2019, 93: 2 161-2 180 DOI:10.1007/s00190-019-01241-1
(  0) 0) |
| [11] |
Luceri V, Pirri M, Rodríguez J, et al. Systematic Errors in SLR Data and Their Impact on the ILRS Products[J]. Journal of Geodesy, 2019, 93(11): 2 357-2 366 DOI:10.1007/s00190-019-01319-w
(  0) 0) |
| [12] |
Zhang H Z, Chen H, Bao L X. An Improved Fuzzy C Means Clustering Algorithm and Its Application in Traffic Condition Recognition[C]. Seventh International Conference on Fuzzy Systems and Knowledge Discovery, Yantai, 2010
(  0) 0) |
| [13] |
Heine K. Potential Application of Fuzzy Methods in Geodetic Fields[C]. First International Symposium on Robust Statistics and Fuzzy Techniques in Geodesy and GIS, Zürich, 2001
(  0) 0) |
| [14] |
寇程, 柯长青. 小波变换与FCM聚类的QuickBird影像特征空间识别分析[J]. 地球信息科学学报, 2010, 12(3): 444-450 (Kou Cheng, Ke Changqing. Feature Space Recognition Analysis of Quick Bird Imagery Based on Wavelet Transform and FCM Clustering[J]. Journal of Geo-Information Science, 2010, 12(3): 444-450)
(  0) 0) |
| [15] |
李毓照, 闫浩文, 杨维芳, 等. 基于模糊聚类分析法的BDS长基线模糊度解算[J]. 大地测量与地球动力学, 2021, 41(10): 1 040-1 044 (Li Yuzhao, Yan Haowen, Yang Weifang, et al. Ambiguity Resolution of BDS Long Baseline Based on Fuzzy Clustering Analysis Method[J]. Journal of Geodesy and Geodynamics, 2021, 41(10): 1 040-1 044)
(  0) 0) |
| [16] |
祖志文, 李秦. 基于马氏距离的模糊聚类优化算法——KM-FCM[J]. 河北科技大学学报, 2018, 39(2): 159-165 (Zu Zhiwen, Li Qin. KM-FCM: A Fuzzy Clustering Optimization Algorithm Based on Mahalanobis Distance[J]. Journal of Hebei University of Science and Technology, 2018, 39(2): 159-165)
(  0) 0) |
| [17] |
Folkner W M, Williams J G, Boggs D H. The Planetary and Lunar Ephemeris DE 421[R]. IPN Progress Report, 2009
(  0) 0) |
| [18] |
Knocke P C, Ries J C, Tapley B D. Earth Radiation Pressure Effects on Satellites[C]. AIAA/AAS Astrodynamics Conference, Minneapolis, 1988
(  0) 0) |
| [19] |
Lyard F, Lefevre F, Letellier T, et al. Modelling the Global Ocean Tides: Modern Insights from FES2004[J]. Ocean Dynamics, 2006, 56(5-6): 394-415 DOI:10.1007/s10236-006-0086-x
(  0) 0) |
| [20] |
Petit G, Luzum B. IERS Conventions(2010), IERS Technical Note 36[Z]. 2010
(  0) 0) |
| [21] |
Altamimi Z, Rebischung P, Métivier L, et al. ITRF2014: A New Release of the International Terrestrial Reference Frame Modeling Nonlinear Station Motions[J]. Journal of Geophysical Research: Solid Earth, 2016, 121(8): 6 109-6 131 DOI:10.1002/2016JB013098
(  0) 0) |
| [22] |
Bizouard C, Lambert S, Gattano C, et al. The IERS EOP 14C04 Solution for Earth Orientation Parameters Consistent with ITRF 2014[J]. Journal of Geodesy, 2019, 93(5): 621-633 DOI:10.1007/s00190-018-1186-3
(  0) 0) |
| [23] |
Mendes V B, Prates G, Pavlis E C, et al. Improved Mapping Functions for Atmospheric Refraction Correction in SLR[J]. Geophysical Research Letters, 2002, 29(10)
(  0) 0) |
| [24] |
Mendes V B, Pavlis E C. High-Accuracy Zenith Delay Prediction at Optical Wavelengths[J]. Geophysical Research Letters, 2004, 31(14)
(  0) 0) |
| [25] |
赵罡, 王小亚, 吴斌. 不同测站卫星质心不同改正对卫星激光测距定轨精度的影响分析[J]. 测绘学报, 2012, 41(2): 165-170 (Zhao Gang, Wang Xiaoya, Wu Bin. Effect Analysis of System-Dependent Center-of-Mass Correction on Precision of SLR Orbit Determination[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 165-170)
(  0) 0) |
2. College of Earth and Planetary Sciences, University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China;
3. Wuhan National Geodetic Observatory, Innovation Academy for Precision Measurement Science and Technology, CAS, 340 Xudong Street, Wuhan 430077, China
 2024, Vol. 44
2024, Vol. 44

