随着低轨(LEO)卫星日益增多,许多科学和业务应用如卫星测高、合成孔径雷达干涉测量、无线电掩星探测和低轨卫星导航增强[1-4]等,在实时性和精度方面,对低轨卫星轨道提出越来越高的要求。星载GNSS因具有可连续观测、精度高等诸多优点,已成为低轨卫星定轨的主要技术手段。基于GNSS的LEO事后精密定轨虽然可达到cm级[5],但严重依赖于时效性不高的精密星历和钟差产品。
目前,可用于LEO实时导航的星历主要为广播星历。早期的低轨卫星实时定轨主要是使用伪距观测值,实时定轨精度只能达到m级[6-7],其影响因素主要有伪距测量误差和广播星历误差等。为了克服伪距测量误差的影响,Montenbruck等率先使用测量误差较小的载波相位观测值。受广播星历轨道和钟差精度制约,基于载波相位的实时定轨精度只能达到dm级[8-11],距离实时cm级精度需求仍存在一定的差距。
为满足实时精密定位技术的发展需求,目前可以通过互联网和导航卫星播发GNSS增强信息。部分学者针对GNSS增强信息在LEO卫星实时精密定轨中的应用展开相关研究,结果表明,在全弧段实时GNSS增强信息产品的支持下,采用实时运动学定轨方法,精度优于20 cm[12],采用简化动力学定轨方法,精度约为5~10 cm[13-15]。
本文针对LEO卫星GPS实时精密定轨伪模糊度随机过程参数优化问题展开研究。首先介绍伪模糊度随机模型的构建过程,并推导LEO卫星GPS实时精密定轨滤波模型;然后使用实测数据,对伪模糊度随机过程噪声开展参数优化实验,并评估采用最优伪模糊度方案对实时精密定轨精度的提升效果。
1 伪模糊度随机模型构建 1.1 星载GPS观测方程LEO星载GPS双频无电离层组合伪距和载波相位观测方程可简化为:
| $ \left\{\begin{array}{l} P_{\mathrm{IF}}=\rho+c \cdot \delta t_{\mathrm{r}}-c \cdot \delta t^{\mathrm{s}}+M_P+\varepsilon_P \\ L_{\mathrm{IF}}=\rho+c \cdot \delta t_{\mathrm{r}}-c \cdot \delta t^{\mathrm{s}}+B_{\mathrm{IF}}+M_L+\varepsilon_L \end{array}\right. $ | (1) |
式中,PIF和LIF分别为GPS双频无电离层组合伪距和载波相位观测值,ρ为GPS卫星与LEO星载接收机之间的几何距离,δtr和δts分别为星载接收机和GPS卫星的钟差参数,c为真空中光速,BIF为无电离层组合载波相位浮点模糊度,(MP, ML)和(εP, εL)分别为GPS双频无电离层组合伪距、载波相位的多路径误差和观测噪声。
1.2 沿传播路径上的星历误差在上述GPS观测方程中,由GPS星历计算的GPS卫星轨道和钟差与真实的GPS卫星轨道和钟差仍存在一定差异,这种差异在沿GPS信号传播路径上引起的星历误差ELOS可表示为[8]:
| $ \begin{gathered} E_{\mathrm{LOS}}=\left(\rho^*-c \cdot \delta t^{\mathrm{s*}}\right)-\left(\rho-c \cdot \delta t^{\mathrm{s}}\right)= \\ \mathrm{d} \rho-c \cdot \mathrm{d} \delta t^{\mathrm{s}} \end{gathered} $ | (2) |
式中,
通常可将星历误差ELOS与式(1)中浮点模糊度BIF合并为一个待估参数(称为伪模糊度参数,A=BIF+ELOS),以减少实时定轨待估参数的个数,进而提高计算效率。因此,可将式(1)中无电离层组合的载波相位观测方程改写为:
| $ L_{\mathrm{IF}}=\rho+c \cdot \delta t_{\mathrm{r}}-c \cdot \delta t^{\mathrm{s}}+A+M_L+\varepsilon_L $ | (3) |
在载波相位无周跳的情况下,由于浮点模糊度参数BIF为常量,伪模糊度参数A的随机模型与ELOS紧密相关。分析表明,与GPS广播星历一样,实时精密星历计算的ELOS也存在缓变的误差变化特性,因此,仍可使用随机游走过程对伪模糊度参数A进行建模:
| $ A_{k+1}=A_k+\omega_k $ | (4) |
式中,Ak+1和Ak分别为tk+1和tk时刻的伪模糊度参数,ωk为具有高斯白噪声的随机变量。
2 实时精密定轨滤波模型基于GPS轨道钟差改正信息的实时精密定轨滤波模型中的状态方程和观测方程可表示为:
| $ \left\{\begin{array}{l} \boldsymbol{X}_k=\boldsymbol{\varPhi}_{k, k-1} \boldsymbol{X}_{k-1}+\boldsymbol{W}_{k-1} \\ \boldsymbol{Z}_k=\boldsymbol{H}_k \boldsymbol{X}_{k-1}+\boldsymbol{V}_k \end{array}\right. $ | (5) |
式中,Xk和 Zk分别为卡尔曼滤波状态量和观测量,Φk, k-1和 Hk分别为状态转移矩阵和观测矩阵,Wk-1和 Vk分为系统噪声和观测噪声。
本文实时精密定轨滤波模型中的待估滤波状态量选取为:
| $ \boldsymbol{X}_k=\left[\begin{array}{llllllll} \boldsymbol{p} & \boldsymbol{v} & \delta t_{\mathrm{r}} & \dot{\delta} t_{\mathrm{r}} & c_d & c_r & \boldsymbol{a}_w & \boldsymbol{A}_{n \times 1} \end{array}\right]^{\mathrm{T}} $ | (6) |
式中,
第i颗GPS卫星的无电离层组合相位观测值LIFi关于滤波器状态量的偏导数 Hki可以表示为:
| $ \boldsymbol{H}_k^i=\left[\begin{array}{lllll} -\left(\boldsymbol{U}^{\mathrm{T}} \cdot \boldsymbol{e}^i\right)^{\mathrm{T}} & \mathbf{0}_{1 \times 3} & 1 & \mathbf{0}_{1 \times 6} & \boldsymbol{I}_{1 \times n} \end{array}\right] $ | (7) |
式中,UT为惯性系到地固系的转换矩阵;ei为低轨卫星相对于第i颗GPS卫星的视线向量;I1×n中第i颗GPS卫星的通道为1,其余通道为0。
3 实验结果及分析 3.1 实验数据选取GRACE-C和SWARM-A两颗LEO卫星2021年doy92~101共计10 d的星载GPS双频数据,两颗LEO卫星的详细信息见表 1。此外,还选取与两颗LEO卫星GPS观测数据同时段的两种实时精密产品(法国CNES发布的CNT和日本JAXA发布的MADOCA),两种实时精密产品的相关信息对比见表 2。
|
|
表 1 GRACE-C和SWARM-A卫星信息 Tab. 1 Information of GRACE-C and SWARM-A satellites |
|
|
表 2 两种实时精密星历产品信息 Tab. 2 Information of the two real-time precise ephemeris products |
如前所述,依据实时精密星历计算的ELOS存在缓变的误差变化特性,可使用随机游走过程对伪模糊度参数A进行建模。伪模糊度参数A的初始方差D0可根据ELOS最大值进行设置,其随机过程噪声σ与ELOS的功率谱密度有关,一般也可根据ELOS的变化率大致设置[9]。本文统计两种实时精密星历计算的ELOS最大变化率在±1 mm/s左右,可通过本文方法合理设置并优化伪模糊度随机过程参数σ,从而吸收沿传播路径上的星历误差ELOS,进而提高实时定轨精度。
为了对伪模糊度随机过程参数进行优化,本文提出在定轨策略及其他变量不变的情况下,使用一种数值步进搜索比较方法确定伪模糊度随机过程参数的最优设置。具体方法为:在实时定轨中使用的定轨策略及其他变量(如地球重力场阶数等)均保持不变,将ELOS最大变化率作为随机过程噪声参数σ的初值,以数值步进的方式增减改变σ值,最终得到表 3中8种不同的σ取值方案(S1~S8);然后以模拟在轨实时模式重复进行实时精密定轨实验,通过比较S1~S8方案下实时定轨结果的三维位置误差,确定伪模糊度随机过程参数的最优设置。
|
|
表 3 伪模糊度随机过程参数设置方案 Tab. 3 Setting schemes of random processes parameters for pseudo-ambiguity |
本文使用两种实时精密星历产品(CNT和MADOCA),在S1~S8方案下,以模拟在轨实时精密定轨的方式重复处理2021年doy92~101共10 d的LEO卫星GPS数据。实验中假设LEO卫星能够在轨全程获取到实时精密星历产品,实时精密定轨策略如表 4所示。
|
|
表 4 实时精密定轨策略及设置 Tab. 4 Real-time precise orbit determination strategies and settings |
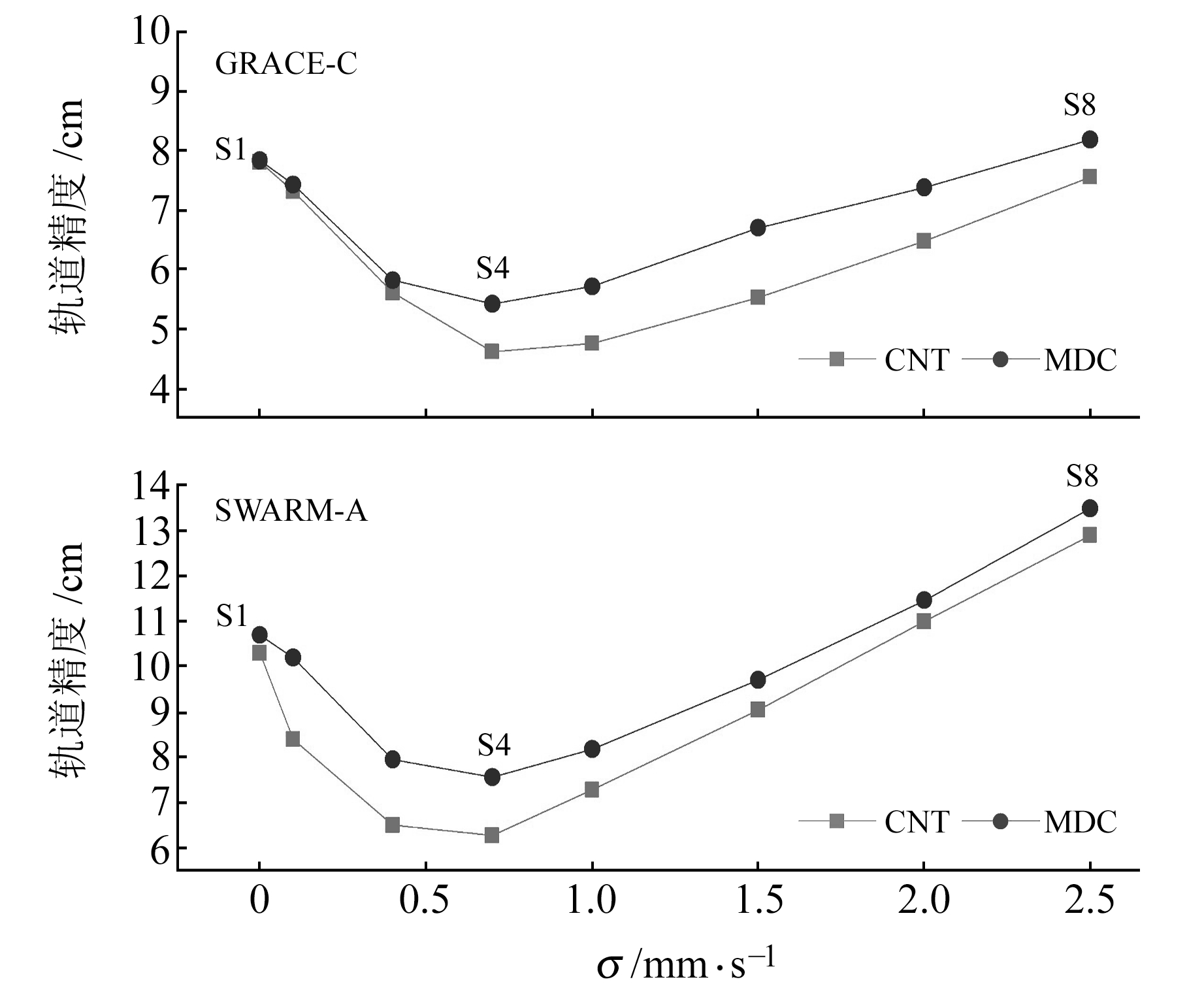
图 1为S1~S8方案下的实时定轨精度对比情况,可以看出,在S4方案下,使用CNT和MADOCA实时产品,两颗LEO卫星实时定轨精度均取得最优值,因此S4方案(σ=0.7 mm/s)可认为是S1~S8方案中的最优值。
|
图 1 S1~S8方案下的实时精密定轨精度对比 Fig. 1 Comparison of RTPOD accuracy under S1-S8 schemes |
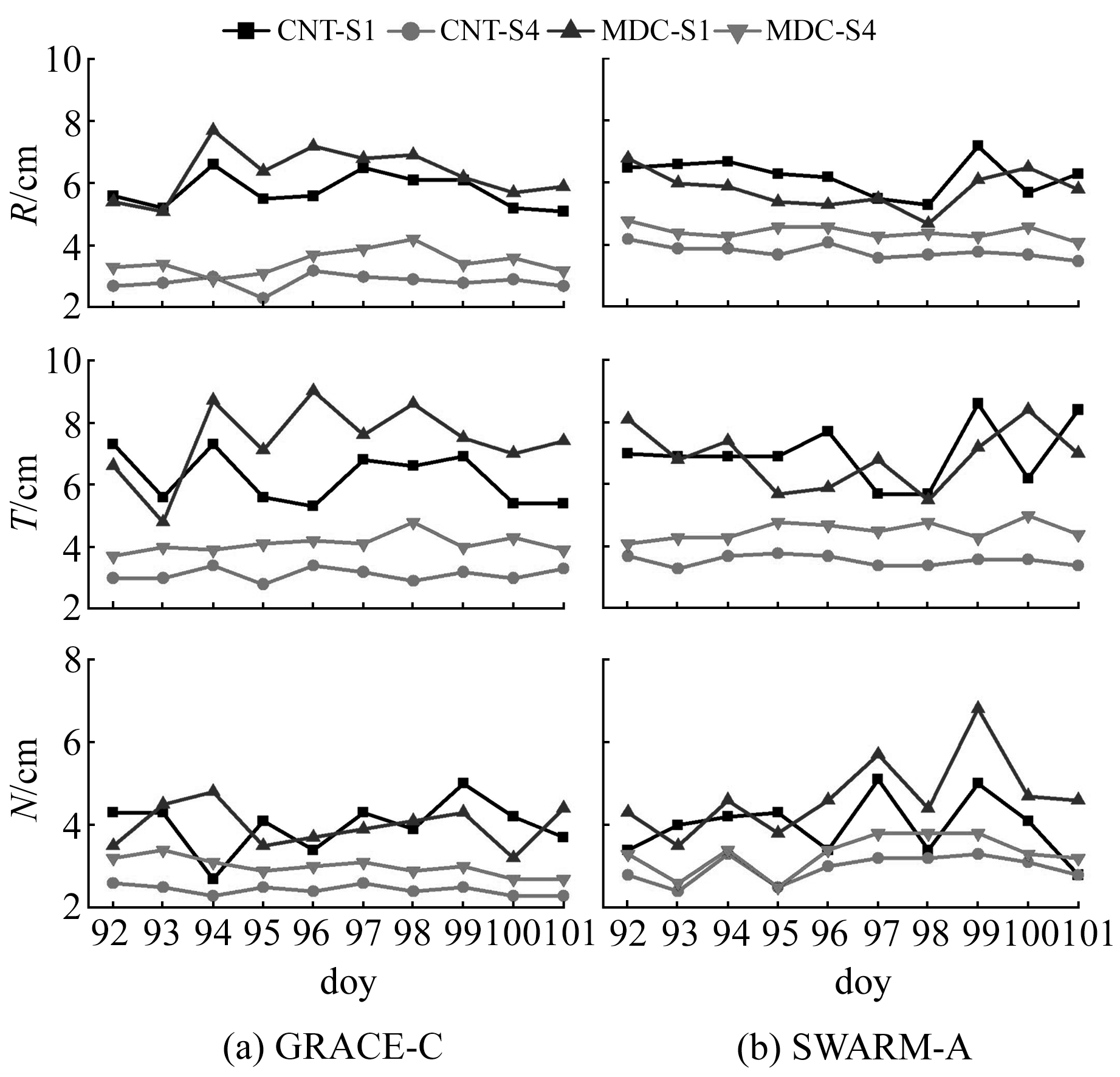
图 2为GRACE-C、SWARM-A两颗卫星在S1、S4两种方案下R、T、N三个方向的实时定轨精度对比情况,表 5为GRACE-C、SWARM-A两颗卫星在S1、S4两种方案下10 d的实时精密定轨精度统计结果。
|
图 2 GRACE-C、SWARM-A卫星在S1、S4方案下的实时精密定轨精度对比 Fig. 2 Comparison of RTPOD accuracy of GRACE-C and SWARM-A satellites under S1 and S4 schemes |
|
|
表 5 GRACE-C、SWARM-A卫星在S1、S4方案下的实时精密定轨精度统计 Tab. 5 RTPOD accuracy statistics of GRACE-C and SWARM-A satellites under S1 and S4 schemes |
1)在相同LEO卫星GPS观测数据条件下,CNT产品的实时精密定轨结果优于MADOCA,可能与CNT产品轨道钟差精度优于MADOCA有关。
2)在相同实时精密星历产品条件下,SWARM-A卫星实时精密定轨结果比GRACE-C卫星稍差,可能与SWARM-A卫星轨道高度更低和GPS观测数据条件稍差(SWARM-A卫星接收机通道数少)有关。
3)GRACE-C、SWARM-A两颗卫星在方案4条件下,实时定轨三维位置误差(RMS)为4.62~7.56 cm,均优于10 cm,其中轨道径向误差均优于5 cm。
4)相比于方案1(该方案伪模糊度参数采用常量模型,伪模糊度参数与传统的浮点模糊度意义相同,即不考虑沿传播路径上的星历误差的影响),使用CNT和MADOCA产品,方案4(最优伪模糊度方案)实时精密定轨精度分别平均提升约39.15%和29.61%。
4 结语本文使用两颗LEO卫星2021年doy92~101共10 d的星载GPS数据及同时段的两种实时精密星历产品,以模拟在轨实时精密定轨的方式,对伪模糊度随机过程参数开展优化实验。结果表明,在参数最优值方案下,两颗LEO卫星的实时精密定轨三维位置误差约为4.62~7.56 cm,相比于传统的模糊度浮点解方案,使用CNT和MADOCA产品的实时定轨精度分别平均提升约39.15%和29.61%。
随着各国GNSS增强系统的建设和逐步完善,未来LEO卫星或能在轨获得实时GNSS轨道和钟差改正信息,通过LEO卫星星载计算可实时获取cm级轨道参数,这一技术将有益于低轨卫星的实时科学和业务应用。
| [1] |
Jayles C, Chauveau J P, Rozo F. DORIS/Jason-2: Better than 10 cm On-Board Orbits Available for Near-Real-Time Altimetry[J]. Advances in Space Research, 2010, 46(12): 1 497-1 512 DOI:10.1016/j.asr.2010.04.030
(  0) 0) |
| [2] |
Wermuth M, Hauschild A, Montenbruck O, et al. TerraSAR-X Precise Orbit Determination with Real-Time GPS Ephemerides[J]. Advances in Space Research, 2012, 50(5): 549-559 DOI:10.1016/j.asr.2012.03.014
(  0) 0) |
| [3] |
Montenbruck O, Hauschild A, Andres Y, et al. (Near-)Real-Time Orbit Determination for GNSS Radio Occultation Processing[J]. GPS Solutions, 2013, 17(2): 199-209 DOI:10.1007/s10291-012-0271-y
(  0) 0) |
| [4] |
Li X X, Ma F J, Li X, et al. LEO Constellation-Augmented Multi-GNSS for Rapid PPP Convergence[J]. Journal of Geodesy, 2019, 93(5): 749-764 DOI:10.1007/s00190-018-1195-2
(  0) 0) |
| [5] |
van den IJssel J, Encarnação J, Doornbos E, et al. Precise Science Orbits for the Swarm Satellite Constellation[J]. Advances in Space Research, 2015, 56(6): 1 042-1 055 DOI:10.1016/j.asr.2015.06.002
(  0) 0) |
| [6] |
Montenbruck O, Ramos-Bosch P. Precision Real-Time Navigation of LEO Satellites Using Global Positioning System Measurements[J]. GPS Solutions, 2008, 12(3): 187-198 DOI:10.1007/s10291-007-0080-x
(  0) 0) |
| [7] |
王甫红. 高精度星载GPS实时定轨卡尔曼滤波模型[J]. 武汉大学学报:信息科学版, 2010, 35(6): 653-656 (Wang Fuhong. A Kalman Filtering Algorithm for Precision Real-Time Orbit Determination with Space-Borne GPS Measurements[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6): 653-656)
(  0) 0) |
| [8] |
Wang F H, Gong X W, Sang J Z, et al. A Novel Method for Precise Onboard Real-Time Orbit Determination with a Standalone GPS Receiver[J]. Sensors, 2015, 15(12): 30 403-30 418 DOI:10.3390/s151229805
(  0) 0) |
| [9] |
Gong X W, Sang J Z, Wang F H, et al. LEO Onboard Real-Time Orbit Determination Using GPS/BDS Data with an Optimal Stochastic Model[J]. Remote Sensing, 2020, 12(20)
(  0) 0) |
| [10] |
郭磊, 王甫红. 星载单频GPS实时精密定轨模型研究[J]. 大地测量与地球动力学, 2020, 40(4): 371-375 (Guo Lei, Wang Fuhong. Precise Real-Time Orbit Determination Model Using Space-Borne Single-Frequency GPS Observations[J]. Journal of Geodesy and Geodynamics, 2020, 40(4): 371-375)
(  0) 0) |
| [11] |
Li M, Qin G E, Jiang K C, et al. Performance Assessment of Real-Time Orbit Determination for the Haiyang-2D Using Onboard BDS-3/GPS Observations[J]. Advances in Space Research, 2023, 71(3): 1 657-1 669 DOI:10.1016/j.asr.2022.09.050
(  0) 0) |
| [12] |
Giordano P, Zoccarato P, Otten M, et al. P2OD: Real-Time Precise Onboard Orbit Determination for LEO Satellites[C]. Proceedings of the 30th International Technical Meeting of the Satellite Division of the Institute of Navigation, Portland, 2017
(  0) 0) |
| [13] |
Hauschild A, Tegedor J, Montenbruck O, et al. Precise Onboard Orbit Determination for LEO Satellites with Real-Time Orbit and Clock Corrections[C]. Proceedings of the 29th International Technical Meeting of the Satellite Division of the Institute of Navigation, Portland, 2016
(  0) 0) |
| [14] |
Allahvirdi-Zadeh A, Wang K, El-Mowafy A. POD of Small LEO Satellites Based on Precise Real-Time MADOCA and SBAS-Aided PPP Corrections[J]. GPS Solutions, 2021, 25(2)
(  0) 0) |
| [15] |
张万威, 王甫红, 龚学文, 等. 一种顾及IGS-RTS数据接收中断的厘米级星载GPS实时定轨方法[J]. 武汉大学学报:信息科学版, 2021, 46(11): 1 620-1 626 (Zhang Wanwei, Wang Fuhong, Gong Xuewen, et al. A Centimeter-Level Real-Time Orbit Determination Method Using Space-Borne GPS Measurements Considering IGS-RTS Data Receiving Interruption[J]. Geomatics and Information Science of Wuhan University, 2021, 46(11): 1 620-1 626)
(  0) 0) |
 2024, Vol. 44
2024, Vol. 44


