2. 中山大学极地环境立体观测与应用教育部重点实验室,广东省珠海市大学路2号,519082
受海平面强反射作用的影响,海洋环境中全球卫星导航系统(global navigation satellite system, GNSS)观测数据多路径效应和观测噪声较大,导致伪距单点定位(single point positioning, SPP)性能显著下降。目前GNSS标准的SPP服务仅能提供精度为3 m的实时海上导航定位[1],这种精度无法满足部分海上较精细作业的需求(精度要求约为1 m)[2]。目前对伪距多路径效应的研究仅在观测站一侧存在水域的海边或浅水环境中[3-5],远海环境中船会被反射系数为1的海水面包围,因此远海环境中的多路径效应会更加严重[6-8]。与高精度分体式大地接收机不同,RTK(real-time kinematic)接收机将接收器和天线部件整合在一起,具有灵活、方便、成本低等优点,市场占有率较高。然而,RTK接收机的天线抗多路径性能较弱,在远海环境中单点定位性能会显著下降。
载波相位平滑伪距以历元间电离层延迟变化较小为前提,利用相位观测值对伪距观测噪声进行平滑,既能有效降低伪距噪声和多路径效应,又能避开求解整周模糊度[9-10]。国内外许多学者采用载波相位平滑伪距来提高伪距单点定位精度。徐宗秋等[11]将载波相位平滑应用于手机端定位,平滑后定位精度提高39.7%;陈正生等[12]提出一种自模型化电离层延迟变化的单频载波相位平滑伪距算法,将陆地动态环境下单频SPP在水平和高程方向的定位精度分别提高5.4倍和3.3倍。以上研究均集中在陆地环境中,而在海洋环境中相位平滑伪距抑制多路径方法对低成本RTK接收机SPP性能的影响尚未可知,这会限制RTK接收机在海洋领域的应用。因此,本文综合分析远海环境中载波相位平滑抑径算法对低成本RTK接收机SPP性能的影响。
1 基本原理 1.1 单点定位模型当采用不同频率观测值进行无电离层组合时,双频无电离层组合伪距观测方程可表示为:
| $ \begin{gathered} P_{\mathrm{IF}}=\alpha P_i+(1-\alpha) P_j= \\ \rho+b_{\mathrm{r}, \mathrm{IF}}-b_{\mathrm{IF}}^{\mathrm{s}}+\varepsilon_{P_{\mathrm{IF}}} \end{gathered} $ | (1) |
式中,
虽然双频无电离层组合可以消除一阶电离层延迟,约占整个电离层总延迟的99%以上[13],但同时对伪距多路径效应及噪声具有放大作用,根据误差传播定律,组合后的双频伪距观测值噪声与多路径效应之和为:
| $ \varepsilon_{P_{\mathrm{IF}}}^2=\alpha^2 \varepsilon_{P_i}^2+(1-\alpha)^2 \varepsilon_{P_j}^2 $ | (2) |
当使用不同频点进行无电离层组合时,为避免组合噪声系数过大,通常将频点相差较大的频率进行组合。
1.2 伪距多路径效应提取模型多路径效应对伪距观测值的影响比载波观测值更显著。伪距多路径效应可由MP(multipath)组合观测值求取,具体计算公式为:
| $ \begin{gathered} \mathrm{MP}_i=P_i-L_i+\frac{2 f_j^2}{f_i^2-f_j^2}\left(L_j-L_i\right)= \\ M_i-\frac{f_i^2+f_j^2}{f_i^2-f_j^2} m_i+\frac{2 f_j^2}{f_i^2-f_j^2} m_j+B+\varepsilon_{\mathrm{MP}_i} \end{gathered} $ | (3) |
式中,Li为i频点的载波观测值,Mi为i频点的伪距多路径效应和伪距观测噪声之和,mi为i频点的载波多路径效应和载波观测值噪声之和,fi为i频点的频率,B为载波相位模糊度和硬件延迟偏差之和。当未发生周跳时,B视为常量,MPi观测值可反映i频点伪距多路径效应和观测噪声的综合影响。
1.3 相位平滑伪距抑径数学模型| $ \begin{gathered} \bar{P}_k=\frac{1}{k} P_1(k)+\frac{k-1}{k} \cdot\left(\bar{P}_1(k-1)+\right. \\ \left.L_1(k)-L_1(k-1)\right) \end{gathered} $ | (4) |
式中,P为平滑后的伪距观测值,k为历元数,P和L分别为原始的伪距和载波相位观测值。根据误差传播定律,平滑后的伪距精度为:
| $ \sigma_{\bar{P}_1(k)}^2=\frac{1}{k} \sigma_P^2+\frac{k-1}{k} \sigma_L^2 $ | (5) |
由式(5)可以看出,平滑窗口越大、历元数越多,平滑后的伪距精度越接近载波观测值精度。本文首先采用单频相位观测值对单频伪距观测值进行平滑处理,然后对平滑后的伪距观测值进行消电离层组合,组合后的双频平滑伪距观测值可表示为:
| $ P_{\mathrm{IF}}=\alpha \bar{P}_1(k)+(1-\alpha) \bar{P}_2(k) $ | (6) |
本文采用RTK接收机(Trimble R10-2)采集陆地和海洋环境实验数据,采样间隔均设置为10 s,该接收机可观测到GPS L1/L2/L5、BDS-3 B1I/B3I/B1C/B2a、Galileo E1/E5频率的信号。选择同设备在陆地和海洋环境中的伪距多路径效应进行定量对比。陆地实验数据采集地点位于中山大学珠海校区内开阔草地,视野无遮挡,观测时长约10 h。远海实验数据采用2021-12-22~27在“中山大学”号科考船上架设RTK接收机采集的观测数据,采集环境如图 1所示,采集地点为距离陆地约524~617 km的南海海域。

|
图 1 远海环境接收机装置 Fig. 1 Receiver device in remote ocean environment |
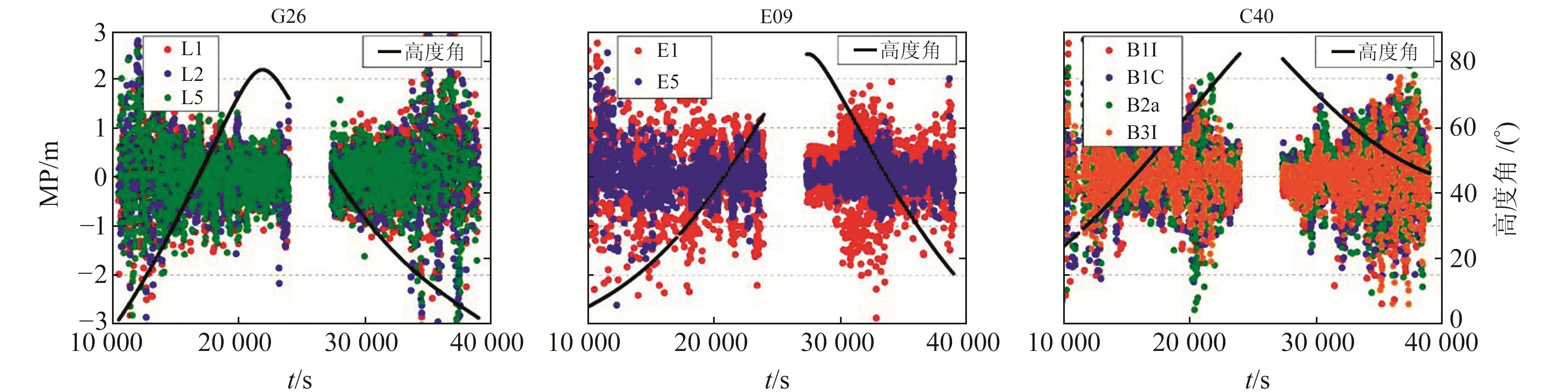
多路径效应MP时间序列与样本分布范围和高度角密切相关,为比较同一接收机在陆地和海洋环境中的伪距多路径效应差异,选取卫星高度角分布相似且样本数量接近的卫星组G24/G26、E15/E09、C40/C39进行比较。图 2、3分别为Trimble R10-2接收机在陆地和海洋环境中的MP时间序列。伪距多路径效应与高度角有关,高度角越低,伪距多路径效应越显著。从图 2可以看出,陆地环境中GPS/Galileo/BDS-3系统各频点的伪距多路径效应均存在明显差异。对于BDS-3系统,各频点伪距多路径效应从大到小依次为:B1I>B1C>B2a>B3I;对于GPS系统,L5频点多路径效应略小于L1、L2频点;Galileo系统E5频点多路径效应远小于其他频点。由图 3可知,海洋环境中GPS系统各频点信号的多路径效应显著大于陆地环境,但各频点的MP时间序列处于同一水平。对于BDS-3系统,B3I频点多路径效应较小,B1I频点多路径效应略大于其他频点。Galileo系统E5频点多路径效应小于其他GNSS系统。

|
图 2 陆地环境中多路径效应时间序列 Fig. 2 Time series of multipath effect in land environment |
|
图 3 海洋环境中多路径效应时间序列 Fig. 3 Time series of multipath effect in marine environment |
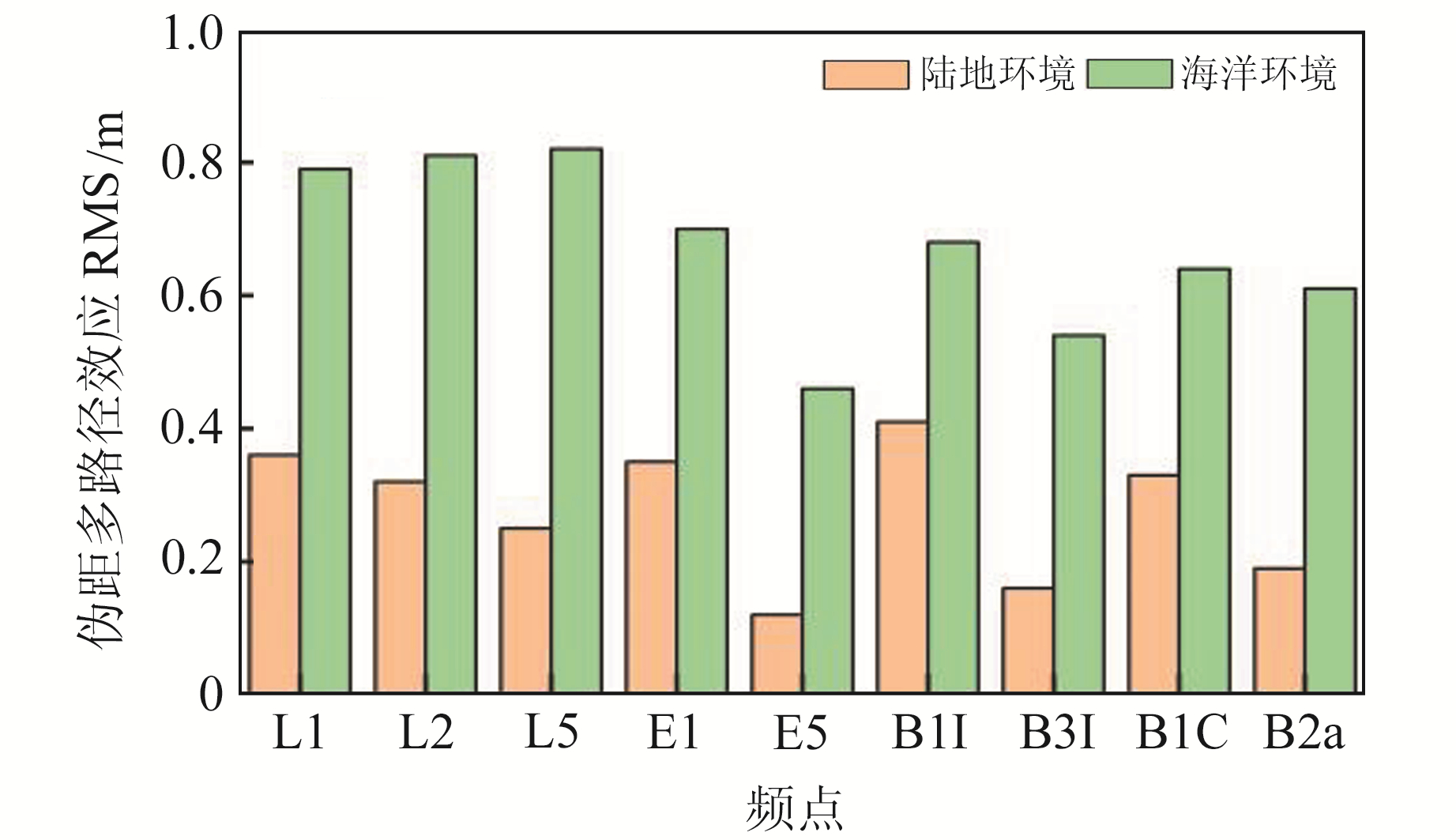
图 4为同型号接收机BDS-3/GPS/Galileo三系统各频率在陆地和海洋环境中MP时间序列RMS值,可以看出,陆地环境中MP值在0.1~0.4 m之间,海洋环境中MP值在0.4~0.8 m之间。由于海平面的强反射作用,相较于陆地环境,海洋环境中GPS/Galileo/BDS-3系统各频点的伪距多路径效应均有所增强。其中,BDS-3系统B1I频点的伪距多路径效应变化最小,增加1.7倍左右;B3I、B2a频点的多路径效应变化最大,增加3.3倍左右。BDS-3系统不同频点的伪距多路径效应变化量不同主要是与不同频点的抗多路径性能差异有关。其中,B3I、B2a频点信号的抗多路径性能较差,受环境影响较大。无论是在海洋还是陆地环境,Galileo系统E5频点的伪距多路径效应最小,表明其抗多路径能力最强。
|
图 4 陆地和海洋环境中MP序列RMS值 Fig. 4 RMS values of multipath effects in land and marine environment |
为对比分析陆地与海洋环境中GPS/BDS-3/Galileo系统滤波平滑抑径对SPP定位性能的影响,利用上述陆地/海洋环境中采集的原始观测数据进行SPP实验。其中,GPS系统采用L1/L2组合频率,Galileo系统采用E1/E5组合频率,BDS-3系统采用B1I/B3I、B1C/B2a组合频率参与解算,具体解算策略见表 1。本次实验采用G/C/E多系统组合的动态PPP结果作为参考真值,将解算的三维坐标转换到站心坐标系下,得到东(E)、北(N)、高(U)方向的定位误差。B-3表示BDS-3,G表示GPS,E表示Galileo。
|
|
表 1 数据处理策略 Tab. 1 Data processing strategy |

|
图 5 海洋环境中可见卫星数及PDOP值 Fig. 5 The number of visible satellites and PDOP value in marine environment |
可见卫星数和精度衰减因子PDOP(position dilution of precision)是影响定位精度的主要因素。对不同系统组合的可见卫星数和PDOP值进行分析。由表 2和图 5可知,对于单系统而言,BDS-3和Galileo系统部分时段可见卫星数低于4颗,PDOP值大于6,无法保证海上动态定位的稳定性和连续性。对于双系统而言,B-3/G和E/G双系统最小可见卫星数为8,最大PDOP值小于3,能充分满足单点定位解算卫星数的需求。B-3/G双系统卫星PDOP值整体优于E/G双系统。因此,本实验采用与GPS系统联合来增加多余观测的卫星数目以保证定位的连续性。对于B-3/G/E三系统组合,相比于B-3/G双系统,平均可见卫星数增加6颗,平均PDOP值减小0.20,其卫星空间几何构型改善28.2%;相比于E/G双系统,平均可见卫星数增加9颗,平均PDOP值减小0.47,其卫星空间几何构型改善14.2%。
|
|
表 2 可见卫星数及PDOP值统计 Tab. 2 Statistics of visible satellite number and PDOP value |
图 6为陆地和海洋环境中GPS+BDS-3(B1I/B3I)系统平滑抑径前后双频SPP定位误差序列,可以看出,海洋环境中单点定位的随机噪声明显大于陆地环境,海洋环境中单点定位精度比陆地环境低1 m以上,这是由于海洋环境中各频点的伪距多路径效应相较于陆地环境放大2~3倍,并且双频消电离层组合又将伪距多路径效应及噪声进一步放大3倍以上。平滑抑径后陆地/海洋环境中定位结果的观测噪声均有所改善,定位误差明显减小。因此,相位平滑伪距能够减弱定位过程中的随机噪声,提高定位结果的稳定性。

|
图 6 陆地环境和海洋环境中B1I/B3I双频SPP在E、N、U方向的定位偏差 Fig. 6 The positioning deviation of B1I/B3I dual-frequency SPP in E, N and U directions in land and marine environment |
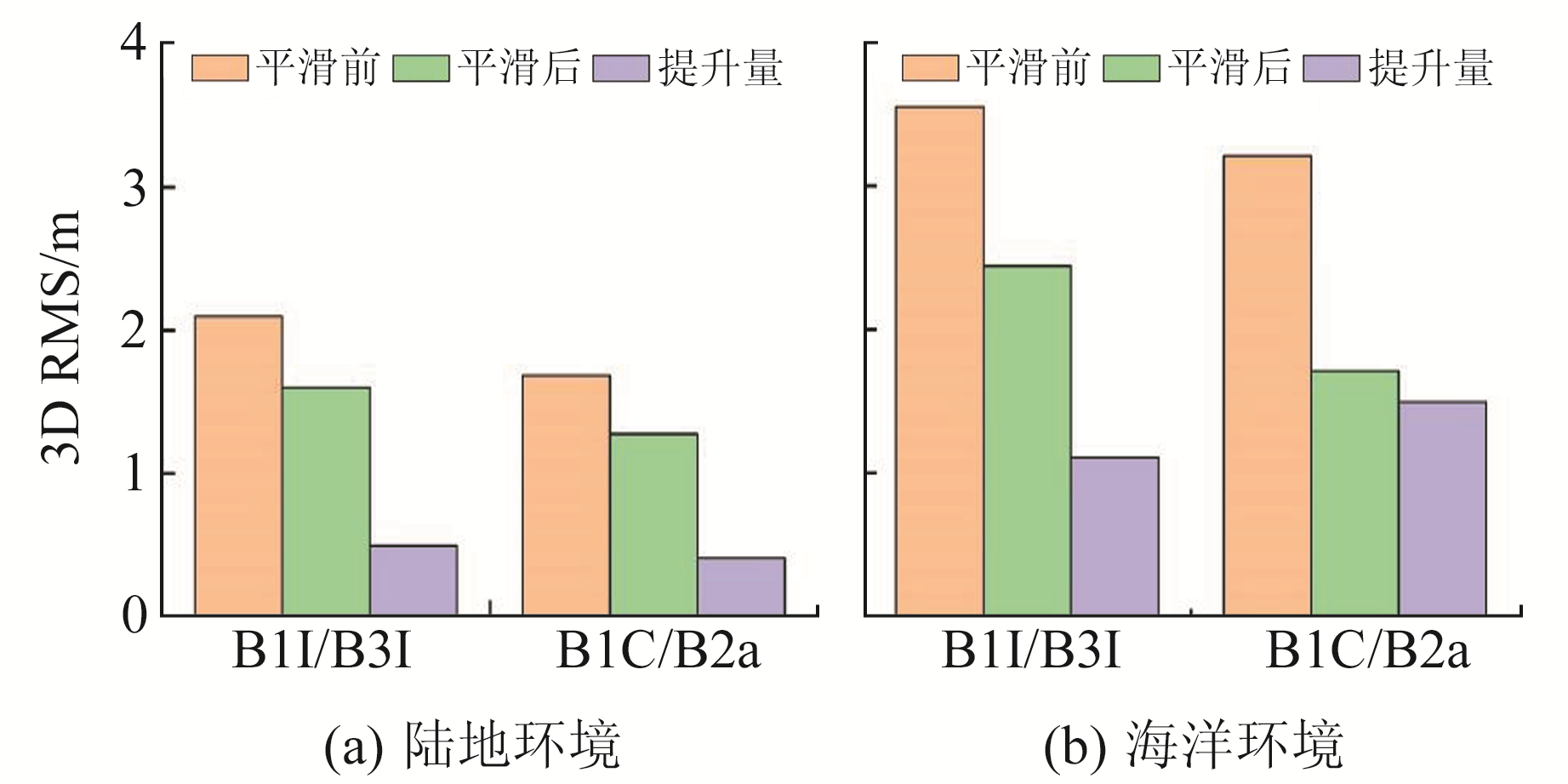
为了直观对比加入平滑抑径算法对海洋/陆地环境中SPP定位精度的影响,图 7为陆地和海洋环境中GPS+BDS-3不同频率组合SPP平滑抑径前后的定位精度。由图 7(a)可知,在陆地环境中,B1C/B2a新频率组合SPP定位精度最高,平滑抑径后3D方向定位精度优于2 m,精度提升量约为0.4 m,提升比例为24%。由图 7(b)可知,平滑抑径对海洋环境中SPP定位精度影响较为明显,在加入平滑抑径算法前,B1C/B2a双频无电离层组合SPP定位精度最高,3D方向定位精度优于3.5 m;加入平滑抑径算法后,B1C/B2a新频率组合SPP定位精度也最高,3D方向定位精度优于2 m,精度提升量约为1.5 m,提升比例为62%。海洋环境中双频无电离层组合SPP经过平滑后的精度提升量约为陆地环境的4~6倍,这也说明海洋环境中的多路径效应更为显著,滤波平滑抑径效果也更为突出。
|
图 7 GPS/BDS-3系统平滑抑径前后SPP定位精度 Fig. 7 SPP accuracy of GPS/BDS-3 system before and after smoothing multipath reduction |
为进一步提高海洋环境中双频单点定位精度,采用多GNSS系统组合定位方式来增加数据观测量。从表 3可以看出,B-3/G/E三系统组合伪距单点定位精度相较于E/G、B-3/G双系统具有一定提升,在水平方向上分别提高19%、12%,在高程方向上分别提高12%、15%。B-3/G/E三系统组合平滑后的伪距单点定位精度在水平方向上优于5 dm,高程方向上优于9 dm,基本可以满足海上石油部分测绘作业的需求。
|
|
表 3 海洋环境滤波平滑抑径前后双频SPP定位精度 Tab. 3 Dual-frequency SPP accuracy before and after filter smoothing multipath reduction in marine environment |
本文定量分析海洋/陆地环境中GPS/Galileo/BDS-3系统各频率的伪距多路径效应,并对平滑抑径前后伪距单点定位性能进行分析,得到以下结论:
1) 相同型号接收机在陆地环境中各频点多路径效应为0.1~0.4 m,在远海环境中各频点多路径效应为0.4~0.8 m,相较于陆地环境增加2~3倍左右;无论是海洋还是陆地环境中,E5频点伪距多路径效应远远小于其他频点。
2) 平滑抑径效果与伪距多路径效应大小有关,加入平滑抑径算法后,海洋环境中的定位精度提升量相比于陆地环境更大,海洋环境双频组合SPP平滑后精度提升量为1.5 m,提升比例为62%;陆地环境精度提升量为0.4 m,提升比例为24%。
3) 使用BDS-3新频率B1C/B2a组合的SPP定位精度优于旧频率组合B1I/B3I,GPS+BDS-3系统使用新频率B1C/B2a组合后的定位精度相较于B1I/B3I在水平方向上提高34%,高程方向上提高33%。
4) GPS/Galileo/BDS-3三系统组合SPP在水平方向上定位精度优于0.5 m,高程方向上优于0.9 m,相比于平滑抑径前分别提升64%和61%。
致谢: 感谢中山大学海洋科考中心为本研究的数据采集提供帮助和支持。
| [1] |
Yan X Y, Liu C C, Jiang M, et al. Performance Analysis of Oceanographic Research Vessel Precise Point Positioning Based on BDS/GNSS RTK Receivers[J]. Measurement, 2023, 211
(  0) 0) |
| [2] |
谌业良. 实时DGPS动态定位在海上石油工程中的应用[J]. 水道港口, 1999, 20(1): 29-32 (Chen Yeliang. Application of Real-Time DGPS Kinematic Positioning in Offshore Petroleum Engineering[J]. Journal of Waterway and Harbor, 1999, 20(1): 29-32)
(  0) 0) |
| [3] |
Tian X Y, Chai H Z, Xiang M Z, et al. The Analysis and Evaluation of the Multipath Error of the BDS Marine Measurement[J]. Advances in Space Research, 2022, 70(2): 496-509 DOI:10.1016/j.asr.2022.04.054
(  0) 0) |
| [4] |
Cai C S, Gao Y, Pan L, et al. An Analysis on Combined GPS/COMPASS Data Quality and Its Effect on Single Point Positioning Accuracy under Different Observing Conditions[J]. Advances in Space Research, 2014, 54(5): 818-829 DOI:10.1016/j.asr.2013.02.019
(  0) 0) |
| [5] |
Su M K, Chang X, Zheng F, et al. Theory and Experiment Analysis on the Influence of Floods on a GNSS Pseudo-Range Multipath and CNR Signal Based on Two Cases Study in China[J]. Remote Sensing, 2022, 14(22)
(  0) 0) |
| [6] |
牟哲晗, 郭博峰, 唐龙. 海洋环境对GPS多路径效应影响分析[J]. 海洋学研究, 2019, 37(4): 36-47 (Mu Zhehan, Guo Bofeng, Tang Long. Analysis of the Influence of Marine Environment on GPS Multipath Effect[J]. Journal of Marine Sciences, 2019, 37(4): 36-47)
(  0) 0) |
| [7] |
白腾飞, 柴洪洲, 王敏, 等. 智能手机海上GNSS数据质量分析与动态定位评估[J]. 海洋测绘, 2022, 42(2): 42-47 (Bai Tengfei, Chai Hongzhou, Wang Min, et al. GNSS Observation Quality Assessment and Kinematic Positioning Analysis of Smartphone in Marine Environment[J]. Hydrographic Surveying and Charting, 2022, 42(2): 42-47)
(  0) 0) |
| [8] |
Geng T, Li Z Q, Xie X, et al. Real-Time Ocean Precise Point Positioning with BDS-3 Service Signal PPP-B2b[J]. Measurement, 2022, 203
(  0) 0) |
| [9] |
Park B, Sohn K, Kee C. Optimal Hatch Filter with an Adaptive Smoothing Window Width[J]. Journal of Navigation, 2008, 61(3): 435-454 DOI:10.1017/S0373463308004694
(  0) 0) |
| [10] |
Yan F J, Gao Y, Zhang C, et al. A Multipath Elimination Algorithm Combined with MEDLL Loop and Hatch Filtering[C]. The 11th China Satellite Navigation Conference, Chengdu, 2020
(  0) 0) |
| [11] |
徐宗秋, 韩澎涛, 赵洪涛, 等. BDS-3基本系统载波相位平滑伪距分析[J]. 测绘科学, 2020, 45(12): 62-68 (Xu Zongqiu, Han Pengtao, Zhao Hongtao, et al. Analysis of Carrier Phase Smoothing Pseudorange of BDS-3 Preliminary System[J]. Science of Surveying and Mapping, 2020, 45(12): 62-68)
(  0) 0) |
| [12] |
陈正生, 张清华, 李林阳, 等. 电离层延迟变化自模型化的载波相位平滑伪距算法[J]. 测绘学报, 2019, 48(9): 1 107-1 118 (Chen Zhengsheng, Zhang Qinghua, Li Linyang, et al. An Improved Carrier Phase Smoothing Pseudorange Algorithm with Self-Modeling of Ionospheric Delay Variation[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(9): 1 107-1 118)
(  0) 0) |
| [13] |
Cui H M, Zhang S J, Li J C. An Improved Phase-Smoothed-Code Algorithm Using GNSS Dual-Frequency Carrier Epoch-Difference Geometry-Free Combination Observations[J]. Advances in Space Research, 2023, 71(8): 3 433-3 443
(  0) 0) |
| [14] |
岑铭. BDS-3载波相位平滑伪距单点定位性能分析[J]. 地理空间信息, 2022, 20(10): 82-85 (Cen Ming. Performance Analysis of BDS-3 Carrier Phase Smoothing Pseudo-Range Single Point Positioning[J]. Geospatial Information, 2022, 20(10): 82-85)
(  0) 0) |
| [15] |
邝英才, 吕志平, 李林阳, 等. GPS/BDS/Galileo相位平滑伪距单点定位性能分析[J]. 导航定位学报, 2018, 6(2): 68-76 (Kuang Yingcai, Lü Zhiping, Li Linyang, et al. Performance Analysis of GPS/BDS/Galileo Phase-Smoothed Pseudorange Point Positioning[J]. Journal of Navigation and Positioning, 2018, 6(2): 68-76)
(  0) 0) |
| [16] |
Zhang Q H, Chen Z S, Rong F J, et al. An Improved Hatch Filter and Its Application in Kinematic Positioning with Single-Frequency GPS[J]. Measurement, 2019, 146: 868-878
(  0) 0) |
| [17] |
杜彦君, 贾小林, 姚顽强, 等. TGD改正对BDS-3新频点单点定位的影响分析[J]. 大地测量与地球动力学, 2023, 43(5): 447-451 (Du Yanjun, Jia Xiaolin, Yao Wanqiang, et al. Influence of Timing Group Delay on BDS-3 New Signals Single Point Positioning[J]. Journal of Geodesy and Geodynamics, 2023, 43(5): 447-451)
(  0) 0) |
2. Key Laboratory of Comprehensive Observation of Polar Environment, Ministry of Education, Sun Yat-Sen University, 2 Daxue Road, Zhuhai 519082, China
 2024, Vol. 44
2024, Vol. 44


