整周模糊度解算对载波相位高精度导航定位结果具有重要影响。LAMBDA方法是当前公认的理论最严密、解算最有效、应用最广泛的模糊度求解方法[1]。该方法以整数最小二乘模型为基础,通过降低模糊度方差分量间的相关性缩减搜索空间,以提高搜索效率[2]。在正式进入搜索过程前,设置合理的模糊度初始空间来限定搜索区域的大小至关重要。Teunissen等[3]分析模糊度搜索空间椭球容积的重要性,并利用椭球容积估计GPS模糊度搜索空间内的候选点数量。卢立果[4]研究认为,椭球容积和候选向量个数并不呈近似相等关系,二者之间存在随维数变化的比例系数。Chang等[5]在MLAMBDA算法中将模糊度目标函数值直接转化为搜索空间大小。赵毅等[6]针对高维模糊度固定,提出利用修正法确定模糊度搜索空间,并通过仿真实验验证其性能优于传统的模糊度搜索空间确定方法。吕浩[7]对两类设置搜索空间方法的性能进行对比分析。上述研究表明,利用椭球容积方法确定模糊度初始空间可能会导致搜索空间内模糊度候选向量较少,甚至会造成模糊度真值丢失;而基于目标函数方法确定搜索空间,虽然可保证有足够的模糊度候选整数,但初始搜索空间设置过大,过多的模糊度候选整数将会增加搜索耗时,影响搜索效率。
本文着重研究BDS2和BDS3在不同测量场景中椭球容积与候选点个数的差异,并分析数据冗余对模糊度搜索空间大小的影响。在对比两种目标函数确定搜索空间方法基础上,针对目标函数方法确定搜索空间时相对较为保守的问题,提出一种优化空间方法,并通过实验验证其有效性。
1 模型与方法 1.1 整数最小二乘模型| $ \boldsymbol{y=A a+B b+e} $ | (1) |
式中,a为载波相位模糊度参数,b为基线分量待估参数,e为观测噪声,y为载波相位与伪距观测值,A、B为设计矩阵。
利用最小二乘准则得:
| $ \min \|\boldsymbol{y}-\boldsymbol{A} \boldsymbol{a}-\boldsymbol{B} \boldsymbol{b}\|{ }_{\boldsymbol{Q}_y}^2, \boldsymbol{a} \in \mathbb{Z}^n, \boldsymbol{b} \in \mathbb{R}^m $ | (2) |
式中,
| $ \begin{gathered} \min \|\hat{\boldsymbol{a}}-\boldsymbol{a}\|_{\underline{\boldsymbol{Q}}_{\hat{\boldsymbol{a}}}^2}^2= \\ \min (\hat{\boldsymbol{a}}-\boldsymbol{a})^{\mathrm{T}} \boldsymbol{Q}_{\boldsymbol{a}}^{-1}(\hat{\boldsymbol{a}}-\boldsymbol{a}), \boldsymbol{a} \in \mathbb{Z}^n \end{gathered} $ | (3) |
为保证搜索效率,利用 Z 变换对原始浮点模糊度进行降相关处理,得到新的模糊度目标函数:
| $ F(\boldsymbol{z})=(\hat{\boldsymbol{z}}-\boldsymbol{z})^{\mathrm{T}} \boldsymbol{Q}_{\hat{\boldsymbol{z}}}^{-1}(\hat{\boldsymbol{z}}-\boldsymbol{z}) $ | (4) |
式中,
模糊度搜索空间定义为:
| $ \begin{equation*} F(\boldsymbol{z})=(\hat{\boldsymbol{z}}-\boldsymbol{z})^{\mathrm{T}} \boldsymbol{Q}_{\boldsymbol{z}}^{-1}(\hat{\boldsymbol{z}}-\boldsymbol{z}) \leqslant \boldsymbol{\chi}^{2} \end{equation*} $ | (5) |
其以
模糊度搜索空间(式(5))容积为[10]:
| $ \begin{align*} V_{n} & =\boldsymbol{\chi}^{n} \cdot U_{n} \sqrt{\left|\boldsymbol{Q}_{\hat{\boldsymbol{a}}}\right|} \\ U_{n} & =\frac{{\rm{\mathsf{π}}}^{n / 2}}{\varGamma(n / 2+1)} \end{align*} $ | (6) |
式中,
根据式(6)得:
| $ \begin{equation*} \boldsymbol{\chi}^{2}=\left[\frac{V_{n}}{U_{n} \cdot \sqrt{\left|\boldsymbol{Q}_{\hat{\boldsymbol{a}}}\right|}}\right]^{2 / n}=\frac{\left[V_{n} \cdot \varGamma(n / 2+1)\right]^{2 / n}}{{\rm{\mathsf{π}}} \cdot\left|\boldsymbol{Q}_{\hat{\boldsymbol{a}}}\right|^{1 / n}} \end{equation*} $ | (7) |
通过式(7)即可求出χ2值。
1.3 基于目标函数确定搜索空间当候选点个数
首先利用Bootstrapping估计获得模糊度估计值
| $ \begin{gathered} \boldsymbol{a}_i=\left[\left[\bar{z}_1\right], \cdots,\left[\bar{z}_{i-1}\right],\left[\bar{z}_i\right]+\right. \\ \left.\quad \operatorname{sign}\left(\bar{z}_i-\left[\bar{z}_i\right]\right), \cdots,\left[\bar{z}_n\right]\right] \end{gathered} $ | (8) |
式中,
为得到
为了验证椭球容积
| $ p \approx \operatorname{int}\left(V_{n}\right) $ | (9) |
|
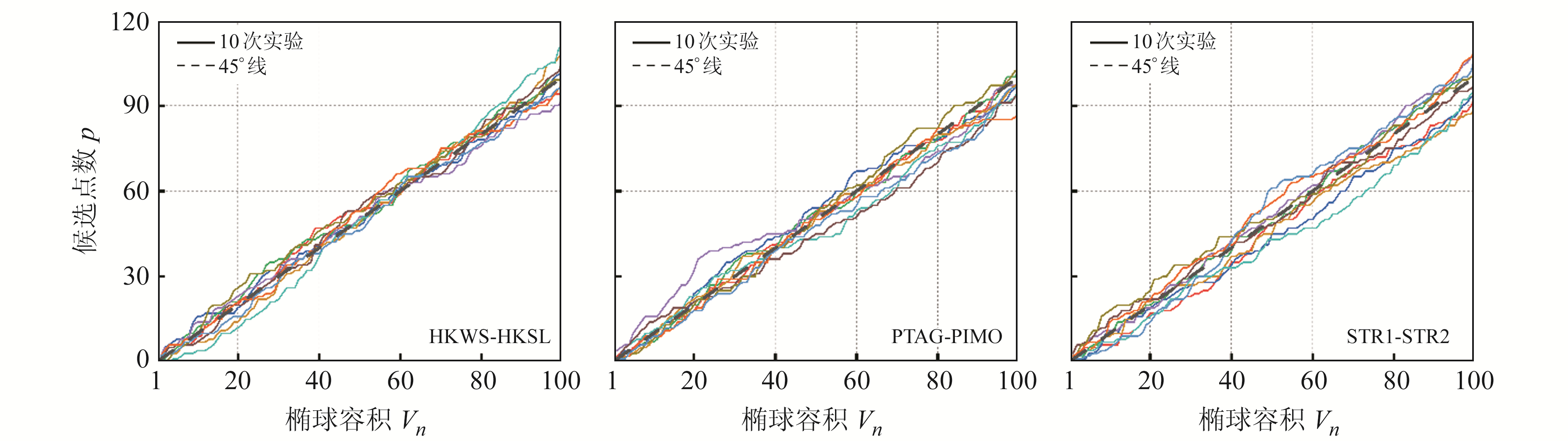
图 1 12维模糊度下椭球容积与候选点个数的关系 Fig. 1 Relationship between ellipsoid volume and the number of candidate points under 12-dimensional ambiguity |
为进一步探讨BDS2和BDS3在不同场景下椭球容积与候选点个数的差异,选取2023-08-16~18(doy228~230)西南交通大学4号教学楼的模拟轨道实测BDS数据。每种场景展示10次实验结果,每次实验使用相邻两个历元的数据,时间间隔30 s,椭球容积Vn∈[1, 100],增量为1。为削弱卫星几何构型和GEO卫星多路径误差等因素的影响,基于卫星高度角和位置精度因子(PDOP),分别选取6颗和8颗卫星讨论在不同测量场景下椭球容积与候选点个数的差异。表 1为不同卫星数(m=6和8)、不同频率(B1I和B3I)相互组合的12种测量场景。
|
|
表 1 不同卫星数、不同频率相互组合的12种测量场景 Tab. 1 Twelve measurement scenarios with different number of satellites and different frequencies |
图 2~4为表 1中所列12种测量场景的椭球容积与搜索空间内包含的模糊度候选向量个数之间的关系,可以看出,椭球容积与候选点数之间存在很好的一致性。在所有情形中,每次实验结果均在45°线附近上下浮动。由图 2可知,使用6颗BDS2卫星的单频结果比使用8颗BDS2卫星的双频结果表现出更好的一致性,其主要由接收机与卫星间的几何形状和模糊度搜索空间的收缩率不同所致。由图 3和图 4可知,无论是增加卫星数还是增加频率,均对椭球容积与候选点数之间的一致性产生正向影响。

|
图 2 BDS2椭球容积与候选点个数的关系 Fig. 2 Relationship between ellipsoid volume and the number of candidate points of BDS2 |

|
图 3 BDS3椭球容积与候选点个数的关系 Fig. 3 Relationship between ellipsoid volume and the number of candidate points of BDS3 |

|
图 4 BDS2+BDS3椭球容积与候选点个数的关系 Fig. 4 Relationship between ellipsoidal volume and the number of candidate points of BDS2+BDS3 |
利用椭球容积与搜索空间内包含的候选向量个数近似相等的特性,既可以用于设置模糊搜索空间的大小,也可以用于验证模糊度候选整数的正确性。根据所需候选向量的大致数量来设置椭球容积,通过式(7)求得χ2值。由于容积只是候选点数的近似指标,最终结果虽然不是精确的数值,但其数量级对搜索空间才是至关重要的。对于模糊度候选整数是否正确,可采用卡方分布求得χ2值对应的α分位点来判定。
前文中在考虑椭球容积与搜索空间内包含的候选向量个数之间的关系时,采用相邻两个历元、时间间隔30 s的数据。因此,有必要探究增加历元数和采用不同时间间隔对模糊度搜索空间大小的影响,分别采用BDS单频/双频的单历元解算数据作进一步验证分析。为节省篇幅,此处仅展示表 1中BDS2+BDS3卫星的4种情形。由于需要讨论体积曲线的定性行为,将χ2设置为1。
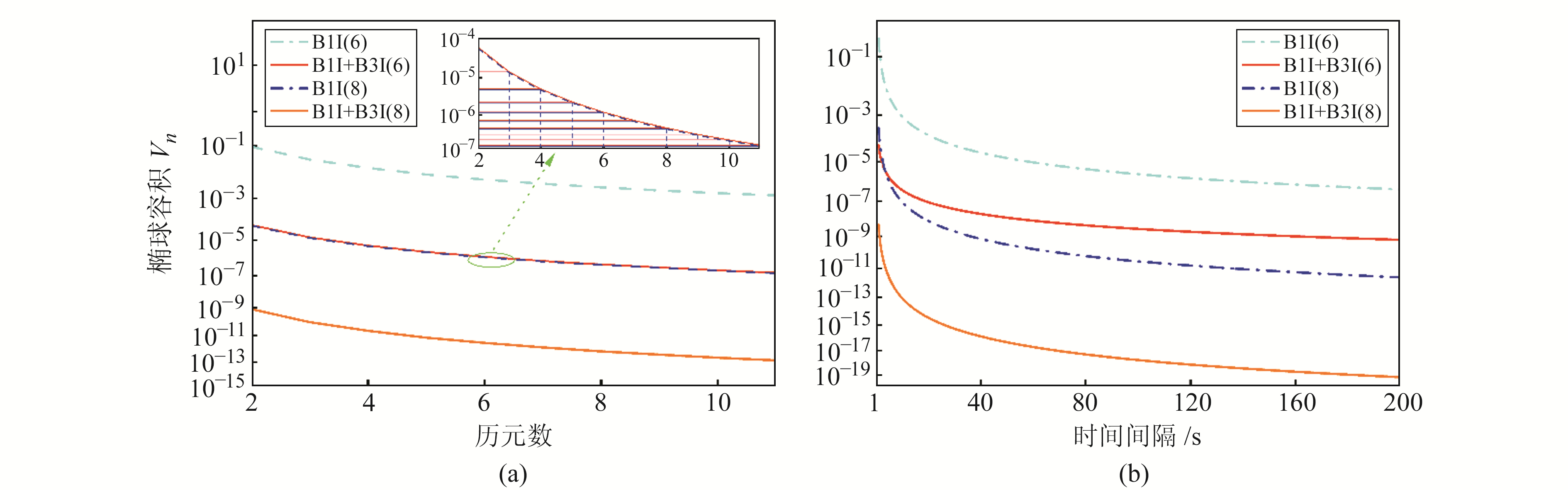
图 5为BDS2+BDS3四种情形的椭球容积与观测历元数及时间间隔的关系。由图 5(a)可知,B1I(6)情形的椭球容积最大,椭球容积随历元数的增加而减小,这是由接收机与卫星几何结构变化和观测历元数累加所致。在单一频率下,增加2颗卫星可使椭球容积减少104个数量级。B1I+B3I(6)情形的椭球容积小于B1I(6)情形,与B1I(8)情形相当。当考虑双频情形下额外增加2颗卫星时,也可以得到类似结论。由图 5(b)可知,B1I+B3I(6)和B1I+B3I(8)之间的间隔远大于B1I(6)和B1I(8)之间的间隔。产生这种现象的原因在于,随着时间间隔的增加,可用的数据冗余增多。
|
图 5 BDS2+BDS3四种情形的椭球容积与观测历元数及时间间隔的关系 Fig. 5 Relationship between ellipsoid volume and the number of observed epochs and time interval in four scenarios of BDS2+BDS3 |
为分析两种方法中模糊度维数对实际候选向量个数的影响, 参考文献[5]中随机模拟方法, 模拟4种方案下
| $ \left\{\begin{array}{l} \hat{\boldsymbol{a}}=100 \times \operatorname{randn}(n, 1) \\ \boldsymbol{Q}_{\hat{a}}=\boldsymbol{L D L}^{\mathrm{T}} \end{array}\right. $ | (10) |
方案1:
方案2:
方案3:L生成方案与方案1相同,
方案4:L生成方案与方案2相同,
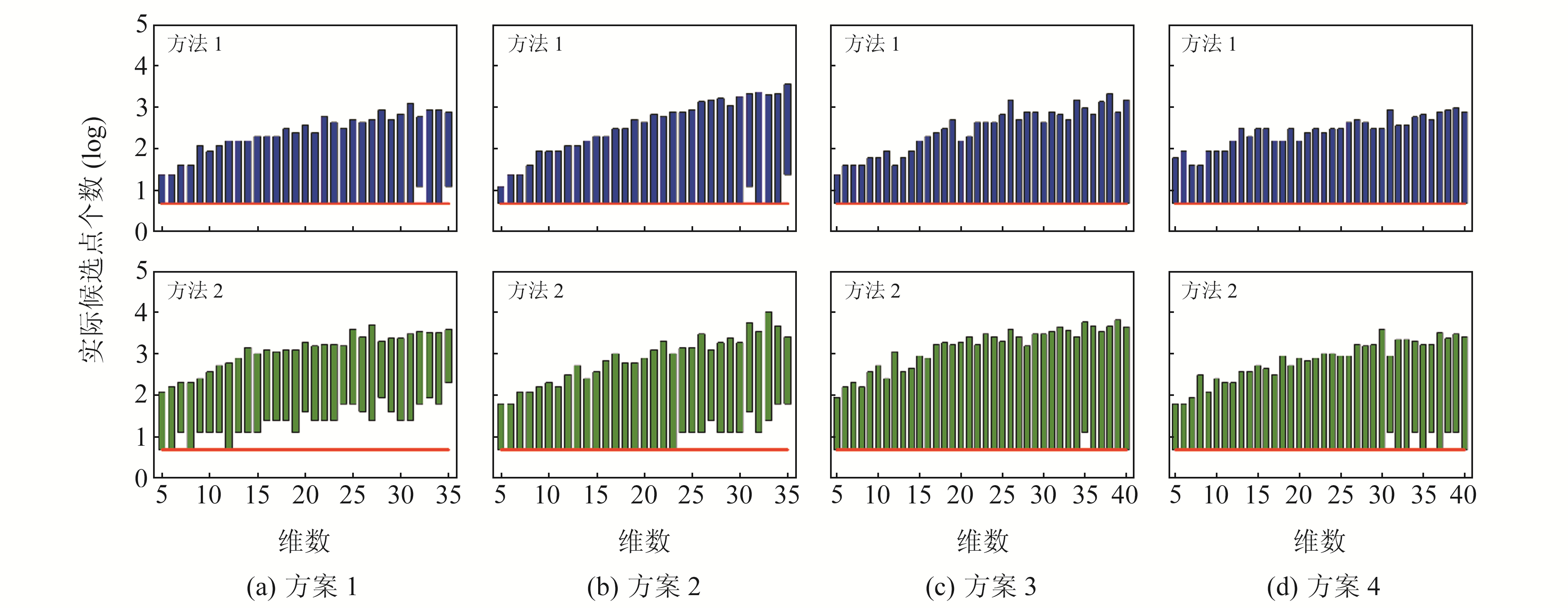
图 6为不同方案在不同维数下采用两种方法所对应的实际候选向量个数变化情况,图中红线表示期望的模糊度候选向量个数p=2所在位置。可以看出,两种方法在不同维数下均能保证至少获得p个模糊度候选向量。随着维数增加,方法1的实际模糊度候选向量个数的变化范围明显变大,但按照同样的构造方式,方法2变化范围则较为稳定。纵向对比同一种方案采用不同方法的变化情况可以看出,方法1除个别情况(如方案2中27、35维)外,均离期望的模糊度候选向量个数(红线)更近。综合而言,方法1较方法2更优。需要说明的是,此处讨论的是模糊度初始搜索空间大小的设置,并不涉及具体的搜索策略。
|
图 6 不同方案、不同维数下两种方法的实际候选向量个数变化 Fig. 6 Variation of the actual number of candidate vectors applying two methods under different schemes and dimensions |
通过上述分析可以发现,基于目标函数确定搜索空间相对较为保守。考虑到模糊度搜索过程是在降相关操作后进行,其搜索椭球以降相关变换后的浮点解
| $ \eta=\sum\limits_{i=1}^n\left(\hat{\boldsymbol{z}}_i-\left[\hat{\boldsymbol{z}}_i\right]\right)^2 $ | (11) |
为分析搜索空间因子η对初始空间大小χ2的影响,利用目标函数值确定的初始空间大小与刚好满足期望要求的空间大小的差值来表征椭球空间冗余度,即
| $ \Delta \boldsymbol{\chi}^{2}=\boldsymbol{\chi}^{2}-\boldsymbol{\chi}_{p}^{2} $ | (12) |
式中,χp2表示刚好包含p个候选向量对应的搜索空间大小。通过建立椭球空间冗余度的函数关系对初始空间大小进行修正,以期能够最大限度地消除冗余模糊度候选向量,提高模糊度搜索效率。
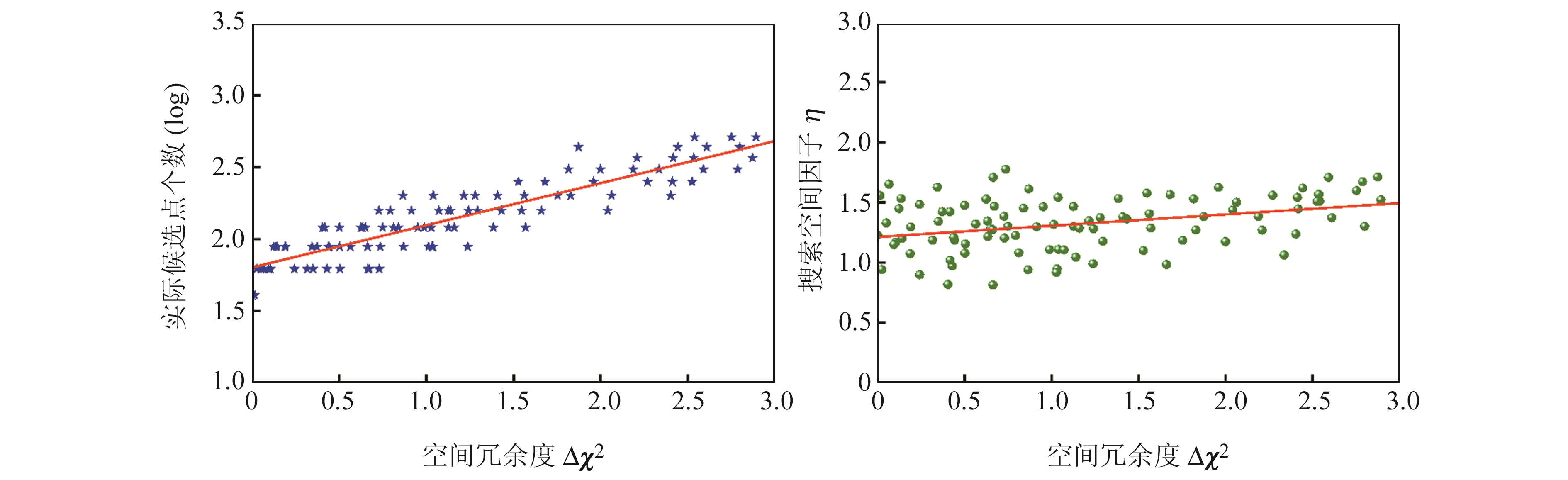
利用§2.2中随机模拟方法构建100组模糊度浮点解和方差协方差阵,分析实际模糊度候选向量个数、搜索空间因子η和椭球空间冗余度Δχ2之间的关系,结果如图 7所示。
|
图 7 空间冗余度Δχ2与实际候选点个数、搜索空间因子η的关系 Fig. 7 Relationship between space redundancy Δχ2 and the number of actual candidate points and search space factor η |
由图 7可知,采用目标函数方法可能出现实际模糊度候选向量个数等于期望模糊度候选向量个数的情况,此时改进后的搜索空间内期望候选向量个数反而无法满足要求。由于椭球容积方法获得的实际候选向量个数变化范围较小,设椭球容积法确定的空间大小为 χV2,则最终选择的最优初始搜索空间如下:
| $ \boldsymbol{\chi}_{\text {opt }}^2=\max \left(\boldsymbol{\chi}_M^2, \boldsymbol{\chi}_V^2\right) $ | (13) |
通过模拟不同维数的实验数据,利用空间冗余度Δχ2与实际模糊度候选向量个数、搜索空间因子η之间的近似线性拟合表达式联合确定修正系数A和B,建立不同维数、不同期望候选点数的修正系数索引表。在实际应用中,用户可以根据需求直接调用所需修正值,快速确定修正的初始空间大小,提升模糊度搜索效率。
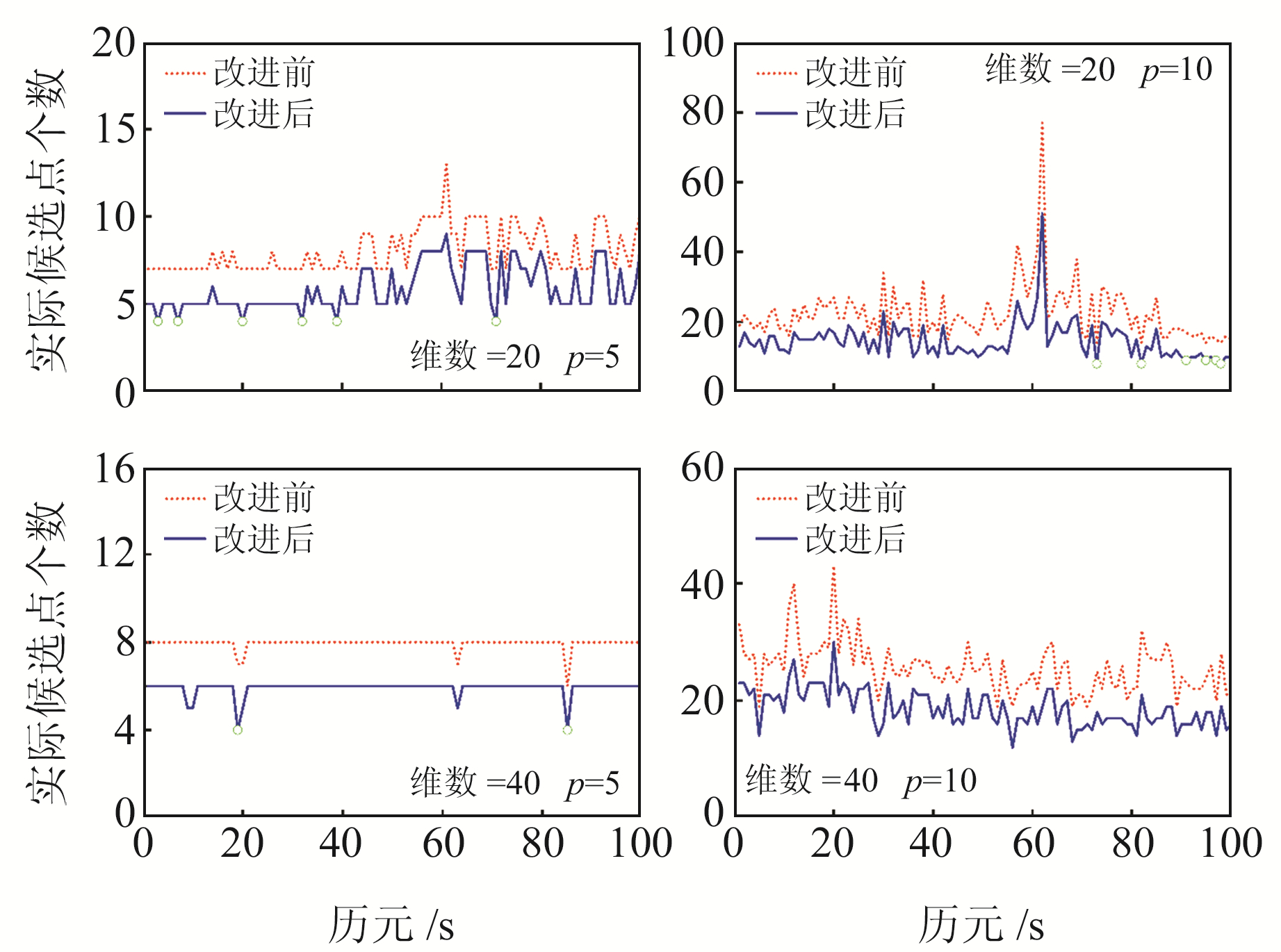
为验证优化的搜索空间设置方法的有效性,利用§2.1中模拟轨道实测GPS/BDS数据,基线长度9.80 m,采样间隔1 s。选取两个时段连续100个历元的模糊度浮点解和方差协方差矩阵,模糊度维数分别为20和40。图 8为不同维数下期望候选点数p=5和p=10时实际候选点个数变化情况,其中绿色圆圈表示不满足期望要求的历元。由图可知,改进后搜索空间内的实际模糊度候选向量个数的浮动范围明显减小,可有效降低椭球空间冗余度。在个别历元存在实际模糊度向量个数不满足期望要求的现象,但仍能保证至少90%以上的搜索空间内的候选向量个数满足期望要求。
|
图 8 不同维数下期望候选点数p=5和10时实际候选点个数变化 Fig. 8 Variation of the actual number of candidate points when the expected number of candidate points p=5 and 10 in different dimensions |
表 2为改进前后各项指标变化情况,可以看出,p=5时,改进后实际模糊度候选向量个数的平均值接近6;p=10时,改进后实际模糊度候选向量个数基本在16附近变化。利用改进的搜索空间确定方法,平均改进率为25%~35%,且可保证94%以上的空间内所包含的候选向量个数符合期望要求。图 9为20维下期望候选点数p=5和p=10时利用不同搜索算法改进搜索空间前后的搜索时间变化情况。表 3为20维下不同搜索算法在改进前后的平均搜索时间与改进率。结合图 9与表 3可以看出,FP算法、VB算法和SE算法应用改进的搜索空间方法后,搜索效率明显提升,改进率为33%~40%。对于SEVB算法,在期望候选点数p=10时搜索时间具有较为显著的提升,而在p=5时效果稍差,仅为18%左右。总体而言,不同搜索算法应用改进的搜索空间确定方法后搜索效率平均提升约33%。因此,改进的搜索空间确定方法有利于分离出初始搜索空间中的冗余候选向量,从而提升模糊度搜索效率。
|
|
表 2 搜索空间改进前后各项指标统计 Tab. 2 Statistical results of each indicator before and after search space improvement |

|
图 9 20维下不同搜索算法在p=5和10时搜索空间改进前后的耗时变化 Fig. 9 Variation of time consuming of different search algorithms before and after search space improvement at p=5 and 10 in 20 dimension |
|
|
表 3 20维下不同搜索算法在搜索空间改进前后的平均搜索时间与改进率 Tab. 3 Average search time and improvement of different search algorithms before and after search space improvement in 20 dimension |
本文在用目标函数确定搜索空间方法基础上,引入搜索空间因子对模糊度搜索空间进行优化,并通过实验验证所提方法的有效性,得到以下结论:
1) 重点分析BDS2和BDS3在不同卫星数、不同频率下椭球容积与候选向量个数的差异,以及数据冗余对椭球容积的影响。结果表明,12种场景下椭球容积和候选点数之间均存在很好的一致性;在低维情形下,椭球容积随着数据冗余的增加而减小,仅增加2颗卫星即可使得椭球容积减少104个数量级。
2) 对比分析两种目标函数确定搜索空间方法在不同方案、不同维数下实际候选向量个数的变化。结果表明,方法1优于方法2。
3) 改进的搜索空间确定方法可明显减少实际模糊度候选向量个数,平均改进率为25%~35%,且可保证94%以上的空间内所包含的候选向量个数符合要求。不同搜索算法应用改进的搜索空间方法后搜索效率平均提升约33%。
| [1] |
Teunissen P J G. Least-Squares Estimation of the Integer GPS Ambiguities[C]. IAG General Meeting, Beijing, 1993
(  0) 0) |
| [2] |
Teunissen P J G. The Least-Squares Ambiguity Decorrelation Adjustment: A Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy, 1995, 70(1): 65-82
(  0) 0) |
| [3] |
Teunissen P J G, Jonge P J, Tiberius C C J M. The Volume of the GPS Ambiguity Search Space and Its Relevance for Integer Ambiguity Resolution[C]. International Technical Meeting of the Satellite Division of the Institute of Navigation, Kansas City, 1996
(  0) 0) |
| [4] |
卢立果. GNSS整数最小二乘模糊度解算理论与方法研究[J]. 测绘学报, 2017, 46(9): 1 204 (Lu Liguo. Study on Theory and Method of GNSS Integer Least Squares Ambiguity Resolution[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(9): 1 204)
(  0) 0) |
| [5] |
Chang X W, Yang X, Zhou T. MLAMBDA: A Modified LAMBDA Method for Integer Least-Squares Estimation[J]. Journal of Geodesy, 2005, 79(9): 552-565 DOI:10.1007/s00190-005-0004-x
(  0) 0) |
| [6] |
赵毅, 龚诚, 邓宁. GPS/Galileo组合导航的模糊度搜索空间[J]. 中国空间科学技术, 2011, 31(2): 9-15 (Zhao Yi, Gong Cheng, Deng Ning. Determination of the Ambiguity Search Space in Hybrid GPS/Galileo Navigation[J]. Chinese Space Science and Technology, 2011, 31(2): 9-15)
(  0) 0) |
| [7] |
吕浩. GNSS整周模糊度估计关键方法研究[D]. 郑州: 信息工程大学, 2019(Lü (Hao. Research on Key Methods of GNSS Integer Ambiguity Estimation[D]. Zhengzhou: Information Engineering University, 2019)
(  0) 0) |
| [8] |
Teunissen P J G. Integer Least-Squares Theory for the GNSS Compass[J]. Journal of Geodesy, 2010, 84(7): 433-447 DOI:10.1007/s00190-010-0380-8
(  0) 0) |
| [9] |
刘经南, 于兴旺, 张小红. 基于格论的GNSS模糊度解算[J]. 测绘学报, 2012, 41(5): 636-645 (Liu Jingnan, Yu Xingwang, Zhang Xiaohong. GNSS Ambiguity Resolution Using the Lattice Theory[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 636-645)
(  0) 0) |
| [10] |
Jonge P J, Tiberius C C J M. The LAMBDA Method for Integer Ambiguity Estimation: Implementation Aspects[R]. Delft Geodetic Computing Centre, 1998
(  0) 0) |
 2024, Vol. 44
2024, Vol. 44


