2. 武汉引力与固体潮国家野外科学观测研究站,武汉市洪山侧路40号,430071;
3. 甘肃省地震局陇南地震监测中心站,甘肃省陇南市汉王镇,746000;
4. 辽宁省地震局,沈阳市黄河北大街44号,110031
VP型宽频带倾斜仪[1-4]常用作同震响应分析和仪器比测实验,是一种较为常见且有效的形变观测仪器。受仪器精密设计特性和安装环境影响,其记录中包含大量的环境噪声和气象干扰数据,会极大影响固体潮曲线观测和地震前兆信号采集,在实际数据处理时需提前进行必要的滤波或去噪操作。
常见的仪器信号去噪模型有卡尔曼滤波、小波去噪、低通FIR滤波、Savitzky-Golay滤波等方法,具有一定的去噪或光滑作用,但存在重构误差较大或信噪比不高的问题。改进型自适应噪声完备集合经验模态分解(ICEEMDAN)[5-6]是一种基于集合经验模态分解(EEMD)和经验模态分解(EMD)的新型信号分解技术。与EEMD不同的是,ICEEMDAN通过引入一对性质相反的白噪声进行经验模态分解,而不是在原始信号中加入随机白噪声,可在一定程度上压制引入白噪声带来的重构误差。
基于信号分解的去噪方法能将原始含噪信号细分为噪声成分较多、含噪较少及几乎不含噪的固有模态函数(IMF),但分解后存在IMF噪声含量大小判别不明、包含主要幅值能量的IMF波形单调易被舍弃、重构对象难以抉择等问题。由于目前尚未构建恰当的评价指标体系衡量IMF的质量优劣或含噪量,亟需一种行之有效的评判方法精准识别能够参与最后重构的有效的IMF分量,并给出合理的IMF筛选依据。为改善传统去噪模型效果,增强信号分解结果的可读性,本文提出一种基于灰色关联分析(GRA)[7-8]优化ICEEMDAN的VP倾斜仪信号去噪模型。该模型综合考虑相关系数、互信息(MI)、样本熵、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、判定系数(R2)、均方根误差(RMSE)、均方误差(MSE)、方差(SSE)、Adj-R2(调整后的判定系数)等10个指标,筛选IMF分量的影响力,利用GRA进行IMF特征指标矩阵的多维压缩,构建IMF分量质量综合评价函数,并根据函数值排名结果完成原始含噪信号的线性重构。同时,设计仿真信号实验和VP倾斜仪实测信号去噪实验,选择卡尔曼滤波、低通FIR滤波、Savitzky-Golay等经典去噪模型进行GRA-ICEEMDAN模型的综合去噪性能对比。
1 GRA-ICEEMDAN信号去噪模型GRA[7-8]是一种依据指标相似性和差异性得到关联度的综合评价方法,一般步骤为:1)设定评价对象和评价指标的个数分别为m和n,对原始数据进行标准化并设置参考数列和比较数列;2)确定各评价指标相应的权重,构建一维权重向量w =[w1, w2, …, wn],其中wk(k=1, 2, …, n) 表示第k个评价指标的权重;3)依据参考数列、分辨系数ρ∈[0, 1],比较数列x0与参考数列xi在第k个评价指标上的灰色关联系数;4)依据指标权重向量w和m×n个灰色关联系数ξi(k),计算第i个评价对象的灰色加权关联度;5)利用步骤4)得到的灰色加权关联度对m个评价对象进行打分排序,关联度越大,说明可信度越高。
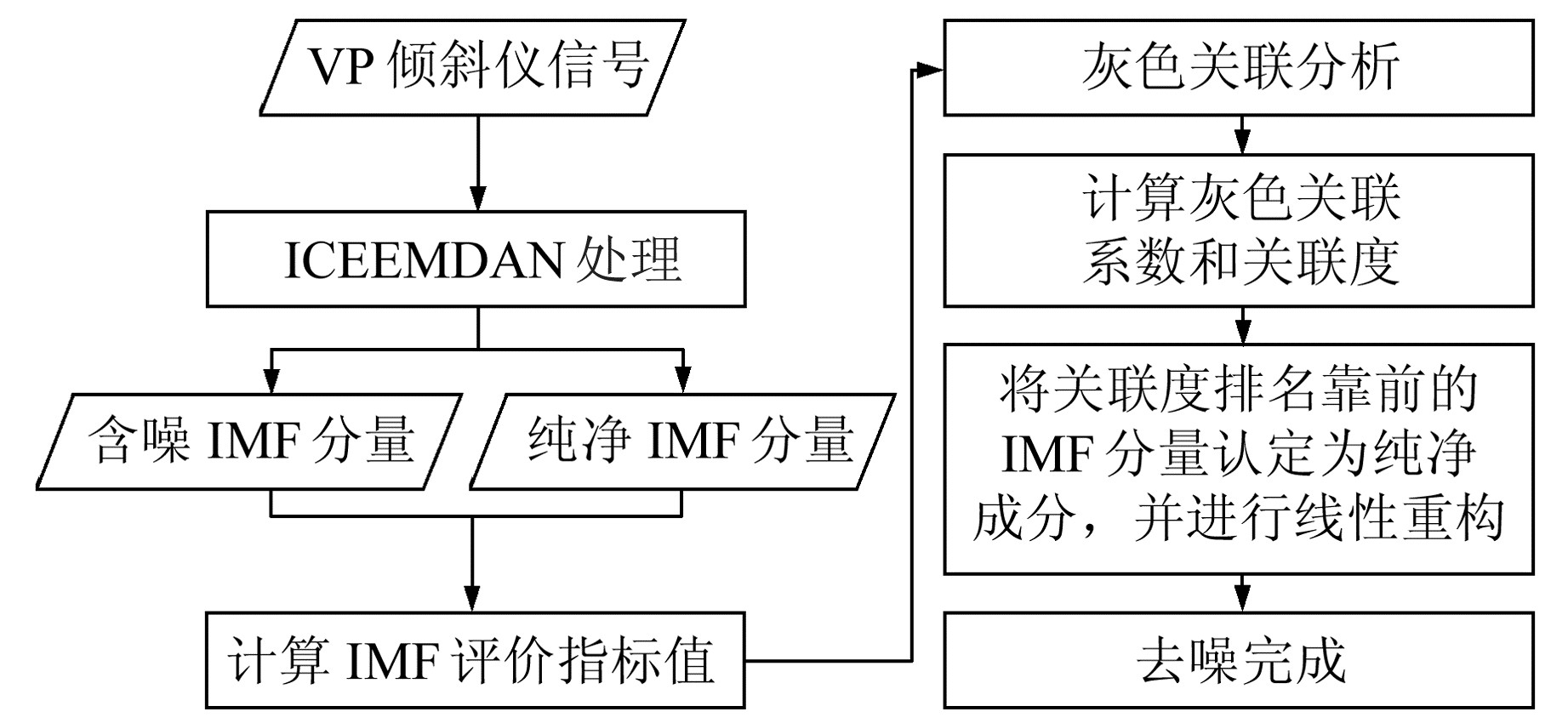
为测算GRA-ICEEMDAN模型的有效性,进行仿真含噪数据和实测VP倾斜仪信号去噪实验,并选用相关系数、互信息、样本熵、平均绝对误差、平均绝对百分比误差、R2、均方根误差、均方误差、方差、Adj-R2等10个指标作为去噪结果准确性及一致性的评价标准。GRA-ICEEMDAN模型的信号处理流程如图 1所示。
|
图 1 GRA-ICEEMDAN模型流程 Fig. 1 Process of GRA-ICEEMDAN model |
为测试GRA-ICEEMDAN模型的真实效果,进行仿真含噪信号去噪实验和VP倾斜仪信号去噪实验,融合相关系数、样本熵、MSE、R2、SSE、RMSE、MAE、MAPE等多个指标评价ICEEMDAN处理的IMF分量质量,然后利用相关系数、信噪比、MSE等3个指标评价去噪效果,并与多个经典去噪模型进行对比。
实验平台和算法参数为:仿真平台为MATLAB 2023a,仿真含噪信号信噪比为20 dB,信号长度为200,采样率为100 sps,通过awgn函数添加纯净信号y=-sin(2πt)+2cos(t)+0.5sin(5πt);ICEEMDAN模型的噪声标准差比、平均次数分别为0.15和20。
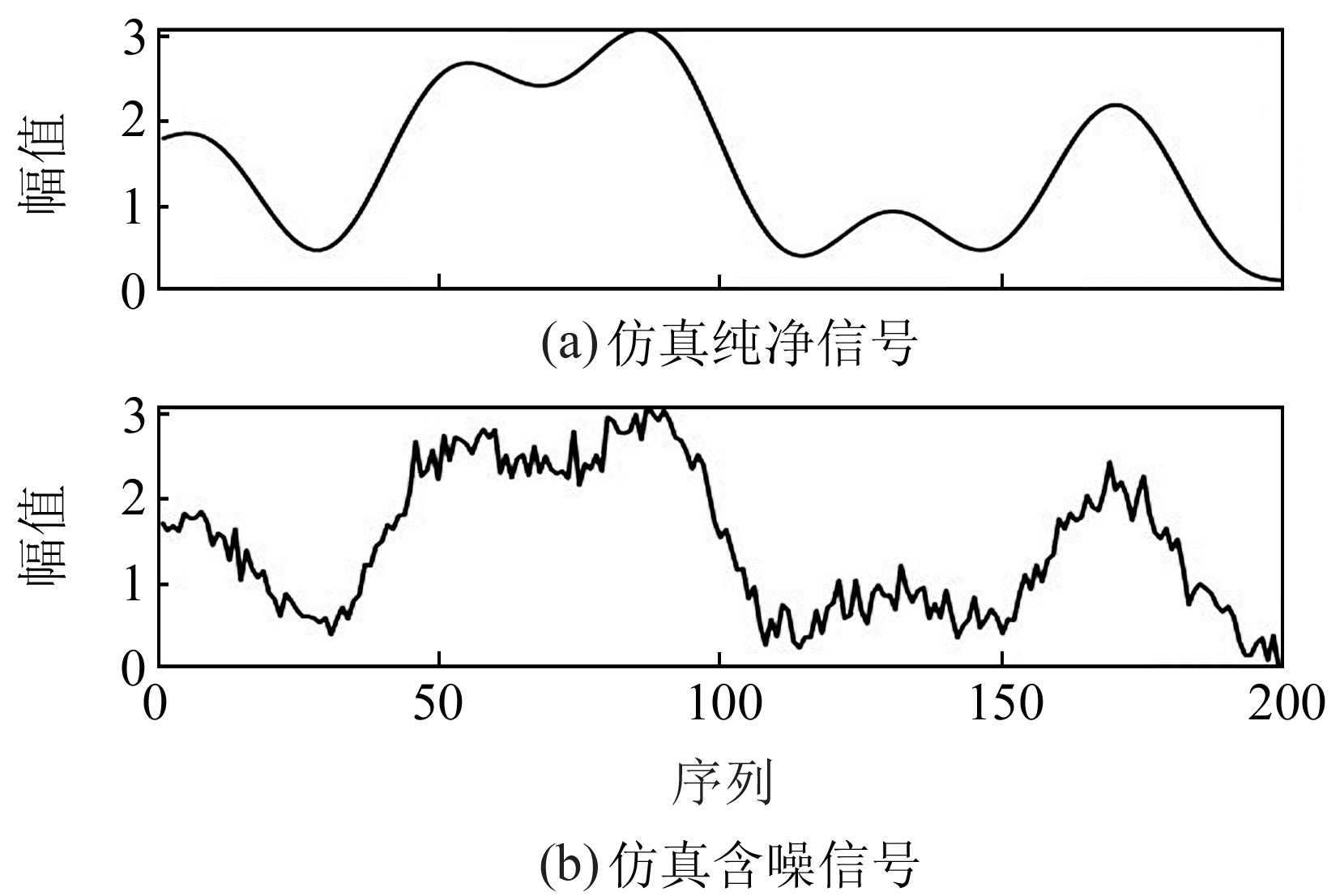
基于MATLAB 2023a软件设计仿真信号去噪实验,根据复合正余弦函数生成纯净信号和加噪信号,得到实验所需数据(图 2)。
|
图 2 仿真纯净信号与加噪波形 Fig. 2 Simulated pure signal and noise-added waveform |
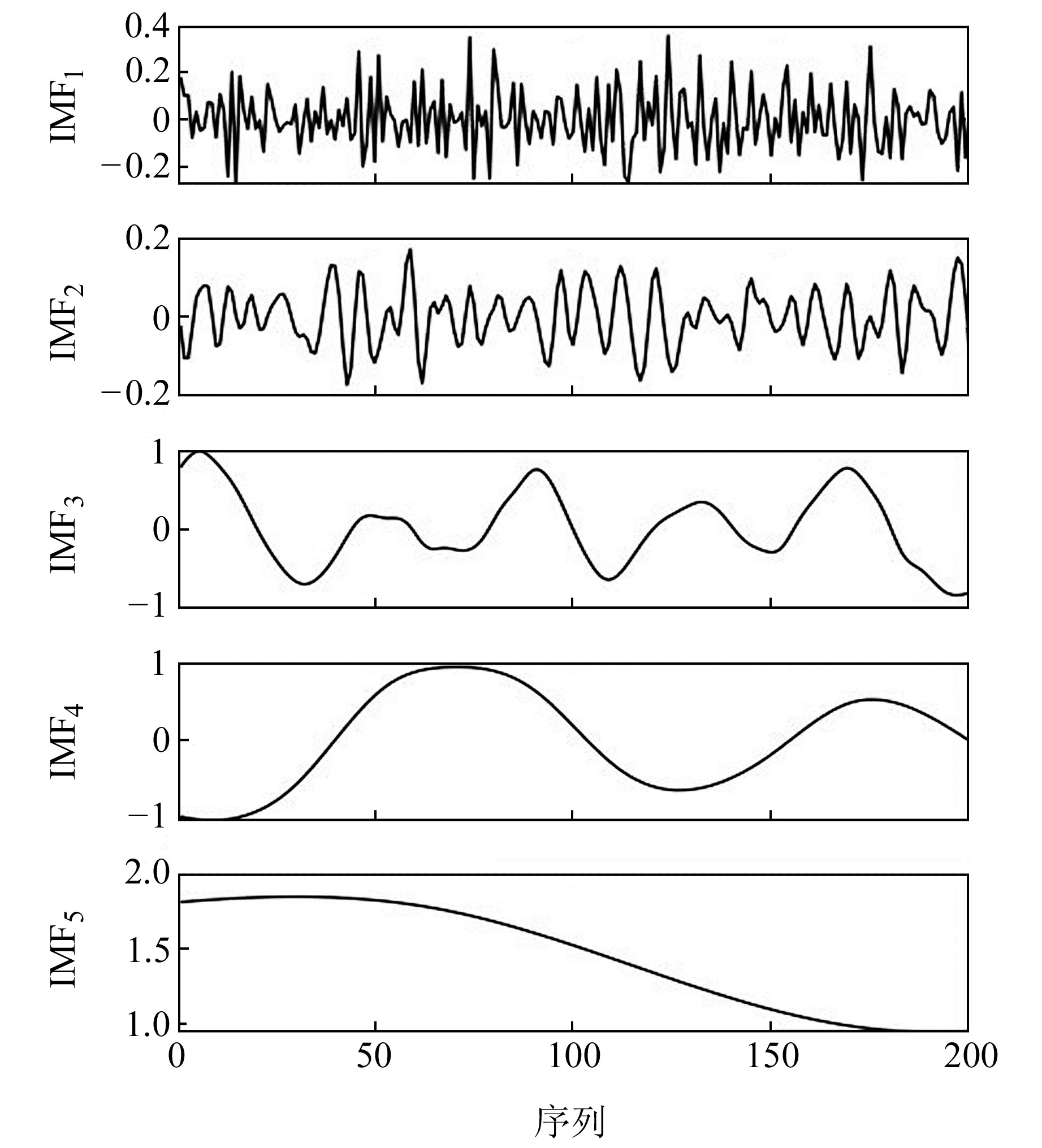
图 3为仿真含噪信号的ICEEMDAN处理结果,由图可知,含噪信号被ICEEMDAN模型分解成5个IMF分量,其中IMF1、IMF2存在较频繁的波形振荡且幅值相对较小,基本可断定为需要剔除的噪声成分;IMF3~IMF5曲线相对较为光滑,幅值较大,属于ICEEMDAN处理得到的主要幅值成分,包含原始信号的大部分能量。同时可以发现,IMF3、IMF4与原始信号曲线整体趋势极为相似。
|
图 3 仿真含噪信号ICEEMDAN模型处理结果 Fig. 3 Decomposition results of simulated signals by ICEEMDAN model |
表 1为原始含噪信号经ICEEMDAN处理后各IMF分量的特征值,可以看出,IMF3、IMF4、IMF5的指标值与其他IMF分量差异较大,如IMF1、IMF2的相关系数均在0.2以下,样本熵值均大于1.5,Adj-R2均小于0.04,这些特征差异表示IMF3、IMF4、IMF5与原始信号形态更为相似,可能是有效成分,需要尽可能保留。此外,IMF5的指标值差异更为显著,在多个指标值中排序第1,如在反映绝对误差程度的SSE、RMSE、MAE、MAPE等指标中值最小,在侧面反映曲线平稳光滑的样本熵中值为0.019 3。
|
|
表 1 ICEEMDAN分解后各IMF的特征参数值 Tab. 1 Feature parameter values of each IMF after ICEEMDAN decomposition |
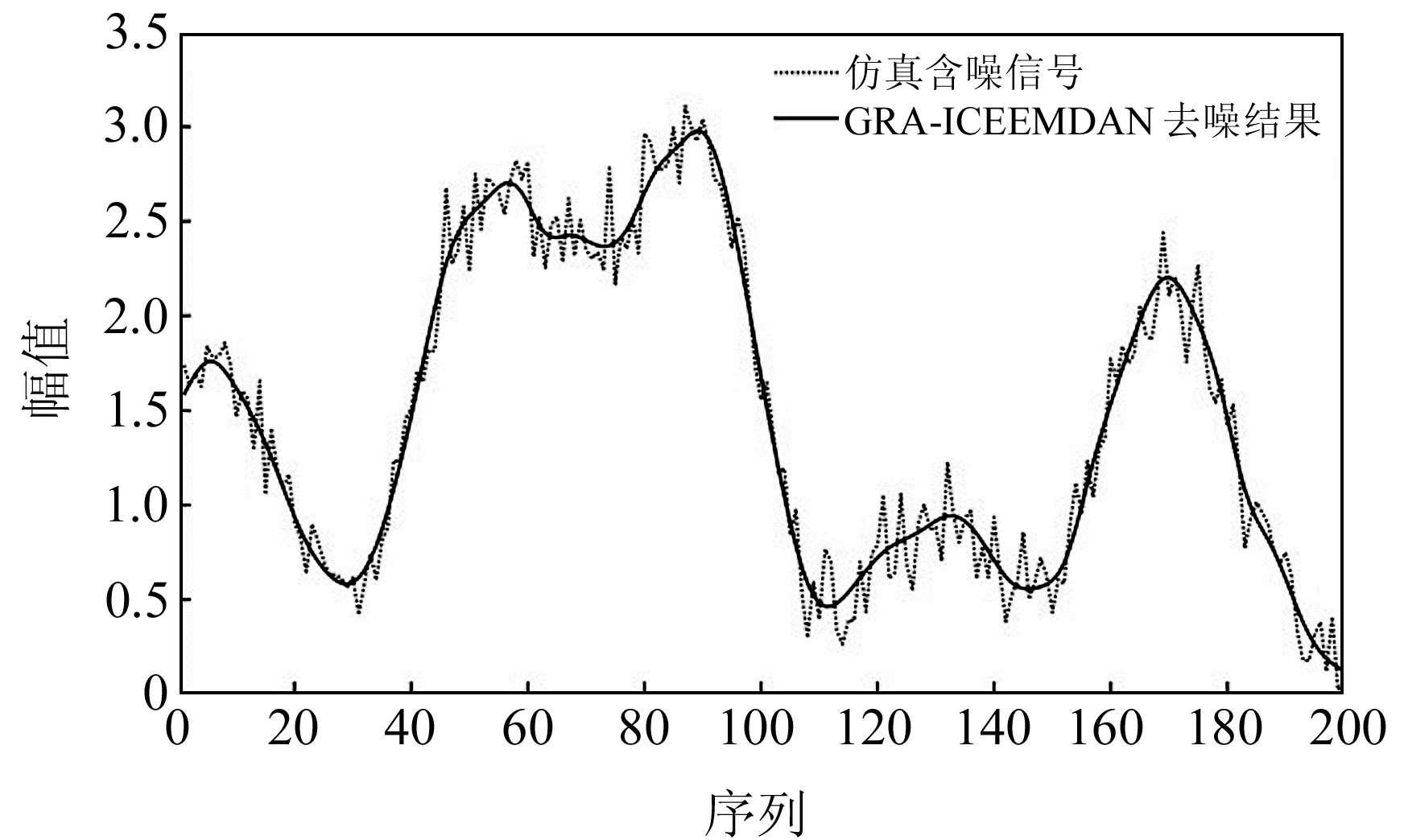
由原始含噪信号的5个IMF分量得到的特征矩阵经标准化、两级最小/最大差计算、灰色关联系数计算、指标权重主观赋值及IMF关联度分析,得到IMF分量最终排名结果,具体数据如表 2~4所示。由表可知:1)部分评价指标针对不同IMF计算结果的差异化程度较高,如相关系数、样本熵、R2等指标,特别是样本熵的最大值和最小值相差约121倍;同时,也有部分指标差异化分布不明显,如互信息、MAPE,其中互信息的极差在0.023 2以内,较难看出各IMF分量的区别。2)互信息指标与IMF3的关联系数最大,相关系数、Adj-R2与IMF4的关联系数值最大,其他指标皆与IMF5的关联系数最大。3)GRA综合评价函数值排名结果为:IMF5>IMF4>IMF3>IMF2>IMF1,本文取前3位IMF分量参与线性重构,得到的去噪结果如图 4所示。
|
|
表 2 ICEEMDAN各IMF的比较数列和参考数列值 Tab. 2 Comparison and reference series values for each IMF of ICEEMDAN |
|
|
表 3 GRA关联系数和关联度值 Tab. 3 GRA correlation coefficients and correlation degree values |
|
|
表 4 基于仿真实验数据的GRA综合评价函数值与排名 Tab. 4 GRA comprehensive evaluation function values and rankings based on simulated experimental data |
|
图 4 基于ICEEMDAN-GRA的仿真信号去噪结果 Fig. 4 Simulated signal denoising results based on ICEEMDAN-GRA |
从图 4可以看出,GRA-ICEEMDAN模型的去噪结果较光滑,可保留原始含噪信号的主要成分,重构误差较小,是一种可取的去噪模型。该模型的具体去噪评价结果中,相关系数、MSE、信噪比分别为0.972 2、0.087 3、12.957 4 dB。
表 5为不同去噪模型的效果对比,可以看出,GRA-ICEEMDAN模型在多个评价指标上都优于卡尔曼滤波、低通FIR滤波、Savitzky-Golay等经典去噪模型,尤其是在信号特征还原上具有显著效果,MSE值在0.008 5以下。
|
|
表 5 基于仿真实验数据的去噪模型效果对比 Tab. 5 Comparison of denoising effect based on simulated experimental data |
GRA-ICEEMDAN模型去噪实验数据来源于河北省地震局易县地震台,VP倾斜仪布设在华北平原与太行山交界的地震断裂带附近山洞中。该区域多出露闪长岩、石灰岩及页岩等,且在2016-04-15遭受异常天气影响,固体潮曲线出现大量环境噪声。首先针对典型含噪信号进行GRA-ICEEMDAN去噪分析,信号分解结果和去噪结果如图 5~6和表 6~9所示;然后针对多条含噪信号进行多轮GRA-ICEEMDAN去噪分析,探讨该模型的稳定性和可靠性。
|
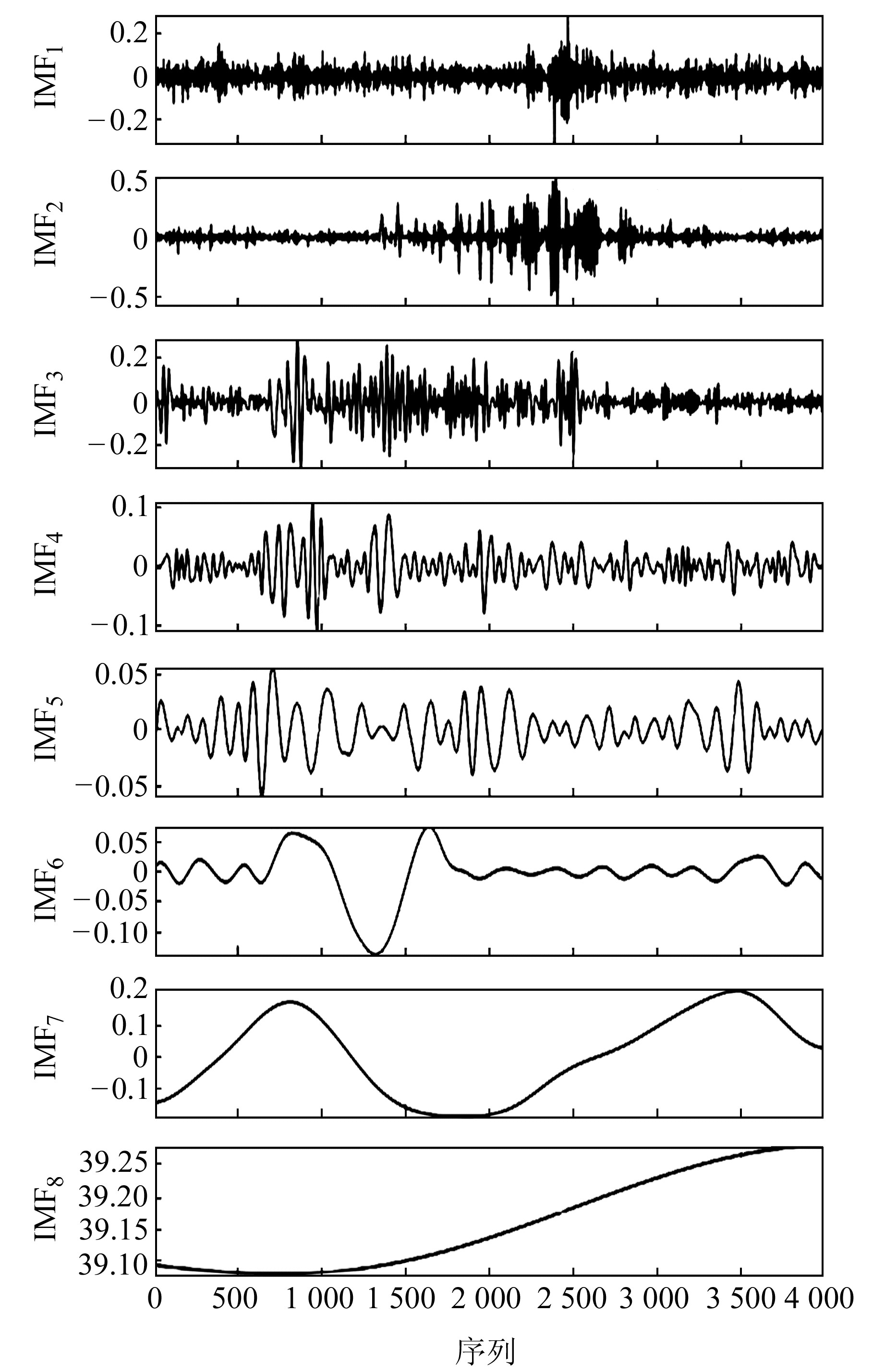
图 5 VP倾斜仪信号经过ICEEMDAN处理结果 Fig. 5 VP inclinometer signals after ICEEMDAN decomposition |
|
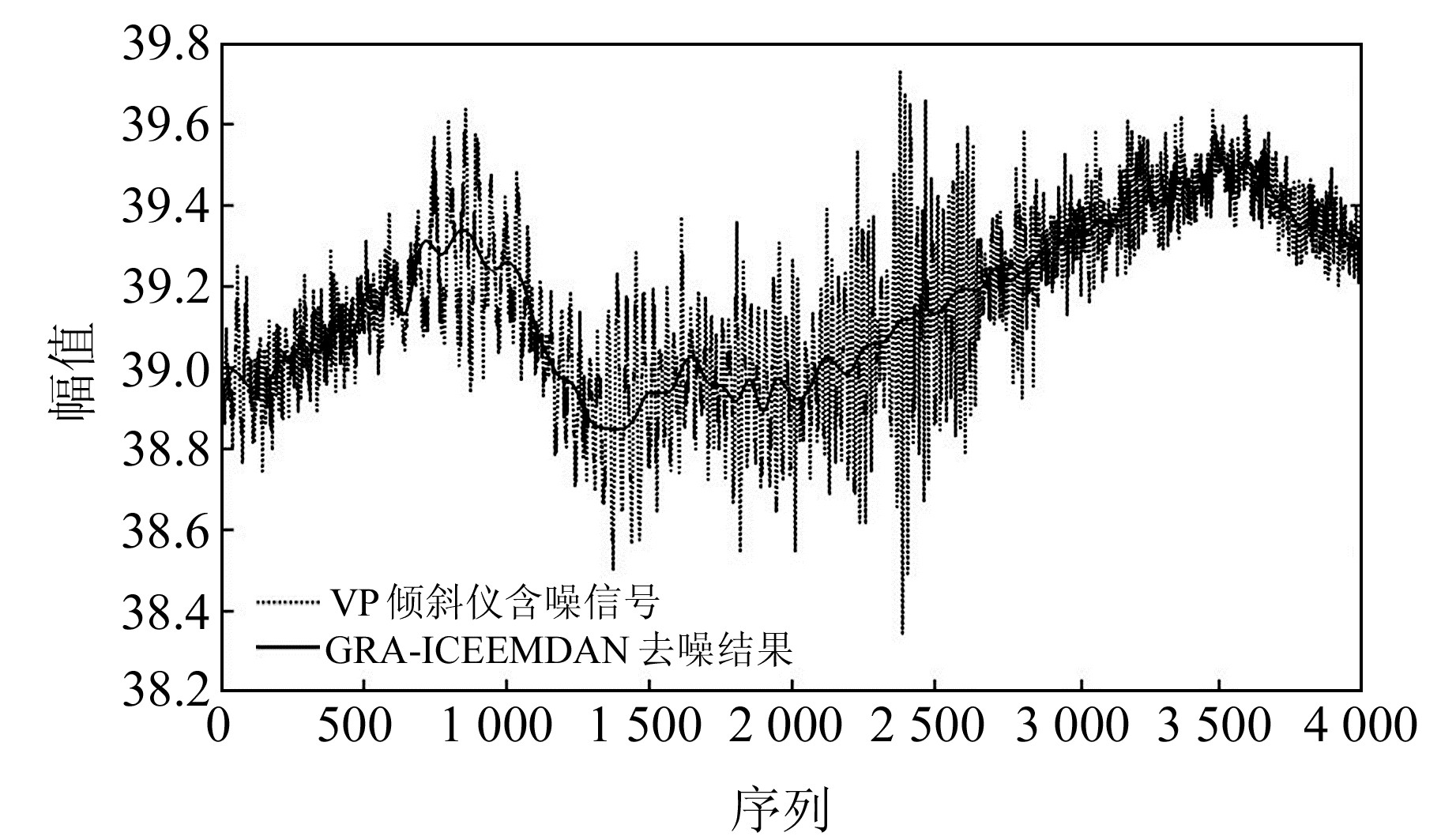
图 6 VP倾斜仪信号的GRA-ICEEMDAN去噪结果 Fig. 6 GRA-ICEEMDAN denoising results of VP inclinometer signals |
|
|
表 6 ICEEMDAN处理后各个IMF的特征参数值 Tab. 6 Feature parameter values of each IMF after ICEEMDAN decomposition |
|
|
表 7 ICEEMDAN各IMF比较数列和参考数列值 Tab. 7 Comparison and reference series values for each IMF of ICEEMDAN |
|
|
表 8 各IMF的GRA关联系数和关联度值 Tab. 8 GRA correlation coefficients and correlation degree values for each IMF |
|
|
表 9 不同模型下的VP倾斜仪信号去噪效果对比 Tab. 9 Comparison of denoising effect of VP inclinometer signals under different models |
图 5为VP倾斜仪含噪信号经ICEEMDAN处理得到的8个IMF结果,由图可知:1)IMF1~IMF3含有大量噪声且幅值整体极小,最大峰值绝对值分别趋于0.2、0.5、0.2,在零点位置上下的振荡频率较高,且噪声能量有较为集中的区段,分别集中于N=2 500、2 400、1 400附近,其他位置噪声能量相对较低;2)IMF4~IMF7曲线相对IMF1~IMF3具有显著的平稳与光滑特性,不存在能量集中的现象,幅值大小同样持续在较低范围内,最大幅值绝对值分别接近于0.2、0.1、0.05、0.2;3)IMF8整体幅值明显较大,峰值超过39.25,包含初始含噪信号的主要幅频能量,说明该IMF分量必须被保留,否则会影响去噪重构精度和信号失真程度,并推断IMF4~IMF7中一定存在一个或多个决定曲线形状的有效分量,判断该分量波形与原始信号的相似性可通过相关系数或互信息指标来验证。
表 6为VP倾斜仪信号经ICEEMDAN处理后各IMF分量的评价指标值,可以看出,IMF7、IMF8与其他IMF分量的多个评价指标值存在较大差异,如样本熵、Adj-R2、相关系数、互信息中IMF8分量在数量级上出现极大反差,而在表达2个信号绝对误差程度的MSE、SSE、RMSE、MAE、MAPE等指标中呈极小值;此外,IMF6样本熵值也较小,仅为0.025 8,说明其曲线具有一定的平稳特性。
表 7为ICEEMDAN各IMF分量特征值比较数列和参考数列值。结合表 6、7和图 5可知:1)在相关系数指标上,IMF7、IMF8与原始含噪信号之间存在较大的正向相关性(相关系数值分别达到0.743 9、0.601 6),其他IMF分量的相关系数均在0.5以下,表明IMF7、IMF8属于真实信号的形状成分,参与重构可避免去噪后信号严重失真;2)样本熵指标可以判断序列的分布规律性或曲线光滑特性,IMF1~IMF8样本熵值依次从1.656 7减小到0.001,与其曲线的光滑程度相呼应,IMF8曲线最为平稳,样本熵值最小;3)MSE、SSE、RMSE、MAE、MAPE等指标可反映各IMF分量与原始信号的绝对误差情况,数值越大说明该IMF曲线相对原始信号的畸变越严重,表 6显示IMF8与原始信号的误差最小,证明其幅值分布最接近原始信号,整体数值较大;4)互信息指标的数值分布整体差异不大且无显著分布规律,无法明显区分出较好或较差的IMF分量,在对各IMF分量的可靠度进行评判时,对结果的影响可能较小。
由表 8可知,GRA关联度排名结果为:IMF8>IMF7>IMF6>IMF5>IMF3>IMF4>IMF2>IMF1,GRA评分分别为0.915 6、0.599 2、0.424 7、0.410 7、0.395 0、0.385 9、0.383 5、0.343 2。在所有固有模态函数中,IMF8与理想IMF的关联度最大(0.915 9),且3项指标的关联系数均为1,证明其优于其他IMF分量;其次为IMF7,有3项关联系数为1,关联度大小(0.599 2)仅次于IMF8;其他固有模态函数的关联度均小于0.5,其间差值也较小,在不损失信号主体能量的前提下,对这些IMF分量的具体取舍需要作进一步分析。
图 6为VP倾斜仪单条信号的GRA-ICEEMDAN去噪结果。由图 5和6可知,ICEEMDAN处理后的IMF7与原始含噪信号波形较为相似,而IMF8的幅值分布范围与原始信号也较为接近,说明GRA-ICEEMDAN模型能准确地从原始含噪信号中分离出关键波形分量和幅值分量;同时,去噪后曲线的居中式游走走势整体遵循原始信号的曲线规律,能精准找到高频随机噪声位置,并减少大量毛刺或尖刺现象的发生,在信号平稳性上有明显改善。
为测算GRA-ICEEMDAN模型在VP倾斜仪信号处理中的有效性,将卡尔曼滤波、70阶低通FIR滤波等作为比对模型,评价指标为相关性、MSE、信噪比等量化参数,具体结果见表 9。由表可知,GRA-ICEEMDAN模型的去噪效果明显优于卡尔曼滤波、70阶低通FIR滤波等经典去噪模型,其相关系数、MSE、信噪比分别为0.816 8、0.017 0、49.558 7 dB,具有更高的随机噪声压制效率;相比之下,另外2个模型面对较复杂的真实含噪波形时的去噪结果极易失真,在一定程度上可解决非平稳性问题,但会损失掉原始信号的幅值成分,导致去噪前后的波形不一致及处理后信号的幅值较小,严重偏离原始信号。对比仿真信号去噪实验,卡尔曼滤波与70阶低通FIR滤波模型的适应性较差,在实际应用中更适合线性、尖刺少或较平稳的信号去噪。
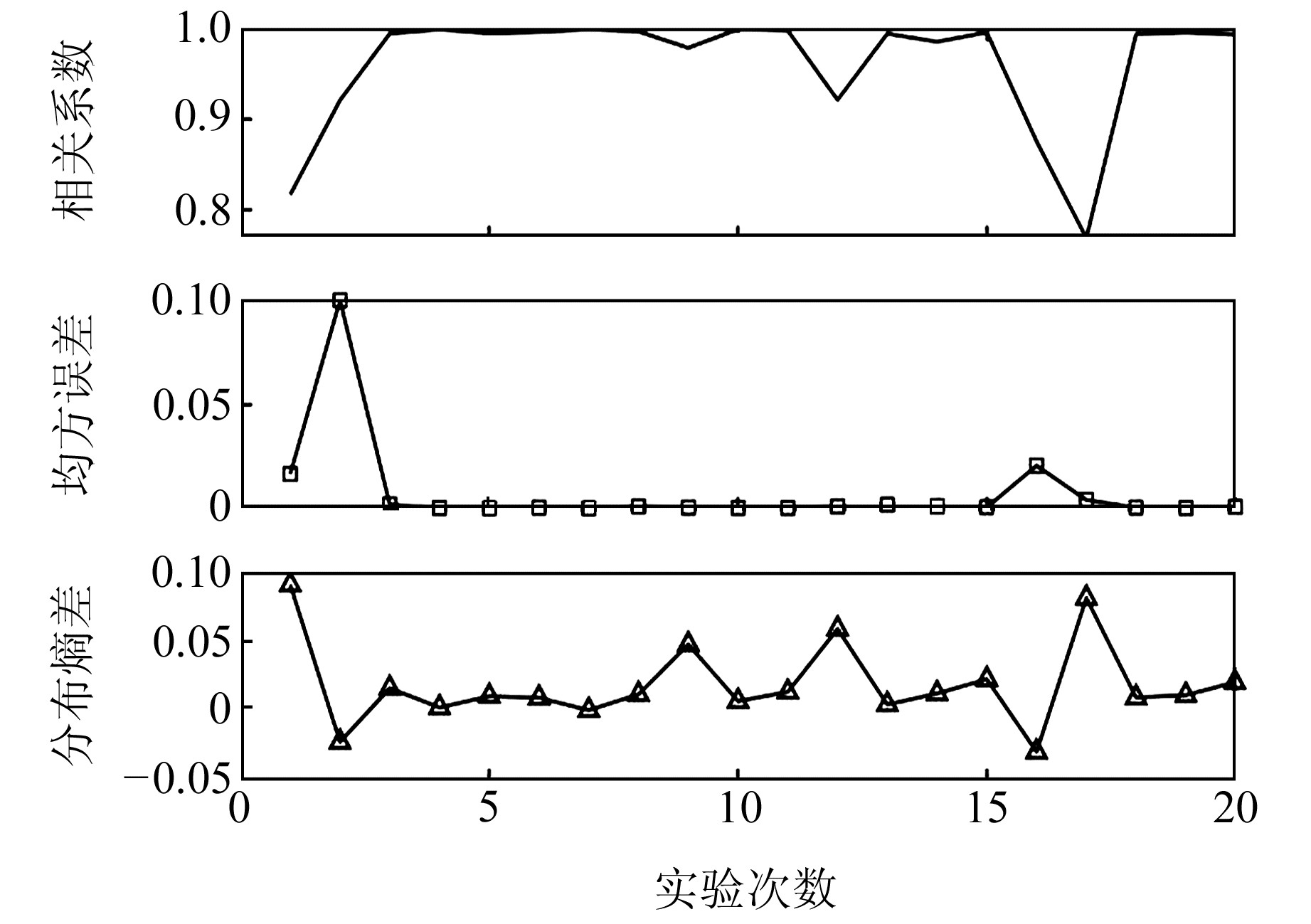
选取2016-04-15~2021-09-09期间20条天气干扰信号,设计包含多条VP倾斜仪含噪数据的去噪实验,用以检验GRA-ICEEMDAN模型的稳定性和适应性,评价指标采用相关系数、分布熵差(去噪后信号分布熵与原始信号分布熵之差)和MSE,结果如图 7和表 10所示。可以看出,3种评价指标的发展趋势具有明显的联动性。
|
图 7 20条VP倾斜仪信号的GRA-ICEEMDAN去噪结果 Fig. 7 Denoising results of 20 VP inclinometer signals based on GRA-ICEEMDAN |
|
|
表 10 20条VP倾斜仪信号去噪结果统计 Tab. 10 Statistics of denoising results of 20 VP inclinometer signals |
本文提出一种结合ICEEMDAN和灰色关联分析的VP倾斜仪信号去噪方法,通过融合多种不同类型的固有模态函数评价指标来构建信号模态分解结果精准评价体系,可以更精确地从全部IMF中识别出含噪IMF分量和较纯净的IMF分量,重构误差较小,无显著失真现象,可避免其他方法存在主要幅值能量IMF易丢失的问题,在仪器信号去噪领域具有一定的应用价值。
下一步将重点关注去噪效率的提升和更多噪声评价指标的有机融合与挑选,以得到更加可信的含噪信号分解结果IMF筛选依据。此外,还将继续加强对雷暴、强降雨、人工干扰、爆破、天然地震等多种含噪数据的采集分析,验证该方法在不同噪声背景下的噪声压制效果。
| [1] |
庞聪, 马武刚, 李查玮, 等. 一种GOA优化SOM神经网络的VP型倾斜仪故障智能诊断方法[J]. 大地测量与地球动力学, 2023, 43(3): 322-326 (Pang Cong, Ma Wugang, Li Chawei, et al. An Intelligent Fault Identification Method for VP Tiltmeter Using GOA-Optimized SOM Neural Network[J]. Journal of Geodesy and Geodynamics, 2023, 43(3): 322-326)
(  0) 0) |
| [2] |
庞聪, 马武刚, 李查玮, 等. 基于CEEMDAN多尺度模糊熵和SSA-BP神经网络的VP型垂直摆倾斜仪故障辨识[J]. 科学技术与工程, 2022, 22(35): 15 612-15 616 (Pang Cong, Ma Wugang, Li Chawei, et al. Determination of Troubles for VP Vertical Pendulum Inclinometer Using CEEMDAN Multi-Scale Approximate Entropy and SSA-BP Neural Networks Model[J]. Science Technology and Engineering, 2022, 22(35): 15 612-15 616)
(  0) 0) |
| [3] |
马武刚, 庞聪, 龚燕民, 等. VP型宽频带倾斜仪故障信号的BBA-SOM智能诊断[J]. 科学技术与工程, 2023, 23(14): 6 012-6 017 (Ma Wugang, Pang Cong, Gong Yanmin, et al. Determination of Troubles for VP-Type Broadband Inclinometer Using CEEMD Multi-Scale Approximate Entropy and BBA-SOM Model[J]. Science Technology and Engineering, 2023, 23(14): 6 012-6 017)
(  0) 0) |
| [4] |
Zhao Y J, Yan S Q, He J L, et al. A Hybrid Denoising Algorithm for HIFU Echo Signal Based on ICEEMDAN Combined with MMSVC and WT[J]. Journal of Measurement Science and Instrumentation, 2023, 14(1): 35-44 DOI:10.62756/jmsi.1674-8042.2023005
(  0) 0) |
| [5] |
梁沛, 杨志强, 杨兵, 等. 顾及GNSS坐标时间序列中季节信号的CEEMD降噪方法[J]. 大地测量与地球动力学, 2022, 42(10): 1 010-1 014 (Liang Pei, Yang Zhiqiang, Yang Bing, et al. CEEMD Denoising Method with Seasonal Signals in GNSS Coordinate Time Series[J]. Journal of Geodesy and Geodynamics, 2022, 42(10): 1 010-1 014)
(  0) 0) |
| [6] |
王民顿, 尚俊娜. 基于CEEMD和改进小波阈值法的钢架结构沉降数据去噪方法[J]. 大地测量与地球动力学, 2022, 42(11): 1 191-1 195 (Wang Mindun, Shang Junna. Denoising Method of Steel Frame Structure Settlement Data Based on CEEMD and Improved Wavelet Threshold Method[J]. Journal of Geodesy and Geodynamics, 2022, 42(11): 1 191-1 195)
(  0) 0) |
| [7] |
贾婧, 窦圣宇, 范国玺, 等. 基于熵权法和灰色关联分析法的海岛地震应急能力评价研究[J]. 世界地震工程, 2020, 36(3): 233-241 (Jia Jing, Dou Shengyu, Fan Guoxi, et al. Research on the Evaluation for Earthquake Emergency Response Capacity of Islands Based on Entropy Weight Theory and Grey Relational Analysis[J]. World Earthquake Engineering, 2020, 36(3): 233-241)
(  0) 0) |
| [8] |
李静波, 崔春义, 许民泽, 等. 连续刚构桥地震响应灰色关联参数敏感性分析[J]. 防灾减灾工程学报, 2022, 42(4): 805-811 (Li Jingbo, Cui Chunyi, Xu Minze, et al. Parameter Sensitivity Analysis of Seismic Response of a Continuous Rigid Frame Bridge Based on Grey Correlation Method[J]. Journal of Disaster Prevention and Mitigation Engineering, 2022, 42(4): 805-811)
(  0) 0) |
2. Wuhan Gravitation and Solid Earth Tides National Observation and Research Station, 40 Hongshance Road, Wuhan 430071, China;
3. Longnan Earthquake Monitoring Center Station of Gansu Earthquake Agency, Hanwang Town, Longnan 746000, China;
4. Liaoning Earthquake Agency, 44 North-Huanghe Street, Shenyang 110031, China
 2024, Vol. 44
2024, Vol. 44


