2. 中国科学院精密测量科学与技术创新研究院大地测量与地球动力学国家重点实验室,武汉市徐东大街340号,430077
固体地球是一种弹性体,容易受一些地球物理现象的影响,如海潮、大气潮和固体潮等潮汐效应及非潮汐大气和海洋、剥蚀、水文、构造运动等非潮汐效应,这些现象会产生或伴随质量的迁移,随之而来的负荷效应会使地壳变形,且形变主要发生在垂直方向[1]。潮汐效应导致的地壳形变能从理论上预先进行计算,因此目前大部分学者主要研究非潮汐效应对地壳的影响[2]。GNSS可以精确观测到地表环境变化和构造活动导致的地面站点形变,但观测站点的数量经常不足以覆盖整个研究区域,且观测结果包含构造运动的影响,不能完全代表由环境负荷引起的地壳形变。GRACE卫星及后续GRACE-FO卫星数据已被广泛应用于地球水运动和地表质量变化探测,基于弹性负荷理论,GRACE的时变重力场数据还可用于计算地壳负荷形变[3]。但GRACE球谐系数处理过程中的滤波和截断会导致GRACE信号衰减和泄露,分辨率约为300 km[3]。
根据Farrell[4]的负荷形变理论,使用格林函数法可准确计算质量变化引起的地壳形变[5]。但精确的环境质量变化模型很难构建,因此大多数人使用GRACE球谐函数法来计算地壳负荷形变,很少有人定量分析2种方法的差异。
三峡水库最大蓄水量为393亿m3,水位每年大约在145~175 m之间波动。三峡水库巨大的储水量变化导致该地区地震、滑坡、塌方、泥石流等地质灾害频发[6],因此研究三峡地区环境变化与地壳形变的响应关系意义重大。本文利用基于GRACE-FO数据的球谐函数法和结合质量变化模型的格林函数法研究三峡地区环境负荷引起的地壳垂直形变时空分布特征,并给出三峡地区2019~2022年各月环境负荷垂直形变量及垂直形变速度场。
1 基本原理 1.1 球谐函数法根据GRACE-FO重力位球谐系数变化量ΔClm和ΔSlm计算环境负荷引起的地壳垂直形变ΔU(θ, λ)[7]:
| $ \begin{gathered} \Delta U(\theta, \lambda)=R \sum\limits_{l=1}^{\infty} \sum\limits_{m=0}^l \frac{h_l}{k_l+1} \cdot \\ \bar{P}_{l m}(\cos \theta)\left[\Delta C_{l m} \cos (m \lambda)+\Delta S_{l m} \sin (m \lambda)\right] \end{gathered} $ | (1) |
式中,R为地球平均半径,l、m为球谐系数的阶和次,θ和λ分别为地心余纬和经度,Plm为完全规格化缔合勒让德函数,kl和hl为Love数。
1.2 格林函数法基于地表负荷形变理论,将大气压、陆地水等环境的质量变化用等效水高的形式构建质量变化模型,则(φ′, λ′)处的质量变化Δhw对地表(φ, λ)点的负荷垂直形变影响(大地高变化)Δμ(φ, λ)为[2]:
| $ \Delta \mu(\varphi, \lambda)=G \rho_{\mathrm{w}} \iint_S \frac{\Delta h_{\mathrm{w}}\left(\varphi^{\prime}, \lambda^{\prime}\right)}{r} G(\psi) \mathrm{d} S $ | (2) |
式中,G为万有引力常数,ρw为水的密度,φ和λ为纬度和经度,ψ和r分别为计算点(φ, λ)到负荷源(φ′, λ′)的球面角距和距离,S为地球表面, G(ψ)为径向格林函数[4]。本文计算三峡地区地壳垂直形变时采用5′× 5′分辨率的计算点。
2 数据及方法 2.1 GRACE-FO数据采用2018-11~2022-12由得克萨斯大学空间研究中心发布的GRACE-FO Level-2 GSM球谐数据产品,阶数为60,GSM数据扣除了潮汐运动、非潮汐海洋和大气的影响。替换GRACE-FO原始数据的一阶项[8]、C20项和C30项[9];为减少高频噪声信号的影响,对球谐系数进行P4M6去相关滤波和300 km高斯滤波处理;由于冰川均衡调整,对球谐系数进行GIA改正[10];滤波和截断处理导致的信号衰减和泄露采用尺度因子法进行恢复[11]。
2.2 环境质量变化模型在使用格林函数法计算负荷垂直形变时,需首先建立环境质量变化模型。由于三峡地区处于内陆,受非潮汐海洋效应影响较小,因此本文构建江河湖库水、土壤水、雪水和植被冠层水这些陆地水的质量变化模型及非潮汐大气质量变化模型。
使用2019年Sentinel-2 MSI影像,采用AWEI、MNDWI、NDVI多个水体指数组合提取三峡地区江河湖泊的水体范围[12](图 1蓝色区域)。结合该地区21个水位站月平均水位数据,通过克里金插值法获得三峡地区2018-11~2022-12每月江河湖库水等效水高格网,分辨率为6″×6″。地表大气压数据由欧洲中期天气预报中心发布的ERA5月产品数据集中获得,将地表压力(单位Pa)数据换算成等效水高(单位mm)格网模型,换算系数为0.101 97 mm/Pa[4],时间为2018-11~2022-12,空间分辨率为0.25°×0.25°。从全球陆地数据同化系统GLDAS Noah 2.1月数据集中获取土壤水、雪水和植被冠层水的等效水高格网,时间为2018-11~2022-12,空间分辨率为0.25°×0.25°。

|
图 1 三峡地区GNSS站、水位站及水体分布 Fig. 1 Distribution of GNSS stations, water level stations and water in the Three Gorges area |
以2018年三峡水库月平均水位最高的11月为基准,对构建的质量变化模型进行基准扣除,分别获取各环境变量2019~2022年的质量月变化格网。
2.3 GNSS数据从国家地震科学数据中心获取三峡地区GNSS站点垂直形变线性时间序列,该数据扣除了海潮、固体潮与极潮的影响。对GNSS时序进行粗差和阶跃项误差剔除处理,使用德国地学中心NTOL数据产品扣除非潮汐海洋负荷引起的垂直形变,对时间序列缺失的数据采用三次样条插值补齐,求得各月平均垂直形变,并以2018-11为基准,得到2019~2022年地壳垂直形变月变化时序。
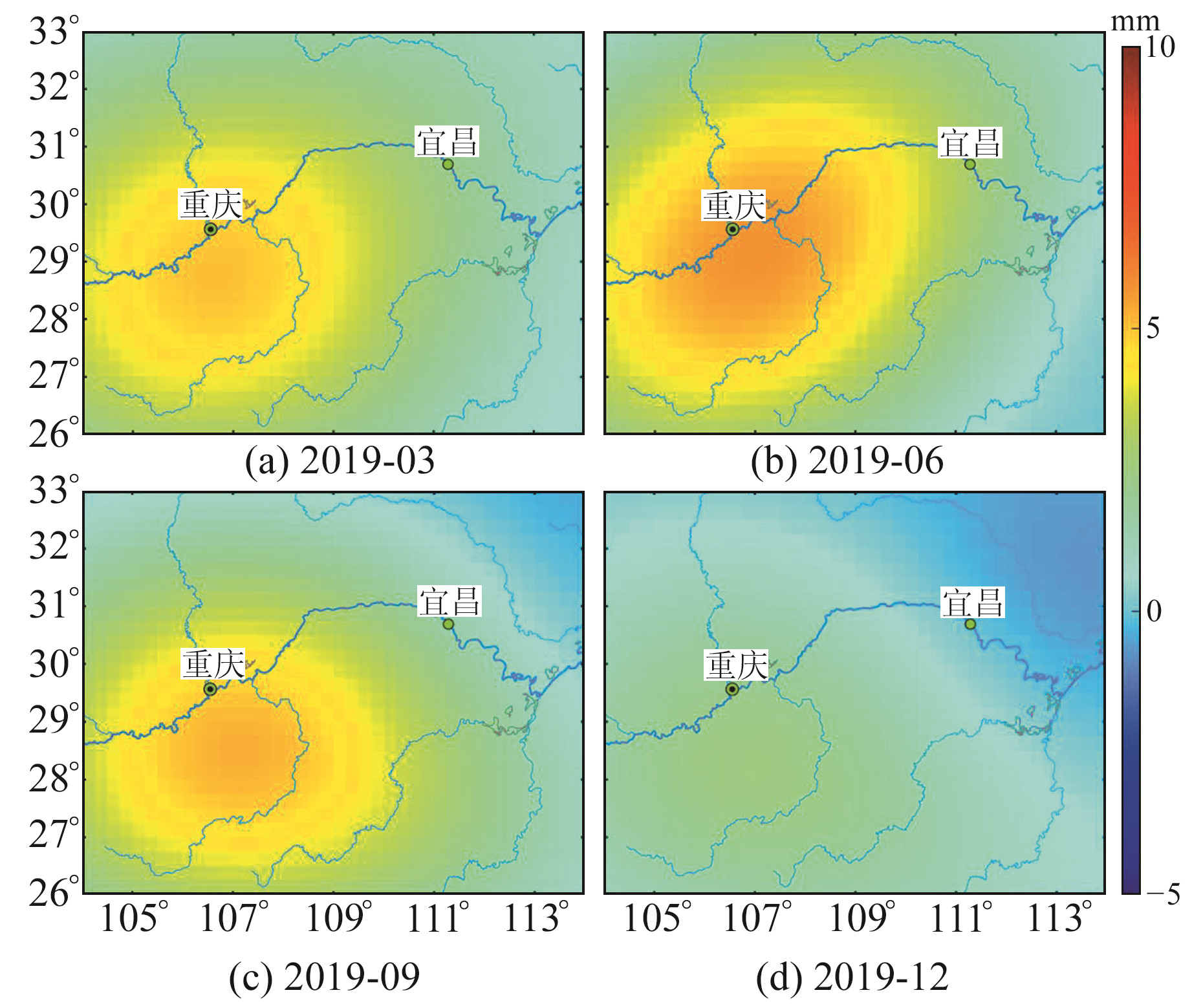
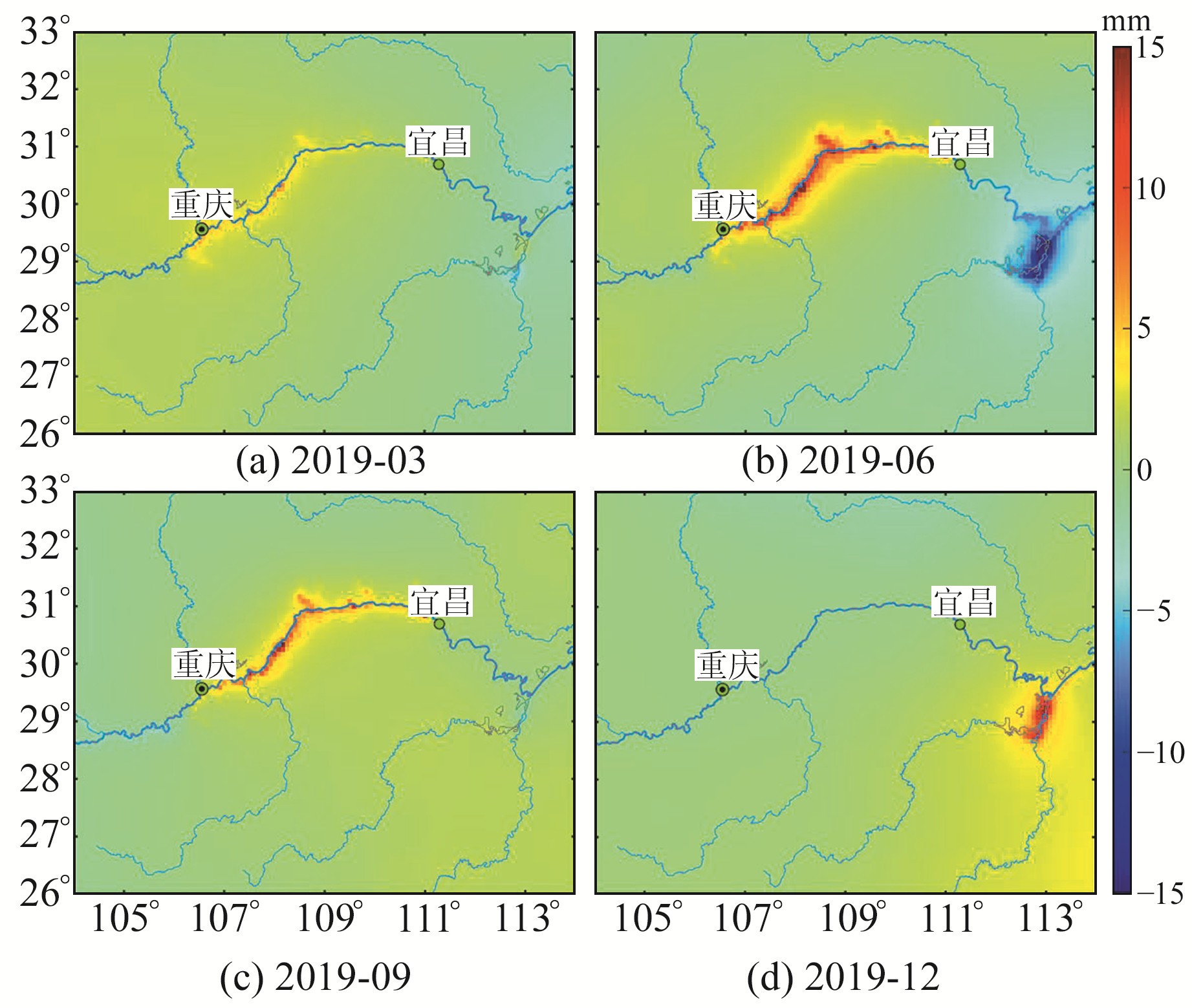
3 结果与分析 3.1 球谐函数法和格林函数法的比较为比较基于GRACE-FO数据的球谐函数法和结合质量变化模型的格林函数法在计算负荷垂直形变上的差异,分别使用2种方法计算三峡地区2019~2022年48个月陆地水负荷导致的地壳垂直形变(相对于2018-11),图 2和3绘制了2种方法在2019-03、2019-06、2019-09和2019-12的计算结果。可以发现,在3、6、9月,2种方法计算的垂直形变在水库库区附近均表现为正值,且地壳都在6月隆升到最大值。从空间分布来看,GRACE-FO结果的空间分辨率低,局部信号不明显,这是由于GRACE-FO数据的滤波和截断处理导致形变信号中的高频信息缺失,剩余的低频信息仅反映区域平均负荷形变;相比之下,陆地水质量变化模型的计算结果分辨率更高,局部信号更加突出,尤其在三峡水库库区附近质量变化较大的区域。
|
图 2 基于GRACE-FO的2019年三峡地区陆地水负荷垂直形变 Fig. 2 Vertical deformation of terrestrial water load in Three Gorges region in 2019 based on GRACE-FO |
|
图 3 基于质量变化模型的2019年三峡地区陆地水负荷垂直形变 Fig. 3 Vertical deformation of terrestrial water load in the Three Gorges region in 2019 based on mass change model |
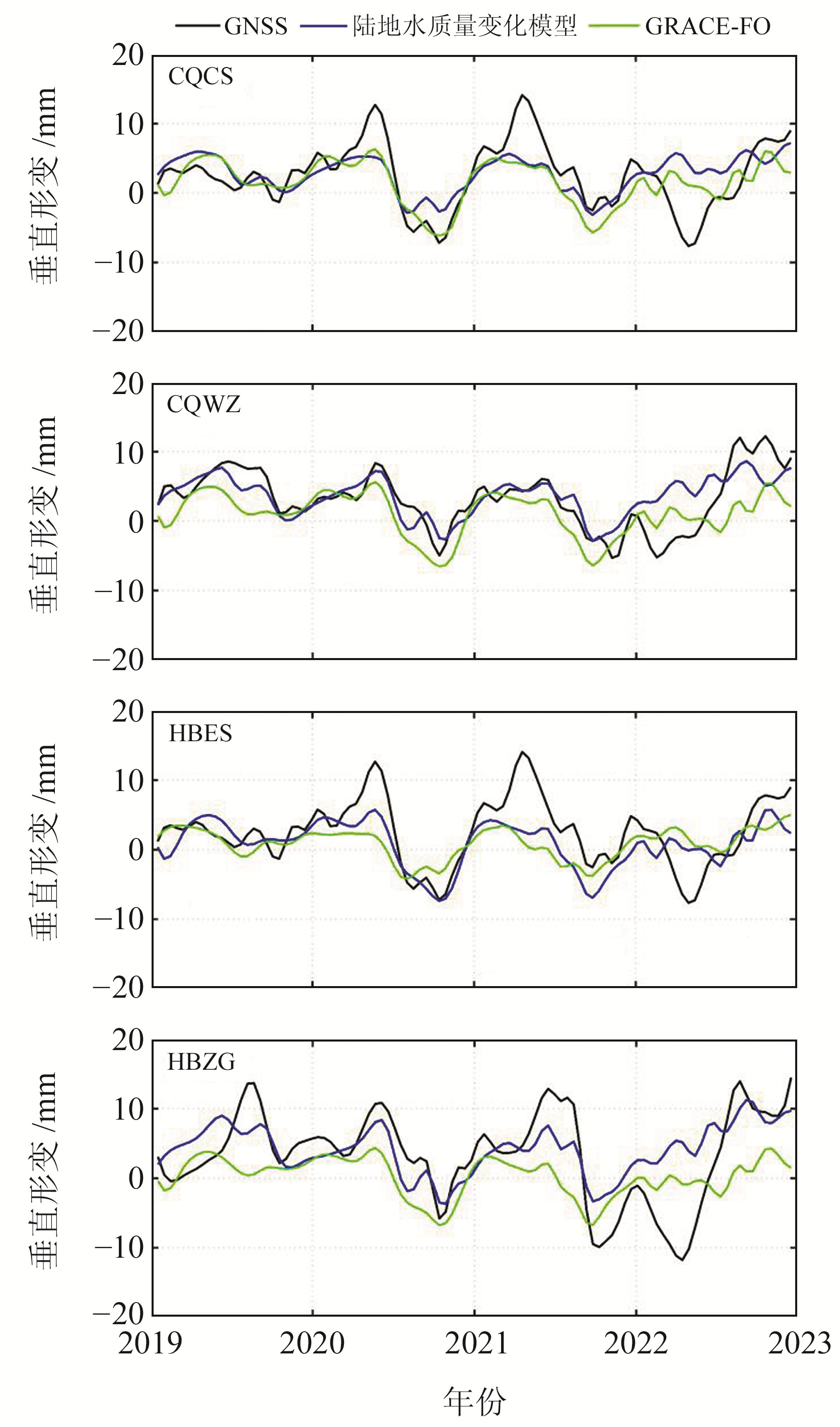
使用位于水库附近的4个GNSS站点实测结果验证2种方法的差异。图 4绘制了2019~2022年GNSS实测垂直形变月变化及GRACE-FO和陆地水质量变化模型计算的地壳垂直形变,表 1统计了2种方法的计算结果及其与GNSS的相关系数。可以发现,GRACE-FO和陆地水质量变化模型计算的地壳垂直形变与GNSS具有一定的相关性,二者与GNSS的相关系数平均为0.60和0.69,说明使用质量变化模型计算负荷垂直形变的精度更高。
|
图 4 2019~2022年GNSS站的陆地水负荷垂直形变 Fig. 4 Vertical deformation of terrestrial water load at GNSS stations from 2019 to 2022 |
|
|
表 1 2种方法计算的陆地水负荷垂直形变以及与GNSS的相关性 Tab. 1 The vertical deformation of terrestrial water load calculated by two methods and their correlation with GNSS |
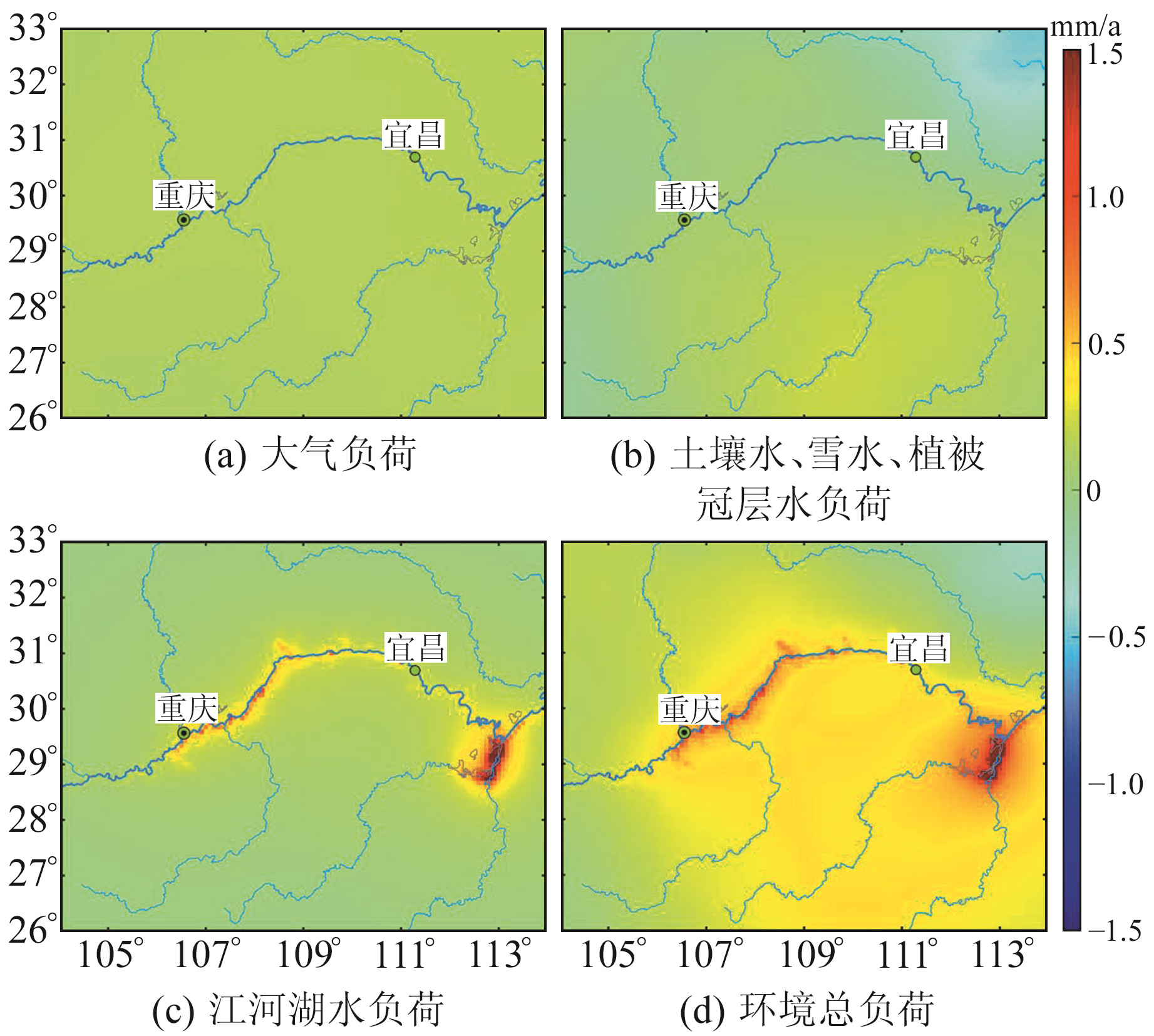
基于§2.2构建的大气压、江河湖库水、土壤水、植被冠层水和雪水质量变化模型,采用格林函数法计算三峡地区2019~2022年各月地壳垂直形变(相对于2018-11),并对48个月的垂直形变格网进行最小二乘拟合,得到2019~2022年各种环境负荷的垂直形变速率分布。由图 5可知,2019~2022年三峡库区和洞庭湖流域的地壳隆升较为明显,垂直形变速率分别达到0.5~0.7 mm/a和0.6~1.5 mm/a,主要受江河湖库水负荷的影响所致。
|
图 5 2019~2022年三峡地区环境负荷的垂直形变速度场 Fig. 5 Vertical deformation velocity field of environmental load in the Three Gorges region from 2019 to 2022 |
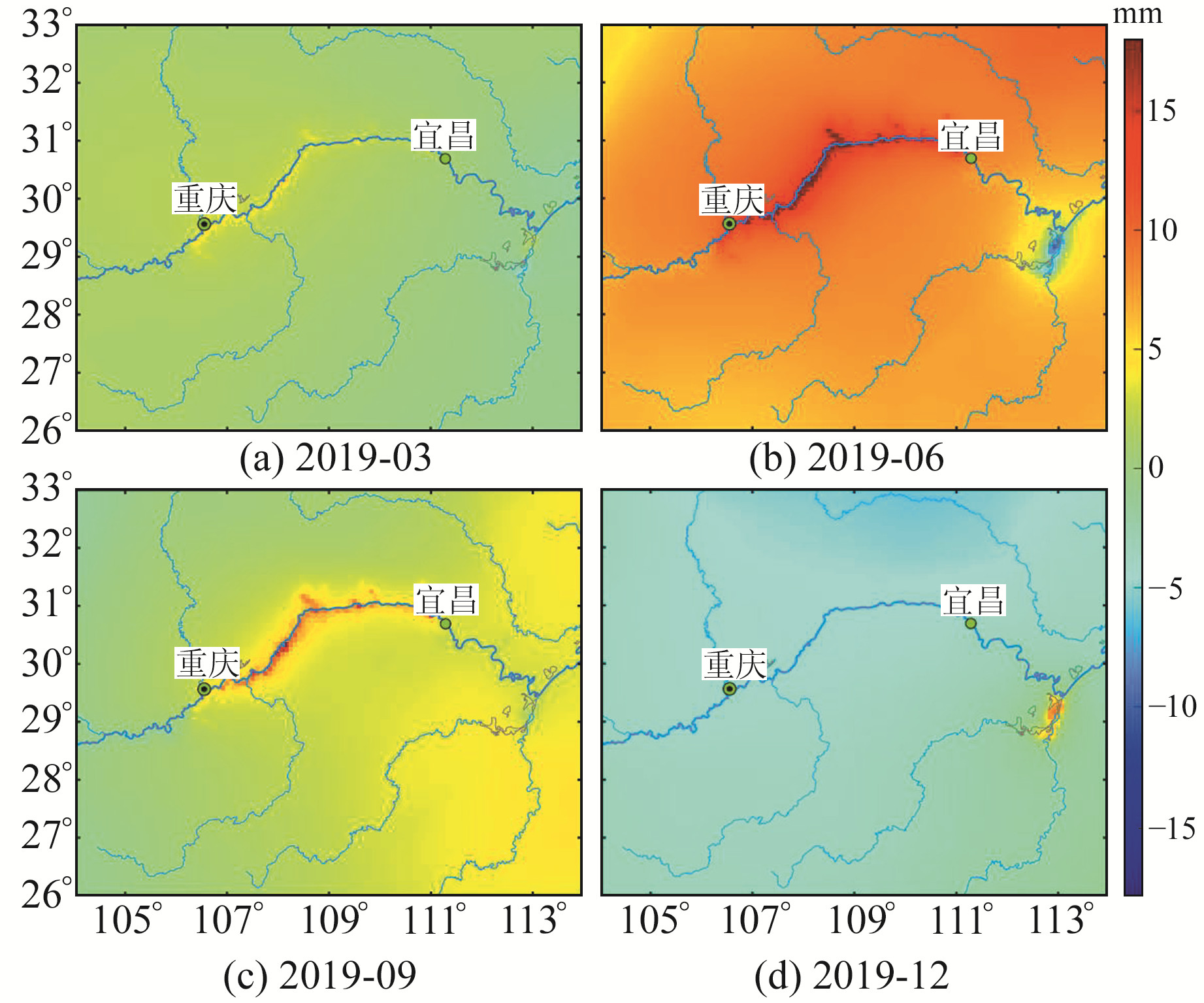
为分析三峡地区环境总负荷变化导致的地壳垂直形变季节性空间变化特征,绘制2019-03、2019-06、2019-09和2019-12地壳垂直形变空间分布,并将大于18 mm的区域表示为18 mm。由图 6可知,3、6、9月三峡水库库区附近地壳均有上升,在6月地壳垂直形变达到最大,库区中心地带垂直形变超过15 mm;6月大坝下游及洞庭湖水域地壳发生轻微沉降,12月地壳轻微上升。根据三峡水库和大坝下游实际水位变化可以发现,地壳垂直形变与环境质量变化具有明显的特征关系,三峡水库水位在6~8月最低,而大坝下游水位却处于每年最高时期,11~12月水库蓄水导致大坝下游水位降低,因此图 6中地壳发生相应变化。对比图 3和6还可以发现,大气负荷对地壳的影响主要在6月,此时三峡地区地壳整体抬升超过5 mm。
|
图 6 三峡地区2019年环境总负荷变化引起的地壳垂直形变 Fig. 6 Vertical crustal deformation due to changes in the total environmental load in the Three Gorges region in 2019 |
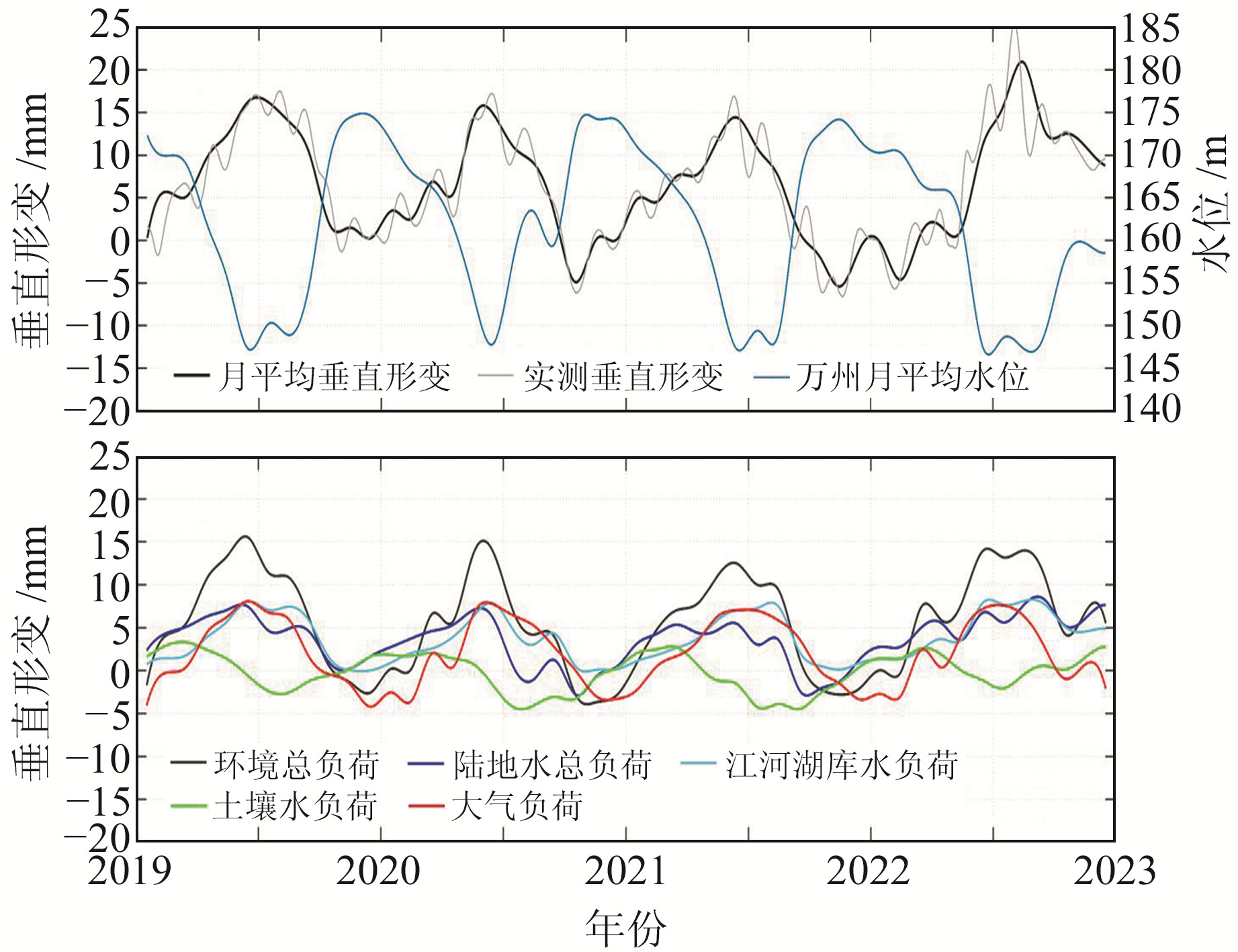
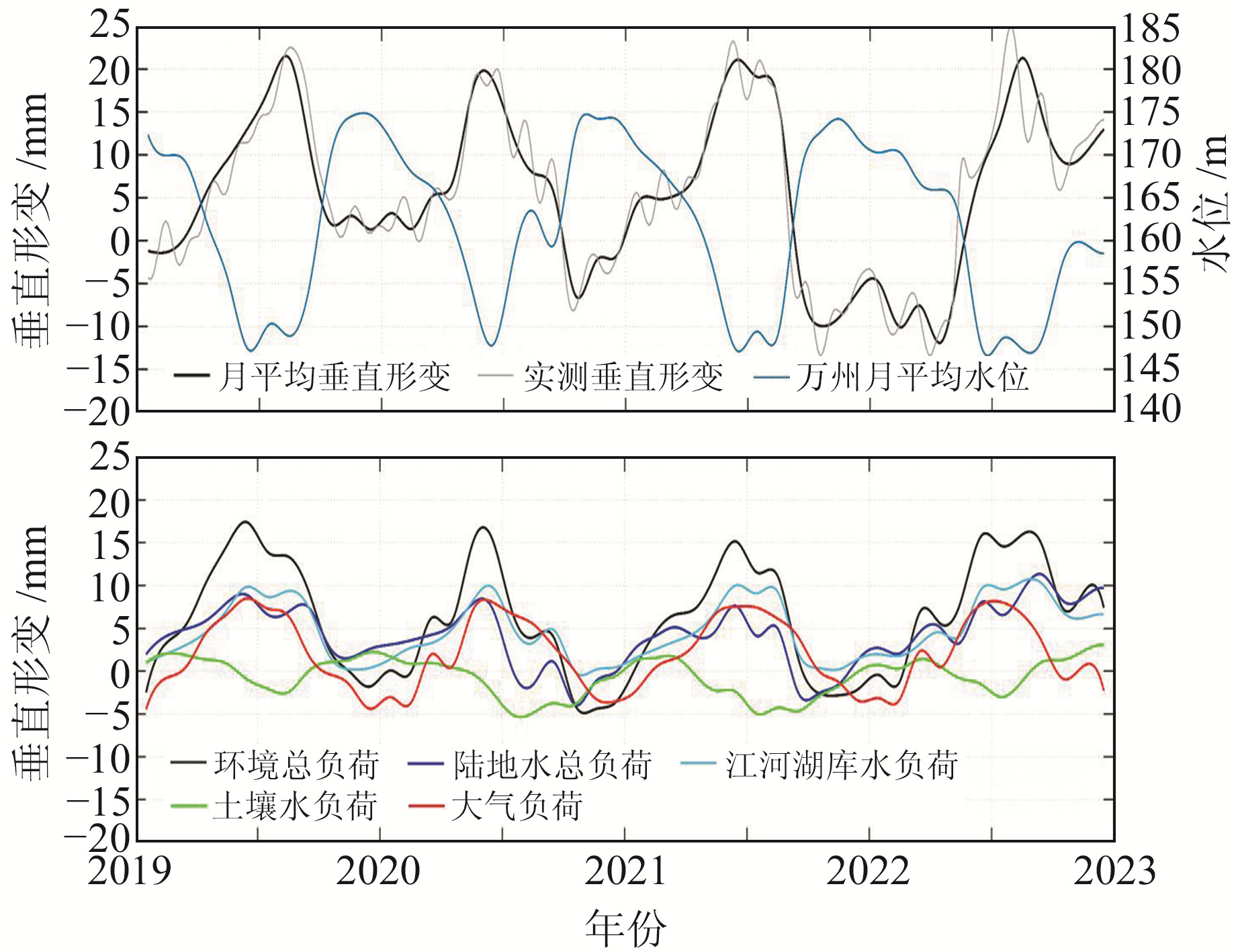
为定量分析环境负荷垂直形变和GNSS监测结果的一致性,图 7和8分别绘制了距离库区最近的CQWZ站和HBZG站2019~2022年实测垂直形变和环境负荷垂直形变时间序列。在加上大气负荷后,环境总负荷引起的地壳垂直形变与GNSS实测结果在CQWZ站和HBZG站的相关系数由0.72和0.65增至0.88和0.83,且两者变化趋势非常吻合。
|
图 7 CQWZ站实测垂直形变及环境负荷的垂直形变 Fig. 7 Measured vertical deformation and vertical deformation of environmental load at CQWZ station |
|
图 8 HBZG站实测垂直形变及环境负荷的垂直形变 Fig. 8 Measured vertical deformation and vertical deformation of environmental load at HBZG station |
由图 7和8可知,江河湖库水负荷垂直形变与三峡水库水位呈负相关,大气负荷对地壳的影响具有夏季隆升、冬季下沉的特点,而土壤水对地壳的影响与大气负荷刚好相反。在三峡水库库区附近,江河湖库水负荷对地壳垂直形变的影响最大,幅度约为-5~10 mm,其次是大气负荷,幅度约为-5~8 mm,土壤水、雪水和植被冠层水对地壳垂直形变的影响最小,幅度约为-5~5 mm。三者总负荷对地壳垂直形变的影响幅度大约在-5~18 mm之间,贡献了地面GNSS站点垂直形变量的90%左右。表明GNSS垂直形变时序的季节性变化主要由环境负荷造成,但环境总负荷垂直形变时序的振幅低于GNSS时序,这可能是由于未考虑构造运动和地下水的影响。
从图 7和8可以发现,2022年下半年地壳较往年同时期有上升的趋势,主要是受江河湖库水负荷的影响。根据气候资料和水位变化可知,2022年气候高温干旱,降雨量减少,三峡水库水位持续低于历年平均水位,洞庭湖水域面积剧减,水位为近30 a最低,地表水质量的减少导致地壳回弹上升,这也是图 6中三峡水库库区和洞庭湖流域地壳垂直形变速率上升的原因。
4 结语本文利用GNSS、GRACE-FO和环境质量变化模型分析计算了三峡地区环境负荷导致的季节性和长期垂直形变,主要结论如下:
1) GRACE-FO和质量变化模型计算的陆地水负荷垂直形变在时空分布上具有一定的一致性,但后者的精度和空间分辨率更高,GRACE-FO和陆地水质量变化模型的计算结果与GNSS实测垂直形变的相关系数平均为0.60和0.69。在加上大气负荷后,采用质量变化模型计算的CQWZ站和HBZG站环境总负荷垂直形变与GNSS的相关系数由0.72和0.65增至0.88和0.83,两者趋势具有较高的一致性。
2) 利用质量变化模型和格林函数法计算三峡地区2019~2022年环境总负荷的地壳垂直形变,结果发现,2019~2022年三峡库区和洞庭湖流域的地壳分别以0.5~0.7 mm/a和0.6~1.5 mm/a的速率上升,原因是2022年高温干旱,使该区域水位降低,地表质量的减少导致地壳回弹上升。
3) 环境总负荷对库区附近地壳垂直形变的影响大约在-5~18 mm之间,且地壳具有夏季上升、冬季下沉的变化特征,主要受江河湖库水负荷和大气负荷的影响较多,环境总负荷垂直形变达到GNSS实测垂直形变量的90%左右,差异部分可能是未考虑地下水和构造运动导致的。
致谢: 感谢章传银教授及其团队提供的地球潮汐负荷效应与形变监测计算系统。
| [1] |
许厚泽. 固体地球潮汐[M]. 武汉: 湖北科学技术出版社, 2010 (Xu Houze. Solid Earth Tide[M]. Wuhan: Hubei Science and Technology Press, 2010)
(  0) 0) |
| [2] |
章传银, 王伟, 甘卫军, 等. 利用CORS站网监测三峡地区环境负荷引起的地壳形变与重力场时空变化[J]. 武汉大学学报: 信息科学版, 2018, 43(9): 1 287-1 294 (Zhang Chuanyin, Wang Wei, Gan Weijun, et al. Monitoring Temporal and Spatial Changes of Crustal Deformation and Gravity Field Caused by Environmental Load in the Three Gorges Reservoir Region Based on CORS Network[J]. Geomatics and Information Science of Wuhan University, 2018, 43(9): 1 287-1 294)
(  0) 0) |
| [3] |
Rao W L, Sun W K. Uplift of the Tibetan Plateau: How to Accurately Compute the Hydrological Load Effect?[J]. Journal of Geophysical Research: Solid Earth, 2022, 127(1)
(  0) 0) |
| [4] |
Farrell W E. Deformation of the Earth by Surface Loads[J]. Reviews of Geophysics, 1972, 10(3): 761-797 DOI:10.1029/RG010i003p00761
(  0) 0) |
| [5] |
Wen Z Q, Rao W L, Sun W K. Contribution of Loading Deformation to the GNSS Vertical Velocity Field in the Chinese Mainland[J]. Geophysical Journal International, 2023, 233(3): 1 655-1 670 DOI:10.1093/gji/ggac508
(  0) 0) |
| [6] |
Wang W, Zhang C Y, Hu M Z, et al. Monitoring and Analysis of Geological Hazards in Three Gorges Area Based on Load Impact Change[J]. Natural Hazards, 2019, 97: 611-622 DOI:10.1007/s11069-019-03661-w
(  0) 0) |
| [7] |
Fu Y N, Freymueller J T. Seasonal and Long-Term Vertical Deformation in the Nepal Himalaya Constrained by GPS and GRACE Measurements[J]. Journal of Geophysical Research: Solid Earth, 2012, 117(B3)
(  0) 0) |
| [8] |
Swenson S, Chambers D, Wahr J. Estimating Geocenter Variations from a Combination of GRACE and Ocean Model Output[J]. Journal of Geophysical Research: Solid Earth, 2008, 113(B8)
(  0) 0) |
| [9] |
Cheng M K, Ries J. The Unexpected Signal in GRACE Estimates of C20[J]. Journal of Geodesy, 2017, 91(8): 897-914 DOI:10.1007/s00190-016-0995-5
(  0) 0) |
| [10] |
Swenson S, Wahr J. Post-Processing Removal of Correlated Errors in GRACE Data[J]. Geophysical Research Letters, 2006, 33(8)
(  0) 0) |
| [11] |
李嘉, 唐河, 饶维龙, 等. 南水北调工程对华北平原水储量变化的影响[J]. 中国科学院大学学报, 2020, 37(6): 775-783 (Li Jia, Tang He, Rao Weilong, et al. Influence of South-to-North Water Transfer Project on the Changes of Terrestrial Water Storage in North China Plain[J]. Journal of University of Chinese Academy of Sciences, 2020, 37(6): 775-783)
(  0) 0) |
| [12] |
刘宇晨, 高永年. Sentinel时序影像的长江流域地表水体提取[J]. 遥感学报, 2022, 26(2): 358-372 (Liu Yucheng, Gao Yongnian. Surface Water Extraction in Yangtze River Basin Based on Sentinel Time Series Image[J]. National Remote Sensing Bulletin, 2022, 26(2): 358-372)
(  0) 0) |
2. State Key Laboratory of Geodesy and Earth's Dynamics, Innovation Academy for Precision Measurement Science and Technology, CAS, 340 Xudong Street, Wuhan 430077, China
 2024, Vol. 44
2024, Vol. 44

