2. 武汉地震工程研究院有限公司,武汉市洪山侧路40号,430071
土体剪切波波速是描述地震荷载作用下土层动力反应的重要参数之一,也是我国建筑抗震设计规范中划分场地类别的主要依据,在土动力学和地震工程学中应用十分广泛[1]。随着国家重大工程项目的不断建设,我国开展了大量场地土层剪切波波速测试工作,积累了丰富的土层剪切波波速数据。依据这些实测数据,国内学者们获得了不同地区土层剪切波波速和埋深之间的经验公式[2-8]。综合已有的研究成果可以得出:1)同一地区较固结的不同土类剪切波波速和深度之间存在明显的相关性,可用线性模型、幂函数模型、一元二次函数等模型进行拟合回归,获得两者的经验公式;2)由于岩土类别、土体状态、沉积环境、地貌单元及地质年代等因素的影响,不同地区、不同深度、不同土类的剪切波波速会有较大差异,不同地区、不同土类剪切波波速和深度的经验公式差别也较大。
本文利用襄阳市重大工程场地地震安全性评价工作中的102个场地钻孔实测剪切波资料,采用线性函数、幂函数和一元二次函数3种模型,给出该地区人工填土、粘性土(粘土、粉质粘土)、粉土、砂土(细砂、中砂、粗砂)及碎石土(圆砾、卵石)剪切波波速与深度的统计关系,同时讨论土体状态对二者相关性的影响,最后利用实测钻孔数据验证统计公式的合理性和可靠性,为襄阳地区工程勘察、地震灾害风险普查等提供参考。
1 数据来源本文数据均来源于湖北省襄阳市重大工程场地地震安全性评价工作中的实测钻孔资料,并剔除了明显不合理和错误的数据。为避免同一地区同一场地数据比重过大,使结果产生偏差,按1个工程场地不超过2个钻孔的原则进行选取[9],其中回填土、杂填土、耕植土、素填土等合并统称为人工填土。
基于本文选取原则和处理方法,最终收集到襄阳地区102个钻孔资料,得到剪切波测点数据3 356条,其中Ⅱ类场地钻孔95个,剪切波测点数据2 901条;Ⅲ类场地钻孔7个,剪切波测点数据455条。表 1为襄阳地区人工填土、粘土、粉质粘土、粉土、细砂、中砂、粗砂、圆砾、卵石等9类土层剪切波波速测试点数据统计结果。
|
|
表 1 襄阳地区常见土层剪切波波速测试点数据统计 Tab. 1 Statistics of common soil shear wave velocity test points in Xiangyang area |
根据已有研究结果,利用线性函数、幂函数和一元二次函数3种数学模型,对襄阳地区土层剪切波波速与深度数据进行拟合回归分析,得到不同数学模型的拟合系数和拟合优度。其中,拟合优度R2范围为0~1,其值越接近1,实际观测点离样本越近,拟合效果越好。具体回归模型为:
1) 线性函数模型:
2) 幂函数模型:
3) 一元二次函数模型:
式中,VS为土层剪切波波速,单位m/s;H为土层埋深,单位m;a、b、c、d、e、f、g为不同回归模型的拟合系数。
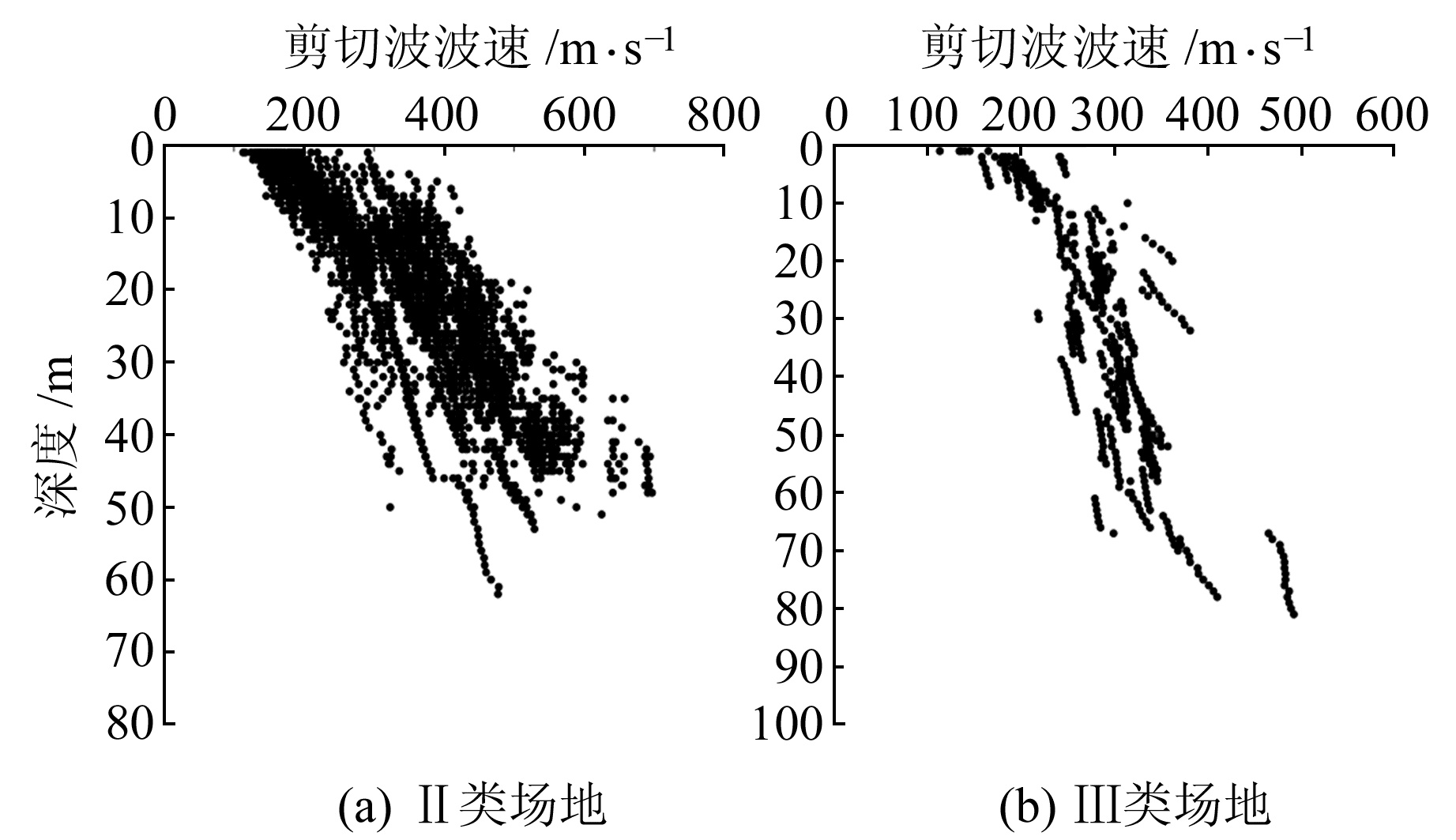
依据场地分类结果,绘制襄阳地区Ⅱ类和Ⅲ类场地的土层剪切波波速与深度的散点分布,如图 1所示。可以看出,襄阳地区土层剪切波波速与深度相关性明显,剪切波波速随深度的增加有增大趋势,且随着深度的不断变大,其离散程度也变大。由于Ⅲ类场地钻孔数据较少,本文不再具体讨论不同场地条件下不同土类剪切波波速与深度的关系。
|
图 1 襄阳地区Ⅱ类和Ⅲ类场地土层剪切波波速与深度的散点分布 Fig. 1 Scatter plot of shear wave velocity and depth in soil layers of Class Ⅱand Ⅲ sites in Xiangyang areas |
为进一步揭示襄阳地区不同土类剪切波波速与深度的相关性,利用不同土类剪切波数据,分别绘制人工填土、粘性土(粘土、粉质粘土)、粉土、砂土(细砂、中砂、粗砂)和碎石土(圆砾、卵石)共5大类9种土层剪切波波速与深度的散点分布。从图 2(a)可以看出,人工填土剪切波波速介于100~200 m/s之间,深度在4 m以内,剪切波波速与深度之间没有明显的相关性,可能和人工填土土体状态较松散、形成时间短、固结程度低有关[3]。其余类型土层剪切波波速随深度的增大而变大,但其变化率逐渐变小。综上分析认为,襄阳地区形成时间短,欠固结的人工填土剪切波波速与深度之间相关性较弱,其余固结较好的土类剪切波波速与深度之间相关性较好。

|
图 2 襄阳地区9种常见土类剪切波波速与深度的散点分布 Fig. 2 Scatter plots of shear wave velocity and depth for 9 common soil types in Xiangyang area |
利用线性函数、幂函数及一元二次函数3种模型,对粘土、粉质粘土、粉土、细砂、中砂、粗砂、圆砾和卵石的剪切波波速与深度的关系进行拟合回归,得到不同土类、不同模型的拟合参数、拟合优度及推荐模型。从表 2看出,一元二次函数模型的拟合优度R2整体大于线性函数模型和幂函数模型。拟合优度最好的为粗砂(0.925 3),最差的为卵石(0.755 2),除细砂和卵石2个回归模型的拟合优度均小于0.8外,其余各土层的拟合优度都在0.8以上,说明该统计结果的相关性较好。
|
|
表 2 襄阳地区9种常见土类剪切波波速与深度关系拟合结果 Tab. 2 Fitting results of shear wave velocity and depth relationship for 9 common soil types in Xiangyang area |
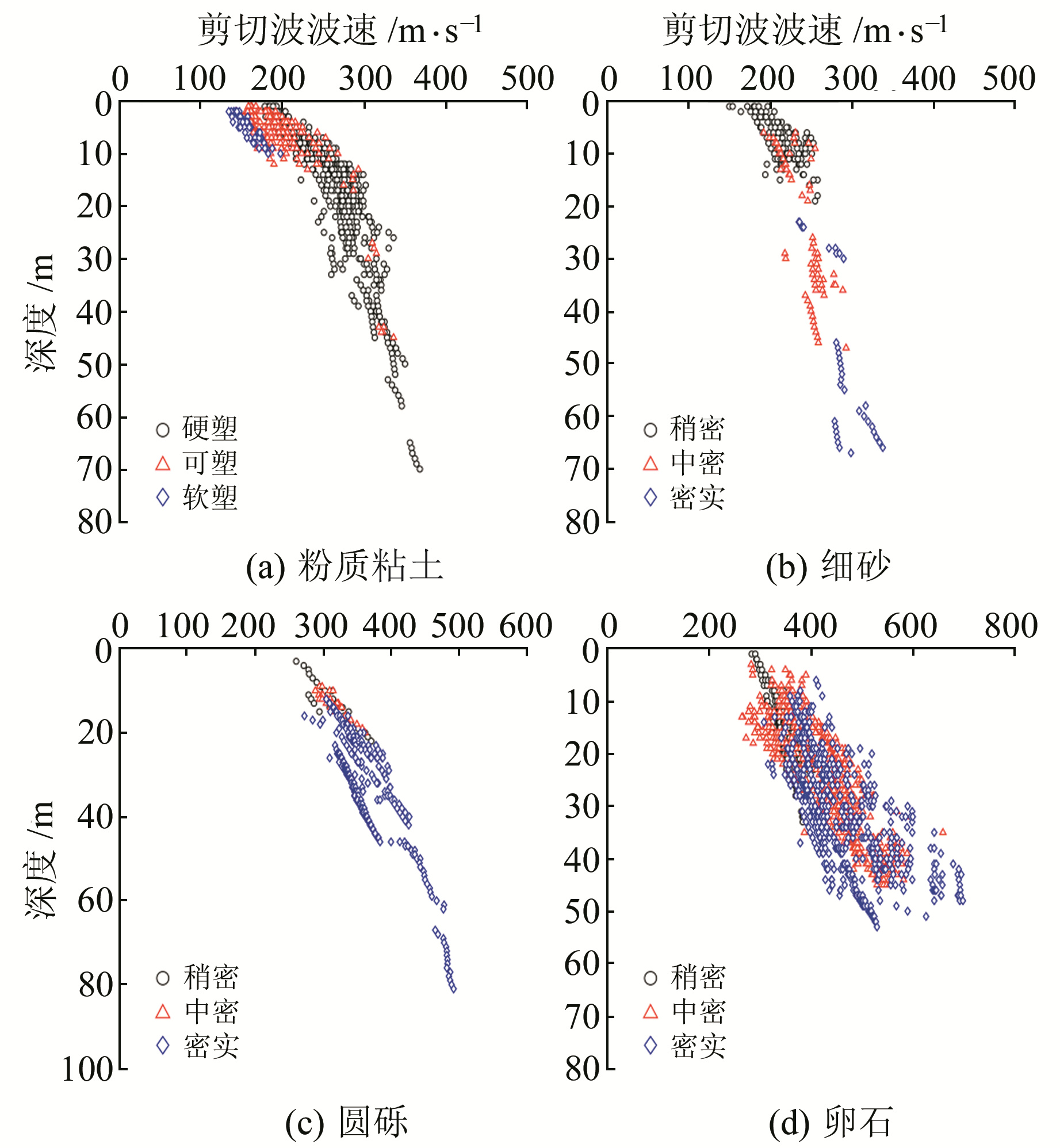
为探究土体状态对土层剪切波波速与深度相关性的影响,对襄阳地区土层的土体状态进行详细划分。TB 10077-2001《铁路工程岩土分类标准》中利用液性指数将粘性土的土体状态分为坚硬、硬塑、可塑、软塑和流塑5种,GB 50021-2001 《岩土工程勘察规范》中使用标贯锤击数将非粘性土的土体状态分为密实、中密、稍密和松散4种。依据规范标准,将研究区内测点数据较多的粉质粘土、细砂、圆砾和卵石4种土类按土体状态进行细分,相关统计数据如表 3和图 3所示。
|
|
表 3 不同土类不同土体状态下剪切波波速和深度拟合结果 Tab. 3 Fitting results of shear wave velocity and depth under different soil types and soil states |
|
图 3 不同土类、不同土体状态下剪切波波速与深度的散点分布 Fig. 3 Scatter plots of shear wave velocity and depth under different soil types and soil states |
从图 3和表 3可看出:1)整体而言,不同土体状态下粉质粘土、细砂、圆砾及卵石的剪切波波速与深度之间也具有较明显的相关性,随着深度的不断增加,其剪切波波速离散程度也不断增加。2)硬塑状粉质粘土深度分布范围最广,为1~70 m,其次为可塑状粉质粘土,软塑状粉质粘土分布深度最为集中,为2~10 m。硬塑状粉质粘土的平均剪切波波速最大,为257 m/s,可塑状粉质粘土次之,为197 m/s,软塑状粉质粘土最小,为160 m/s。划分土体状态后,可塑状粉质粘土的拟合优度变小,硬塑状和软塑状粉质粘土的拟合优度变化不大。3)稍密状、中密状和密实状细砂的分布深度范围区别较大,稍密状细砂分布最浅,为1~19 m,中密状细砂次之,在6~47 m,密实状细砂最深,在23~67 m。密实状细砂的平均剪切波波速最大,为289 m/s,中密状细砂次之,为242 m/s,稍密状细砂最小,为217 m/s;区分土体状态后,密实状、中密状和稍密状细砂的拟合优度均变小,可能与不同状态下细砂的剪切波波速数据较少且离散有关。4)不同土体状态下圆砾的分布深度规律和平均剪切波波速变化与细砂相似,其中密实状、中密状和稍密状圆砾的拟合优度较不区分土体状态的拟合优度变化不大。5)稍密状卵石分布深度较浅,多在20 m以内,中密状和密实状卵石的分布深度范围较一致,3~50 m均有出露。在同一深度,中密状及密实状卵石的剪切波波速离散程度较大,在100~200 m/s之间,且随深度的变大离散程度也变大。密实状卵石的平均剪切波波速最大,为465 m/s,中密状卵石次之,为436 m/s,稍密状卵石最小,为354 m/s。较不区分土体状态的拟合优度,稍密状和密实状卵石的拟合优度明显变小,中密状卵石的拟合优度也减小,但变化幅度不大。
综上所述,土体状态会对土层剪切波波速与深度关系的拟合结果产生影响,考虑了土体状态的统计结果比不考虑土体状态的统计结果更具体,但同一土类区分土体状态后,推荐模型拟合优度的变化存在不确定性。
3 结果验证 3.1 不同土类剪切波波速与深度回归模型的可靠性验证以襄阳市东西轴线道路和庞公大桥工程勘察中ZK1和ZK2号钻孔的实测剪切波波速数据为例,对实测数据、本文模型与刘红帅等[2]提供的模型进行对比分析,并给出对应误差,结果如表 4和5所示。
|
|
表 4 ZK1钻孔实际剪切波波速、本文模型和文献模型所得剪切波波速对比 Tab. 4 Comparison between the actual shear wave velocity of ZK1 borehole and the shear wave velocity obtained from the model presented in this paper and literature's model |
|
|
表 5 ZK2钻孔实际剪切波波速、本文模型和文献模型所得剪切波波速对比 Tab. 5 Comparison between the actual shear wave velocity of ZK2 borehole and the shear wave velocity obtained from the model presented in this paper and literature's model |
可以看出,基于刘红帅等[2]利用全国范围内剪切波数据得到的模型预测的剪切波波速误差相对较大,最大误差接近30%,而基于本文模型计算得到的剪切波波速与实测值之间的误差浮动较稳定,基本在9%以内,预测值更接近实测值。两者误差对比表明,土层剪切波波速与深度之间的相关性存在明显的区域性特征。
3.2 土体状态对土层剪切波波速与深度关系的精度影响选取襄阳市图书馆和普陀龙湾项目工程勘察中ZK3和ZK4号钻孔的实测剪切波波速数据,对比粉质粘土、细砂、圆砾和卵石区分土体状态和不区分土体状态拟合回归模型计算得到的剪切波波速,并给出对应的误差值,结果如表 6和7所示。
|
|
表 6 ZK3钻孔实际剪切波波速、区分土体状态模型和不区分土体状态模型所得剪切波波速对比 Tab. 6 Comparison of actual shear wave velocity obtained from ZK3 borehole, distinguishing soil state models and indistinguishable soil state models |
|
|
表 7 ZK4钻孔实际剪切波波速、区分土体状态模型和不区分土体状态模型所得剪切波波速对比 Tab. 7 Comparison of actual shear wave velocity obtained from ZK4 borehole, distinguishing soil state models and indistinguishable soil state models |
可以看出,不区分土体状态下本文模型给出的剪切波波速与实测值之间的误差基本在20%以内;而区分土体状态下,本文模型给出的剪切波波速与实测值之间的误差在16%以内,且大部分在12%以内。结果表明,相对于不区分土体状态,区分土体状态下本文模型剪切波波速的误差更小。两者的误差对比表明,土体状态对土层剪切波波速与深度的回归模型的精度存在影响。
4 结语本文基于湖北襄阳地区地震安全性评价项目中的实测钻孔资料,对常见土层剪切波波速与深度的关系进行拟合回归分析计算,并给出该地区粘性土、粉土、砂土及碎石土剪切波波速与深度的最优经验公式,同时讨论土体状态对二者关系的影响,最后利用实测钻孔数据验证本文模型的可靠性。结果表明:
1) 襄阳地区人工填土剪切波波速与深度的相关性较差,粘性土、粉土、砂土和碎石土的剪切波波速与深度之间存在明显的相关性,且随着深度的增大,剪切波波速的离散程度逐渐变大。
2) 土体状态对不同类型土体剪切波波速的影响规律基本一致,同一土类随密实度或塑性状态的变大,其平均剪切波波速也变大。
3) 不同土体状态对相同土类的回归模型拟合效果产生影响,考虑土体状态可使回归模型的预测结果更接近真实值,但对本文推荐模型拟合优度的变化存在不确定性。
4) 剪切波波速与深度的相关性具有明显的地域性特征,襄阳地区各土类剪切波波速的回归模型较全国土类模型具有更好的预测精度和误差平稳性,可为该地区岩土工程的施工提供土层剪切波波速参考。
影响土层剪切波波速的因素是多样的,如土体类型、土层埋深、土体状态、场地类别、土层地质成因、地质年代、地貌分区等,本文研究过程中仅考虑了土体类型、埋深及土体状态和场地类别划分等,今后将以相同或相近地质成因钻孔为基础统计单元,再依据场地类别、土体类别及土体状态进行具体细分,建立不同土层、不同条件下剪切波波速与深度的经验公式,使结果更加准确可信。
| [1] |
汪闻韶. 土工地震减灾工程中的一个重要参量: 剪切波速[J]. 水利学报, 1994, 25(3): 80-84 (Wang Wenshao. An Important Parameter in Geotechnical Engineering for Earthquake Disaster Mitigation——Shear Wave Velocity[J]. Journal of Hydraulic Engineering, 1994, 25(3): 80-84)
(  0) 0) |
| [2] |
刘红帅, 郑桐, 薄景山, 等. 粘性土剪切波速不确定性的统计分析[J]. 世界地震工程, 2010, 26(增1): 99-103 (Liu Hongshuai, Zheng Tong, Bo Jingshan, et al. Statistical Analysis of Uncertainty for Shear Wave Velocities of Cohesive Soils[J]. World Earthquake Engineering, 2010, 26(S1): 99-103)
(  0) 0) |
| [3] |
战吉艳, 陈国兴, 刘建达. 苏州城区深软场地土剪切波速与土层深度的经验关系[J]. 世界地震工程, 2009, 25(2): 11-17 (Zhan Jiyan, Chen Guoxing, Liu Jianda. Empirical Relationship between Shear Wave Velocity and Soil Depth on Deep Soft Sites in Urban Area of Suzhou City[J]. World Earthquake Engineering, 2009, 25(2): 11-17)
(  0) 0) |
| [4] |
王琦, 刘红帅, 郑桐, 等. 天津地区覆盖土层剪切波速与埋深的相关性分析[J]. 地震工程与工程振动, 2018, 38(6): 190-201 (Wang Qi, Liu Hongshuai, Zheng Tong, et al. Correlation Analysis between Shear Wave Velocity and Depth of Covering Soils in Tianjin[J]. Earthquake Engineering and Engineering Dynamics, 2018, 38(6): 190-201)
(  0) 0) |
| [5] |
李敏, 杨立国, 陈海鹏, 等. 杭州市典型土层剪切波速与埋深间的关系分析[J]. 震灾防御技术, 2020, 15(1): 77-88 (Li Min, Yang Liguo, Chen Haipeng, et al. Relationship between Shear Wave Velocity and Soil Depth of Typical Soil Layers in Hangzhou Area[J]. Technology for Earthquake Disaster Prevention, 2020, 15(1): 77-88)
(  0) 0) |
| [6] |
乔峰, 薄景山, 张兆鹏, 等. 广西柳州地区常见土类剪切波速与埋深之间的相关性[J]. 地震学报, 2020, 42(1): 109-119 (Qiao Feng, Bo Jingshan, Zhang Zhaopeng, et al. Correlation between Shear Wave Velocity and Buried Depth of Common Soils in Liuzhou City of Guangxi Region[J]. Acta Seismologica Sinica, 2020, 42(1): 109-119)
(  0) 0) |
| [7] |
乔峰, 阮雪飞, 王亮, 等. 廊坊地区常规土类剪切波速与埋深之间的相关性[J]. 科学技术与工程, 2023, 23(15): 6 549-6 559 (Qiao Feng, Ruan Xuefei, Wang Liang, et al. Correlation between Shear Wave Velocity and Buried Depth of Conventional Soils in Langfang Area[J]. Science Technology and Engineering, 2023, 23(15): 6 549-6 559)
(  0) 0) |
| [8] |
贺为民, 刘明军, 杨杰. 土层剪切波速与埋深关系统计分析和应用[J]. 地震地质, 2016, 38(4): 937-949 (He Weimin, Liu Mingjun, Yang Jie. Application and Statistical Analysis of Relationship between Shear Wave Velocity and Depth of soil-Layers[J]. Seismology and Geology, 2016, 38(4): 937-949)
(  0) 0) |
| [9] |
孔宇阳, 雷东宁, 廉超, 等. 武汉市区土体剪切波速与深度的经验关系[J]. 地震工程学报, 2017, 39(2): 336-342 (Kong Yuyang, Lei Dongning, Lian Chao, et al. Relationship between Shear-Wave Velocity and Soil Depth in the Wuhan Area[J]. China Earthquake Engineering Journal, 2017, 39(2): 336-342)
(  0) 0) |
2. Wuhan Institute of Earthquake Engineering Co Ltd, 40 Hongshance Side Road, Wuhan 430071, China
 2024, Vol. 44
2024, Vol. 44

