2. 引力与固体潮国家野外观测研究站,武汉市洪山侧路40号,430071;
3. 湖北省地震局,武汉市洪山侧路48号,430071
开展超导重力仪(SG)长期定点观测并保持其持续稳定运行,是获取连续高质量重力数据的重要前提[1]。SG的格值精度是评价其数据观测质量的重要指标之一[2]。目前在用于标定的仪器选择上,几乎所有研究者都使用FG5型绝对重力仪,而未采用A10型绝对重力仪,这可能是由于A10型绝对重力仪精度略低于FG5,标定效果欠佳,但具体差异无从得知。本文利用同期同址的A10-057、FG5X-265及iGrav-053观测数据,基于最小二乘和迭代算法,对比其标定结果差距,以验证A10型绝对重力仪标定SG的可行性。
1 同址观测 1.1 FG5X-265与A10-057的各项指标FG5型绝对重力仪的观测精度优于2 μGal;A10型绝对重力仪的观测精度优于10 μGal,在较好的环境下其观测精度可优于5 μGal。虽然测量原理一致,但这2种仪器的测量方式略有区别,最直接的体现就是激光器不同。FG5型绝对重力仪采用碘稳频氦氖激光器,温度在15~25 ℃范围内,其稳频度最高可达2.5×10-11。而A10型绝对重力仪具有野外快速观测的特点,为使仪器能在户外正常工作,配置了ML-1型偏振氦氖稳频激光器(热稳频激光器)。该激光器通过在激光管中平衡两种TM00模式的强度来获得频率的稳定性,这两种模式都具有线性正交偏振现象,允许使用偏振光学的独立光探测器单独检测两种模式对应激光增益曲线中心两侧的锁定点,即红光模式和蓝光模式[3-4],频率稳定度最高仅达10-9。在仪器测量时,落体组与组之间交替采用红、蓝光模式,可消减温度变化及激光波长慢速线性漂移对观测结果的影响,因此A10型绝对重力仪的测量结果是红、蓝光测量的均值。相比之下,除主要的激光器稳频精度不同外,在落体质量块行程、隔振系统及观测精度等方面,A10型绝对重力仪的性能指标都低于FG5。
湖北省地震局于2022-08采购的4台绝对重力仪均已通过武汉地震计量检定与测量工程研究院有限公司检测,检定时间为2022-06~08与2023-02,检定内容包含测量气压测试、重复性、准确度检验,检定地点为武汉市九峰山洞内[5]。
值得注意的是,A10型绝对重力仪采用偏正稳定的氦氖激光器(ML-1)作为标准距离标尺[6]。经对该类激光的长期标定检验[7]认为,激光频率会以至少1 MHz/a的速率发生变化,进而导致重力值平均每年产生2 μGal的变化[8],因此建议至少每半年对A10型绝对重力仪进行一次激光拍频,以校正其测量值。A10-057在2023-03进行了首次拍频实验,以FG5激光为基准值,分别测试了A10-057红、蓝光与FG5X-265激光数值的差值。结果发现,A10-057蓝光频率为473 612 315.820 MHz,波长为632.991 263 08 nm,与标称频率和标称波长差值分别为-10.233 MHz、0.000 0136 8 nm;A10-057红光频率为473 613 051.560 MHz,波长为632.990 279 75 nm,与标称频率和标称波长差值分别为3.030 MHz、-0.000 004 05 nm;最终绝对重力校正值约为7 μGal。
1.2 FG5标定格值计算原理设在测量时刻i,绝对重力仪输出量重力值gAi为纵轴,超导重力仪输出量电压Vi为横轴,则观测方程为:
| $ g_A^i=K \cdot V_i+D \cdot \mathrm{d} t_i+C $ | (1) |
式中,K为格值因子,D为超导重力仪漂移率,dti为测量时刻i相对起始测量时刻的时间差值,C为待求常数。
令
| $ v=\boldsymbol{B} \tilde{x}-l $ | (2) |
每次测量按等精度定权,采用最小二乘法计算:
| $ \tilde{\boldsymbol{x}}=\left(\boldsymbol{B}^{\mathrm{T}} \boldsymbol{B}\right)^{-1} \boldsymbol{B}^{\mathrm{T}} \boldsymbol{l} $ | (3) |
则格值因子K可由下式算得:
| $ K=\tilde{x}(1) $ | (4) |
如不同时段测量数据的分散性较大,为减小拟合残差,可采用分组加权的方式进行处理。实际中,因超导重力仪在5 d内的漂移可以忽略不计,因此其格值因子可简化为:
| $ K=\Delta g_A / \Delta V $ | (5) |
式中,K为台站重力仪格值因子,ΔgA为绝对重力仪的观测重力值最大变化量(波峰与波谷差值),ΔV为台站重力仪的输出电压最大变化量。
1.3 A10标定格值计算原理A10型绝对重力仪利用红、蓝光测量取均值,才可得到绝对重力的真值,总体计算方法与FG5标定时一致。需要格外注意的是,如何将超导重力仪的测量时间与A10型绝对重力仪的红、蓝光测量均值(即实际重力值)时间匹配一致。本文比较了2种计算模型,即直接利用FG5型绝对重力仪的计算原理,套用A10型绝对重力仪,分别计算红、蓝光测得的绝对重力值均值。第2种模型可表示为:
| $ K_{A 10}=\left(\frac{\Delta g_{A\text {知光 }}}{\Delta V}+\frac{\Delta g_{A\text {蓝光 }}}{\Delta V}\right) / 2 $ | (6) |
本文将详细对比2种标定方法的数值差异。
1.4 格值不确定度计算原理在实际测量中,由于环境及仪器自身误差等影响会造成测量偏差,观测点也无法完全与拟合直线重合。为此引入影响超导格值因子不确定度来源的2个指标:1)由测量重复性引入的标准不确定度u1,其结果等于最小二乘拟合残差的标准差;2)由绝对重力仪和超导重力仪自身引入的不确定度u2。最终不确定度需综合u1和u2的影响进行计算:
| $ u_1=\sqrt{\frac{\boldsymbol{v}^{\mathrm{T}} \boldsymbol{v}}{n-3}} $ | (7) |
| $ u_2=|K| \sqrt{\left(\frac{u_{\Delta g_A}}{\Delta g_A}\right)^2+\left(\frac{u_{\Delta V}}{\Delta V}\right)^2} $ | (8) |
式中,uΔgA为绝对重力仪测得的重力变化量的标准不确定度,uΔV为超导重力仪测得的电压变化量的标准不确定度。最终不确定度为:
| $ u_{\text {综合 }}=\sqrt{u_1^2+u_2^2} $ | (9) |
为获得高精度iGrave-053格值,标定时间选在2023-06-18大潮前后5 d。期间3台仪器架设在相距不到5 m的观测室内,观测环境保持一致,温度恒定为16 ℃,测点重力场变化相同。为使FG5型绝对重力仪与超导重力仪观测保持长时间的一致性与连续性,FG5X-265观测方案如下:每30 min观测1组数据,每组数据单次落体观测时间为10 s,每组120次下落,停测10 min后进行下一组测量,总测量组数249组,共获得29 280个观测值。由于A10型绝对重力仪的测量模式与FG5略有不同,具体测量方案设计如下:每30 min观测1组数据,每组数据单次落体时间为6 s,单次激光60次下落,红、蓝光视为一组共120次下落,与FG5保持一致,红、蓝光间距4 min,每组停测14 min,总测量组数为262组。期间因状态检查停测2次(共计1.5 h),共获得31 440个观测值。
iGrav-053的采样率为1 Hz,为保证AG与SG的变化一致,同址观测时FG5与A10均未扣除固体潮与海潮,保留了原始采集数据。因大潮期间潮汐变化较大,有利于比测精度的提升。测量期间A10-057、FG5X-265与iGrav-053均有零散且偏离较大的误差值,这是由激光问题、环境因素及仪器自身误差等原因引起的,该离散值会影响格值标定精度,计算时需剔除。
2.2 数据处理目前主流潮汐模型参数与大部分标定实验精度均为0.1%或更优,为保证线性拟合的准确性,定义超出拟合结果3倍中误差的点对为异常值,循环迭代计算时去除异常值,再进行最小二乘拟合,直至没有异常值[9-10]。
本次标定中FG5X-265共测得29 280个值,利用迭代循环去除异常值,最终保留28 658个,求得σFG5=63.482 mGal,最终实际迭代次数为5,整体保留率为97.88%。A10-057共测得31 440个值,利用FG5去除模型直接迭代循环去除异常值,最终保留30 888个,求得σA10=126.911 mGal,最终实际迭代次数为8,整体保留率为98.24%。利用红、蓝光测量值分别迭代计算去除异常值,求得σA10红=124.593 mGal,σA10蓝=124.844 mGal,A10-057整体σA10=124.718 mGal,最终保留30 883个值,整体保留率为98.23%。由此可得,在计算模型的选择上,分开计算σA10红、蓝光最终加权平均的结果更接近FG5型绝对重力仪,二者去除异常值前后的对比结果见图 1和2。
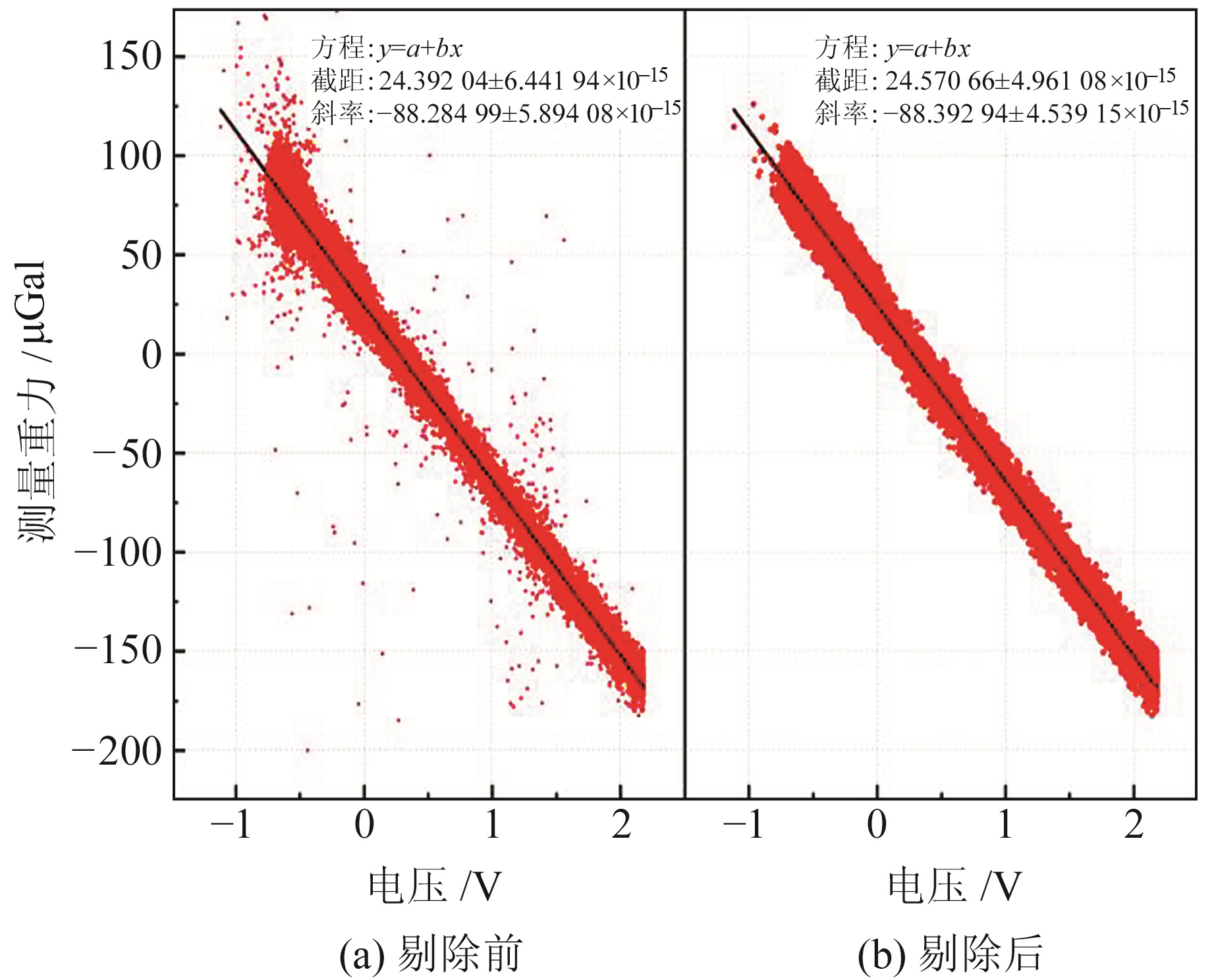
|
图 1 FG5X-265重力观测异常值剔除前后对比 Fig. 1 Comparison of FG5X-265 gravity observation before and after outlier eliminator |
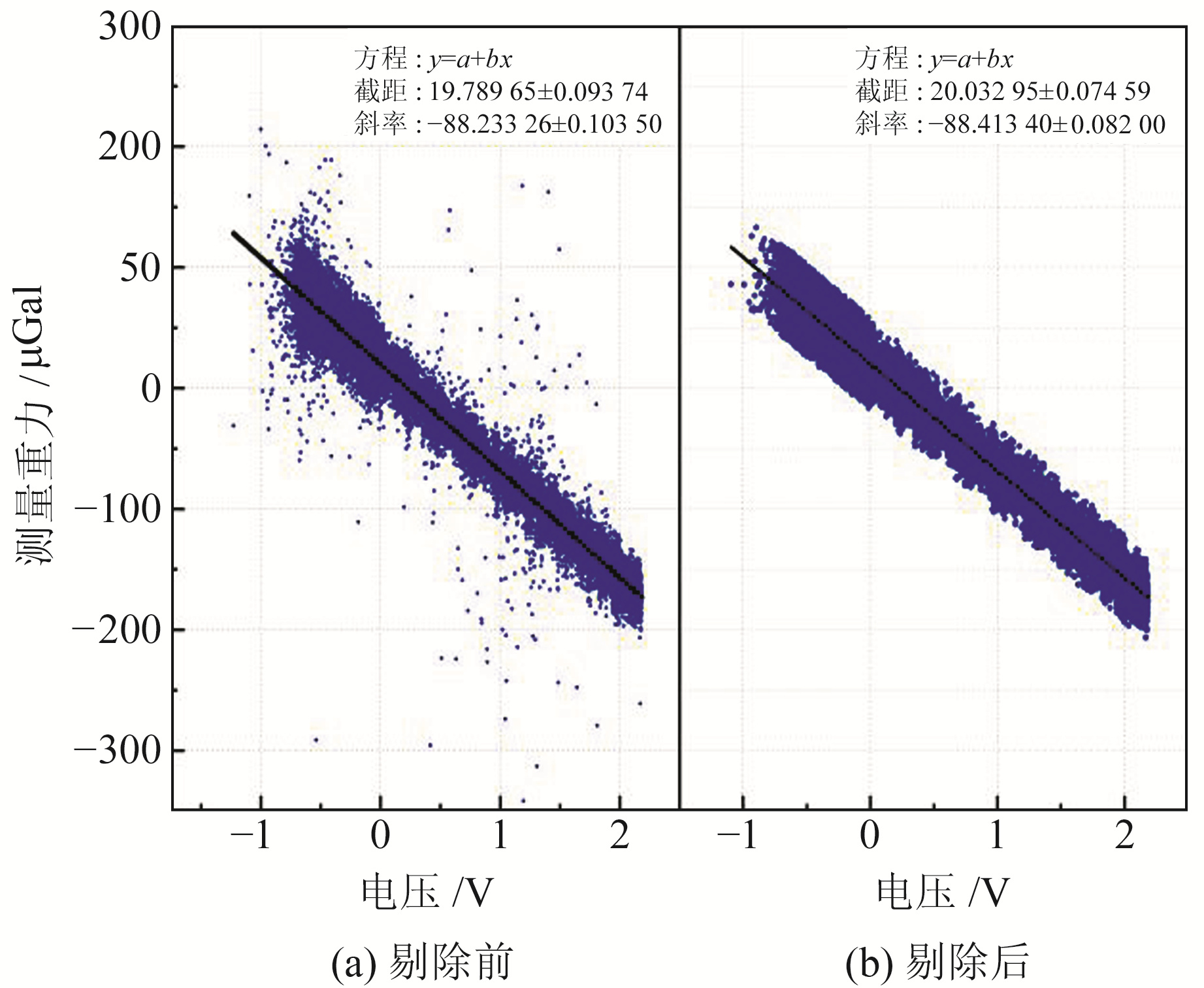
|
图 2 A10-057重力观测异常值剔除前后对比 Fig. 2 Comparison of A10-057 gravity observation before and after outlier eliminator |
总体来看,二者的标定数值相差不大,但A10-057的标准中误差约为FG5X-265的2倍,从95%置信区间来看,A10-057整体残差标准差也约为FG5X-265的2倍。为验证该结论,本文分别计算了σFG5与σA10的正态分布区间,如图 3和4所示。
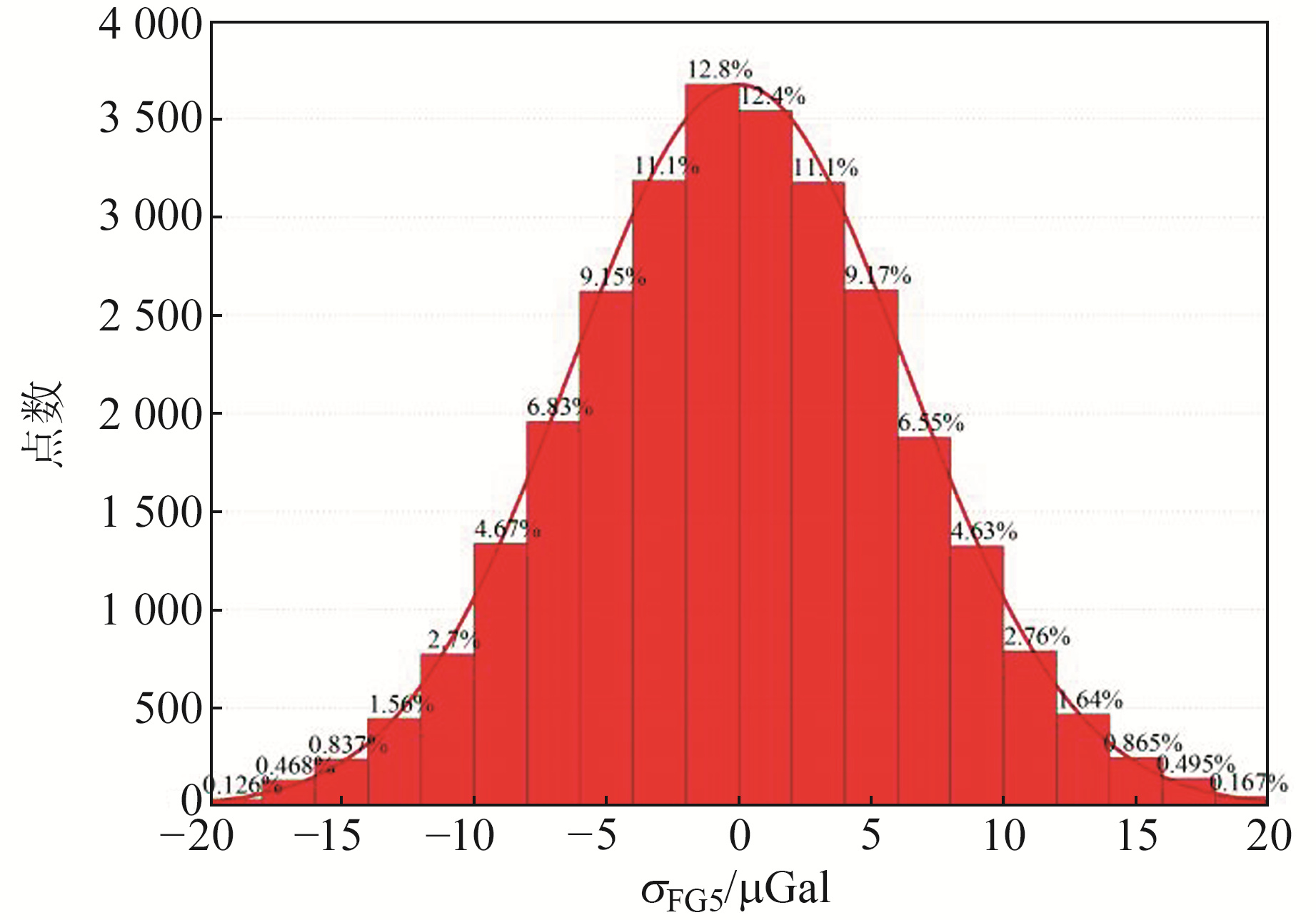
|
图 3 σFG5正态分布 Fig. 3 σFG5 normal distribution |
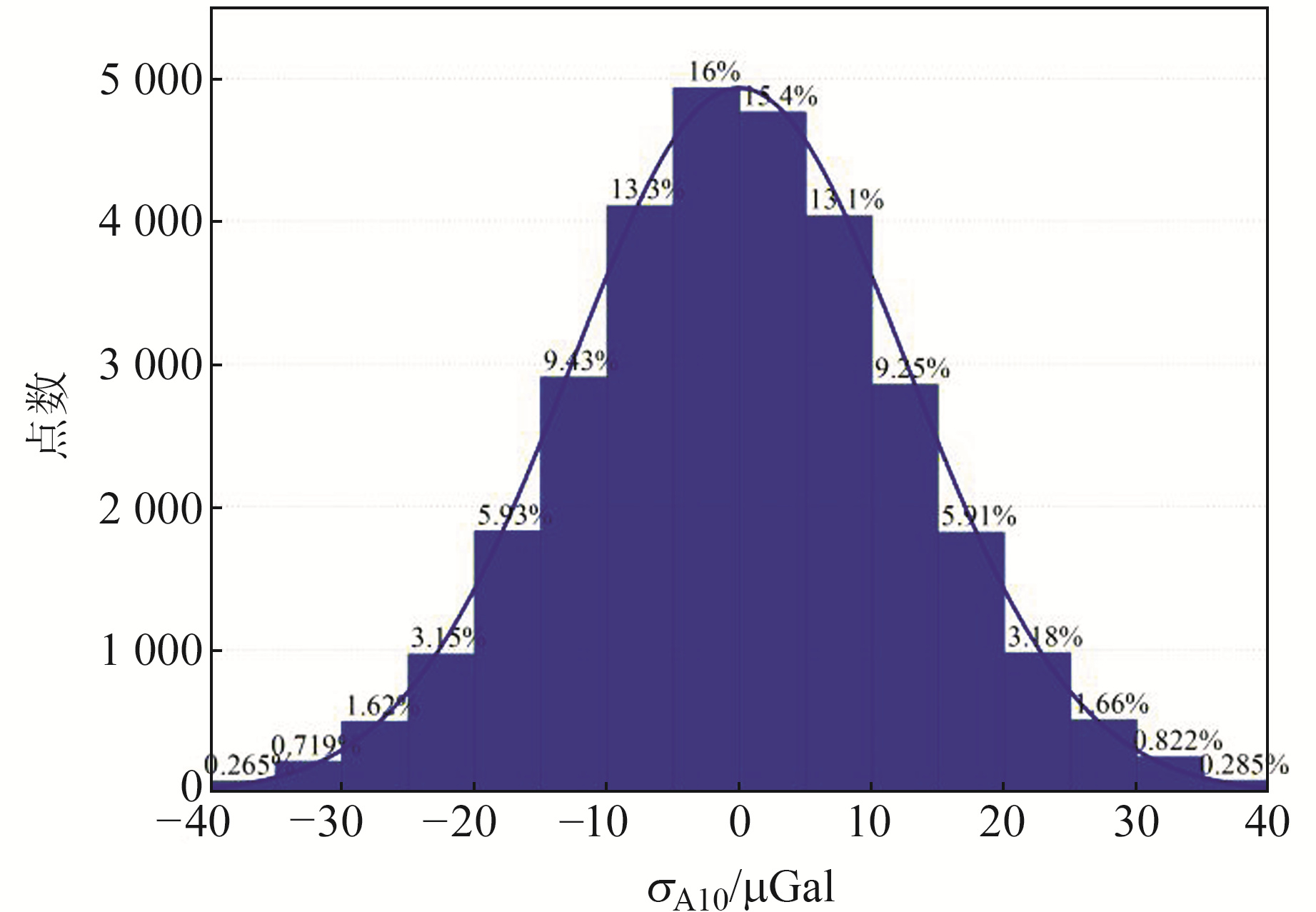
|
图 4 σA10正态分布 Fig. 4 σA10 normal distribution |
根据测量结果,FG5X-265最终测得iGrav-053的格值为-883.929 4 ns-2/V,标定精度为0.0482 6%,优于0.1%;A10-057最终测得的格值为-884.134 ns-2/V,标定精度为0.093 7%,优于0.1%。iGrav-053的原出场格值为-882.9 ns-2/V,2种绝对重力仪标定的格值与出厂格值相近。为计算FG5与A10标定精度的差距,本文分别列举不同次数的测量值,对比其精度与综合不确定度,结果见表 1和图 5。
|
|
表 1 A10-057与FG5X-265标定结果 Tab. 1 Calibration results of A10-057 and FG5X-265 |
|
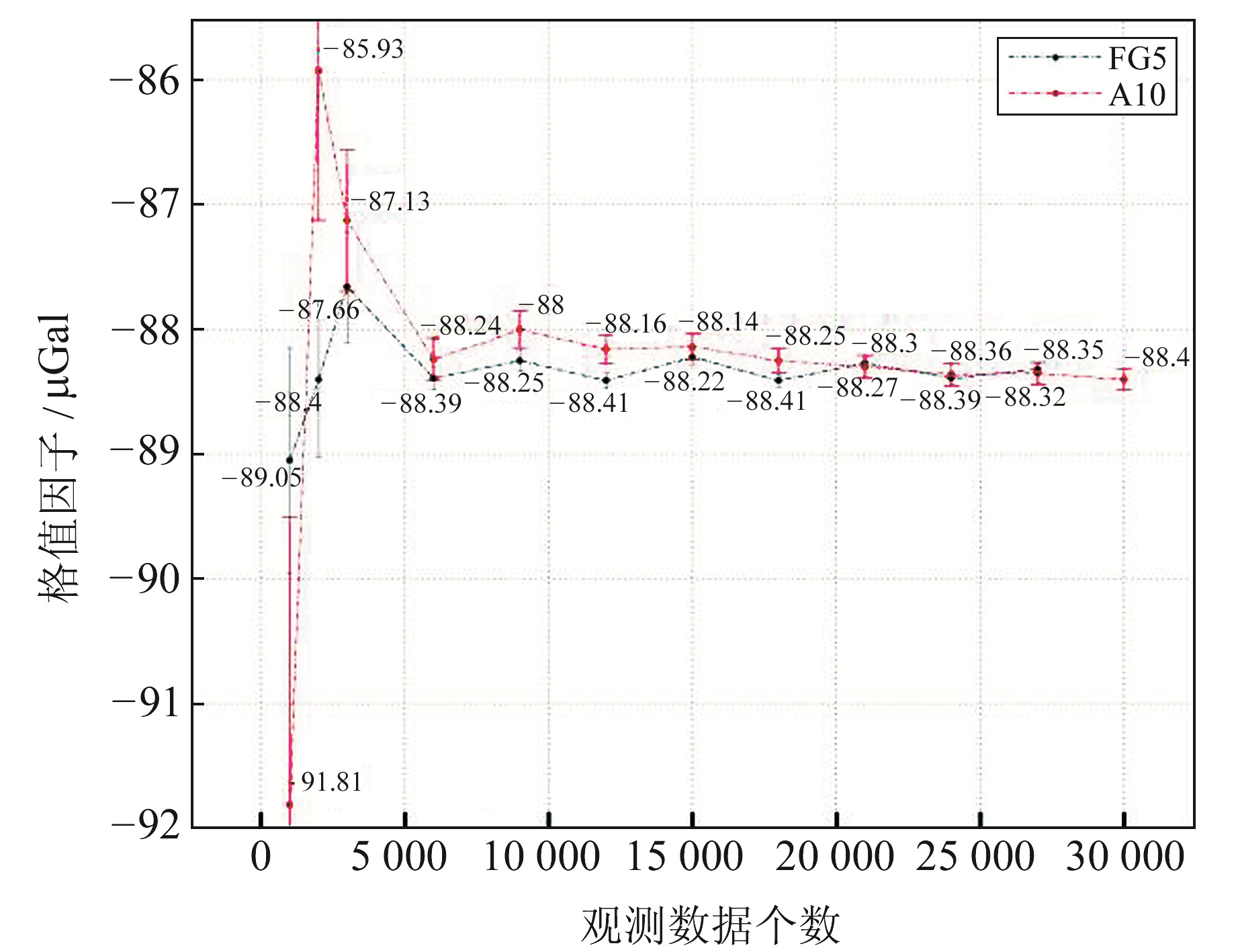
图 5 A10-057与FG5X-265标定结果 Fig. 5 A10-057 and FG5X-265 calibration results |
本文利用FG5X-265与A10-057对iGrav-053在大潮期间进行了连续5 d的标定,结果显示,24 h、72 h及5 d的标定结果精度均优于目前国内外相对重力仪的标定精度,最高可达0.05%。此外,作为对比,A10型绝对重力仪获得的标定精度可满足观测需要。A10稳定观测1 d后格值标定精度收敛于0.2%,4.5 d后优于0.1%。从图 5还可看出,在获取第6 000个测量值后,FG5-265与A10-057的标定结果已非常接近;在获取第21 000个测量值后,二者的标定数值已基本重合。
3 结语当前重力潮汐的变化幅度为350 μGal,格值因子0.2%的变化最大可引起重力潮汐的总变化为0.7 μGal。对于超导重力仪这类超高精度仪器,残差标准差基本小于0.7 μGal,而其他大多数相对重力仪的残差标准差远大于该值。在实际标定工作中,要获得优于0.1% 精度的格值,基本需观测5 d及以上,这对于绝对重力仪的损耗是不可逆的。考虑到A10型绝对重力仪的标定成本较FG5低,在不需要超高精度格值标定的情况下,A10型绝对重力仪可满足格值标定需求。
此外,鉴于在标定工作中由于斜率K基本只与绝对重力值的最大差值Δg、电压最大差值ΔV相关,中间测量值大多为无用值。在未来标定中,可提前计算测量峰值出现时间,并设定测量计划,加大峰值期间测量频率,适当缩短期间停测时间,或在测量g9软件中植入动态测量程序等,以减小标定成本。
致谢: 标定中武汉地震计量检定与测量工程研究院有限公司提供野外测量帮助,中国科学院精密测量科学与技术创新研究院陈晓东副研究员提供基于绝对重力测量的超导重力仪标定方法原理作参考,在此一并表示感谢。
| [1] |
Xing L L, Niu X W, Bai L, et al. Monitoring Groundwater Storage Changes in a Karst Aquifer Using Superconducting Gravimeter OSG-066 at the Lijiang Station in China[J]. Pure and Applied Geophysics, 2022, 179(5): 1 853-1 870 DOI:10.1007/s00024-022-03024-w
(  0) 0) |
| [2] |
Yuichi I. Inertial Effects Due to Eruption-Induced Atmospheric Disturbances Identified by Superconducting Gravimeter Observations at Matsushiro, Japan[J]. Earth, Planets and Space, 2022, 74(1)
(  0) 0) |
| [3] |
张锐, 韦进, 刘子维, 等. 用SGC053超导重力仪观测资料对gPh058重力仪格值的精密测定[J]. 大地测量与地球动力学, 2011, 31(5): 151-155 (Zhang Rui, Wei Jin, Liu Ziwei, et al. Accurate Determination of Scale Value of gPh058 Gravimeter by Use of Observations with SGC053 Superconducting Gravimeter[J]. Journal of Geodesy and Geodynamics, 2011, 31(5): 151-155)
(  0) 0) |
| [4] |
王应建, 邱雪峰, 张松堂, 等. A10/35绝对重力仪测试及性能分析[J]. 海洋测绘, 2015, 35(6): 65-68 (Wang Yingjian, Qiu Xuefeng, Zhang Songtang, et al. Test and Analysis of the A10 /35 Absolute Gravimeter[J]. Hydrographic Surveying and Charting, 2015, 35(6): 65-68)
(  0) 0) |
| [5] |
Zhang X T, Zhou H, Jiang Y, et al. First Acceptance Testing of Multiple A10 Absolute Gravimeters in China and Analysis of the Comparison Results[J]. Geodesy and Geodynamics, 2023, 14(4): 401-410 DOI:10.1016/j.geog.2023.02.001
(  0) 0) |
| [6] |
Micro-g LaCoste Inc. ML-1 Polarization Stabilized Laser[Z]. Colorado: Micro-g LaCosteInc, 2005
(  0) 0) |
| [7] |
Niebauer T M, Faller J E, Godwin H M, et al. Frequency Stability Measurements on Polarization-Stabilized He-Ne Lasers[J]. Applied Optics, 1988, 27(7): 1 285-1 289 DOI:10.1364/AO.27.001285
(  0) 0) |
| [8] |
王林松, 陈超, 王同庆, 等. A-10绝对重力仪野外测量精度分析[J]. 大地测量与地球动力, 2012, 32(1): 60-63 (Wang Linsong, Chen Chao, Wang Tongqing, et al. Analysis of Measuring Accuracy in Field with A-10 Absolute Gravimeter[J]. Journal of Geodesy and Geodynamics, 2012, 32(1): 60-63)
(  0) 0) |
| [9] |
Merlet S, Gillot P, Cheng B, et al. Calibration of a Superconducting Gravimeter with an Absolute Atom Gravimeter[J]. Journal of Geodesy, 2021, 95(5)
(  0) 0) |
| [10] |
Riccardi U, Rosat S, Hinderer J. On the Accuracy of the Calibration of Superconducting Gravimeters Using Absolute and Spring Sensors: A Critical Comparison[J]. Pure and Applied Geophysics, 2012, 169(8): 1 343-1 356 DOI:10.1007/s00024-011-0398-8
(  0) 0) |
2. Gravitation and Earth Tides National Observation and Research Station, 40 Hongshance Road, Wuhan 430071, China;
3. Hubei Earthquake Agency, 48 Hongshance Road, Wuhan 430071, China
 2024, Vol. 44
2024, Vol. 44


