2. 地理国情监测技术应用国家地方联合工程研究中心,兰州市安宁西路88号,730070;
3. 甘肃省地理国情监测工程实验室,兰州市安宁西路88号,730070;
4. 江苏师范大学地理测绘与城乡规划学院,江苏省徐州市上海路101号,221116;
5. 中国矿业大学环境与测绘学院,江苏省徐州市大学路1号,221116
大气水汽作为对流层中较为活跃和较难监测的成分之一,在恶劣灾害天气和暴雨预测中起到关键作用。MODIS具有空间分辨率高、全谱段观测等特点,同时在空间上进行插值可得到面状连续的PWV分布情况,但其精度受云层、地面光谱反射误差等影响,相对误差超过10%[1-2]。GNSS水汽探测技术利用卫星信号传播路径上的大气延迟来反演大气中的水汽含量,其相对精度可达1~2 mm[3-4],但其站点较稀疏,空间分辨率有限,PWV呈离散的空间分布特征。综合GNSS和MODIS两者优势,采用插值方法使MODIS像元点与GNSS测站点完全重合,然后构建合适的校正模型,利用GNSS PWV校正MODIS PWV,提高其精度和可靠性,得到高空间分辨率、连续的PWV。
利用GNSS PWV观测数据通过插值和校正可有效提高MODIS PWV精度[5-6]。在空间插值方面,MODIS像元点与GNSS测站在空间上不完全匹配,需要采用合适的插值方法使两者在空间上一致。胡波等[7]使用反距离加权法、克里金法和径向基函数法对MODIS水汽进行插值实验,但该研究仅使用1 d的MODIS数据,结果精度有限。在水汽校正方面,大多数学者使用最近邻法,且对于GNSS PWV校正MODIS PWV的相关研究主要集中在构建合适的校正模型[8-11],校正后精度可达mm级。
综上,在MODIS水汽校正实验中,插值方法研究较少且多为最近邻法,校正模型多为线性回归模型。基于此,本文对MODIS PWV校正过程中基于1 a的GNSS和MODIS数据,在最近邻法、线性插值三角网法、自然邻点法、三次样条插值法、反距离加权法和克里金法6种插值方法中选取最优插值方法,在线性拟合、多元线性拟合和傅里叶变换非线性校正模型中选取最优校正模型进行研究。
1 研究区域与数据本文采用GNSS PWV和MODIS PWV两种数据,以香港地区为例,研究时段选取2022-01~12,使用不同插值方法估计GNSS测站水汽值,以建立MODIS水汽校正模型。
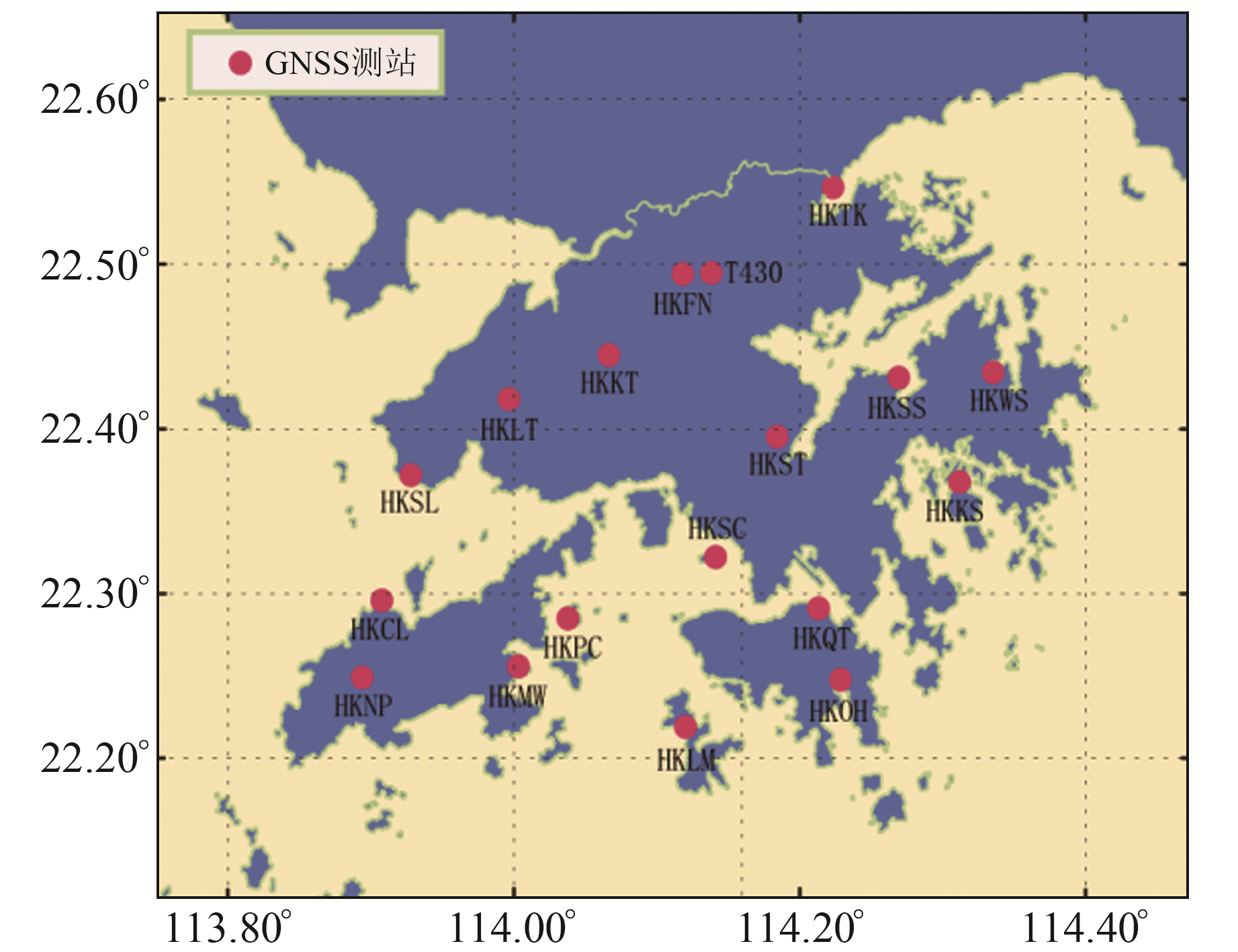
1.1 研究区域本文选取香港地区为研究区域(图 1),范围为113°48′~114°24′E、22°06′~22°36′N。香港地区地处中国南部,位于珠江三角洲,东临南海,西北与广东省接壤。该地区属亚热带季风气候,四季分明,夏季炎热潮湿,冬季相对凉爽干燥。
|
图 1 香港地区GNSS测站位置 Fig. 1 GNSS station location in Hong Kong |
本文使用GAMIT 10.71软件处理GNSS观测数据,结合IGS精密星历和广播星历,引入BAKO、CHAN和GUAM三个IGS辅助站联合解算PWV。其中,对流层延迟可通过映射函数转换到天顶方向上得到天顶总延迟(ZTD),其由天顶静力学干延迟(ZHD)和天顶湿延迟(ZWD)组成。ZHD可通过Saastamoinen模型获得,计算公式为:
| $ \mathrm{ZHD}=\frac{2.2767 \times P}{1-0.00266 \cos (2 \varphi)-0.00028 \times H} $ | (1) |
式中,P表示气压,单位mbar;H表示测站水准高,单位km;φ表示测站纬度。ZTD减去ZHD可得到ZWD,并且根据公式PWV=Π×ZWD计算得到PWV,其中Π由Bevis公式[12]决定。
本文采用香港连续运行参考站(CORS)中17个测站的GNSS观测数据进行实验,站点位置如图 1所示,GAMIT软件解算策略见表 1。解算后的GNSS PWV精度可达1~2 mm,满足气象科学研究需求。
|
|
表 1 GAMIT 10.71解算策略 Tab. 1 Calculation strategy of GAMIT 10.71 |
在MODIS数据中,第17(0.905 μm)、18(0.936 μm)、19(0.940 μm)通道对于水汽反演具有较高的灵敏度,这3个波段受大气水汽吸收和散射的影响较大,因此可用于反演大气水汽含量。MODIS水汽产品由美国航空航天局(NASA)提供,包括Terra卫星平台的MOD05_L2和Aqua卫星平台的MYD05_L2两种水汽产品。2种产品为同一地区不同观测时段的水汽观测数据,包括红外和近红外2种水汽产品,近红外水汽产品的分辨率为1 km×1 km,红外水汽产品的分辨率为5 km×5 km。MODIS红外产品数据在昼夜均可提供,本文使用5 km×5 km分辨率的红外水汽产品开展实验。MOD/MYD05_L2产品包括每个像元的经纬度、扫描时间、太阳天顶角、太阳方位角、近红外水汽观测值、红外水汽观测值及云掩膜产品等多个参数信息,本文利用云掩膜产品将置信区间大于95%的红外水汽产品挑选出来[13],得到香港地区2022-01~12质量较好的MOD05和MYD05红外影像。
GNSS PWV时间分辨率为5 min,而MODIS PWV时间分辨率远远低于GNSS PWV。故本文以MODIS PWV时间作为参考,选择与MODIS时间对应的GNSS时间进行观测。
2 融合反距离加权和傅里叶变换的MODIS水汽校正方法本文基于GNSS PWV对MODIS PWV进行校正,对每个GNSS测站附近的MODIS像元点按照与GNSS测站的距离进行排序,并根据距离优先级筛选合适的MODIS像元点数量,使用6种插值方法分别估计GNSS测站的水汽值,开展GNSS PWV与MODIS PWV相关性分析,以此建立MODIS水汽校正模型,同时构建线性拟合模型、多元线性拟合模型和傅里叶变换模型,并对模型可靠性进行分析。基于此,本文提出一种融合反距离加权和傅里叶变换(FIDWFT)的MODIS水汽校正方法。
2.1 区域MODIS PWV产品空间插值 2.1.1 插值方法对比GNSS PWV与MODIS PWV在空间上不一致,因此需要对MODIS PWV进行插值,进而对MODIS PWV与GNSS PWV进行空间配准。本文对每幅遥感影像的MODIS像元点至GNSS测站的距离进行排序,选取距离和最小的1~20个MODIS像元点,分别采用6种不同的插值方法对MODIS PWV进行比较分析,根据均方根误差(RMSE)、标准差(STD)、平均偏差(MB)、平均相对误差(MRE)和相关系数来评价插值方法的效果。图 2为采用6种插值方法选取1~20个所有参数的综合相关性分析,可以看出,每种插值方法得到的MODIS PWV均与GNSS PWV总体变化趋势一致,相关性良好,但误差离散程度较大,并且反距离加权法的相关性最强。同时,不同插值方法选取参与插值的参数不同,散点图的疏密程度也不同。

|
图 2 不同插值方法下的GNSS PWV与MODIS PWV相关关系 Fig. 2 Correlation between GNSS PWV and MODIS PWV under different interpolation methods |
表 2为香港地区17个测站选取不同插值方法的GNSS PWV与MODIS PWV相关性分析,可以看出,2022年该地区GNSS PWV与MODIS PWV相关性较好,但RMSE、STD和MRE误差较大。最近邻法(nearest)仅考虑最近点对插值点的影响,误差最大,相关性最差;线性插值三角网法(TLI)会将研究区数据均匀分配,未考虑区域内不同站点水汽的差异性;自然邻点法(natural)基于Delaunay三角网和Voronoi图,插值点权重受邻点权重平均值影响;三次样条插值法(cubic)采用分段插值,无法保证整个研究区插值点的光滑性;反距离加权法(IDW)采用插值点与样本点的距离作为权重,考虑了水汽分布的差异性;克里金法(Kriging)考虑了插值点与样本点之间的距离及空间关系,但该方法计算量较大,容易产生极值。综合来看,插值效果由好到坏依次为:IDW、Kriging、natural、TLI、cubic、nearest。
|
|
表 2 MODIS PWV与GNSS PWV的相关性与误差统计 Tab. 2 Correlation and error statistics of MODIS PWV and GNSS PWV |
本文参数指MODIS像元点参与插值的数量。在插值过程中,根据实验内容选取合适的参数可以提高插值结果的准确性和可靠性,若不对实验结果中的插值参数进行分析,往往会忽略其他因素对数据的影响,进而导致插值结果偏差较大。因此,本文对每幅遥感影像的MODIS像元点至GNSS测站的距离进行排序,选取距离和最小的1~20个参数,每个参数可以使用的插值方法不同,误差统计结果也不同。
图 3为选取不同参数插值得到的MODIS PWV与GNSS PWV误差统计。在实验中,1个参数只能使用nearest插值,得到的MODIS PWV与GNSS PWV相关性较低,误差较大;2个参数使用IDW插值,相比1个参数其RMSE和MB有所降低;3个参数可使用natural、IDW和Kriging插值,插值精度存在差异,其中natural插值效果最差;4~20个参数可使用TLI、natural、cubic、IDW和Kriging插值,其中TLI、natural、cubic在选取4个参数时插值效果较好,同时RMSE和MB误差较小,其后随着参数的增加,相关系数和RMSE开始趋于稳定,MB逐步减小;IDW插值误差随选取参数数量的增加而逐渐减小;Kriging插值误差随选取参数数量的增加而逐渐减小,并在选取11个参数时误差趋于稳定。可以看出,6种插值方法在选取4~11个参数时插值效果最好,随着插值参数数量的增加,RMSE和MB会出现先逐步下降趋于稳定,后误差缓慢增大的现象。

|
图 3 不同插值参数数量的MODIS PWV与GNSS PWV误差统计 Fig. 3 Error statistics of MODIS PWV and GNSS PWV for different interpolation parameters |
综上所述,随着参数数量的增加,插值复杂度也随之增加,可能会出现过拟合现象,从而使插值效果不佳,误差开始增大。根据本文实验结果,插值参数选取4~11时效果最佳,插值方法选择IDW、Kriging和natural精度最高。选取不同的参数和不同的插值方法得到的MODIS PWV与GNSS PWV相关关系不同,均存在一定误差,因此有必要选择合适的模型来校正MODIS PWV。
2.2 区域MODIS PWV产品校正 2.2.1 MODIS PWV校正模型由前文可知,GNSS PWV与MODIS PWV之间并非是简单的线性关系,利用GNSS PWV校正MODIS PWV可以提高大气水汽的估算精度,更好地反映水汽时空变化。使用不同的插值方法得到的MODIS PWV与GNSS PWV相关性均较低,因此需要根据实际情况采用不同的校正模型。本文利用GNSS PWV对插值得到的MODIS PWV进行模型构建,经过实验对比,构建线性拟合模型(LT)、多元线性拟合(MLT)和傅里叶变换(FT)模型,结果如图 4所示。需要注意的是,FT模型具有周期性变化,而研究区PWV值很少超过90 mm,故FT模型只在PWV低于90 mm时可用。

|
图 4 3种拟合模型散点图 Fig. 4 Scatter diagram ofthe three fitting models |
上述模型的表达式分别为:
| $ \text {PWV}_{ \text {MODIS}_{\text {校正 }}}= p_0+p_1 \times \text {PWV}_{ \text {MODIS}_{\text {初始 }}} $ | (2) |
| $ \begin{array}{c} \text {PWV}_{ \text {MODIS}_{\text {校正 }}}= p_0+p_1 \times \text {PWV}_{ \text {MODIS}_{\text {初始 }}}+ \\ p_2 \times \text {PWV}_{ \text {MODIS}_{\text {初始 }}}^2 \end{array} $ | (3) |
| $ \begin{array}{c} \text {PWV}_{ \text {MODIS}_{\text {校正 }}}= \\ p_0+p_1 \times \cos \left(\mathrm{PWV}_{ \mathrm{MODIS}_{\text {初始 }}} \times w\right)+ \\ p_2 \times \sin \left(\mathrm{PWV}_{ \mathrm{MODIS}_{\text {初姶 }}} \times w\right) \end{array} $ | (4) |
其中,式(2)为线性拟合模型,式(3)为多元线性拟合模型,式(4)为傅里叶变换模型;PWVMODIS校正为GNSS测点处校正后的MODIS PWV;PWVMODIS初始为校正前的MODIS PWV;p0为常数项;p1~p2为模型系数;w为傅里叶变换模型的角频率。所构建模型的各个参数如表 3所示。
|
|
表 3 MODIS PWV校正模型 Tab. 3 MODIS PWV correction model |
本文以GNSS PWV为标准,分别对将LF模型、MLF模型和FT模型应用于不同插值方法得到的MODIS PWV进行校正模型精度评价。由表 4可知,FT模型精度最高,每种插值方法的精度均有所提升,nearest、TLI、natural、cubic、IDW和Kriging的RMSE改进率分别为74.5%、73.4%、72.9%、74.2%、69%和71.6%;MLF模型的RMSE均有所降低,平均改进率为59.7%;LF模型校正效果较不理想,6种插值方法的RMSE平均改进率为21.9%。在FT模型中,使用IDW插值的拟合效果最好,RMSE为2.3 mm,MB为0.75 mm,误差最小。
|
|
表 4 MODIS PWV校正模型精度 Tab. 4 Accuracy of MODIS PWV correction model |
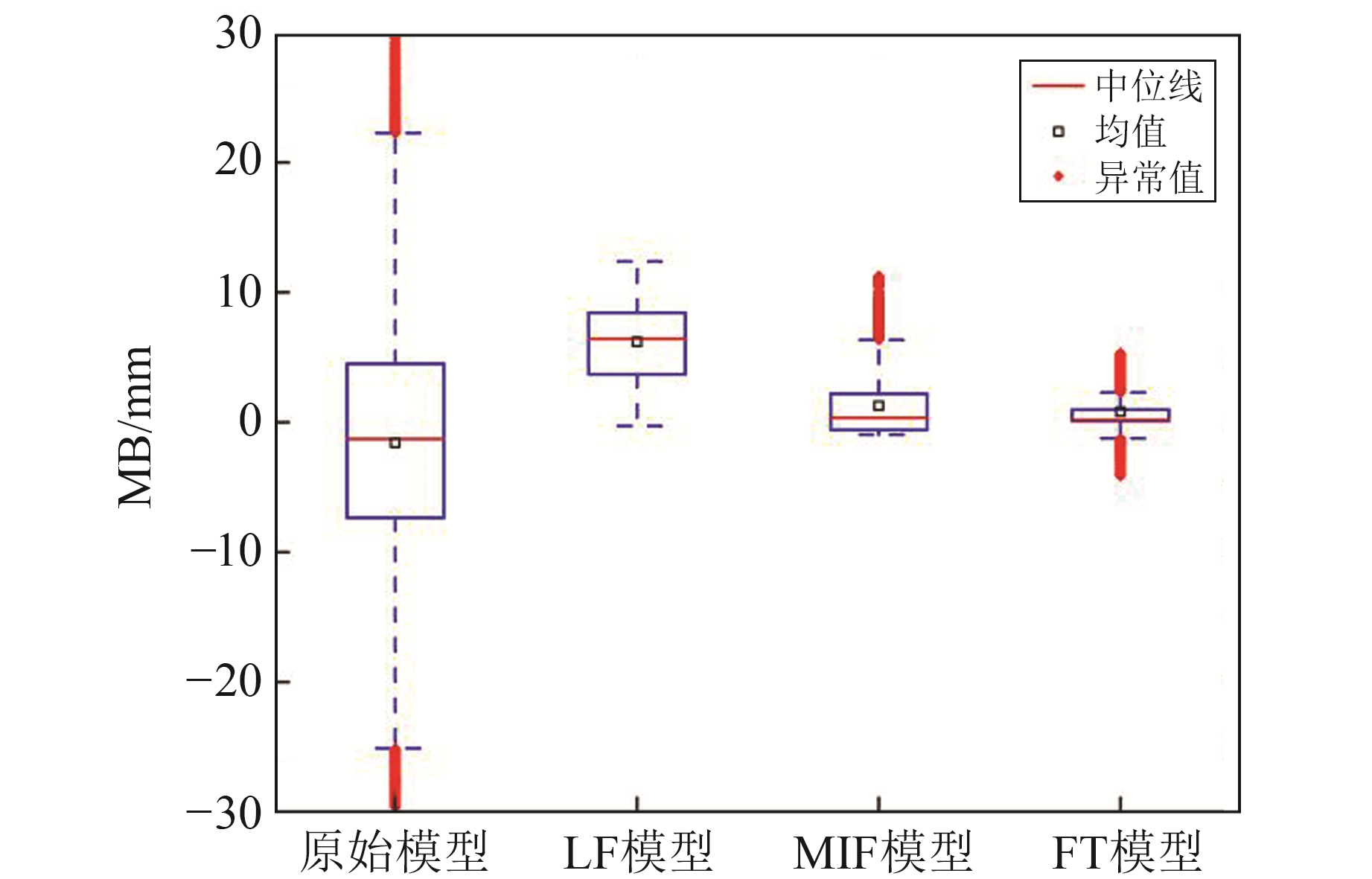
图 5为使用3种校正模型与原始数据的整体偏差箱形图,可以看出,LF模型的中位线较偏,远大于0,但几乎无异常值;MLF模型的均值和中位线均在0上方;FT模型的均值和中位线均在0附近,误差比较集中,异常值分布均匀。在3种校正模型中,FT模型误差呈近似对称分布,上下边界的绝对值更小,说明FT模型相对其他模型具有良好的鲁棒性。
|
图 5 MODIS校正模型与原始数据箱形图 Fig. 5 Box diagram of MODIS correction model and original data |
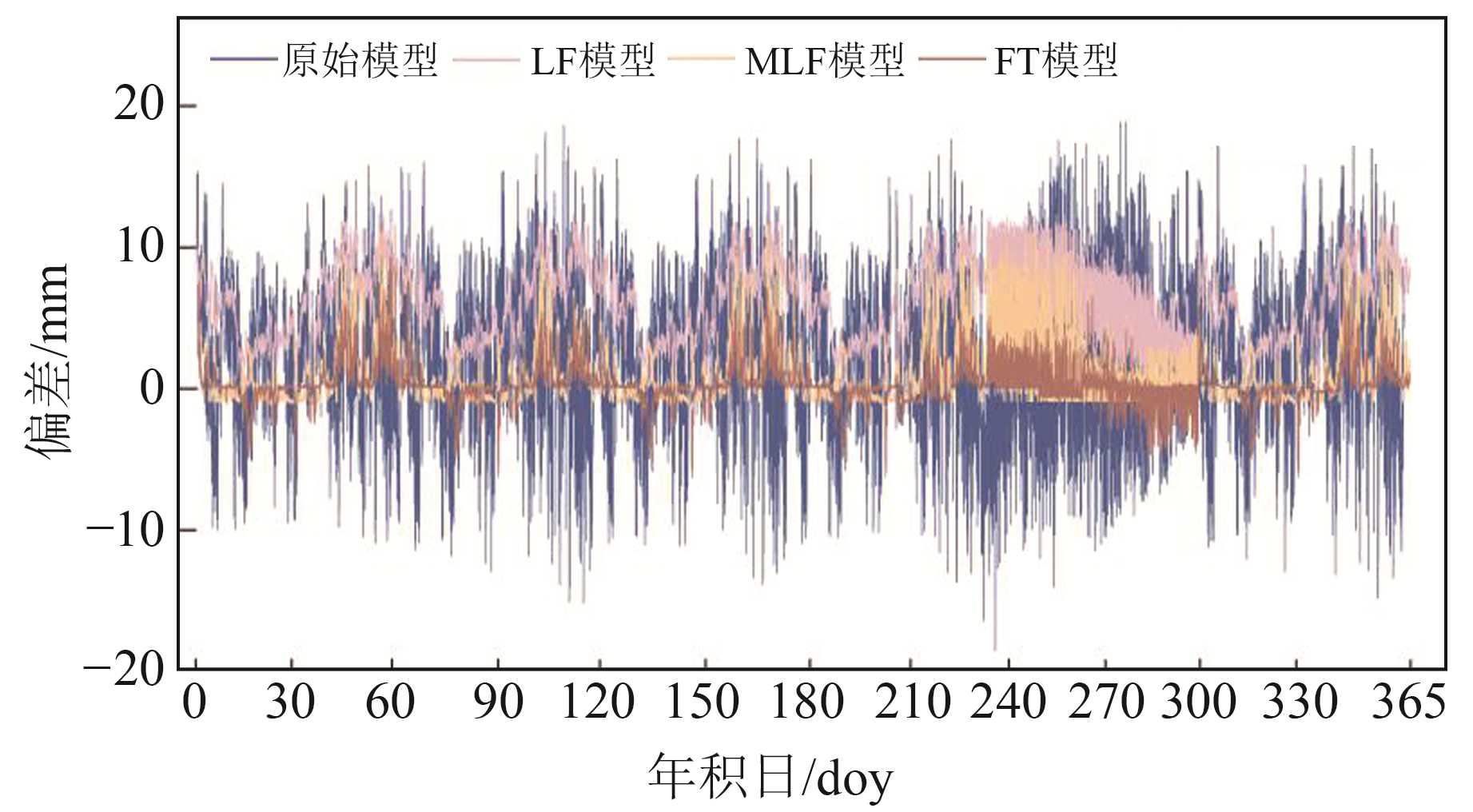
本文选取5个插值参数,分别使用nearest、TLI、natural、cubic、IDW和Kriging六种不同插值方法获取MODIS PWV,同时分别组合LF模型、MLF模型和FT模型对MODIS PWV进行校正。图 6为MODIS PWV校正前后的误差时间序列,可以看出,FT模型精度最高,其次为MLF模型,LF模型误差较大。表 5为不同模型组合校正前后的误差统计情况,可以看出,IDW和FT组合模型(IDW+FT)精度最高,误差最小;其次为Kriging和FT组合模型(Kriging+FT)、natural和FT组合模型(natural+FT)、TLI和FT组合模型(TLI+FT),RMSE均低于2.43 mm,STD均低于12.05 mm,MRE均在4.0%以下;cubic和FT组合模型(cubic+FT)及nearest和FT组合模型(nearest+FT)精度最低,误差分布最不稳定。
|
图 6 不同模型校正前后的时间序列 Fig. 6 Time series of different correction models before and after correction |
|
|
表 5 不同模型组合校正前后的误差统计 Tab. 5 Error statistics of different correction model combinations before and after correction |
本文基于GNSS水汽数据,以香港地区为研究区,采用6种不同的插值方法根据距离优先级对MODIS PWV进行插值,使其与GNSS PWV在空间点位上一致,同时开展GNSS PWV与MODIS PWV相关性分析,构建融合反距离加权和傅里叶变换的MODIS水汽校正模型,并对该模型进行验证分析,得到以下结论:
1) 空间插值部分,插值参数选取4~11个时效果最优;不同插值方法得到的MODIS PWV与GNSS PWV相关性良好,但误差分布较大,两者之间并非单纯的线性关系,其中插值方法选取IDW时精度最高。
2) 水汽校正部分,采用线性拟合、多元线性拟合和傅里叶变换模型分别构建MODIS水汽校正模型,与原始模型对比发现,傅里叶变换模型精度优于其他2种模型,且在使用傅里叶变换校正模型时,每种插值方法的精度和相关性均有所提升,RMSE平均误差改进率可达73%。
3) 综合MODIS水汽的空间插值和校正问题,本文提出的融合反距离加权和傅里叶变换的MODIS水汽校正模型得到的MODIS水汽精度较高,且具有空间连续性,可有效改善MODIS PWV精度不高的问题,提高校正区域的空间分辨率,更准确地反映该地区的水汽分布情况。
在MODIS水汽校正过程中,傅里叶变换模型精度较高,但在PWV低于90 mm时才可使用该模型,这会限制模型的使用范围,且未在模型中引入误差改正项,在后续研究中有必要对该模型作进一步研究。同时,考虑到水汽存在明显的季节性差异,在后续研究中会延长时间区间,使用不同的插值方法和水汽校正模型,分区域、分季节进行周期性分析,进一步提高MODIS水汽精度,拓展MODIS水汽的研究价值与意义。
| [1] |
Gurbuz G, Jin S G. Long-Time Variations of Precipitable Water Vapour Estimated from GPS, MODIS and Radiosonde Observations in Turkey[J]. International Journal of Climatology, 2017, 37(15): 5170-5180 DOI:10.1002/joc.5153
(  0) 0) |
| [2] |
Oliveira G, Brunsell N A, Moraes E C, et al. Evaluation of MODIS-Based Estimates of Water-Use Efficiency in Amazonia[J]. International Journal of Remote Sensing, 2017, 38(19): 5291-5309 DOI:10.1080/01431161.2017.1339924
(  0) 0) |
| [3] |
丁楠. 地基GNSS水汽层析关键技术研究[D]. 徐州: 中国矿业大学, 2018 (Ding Nan. Study on the Key Technologies in Ground-Based GNSS Tomography[D]. Xuzhou: China University of Mining and Technology, 2018)
(  0) 0) |
| [4] |
Ware R, Rocken C, Solheim F, et al. Pointed Water Vapor Radiometer Corrections for Accurate Global Positioning System Surveying[J]. Geophysical Research Letters, 1993, 20(23): 2635-2638 DOI:10.1029/93GL02936
(  0) 0) |
| [5] |
McAtee B K, Maier S W. A Comparison of Algorithms for Near-Real Time Water Vapour Retrieval from MODIS[J]. International Journal of Remote Sensing, 2006, 27(23): 5145-5163 DOI:10.1080/01431160600707383
(  0) 0) |
| [6] |
Prasad A K, Singh R P. Validation of MODIS Terra, AIRS, NCEP/DOE AMIP-II Reanalysis-2, and AERONET Sun Photometer Derived Integrated Precipitable Water Vapor Using Ground-Based GPS Receivers over India[J]. Journal of Geophysical Research: Atmospheres, 2009, 114(D5)
(  0) 0) |
| [7] |
胡波, 汪汉胜, 侯建国, 等. 基于MODIS水汽数据改正InSAR中的大气效应[J]. 大地测量与地球动力学, 2013, 33(2): 82-86 (Hu Bo, Wang Hansheng, Hou Jianguo, et al. Correction of InSAR Atmosphere Effect Based on Modis Water Vapor Data[J]. Journal of Geodesy and Geodynamics, 2013, 33(2): 82-86)
(  0) 0) |
| [8] |
张俊东, 陈秀万, 李颖, 等. 基于GPS数据的MODIS近红外水汽改进反演算法研究[J]. 地理与地理信息科学, 2013, 29(2): 40-44 (Zhang Jundong, Chen Xiuwan, Li Ying, et al. Research on Improved Retrieval Algorithm of MODIS Near-IR Water Vapor Based on GPS Data[J]. Geography and Geo-Information Science, 2013, 29(2): 40-44)
(  0) 0) |
| [9] |
王勇, 刘晓, 刘严萍, 等. CMONOC约束下的MODIS水汽分区域函数模型校正[J]. 武汉大学学报: 信息科学版, 2023, 48(2): 224-231 (Wang Yong, Liu Xiao, Liu Yanping, et al. MODIS PWV Correction Based on CMONOC and Regional Function Model[J]. Geomatics and Information Science of Wuhan University, 2023, 48(2): 224-231)
(  0) 0) |
| [10] |
Zhang W Y, Zhang S B, Zheng N S, et al. A New Integrated Method of GNSS and MODIS Measurements for Tropospheric Water Vapor Tomography[J]. GPS Solutions, 2021, 25(2)
(  0) 0) |
| [11] |
Chang L, Gao G P, Jin S G, et al. Calibration and Evaluation of Precipitable Water Vapor from MODIS Infrared Observations at Night[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(5): 2612-2620 DOI:10.1109/TGRS.2014.2363089
(  0) 0) |
| [12] |
Bevis M, Businger S, Herring T A, et al. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research: Atmospheres, 1992, 97(D14): 15787-15801
(  0) 0) |
| [13] |
Li Z H, Muller J P, Cross P. Comparison of Precipitable Water Vapor Derived from Radiosonde, GPS, and Moderate-Resolution Imaging Spectroradiometer Measurements[J]. Journal of Geophysical Research: Atmospheres, 2003, 108(D20)
(  0) 0) |
2. Nation-Local Joint Engineering Research Center of Technologies and Applications for National Geographic State Monitoring, 88 West-Anning Road, Lanzhou 730070, China;
3. Gansu Provincial Engineering Laboratory for National Geographic State Monitoring, 88 West-Anning Road, Lanzhou 730070, China;
4. School of Geography, Geomatics and Planning, Jiangsu Normal University, 101 Shanghai Road, Xuzhou 221116, China;
5. School of Environment and Spatial Informatics, China University of Mining and Technology, 1 Daxue Road, Xuzhou 221116, China
 2024, Vol. 44
2024, Vol. 44

