2. 长江设计集团有限公司,武汉市解放大道1863号,430010;
3. 广州市城市规划勘测设计研究院,广州市建设大马路10号,510000
随着BDS的不断发展,其观测信息日益丰富,观测信号由双频扩展至三频、四频甚至多频。截至2023-02,BDS在轨卫星共45颗,其中15颗BDS-2能播发B1I、B2I和B3I信号,而BDS-3除能播发BII与B3I信号外,还能播发新信号B1C、B2a、B2b,为用户提供定位、导航、授时、星基增强、短报文通信和中轨搜救等服务。截至2022年底,全球能接收到B2b信号的MGEX监测站数量可达120多个,且其对应的可视卫星数基本超过5颗。因此,B2b信号也可作为基础导航信号开展GNSS精密定位和授时服务。
在BDS-3精密授时和时间传递方面,许多学者进行了大量研究工作,且集中于多系统和多频观测数据融合的时间传递技术[1-4],而对作为新信号的B2b用于GNSS高精度定位和授时服务的研究相对较少。且传统PPP授时研究主要将接收机钟差作为白噪声进行估计,忽略了接收机钟差历元间的相关性会吸收部分未被模型化的误差或噪声,进而影响授时精度[5]。因此,本文以基于BDS-3的B2b观测信号对接收机钟差添加随机游走噪声约束,来降低未被模型化噪声的影响,从而更准确地分析B2b观测信号的服务性能。
1 基于B1C/B2b组合观测值的PPP授时模型构建基于BDS-3观测数据,分别开展B1I/B3I、B1C/B2b频点组合定位性能对比及B1C/B2b观测值精密授时测试,在此过程中对接收机钟差的随机模型进行约束,并对其授时性能进行测试分析。
1.1 PPP授时函数模型构建GNSS原始非组合PPP伪距和载波相位观测方程可表示为[6-7]:
| $ \left\{\begin{array}{l} E\left[\Delta P_{\mathrm{r}, f}^{\mathrm{s}}(i)\right]=e_{\mathrm{r}}^{\mathrm{s}} x+m_{\mathrm{r}}^{\mathrm{s}}(i) T_{\mathrm{r}}(i)+\mathrm{d} t_{\mathrm{r}}(i)-\mathrm{d} t^{\mathrm{s}}(i)+\mu_{f} I_{\mathrm{r}, 1}^{\mathrm{s}}(i)+b_{\mathrm{r}, f}-b_{f}^{\mathrm{s}} \\ E\left[\Delta L_{\mathrm{r}, f}^{\mathrm{s}}(i)\right]=e_{\mathrm{r}}^{\mathrm{s}} x+m_{\mathrm{r}}^{\mathrm{s}}(i) T_{\mathrm{r}}(i)+\mathrm{d} t_{\mathrm{r}}(i)-\mathrm{d} t^{\mathrm{s}}(i)-\mu_{f} I_{\mathrm{r}, 1}^{\mathrm{s}}(i)+N_{\mathrm{r}, f}^{\mathrm{s}} \end{array}\right. $ | (1) |
式中,E[]为期望算子;i为对应的历元号;ΔPr, fs(i)和ΔLr, fs(i)分别为第i个历元的伪距和载波相位观测值与计算值之差,上标s为卫星号,下标r为接收机号,下标f为频段号;ers和x分别为卫星至接收机的单位向量及三维坐标向量;dtr(i)为接收机钟差,dts(i)为卫星钟差;mrs(i)为对流层投影函数,Tr(i)为天顶对流层延迟;μf=(λf2/λ12)为其他频率电离层与第一频率间的比值,Ir, 1s(i)第一频率的电离层延迟;br, f为接收机端伪距硬件延迟,bfs为卫星端伪距硬件延迟,Nr, fs为载波相位浮点模糊度,吸收接收机端和卫星端相位硬件延迟。
根据原始观测值进行参数估计,保留所有参数信息。在实际PPP授时观测方程中,伪距硬件延迟和卫星钟差、接收机钟差、电离层延迟及模糊度参数之间存在一定的相关性,对应的法方程无法直接进行参数求解。通常的处理方法是将对应参数进行重组,如式(2)所示:在双频IF组合伪距观测方程中,接收机钟差吸收接收机伪距硬件延迟的IF组合,卫星钟差吸收卫星伪距硬件延迟的IF组合。在相位观测方程式(3)中,基于与伪距公共的接收机和卫星钟差参数,模糊度会吸收剩余伪距硬件延迟的线性组合。
| $ \left\{\begin{array}{l} E\left[\Delta P_{\mathrm{r}, i f 12}^{\mathrm{s}}(i)\right]=e_{\mathrm{r}}^{\mathrm{s}} x+m_{\mathrm{r}}^{\mathrm{s}}(i) T_{\mathrm{r}}(i)+[\tilde{\mathrm{d}}t_{\mathrm{r}}(i)+\underbrace{\alpha_{12} b_{\mathrm{r}, 1}}_{\tilde{\mathrm{d}} t_{\mathrm{r}, i f 12}{(i)}}+\beta_{12} b_{\mathrm{r}, 2}]-[\mathrm{d} t^{\mathrm{s}}(i)+\underbrace{\alpha_{12} b_{1}^{\mathrm{s}}+\beta_{12} b_{\mathrm{s}}^{\mathrm{s}}}_{\tilde{\mathrm{d}}t^{\mathrm{s}}(i)}] \\ E\left[\Delta P_{\mathrm{r}, i f 12}^{\mathrm{s}}(i)\right]=e_{\mathrm{r}}^{\mathrm{s}} x+m_{\mathrm{r}}^{\mathrm{s}}(i) T_{\mathrm{r}}(i)+\underbrace{\left[{\mathrm{d}}t_{\mathrm{r}}(i)+b_{\mathrm{r}, i f 12}\right]}_{\tilde{\mathrm{d}}t_{\mathrm{r}, i f 12}(i)}-\underbrace{\left[\mathrm{d} t^{\mathrm{s}}(i)+b_{if12}^{\mathrm{s}}\right]}_{\tilde{\mathrm{d}}t^{\mathrm{s}}(i)} \end{array}\right. $ | (2) |
| $ \left\{\begin{array}{l} E\left[\Delta L_{\mathrm{r}, f}^{\mathrm{s}}(i)\right]=e_{\mathrm{r}}^{\mathrm{s}} x+m_{\mathrm{r}}^{\mathrm{s}}(i) T_{\mathrm{r}}(i)+\mathrm{d} t_{\mathrm{r}}(i)-\mathrm{d} t^{\mathrm{s}}(i)-\mu_f I_{\mathrm{r}, 1}^{\mathrm{s}}(i)+N_{\mathrm{r}, f}^{\mathrm{s}} \\ E\left[\Delta L_{\mathrm{r}, i f 12}^{\mathrm{s}}(i)\right]=e_{\mathrm{r}}^{\mathrm{s}} x+m_{\mathrm{r}}^{\mathrm{s}}(i) T_{\mathrm{r}}(i)+\mathrm{d} t_{\mathrm{r}}(i)+b_{i f 12}^{\mathrm{s}}-\mathrm{d} t^{\mathrm{s}}(i)-b_{\mathrm{r}, i f 12}+\alpha_{12} N_{\mathrm{r}, 1}^{\mathrm{s}}+\beta_{12} N_{\mathrm{r}, 2}^{\mathrm{s}} \\ E\left[\Delta L_{\mathrm{r}, i f 12}^{\mathrm{s}}(i)+\tilde{\mathrm{d}} t^{\mathrm{s}}(i)\right]=e_{\mathrm{r}}^{\mathrm{s}} x+m_{\mathrm{r}}^{\mathrm{s}}(i) T_{\mathrm{r}}(i)+\tilde{\mathrm{d}} t_{\mathrm{r}, i f 12}(i)+\underbrace{b_{i f 12}^{\mathrm{s}}-b_{\mathrm{r}, i f 12}+\alpha_{12} N_{\mathrm{r}, 1}^{\mathrm{s}}+\beta_{12} N_{\mathrm{r}, 2}^{\mathrm{s}}}_{\tilde{N}_{\mathrm{r}, i f 12}^{\mathrm{s}}} \end{array}\right. $ | (3) |
经参数重组后的消电离层组合双频PPP授时模型可表示为:
| $ \left\{\begin{array}{l} E\left[P_{\mathrm{r}, i f 12}^{\mathrm{s}}(i)+\tilde{\mathrm{d}} t^{\mathrm{s}}(i)\right]=e_{\mathrm{r}}^{\mathrm{s}} x+m_{\mathrm{r}}^{\mathrm{s}}(i) T_{\mathrm{r}}(i)+\tilde{\mathrm{d}} t_{\mathrm{r}, i f 12}(i) \\ E\left[L_{\mathrm{r}, i f 12}^{\mathrm{s}}(i)+\tilde{\mathrm{d}} t^{\mathrm{s}}(i)\right]=e_{\mathrm{r}}^{\mathrm{s}} x+m_{\mathrm{r}}^{\mathrm{s}}(i) T_{\mathrm{r}}(i)+\tilde{\mathrm{d}} t_{\mathrm{r}, i f 12}(i)+\widetilde{N}_{\mathrm{r}, i f 12}^{\mathrm{s}} \end{array}\right. $ | (4) |
在此过程中对应的重组参数的详细表达式为:
| $ \left\{\begin{array}{l} \tilde{\mathrm{d}} t_{\mathrm{r}, i f 12}(i)=\mathrm{d} t_{\mathrm{r}}(i)+b_{\mathrm{r}, i f 12}, \tilde{\mathrm{d}} t^{\mathrm{s}}(i)=\mathrm{d} t^{\mathrm{s}}(i)+b_{i f 12}^{\mathrm{s}} \\ b_{\mathrm{r}, i f 12}=\alpha_{12} b_{\mathrm{r}, 1}+\beta_{12} b_{\mathrm{r}, 2}, b_{i f 12}^{\mathrm{s}}=\alpha_{12} b_{1}^{\mathrm{s}}+\beta_{12} b_{2}^{\mathrm{s}} \\ \widetilde{N}_{\mathrm{r}, i f 12}^{\mathrm{s}}=\alpha_{12} N_{\mathrm{r}, 1}^{\mathrm{s}}+\beta_{12} N_{\mathrm{r}, 2}^{\mathrm{s}}-b_{\mathrm{r}, i f 12}+b_{i f 12}^{\mathrm{s}}, \alpha_{12}=\frac{f_{1}^{2}}{f_{1}^{2}-f_{2}^{2}}, \beta_{12}=\frac{-f_{2}^{2}}{f_{1}^{2}-f_{2}^{2}} \end{array}\right. $ | (5) |
同样地,在B1C/B2b组合观测值对应的消电离层组合PPP授时观测方程中,考虑到精密卫星钟差产品是以B1I/B3I组合观测值解算得到,在构建观测方程时需考虑伪距硬件延迟差异对模型构建的影响。在函数模型推导过程中,分别将B1C和B2b以频率编号f=3和f=4表示,基于3、4频率函数模型的参数重组过程为:
| $ \left\{ {\begin{array}{*{20}{l}} {E\left[ {\Delta P_{{\rm{r}}, if34}^{\rm{s}}(i)} \right] = e_{\rm{r}}^{\rm{s}}x + m_{\rm{r}}^{\rm{s}}(i){T_{\rm{r}}}(i) + {\rm{d}}{t_{\rm{r}}}(i) - {\rm{d}}{t^{\rm{s}}}(i) + {\alpha _{34}}\left( {{b_{{\rm{r}}, 3}} - b_3^{\rm{s}}} \right) + {\beta _{34}}\left( {{b_{{\rm{r}}, 4}} - b_4^{\rm{s}}} \right)}\\ {E\left[ {\Delta P_{{\rm{r}}, if34}^{\rm{s}}(i) + \widetilde {\rm{d}}{t^{\rm{s}}}(i)} \right] = e_{\rm{r}}^{\rm{s}}x + m_{\rm{r}}^{\rm{s}}(i) \cdot {T_{\rm{r}}}(i) + }\\ {\underbrace {\left[ {{\rm{d}}{t_{\rm{r}}}(i) + {\alpha _{34}}{b_{{\rm{r}}, 3}} + {\beta _{34}}{b_{{\rm{r}}, 4}}} \right]}_{{\rm{\tilde d}}{t_{{\rm{r}}, if13}}(i)} + \underbrace {\left( {{\alpha _{12}}b_1^{\rm{s}} - {\alpha _{34}}b_3^{\rm{s}}} \right) + \left( {{\beta _{12}}b_2^{\rm{s}} - {\beta _{34}}b_4^{\rm{s}}} \right)}_{\varOmega _{if12, 34}^{\rm{s}}}} \end{array}} \right. $ | (6) |
| $ \left\{ \begin{array}{l} E\left[ {\Delta L_{{\rm{r}}, if34}^{\rm{s}}(i)} \right] = e_{\rm{r}}^{\rm{s}}x + m_{\rm{r}}^{\rm{s}}(i){T_{\rm{r}}}(i) + {\rm{d}}{t_{\rm{r}}}(i) - {\rm{d}}{t^{\rm{s}}}(i) + {\alpha _{34}}N_{{\rm{r}}, 3}^{\rm{s}} + {\beta _{34}}N_{{\rm{r}}, 4}^{\rm{s}}\\ E\left[ {\Delta L_{{\rm{r}}, if34}^{\rm{s}}(i) + \widetilde {\rm{d}}{t^{\rm{s}}}(i)} \right] = e_{\rm{r}}^{\rm{s}}x + m_{\rm{r}}^{\rm{s}}(i){T_{\rm{r}}}(i) + \widetilde {\rm{d}}{t_{{\rm{r}}, if34}}(i) + \underbrace {{\alpha _{34}}N_{{\rm{r}}, 3}^{\rm{s}} + {\beta _{34}}N_{{\rm{r}}, 4}^{\rm{s}} - {b_{{\rm{r}}, if34}} + b_{if12}^{\rm{s}}}_{\tilde N_{{\rm{r}}, if{\rm{ }}34}^{\rm{s}}} \end{array} \right. $ | (7) |
对于B1C/B2b组合的双频消电离层组合,PPP授时函数模型固定测站坐标后可表示为:
| $ \left\{\begin{array}{l} E\left[\Delta P_{\mathrm{r}, i f 34}^{\mathrm{s}}(i)+\tilde{\mathrm{d}} t^{s}(i)\right]= \\ \quad m_{\mathrm{r}}^{\mathrm{s}}(i) T_{\mathrm{r}}(i)+\tilde{\mathrm{d}} t_{\mathrm{r}, i j 34}(i)+\varOmega_{i f 12, 34}^{\mathrm{s}} \\ E\left[\Delta L_{\mathrm{r}, i f 34}^{\mathrm{s}}(i)+\tilde{\mathrm{d}} t^{\mathrm{s}}(i)\right]= \\ \quad m_{\mathrm{r}}^{\mathrm{s}}(i) T_{\mathrm{r}}(i)+\tilde{\mathrm{d}} t_{\mathrm{r}, i f 34}(i)+\widetilde{N}_{\mathrm{r}, i f 34}^{\mathrm{s}} \end{array}\right. $ | (8) |
值得注意的是,相比于式(4),式(6)中多出一个与频率相关的卫星端伪距偏差参数Ωif12, 34s,包含了不同形式的DCB线性组合信息,对应的卫星端伪距偏差可通过MGEX发布的多模DCB产品进行改正。经DCB改正后,对应的B1C/B2b和B1I/B3I组合函数模型表达形式基本一致,但部分待估参数的具体包含信息存在差异,即接收机钟差分别吸收对应频点的伪距硬件延迟IF组合。此外,参数重组后模糊度参数的表达形式也基本一致,考虑到同样是基于B1I/B3I频率估计的卫星钟差产品,模糊度参数吸收与B1I/B3I相同的卫星端伪距硬件延迟,而吸收的接收机端伪距硬件延迟与其组合观测值类型各自对应。
| $ \begin{aligned} & \varOmega_{i f 12, 34}^{\mathrm{s}}=\left(\alpha_{12} b_{1}^{\mathrm{s}}-\alpha_{34} b_{3}^{\mathrm{s}}\right)+\left(\beta_{12} b_{2}^{\mathrm{s}}-\beta_{34} b_{4}^{\mathrm{s}}\right)= \\ & \quad\left(\mathrm{DCB}_{12}^{\mathrm{s}}-\mathrm{DCB}_{23}^{\mathrm{s}}\right)-\beta_{12} \mathrm{DCB}_{12}^{\mathrm{s}}-\beta_{34} \mathrm{DCB}_{34}^{\mathrm{s}} \end{aligned} $ | (9) |
同样地,各项组合参数的具体表达式为:
| $ \left\{\begin{array}{l} \tilde{\mathrm{d}} t_{\mathrm{r}, i f 34}(i)=\mathrm{d} t_{\mathrm{r}}(i)+b_{\mathrm{r}, i f 34} \\ b_{\mathrm{r}, i f 34}=\alpha_{34} b_{\mathrm{r}, 3}+\beta_{34} b_{\mathrm{r}, 4} \\ \widetilde{N}_{\mathrm{r}, i f 34}^{\mathrm{s}}=\alpha_{34} N_{\mathrm{r}, 3}^{\mathrm{s}}+\beta_{34} N_{\mathrm{r}, 4}^{\mathrm{s}}-b_{\mathrm{r}, i f 34}+b_{i f 12}^{\mathrm{s}} \\ \alpha_{34}=\frac{f_{3}^{2}}{f_{3}^{2}-f_{4}^{2}}, \beta_{34}=-\frac{f_{4}^{2}}{f_{3}^{2}-f_{4}^{2}} \\ \varOmega_{i f 12, 34}^{\mathrm{s}}=\left(\mathrm{DCB}_{12}^{\mathrm{s}}-\mathrm{DCB}_{23}^{\mathrm{s}}\right)- \\ \quad \beta_{12} \mathrm{DCB}_{12}^{\mathrm{s}}-\beta_{34} \mathrm{DCB}_{34}^{\mathrm{s}} \end{array}\right. $ | (10) |
在常规PPP中,接收机钟差一般都作为白噪声逐历元进行参数估计,未充分发掘接收机钟差在相邻历元间变化的特点。考虑到原子钟对应站钟钟差在历元间平稳变化的特征,采用Allan方差计算原子钟稳定性,然后根据稳定性与噪声系数之间的关系,确定精密授时过程对应采样间隔的随机游走噪声,并引入参数估计的随机模型对接收机钟差参数的方差进行更新。对于随机游走噪声,首先提取关于外接原子钟的站钟钟差序列,采用Allan方差分析其不同平滑时间的稳定性;然后根据噪声(调相白噪声q0、调频白噪声q1、调频随机游走噪声q2及调频随机奔跑噪声q3)系数和Allan方差之间的对应关系式(11)拟合得到对应的噪声系数;最后通过式(12)根据采样间隔和噪声系数确定对应采样率的随机游走噪声[8-9]。
| $ \delta_{\text {Allan }}^{2}=3 q_{0} \tau^{-2}+q_{1} \tau^{-1}+\frac{q_{2} \tau}{3}+\frac{1}{20} q_{3} \tau^{3} $ | (11) |
| $ \sigma_{w}^{2}=\left(\delta_{\text {Allan }} \tau c\right)^{2} $ | (12) |
式中,σw2为确定的噪声方差,δAllan2为原子钟对应的Allan方差。基于卡尔曼滤波参数求解过程,结合上一历元的接收机钟差估计值,通过一步预测得到当前接收机钟差一步预测值及其方差:
| $ \left\{\begin{array}{l} \tilde{\mathrm{d}} t_{k, k-1}=\varPhi_{k, k-1} \tilde{\mathrm{d}} t_{k-1} \\ D_{\tilde{\mathrm{d}} t_{k, k-1}}=\varPhi_{k, k-1} D_{\tilde{\mathrm{d}} t_{k-1}} \varPhi_{k, k-1}^{\mathrm{T}}+D_{w_{k-1}} \end{array}\right. $ | (13) |
式中,
附加随机游走噪声的接收机钟差先验约束是将接收机钟差的一步预测方差添加过程噪声信息,然后引入滤波计算过程进行参数求解。
| $ D_{\tilde{\mathrm{d}} t_{k, k-1}}=D_{\tilde{\mathrm{d}} t_{k-1}}+\sigma_{w}^{2} $ | (14) |
式中,σw2为添加的过程噪声方差信息。
2 实验结果与分析基于BDS-3的B1I/B3I和B1C/B2b两组频点进行精密单点定位性能对比,同时开展B1C/B2b组合观测值PPP授时测试分析。在此之前,分析全球范围内能观测到B2b信号的测站分布及可视卫星数,为研究基于B1C/B2b的数据处理提供支持。另外,考虑到氢原子钟相比于石英钟、铯原子钟及铷原子钟具有更高的稳定性,为充分验证添加过程噪声约束前后的授时性能,避免原子钟本身性能对算法结果产生影响,选择性能更优的氢原子钟站点进行测试。在进行授时测试之前,对基于部分外接高性能氢原子钟的测站进行先验信息解算工作,为附加过程噪声的精密授时获取准确的过程噪声约束。
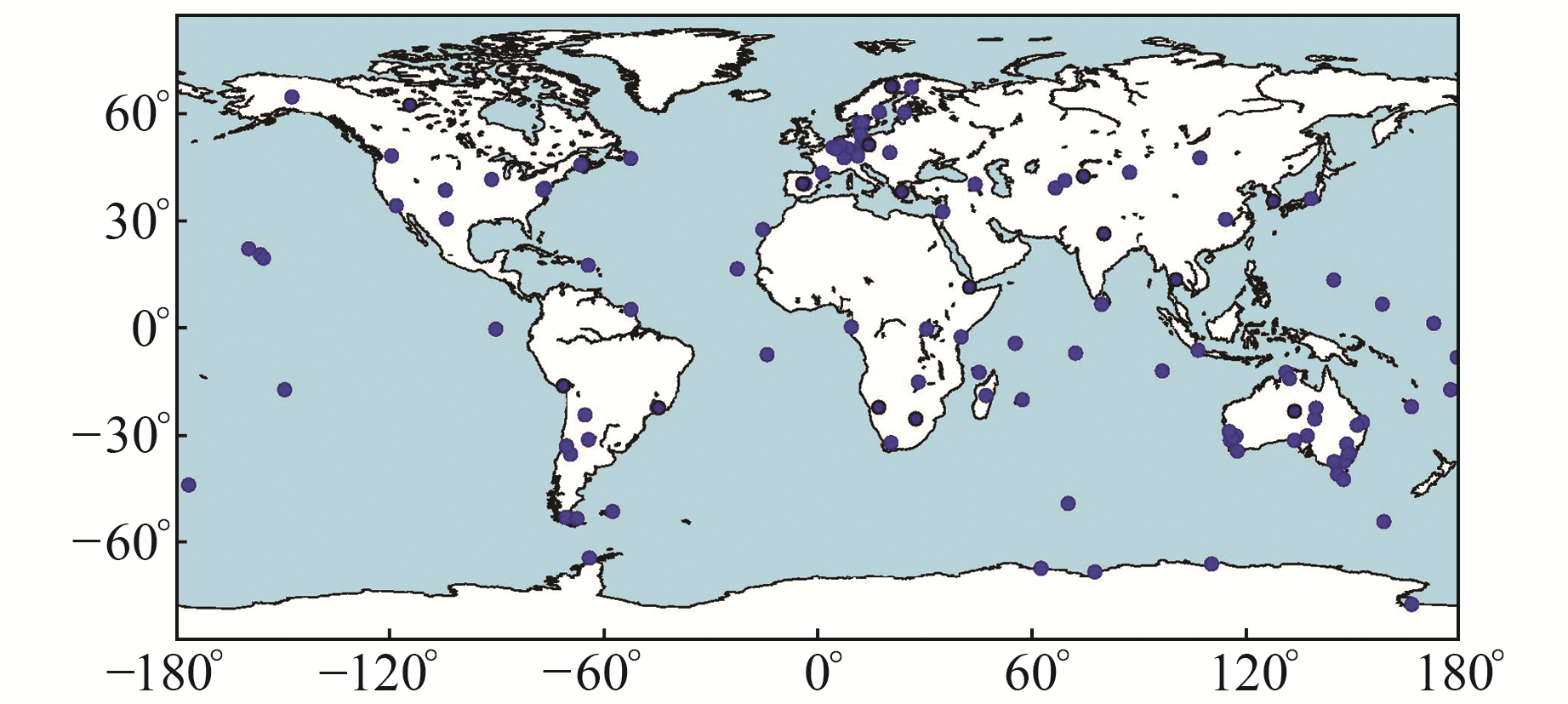
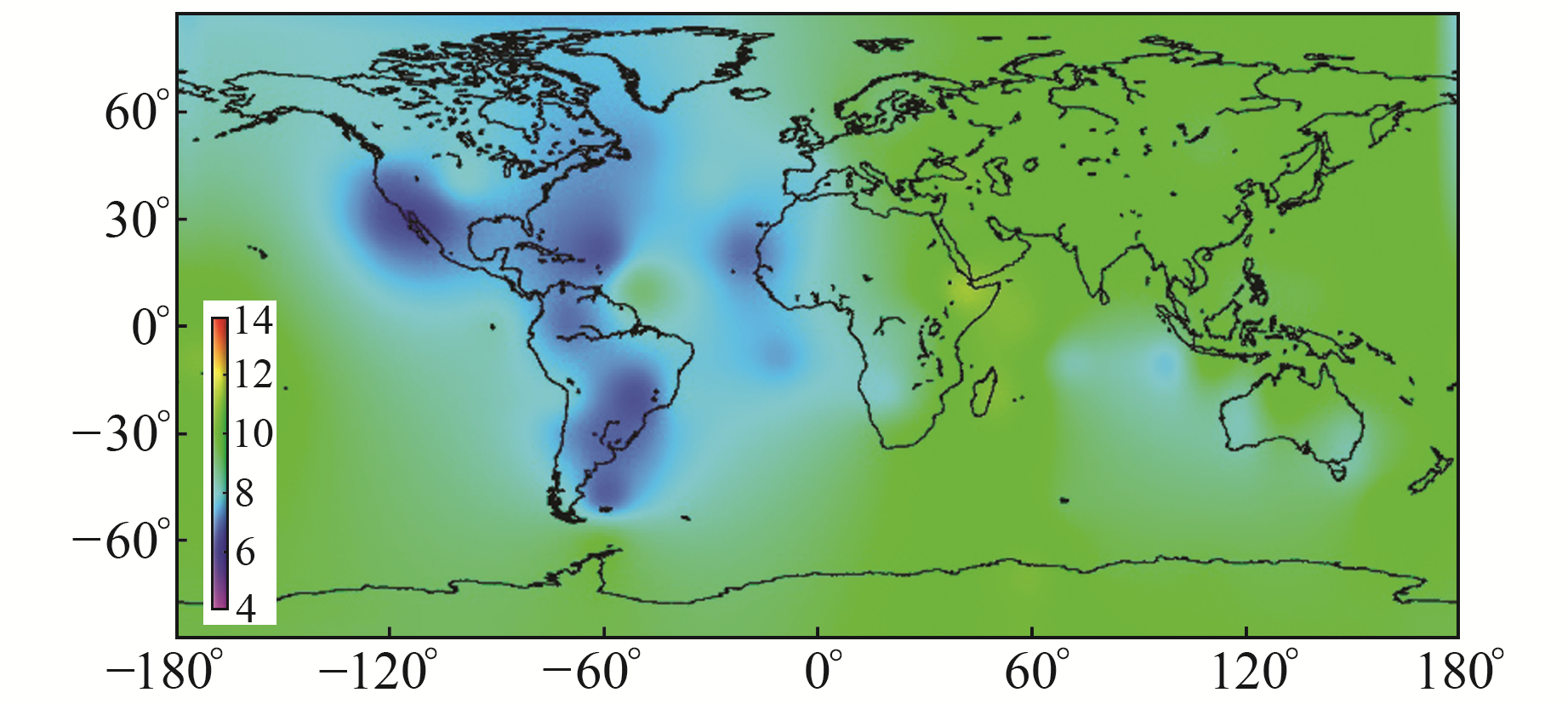
2.1 BDS的B2b观测信息分析本文首先对全球范围内能观测到B2b信号的测站进行统计。截至目前,能观测到播发B2b在内的5频信号的测站多达129个,其站点分布如图 1所示。全球范围内接收B2b信号的监测站点分布较为均匀,亚太地区站点分布相对集中。此外,本文对全球范围内能观测到B2b信号的测站的可视卫星数进行了分析。由图 2可知,亚太地区能观测到B2b信号的卫星数量较多,基本在10颗以上;北美和南美区域观测到该信号的卫星数量相对较少,基本在6~8颗。在全球范围内,能观测到B2b信号的站点可有效支持基于B2b信号的精密单点定位和精密授时服务。
|
图 1 接收B2b信号的MGEX站点分布 Fig. 1 Distribution of MGEX stations track B2b signals |
|
图 2 全球范围内观测到B2b信号的可视卫星数 Fig. 2 The amount of visible satellites track B2b signals on a global scale |
为验证原子钟对应测站接收机钟差历元间的相关性,准确获取过程噪声先验信息,选取9个分布在全球不同区域接收B2b信号外接氢原子钟的MGEX站点,观测时段为2023-01-01~31。基于常规PPP方法在滤波解算过程中将接收机钟差当作白噪声进行处理,然后对解算的接收机钟差序列进行自相关性分析和过程噪声确定。
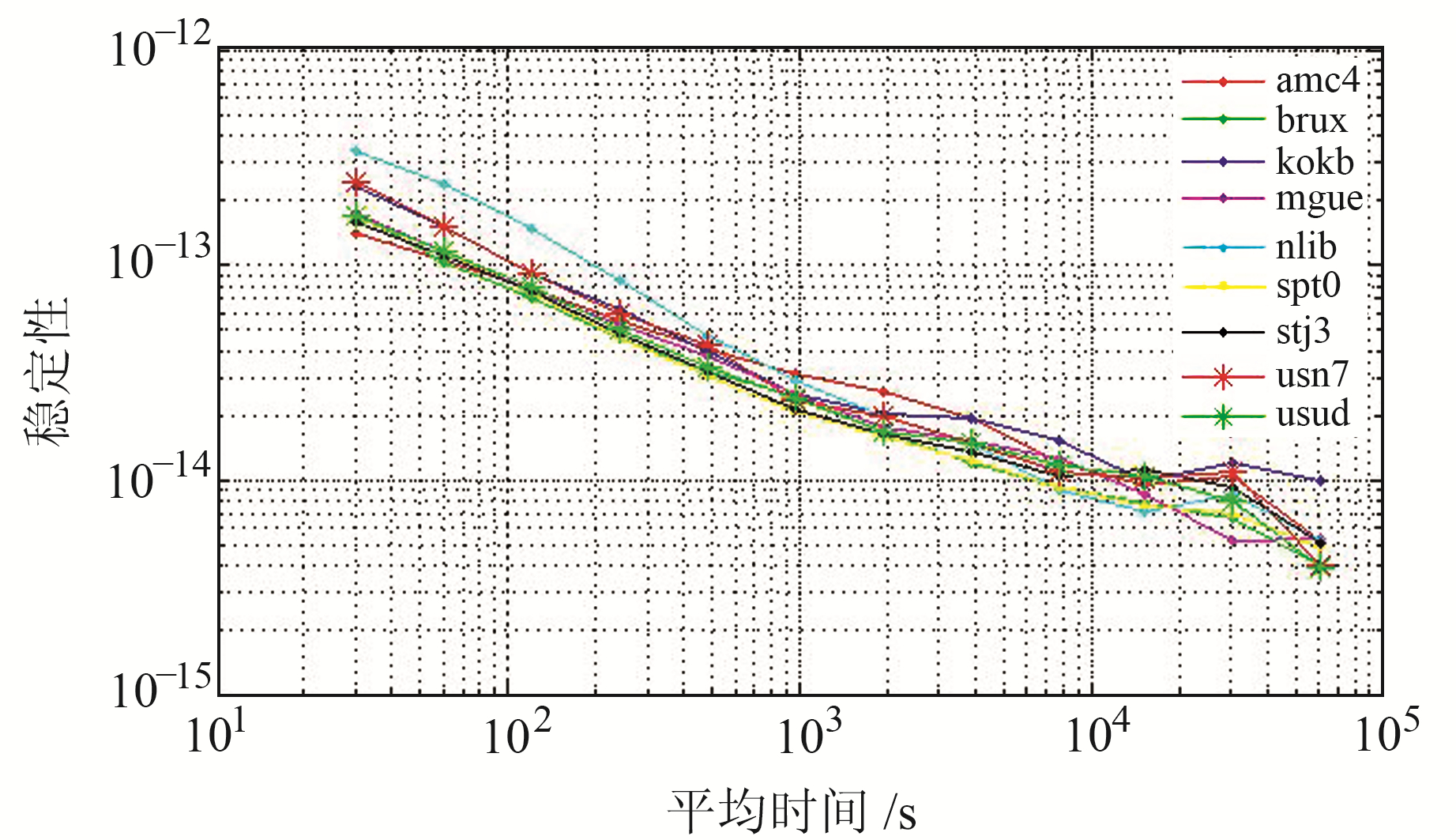
从表 1可以看出,钟差历元间相关性较强,基本在0.91~0.98之间,并且接收机钟差的历元间变化较为平稳,基本都在ps量级。此外,从接收机钟差序列的性能评估分析(图 3)可以发现,外接氢原子钟的接收机钟差稳定性很高,万秒稳能到达10-14量级,天稳基本都在10-15量级。因此可基于历元间强相关性和历元间平稳变化特点,在PPP授时过程中对接收机钟差添加先验信息加以约束,增加对应随机模型强度。
|
|
表 1 接收B2b信号的氢钟站点过程噪声信息 Tab. 1 Process noise of hydrogen clock stations track B2b signals |
|
图 3 接收B2b信号的氢钟站点对应的站钟稳定性 Fig. 3 Stability of station clocks with hydrogen clock track B2b signals |
采用卫星钟差产品中对应的接收机钟差序列,通过式(11)和式(12)可准确获得对应测站的过程噪声信息,对应30 s采样间隔的随机游走噪声基本在2 mm。
2.3 BDS-3精密定位和精密授时性能测试为验证B2b信号在附加先验信息条件下的PPP授时性能,采用前文提及的9个测站进行PPP和精密授时测试,观测时段为2023-01-01~07,测试模型采用双频无电离层组合IF模型。
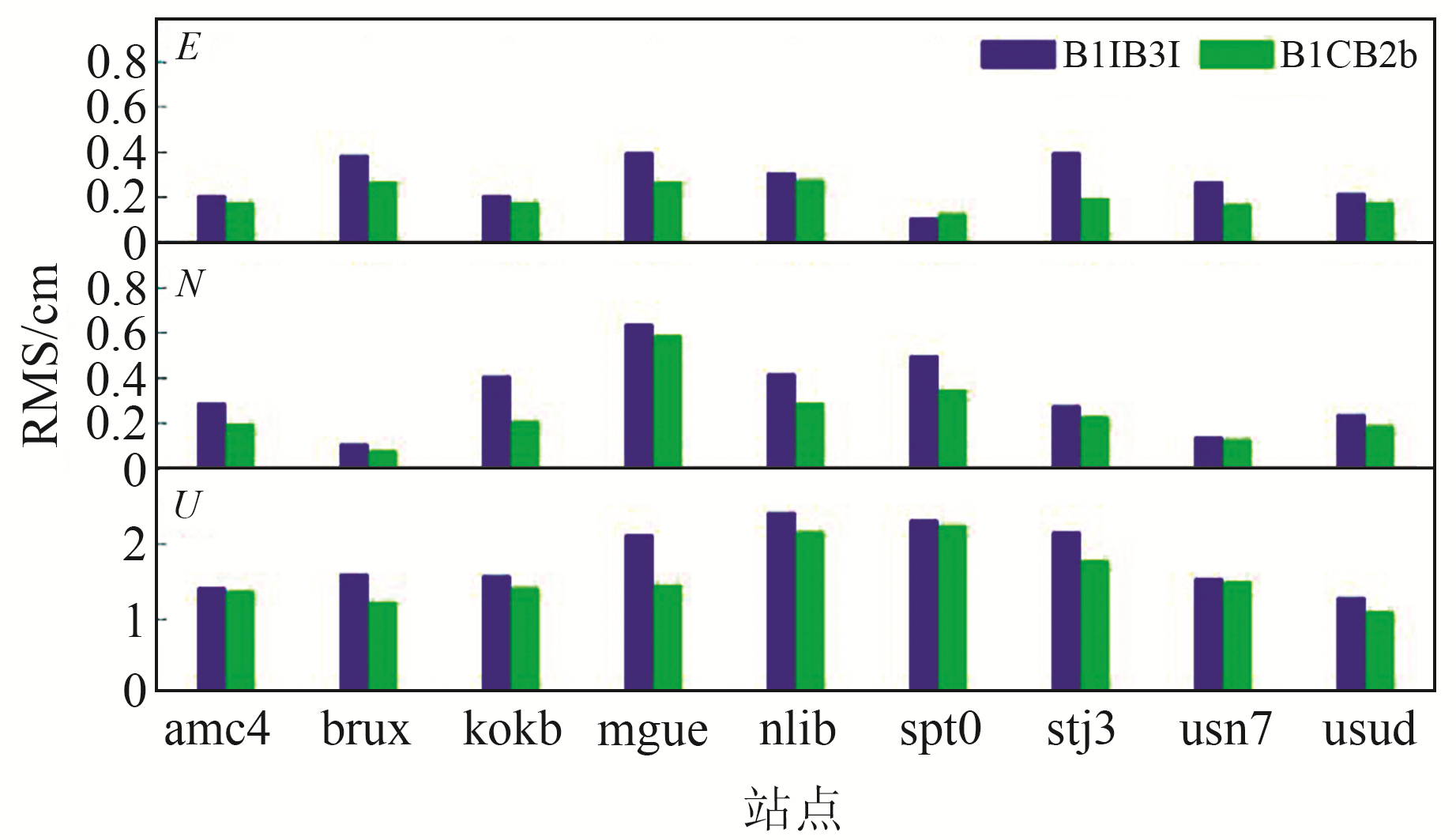
如图 4所示,BDS-3系统的定位精度较为可观,基于观测信号B1I/B3I和新信号B1C/B2b进行静态PPP在不同测站的定位结果存在很好的一致性。B1I/B3I组合在水平N、E方向的定位精度与B1C/B2b基本相当,精度基本都在0.5 cm以内;U方向精度差异较水平方向显著,最大差异可达7 mm,2种模型U方向精度基本在1~2 cm。结合表 2(单位cm)可以发现,相比于B1I/B3I,3D方向B1C/B2b的精度优势可达13.8%,这主要得益于新信号更好的数据质量[10]。新频点B1C和B2b的观测数据质量较为可观,能为进一步提升BDS-3精密定位服务提供支持。
|
图 4 BDS-3不同组合观测值精密定位精度统计 Fig. 4 Accuracy of BDS-3 precise positioning with different combination observations |
|
|
表 2 BDS-3 B1I/B3I和B1C/B2b PPP静态定位精度 Tab. 2 Accuracy of BDS-3 static positioning with the B1I/B3I and B1C/B2b mode |
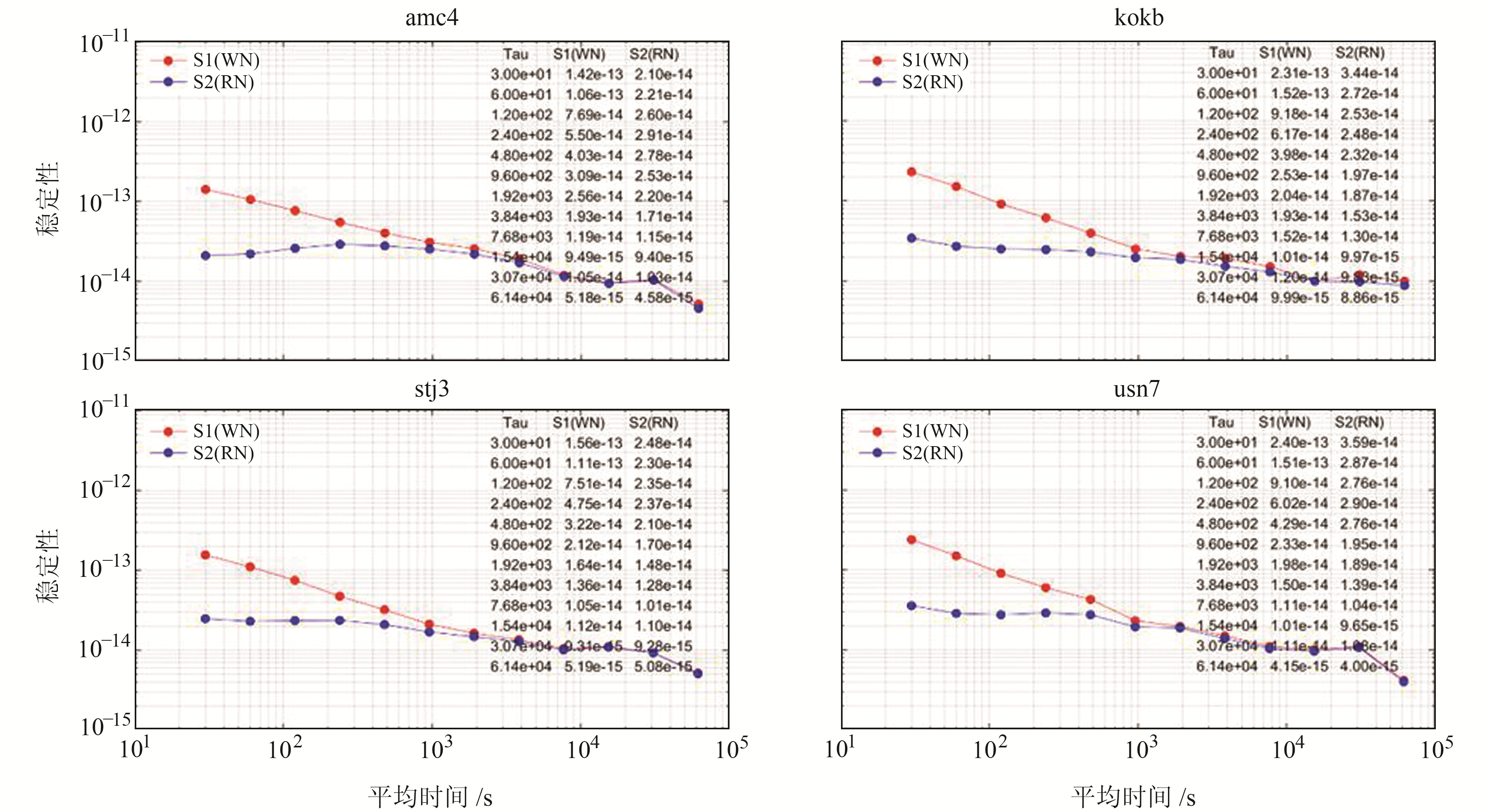
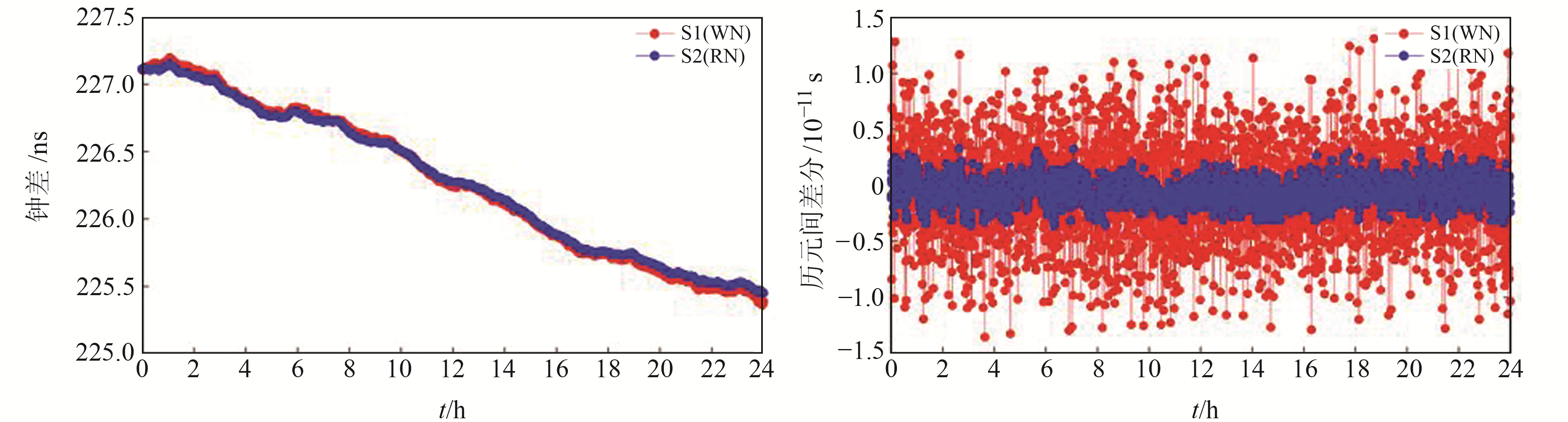
图 5为部分测站精密单点定位授时结果,S1和S2分别对应传统的白噪声(WN)模型和附加先验信息的随机游走噪声(RN)模型。从图中可以看出,附加随机游走噪声的PPP授时模型较传统模型的授时性能更高,在各测站均有体现,尤其是短期稳定性非常显著,提升程度基本可达1个量级。结合表 3可以发现,短期稳定性(平滑时间Tau<100 s)提升幅度超过66%,这是由于短期内模型约束较紧,模型强调显著提升,尤其是与采样间隔(30 s)相同的平滑时段,性能提升幅度最大。千秒稳(Tau=960 s)提升幅度接近20%,万秒稳(Tau=15 360 s)提升幅度接近5%。随着平滑时间的增加,约束强度逐渐减弱,对应授时性能提升幅度有所下降,但总体仍优于传统PPP模型。图 6为spt0测站的接收机钟差序列及其对应的历元间差分序列,可以看出,2种不同处理模式对应的接收机钟差具有较好的一致性,说明添加过程噪声的处理模式具有合理性;S2(RN)(图 5蓝线)对应的时间序列具有更小的噪声,充分说明接收机钟差添加合理的过程噪声后,其授时性能可得到有效提升。
|
图 5 基于不同站钟处理模式的单站授时性能 Fig. 5 The timing performance based on different clock processing modes |
|
|
表 3 附加随机游走噪声的PPP精密授时相对于传统模型的稳定性提升率 Tab. 3 Stability improvement rate of PPP timing with additional random walk noise compared to traditional models |
|
图 6 基于spt0站钟处理模式的接收机钟差和历元间差分序列 Fig. 6 Receiver clock bias and epoch differential series based on spt0 station clock processing modes |
本文基于传统B1I/B3I精密单点定位模型严格推导非公共频率的B1C/B2b精密单点定位授时模型。在此基础上,充分顾及氢原子钟高稳定性及钟差历元间强相关性的特点,对精密单点定位授时模型的接收机钟差参数添加过程噪声进行先验约束,采用新频点B1C/B2b组合验证B2b信号授时性能。为进一步明确B2b信号的定位服务性能,基于B1I/B3I和B1C/B2b两组不同频点组合进行PPP测试。结果表明:1) BDS-3不同频点组合静态PPP精度在水平方向基本优于0.5 cm,高程方向基本在2 cm左右,基于新频点B1C/B2b的静态PPP性能优于传统B1I/B3I组合,其精度优势可达13.8%。2) 对氢原子钟附加过程噪声先验约束可有效提升精密单点定位授时精度,尤其是短期稳定性提升效果较为显著,提升率基本可达66%。因此,基于BDS-3的B2b信号不仅能作为数据广播信道用于播发导航增强信息,还可作为基础信号用于GNSS高精度定位和授时服务。
| [1] |
张小红, 程世来, 李星星, 等. 单站GPS载波平滑伪距精密授时研究[J]. 武汉大学学报: 信息科学版, 2009, 34(4): 463-465 (Zhang Xiaohong, Cheng Shilai, Li Xingxing, et al. Precise Timing Using Carrier Phase Smoothed Pseudorange from Single Receiver[J]. Geomatics and Information Science of Wuhan University, 2009, 34(4): 463-465)
(  0) 0) |
| [2] |
Tu R, Zhang P F, Zhang R, et al. Modeling and Performance Analysis of Precise Time Transfer Based on BDS Triple-Frequency Un-Combined Observations[J]. Journal of Geodesy, 2019, 93(6): 837-847 DOI:10.1007/s00190-018-1206-3
(  0) 0) |
| [3] |
葛玉龙. 多频多系统精密单点定位时间传递方法研究[D]. 西安: 中国科学院国家授时中心, 2020 (Ge Yulong. Research on Methodology of Multi-Frequency and Multi-GNSS Precise Point Positioning Time Transfer[D]. Xi'an: National Time Service Center, CAS, 2020)
(  0) 0) |
| [4] |
张鹏飞. GNSS载波相位时间传递关键技术与方法研究[D]. 西安: 中国科学院国家授时中心, 2019 (Zhang Pengfei. The Research of Key Technology and Approach for Time and Frequency Transfer Based on GNSS Carrier Phase Observation[D]. Xi'an: National Time Service Center, CAS, 2019)
(  0) 0) |
| [5] |
艾青松. GNSS卫星钟差估计与精密单点定位时间传递方法研究[D]. 武汉: 中国科学院精密测量科学与技术创新研宄院, 2021 (Ai Qingsong. Research on Methodology of GNSS Satellite Clock Offset Estimation and Precise Point Positioning Time Transfer[D]. Wuhan: Innovation Academy for Precision Measurement Science and Technology, CAS, 2021)
(  0) 0) |
| [6] |
章红平, 高周正, 牛小骥, 等. GPS非差非组合精密单点定位算法研究[J]. 武汉大学学报: 信息科学版, 2013, 38(12): 1 396-1 399 (Zhang Hongping, Gao Zhouzheng, Niu Xiaoji, et al. Research on GPS Precise Point Positioning with Un-Differential and Un-Combined Observations[J]. Geomatics and Information Science of Wuhan University, 2013, 38(12): 1 396-1 399)
(  0) 0) |
| [7] |
张小红, 左翔, 李盼. 非组合与组合PPP模型比较及定位性能分析[J]. 武汉大学学报: 信息科学版, 2013, 38(5): 561-565 (Zhang Xiaohong, Zuo Xiang, Li Pan. Mathematic Model and Performance Comparison between Ionosphere-Free Combined and Uncombined Precise Point Positioning[J]. Geomatics and Information Science of Wuhan University, 2013, 38(5): 561-565)
(  0) 0) |
| [8] |
Wang K, Rothacher M. Stochastic Modeling of High-Stability Ground Clocks in GPS Analysis[J]. Journal of Geodesy, 2013, 87(5): 427-437 DOI:10.1007/s00190-013-0616-5
(  0) 0) |
| [9] |
Ge Y L, Zhou F, Liu T J, et al. Enhancing Real-Time Precise Point Positioning Time and Frequency Transfer with Receiver Clock Modeling[J]. GPS Solutions, 2019, 23(1)
(  0) 0) |
| [10] |
Tan B F, Ai Q S, Yuan Y B. Analysis of Precise Orbit Determination of BDS-3 MEO and IGSO Satellites Based on Several Dual-Frequency Measurement Combinations[J]. Remote Sensing, 2022, 14(23)
(  0) 0) |
2. Changjiang Institute of Survey, Planning, Design and Research Co Ltd, 1863 Jiefang Road, Wuhan 430010, China;
3. Guangzhou Urban Planning and Design Survey Research Institute, 10 Jianshedama Road, 510000
 2024, Vol. 44
2024, Vol. 44

