2. 海军航空大学信息融合研究所,山东省烟台市二马路188号,264001;
3. 山东南山铝业股份有限公司,山东省龙口市南山工业园,265706
GNSS/SINS组合导航系统由于其优异的性能,已成为导航应用的主要选择,而卡尔曼滤波器作为组合导航系统常用的信息融合方法,其滤波性能严重依赖于准确的系统噪声及测量噪声先验统计特性,利用错误的噪声统计特性将会导致滤波性能下降甚至发散[1]。然而,在实际应用环境下,由于内部及外部原因,惯性导航传感器存在较大的动态误差,标度因子导致的误差在滤波过程中很难得到补偿,进而导致系统噪声统计特性不准确。当GNSS接收机处于电磁干扰环境下时,测量噪声的统计模型无法准确进行描述[2]。
自适应滤波方法是解决上述问题的有效途径[3]。Sage Husa自适应滤波是一种研究较早的方法[4-6],然而在实际应用中,该滤波存在无法同时估计系统噪声及测量噪声统计特性、用于组合导航系统时经常存在滤波发散现象等缺陷。交互式多模型滤波器利用多个滤波模型来解决参数变化系统的状态估计问题,并被应用于组合导航测量多模型的切换[7-9],但该方法存在运行时间较长、多模型独立参数构成的模型集需涵盖参数范围等缺陷。近年来,基于变分贝叶斯的自适应滤波方法得到长足发展,并被成功应用于组合导航系统中[10],以克服Sage Husa自适应滤波在应用中出现的发散现象。但该方法目前只能在线实时估计测量噪声方差的变化,无法克服不准确的系统噪声方差统计特性对滤波精度的影响[11]。林雪原等[12]将变分贝叶斯估计方法与抗野值估计方法相结合,以解决测量噪声方差变化、测量值存在硬故障等问题,但对软故障的处理效果不佳。根据卡尔曼滤波方程可以发现,系统噪声方差矩阵会直接影响状态估计的一步预测误差协方差矩阵,且相对于系统噪声方差矩阵,状态估计的一步预测误差协方差矩阵对状态估计的影响更直接,更容易被估计。
为此,针对不准确的系统噪声及测量噪声先验统计,本文基于变分贝叶斯理论,在对系统状态估计的一步预测协方差矩阵及测量噪声的联合后验分布进行近似的基础上,提出GNSS/INS组合导航系统的改进变分贝叶斯自适应滤波方法,以得到复杂环境下组合导航系统的准确滤波结果。
1 组合导航滤波模型GNSS/INS组合导航系统松组合滤波模型为:
| $ \left\{\begin{array}{l} \boldsymbol{X}_{k}=\boldsymbol{\varPhi}_{k / k-1} \boldsymbol{X}_{k-1}+\boldsymbol{\varGamma}_{k-1} \boldsymbol{W}_{k-1} \\ \boldsymbol{Z}_{k}=\boldsymbol{H}_{k} \boldsymbol{X}_{k}+\boldsymbol{V}_{k} \end{array}\right. $ | (1) |
式中,Xk为n×1维状态向量;Φk/k-1为k-1时刻到k时刻的状态转移矩阵;Γk-1为系统噪声分配矩阵;Wk-1为系统噪声向量,且Wk~N(0, Qk);Zk为m×1维测量向量;Hk为测量矩阵;Vk为测量噪声向量,且Vk~N(0, Rk)。
选取“东北天”导航坐标系,记为n系;“右前上”载体坐标系,记为b系;地心地固系,记为e系;采用15维误差状态向量:
| $ \boldsymbol{X}=\left[\begin{array}{l} \left(\boldsymbol{\varphi}^n\right)^{\mathrm{T}}\quad\left(\delta \boldsymbol{v}^n\right)^{\mathrm{T}}\quad\left(\delta \boldsymbol{p}^e\right)^{\mathrm{T}}\quad\left(\boldsymbol{\varepsilon}^b\right)^{\mathrm{T}}\quad\left(\boldsymbol{\nabla}^b\right)^{\mathrm{T}} \end{array}\right]^{\mathrm{T}} $ | (2) |
式中,φn=[φE φN φU]T为n系下的姿态误差角,δvn=[δvEn δvNn δvUn]T为东、北、天3个方向的速度误差,δpe=[δL δλ δh]T为e系下的纬度、经度和高度3个方向的位置误差,εb=[εxb εyb εzb]T为载体系下陀螺仪三轴一阶马尔科夫误差,▽b=[▽xb ▽yb ▽zb]T为载体系下加速度计三轴一阶马尔科夫误差。
观测向量Zk取为GNSS与SINS提供的三维位置和三维速度的对应差值。
基于式(1)和式(2),卡尔曼滤波方程表示为:
| $ \left\{\begin{array}{l} \hat{\boldsymbol{X}}_{k \mid k-1}=\boldsymbol{\varPhi}_{k, k-1} \hat{\boldsymbol{X}}_{k-1 \mid k-1} \\ \boldsymbol{P}_{k \mid k-1}=\boldsymbol{\varPhi}_{k, k-1} \boldsymbol{P}_{k-1 \mid k-1} \boldsymbol{\varPhi}_{k, k-1}^{\mathrm{T}}+\boldsymbol{\varGamma}_{k-1} \boldsymbol{Q}_{k-1} \boldsymbol{\varGamma}_{k-1}^{\mathrm{T}} \\ \boldsymbol{K}_{k}=\boldsymbol{P}_{k \mid k-1} \boldsymbol{H}_{k}^{\mathrm{T}}\left(\boldsymbol{H}_{k} \boldsymbol{P}_{k \mid k-1} \boldsymbol{H}_{k}^{\mathrm{T}}+\boldsymbol{R}_{k}\right)^{-1} \\ \boldsymbol{P}_{k \mid k}=\left[\boldsymbol{I}-\boldsymbol{K}_{k} \boldsymbol{H}_{k}\right] \boldsymbol{P}_{k \mid k-1} \\ \hat{\boldsymbol{X}}_{k \mid k}=\hat{\boldsymbol{X}}_{k \mid k-1}+\boldsymbol{K}_{k}\left(\boldsymbol{Z}_{k}-\boldsymbol{H}_{k} \hat{\boldsymbol{X}}_{k \mid k-1}\right) \end{array}\right. $ | (3) |
式中,
根据式(3),Qk-1的不准确性将直接影响Pk|k-1。所以,当Qk-1和Rk不准确时,在估计Xk的同时需估计Pk|k-1和Rk,以保证滤波精度。
将Pk|k-1和Rk的先验分布p(Pk|k-1|Z1:k-1)和p(Rk|Z1:k-1)选为逆Wishart概率密度函数(probability density function, PDF)[13]:
| $ p\left(\boldsymbol{P}_{k \mid k-1} \mid \boldsymbol{Z}_{1: k-1}\right)=\operatorname{IW}\left(\boldsymbol{P}_{k \mid k-1} ; {t_{\hat{k} \mid k-1}}, \hat{\boldsymbol{T}}_{k \mid k-1}\right) $ | (4) |
| $ p\left(\boldsymbol{R}_{k} \mid \boldsymbol{Z}_{1: k-1}\right)=\operatorname{IW}\left(\boldsymbol{R}_{k} ; \hat{u}_{k \mid k-1}, \hat{\boldsymbol{U}}_{k \mid k-1}\right) $ | (5) |
式中,IW(B; λ, Ψ)代表自由度参数为λ和逆尺度矩阵为Ψ的逆Wishart PDF;B和Ψ均为对称正定矩阵,并假设其维数为d×d。
IW(B; λ, Ψ)可以表示为:
| $ \begin{gathered} \operatorname{IW}(\boldsymbol{B} ; \lambda, \boldsymbol{\varPsi})=\\ \frac{|\boldsymbol{\varPsi}|^{\lambda / 2}|\boldsymbol{B}|^{-(\lambda+d+1) / 2} \exp \left\{-0.5 \operatorname{tr}\left(\boldsymbol{\varPsi} \cdot \boldsymbol{B}^{-1}\right)\right\}}{2^{d \lambda / 2} T_{d}(\lambda / 2)} \end{gathered} $ | (6) |
式中,|·|和tr(·)分别为行列式运算和求迹运算,Td(·)是一个d元伽马函数。
如果B~IW(B; λ, Ψ),当λ>d+1时有:
| $ E\left[\boldsymbol{B}^{-1}\right]=(\lambda-d-1) \boldsymbol{\varPsi}^{-1} $ | (7) |
为获取Pk|k-1的先验信息,利用式(7)得到Pk|k-1的均值为:
| $ \begin{gather*} \frac{\hat{\boldsymbol{T}}_{k \mid k-1}}{\hat{t}_{k \mid k-1}-n-1}=\widetilde{\boldsymbol{P}}_{k \mid k-1}= \\ \boldsymbol{\varPhi}_{k, k-1} \boldsymbol{P}_{k-1 \mid k-1} \boldsymbol{\varPhi}_{k, k-1}^{\mathrm{T}}+\boldsymbol{\varGamma}_{k-1} \widetilde{\boldsymbol{Q}}_{k-1} \boldsymbol{\varGamma}_{k-1}^{\mathrm{T}} \end{gather*} $ | (8) |
式中,
| $ \hat{t}_{k \mid k-1}=n+\tau+1 $ | (9) |
式中,τ≥0是一个调整因子。将式(9)代入式(8),得:
| $ \hat{\boldsymbol{T}}_{k \mid k-1}=\tau \widetilde{\boldsymbol{P}}_{k \mid k-1} $ | (10) |
同理,为获取Rk的先验信息,R0的均值可表示为:
| $ \widetilde{\boldsymbol{R}}_{0}=\frac{\hat{\boldsymbol{U}}_{0 \mid 0}}{\hat{u}_{0 \mid 0}-m-1} $ | (11) |
式中,
| $ \hat{u}_{k \mid k-1}=\rho\left(\hat{u}_{k-1 \mid k-1}-m-1\right)+m+1 $ | (12) |
| $ \hat{\boldsymbol{U}}_{k \mid k-1}=\rho \hat{\boldsymbol{U}}_{k-1 \mid k-1} $ | (13) |
为同时估计Xk、Pk|k-1和Rk,需计算联合后验PDFp(Xk, Pk|k-1, Rk|Z1:k),利用变分贝叶斯方法可得[14-15]:
| $ p\left(\boldsymbol{X}_{k}, \boldsymbol{P}_{k \mid k-1}, \boldsymbol{R}_{k} \mid \boldsymbol{Z}_{1: k}\right) \approx q\left(\boldsymbol{X}_{k}\right) q\left(\boldsymbol{P}_{k \mid k-1}\right) q\left(\boldsymbol{R}_{k}\right) $ | (14) |
式中,q(·)代表p(·)的近似后验PDF。
通过最小化近似后验PDF与真实后验PDF之间的KLD距离,得到:
| $ \log q(\theta) =E_{\varXi^{(-\theta)}}\left[\log p\left(\boldsymbol{\varXi}, \boldsymbol{Z}_{1: k}\right)\right]+c_{\theta} $ | (15) |
| $ \boldsymbol{\varXi} \triangleq\left\{\boldsymbol{X}_{k}, \boldsymbol{P}_{k \mid k-1}, \boldsymbol{R}_{k}\right\} $ | (16) |
式中,联合PDF logp(Ξ, Z1:k)可以表示为:
| $ \begin{gather*} p\left(\boldsymbol{\varXi}, \boldsymbol{Z}_{1: k}\right)=\\ p\left(\boldsymbol{Z}_{k} \mid \boldsymbol{X}_{k}, \boldsymbol{R}_{k}\right) p\left(\boldsymbol{X}_{k} \mid \boldsymbol{Z}_{1: k-1}, \boldsymbol{P}_{k \mid k-1}\right) \times \\ p\left(\boldsymbol{P}_{k \mid k-1} \mid \boldsymbol{Z}_{1: k-1}\right) p\left(\boldsymbol{R}_{k} \mid \boldsymbol{Z}_{1: k-1}\right) p\left(\boldsymbol{Z}_{1: k-1}\right)= \\ N\left(\boldsymbol{Z}_{k} ; \boldsymbol{H}_{k} \boldsymbol{X}_{k}, \boldsymbol{R}_{k}\right) N\left(\boldsymbol{X}_{k} ; \hat{\boldsymbol{X}}_{k \mid k-1}, \boldsymbol{P}_{k \mid k-1}\right) \times \\ \operatorname{IW}\left(\boldsymbol{P}_{k \mid k-1} ; \hat{t}_{k \mid k-1}, \hat{\boldsymbol{T}}_{k \mid k-1}\right) \\ \operatorname{IW}\left(\boldsymbol{R}_{k} ; \hat{u}_{k \mid k-1}, \hat{\boldsymbol{U}}_{k \mid k-1}\right) p\left(\boldsymbol{Z}_{1: k-1}\right) \end{gather*} $ | (17) |
式中,log(·)代表对数函数,E(·)代表期望运算,θ是Ξ中的任一元素,Ξ(-θ)是除了θ以外所有元素的集合,cθ代表变量θ的常数,N(·;μ, Σ)代表均值为μ、协方差矩阵为Σ的高斯PDF。
基于式(17),logp(Ξ, Z1:k)可表示为:
| $\begin{gathered} \log p\left(\boldsymbol{\varXi}, \boldsymbol{Z}_{1: k}\right)=-\\ 0.5\left(\boldsymbol{Z}_{k}-\boldsymbol{H}_{k} \boldsymbol{X}_{k}\right){ }^{\mathrm{T}} \boldsymbol{R}_{k}^{-1}\left(\boldsymbol{Z}_{k}-\boldsymbol{H}_{k} \boldsymbol{X}_{k}\right)-\\ 0.5\left(m+\hat{\mu}_{k \mid k-1}+2\right) \log \left|\boldsymbol{R}_{k}\right|-0.5\\ \operatorname{tr}\left(\hat{\boldsymbol{U}}_{k \mid k 1} \boldsymbol{R}_{k}^{-1}\right)-0.5\left(n+\hat{t}_{k \mid k-1}+2\right)\\ \log \left|\boldsymbol{P}_{k \mid k-1}\right|-0.5 \operatorname{tr}\left(\hat{\boldsymbol{T}}_{k \mid k-1} \boldsymbol{P}_{k \mid k-1}^{-1}\right)-\\ 0.5\left(\boldsymbol{X}_{k}-\hat{\boldsymbol{X}}_{k \mid k-1}\right)^{\mathrm{T}} \boldsymbol{P}_{k \mid k-1}^{-1}\left(\boldsymbol{X}_{k}-\hat{\boldsymbol{X}}_{k \mid k-1}\right)+c_{\varXi} \end{gathered} $ | (18) |
令θ=Pk|k-1,且将式(18)代入式(15),得:
| $ \begin{gather*} \log q^{(i+1)}\left(\boldsymbol{P}_{k \mid k-1}\right)=- \\ 0.5\left(n+\hat{t}_{k \mid k-1}+2\right) \log \mid \boldsymbol{P}_{k \mid k-1}- \\ 0.5 \operatorname{tr}\left(\left(\hat{\boldsymbol{T}}_{k \mid k-1}+\boldsymbol{A}_{k}^{(i)}\right) \boldsymbol{P}_{k \mid k-1}^{-1}\right)+c_{p} \end{gather*} $ | (19) |
式中,q(i+1)(·)为第i+1次迭代的近似PDF,且Ak(i)可表示为:
| $ \boldsymbol{A}_{k}^{(i)}=\boldsymbol{P}_{k \mid k}^{(i)}+\left(\boldsymbol{X}_{k \mid k}^{(i)}-\boldsymbol{X}_{k \mid k-1}\right)\left(\boldsymbol{X}_{k \mid k}^{(i)}-\boldsymbol{X}_{k \mid k-1}\right)^{\mathrm{T}} $ | (20) |
基于式(19),可以更新为逆Wishart PDF:
| $ q^{(i+1)}\left(\boldsymbol{P}_{k \mid k-1}\right)=\operatorname{IW}\left(\boldsymbol{P}_{k \mid k-1} ; \hat{t}_{k}^{(i+1)}, \hat{\boldsymbol{T}}_{k}^{(i+1)}\right) $ | (21) |
其中,
| $ \hat{t}_{k}^{(i+1)}=\hat{t}_{k \mid k-1}+1 $ | (22) |
| $ \hat{\boldsymbol{T}}_{k}^{(i+1)}=\hat{\boldsymbol{T}}_{k \mid k-1}+\hat{\boldsymbol{A}}_{k}^{(i)} $ | (23) |
基于式(21),得到修正的Pk|k-1(i+1)为:
| $ \boldsymbol{P}_{k \mid k-1}^{(i+1)}=\frac{\hat{\boldsymbol{T}}_{k}^{(i+1)}}{\hat{t}_{k}^{(i+1)}-n-1} $ | (24) |
令θ=Rk,且将式(18)代入式(15),得:
| $ \begin{gather*} \log q^{(i+1)}\left(\boldsymbol{R}_{k}\right)=-0.5\left(m+\hat{\mu}_{k \mid k-1}+2\right) \log \left|\boldsymbol{R}_{k}\right|- \\ 0.5 \operatorname{tr}\left(\left(\hat{\boldsymbol{U}}_{k \mid k 1}+\boldsymbol{B}_{k}^{(i)}\right) \boldsymbol{R}_{k}^{-1}\right)+c_{\boldsymbol{R}} \end{gather*} $ | (25) |
式中,Bk(i)可以表示为:
| $ \begin{gather*} \boldsymbol{B}_{k}^{(i)}=\left(\boldsymbol{Z}_{k}-\boldsymbol{H}_{k} \hat{\boldsymbol{X}}_{k \mid k}^{(i)}\right)\left(\boldsymbol{Z}_{k}-\boldsymbol{H}_{k} \hat{\boldsymbol{X}}_{k \mid k}^{(i)}\right)^{\mathrm{T}}+ \\ \boldsymbol{H}_{k} \boldsymbol{P}_{k \mid k}^{(i)} \boldsymbol{H}_{k}^{\mathrm{T}} \end{gather*} $ | (26) |
基于式(25),q(Rk)更新为逆Wishart PDF:
| $ q^{(i+1)}\left(\boldsymbol{R}_{k}\right)=\operatorname{IW}\left(\boldsymbol{R}_{k} ; \hat{u}_{k}^{(i+1)}, \hat{\boldsymbol{U}}_{k}^{(i+1)}\right) $ | (27) |
其中,
| $ \hat{u}_{k}^{(i+1)}=\hat{u}_{k \mid k-1}+1 $ | (28) |
| $ \hat{\boldsymbol{U}}_{k}^{(i+1)}=\hat{\boldsymbol{U}}_{k \mid k 1}+\boldsymbol{B}_{k}^{(i)} $ | (29) |
则修正后的Rk(i+1)可以表示为:
| $ \boldsymbol{R}_{k}^{(i+1)}=\frac{\hat{\boldsymbol{U}}_{k}^{(i+1)}}{\hat{u}_{k}^{(i+1)}-m-1} $ | (30) |
同理,令θ=Xk,且将式(18)代入式(15),q(Xk)更新为高斯PDF,得:
| $ q^{(i+1)}\left(\boldsymbol{X}_{k}\right)=N\left(\boldsymbol{X}_{k} ; \hat{\boldsymbol{X}}_{k \mid k}^{(i+1)}, \boldsymbol{P}_{k \mid k}^{(i+1)}\right) $ | (31) |
式中,
| $ \boldsymbol{K}_{k}^{(i+1)}=\boldsymbol{P}_{k \mid k-1}^{(i+1)} \boldsymbol{H}_{k}^{\mathrm{T}}\left(\boldsymbol{H}_{k} \boldsymbol{P}_{k \mid k-1}^{(i+1)} \boldsymbol{H}_{k}^{\mathrm{T}}+\boldsymbol{R}_{k}^{(i+1)}\right)^{-1} $ | (32) |
| $ \boldsymbol{X}_{k \mid k}^{(i+1)}=\boldsymbol{X}_{k \mid k-1}+\boldsymbol{K}_{k}^{(i+1)}\left(\boldsymbol{Z}_{k}-\boldsymbol{H}_{k} \boldsymbol{X}_{k \mid k-1}\right) $ | (33) |
| $ \boldsymbol{P}_{k \mid k}^{(i+1)}=\left(I-\boldsymbol{K}_{k}^{(i+1)} \boldsymbol{H}_{k}\right) \boldsymbol{P}_{k \mid k-1}^{(i+1)} $ | (34) |
经过N次定点迭代运算后,后验PDF q(Xk)、q(Pk|k-1)和q(Rk)的变分近似可以表示为:
| $ \begin{gather*} q\left(\boldsymbol{X}_{k}\right) \approx q^{(N)}\left(\boldsymbol{X}_{k}\right)=N\left(\boldsymbol{X}_{k} ; \hat{\boldsymbol{X}}_{k \mid k}^{(N)}, \boldsymbol{P}_{k \mid k}^{(N)}\right)= \\ N\left(\boldsymbol{X}_{k} ; \hat{\boldsymbol{X}}_{k \mid k}, \boldsymbol{P}_{k \mid k}\right) \end{gather*} $ | (35) |
| $ \begin{gather*} q\left(\boldsymbol{P}_{k \mid k-1)} \approx q^{(N)}\left(\boldsymbol{P}_{k \mid k-1}\right)=\operatorname{IW}\left(\boldsymbol{P}_{k \mid k-1} ; {t_{\hat{k}}^{( N)}}, \hat{\boldsymbol{T}}_{k}^{(N)}\right)=\right.\\ \operatorname{IW}\left(\boldsymbol{P}_{k \mid k-1} ; \hat{t}_{k \mid k}, \hat{\boldsymbol{T}}_{k \mid k}\right) \end{gather*} $ | (36) |
| $ \begin{gather*} q\left(\boldsymbol{R}_{k}\right) \approx q^{(N)}\left(\boldsymbol{R}_{k}\right)=\operatorname{IW}\left(\boldsymbol{R}_{k} ; \hat{u}_{k}^{(N)}, \hat{\boldsymbol{U}}_{k}^{(N)}\right)= \\ \operatorname{IW}\left(\boldsymbol{R}_{k} ; \hat{u}_{k \mid k}, \hat{\boldsymbol{U}}_{k \mid k}\right) \end{gather*} $ | (37) |
式(35)~(37)表明,经过N次定点迭代运算后,MVBAKF算法的最终滤波值为:
| $ \hat{\boldsymbol{R}}_{k} \approx \boldsymbol{R}_{k}^{(N)}=\frac{\hat{\boldsymbol{U}}_{k}^{(N)}}{\hat{u}_{k}^{(N)}-m-1} $ | (38) |
| $ \hat{\boldsymbol{P}}_{k \mid k-1} \approx \boldsymbol{P}_{k \mid k-1}^{(N)}=\frac{\hat{\boldsymbol{T}}_{k}^{(N)}}{\hat{t}_{k}^{(N)}-n-1} $ | (39) |
为验证本文MVBAKF算法的有效性与优越性,设计了GNSS/SINS组合导航系统仿真实验,并将MVBAKF算法及传统的VBAKF算法进行比较。为了保证仿真实验结果的严谨性,对上述两种滤波器设置了相同的滤波初值、测量噪声、系统噪声及测量数据(即具有相同的初始条件及相同的输入等)。各导航传感器的误差参数设置如表 1所示。
|
|
表 1 导航传感器误差参数 Tab. 1 Error parameters of navigation sensors |
设置包含加速、减速、爬升、俯冲及转弯等机动过程的航迹作为导航基准,时长为3 600 s,其飞行轨迹如图 1所示。MVBAKF算法中遗忘因子选取为ρ=0.95,VBAKF算法中遗忘因子向量的每个元素均为0.95,以保证两种算法对历史测量信息的保留度相同。仿真时,在GNSS测量噪声方差中引入突变及缓变两个不同阶段,如图 2中黑色实线部分;根据表 1的设置,将滤波器实际的系统噪声方差设置为真实值的9倍,以模拟滤波过程中未知的系统噪声及测量噪声。

|
图 1 载体飞行轨迹 Fig. 1 Flight trajectory of carrier |

|
图 2 测量噪声均方差估计曲线 Fig. 2 Measurement noise mean square error estimation curves |
对于MVBAKF算法,当循环次数选取为N=5、调整因子选取为τ=6时,图 2给出基于VBAKF算法和MVBAKF算法的测量噪声均方差估计曲线。可以看出,两种算法对测量噪声方差的估计效果基本相同,估计值基本与真实值一致,且随真实值的变化而变化。
图 3给出基于VBAKF算法、MVBAKF算法的组合导航系统的位置误差对比曲线、速度误差对比曲线及姿态误差对比曲线。为更加直观地评估滤波器对状态参数的滤波精度,选取位置和速度的均方根误差(root mean square error,RMSE)为性能指标,定义如下:
| $ \begin{array}{c} \mathrm{RMSE} \triangleq\\ \sqrt{\frac{1}{M} \sum\limits_{k=1}^{M}\left[\left(\hat{x}_{k}-x_{k}\right)^{2}+\left(\hat{y}_{k}-y_{k}\right)^{2}+\left(\hat{z}_{k}-z_{k}\right)^{2}\right]} \end{array} $ | (40) |

|
图 3 基于VBAKF和MVBAKF的导航参数误差对比曲线 Fig. 3 Comparison curves of navigation parameter error based on VBAKF and MVBAKF |
式中,(xk, yk, zk)代表k时刻真实的位置信息(或速度信息),(
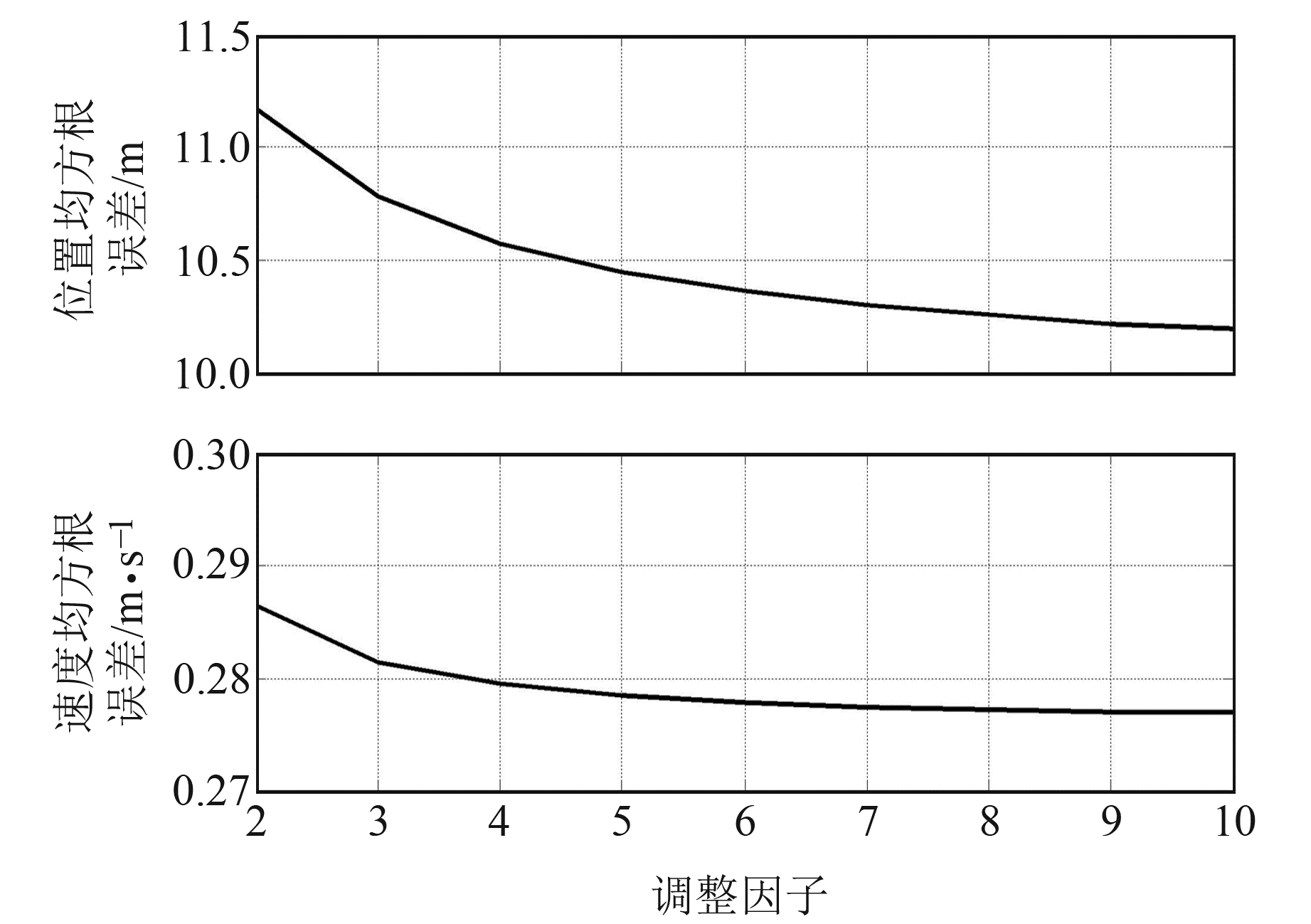
为评估MVBAKF算法中调整因子τ对滤波精度的影响,在循环次数N=5不变的基础上,图 4给出了τ=2、3、4、5、6、7、8、9、10时的位置均方根误差及速度均方根误差曲线。由图 4可见,当调整因子较小时(如τ=2, 3, 4),位置均方根误差及速度均方根误差较大;当调整因子较小时(如τ=9, 10),位置均方根误差及速度均方根误差较小;当调整因子继续增大时(τ>10),位置均方根误差及速度均方根误差基本稳定。
|
图 4 当τ=2, 3, 4, 5, 6, 7, 8, 9, 10时位置及速度RMSE Fig. 4 Position and velocity RMSE when τ=2, 3, 4, 5, 6, 7, 8, 9, 10 |
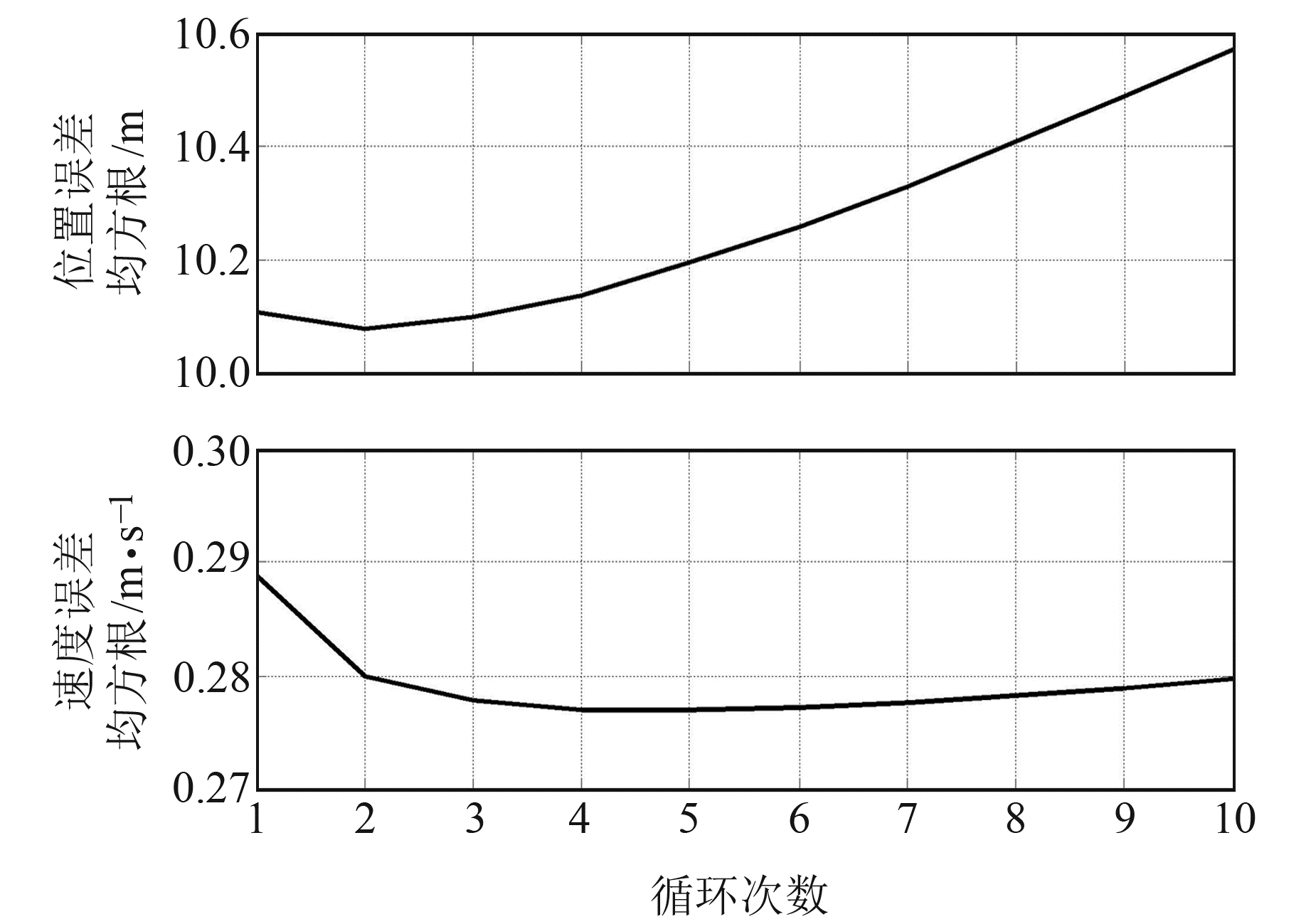
为评估MVBAKF算法中循环次数N对滤波精度的影响,在调整因子为τ=10不变的基础上,图 5给出了N=1~10时的位置均方根误差及速度均方根误差曲线。
|
图 5 当N=1~10时位置及速度RMSE Fig. 5 Position and velocity RMSE when N=1~10 |
可以看出,当循环次数N=2~4时,位置均方根误差及速度均方根误差达到较小的值,否则位置均方根误差及速度均方根误差较大。
4 结语在实际环境中,针对具有不准确测量噪声及系统噪声统计特性的线性高斯状态空间GNSS/SINS组合导航系统滤波,提出一种改进的变分贝叶斯自适应滤波算法。在该算法中,将对系统噪声的估计问题变换成对状态向量估计的一步预测误差协方差估计问题,进而将状态估计及其一步预测误差协方差、测量噪声方差通过逆Wishart分布进行推断。
仿真结果表明,与VBAKF算法相比,本文MVBAKF算法具有更好的鲁棒性,且能提高组合导航系统的滤波精度,这是由于MVBAKF算法可以迭代地找到更优的状态估计一步预测误差协方差及测量噪声方差。
| [1] |
林雪原, 姚力波, 孙炜玮. 基于多尺度的组合导航系统状态估计及应用[M]. 北京: 科学出版社, 2020 (Lin Xueyuan, Yao Libo, Sun Weiwei. State Estimation of Integrated Navigation System Based on Multi-Scale and Its Application[M]. Beijing: Science Press, 2020)
(  0) 0) |
| [2] |
张小红, 陶贤露, 王颖喆, 等. 城市场景智能手机GNSS/MEMS融合车载高精度定位[J]. 武汉大学学报: 信息科学版, 2022, 47(10): 1740-1749 (Zhang Xiaohong, Tao Xianlu, Wang Yingzhe, et al. MEMS-Enhanced Smartphone GNSS High-Precision Positioning for Vehicular Navigation in Urban Conditions[J]. Geomatics and Information Science of Wuhan University, 2022, 47(10): 1740-1749)
(  0) 0) |
| [3] |
Huang Y L, Zhang Y G. A New Process Uncertainty Robust Student's t-Based Kalman Filter for SINS/GPS Integration[J]. IEEE Access, 2017(5): 14391-14404
(  0) 0) |
| [4] |
孙淑光, 温启新. 改进Sage-Husa算法在飞机组合导航中的应用[J]. 全球定位系统, 2021, 46(3): 54-60 (Sun Shuguang, Wen Qixin. The Application of Improved Sage-Husa Algorithm in Aircraft Integrated Navigation[J]. GNSS World of China, 2021, 46(3): 54-60)
(  0) 0) |
| [5] |
付梦印, 邓志红, 闫莉萍. Kalman滤波理论及其在导航系统中的应用(2版)[M]. 北京: 科学出版社, 2010 (Fu Mengyin, Deng Zhihong, Yan Liping. Kalman Filtering Theory and Its Application in Navigation System(2nd ed)[M]. Beijing: Science Press, 2010)
(  0) 0) |
| [6] |
Yu M J. INS/GPS Integration System Using Adaptive Filter for Estimating Measurement Noise Variance[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 1786-1792 DOI:10.1109/TAES.2012.6178100
(  0) 0) |
| [7] |
Song J H, Li J, Wei X K, et al. Improved Multiple-Model Adaptive Estimation Method for Integrated Navigation with Time-Varying Noise[J]. Sensors, 2022, 22(16): 5976 DOI:10.3390/s22165976
(  0) 0) |
| [8] |
Liu X H, Liu X X, Zhang W G, et al. Interacting Multiple Model UAV Navigation Algorithm Based on a Robust CubatureKalman Filter[J]. IEEE Access, 2020(8): 81034-81044
(  0) 0) |
| [9] |
徐博, 陈崇, 王连钊. 基于交互式多模型的车载INS/OD/GPS的定位方法[J]. 中国惯性技术学报, 2022, 30(1): 58-64 (Xu Bo, Chen Chong, Wang Lianzhao. Vehicle-Mounted INS/OD/GPS Integrated Navigation Based on IMM Filtering[J]. Journal of Chinese Inertial Technology, 2022, 30(1): 58-64)
(  0) 0) |
| [10] |
Sarkka S, Nummenmaa A. Recursive Noise Adaptive Kalman Filtering by Variational Bayesian Approximations[J]. IEEE Transactions on Automatic Control, 2009, 54(3): 596-600 DOI:10.1109/TAC.2008.2008348
(  0) 0) |
| [11] |
荆蕾, 孙炜玮, 乔玉新, 等. GNSS/SINS组合导航系统的自适应UKF算法[J]. 大地测量与地球动力学, 2023, 43(3): 255-258 (Jing Lei, Sun Weiwei, Qiao Yuxin, et al. Adaptive UKF Algorithm for GNSS/SINS Integrated Navigation System[J]. Journal of Geodesy and Geodynamics, 2023, 43(3): 255-258)
(  0) 0) |
| [12] |
林雪原, 刘丽丽, 董云云, 等. 改进的GNSS/SINS组合导航系统自适应滤波算法[J]. 武汉大学学报: 信息科学版, 2023, 48(1): 127-134 (Lin Xueyuan, Liu Lili, Dong Yunyun, et al. Improved Adaptive Filtering Algorithm for GNSS/SINS Integrated Navigation System[J]. Geomatics and Information Science of Wuhan University, 2023, 48(1): 127-134)
(  0) 0) |
| [13] |
Huang Y L, Zhang Y G, Wu Z M, et al. A Novel Adaptive Kalman Filter with Inaccurate Process and Measurement Noise Covariance Matrices[J]. IEEE Transactions on Automatic Control, 2017, 63(2): 594-601
(  0) 0) |
| [14] |
Davari N, Gholami A. Variational Bayesian Adaptive Kalman Filter for Asynchronous Multirate Multi-Sensor Integrated Navigation System[J]. Ocean Engineering, 2019, 174: 108-116
(  0) 0) |
| [15] |
Sarkka S, Nummenmaa A. Recursive Noise Adaptive Kalman Filtering by Variational Bayesian Approximations[J]. IEEE Transactions on Automatic Control, 2009, 54(3): 596-600
(  0) 0) |
2. Institute of Information Fusion, Naval Aeronautical University, 188 Erma Road, Yantai, 264001, China;
3. Shandong Nanshan Aluminium Co Ltd, Nashan Industrial Park, Longkou 265706, China
 2024, Vol. 44
2024, Vol. 44


