2. 太原大陆裂谷动力学国家野外科学观测研究站,太原市晋祠镇,030025
准确的震源位置是研究地震学和深部地球物理学重要的数据基础[1],对深入认识板块构造[2]、断层结构[3]、强震发震机制[4]及其演化过程[5]等有重要意义。研究表明,影响地震震源位置测定的因素包括传感器坐标定位精度、地壳速度模型、监测台网几何布局及到时震相拾取精度等[1, 6]。有学者利用定位残差[7]、重复地震事件[8]、人工爆破事件[9-10]及数值模拟[11]等手段定性分析并评估不同区域的地震定位精度[6],但鲜有针对定位结果偏差开展定量分析的研究[12]。
本文利用数值模拟方法,基于山西地震台网数据,结合地壳速度模型计算各台站理论到时,同时分别改变速度模型、走时拾取误差及台站布局,采用同一种定位方法测定震源位置,以对比分析测定位置与初始位置的偏差,定量分析各类因素对震源位置测定的影响。
1 研究方法山西地区北邻内蒙古,南邻河南,东以太行山为界,西与陕西隔河相望,两侧为隆起区,中部为S形展布的断陷盆地。由于地形起伏显著,地质构造复杂,山西地区地震活动比较强烈,历史上发生7级以上地震8次,震中主要位于人口稠密、经济发达的五大盆地及其边缘山区。近10 a来,山西地区虽未发生5级以上强震,但小震不断,多数有感地震以3~4级为主。山西地震台网当前共有测震台站57个,平均台间距为40~50 km(图 1)。

|
图 1 山西地区台站和假设震中位置分布 Fig. 1 Location distribution of stations and assumed epicenter in Shanxi region |
为尽可能接近实际情况,同时便于测试不同因素对山西台网地震定位结果的影响,本文模拟地震震中位于山西中部太原市清徐县(37.594°N、112.482°E,见图 1),震源深度为18 km。参考历史地震数据,通常ML3.0以上地震事件全省80% 台站有记录,据此假设地震震级为ML3.0,有45个台站记录到,震中距大于180 km的台站有22个,最近及最远台站的震中距分别为11 km和285 km,台站最大空隙角为31°。结合台站坐标和山西2015速度模型[13],计算各台站的理论走时,其中震中距小于180 km的台站仅计算直达波到时,大于180 km的台站另外计算首波到时。考虑到Sn震相信号较弱,不易识别,仅随机计算11个台站的Sn震相理论到时,共得到Pg和Sg震相各45个,Pn震相22个,Sn震相11个,总计123个震相数据。在此基础上,定量改变速度模型参数、震相走时拾取精度及台网布局等单一变量参数,利用Hyposat定位方法[14]对地震进行重新定位,对比不同参数的测定结果与初始震中的差异,定量分析各影响因素对定位结果造成的偏差。
2 影响因素定量分析 2.1 计算理论走时当震源位置已知时,根据现有台站坐标,利用近震地震波走时规律,可以计算一维分层模型下常用的P、S震相理论走时。假设震源为点源,地震波传播路径上的各层面为平面,各层内的介质均匀分布,地震波的传播速度恒定,地震波射线为直线。因此,当地壳速度模型为单层模型或双层模型,且震源位于上地壳时,直达波的走时方程可表示为:
| $\frac{t^2}{t_0^2}-\frac{\varDelta^2}{h^2}=1 $ | (1) |
首波的走时方程为:
| $t=\frac{\varDelta}{v_3}+(2 H-h) \frac{\cos i_0}{v_1} $ | (2) |
当地壳速度模型为双层模型,且震源位于下地壳时,直达波的走时方程可表示为:
| $ t=\frac{H_1}{\nu_1 \operatorname{sine}_2}+\frac{h-H_1}{\nu_2 \operatorname{sine}_2} $ | (3) |
| $ \begin{gathered} \varDelta=H_1 \cot e_1+\left(h-H_1\right) \cot e_2 \end{gathered} $ | (4) |
首波的走时方程为:
| $ \begin{gathered} t=\frac{\varDelta}{v_3}+(2 H-h) \sqrt{\frac{1}{v_1^2}-\frac{1}{v_3^2}}+ \\ 2 H_2 \sqrt{\frac{1}{v_2^2}-\frac{1}{v_3^2}} \end{gathered} $ | (5) |
式中,t为相应震相的走时,Δ为震中距,h为震源深度,H1、H2分别为上、下地壳厚度,v1、v2和v3分别为上、下地壳和莫霍面地震波传播速度,e1、e2分别为上、下地壳直达波的出射角,i0为首波入射的临界角,t0=h/v1[15]。
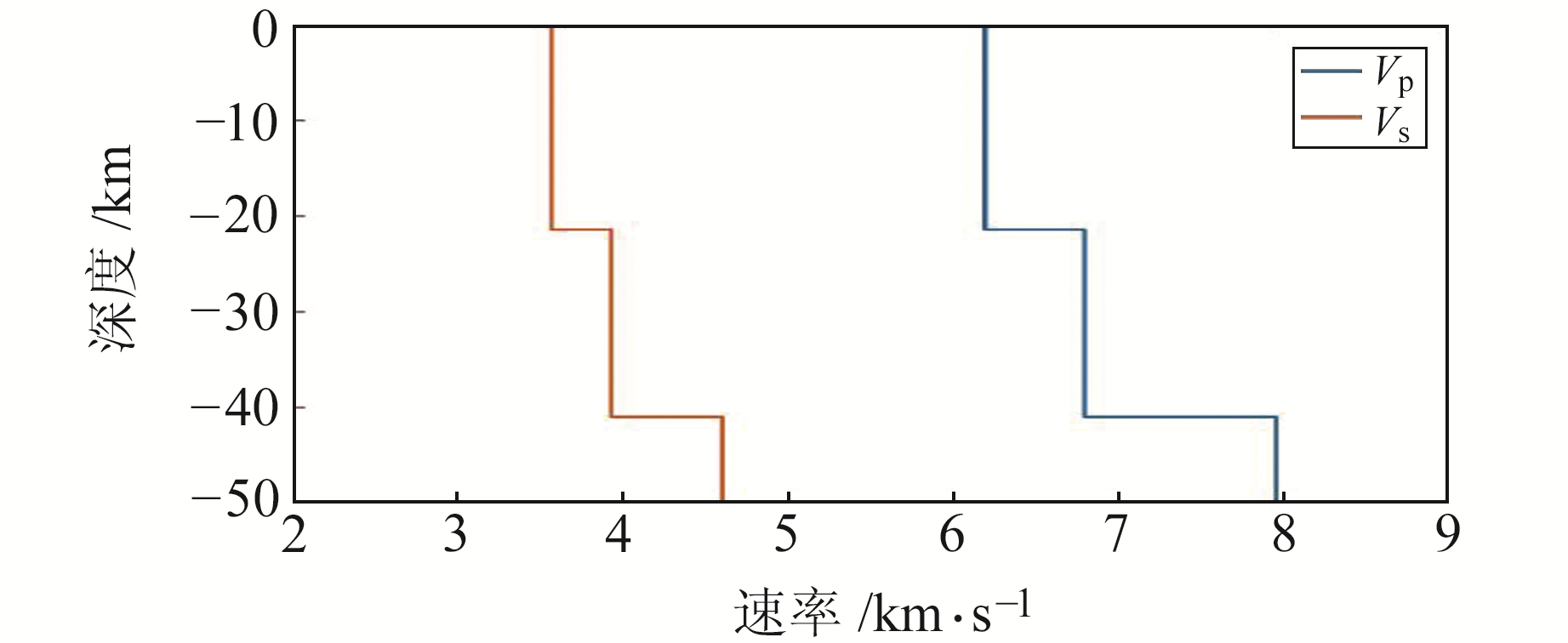
2.2 地壳速度模型对震源位置的影响在区域台网地震定位过程中,地壳速度模型对震源位置测定的影响极为突出,尤其是震源深度[16]。本文P波速度选自山西地震台网使用的山西2015速度模型[13],波速比设定为1.73,模型如图 2所示。
|
图 2 地壳速度模型参数 Fig. 2 Parameters of crustal velocity model |
根据地壳速度模型,结合震源位置和台站分布,利用式(2)~(5)计算各台站初至波和首波等不同震相的理论到时,然后不断改变速度模型参数进行定位。在模型参数变化过程中,每次仅变化单一参数,其中上、下地壳和莫霍面P波速度波动范围在±1 km/s,每次波动幅度为0.02 km/s;深度波动范围为±10 km,每次波动幅度为0.2 km,详情见表 1。
|
|
表 1 地壳速度模型参数变化 Tab. 1 Parameters change of crustal velocity model |
计算重定位结果和初始位置之间的距离,得到震中位置差随地壳速度模型的变化趋势,如图 3所示。图 3(a)为模型参数中速度变化对震源位置的影响,由图可知,随着地壳速度模型中速度值逐步偏离模型初始值,震中位置出现不同程度的偏差,当速度正负偏差增大到一定程度后,震中位置呈宽幅震荡态势。震中位置偏差最大值小于4 km,符合Ⅰ类定位精度(5 km)要求。对于地壳速度模型中的3种速度值,上地壳P波速度(v1)造成的影响最为明显,震中位置差随速度偏差的增大而增大,速度值减小造成的震中偏差较速度值增大略大,变化速率也更快;下地壳P波速度(v2)的影响最小,震中偏差在1 km以内,可能是由于震源处于上地壳,参与定位的震相以上地壳传播的直达波为主;莫霍面P波速度(v3)的影响居于二者之间,最大偏差约为2 km。由于震中位置最大差对应的莫霍面P波速度(v3)偏差小于上地壳P波速度(v1)偏差,可知震中位置差对莫霍面P波速度(v3)的变化更为敏感。图 3(b)为模型参数中康拉德面和莫霍面深度对震源位置的影响,不难发现,莫霍面和康拉德面深度的变化造成的震中位置偏差均不超4 km,但二者的影响区间却存在显著不同。在莫霍界面深度逐渐减小的过程中,震中位置几乎没有变化,而增大时震中位置差呈上升趋势,尤其当莫霍面深度大于初始值6 km后,震中位置差加速上升;康拉德面深度引发的震中位置差变化趋势与莫霍界面深度相反,震中位置差变化明显处对应康拉德面深度减小区域,而康拉德面深度增大时对震中位置的影响较小。

|
图 3 震中位置差与地壳速度模型变化的关系 Fig. 3 Relation between epicenter position difference and crustal velocity model change |
图 4(a)和4(b)分别为地壳速度模型中速度和界面深度对震源深度测定的影响,整体而言,速度值对震源深度的影响大于界面深度。3类速度值波动引发的震源深度最大偏差均可达20 km左右,不同之处在于震源深度出现最大偏差时对应的速度偏离初始值的幅度,具体表现为:上地壳速度(v1)在比初始值低0.4 km/s区域,下地壳速度(v2)在比初始值高0.8 km/s区域,而莫霍面P波速度(v3)在大于初始值0.1~0.4 km/s区间。速度值负偏差造成的震源深度波动最快的因素依次为上地壳速度(v1)、下地壳速度(v2)和莫霍面P波速度(v3);在速度值正偏差范围内,上地壳速度(v1)对震源深度的影响最小,其余二者的影响都超过15 km。康拉德面和莫霍面深度的变化均会导致震源深度出现明显偏差,但莫霍面深度变化的影响更为剧烈。当界面深度偏离初始值逐渐增大时,二者造成的震源深度偏差增加,莫霍面深度变化引起的偏差幅度较大;当界面深度值偏离初始值逐渐减小时,莫霍面深度变化造成的震源深度差随地壳深度呈线性变化态势,最大可达近14 km,而康拉德面深度变化引起的震源深度差较小,最大值小于4 km,并且当康拉德面深度减小至5 km左右时,震源深度偏差出现显著降低,这可能与康拉德面深度减小至震源深度附近有关。

|
图 4 震源深度偏差与地壳速度模型变化的关系 Fig. 4 Relation between focal depth deviation and crustal velocity model change |
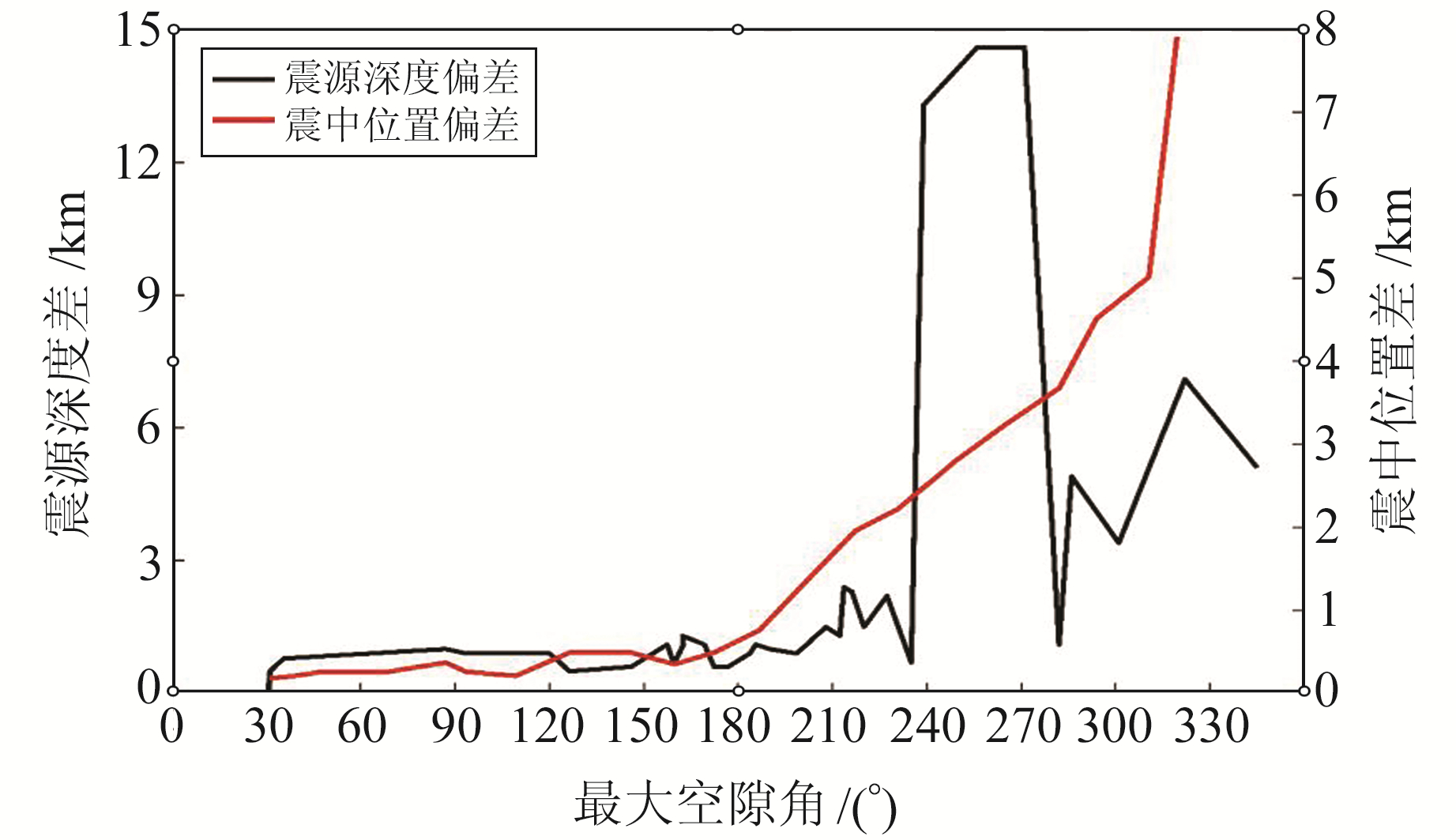
台站布局包括参与定位的台站数量、台站分布、最大空隙角和最小震中距等,相对而言,最小震中距的影响不明显[17]。本文模拟地震震中位于山西中部,台站几乎均匀分布于以震中为中心的四象限内,另外台站数量和最大空隙角并非相互独立,通常参与定位的台站越多最大空隙角越小。因此,本文采用抛台法逐步减小台站数,从而增加最大空隙角,同时改变台站分布结构,每减少1个台站均重新定位,计算震源位置和初始位置的偏差,得到最大空隙角与震源位置差之间的关系(图 5)。由图可知,震中位置和震源深度随最大空隙角的增大整体呈逐步上升趋势,当最大空隙角为0°~90°时,震中位置差普遍小于0.3 km,震源深度偏差小于2 km;当最大空隙角增大至150°时,震中位置差略有增加,但也基本小于0.5 km;当最大空隙角为180°~270°时,震中位置和震源深度的偏差开始增大,且随最大空隙角的增加变化明显,震中位置差由不足1 km增大至近4 km,几乎呈线性增长。与此同时,震源深度差也呈突跳变化,最大近15 km;当最大空隙角超过270°后,震中位置差进一步增大,最大达7.91 km,而震源深度偏差有所回落,可能受震中位置出现较大偏差的影响。
|
图 5 最大空隙角和震源位置差变化的关系 Fig. 5 Relationship between maximum void angle and source position difference |
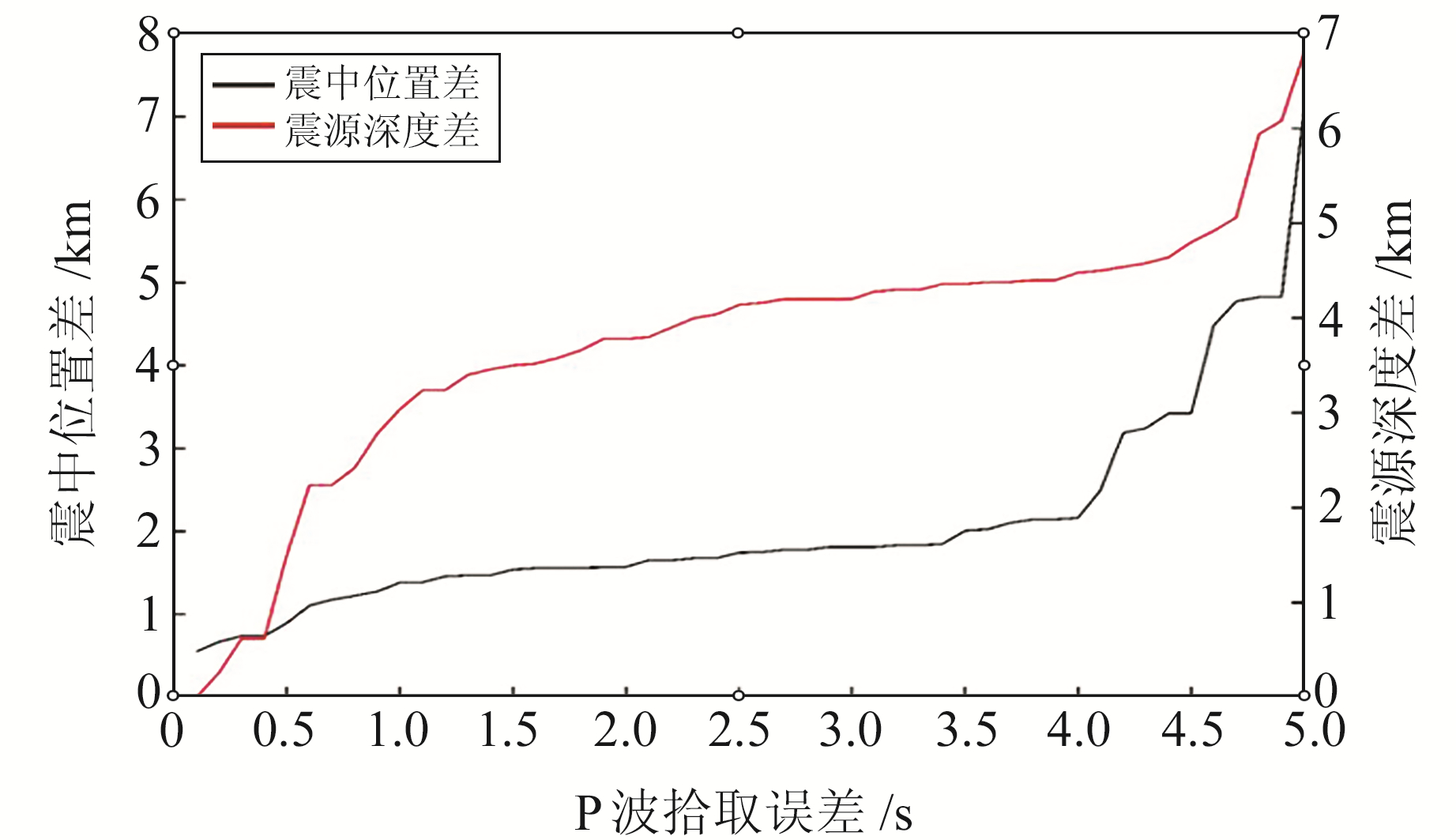
人工拾取震相会不可避免地存在一定误差,但大量震相拾取的结果基本满足高斯分布。本文在理论走时的基础上增加符合高斯分布的扰动,扰动标准差由0 s开始,以0.2 s为步长逐步增大到5 s。由于S波是后续震相,拾取精度小于P波,因此扰动幅度设定为P波的2倍。重新测定震源位置,得到震中位置和震源深度的偏差随P波震相扰动的变化规律,具体见图 6。显然,震中位置和震源深度偏差随P波拾取误差的增大而增大,且震源深度变化更为明显。震中位置和震源深度偏差在P波拾取误差不足4 s时变化平稳,偏差较小,超过4 s后偏差明显增大。当误差标准差达到5 s时,震中位置差最大为6 km,震源深度差则接近7 km,若再叠加地壳速度模型和台网布局的误差,偏差值可能会更大。所以,震相拾取精度直接影响台网的地震定位误差,P波震相最大误差不应该超过4 s。
|
图 6 P波拾取误差和震源位置差变化的关系 Fig. 6 Relation between P wave picking errorand source position difference |
本文利用数值模拟方法,定量分析地壳速度模型、台网布局及震相拾取精度等因素对山西台网地震定位的影响,得到如下结论:
1) 地壳速度模型、台网布局及震相拾取精度均可对震源位置的准确测定造成不同程度的影响,尤其对震源深度的影响更明显。
2) 当最大空隙角小于30°且震相拾取精度较高时,由地壳速度模型差异导致的山西台网地震定位震中位置差不超过5 km,但震源深度偏差可能大于20 km;上地壳P波速度(v1)对震中位置的影响最大,而震源深度受莫霍面深度的影响显著。
3) 震相拾取精度直接影响着震中位置的测定,当速度模型选取恰当、台站分布均匀、最大空隙角小于30°时,为使震中位置符合Ⅰ类精度(5 km)要求,P波拾取误差不得超过4 s。
4) 在条件允许的情况下,为保证地震定位有较高的精度,应尽可能减小最大空隙角,使其保持在180°以内。
| [1] |
朱元清, 赵仲和. 提高地震定位精度新方法的研究[J]. 地震地磁观测与研究, 1997, 18(5): 59-67 (Zhu Yuanqing, Zhao Zhonghe. Research on the New Method to Raise Earthquake Location Accuracy[J]. Seismological and Geomangnetic Observation and Research, 1997, 18(5): 59-67)
(  0) 0) |
| [2] |
Hauksson E, Yang W, Shearer P M. Waveform Relocated Earthquake Catalog for Southern California(1981 to June 2011)[J]. Bulletin of the Seismological Society of America, 2012, 102(5): 2 239-2 244 DOI:10.1785/0120120010
(  0) 0) |
| [3] |
Rubin A M, Gillard D, Got J L. Streaks of Microearthquakes along Creeping Faults[J]. Nature, 1999, 400(6 745): 635-641
(  0) 0) |
| [4] |
Rubin A M. Aftershocks of Microearthquakes as Probes of the Mechanics of Rupture[J]. Journal of Geophysical Research: Solid Earth, 2002, 107(B7)
(  0) 0) |
| [5] |
Kato A, Obara K, Igarashi T, et al. Propagation of Slow Slip Leading up to the 2011 MW9.0 Tohoku-Oki Earthquake[J]. Science, 2012, 335(6 069): 705-708
(  0) 0) |
| [6] |
尹陈, 刘鸿, 李亚林, 等. 微地震监测定位精度分析[J]. 地球物理学进展, 2013, 28(2): 800-807 (Yin Chen, Liu Hong, Li Yalin, et al. The Precision Analysis of the Microseismic Location[J]. Progress in Geophysics, 2013, 28(2): 800-807)
(  0) 0) |
| [7] |
李楠. 微震震源定位的关键因素作用机制及可靠性研究[D]. 徐州: 中国矿业大学, 2014 (Li Nan. Research on Mechanisms of Key Factors and Reliability for Microseismic Source Location[D]. Xuzhou: China University of Mining and Technology, 2014)
(  0) 0) |
| [8] |
蒋长胜, 吴忠良, 李宇彤. 首都圈地区"重复地震"及其在区域地震台网定位精度评价中的应用[J]. 地球物理学报, 2008, 51(3): 817-827 (Jiang Changsheng, Wu Zhongliang, Li Yutong. Estimating the Location Accuracy of the Beijing Capital Digital Seismograph Network Using Repeating Events[J]. Chinese Journal of Geophysics, 2008, 51(3): 817-827)
(  0) 0) |
| [9] |
黄文辉, 吕作勇, 康英, 等. 人工爆破检验区域地震台网地震定位精度[J]. 地震地磁观测与研究, 2017, 38(2): 77-80 (Huang Wenhui, Lü Zuoyong, Kang Ying, et al. Testing Earthquake Location Accuracy of Regional Seismic Network by Artificial Explosion[J]. Seismological and Geomagnetic Observation and Research, 2017, 38(2): 77-80)
(  0) 0) |
| [10] |
吕作勇, 杨传成, 房立华. 广东地震台网近震定位精度的经验性GT准则[J]. 震灾防御技术, 2014, 9(增1): 657-664 (Lü Zuoyong, Yang Chuancheng, Fang Lihua. Empirical Ground Truth Criteria for Location Accuracy of near Earthquake on Guangdong Seismic Network[J]. Technology for Earthquake Disaster Prevention, 2014, 9(S1): 657-664 DOI:10.11899/zzfy2014s112)
(  0) 0) |
| [11] |
张志斌, 金花, 王晓飞. 单纯形定位方法在新疆数字地震台网的测定精度分析[J]. 震灾防御技术, 2019, 14(1): 200-209 (Zhang Zhibin, Jin Hua, Wang Xiaofei. Analysis of Precision of the Simplex Location Method in the Xinjiang Digital Seismic Network[J]. Technology for Earthquake Disaster Prevention, 2019, 14(1): 200-209)
(  0) 0) |
| [12] |
Hardy R. Acoustic Emission/Microseismic Activity: VolumeⅠ: Principles, Techniques and Geotechnical Applications[M]. Netherlands: Balkema Publisher, 2003
(  0) 0) |
| [13] |
殷伟伟, 陈存田, 宋秀青, 等. 山西2015地壳速度模型研究[J]. 中国地震, 2018, 34(4): 720-730 (Yin Weiwei, Chen Cuntian, Song Xiuqing, et al. The 2015 Crustal Velocity Model for the Shanxi Region[J]. Earthquake Research in China, 2018, 34(4): 720-730)
(  0) 0) |
| [14] |
Schweitzer J. HYPOSAT-An Enhanced Routine to Locate Seismic Events[J]. Pure and Applied Geophysics, 2001, 158(1-2): 277-289
(  0) 0) |
| [15] |
中国地震局监测预报司. 测震学原理与方法[M]. 北京: 地震出版社, 2017 (Monitoring and Forecasting Department of CEA. Principles and Methods of Seismology[M]. Beijing: Seismological Press, 2017)
(  0) 0) |
| [16] |
朱元清, 宋秀青, 刘双庆, 等. 中国地震测定参考速度结构研究[M]. 北京: 地震出版社, 2017 (Zhu Yuanqing, Song Xiuqing, Liu Shuangqing, et al. Research on Earthquake Reference Velocity Structure of China[M]. Beijing: Seismological Press, 2017)
(  0) 0) |
| [17] |
苏亚军, 靳平, 李莎, 等. 国际监测系统(IMS)对内华达地区地震事件的检测和定位能力分析[J]. 地震学报, 2012, 34(3): 323-330 (Su Yajun, Jin Ping, Li Sha, et al. Evaluation of the Detection and Location Capability of IMS for Seismic Events Occurred in US Nevada[J]. Acta Seismologica Sinica, 2012, 34(3): 323-330)
(  0) 0) |
2. National Continental Rift Valley Dynamics Observatory of Taiyuan, Jinci Town, Taiyuan 030025, China
 2024, Vol. 44
2024, Vol. 44


