2. 中国地震局地震大地测量重点实验室,武汉市洪山侧路40号,430071;
3. 湖北省地震局,武汉市洪山侧路48号,430071
地震是造成人员伤亡和经济损失最为严重的自然灾害之一。自19世纪70年代后期现代地震学创立以来的140余年里,地震孕育与发生的规律和机理一直是地震学研究的重要方向[1]。
地表重力变化包含有丰富的构造运动信息,是研究地震孕育与发生过程的重要数据和手段[2-4]。近年来,我国研究人员利用基于地震重力观测获取的地表重力变化结果,在2008年汶川8.0级地震[5]、2013年芦山7.0级地震[6]、2016年门源6.4级地震[7]等强震地点判定工作中取得良好效果,显示出重力场变化信息在认识地震孕育和发生规律中具有的独特作用。一些学者对地震前后重力变化特征进行总结,进一步获得一些典型的地震前重力变化异常现象指标, 如四象限分布特征中心附近往往对强震发生地点的判定具有指示意义[8]。
然而,前述研究对于重力变化异常特征区的识别主要采用人工判读方式,一方面耗时费力,另一方面也存在对研究人员的经验依赖问题。在分析不同研究区域、不同时间尺度和不同空间尺度的大量重力变化图像时,往往难以对重力异常特征区进行全面统计分析。近年来快速发展的基于机器学习的图像识别方法为重力变化异常特征区的快速自动化识别提供了可能。
2010年,Mikolov等[9]提出初代图像识别算法R-CNN。此后,基于深度学习的目标检测方法不断涌现,如Faster R-CNN、Mask R-CNN、YOLO(you only look once)等。其中,YOLO算法在检测速度上较R-CNN等算法具有明显优势,经过多次迭代升级,其算法结构逐渐完善成熟,已成为当前目标检测研究应用的热点之一。在YOLO各版本算法中,YOLOv5在算法性能和检测速度上具有较好的均衡性,具有更广泛的应用。Liu等[10]对YOLOv5各分支训练的平均精度与速度的对应关系的统计结果表明,YOLOv5s在高精度的情况下识别速度最快。
本文拟采用YOLOv5s算法,以近年来我国南北地震带地区不同时空尺度的重力变化图像为例,研究重力变化四象限异常特征区自动化识别方法。本文结果可为强震前重力变化异常快速识别提供技术支撑,并为重力场变化异常特征与地震孕育发生的机理研究提供参考。
1 模型构建 1.1 YOLOv5模型YOLOv5是目前应用较为广泛的单阶段目标检测模型。该模型不仅在YOLOv4的基础上延续使用Mosaic数据增强功能,同时升级自适应锚框匹配、标签缩放以及图像自适应等数据增强功能,可有效提高对小图像的识别精度,代码结构也更加简洁,运行速度显著提高。
YOLOv5由Input(输入端)、Backbone(骨干网络)、Neck(颈部结构)、Head(头部结构)4个部分组成,网络架构如图 1所示。

|
图 1 YOLOv5结构示意图 Fig. 1 YOLOv5 structure diagram |
算法从Input开始,选取640像素×640像素作为输入,随后传输至Backbone提取图像信息,再将初始输入图像转化为多层特征图,用于后续目标检测。Backbone部分主要由Focus模块、CBL模块、CSP1_X模块组成,其中Focus模块将多个经Slice层切割后的结果综合起来,交由CBL模块处理。CBL模块由卷积层、BN层和激活函数Leaky Relu三个部分组成,主要功能为提取局部空间信息,同时Leaky Relu函数可以避免神经元死亡,从而进一步提高模型的性能。CSP1_X模块是在CBL模块上增加Res单元层、CONV层以及Concate层升级而来,其结构图如图 2所示。

|
图 2 CSP1_X模块结构示意图 Fig. 2 CSP1 _X module structure diagram |
Neck网络处于Backbone与Head之间。YOLOv5中添加FPN+PAN结构,将Concat操作后的CBL模块更换为CSP2_1模块,利用该模块进一步提取Backbone部分的特征,借此提高特征的多样性,同时增强模型的鲁棒性,加强模型的抗噪能力。Head输出端获取网络的输出,完成目标检测结果的处理,利用已经提取的特征作出预测。
YOLOv5模型的分支子模型众多,按模型复杂度可依次排列为YOLOv5n、YOLOv5s、YOLOv5m、YOLOv5l、YOLOv5x等,由于复杂度不同,每个模型具有不同的优缺点,模型复杂程度越高,则训练精度越高,训练时间也越长;相反,模型复杂度越低,则训练精度越低,训练时间也越短。YOLOv5各函数分支训练的平均精度与速度的对应关系表明,YOLOv5s在高精度的情况下识别速度最快。因此,本文选择YOLOv5s模型,在保证对四象限区域识别准确性的前提下,相同时间内可识别更多区域。
1.2 模型评价指标模型预测结果的类别可分为正例(positive, P)与负例(negative, N)两种,正例与负例的布尔类型分为真(true, T)与假(false, F),故预测结果共有4种,4种结果的混淆矩阵如表 1所示。
|
|
表 1 预测结果的混淆矩阵 Tab. 1 Confusion matrix of prediction results |
模型的优劣可用精度(precision)、召回率(recall)、平均精度(average precision, AP)3个指标进行衡量。精度(precision)是衡量模型预测准确率的重要标准,表示预测的正例(TP)在包含正例与反例(FP)所有预测结果总数中的占比,精度越高,模型预测越准确。其计算公式如下:
| $\text { precision }=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}} $ | (1) |
召回率(recall)是预测成功的正例与总正例的比值,总正例包含预测成功的正例与未预测成功的正例(FN)。召回率越高,漏判的情况越少,因此应尽量降低召回率,以提高模型的准确性。召回率计算公式如下:
| $ \text { recall }=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}} $ | (2) |
平均精度是precision-recall曲线所围成的面积值,在全类别内进行平均可得到全类平均精度(mAP)。由于在本次实验中只有四象限特征区一种识别内容,故平均精度与全类平均精度相等,其计算公式如下:
| $ \mathrm{mAP}=\frac{\operatorname{sum}(\mathrm{AP})}{N} $ | (3) |
式中,N为类别数量。
2 数据集处理与模型训练 2.1 重力变化图像南北地震带是我国地震重力监测的重点地区之一。该地区自2014年起形成常态化的整体观测(测点分布如图 3所示,图中蓝色五角星为绝对重力测点,红色圆点为相对重力测点,浅蓝色线为活动块体边界线),至2022年总计获得18期观测成果。根据国家地震科学数据共享中心提供的地震目录,2014~2022年期间南北地震带重力测区内共发生7.0级以上地震2次、6.0~6.9级地震13次、5.0~5.9级地震62次。丰富的观测数据和频繁发生的中强地震使南北地震带地区成为研究重力场变化与地震发生关系的理想区域。本文将中国地震局重力技术管理组提供的南北地震带地区重力变化图像作为图像识别训练的数据集。经统计,2014~2022年时段内共有153幅不同时间尺度的重力变化图像。

|
图 3 南北地震带地区重力测点分布 Fig. 3 Distribution of gravity measurement points in the north-south seismic zone |
重力变化图像处理时首先要通过人工判别的方式对四象限特征区域进行标注。由于四象限区域的面积具有大小不唯一的特点,故而选取标签区域的大小会影响识别结果,标签区域过小,会导致异常区域的特征不明显;标签区域过大,则会导致背景区域中掺杂的重力变化区域的特征影响实际异常区域的特征,从而影响识别精度。本文利用改变图片大小、固定标签大小的方式,以保证不同范围内的四象限区域标签大小一致,并通过缩放,减少标签中最终划定区域所受边界位置模糊的影响,以保留更多特征。此外,由于重力变化区域的特征较少,为降低识别区域周围的重力变化对最终训练结果产生的负面影响,在划定标签区域时,应尽可能涵盖完整的异常区域,同时提高异常区域占标签总面积的比例。
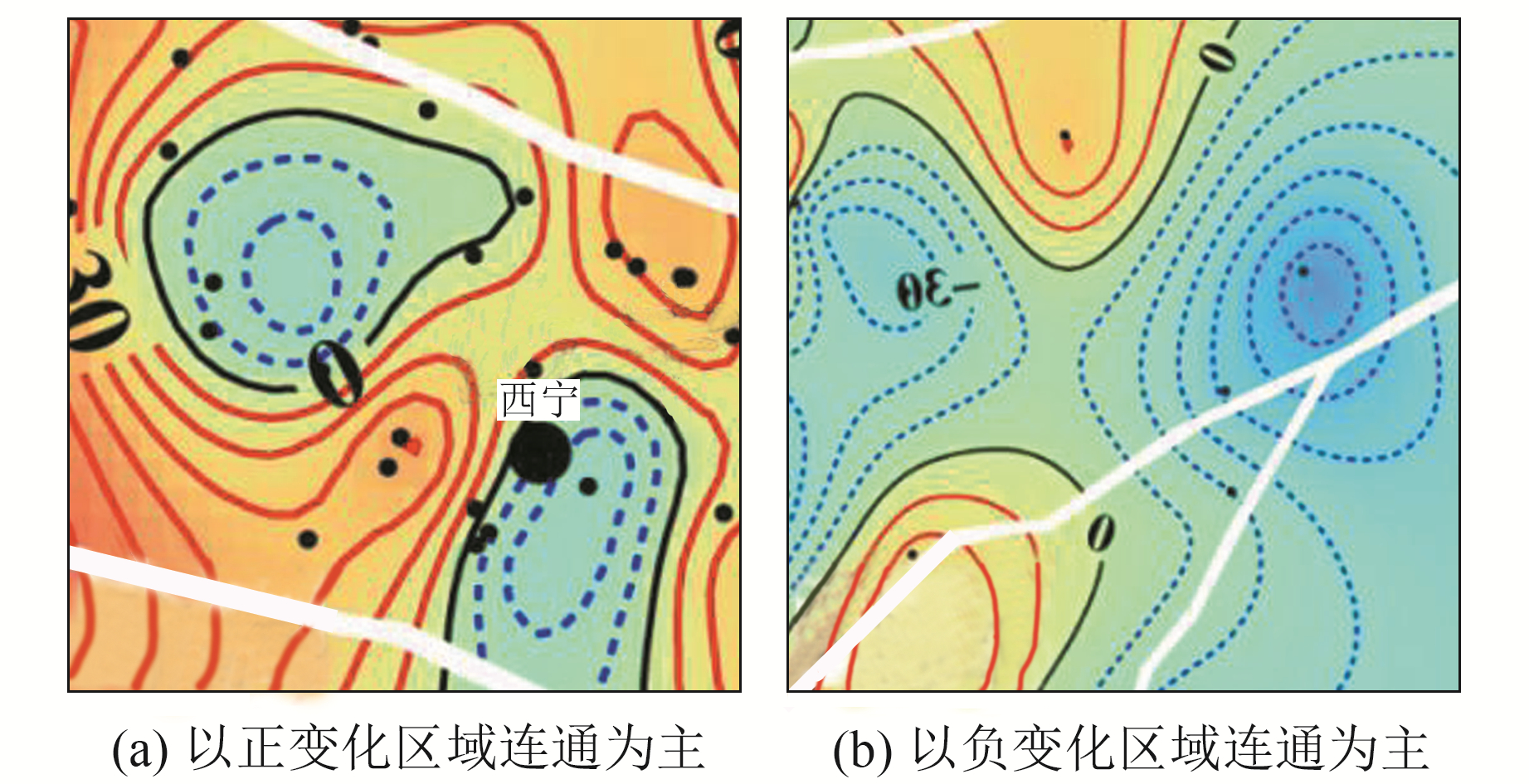
重力变化图像中的四象限区域分为以正变化区域为主的连通类型与以负变化区域为主的连通类型,两种标签类型同属重力异常四象限区域,异常区域的色度结构相反。本文将两种区域标记为相同标签,预测结果中同样标为同种类别,图 4为两种不同相连方式的四象限区域的标签示例。使用LabelImg对153幅图像进行四象限区域标注,共获得237个四象限区域标签。
|
图 4 不同类型的标签示例 Fig. 4 Examples of different types of labels |
为满足机器学习中模型训练对训练集数量的要求,利用翻转、镜像、色度调整、亮度调整、随机添加噪声等数据增强方式对标注好的数据集进行进一步扩增,最终获得2 065幅图像、3 199个四象限标签区域。将数据集制作为VOC格式,按照9 ∶1的比例分为训练集与测试集,其中训练集为1 858幅图像,测试集为207幅图像。图 5为经处理后的训练集示例。

|
图 5 训练集示例 Fig. 5 Example of training set |
Pytorch深度学习框架具有简洁高效、性能优良等优点,本文使用该框架进行模型搭建,模型环境及参数如表 2所示。经过计算,使用该参数总步长可达50 000以上,对模型训练具有良好的效果。
|
|
表 2 实验环境 Tab. 2 Experimental environment |
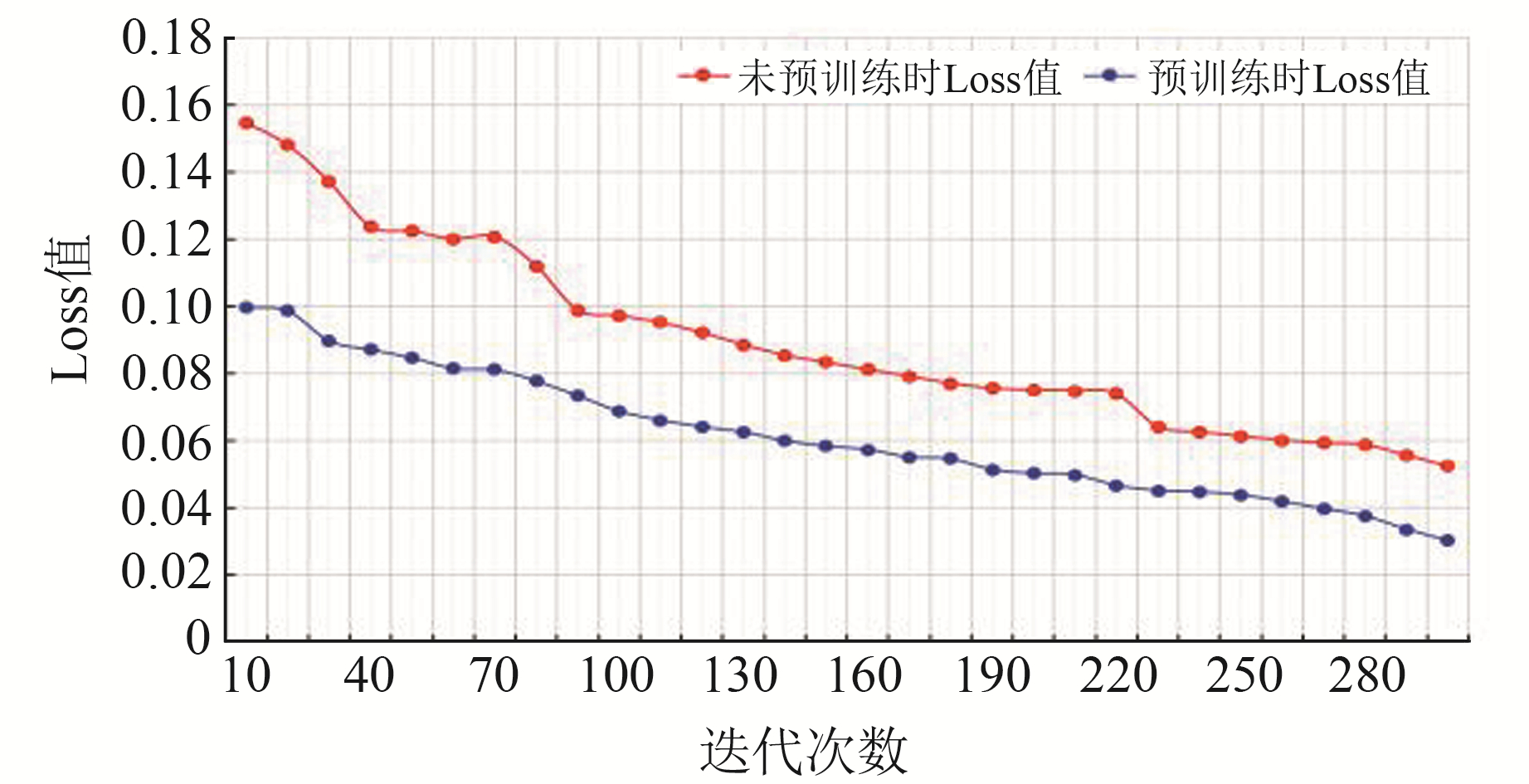
总体训练前,进行预训练能有效提升训练效率,节省计算资源。本文使用少量样本进行预训练,将所得参数作为初始训练参数加入到大样本的训练中。对比结果如图 6所示,图中Loss值代表收敛效果。结果表明,经过预训练,模型获得更快的收敛速度,在相同迭代次数内收敛程度更好。
|
图 6 预训练与非预训练收敛效果对比 Fig. 6 Comparison of convergence effect betweenpre-training and non-pre-training |
利用训练后模型对207幅测试集图像进行识别测试,结果如表 3所示。模型总体精度为94.09%,YOLOv5s在实际图像识别应用中,对于小目标的识别精度普遍优于90%,本模型精度处于合理范围,结果具有参考价值。模型召回率为89.74%,说明能够有效识别约90%的重力变化四象限特征区域,具有较好的预测结果。模型平均精度达到95.25%,表明模型与所识别图像拟合程度达到较好水平,目标区域的识别定位准确且覆盖范围合理。
|
|
表 3 测试结果统计 Tab. 3 Statistics of test results |
对测试集中不同相连类型的重力异常区域进行统计,正变化连通为主的区域共116个,精度为92.92%;负变化连通为主的区域共93个,精度为95.54%。将两种连通类型的不同区域标为同种标签时,二者识别精度接近,对总体精度影响较小,显示模型在不同类型区域的识别效果较为稳定。因此,选择此类标签方式可以在不影响最终结果的情况下减少前期标注工作量,尤其在大量数据需要进行标识的情况下具有较为明显的优势。
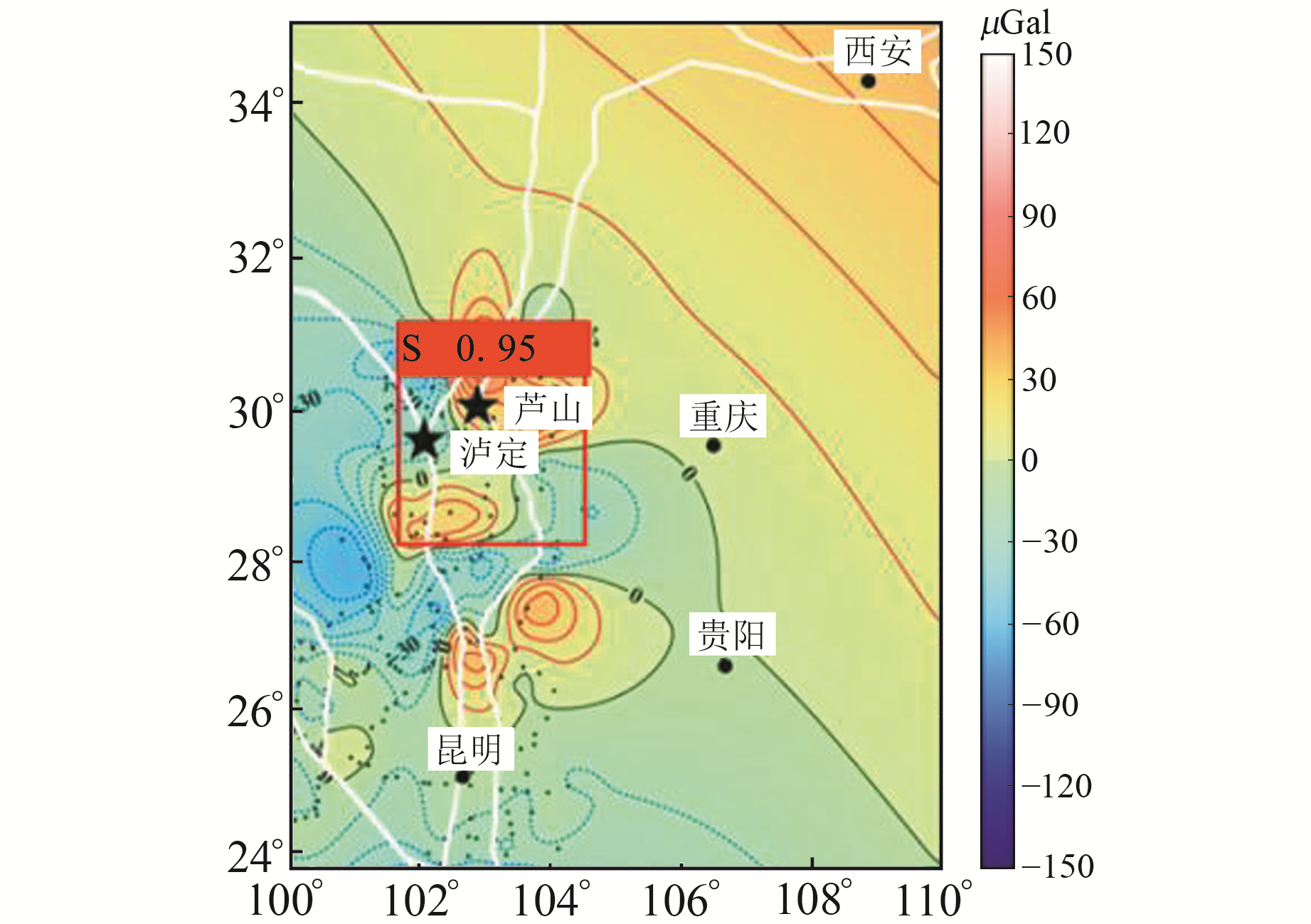
图 7为测试集中2021-09~2022-05约0.5 a时间尺度的重力变化图像识别结果,图中红色方框为模型识别区(S为四象限区域标签名称,0.95为置信度),下部黑色五角星为泸定6.8级地震震中,上部黑色五角星为芦山6.1级地震震中。识别区域预测框较为完整地包含了龙门山断裂南段至安宁河断裂地区重力变化四象限区域。2022-06-01四川芦山地区发生6.1级地震,同年09-05泸定地区发生6.8级地震,两次地震的震中都位于模型识别圈定的四象限特征区范围内。这一方面进一步表明四象限特征对于地震地点判定具有重要的参考意义,另一方面也表明本文基于机器学习的四象限特征区识别方法对于重力异常区域的筛选以及潜在的地震风险研判具有较好的应用潜力。
|
图 7 识别结果示例 Fig. 7 Example of recognition results |
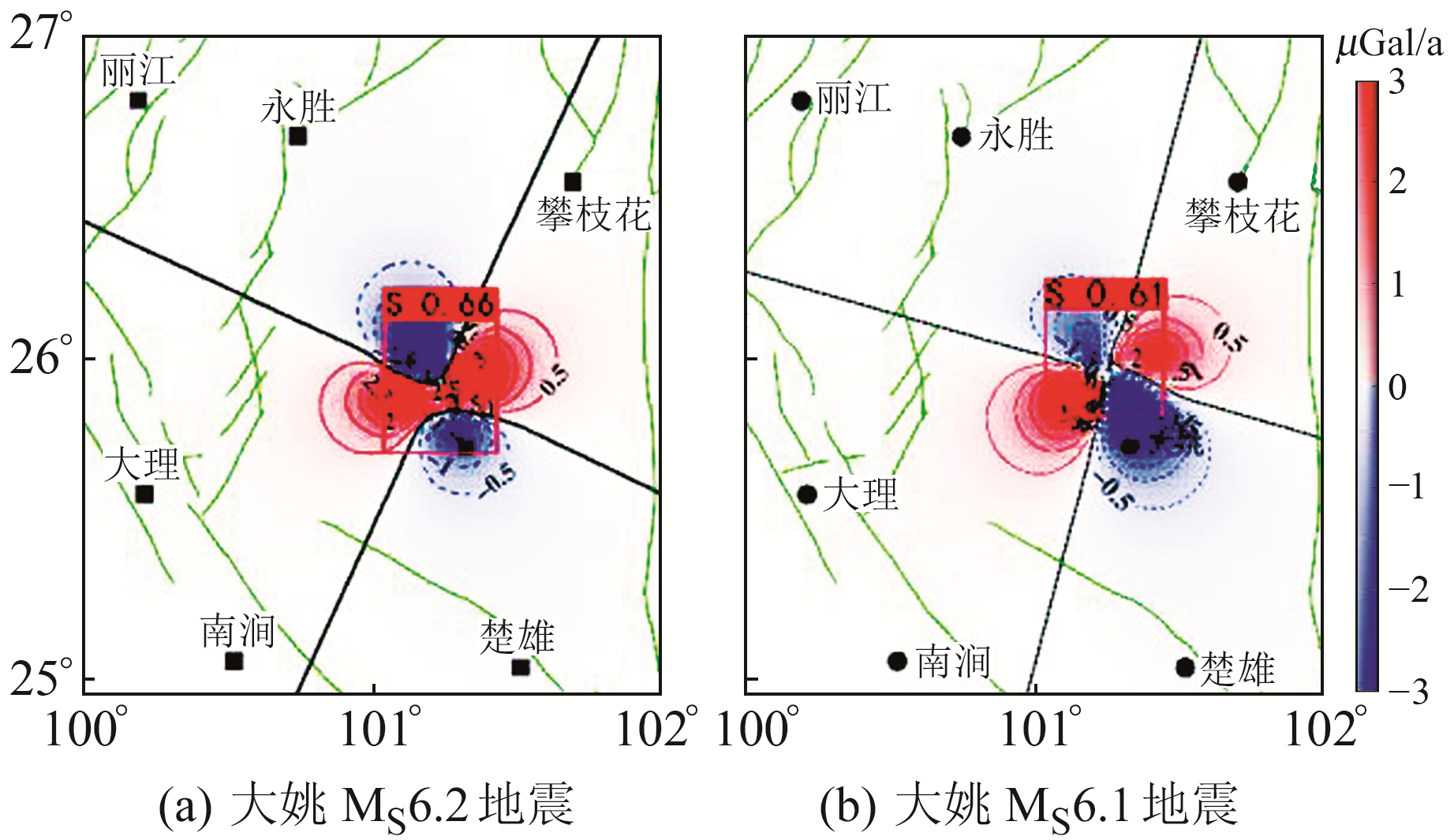
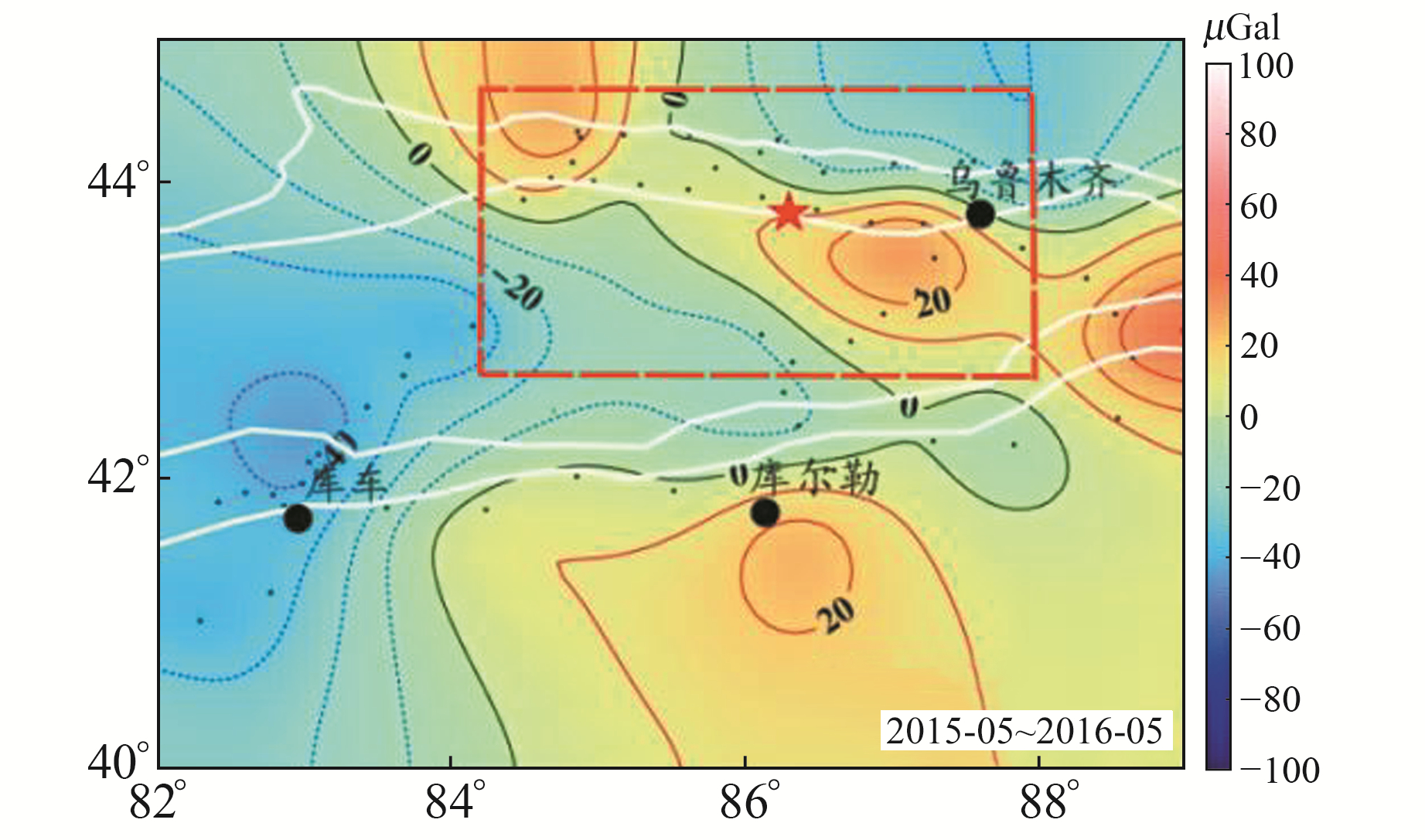
为进一步验证训练模型的识别效果,另选取部分现有文献中发布的具有四象限特征的重力变化图像进行测试。首先,对文献中发表的基于位错理论计算的2003年大姚MS6.2、MS6.1两次地震同震变化结果[11]进行识别测试。由图 8可知,重力变化图像表现出较为标准的四象限分布特征,而识别区域则准确覆盖了四象限中心区域。其次,对文献中发表的基于实测数据计算的2016-12呼图壁6.2级地震前1 a时间尺度重力变化结果[12]进行识别测试,但结果显示(图 9)模型未能识别出红色虚线框内基于人工判读划定的四象限特征区。对图 9进行分析发现,文献中标注的四象限特征相比标准四象限特征存在明显的畸变,这也表明,由于四象限特征区的人工判读仍具备较大的不确定性,异常特征区识别仍需要更多的样本进行训练,以进一步提高模型对于非标准四象限特征区的识别效果。
|
图 8 标准四象限识别结果示例(重力变化图引自文献[11]) Fig. 8 Example of standard four-quadrantrecognition results (the gravity change map is cited from the literature[11]) |
|
图 9 2016年呼图壁MS6.2地震震前重力变化图像(重力变化图引自文献[12]) Fig. 9 Image of gravity change before Hutubi MS6.2 earthquake in 2016(the figure of gravity change is cited from literature[12]) |
针对基于人工判读方式对重力变化异常特征区进行识别存在效率低下的问题,本文提出利用YOLOv5s算法进行重力变化四象限特征区识别的方法, 并基于南北地震带地区实测重力变化图像进行训练和测试,主要得出以下认识:
1) 对基于YOLOv5s进行重力变化异常识别所涉及的训练集建立和训练方法进行探索测试,结果表明,采用图像增强、对图像进行尺寸调整并同时保持标签大小不变等策略,可利用有限数量的重力变化图像构建训练效果较为理想的数据集。采用在总体训练前先进行预训练的策略,可使模型获得更快的收敛速度,在相同迭代次数内收敛程度更好。此外,将正变化为主和负变化为主的两种区域连通类型的四象限特征区域标注为同种标签,对图像识别结果无影响,但可显著减少图像特征区标注的工作量。
2) 测试集图像识别统计结果表明,模型预测结果的精度、召回率、平均精度等指标均处于合理范围。南北地震带2021-09~2022-05时段的重力变化图像识别结果表明,模型较为准确地识别出龙门山断裂南段至安宁河断裂地区重力变化四象限特征区域,且识别区域内先后发生2022-06芦山6.1级地震和2022-09泸定6.8级地震。这也表明,本文方法对于重力异常区域的筛选以及潜在的地震风险研判具有较好的应用潜力。
3) 对现有文献中标注有四象限特征区的重力变化图像的识别测试结果表明,本文模型对标准四象限特征区具有较好的识别能力,但对于非标准四象限特征区的识别仍存在一定不足。由于四象限特征区的判定目前缺少较为严格的标准,因此想要获取更为合理的四象限相关特征,更为全面和准确地识别四象限异常特征区,仍需要构建数量更多、标注更为合理的数据集。
| [1] |
陈运泰. 地震预测: 回顾与展望[J]. 中国科学: 地球科学, 2009, 39(12): 1 633-1 658 (Chen Yuntai. Earthquake Prediction: Review and Prospect[J]. Science China Earth Sciences, 2009, 39(12): 1 633-1 658)
(  0) 0) |
| [2] |
Barnes D F. Gravity Changes during the Alaska Earthquake[J]. Journal of Geophysical Research, 1966, 71(2): 451-456 DOI:10.1029/JZ071i002p00451
(  0) 0) |
| [3] |
Hunt T M. Gravity Changes Associated with the 1968 Inangahua Earthquake[J]. New Zealand Journal of Geology and Geophysics, 1970, 13(4): 1 050-1 051 DOI:10.1080/00288306.1970.10418220
(  0) 0) |
| [4] |
陈运泰, 顾浩鼎, 卢造勋. 1975年海城地震与1976年唐山地震前后的重力变化[J]. 地震学报, 1980(1): 21-31 (Chen Yuntai, GU Haoding, Lu Zaoxun. Gravity Changes before and after the 1975 Haicheng Earthquake and 1976 Tangshan Earthquake[J]. Acta Seismologica Sinica, 1980(1): 21-31)
(  0) 0) |
| [5] |
申重阳, 李辉, 孙少安, 等. 重力场动态变化与汶川MS8.0地震孕育过程[J]. 地球物理学报, 2009, 52(10): 2 547-2 557 (Shen Chongyang, Li Hui, Sun Shaoan, et al. Dynamic Variations of Gravity and the Preparation Process of the Wenchuan MS8.0 Earthquake[J]. Chinese Journal of Geophysics, 2009, 52(10): 2 547-2 557)
(  0) 0) |
| [6] |
祝意青, 闻学泽, 孙和平, 等. 2013年四川芦山MS7.0地震前的重力变化[J]. 地球物理学报, 2013, 6: 1 887-1 894 (Zhu Yiqing, Wen Xueze, Sun Heping, et al. Gravity Changes before the 2013 Lushan MS7.0 Earthquake in Sichuan Province[J]. Chinese Journal of Geophysics, 2013, 6: 1 887-1 894)
(  0) 0) |
| [7] |
祝意青, 李铁明, 郝明, 等. 2016年青海门源MS6.4地震前重力变化[J]. 地球物理学报, 2016, 59(10): 3 744-3 752 (Zhu Yiqing, Li Tieming, Hao Ming, et al. Gravity Changes before the Menyuan, Qinghai MS6.4 Earthquake of 2016[J]. Chinese Journal of Geophysics, 2016, 59(10): 3 744-3 752)
(  0) 0) |
| [8] |
祝意青, 申重阳, 张国庆, 等. 我国流动重力监测预报发展之再思考[J]. 大地测量与地球动力学, 2018, 38(5): 441-446 (Zhu Yiqing, Shen Chongyang, Zhang Guoqing, et al. Rethinking the Development of Earthquake Monitoring and Prediction in Mobile Gravity[J]. Journal of Geodesy and Geodynamics, 2018, 38(5): 441-446)
(  0) 0) |
| [9] |
Mikolov T, Karafiát M, Burget L, et al. Recurrent Neural Network Based Language Model[C]. Conference of the International Speech Communication Association, Makuhari, 2010
(  0) 0) |
| [10] |
Liu K Y, Tang H T, He S, et al. Performance Validation of Yolo Variants for Object Detection[C]. The 2021 International Conference on Bioinformatics and Intelligent Computing, Harbin, 2021
(  0) 0) |
| [11] |
郝洪涛, 王青华, 张新林, 等. 滇西地震预报实验场区重力长期变化特征及其机理[J]. 地震地质, 2022, 44(4): 876-894 (Hao Hongtao, Wang Qinghua, Zhang Xinlin, et al. A Study on Long-Term Gravity Variation and Its Mechanism in the Western Yunnan Earthquake Prediction Study Area[J]. Seismology and Geology, 2022, 44(4): 876-894)
(  0) 0) |
| [12] |
申重阳, 祝意青, 胡敏章, 等. 中国大陆重力场时变监测与强震预测[J]. 中国地震, 2020, 36(4): 729-743 (Shen Chongyang, Zhu Yiqing, Hu Minzhang, et al. Time-Varying Gravity Field Monitoring and Strong Earthquake Prediction on the Chinese Mainland[J]. Earthquake Research in China, 2020, 36(4): 729-743)
(  0) 0) |
2. Key Laboratory of Earthquake Geodesy, CEA, 40 Hongshance Road, Wuhan 430071, China;
3. Hubei Earthquake Agency, 48 Hongshance Road, Wuhan 430071, China
 2024, Vol. 44
2024, Vol. 44


