重力场是地球的基本物理场,通过确定地球重力场及其变化可以反映出地球内部质量分布以及地表物质迁移情况[1]。GRACE(gravity recovery and climate experiment)重力卫星为监测大尺度地球重力场变化、恢复地球重力场提供支持,它的出现解决了人们无法持续有效观测地球重力场这一难题,为地球科学研究作出重要贡献[2]。
由于GRACE采用南、北双星跟踪飞行模式,导致其观测信息也是呈南北条形分布,GRACE获得的地球时变重力场信息会出现严重的南北条带误差,这在很大程度上掩盖了真实重力信号[3]。目前,国内外学者处理条带误差的主要手段分为两大类:一是通过降低含有噪声的高阶项权重来降低噪声,比如高斯滤波等,该类方法虽然可以较好地滤除噪声,但由于是通过降低高阶权重实现的,不可避免地会损失掉一些真实高频信号,而且随着滤波半径的增大,信号损失会更严重;二是通过滤除重力场球谐系数奇偶项之间的相关性而达到滤除噪声的目的[4],如去相关滤波[5]等,此类方法对滤波造成的信号损失较小,但对于低纬度地区的滤波效果较差,仍会存在条带误差。因此,为实现最大程度地保留真实信号并且拥有较好的滤波效果,人们通常采用去相关与高斯滤波相结合的组合滤波方法。同时,在GRACE运行期间存在部分月份数据缺失,对此常用三次样条插值法对短期缺失数据进行填补。而对于GRACE与GRACE-FO两代卫星之间11个月的数据空白,莫绍兴等[6]提出利用贝叶斯卷积神经网络提取时变重力场信号有效特征,从而对缺失数据进行预测;也有专家提出利用奇异谱分析法[7]恢复两代卫星间的缺失值,均取得较好效果。
本文运用上述GRACE时变重力场滤波方法,对时变重力场球谐系数分别进行经典高斯滤波以及去相关滤波与高斯滤波的组合滤波,详细分析不同高斯滤波半径在各阶次下信噪比情况以及高斯权重系数变化情况,并据此提出通过调整高斯滤波在各阶次的权重系数,实现分步高斯滤波的方法。结果表明,在相同滤波半径下,改进后高斯滤波信噪比明显优于经典高斯滤波,同时对高斯滤波造成的区域信号泄漏也有较好改善。
1 滤波处理方法利用GRACE时变重力场反演地球表面质量变化,在大尺度范围内,我们通常近似认为地表质量变化所引起的时变重力场变化实际就是地面水质量的变化。因而通过地表质量变化模型再除以水的密度便可以得到陆地等效水高,进而计算陆地水储量变化[8]:
| $ \begin{gathered} \Delta h(\theta, \lambda)=\frac{a \rho_{\text {ave }}}{3 \rho_\omega} \sum\limits_{l=0}^{\infty} \sum\limits_{m=0}^l \frac{2 l+1}{1+k_l} \cdot \\ {\left[\Delta \bar{C}_{l m} \cos (m \lambda)+\Delta \bar{S}_{l m} \sin (m \lambda)\right] \bar{P}_{l m}(\cos \theta)} \end{gathered} $ | (1) |
式中,Δh为等效水高,λ、θ分别为经度和余纬,ρω为水的密度,a为地球赤道的平均半径,ρave为地球平均密度,l、m分别为地球重力场球谐展开项中的阶数和次数,kl为对应l阶的负荷勒夫数,
Wahr等[8]提出一种基于平滑函数的高斯滤波方法,并推导了一组高斯平滑滤波系数,应用于GRACE数据处理中。高斯滤波削弱条带误差的主要原理就是通过降低球谐系数高阶项的权重,将高阶项中存在的条带误差信号滤除掉。其高斯平滑核函数定义为:
| $ \left\{\begin{array}{l} W(\alpha)=\frac{b}{2 \pi} \frac{\mathrm{e}^{-b(1-\cos \alpha)}}{1-\mathrm{e}^{-2 b}} \\ b=\frac{\ln 2}{1-\cos (r / a)} \end{array}\right. $ | (2) |
式中,α为球面两点夹角,r为滤波半径。给出高斯滤波的递推系数:
| $ \left\{\begin{array}{l} W_0=1 \\ W_1=\frac{1+\mathrm{e}^{-2 b}}{1-\mathrm{e}^{-2 b}}-\frac{1}{b} \\ W_{l+1}=-\frac{2 l+1}{b} W_\iota+W_{l-1} \end{array}\right. $ | (3) |
Chambers等[9]研究发现,当以上高斯滤波算法在球谐系数高于50阶时存在不确定性,因此提出高斯滤波改进算法。改进算法的平滑函数如下:
| $W_l=\exp \left[-\frac{(\operatorname{lr} / a)^2}{4 \ln 2}\right] $ | (4) |
Swenson和Wahr[10]研究发现,GRACE条带误差存在的一个重要原因就是其时变重力场球谐系数奇偶项之间存在明显的相关性,因此国内外专家学者提出利用多项式拟合来去除相关性的去相关滤波方法,其基本原理就是对球谐系数项的奇、偶数阶分别进行滑动固定窗口的多项式拟合,拟合值认为是存在的相关误差,将原始球谐系数减去拟合值即为去相关滤波后的球谐系数。
Chen等[11]根据上述基本思想进行改进,提出PnMl方法。该方法原理主要为:对系数的前l阶位系数不作处理,对大于等于l阶的位系数用n阶多项式进行奇偶项拟合并扣除相关值。
同时研究发现,GRACE时变重力场模型的球谐系数精度与阶次数密切相关,低阶次系数间的相关误差小,但球谐系数的标准差随着阶数和次数的增大而增大。Duan等[12]在Swenson等[10]提出的滑动固定窗口多项式拟合去相关滤波的基础上,建立滑动可变窗口多项式拟合去相关滤波方法。
1.3 组合滤波方法随着高斯滤波半径的增大,对条带误差的滤除效果越好,但由于高斯平滑滤波是通过降低高阶项的权重系数来压制噪声,因此会不可避免地滤除掉高阶项真实信号。去相关滤波也可在一定程度上去除条带误差,但在中纬度地区仍存在噪声信息。因而,为在滤除条带噪声的同时尽量保留真实信号,国内外学者发现组合滤波方法,即去相关滤波与高斯滤波相结合的方法可以最大程度地压制噪声并保留真实信号[4]。
1.4 信噪比估计目前对各种滤波效果的评估国内外尚未有统一标准,通常采用的是通过分析滤波前后误差的RMS(root-mean-square)以及陆地与海洋信噪比(signal-to-noise ratio,SNR)方法。经研究,GRACE测量误差在陆地与海洋上大致处于同一水平,而陆地质量变化信号强于海洋,因此Chen等[11]根据此原理构建出一套基于陆地海洋信噪比最大为准则的滤波器,其信噪比公式为:
| $\text { RMS_Ratio }=\frac{\operatorname{RMS}\left(\text { MASS }_{\text {land }}+\text { Err }\right)}{\operatorname{RMS}\left(\text { MASS }_{\text {ocean }}+\text { Err }\right)} $ | (5) |
式中,MASSland为陆地质量变化,MASSocean为海洋质量变化,Err为GRACE测量误差。
2 实验分析 2.1 数据预处理本文采用得克萨斯空间研究中心(Center for Space Research, CSR)的GRACE RL06月重力场模型,模型截断阶数为60,选取2004-01~2010-12数据作为研究对象,该范围内GRACE卫星运行正常,数据质量较好,且不存在数据空白月份。
由于GRACE卫星对代表地心运动的一阶项不敏感,导致一阶项缺失,这里采用Swenson等[10]计算的一阶项进行补充。受GRACE卫星运行轨道因素影响,其解算的C20项存在较大不确定性,利用卫星激光测距(SLR)获取的C20项对其进行替换。为体现出重力场时变信息,这里选取所有月份球谐系数平均值作为背景重力场,将每月的球谐系数减去该背景重力场,得到各月时变重力场球谐系数。
2.2 高斯滤波信噪比分析郭飞宵等[3]指出,时变重力场模型低于20阶的项主要反映地幔以下的重力场信号,20~30阶项体现信号与噪声混合信息,而高于30阶项则包含更多的噪声信息。由表 1可见,高斯滤波半径为0 km(即对条带误差不进行处理)时,随着阶数的不断增大,信噪比不断变小,在球谐系数大于30阶时信噪比减小较快,至60阶时降低为1.252。这也证实高阶项以噪声为主,对真实信号掩盖严重,造成信噪比急剧减小。随着高斯滤波方法的加入,GRACE球谐系数中的噪声误差被减弱,信噪比有较明显提升,从不同阶下的信噪比情况也可以看出,当高斯滤波半径为400 km时,其信噪比在各阶均处于最优水平,因此在仅用高斯滤波去除条带误差时,常选取400 km半径的高斯滤波作为最优滤波半径。
|
|
表 1 各阶数下不同滤波半径的高斯滤波信噪比 Tab. 1 Gaussian filtering SNR for different filtering radii at different orders |
研究发现,GRACE球谐系数奇偶项之间具有相关性,因此认为GRACE球谐系数误差中存在相关性误差。为有效去除GRACE存在的误差,目前常采用组合滤波的方法,即去相关滤波+高斯滤波方法,可以最大程度地减弱条带误差项。这里选取Duan等[12]提出的去相关滤波与高斯滤波结合的组合滤波方法,不同阶数以及高斯滤波半径下的信噪比如表 2所示。可以看出,在不进行高斯滤波的情况下,经去相关滤波后的时变重力场信噪比有明显提升,这也印证了相关性误差确实存在于时变重力场球谐系数中。同时,分析去相关滤波后不同半径下的高斯滤波信噪比也可以看出,由于去相关滤波减弱了相关性误差,因此在300 km高斯滤波半径下其信噪比在各阶下均处于最优水平。
|
|
表 2 各阶数下不同滤波半径的组合滤波信噪比 Tab. 2 Combined filtering SNR with different filtering radii at different orders |
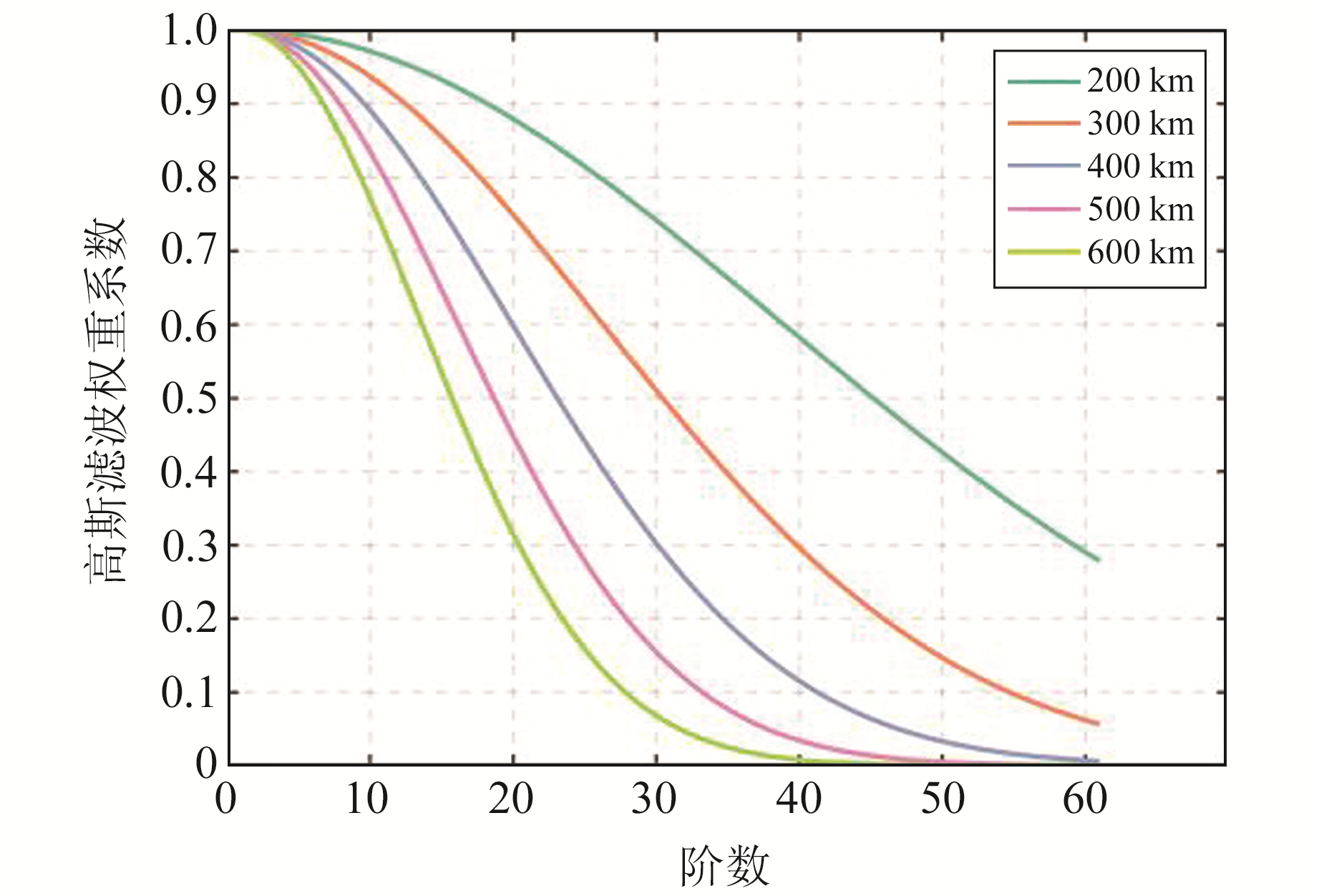
不同半径下的高斯滤波权重系数如图 1所示,可以看出,随着滤波半径的增大,高阶项的权重系数下降得越来越快。虽然压制了高阶项噪声,但由于权重系数下降过快,也会导致信号损失过多,尤其在含误差较少的低阶项部分,由于滤波半径增大,权重系数减小较快会导致真实低频信号损失。
|
图 1 不同滤波半径高斯权重系数 Fig. 1 Gaussian weight coefficients with different filtering radius |
分析表 1可知,当球谐系数阶数较低(如20阶)时,里面所包含的噪声信息较少,不同高斯滤波半径与原始球谐系数相比信噪比变化较小,且随着滤波半径的增大,权重系数下降快,会造成真实信号较快损失。为应对这种情况,本文提出一种混合半径的高斯滤波方法,即通过调整球谐系数不同阶次项的高斯权重系数进行分段高斯滤波,实现在尽可能滤除高频误差的同时尽量多地保留低频信息。
首先确定阶数L、滤波半径R和分段步数S,则可以将阶数和高斯滤波半径按下式划分:
| $ \left\{\begin{array}{l} r_0=\frac{R}{S} \\ l_0=\frac{L}{S} \\ r_i=i \cdot r_0, i=1, 2, \cdots, S \\ l_i=i \cdot l_0, i=1, 2, \cdots, S \end{array}\right. $ | (6) |
式中,r0为原始滤波半径按步长划分的滤波半径段长,l0为给定球谐阶数按步长划分后每段阶数大小,ri、li分别为第i段对应的高斯滤波半径以及所取的部分阶数。
根据式(4)给出的不同阶数半径下的改进高斯滤波权重系数Wl,可计算出每段高斯滤波半径对应的滤波半径下高斯权重系数:
| $w_i=\exp \left[-\frac{\left(l_i r_i / a\right)^2}{4 \ln 2}\right] $ | (7) |
提取不同阶数范围的高斯权重系数并进行重组,便可得到拼接后的高斯滤波权重系数。由于不同阶数对应滤波系数不同,为保证高斯滤波的平稳性,还要对组合拼接的滤波系数进行移动平均平滑处理,最终得到改进的高斯滤波权重系数:
| $ \left\{\begin{array}{l} W_1=w_1 \\ W_i=w_i\left(l_{i-1}, l_i\right), i>1 \end{array}\right. $ | (8) |
根据表 1及表 2可得出结论,只进行高斯滤波情况下,400 km高斯滤波的信噪比最优,进行组合滤波时,Duan等[12]与300 km半径高斯滤波信噪比最优。混合半径高斯滤波方法的目的就是在相同滤波半径下尽可能保留信号、提升信噪比。利用式(8)改进的高斯滤波方法进行信噪比分析(表 3),可以看出,当仅用一步进行分段高斯滤波时,分段高斯滤波即为经典高斯滤波;在仅进行混合半径高斯滤波的情况下,400 km滤波半径分两步进行滤波信噪比最大;在进行组合滤波时,分3步进行的300 km混合半径高斯滤波信噪比最大。
|
|
表 3 混合半径高斯滤波信噪比 Tab. 3 Mixed radius Gaussian filter SNR |
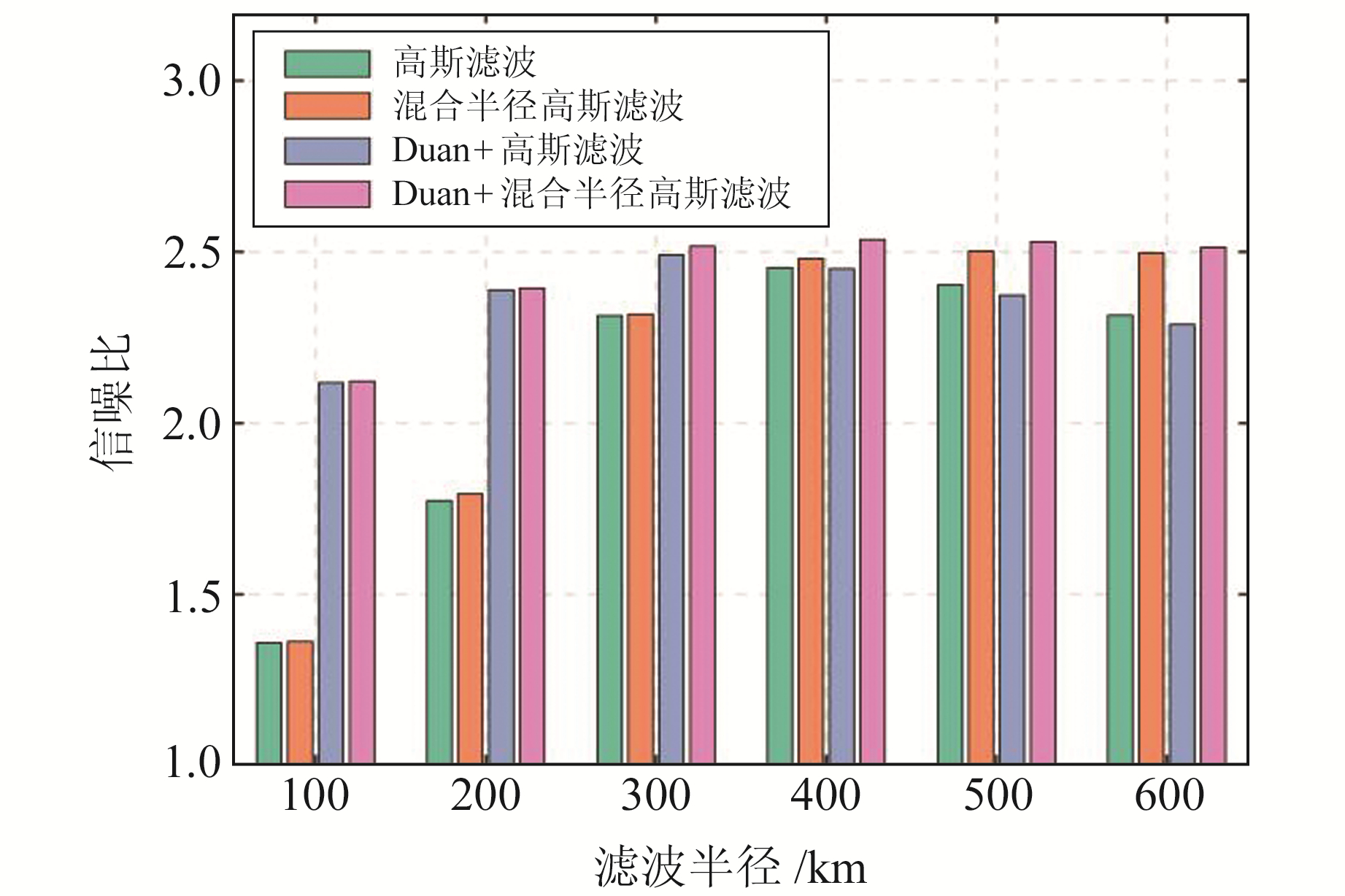
为进一步验证该方法能否更好地保留真实信号,本文对不同滤波半径的传统高斯滤波、传统组合滤波以及混合半径高斯滤波、去相关滤波[12]与混合半径高斯滤波的改进组合滤波方法的信噪比进行对比,结果如图 2所示。可以看出,混合半径高斯滤波方法在不同滤波半径下信噪比均处于较优水平。此外,随着传统高斯滤波半径的增大,因滤波造成的信号损失也越严重,而利用本文的混合半径高斯滤波方法对信号保留效果较好。
|
图 2 不同滤波方法信噪比 Fig. 2 SNR of different filtering methods |
图 3展示了利用GRACE反演全球陆地水储量变化的效果,可以看出,不进行滤波或只进行去相关滤波都无法完全提取真实的等效水高信号,而经过经典高斯滤波、经典组合滤波以及混合半径高斯滤波、Duan等[12]与混合半径高斯滤波的改进组合滤波均对条带噪声有明显压制作用,真实等效水高信号已经显现。

|
图 3 全球陆地水储量变化 Fig. 3 Changes in global land water reserves |
同时,对比分析图 3中高斯滤波(c)和混合半径高斯滤波(d)、组合滤波(e)和Duan等[12]与混合半径高斯滤波的改进组合滤波(f)两组全球陆地水储量变化中水储量信号变化较剧烈的亚马逊流域、刚果盆地地区的等效水高信号可以看出,经典高斯滤波方法对信号平滑效果更强,尤其在刚果盆地地区最为明显,而对信号过度平滑则会造成区域信号泄漏。相比之下,混合半径高斯滤波在保证去条带误差的同时还能较好地减弱信号泄漏,提高区域反演结果的准确性,这也再次印证改进高斯滤波能更好地保留水储量变化信号的判断,证明改进高斯滤波具有可行性。
3 结语本文对GRACE时变重力场条带误差的处理方法进行分析,着重讨论时变重力场球谐系数不同阶数下不同半径的高斯滤波以及组合滤波的信噪比情况。结果表明,在低于20阶时,球谐系数具有较高信噪比,因此不同半径高斯滤波效果近似;当球谐系数大于30阶时信噪比较低,因此需要用滤波手段提高信噪比。
通过不同高斯滤波半径下的经典高斯滤波以及组合滤波信噪比的分析可以发现,仅进行高斯滤波时,400 km半径高斯滤波信噪比最优,在各阶下处于最好水平;在进行Duan等[12]去相关滤波和高斯滤波组合滤波时,由于消除了球谐系数的相关性误差,因此在进行300 km半径高斯滤波时,球谐系数各阶下信噪比处于最好水平。
对得到的最优高斯滤波半径进行改进,结果表明,仅进行经典高斯滤波时,分两步进行的400 km混合半径的高斯滤波信噪比较经典高斯滤波更优;进行组合滤波时,Duan等[12]与分3步进行的300 km混合半径高斯滤波信噪比更优。对全球陆地水储量变化较为剧烈的亚马逊流域、刚果盆地地区信号分析可以看出,混合半径高斯滤波能更好地保留真实信号,减弱因高斯平滑造成的区域信号泄漏。
| [1] |
郭飞霄. 地表物质迁移的卫星大地测量反演理论与方法研究[D]. 郑州: 信息工程大学, 2019 (Guo Feixiao. Research on Satellite Geodesy Inversion Theory and Method of Surface Mass Transport[D]. Zhengzhou: Information Engineering University, 2019)
(  0) 0) |
| [2] |
罗志才, 钟波, 周浩, 等. 利用卫星重力测量确定地球重力场模型的进展[J]. 武汉大学学报: 信息科学版, 2022, 47(10): 1 713-1 727 (Luo Zhicai, Zhong Bo, Zhou Hao, et al. Progress in Determining the Earth's Gravity Field Model by Satellite Gravimetry[J]. Geomatics and Information Science of Wuhan University, 2022, 47(10): 1 713-1 727)
(  0) 0) |
| [3] |
郭飞霄, 孙中苗, 任飞龙, 等. GRACE时变重力场各向异性高斯组合滤波方法[J]. 测绘学报, 2019, 48(7): 898-907 (Guo Feixiao, Sun Zhongmiao, Ren Feilong, et al. Non-Isotropic Gaussian Combination Filtering Method of GRACE Time-Variable Gravity[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(7): 898-907)
(  0) 0) |
| [4] |
何国庆. GRACE时变重力位系数误差处理滤波方法研究[J]. 地球物理学进展, 2022, 37(1): 19-29 (He Guoqing. Study on Filtering Methods of Error Processing in GRACE Time Variable Gravity Data[J]. Progress in Geophysics, 2022, 37(1): 19-29)
(  0) 0) |
| [5] |
Kusche J, Schmidt R, Petrovic S, et al. Decorrelated GRACE Time-Variable Gravity Solutions by GFZ, and Their Validation Using a Hydrological Model[J]. Journal of Geodesy, 2009, 83(10): 903-913 DOI:10.1007/s00190-009-0308-3
(  0) 0) |
| [6] |
Mo S, Zhong Y, Shi X, et al. Improving Prediction of the Terrestrial Water Storage Anomalies during the GRACE and GRACE-FO Gap with Bayesian Convolutional Neural Networks[EB/OL]. https://arxiv.org/abs/2101.09361v2, 2021-01-21
(  0) 0) |
| [7] |
Yi S, Sneeuw N. Filling the Data Gaps within GRACE Missions Using Singular Spectrum Analysis[J]. Journal of Geophysical Research: Solid Earth, 2021, 126(5)
(  0) 0) |
| [8] |
Wahr J, Molenaar M, Bryan F. Time Variability of the Earth's Gravity Field: Hydrological and Oceanic Effects and Their Possible Detection Using GRACE[J]. Journal of Geophysical Research: Solid Earth, 1998, 103(B12): 30 205-30 229 DOI:10.1029/98JB02844
(  0) 0) |
| [9] |
Chambers D P. Evaluation of New GRACE Time-Variable Gravity Data over the Ocean[J]. Geophysical Research Letters, 2006, 33(17)
(  0) 0) |
| [10] |
Swenson S, Wahr J. Post-Processing Removal of Correlated Errors in GRACE Data[J]. Geophysical Research Letters, 2006, 33(8)
(  0) 0) |
| [11] |
Chen J L, Wilson C R, Seo K W. Optimized Smoothing of Gravity Recovery and Climate Experiment(GRACE) Time-Variable Gravity Observations[J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B6)
(  0) 0) |
| [12] |
Duan X, Guo J Y, Shum C, et al. On the Postprocessing Removal of Correlated Errors in GRACE Temporal Gravity Field Solutions[J]. Journal of Geodesy, 2009, 83: 1 095-1 106 DOI:10.1007/s00190-009-0327-0
(  0) 0) |
 2024, Vol. 44
2024, Vol. 44


