地震震级与破裂尺度之间的关系描述断层破裂尺度(长度、宽度、面积)、平均滑动量与震级的关系特征,提供了一种将可观测的地震参数进行转换和比较的工具。震级-破裂尺度关系可用于推断地震的震级、破裂面积和破裂展布等,也可以推估古地震震源参数[1-2],对研究历史地震具有重要的参考价值。
20世纪以来,很多学者研究地震震级与断层滑动尺度的关系[3],提出若干描述断层滑动尺度和震级之间关系的经验公式[4-7]。但这些研究采用的数据来源、破裂参数估算方法和研究区域存在差异,加之地震分类(是否分为大陆地震和俯冲带或海洋地震)和断层滑动类型分类等因素,使得给出的经验关系式存在适用性问题,且不同经验关系间存在差异。比如,Mai等[4]采用自相关方法来确定断层破裂的长度和宽度,但仅使用18次地震的31个已公布的破裂模型,总体地震样本较少;且在拟合过程中,仅将断层类型分为走滑型和斜滑型进行拟合,未考虑更多的断层类型。Wells等[5]统计了4.5级以上浅源地震,将断层分为走滑、逆冲和正断3种类型进行拟合,给出震级与断层滑动尺度的关系式。由于逆冲断层地震的数据量较少,导致逆冲型地震关系式的可靠度较低。Blaser等[6]通过扩展地震样本数据库对Wells等[5]的经验公式进行修正和改进,对于给定震级下的逆冲事件,得到的破裂长度较Wells等[5]的关系小,而破裂宽度则较Wells等[5]的关系大。此外,Blaser等[6]对断层破裂面积的估算存在较大误差。Allen等[7]利用USGS提供的99个7级以上地震,分析俯冲界面和海洋环境下的震级-破裂尺度关系,发现海洋环境下的地震平均滑移和最大滑移量比俯冲界面事件的要大,呈现明显的差异性。总体而言,经验关系式的可靠性依赖于所统计的样本数目和拟合过程中所使用破裂参数的准确性、稳定性,此外,历史地震破裂参数的不确定性较大,也会影响拟合的经验关系式的可靠性。
近年来,地震破裂参数的研究取得长足进步。随着观测技术的快速发展,近场观测手段不断丰富,数据种类(如区域宽频带数据、强震仪数据、GNSS同震位移数据、高频GNSS波形数据、InSAR数据、海啸数据等)和观测量不断增多,加之反演理论不断完善,在大地震发生后,通过联合反演技术可得到相对稳定的震源破裂模型[8-9],这些进展大大提高了破裂模型的可靠性和时空分辨率。美国地质调查局(USGS)采用以上方法研究全球MW≥7.0以上地震的震源破裂模型,与仅使用远震宽频带地震数据得到的结果相比,联合反演的模型精度大幅提高[10],确定的断层破裂参数稳定性和准确性更佳。基于此,本文利用USGS作为统一的数据来源,汇总破裂参数资料,进一步优化强震震级与断层破裂参数之间的经验关系式。
1 数据和方法为了降低由于所用观测数据、断层破裂模型反演方法以及断层破裂参数估算方法不同导致统计结果的不确定性,本文基于USGS公布的有限断层模型,在以往研究的基础上[7],采用统一方法估算1990~2023年MW≥7.0且震源深度小于100 km的195次历史地震事件(图 1)的断层破裂长度RL(rupture length)、破裂宽度RW(rupture width)以及主破裂面积RA(rupture area)。

|
TH:逆冲断层;NO:正断层;SS:走滑断层 图 1 本研究使用的195次地震分布 Fig. 1 Distribution of 195 earthquakes used in this study |
为了使本研究的新经验关系与已有成果[4-7]具有可比性,参考以上文献所使用的经验关系表达式,采用对数线性化(lgy=kx+b)方法对数据进行拟合分析。其中,自变量x代表矩震级,因变量y表示断层的RL、RW和RA。
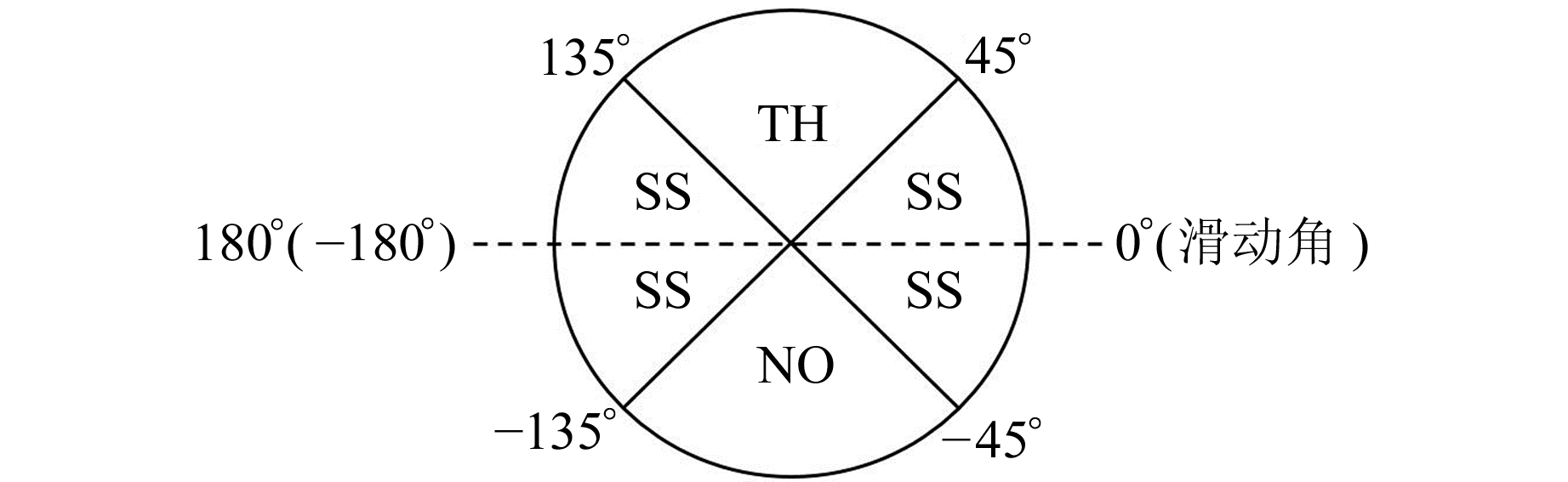
1.1 断层类型划分研究表明,断层的滑动类型或运动方式将会影响震级与破裂参数之间的相关关系[11]。本文使用USGS提供的震源机制解,根据图 2断层滑动角的所在范围,将所有地震事件的发震断层分为正断层(NO)、逆冲断层(TH)以及走滑断层(SS)3类。最终将195次地震事件的断层滑移类型分为123个逆冲断层、47个走滑断层以及25个正断层。
|
图 2 断层类型判断准则 Fig. 2 Criteria for determining fault types |
根据破裂长度与震级的关系估算最大震级是最常用的方式[12]。与Mai等[4]利用断层滑动量分布的自相关来近似断层破裂的长度和宽度的方法不同,本文利用USGS提供的所有地震事件的有限断层模型,将模型沿断层走向和倾向的最大破裂范围分别作为断层破裂的长度和宽度。
通常情况下,断层破裂的分布存在较强的不均匀性,并不是所有断层的破裂区域都可以近似为矩形或者圆形,因此,使用RL×RW估算面积有时是不合理的。考虑到有限断层模型反演的分辨率,本文参考Ye等[13]以及Allen等[7]的处理方式,采用表 1的计算准则,使用断层中滑动量较高的子断层面积之和评估主破裂面积。需要说明的是,虽然不同地震事件的破裂模型子断层面积可能不尽相同,但对于本文统计的地震事件,其单个破裂模型中的每个子断层面积是相同的,因此该方法能够对每个破裂模型的主破裂面积进行合理的评估。
|
|
表 1 破裂面积计算准则 Tab. 1 Calculation criteria for the rupture area |
以2021-05-21中国青海玛多MW7.4地震(以下简称玛多地震)、2020-10-30希腊MW7.0地震(以下简称希腊地震)、2021-07-29美国阿拉斯加MW8.2地震(以下简称阿拉斯加地震)3种不同断层类型的地震事件为例,展示断层的破裂长度、宽度以及断层主破裂区域的计算方法(图 3)。通过以上方法评估断层破裂长度、宽度以及主破裂面积,在此基础上拟合出断层参数与震级的关系。

|
白色虚线矩形框为断层的最大破裂长度和宽度;红色实线框选范围为主破裂面积区域;白色箭头标示破裂滑移方向和大小 图 3 3种不同断层类型地震的有限断层模型的长度、宽度和主破裂面积的测算示例 Fig. 3 Calculation examples of length, width and rupture area of three different fault types of earthquakes using finite fault model |
利用对数线性关系式得到震级与断层破裂长度、宽度及面积之间新的经验关系式,结果如图 4和表 2所示。

|
蓝色、红色、绿色实线为本次研究得到的对于正断层、走滑断层和逆冲断层的震级与破裂参数经验关系结果;褐色、紫色和橙色虚线分别为Mai等[4]、Wells等[5]和Blaser等[6]的经验关系结果 图 4 不同断层滑动类型下矩震级与破裂长度、宽度和断层主破裂面积之间的关系 Fig. 4 The relationship between moment magnitude and rupture length, width and fault main rupture area under different fault slip types |
|
|
表 2 利用最小二乘拟合得到的破裂尺度参数 Tab. 2 Rupture-scaling coefficients determined from least squares fitting |
相比于Wells等[5]的统计结果,本研究在地震数量方面有显著提升,尤其是逆冲断层的数据量几乎增加了1倍。这不仅极大丰富了逆冲断层统计的结果,也提升了其可信度。Mai等[4]仅将地震事件简化为走滑和斜滑2种类型进行回归分析,而本研究利用统一的数据来源将地震事件细分为走滑、逆冲和正断3种类型,这也使得经验关系式能够更加灵活地适用于不同类型的断层。
从拟合结果来看,随着震级的增加,不同断裂类型的RL、RW和RA的增长呈现不同的系统性偏差。特别是正断型和走滑型,由于地震数目较少,且在某一特定震级时,断层破裂长度和宽度在95%的置信区间内存在较大程度的离散(尤其是RW),因此正断型和走滑型的经验关系拟合参数R2仅为0.39和0.14。但在震级增长的同时,RA的增长系统性偏差较低,拟合参数R2分别为0.87、0.83和0.78,可信度较高。本次研究中逆冲类型的数据量为122个,较Wells等[5](破裂长度50个,宽度43个)、Mai等[4](8个)和Blaser等[6](破裂长度96个,宽度83个)有不同程度的增加。从图 4可以看出,逆冲型的破裂长度和宽度随着震级的增加呈现出较好的相关性。
3 讨论 3.1 RL-MW与RW-MW经验关系式对于破裂长度,在正断层离散点7.01~8.16的震级范围内,Wells等[5]与本文结果没有明显差异。本文所得正断层RL-MW关系式中的斜率较大,震级越大,本文结果与Blaser等[6]之间的差异越小。Blaser等[6]与Wells等[5]得到的走滑断层RL-MW关系式接近,本文得到的结果介于两者与Mai等[4]结果之间。
正断层的破裂宽度与Wells等[5]和Blaser等[6]的结果较为吻合。走滑断层的RW-MW关系式与其他经验关系式在不同震级范围内具有不同程度的偏离。震级在8.1以下时,走滑断层宽度均大于其余结果;震级大于8.1时,走滑断层宽度与Wells等[5]和Mai等[4]的结果接近,但偏离Blaser等[6]的关系式。
对于逆冲断层,Wells等[5]所使用的数据库中逆冲断层事件数量少,且绝大多数逆冲事件震级较本文所使用地震事件震级低;同时,在统计方法上,Wells等[5]使用断层上地震活动的深度范围、体波及面波反演和地表形变的几何模型等多种方法对断层破裂长度和宽度进行估算,因此Wells等[5]最终经验关系与本文结果(尤其是RW-MW)具有较为明显的差异。
3.2 RA-MW经验关系式从图 4可以看出,正断层RA-MW经验关系式与已有经验关系式之间存在较明显差异。当震级大于7.0时,对于走滑型和逆冲型地震的主破裂面积,在不同的震级范围内本文结果与其他学者的结果接近。
3.3 实用性分析在以往的历史地震研究中,由于缺少可靠的震源破裂模型,大都采用经验公式来确定历史地震的断层参数和破裂尺度[14-15]。本研究采用了分辨率更高的地震破裂模型,以获取更可靠的断层破裂参数。相对于文献[4-6]的方法,本文采用了更合理的估算方式来评估破裂面积的大小(表 1)。Chinnery[3]指出,大地震产生的破裂与小地震产生的破裂并不相匹配,因此本文仅针对MW≥7.0的强震进行统计分析,得出更适用于强震事件的经验关系式。
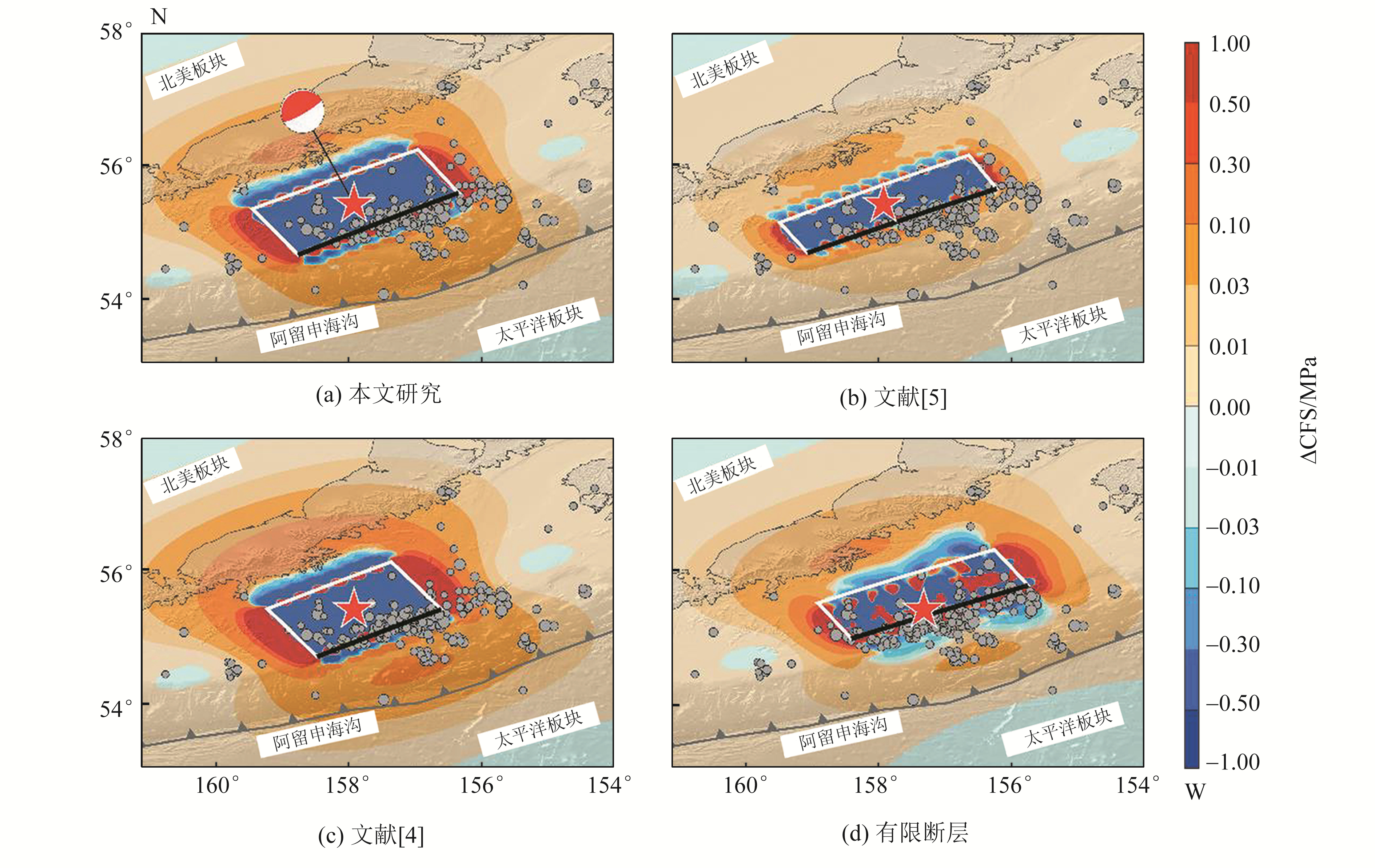
为了分析不同经验关系式得到的强震事件破裂参数的差异性,采用粘弹分层介质PSGRN/PSCMP模拟软件[16]分别计算玛多地震、希腊地震和阿拉斯加地震3种不同断层类型下产生的同震库仑应力变化ΔCFS,并与利用Wells等[5]、Mai等[4]的经验破裂尺度的结果以及实际有限断层反演获得的震源破裂模型[17-19]计算得到的ΔCFS分布进行对比分析,计算结果如图 5~7所示。

|
红色五角星为震中位置,灰色圆圈为余震位置[20],黑色线条为断层靠近地表的一侧,下同 图 5 玛多地震在不同破裂尺度下得到的同震库仑应力变化 Fig. 5 Coseismic Coulomb stress changes obtained by different rupture scales of Maduo earthquake |

|
GF、SF和TF分别为Gülbahçe、Seferihisar、Tuzla and Samos断层[18] 图 6 希腊地震在不同破裂尺度下得到的同震库仑应力变化 Fig. 6 Coseismic Coulomb stress changes obtained by different rupture scales of Greece earthquake |
|
图 7 阿拉斯加地震在不同破裂尺度下得到的同震库仑应力变化 Fig. 7 Coseismic Coulomb stress changes obtained by different rupture scales of Alaska earthquake |
从计算结果来看,虽然根据不同经验关系式预测的断层长度和宽度结果不同,但这并没有明显影响到对断层周边地区触发关系和应力增强以及减弱区域分布的判定,特别是从余震分布来看,所有经验模型都可以很好地预测余震的分布,这也证明了经验关系式的差异并不会影响远场同震库仑应力的计算结果。
但需要强调的是,以上通过经验公式得到的结果均是估计值或预期值,并不代表真实情况下的断层破裂尺度或真实且准确的地震震级大小。比如当震级为MW=7.0时,通过经验公式得到的走滑断层沿倾向的最大破裂宽度约为20 km。而实际上,由于走滑型地震的破裂断层往往具有复杂性,经常呈现多断层同时破裂,如2021年玛多MW7.4地震[17]和2023年土耳其MW7.8地震[21]。对于破裂比较复杂的走滑型地震,采用经验关系式预测往往会低估断层破裂尺度(图 4)。
由于MW9.0以上地震在历史上很少出现[5],因此研究中的样本震例较少。除此之外,特大地震断层破裂的差异性也比较大,如2004年苏门答腊MW9.1地震的同震破裂长度约1 000 km[22],而2011年日本MW9.0地震的同震有效破裂长度仅约350 km[23](图 4)。因此,利用经验关系估算特大地震的断层破裂参数时也应慎重。总之,不建议对所有不同类型的地震使用一种标度关系,最好根据实际情况分别使用不同滑移类型的标度关系。
4 结语基于USGS公布的有限断层模型,采用对断层破裂尺度统一的评判方法,系统收集和整理了1990~2023年全球范围内195次MW≥7.0强震的破裂参数资料,得到不同断层类型下震级与破裂参数之间新的经验关系式。
为验证不同经验关系式的差异性,通过利用新经验关系式得到的破裂参数计算玛多地震、希腊地震以及阿拉斯加地震的同震ΔCFS, 并与使用已有经验关系式以及真实震源破裂模型计算出的结果进行对比。结果显示,虽然使用不同经验公式计算出的断层长度和宽度不同,但计算出的同震ΔCFS分布几乎一致,并不影响断层对周边地区触发关系的判定,这也进一步说明远场同震ΔCFS的计算对所使用的断层滑动的经验关系式并不敏感。
本研究利用更多的破裂模型提高了逆冲型断层滑动经验关系式的可信度,但由于所使用地震事件以及对断层破裂参数的判定方法不同,本研究得出的经验关系式与其他学者的结果存在一定的差异,特别是走滑型和正断型。尽管如此,本研究给出的新的经验关系式可为以后震级-破裂尺度关系的进一步研究提供重要参考。尤其是大地震发生以后,可以与以往的经验关系式[4-7]相结合,快速生成经验断层破裂模型,更好地确定强震产生和滑动的区域,为震后的快速灾害评估、应急响应以及古地震研究提供可靠的参数。值得注意的是,对于破裂较为复杂的地震和特大地震(MW> 9.0),经验关系式所给出的断层破裂参数可能存在较大的估算误差,在使用时需要谨慎对待。
| [1] |
Mccalpin J P. International Geophysics[M]. Amsterdam: Elsevier, 2009
(  0) 0) |
| [2] |
Cinti F R, Pantosti D, Lombardi A M, et al. Modeling of Earthquake Chronology from Paleoseismic Data: Insights for Regional Earthquake Recurrence and Earthquake Storms in the Central Apennines[J]. Tectonophysics, 2021, 816
(  0) 0) |
| [3] |
Chinnery M A. Earthquake Magnitude and Source Parameters[J]. Bulletin of the Seismological Society of America, 1969, 59: 1 969-1 982 DOI:10.1785/BSSA0590051969
(  0) 0) |
| [4] |
Mai P M, Beroza G C. Source Scaling Properties from Finite-Fault-Rupture Models[J]. Bulletin of the Seismological Society of America, 2000, 90(3): 604-615 DOI:10.1785/0119990126
(  0) 0) |
| [5] |
Wells D L, Coppersmith K J. New Empirical Relationships among Magnitude, Rupture Length, Rupture Width, Rupture Area, and Surface Displacement[J]. Bulletin of the Seismological Society of America, 1994, 84(4): 974-1002 DOI:10.1785/BSSA0840040974
(  0) 0) |
| [6] |
Blaser L, Kruger F, Ohrnberger M, et al. Scaling Relations of Earthquake Source Parameter Estimates with Special Focus on Subduction Environment[J]. Bulletin of the Seismological Society of America, 2010, 100(6): 2 914-2 926 DOI:10.1785/0120100111
(  0) 0) |
| [7] |
Allen T I, Hayes G P. Alternative Rupture-Scaling Relationships for Subduction Interface and Other Offshore Environments[J]. Bulletin of the Seismological Society of America, 2017, 107(3): 1 240-1 253 DOI:10.1785/0120160255
(  0) 0) |
| [8] |
Yokota Y, Koketsu K, Fujii Y, et al. Joint Inversion of Strong Motion, Teleseismic, Geodetic, and Tsunami Datasets for the Rupture Process of the 2011 Tohoku Earthquake[J]. Geophysical Research Letters, 2011, 38(7)
(  0) 0) |
| [9] |
Liu C L, An C, Shan B, et al. Insights into the Kinematic Rupture of the 2015 MW8.3 Illapel, Chile, Earthquake from Joint Analysis of Geodetic, Seismological, Tsunami, and Superconductive Gravimeter Observations[J]. Journal of Geophysical Research: Solid Earth, 2018, 123(11): 9 778-9 799 DOI:10.1029/2018JB016065
(  0) 0) |
| [10] |
Goldberg D E, Koch P, Melgar D, et al. Beyond the Teleseism: Introducing Regional Seismic and Geodetic Data into Routine USGS Finite-Fault Modeling[J]. Seismological Research Letters, 2022, 93(6): 3 308-3 323 DOI:10.1785/0220220047
(  0) 0) |
| [11] |
Madariaga R. Extreme Environmental Events[M]. New York: Springer, 2011
(  0) 0) |
| [12] |
Scholz C H. A Reappraisal of Large Earthquake Scaling[J]. Bulletin of the Seismological Society of America, 1994, 84(1): 215-218
(  0) 0) |
| [13] |
Ye L L, Lay T, Kanamori H, et al. Rupture Characteristics of Major and Great (MW≥7.0) Megathrust Earthquakes from 1990 to 2015: 1. Source Parameter Scaling Relationships[J]. Journal of Geophysical Research: Solid Earth, 2016, 121(2): 826-844 DOI:10.1002/2015JB012426
(  0) 0) |
| [14] |
Xiong X, Shan B, Zheng Y, et al. Stress Transfer and Its Implication for Earthquake Hazard on the Kunlun Fault, Tibet[J]. Tectonophysics, 2010, 482(1-4): 216-225 DOI:10.1016/j.tecto.2009.07.020
(  0) 0) |
| [15] |
Xiong X, Shan B, Zhou Y M, et al. Coulomb Stress Transfer and Accumulation on the Sagaing Fault, Myanmar, over the Past 110 years and Its Implications for Seismic Hazard[J]. Geophysical Research Letters, 2017, 44(10): 4 781-4 789 DOI:10.1002/2017GL072770
(  0) 0) |
| [16] |
Wang R J, Lorenzo-Martín F, Roth F. PSGRN/PSCMP: A New Code for Calculating Co- and Post-Seismic Deformation, Geoid and Gravity Changes Based on the Viscoelastic-Gravitational Dislocation Theory[J]. Computers and Geosciences, 2006, 32(4): 527-541 DOI:10.1016/j.cageo.2005.08.006
(  0) 0) |
| [17] |
冯雅杉, 熊熊, 单斌, 等. 2021年玛多MS7.4地震导致的周边地区库仑应力加载及地震活动性变化[J]. 中国科学: 地球科学, 2022, 65(6): 675-686 (Feng Yashan, Xiong Xiong, Shan Bin, et al. Coulomb Stress Changes Due to the 2021 MS7.4 Maduo Earthquake and Expected Seismicity Rate Changes in the Surroundings[J]. Scientia Sinica(Terrae), 2022, 65(4): 675-686)
(  0) 0) |
| [18] |
Taymaz T, Yolsal-çevikbilen S, Irmak T S, et al. Kinematics of the 30 October 2020 Mw 7.0 Néon Karlovásion(Samos) Earthquake in the Eastern Aegean Sea: Implications on Source Characteristics and Dynamic Rupture Simulations[J]. Tectonophysics, 2022, 826
(  0) 0) |
| [19] |
Liu C, Bai Y, Lay T, et al. Megathrust Complexity and the Up-Dip Extent of Slip During the 2021 Chignik, Alaska Peninsula Earthquake[J]. Tectonophysics, 2023, 854
(  0) 0) |
| [20] |
王未来, 房立华, 吴建平, 等. 2021年青海玛多MS7.4地震序列精定位研究[J]. 中国科学: 地球科学, 2021, 51(7): 1 193-1 202 (Wang Weilai, Fang Lihua, Wu Jianping, et al. Aftershock Sequence Relocation of the 2021 MS7.4 Maduo Earthquake, Qinghai, China[J]. Scientia Sinica(Terrae), 2021, 51(7): 1 193-1 202)
(  0) 0) |
| [21] |
Reitman N G, Briggs R W, Barnhart W D, et al. Preliminary Fault Rupture Mapping of the 2023 M7.8 and M7.5 Türkiye Earthquakes[R]. USGS, 2023
(  0) 0) |
| [22] |
Lay T, Kanamori H, Ammon C J, et al. The Great Sumatra-Andaman Earthquake of 26 December 2004[J]. Science, 2005, 308: 1 127-1 133 DOI:10.1126/science.1112250
(  0) 0) |
| [23] |
Ammon C J, Lay T, Kanamori H, et al. A Rupture Model of the 2011 off the Pacific Coast of Tohoku Earthquake[J]. Earth, Planets and Space, 2011, 63(7): 693-696 DOI:10.5047/eps.2011.05.015
(  0) 0) |
 2024, Vol. 44
2024, Vol. 44

