2. 湖北省地震局,武汉市洪山侧路48号,430071
同震地表形变量及其在空间上的分布特征,是理解地壳弹性应变转换为不可逆的永久性构造变形和构造地震破裂行为的关键,也是构造活动区各种重要基础设施抗震设防的重要依据[1]。目前,获取同震形变的方法主要有GNSS、InSAR、精密水准、地震波反演、遥感及多源数据联合反演等。受限于仪器成本和信号传输等因素,GNSS、测震台站多布设于重点监测区,无法精细刻画地震同震形变的空间分布与变化特征[2]。自1993年首个InSAR同震形变场获取以来,InSAR技术因其低成本、面状覆盖等优势迅速成为研究同震形变的最重要方法之一。但该技术最大只能监测出相邻像元间小于半波长的形变[3],且近断层强震动作用会导致相位失相干,造成近场形变缺失[2]。此外,中强地震多发生于构造活动强烈的造山带,地形效应对相位解缠影响较大,有望借助深度学习等方法突破瓶颈,但需要海量训练集的支撑。为此,近年来一些学者利用光学影像中的像素点偏移来快速获取大范围中强地震同震形变,以弥补GNSS和InSAR技术的不足[4-5]。本文将重点讨论基于光学影像的同震形变处理技术及具可操作性的优化流程,以2021年玛多地震为例对比两款主流软件的差异,基于同震形变场的一阶和二阶导数推导具有地学意义的形变算子,旨在为光学同震形变技术的深入应用提供参考。
1 光学同震形变处理技术理论上,同一区域、不同时相(时间基线较短)的光学影像对中相同坐标的像素点应当完全重合。但由于大气辐射、几何畸变及地震引起的地表变化等因素,使得不同时相影像对存在像素偏移。因此,在剔除大气辐射、几何畸变等影响后,影像对产生的像素偏移可用于描述同震地表形变,利用亚像素相关性匹配技术甚至可检测1/10亚像素级别的形变[6]。
1.1 亚像素相关性匹配技术亚像素相关性匹配技术指利用经过辐射校正、正射校正和控制点匹配等预处理后的光学影像对进行亚像素级别的匹配,计算不同时相影像对偏差带来的位移量[6]。相位相关法[7]能精准计算偏移量估计,利用傅里叶变换将加窗后的光学影像对包含的空间域信息变换到频率域,获取图像的变换关系并计算归一化互功率谱函数相位信息,经过傅里叶逆变换后的互功率谱相位矩阵最大值即为图像间的相对偏移量,并采用内插或者奇异值(singular value decomposition, SVD)分解等方法进行拟合估计,从而获得亚像素级别偏移检测精度[8]。具体计算如下:
假设fpre(x, y)和fpost(x, y)分别为震前、震后影像的像元点,(Δx, Δy)为同震地表形变量,有:
| $ f_{\text {post }}(x, y)=f_{\text {pre }}(x-\Delta x, y-\Delta y) $ | (1) |
式中,(x, y)为像元坐标。设Fpost(u, v)为fpost(x, y)的傅里叶变换,Fpre(u, v)为fpre(x, y)的傅里叶变换,将两幅影像加窗后经过傅里叶变换转化为频率域:
| $ \begin{gather*} F_{\text {post }}(u, v)= \\ F_{\text {pre }}(u, v) * \exp (-\mathrm{j} 2 {\mathsf{π}}(u \Delta x+v \Delta y)) \end{gather*} $ | (2) |
式中,u、v分别为行、列的频率变化,j为复数单位。以Fpre(u, v)为参考得到归一化互功率谱函数H(u, v):
| $ \begin{gather*} \boldsymbol{H}(u, v)=\frac{\boldsymbol{F}_{\text {post }}(u, v) \boldsymbol{F}_{\text {pre }}(u, v)^{*}}{\left|\boldsymbol{F}_{\text {post }}(u, v) \boldsymbol{F}_{\text {pre }}(u, v)^{*}\right|}= \\ \exp (-\mathrm{j} 2 {\mathsf{π}}(u \Delta x+v \Delta y)) \end{gather*} $ | (3) |
式中,上标*为共轭。理论上,归一化互功率谱矩阵H是一个秩为1的矩阵,因此可将归一化互功率谱函数H(u, v)分解为:
| $ \begin{gather*} \boldsymbol{H}(u, v)=\exp (-\mathrm{j} 2 {\mathsf{π}} u \Delta x) \exp (-\mathrm{j} 2 {\mathsf{π}} u \Delta y)= \\ \boldsymbol{q}_{\Delta x}(u) \boldsymbol{q}_{\Delta y}^{\mathrm{G}}(v) \end{gather*} $ | (4) |
式中,上标G为共轭转置。进行SVD分解,用最大奇异值及相应的奇异向量对归一化互功率谱矩阵H进行秩1估计:
| $ \boldsymbol{H} \approx \boldsymbol{u}_{\max } * \sigma_{\max } * \boldsymbol{v}_{\max }^{\mathrm{G}} $ | (5) |
式中,σmax为最大奇异值,umax和vmax为对应的奇异向量。将umax和vmax相位解缠,得到相位PΔx和PΔy,拟合线性相位得到平移量:
| $ \Delta x=\frac{-k_{x}}{2 {\mathsf{π}}}, \Delta y=\frac{-k_{y}}{2 {\mathsf{π}}} $ | (6) |
式中,kx和ky分别为pΔx和pΔy的斜率。最终,由震前、震后光学影像经过亚像素相关性匹配后即可得到东西向(EW)和南北向(NS)的水平向形变分量。
1.2 光学同震形变提取的优化流程通过对不同时相的影像进行正射校正、几何校正、掩膜、地理配准等预处理,可消除几何畸变、地形、水体等带来的噪声。但亚像素匹配后得到的水平向形变场还存在诸多噪声,不利于定量化的形变分析。例如,不同时相的轨道参数变化导致轨道误差,多光谱探测器中电耦合器件(charge coupled device,CCD)线阵列错位排列、抖动震荡引起波动伪影条带误差,地表辐射性能变化造成失相关噪声,大气噪声、时间失相关(区域内随时间发生的变化)和阴影等与场地相关的因素以及热波动和信号量化等传感器因素导致白噪声和加性噪声[9]等,但这些因素在已有研究中很少被综合考虑[10]。为有效消除上述误差影响,经过实验对比,提出以下对水平向形变场的精化后处理:
1) 失相关区域掩膜。对同震形变场中信噪比(signal-noise ratio,SNR)低于设定经验阈值的像素点进行掩膜,抑制失相关噪声点对后续误差处理的影响。
2) 条带误差处理。为消除CCD线阵列姿态变化引起的条带误差,将每列条带区域内像元形变值叠加求平均,再由每个像元形变值减去平均值,去除条带误差。
3) 非局部均值滤波(NL-means)。相对于传统的中值滤波,实验选择非局部均值滤波(NL-means)平滑噪声、减少突跳点。NL-means滤波是基于图像自相似性的邻域滤波方法,充分利用图像中的冗余信息,在去噪的同时最大程度地保持图像的细节特征。在条带误差处理后,进行NL-means滤波,可进一步平滑噪声、突出同震形变场细节特征。其核心是计算图像中所有像素与当前像素间的相似性,一般会设定两个固定大小的窗口——一个大的搜索窗口和一个小的邻域窗口,邻域窗口在搜索窗口中进行滑动,根据邻域间的相似性修改权值来确定对应中心像素对当前像素的影响度。
假设含噪声图像为m,去噪图像为
| $ \tilde{m}(a)=\sum\limits_{b \in I} w(a, b) * m(b) $ | (7) |
式中,I为搜索窗口区域;权值w(a, b)为像素点a和b间的相似度,它的值由以a、b为中心的矩形邻域M(a)、M(b)间的距离||M(a)-M(b)||2决定:
| $ \begin{aligned} w(a, b)=\frac{1}{\sum\limits_{b} \exp \left(-\frac{\|M(a)-M(b)\|^{2}}{h^{2}}\right)} \\ \;\;\;\;\;\;\;\; \exp \left(-\frac{\|M(a)-M(b)\|^{2}}{h^{2}}\right) \end{aligned} $ | (8) |
| $ \begin{array}{*{20}{c}} \|M(a)-M(b)\|^{2}= \\ \frac{1}{d^{2}} \sum\limits_{c_{a} \in M(a), c_{b} \in M(b)}\left\|m\left(c_{a}\right)-m\left(c_{b}\right)\right\|^{2} \end{array} $ | (9) |
式中,M为邻域窗口区域,控制高斯函数的衰减程度;c为邻域窗口中的像元点;d为邻域窗口尺寸;h为平滑系数,h越大高斯函数变化越平缓,去噪水平越高,但同时也会导致图像越模糊,建议采取小平滑系数的多次滤波策略。
4) 轨道误差处理。为剔除图像中的多项式趋势,在非形变区域均匀选取若干个像素点,通过最小二乘平差求得4个参数和多项式轨道误差,即将一个多项式曲面拟合到图像上,并将其从图像中移除[5]。
5) 赋空值-中值滤波。当形变场的空值较多时,会在一定程度上影响形变表达和解读,传统方法中对此不加考虑。实验通过中值滤波法将失相关掩膜空值区域赋值,只对失相关区域进行中值滤波,可以在不失真的情况下尽可能减小噪声影响。
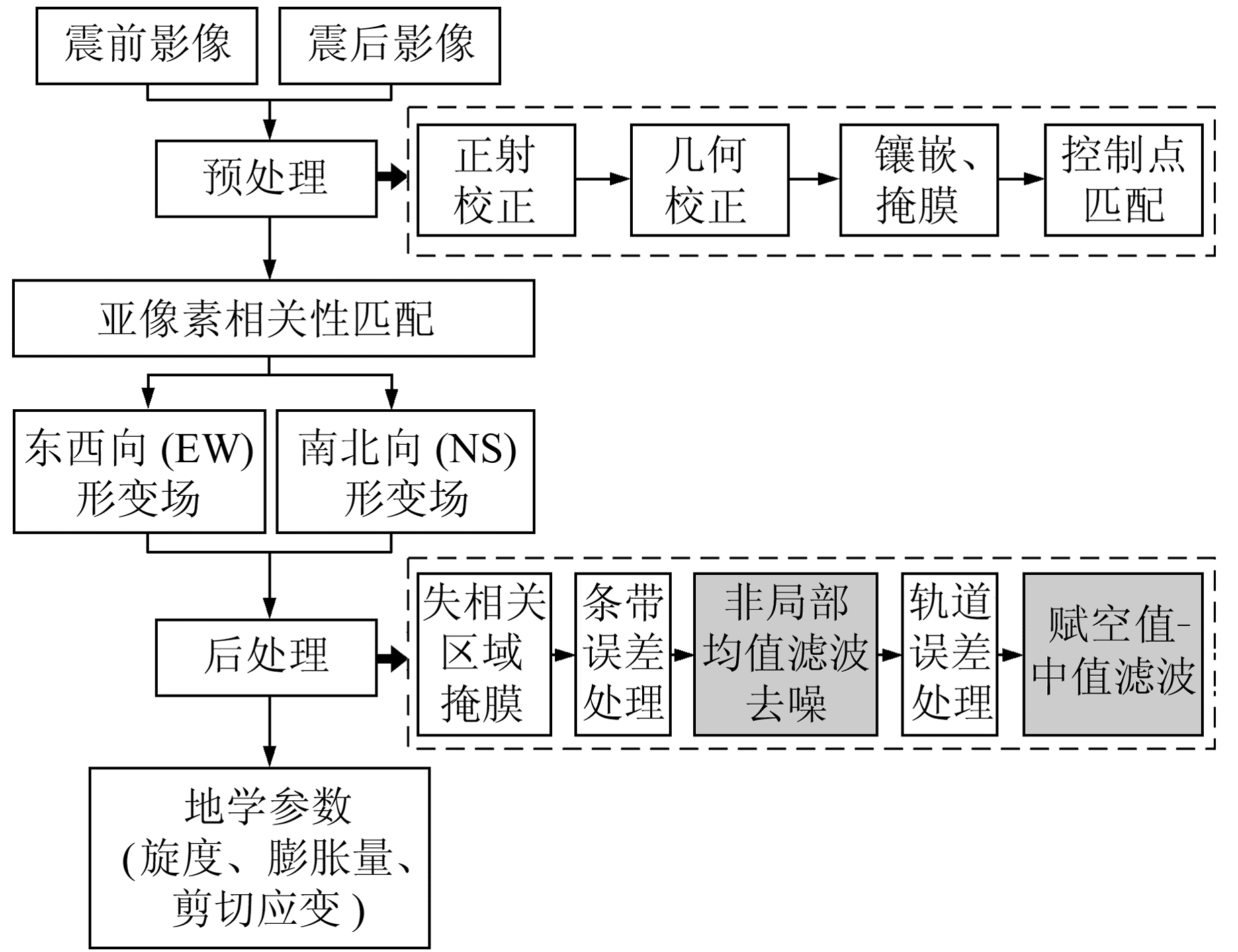
基于精化后处理的水平形变分量,即可进一步定量化分析,提取具有地学意义的形变算子。完整的光学同震形变提取优化流程如图 1所示。
|
图 1 光学同震形变提取优化流程 Fig. 1 Optimization process for optical coseismic deformation extraction |
目前,用于光学地表形变处理的亚像素相关性匹配软件包括COSI-Corr、MicMac和Medicis等[10]。其中,COSI-Corr和Medicis均采用频域相关器,但后者去噪效果较差[11],这里不作讨论。COSI-Corr、MicMac的差异主要在于像素对偏移检测相关器的影响、检测窗口设置、噪声抑制等方面。
COSI-Corr是一款依赖ENVI平台的非开源免费软件。COSI-Corr软件采用频域相关器完成像素偏移检测。首先对固定尺寸的初始窗口内逐像素偏移进行粗略估计,并以此设定截止窗口进行亚像素相关性检测。当影像噪声较大或预期形变较大时,初始窗口尺寸设置较大为宜,而截止窗口尺寸应设计成能容纳一定噪声的最小尺寸。COSI-Corr软件根据对数-交叉频谱振幅大小对噪声频率进行屏蔽,筛选噪声值,修改每次重新计算的频率屏蔽次数,减少测量中的噪声值。
MicMac是完全开源的数字摄影测量和三维重建软件,采用正则化相关器,通过检测窗口尺寸和移动步长来调整检测精度和速度,从而完成亚像素相关性匹配[10];采用非线性相关性系数(式(10))在像素对偏移检测的同时限制噪声对形变检测结果的影响:
| $ \text { Cost }=C_{1} *\left(1-C_{3}\right) $ | (10) |
| $ C_{1}=1-C^{\min } $ | (11) |
| $ C_{2}=\frac{\operatorname{Max}\left(\text { Cor }, C^{\min }\right)-C^{\min }}{C_{1}} $ | (12) |
| $ C_{3}=C_{2}^{\gamma} $ | (13) |
式中,Cor为归一化相关性系数,Cmin为相关性最小阈值,γ为相关影响程度。
针对相同的影像对数据,两款软件相关器窗口大小对噪声的敏感度稍有差异,如表 1所示。对比结果表明,MicMac始终保持较好的去噪效果。
|
|
表 1 COSI-Corr与MicMac结果差异 Tab. 1 Differences in results between COSI-Corr and MicMac |
在数学上,梯度作为矢量表示为函数在某点沿法向的变化。将光学同震形变场看作二维离散函数,同理可进行梯度计算。基于像素偏移的梯度计算可得到位移在空间某一位置沿某一方向的变化量,即位移矢量场。梯度变化最大的方向和变化量指示同震破裂在地表的投影。
图像梯度算子有多种,与Milliner[11]采用的二阶精准中心差分近似,本文选择具有较强抗噪声能力的Sobel算子,它通过对空间邻域加权计算位移梯度,能充分考虑在整个空间邻域对中心形变像素点求取梯度的影响,还可以降低场地因素和传感器因素带来的复合噪声对梯度的直接影响,对形变反映更加敏感,如式(14)、(15):
| $ \begin{array}{*{20}{c}} {\partial u(x, y) / \partial x=}\\ {\frac{2 u(x+1, y)+u(x+1, y-1)+u(x+1, y+1)-(2 u(x-1, y)+u(x-1, y-1)+u(x-1, y+1))}{8\;\mathrm{px}}} \end{array} $ | (14) |
| $ \begin{gather*} \partial u(x, y) / \partial y= \\ \frac{2 u(x, y+1)+u(x-1, y+1)+u(x+1, y+1)-(2 u(x, y-1)+u(x-1, y-1)+u(x+1, y-1))}{8\;\mathrm{px}} \end{gather*} $ | (15) |
式中,u为同震位移场,px为同震位移场分辨率,下文同理。
场是指物体在空间的分布情况。根据场的定义,可由位移梯度进一步计算形变场的旋度(curl,ω)、膨胀量(dilatation,δ)和剪切应变(shear-strain,γ):
| $ \omega=(\nabla \times u)_{z}=\frac{\partial u_{\mathrm{EW}}}{\partial y}-\frac{\partial u_{\mathrm{NS}}}{\partial x} $ | (16) |
| $ \delta=\nabla_{h} \cdot u=\frac{\partial u_{\mathrm{EW}}}{\partial x}+\frac{\partial u_{\mathrm{NS}}}{\partial y} $ | (17) |
| $ \gamma=(\Delta \times u)_{z}=\frac{\partial u_{\mathrm{EW}}}{\partial y}+\frac{\partial u_{\mathrm{NS}}}{\partial x} $ | (18) |
式中,uEW和uNS为同震位移场的东西(EW)和南北(NS)形变分量。其中旋度(ω)是指矢量作旋转运动的方向和强度,其正负符号指示了断层的运动性质,旋度为正表示逆时针旋转,为左旋走滑;旋度为负表示顺时针旋转,为右旋走滑。膨胀量(δ)是指矢量场中某点周围的矢量向该点聚集或发散,指示断层的挤压或拉张运动性质,膨胀量不为0表示该点处存在垂向运动,为正表示拉张性,为负表示挤压性。剪切应变(γ)是指南北、东西向位移分量分别在正东、正北方向的梯度之和,指示剪切应力的集中程度,剪切应变为正(夹角减小)表示左旋走滑为主,为负(夹角增大)表示右旋走滑为主。
综上,位移梯度的旋度、膨胀量、剪切应力算子可以直观地刻画同震地表破裂形迹、指示发震断层的运动学性质,还可以基于其数值开展统计分析。
3 2021年玛多MW7.4地震实例分析2021-05-22青海玛多发生MW7.4地震,是继2008年汶川地震之后中国大陆发生的震级最高的一次地震,造成沿昆仑山口-江错断层158 km长的地表破裂[12],并在东、西尾端发生分叉破裂[13]。玛多地震发生后,我们选用完全覆盖震区的10 m分辨率的Sentinel-2影像提取同震形变场。考虑到气候、时间、拍摄角度等影响,选择地震前、后同一时间段(震前:2020-10-12,震后:2021-10-17)、太阳方位角相近(159°~ 163°)、含云量低的各3景数据。考虑到短波红外波段(Band8)形变值标准差最小,选择Band8作为输入进行亚像素相关性匹配处理。震区水系分布较广,为最大程度抑制水体噪声,对其进行掩膜和空值赋值处理。其中将COSI-Corr中的初始窗口和截止窗口分别设置32×32 px和16×16 px、迭代次数为2、掩膜阈值为0.9;MicMac中的滑动窗口设置为3×3 px、相关性最小阈值为0.5、相关影响程度为2、正则化系数为0.3。
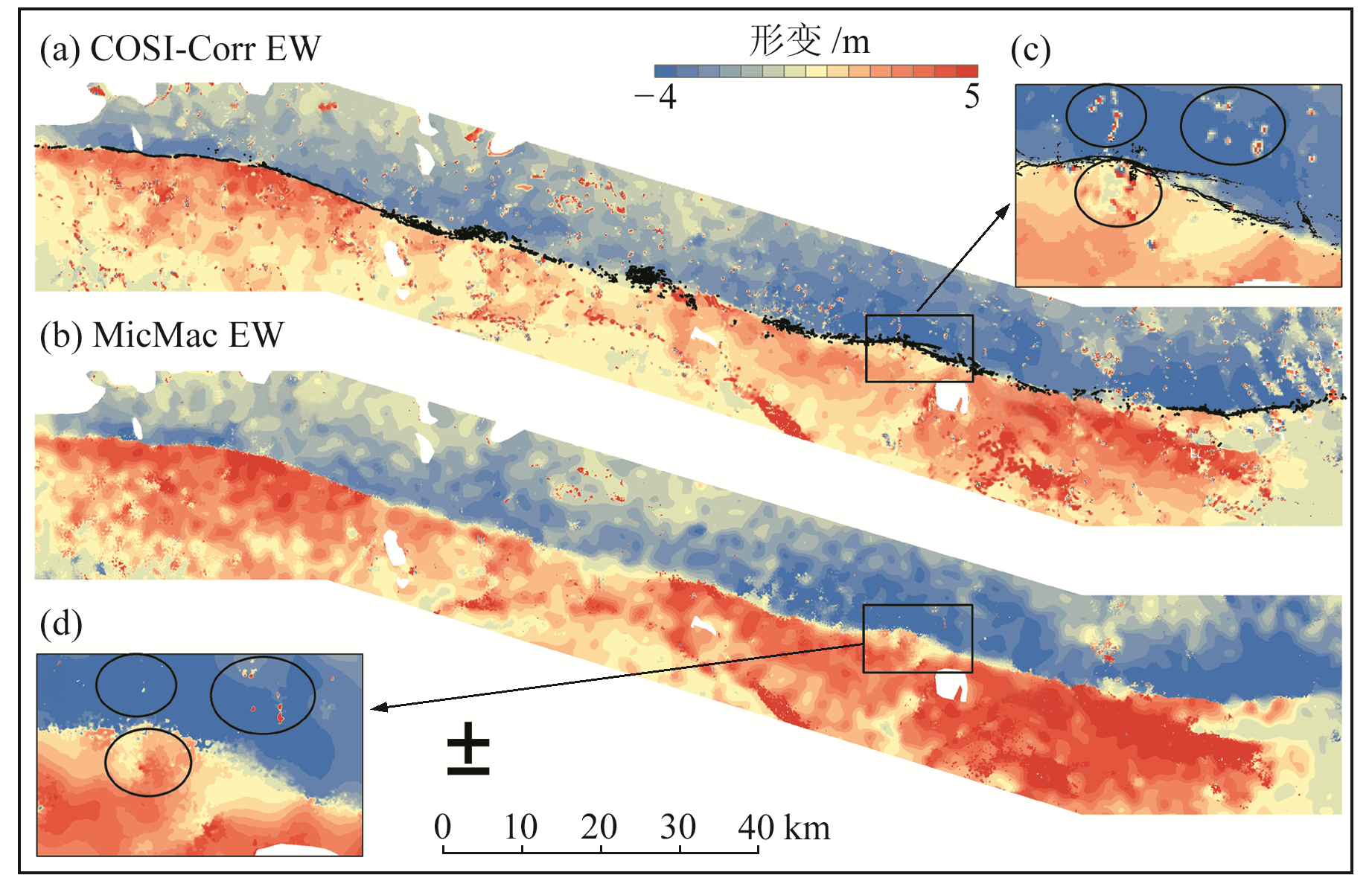
基于COSI-Corr和MicMac软件得到的亚像素相关性匹配检测结果整体趋势接近,一致地刻画了发震断层的空间位置,与基于cm级无人机航片解译的地表破裂带形迹(图 2(a)中黑色实线)吻合度较高。比较分析可见,MicMac软件降噪抑制效果更佳(图 2(d))。亚像素相关性匹配后得到的同震形变场含有大量的白噪声和加性噪声(图 3(a))。经过条带误差处理后,能有效去除条带误差和卫星姿态角误差带来的影响(图 3(b))。经过非局部均值滤波后的形变场更加平滑(图 3(c)),有利于快速判定跨断层的位错量和断层的精准位置。经过轨道误差处理后整体趋势不变,但跨断层的位错量有约5%的减小(图 3(d))。精化后处理(图 3(e))的结果在有效降低干扰噪声和抑制误差的同时细节特征得到保留(图 2(b)、2(d)),图 2(c)跨断层形变剖线拐点指示破裂在局部出现次级分支,与野外调查结果完全吻合[14]。
|
图 2 EW方向同震形变场 Fig. 2 EW coseismic displacement field |

|
图 3 玛多地震精细化后处理 Fig. 3 Refined post-processing of the Maduo earthquake |
旋度场(图 4(a))、膨胀量场(图 4(b))、剪切应变场(图 4(c))直观刻画了地表破裂形迹。沿断层走向,旋度普遍大于0(图 4(d)、(e)),表示逆时针旋转运动,指示断层发生了左旋走滑运动;膨胀量值较小、稳定性差,局部段落出现连续正值或负值(图 4(f)、(g)),表示断层局部存在垂向运动(隆升或沉降)。剪切应变与旋度符号一致(图 4(h)、(i)),表明地震以左旋走滑为主,局部段落兼倾滑分量,与已有结果基本一致[13]。

|
图 4 旋度、膨胀量、剪切应变 Fig. 4 Curl, dilatation, and shear strain |
本文系统介绍光学同震形变提取的关键技术和优化流程,改进滤波平滑方法,提出精细化后处理能有效减小噪声、降低误差。分析COSI-Corr和MicMac两款主流软件的关键差异,结果显示,COSI-Corr采用小相关窗口噪声会比较突出且位错振幅减少,随着滑动窗口尺寸减小,其噪声抑制受到弱化,而MicMac因采用正则化算法,即使采用较小的滑动窗口也不会降低噪声抑制效果。基于同震形变场采用Sobel算子推导具有地学意义的位移梯度、旋度、膨胀量、剪切应变等算子。最后以2021年青海玛多MW7.4地震为例,验证了基于Sentinel-2光学影像的同震形变场提取以及精细化后处理优化流程,并推导出玛多地震的旋度场、膨胀量场和剪切应变场,由此得出玛多地震的发震断层为左旋走滑,断层两盘存在倾滑(逆冲)运动。研究表明,对亚像素相关性匹配结果的后处理可有效消除轨道误差、条带误差、场地因素和传感器因素导致的白噪声和加性噪声,精化形变场,更加客观地描述同震形变的空间分布特征。
| [1] |
Ferrario M F, Livio F. Conditional Probability of Distributed Surface Rupturing during Normal-Faulting Earthquakes[J]. Solid Earth, 2021, 12(5): 1 197-1 209 DOI:10.5194/se-12-1197-2021
(  0) 0) |
| [2] |
Xu X H, Tong X P, Sandwell D T, et al. Refining the Shallow Slip Deficit[J]. Geophysical Journal International, 2016, 204(3): 843-862
(  0) 0) |
| [3] |
Massonnet D, Feigl K L. Radar Interferometry and Its Application to Changes in the Earth's Surface[J]. Reviews of Geophysics, 1998, 36(4): 441-500 DOI:10.1029/97RG03139
(  0) 0) |
| [4] |
Van Puymbroeck N, Michel R, Binet R, et al. Measuring Earthquakes from Optical Satellite Images[J]. Applied Optics, 2000, 39(20): 3 486 DOI:10.1364/AO.39.003486
(  0) 0) |
| [5] |
贺礼家, 冯光财, 冯志雄, 等. 哨兵-2号光学影像地表形变监测: 以2016年MW7.8新西兰凯库拉地震为例[J]. 测绘学报, 2019, 48(3): 339-351 (He Lijia, Feng Guangcai, Feng Zhixiong, et al. Coseismic Displacements of 2016 MW7.8 Kaikoura, New Zealand Earthquake, Using Sentinel-2 Optical Images[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(3): 339-351)
(  0) 0) |
| [6] |
Leprince S, Ayoub F, Klinger Y, et al. Co-Registration of Optically Sensed Images and Correlation(COSI-Corr): An Operational Methodology for Ground Deformation Measurements[C]. 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, 2008
(  0) 0) |
| [7] |
Foroosh H, Zerubia J B, Berthod M. Extension of Phase Correlation to Subpixel Registration[J]. IEEE Transactions on Image Processing, 2002, 11(3): 188-200 DOI:10.1109/83.988953
(  0) 0) |
| [8] |
Hermas E, Leprince S, Abou El-Magd I. Retrieving Sand Dune Movements Using Sub-Pixel Correlation of Multi-Temporal Optical Remote Sensing Imagery, Northwest Sinai Peninsula, Egypt[J]. Remote Sensing of Environment, 2012, 121: 51-60 DOI:10.1016/j.rse.2012.01.002
(  0) 0) |
| [9] |
Leprince S, Barbot S, Ayoub F, et al. Automatic and Precise Orthorectification, Coregistration, and Subpixel Correlation of Satellite Images, Application to Ground Deformation Measurements[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(6): 1 529-1 558 DOI:10.1109/TGRS.2006.888937
(  0) 0) |
| [10] |
Rosu A M, Pierrot-Deseilligny M, Delorme A, et al. Measurement of Ground Displacement from Optical Satellite Image Correlation Using the Free Open-Source Software MicMac[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2015, 100: 48-59 DOI:10.1016/j.isprsjprs.2014.03.002
(  0) 0) |
| [11] |
Milliner C W D, Dolan J F, Hollingsworth J, et al. Quantifying Near-Field and Off-Fault Deformation Patterns of the 1992 MW7.3 Landers Earthquake[J]. Geochemistry, Geophysics, Geosystems, 2015, 16(5): 1 577-1 598 DOI:10.1002/2014GC005693
(  0) 0) |
| [12] |
姚文倩, 王子君, 刘静, 等. 2021年青海玛多MW7.4地震同震地表破裂长度的讨论[J]. 地震地质, 2022, 44(2): 541-559 (Yao Wenqian, Wang Zijun, Liu Jing, et al. Discussion on Coseismic Surface Rupture Length of the 2021 MW7.4 Madoi Earthquake, Qinghai, China[J]. Seismology and Geology, 2022, 44(2): 541-559)
(  0) 0) |
| [13] |
刘小利, 夏涛, 刘静, 等. 2021年青海玛多MW7.4地震分布式同震地表裂缝特征[J]. 地震地质, 2022, 44(2): 461-483 (Liu Xiaoli, Xia Tao, Liu Jing, et al. Distributed Characteristics of the Surface Deformations Associated with the 2021 MW7.4 Madoi Earthquake, Qinghai, China[J]. Seismology and Geology, 2022, 44(2): 461-483)
(  0) 0) |
2. Hubei Earthquake Agency, 48 Hongshance Road, Wuhan 430071, China
 2024, Vol. 44
2024, Vol. 44


