2. 安徽理工大学矿山采动灾害空天地协同监测与预警安徽普通高校重点实验室,安徽省淮南市泰丰大街168号,232001;
3. 安徽理工大学矿区环境与灾害协同监测煤炭行业工程研究中心,安徽省淮南市泰丰大街168号,232001
GNSS的快速发展,对当前卫星导航系统的实时性、可靠性以及定位精度提出更高的要求。对高动态接收机而言,会大大增加接收机硬件设计的成本与难度[1]。当可见卫星达到一定数目,其定位精度并不会得到有效提升,相反其冗余信息会使计算量增大。因此,通过对当前可见卫星进行选取,获取几何构型良好的卫星组合进行定位解算,降低定位所需计算量,提高实时解算能力很有必要。
传统的选星算法主要是基于遍历法思想,即通过将当前观测到的所有可见卫星进行合适数目卫星排列组合,计算各个卫星组合下的几何精度因子(geometric dilution of precision, GDOP),并从全部组合中找出最小GDOP作为最终结果[2-3]。当前,选星算法多数从单目标优化问题和聚类2个方面出发。单目标优化方法是指将GDOP值作为适应度函数,通过智能优化算法求解适应度函数的最小值。聚类方法是指将所有可见卫星进行分类,从每类卫星中选取1颗卫星,从而获得与遍历法相近的GDOP值,提高选星效率,但该方法在卫星分布分散情况下效果较差[4-5]。随着研究的深入,针对传统选星算法计算量大、耗时长等缺点,许多学者对其进行大量研究。霍航宇等[6]基于遗传算法,比较选星数目和GDOP的关系,根据所需精度来确定卫星数目,进而进行定位解算;Azami等[7]结合神经网络和主成分分析,对当前可见卫星进行分类,从而选出最小GDOP值的卫星组合;余德荧等[8]采用灰狼优化算法,通过固定选星数目,根据最小GDOP值进行选择,降低选星耗时;王尔申等[9-10]提出基于粒子群优化算法(particle swarm optimization, PSO)的快速选星,并比较PSO参数设置对选星结果的影响;朱军等[11]结合几何分布和差分进化算法,自适应改变种群大小,从而实现快速选星。
综上可知,现有的研究成果在一定程度上可提高选星实时性,但并未对选星算法在不同卫星系统组合下的普适性进行系统分析,且免疫算法在选星领域还未被使用。该方法具有并行分布式搜索、鲁棒性强等特点,可以克服一般“寻优”中不可避免的过早收敛问题,更加快速地寻求全局最优解。因此,本文提出基于改进免疫算法的GNSS快速选星算法,分析初始化种群数目、最大迭代次数对结果的影响,获得参数的最佳取值,并通过实测数据验证所提方法的普适性和有效性。
1 免疫算法免疫算法的运行过程与其他智能算法类似[12],均是基于算子来进行计算,每个算子均有其各自的功能。
1) 亲和度评价算子。亲和度是指生成的种群个体与全局最优解的结合强度,其通常表示为aff(x): S∈R,其中aff(x) 为适应度函数,S为适应度函数的可行解区间,R为实数域。
2) 抗体浓度评价算子。抗体浓度是指生成种群多样性的好坏。抗体浓度通常定义为:
| $ \operatorname{den}\left(a b_i\right)=\frac{1}{N} \sum\limits_{j=1}^N S\left(a b_i, a b_j\right) $ | (1) |
式中,N为种群数目;S(abi, abj) 为种群个体间的相似度,其中abi为种群中的第i个个体。
3) 克隆算子。克隆是将符合要求的种群个体进行复制,其可以描述为Tc(abi)=clone(abi),其中clone(abi) 为mi个与abi相同的克隆构成集合,mi为克隆数目,根据实际情况设定。
免疫算法的寻优过程为:通过生成初始化种群,利用抗体浓度评价算子和亲和度评价算子获取种群个体质量信息,选择出优质个体,利用克隆算子对优质个体进行克隆复制,并进行变异等操作,从而获取全局最优解。
2 基于改进免疫算法的GNSS快速选星方法 2.1 适应度函数适应度函数选取的原则为能够衡量所选卫星组合的定位精度。免疫算法对种群每个个体的适应度函数值进行计算,其选取直接影响到算法能否正确求解问题以及计算的时间复杂度[13]。本文采用GDOP值作为适应度函数,定位精度与其关系可表示为:
| $ \sigma=\sigma_{\text {UERE }} \cdot \mathrm{GDOP} $ | (2) |
式中,σUERE为等效距离误差,假设在不同卫星系统组合情况下,其等效距离误差大致相同;σ为定位精度。GDOP计算公式如下:
| $ \text { GDOP }=\sqrt{\operatorname{trace}\left[\left(\boldsymbol{H}^{\mathrm{T}} \boldsymbol{H}\right)\right]^{-1}} $ | (3) |
式中,
| $ \boldsymbol{H}=\left[\begin{array}{cccccc} \boldsymbol{H}_{\mathrm{C}} & \boldsymbol{I}_{\mathrm{C}} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \boldsymbol{H}_{\mathrm{G}} & \mathbf{0} & \boldsymbol{I}_{\mathrm{G}} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \boldsymbol{H}_{\mathrm{E}} & \mathbf{0} & \mathbf{0} & \boldsymbol{I}_{\mathrm{E}} & \mathbf{0} & \mathbf{0} \\ \boldsymbol{H}_{\mathrm{R}} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \boldsymbol{I}_{\mathrm{R}} & \mathbf{0} \\ \boldsymbol{H}_{\mathrm{J}} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \boldsymbol{I}_{\mathrm{J}} \end{array}\right] $ | (4) |
| $ \boldsymbol{H}_x=\left[\begin{array}{ccc} l_x^1 & m_x^1 & n_x^1 \\ l_x^2 & m_x^2 & n_x^2 \\ \vdots & \vdots & \vdots \\ l_x^k & m_x^k & n_x^k \end{array}\right] $ | (5) |
式中,trace(·)表示矩阵的迹,H表示可见卫星的观测矩阵,下标C、R、G、E、J分别代表BDS、GLONASS、GPS、Galileo和QZSS(quasi-zenith satellite system, 准天顶卫星系统),I为单位矩阵,下标x指代卫星系统,l、m、n为接收机位置到可见卫星的方向余弦,上标k为当前系统可见卫星数目。
2.2 算法实现步骤在免疫算法中,免疫个体数为Np,最大迭代次数为G,X={x1, x2, ⋯, xNp} 为初始化种群个体集合,xi={y1,y2,⋯,yn} 为每个个体所选的卫星组合,算法详细流程如图 1所示。

|
图 1 算法流程 Fig. 1 Algorithm flow chart |
其具体算法步骤如下:
1) 根据导航电文,获取历元可见卫星的高度角。
2) 设置截止高度角(10°),对可见卫星进行提取,并计算可用卫星的观测矩阵 H。
3) 根据观测矩阵的行数获取可用卫星数目m,对可用卫星从1到m进行编号,使之一一对应;将初始化种群数目和最大迭代次数作为改进免疫算法的输入参数,进行免疫计算,此时计时开始。
4) 初始化种群。根据GNSS接收机所能接收到卫星系统下的必要观测卫星数n,从Cmn个卫星组合中选取 Np个个体作为初始化种群,每个个体中包含n颗卫星组合。
5) 根据设置的最大迭代次数进行迭代运算,对每个个体计算GDOP值即适应度函数,每次迭代保留适应度函数值最好的个体。
6) 当迭代数目达到设置的最大迭代次数G之后,免疫算法结束,停止计时,输出最小GDOP值和耗时。
2.3 免疫算法参数选取免疫算法通过迭代次数和初始化种群大小从全局寻优缓慢收敛到局部寻优。为了寻求免疫算法运算过程中最佳的迭代次数和初始化种群数目,本文利用CUT0测站2023-02-02观测数据进行实验,所使用软件为MATLAB R2018b,电脑搭载R5-4600H,3.00 GHz处理器,16GB RAM。其中GDOP差值指免疫算法所寻找的最小GDOP值与遍历法之间的差值,时间的度量从计算出当前所有观测卫星的观测矩阵 H进入免疫算法开始,判断免疫算法迭代次数是否到达设置的最大迭代次数,满足条件则结束。本文设置截止高度角为10°,通过固定初始化种群数目(从20开始,步长为20,直至60结束),分别对最大迭代次数取不同值(从80开始,步长为20,直至140结束)进行讨论,实验结果如图 2、表 1所示。

|
图 2 初始化种群数目与迭代次数对性能的影响 Fig. 2 Effects of initial population number and iterations on positioning performance |
|
|
表 1 初始化种群数目与迭代次数对选星性能的影响 Tab. 1 Effects of initial population number and iterations on satellite selection performance |
由图 2、表 1可知,GDOP差值均在0~0.5之间波动,且较为稳定,表明免疫算法能够大概率搜索到与遍历法结果一致的GDOP值,而小部分由于随机生成的初始化种群而无法保证其良好的多样性,从而获取与遍历法相近略大的GDOP值,即局部最优解[14]。当初始化种群数目固定时,随着迭代次数增加,其GDOP差值呈现减小的趋势,但耗时明显增加。初始化种群数目为60和最大迭代次数为140时,平均GDOP值差值仅为0.128,说明免疫算法能够搜索到最佳的卫星组合。当固定最大迭代次数为120、初始化种群数目为20时,平均耗时最少,为0.860 s。为了更加直观地分析初始化种群数目与最大迭代次数对选星实时性的影响,表 2(单位%)为选星耗时百分比。
|
|
表 2 选星耗时百分比 Tab. 2 Percentage of satellite selection time consuming |
从表 2可知,在最大迭代次数固定的前提下,初始化种群数目从20到60,其耗时比((t遍历法-t免疫算法)/t遍历法×100%)减少,减小幅度大致相当;在初始化种群固定的前提下,最大迭代次数从80到140,耗时比减小,从120到140减小幅度最大。因此,在考虑实时性与定位精度双重因素下,初始化种群数目可选在20附近、最大迭代次数可选择在120附近。
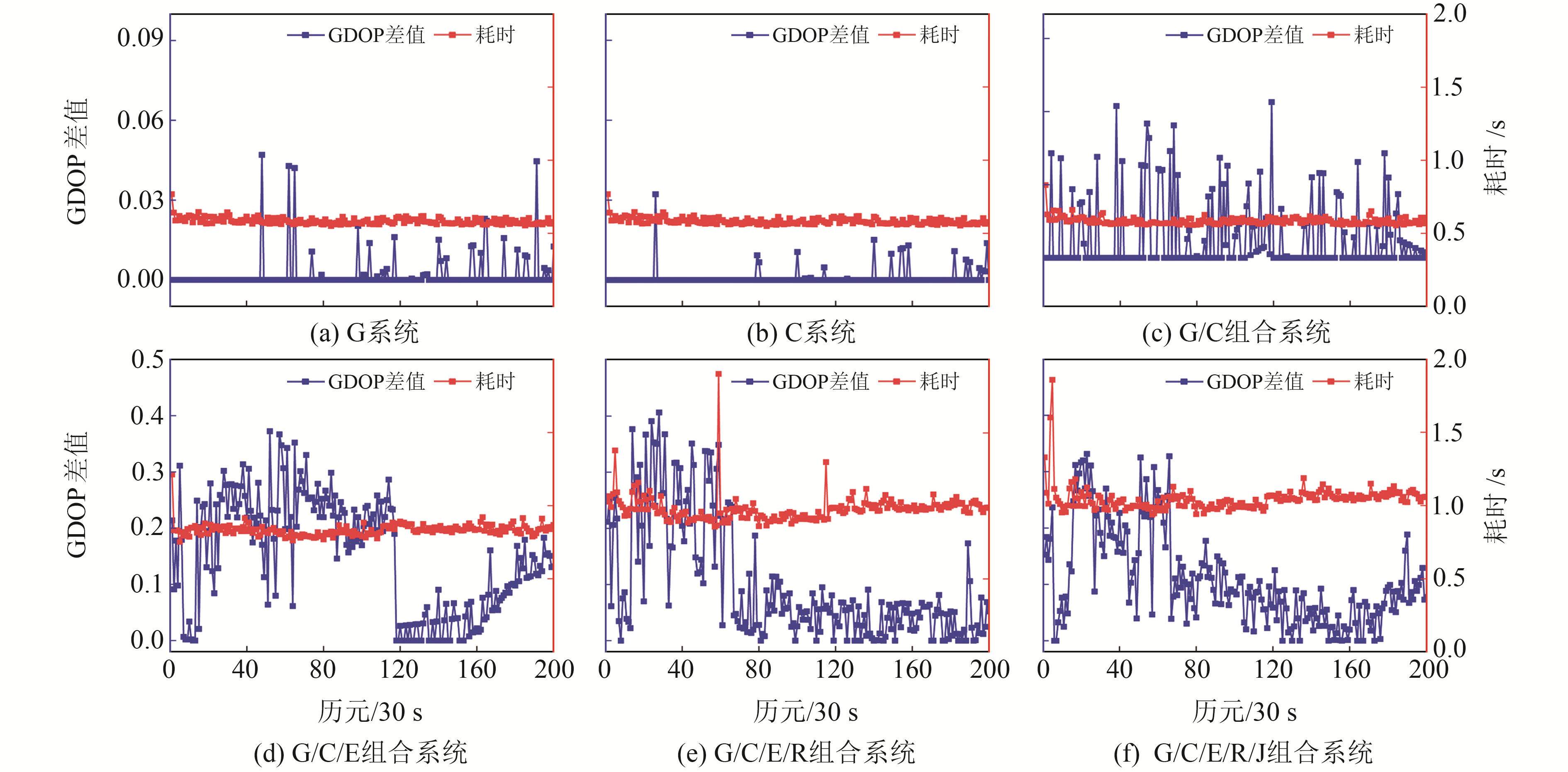
3 实验验证与分析为了验证本文所提算法对不同卫星系统组合是否具有普适性,在初始化种群数目设置为20、最大迭代次数设置为120的前提下,系统分析不同卫星系统组合(G、C、G/C、G/C/E、G/C/E/R、G/C/E/R/J)下的选星耗时和平均GDOP差值,结果如图 3所示。
|
图 3 不同卫星系统组合下的选星耗时和GDOP差值 Fig. 3 Satellite selection time consuming and GDOP difference under different satellite system combinations |
由图 3(a)~(c)可知,利用G、C单系统和C/G双系统进行定位时,在固定选星数目情况下改进免疫算法求得的最小GDOP与遍历法结果几乎一致,且GDOP差值最大不超过0.07。平均耗时在0.5~0.6 s内波动,处于平稳状态。由图 3(d)~(f)可知,GDOP差值存在较大波动,总体介于0~0.4之间,部分历元平均耗时明显上升,但最大耗时不超过2.0 s。为了量化所提算法的性能,表 3为不同系统组合下2种选星算法的GDOP值以及计算耗时。
|
|
表 3 两种选星算法的GDOP值和平均耗时 Tab. 3 GDOP values and average time consuming of the two satellite selection algorithms |
由表 3可知,随着卫星数增加,遍历法平均耗时急剧上升,当可见卫星数目为45时,遍历法耗时高达29.976 s,严重影响接收机的实时性。改进免疫算法的平均耗时虽然也随可见卫星数的上升而增加,但上升幅度较小,在五系统组合情况下,耗时仅为1.06 s。改进免疫算法计算的GDOP值与遍历法结果相差较小,最大差值约为0.2。与遍历法相比,本文所提方法在进行GPS、BDS单系统定位时平均耗时分别缩短40.58%、53.27%,平均GDOP差值与遍历法的比值分别为0.44%、0.57%。在GPS/BDS组合系统下,与遍历法相比,改进的免疫算法平均GDOP差值仅为0.011,耗时缩短69.74%。在GPS/BDS/Galileo三系统、GPS/BDS/Galileo/GLONASS四系统、GPS/BDS/Galileo/GLONASS/QZSS五系统组合定位时,本文算法的平均耗时分别缩短93.37%、96.21%、96.47%,其平均GDOP与遍历法相差分别为0.159、0.152、0.122,因此改进的免疫算法在多GNSS系统组合定位时均具有良好的性能。
4 结语本文提出一种基于改进免疫算法的GNSS快速选星方法,可有效降低运算量,提高接收机定位实时性。在考虑实时性与定位精度双重因素下,选择最佳的初始化种群数目与最大迭代次数。最后,通过实测数据验证所提方法的有效性及普适性,结论如下:
1) 初始化种群数目在20附近、最大迭代次数在120附近,免疫算法的选星性能最优,其耗时与遍历法相比缩短93.42%。
2) 在单BDS系统定位时,本文所提算法平均GDOP值与遍历法相差仅为0.01,平均GDOP差值与遍历法的比值仅为0.57%,耗时比遍历法缩短53.27%。
3) 在不同系统组合下,包括GPS/BDS/Galileo、GPS/BDS/Galileo/GLONASS和GPS/BDS/Galileo/GLONASS/QZSS,本文所提算法相对于遍历法,GDOP误差不超过0.5,并且平均耗时分别缩短93.37%、96.21%和96.47%。因此,该算法适用于多个GNSS系统组合下的定位,具有良好的普适性。
| [1] |
宋玉龙, 廉保旺, 宋佳驹. BDS/GPS双系统软件接收机实现与性能分析[J]. 西北工业大学学报, 2016, 34(4): 656-662 (Song Yulong, Lian Baowang, Song Jiaju. Implementation and Performance of BDS/GPS Dual-System Software Receiver[J]. Journal of Northwestern Polytechnical University, 2016, 34(4): 656-662)
(  0) 0) |
| [2] |
Wang H B, Cheng Y M, Cheng C, et al. Research on Satellite Selection Strategy for Receiver Autonomous Integrity Monitoring Applications[J]. Remote Sensing, 2021, 13(9)
(  0) 0) |
| [3] |
Blanco-Delgado N, Nunes F D. Satellite Selection Method for Multi-Constellation GNSS Using Convex Geometry[J]. IEEE Transactions on Vehicular Technology, 2010, 59(9): 4 289-4 297 DOI:10.1109/TVT.2010.2072939
(  0) 0) |
| [4] |
董天宝, 唐健, 曾芳玲. 基于K均值聚类的新型选星算法[J]. 计算机仿真, 2022, 39(11): 22-26 (Dong Tianbao, Tang Jian, Zeng Fangling. A New Satellite Selection Algorithm Based on K-Means[J]. Computer Simulation, 2022, 39(11): 22-26)
(  0) 0) |
| [5] |
Hao P Y, Wu C Y. GPS GDOP Approximation Using Support Vector Regression Algorithm with Parametric Insensitive Model[C]. 2012 International Conference on Machine Learning and Cybernetics. Xi'an, 2012
(  0) 0) |
| [6] |
霍航宇, 张晓林. 组合卫星导航系统的快速选星方法[J]. 北京航空航天大学学报, 2015, 41(2): 273-282 (Huo Hangyu, Zhang Xiaolin. Fast Satellite Selection Method for Integrated Navigation Systems[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(2): 273-282)
(  0) 0) |
| [7] |
Azami H, Sanei S. GPS GDOP Classification via Improved Neural Network Trainings and Principal Component Analysis[J]. International Journal of Electronics, 2014, 101(9): 1 300-1 313 DOI:10.1080/00207217.2013.832390
(  0) 0) |
| [8] |
余德荧, 李厚朴, 纪兵, 等. 基于灰狼优化算法的快速选星方法[J]. 系统工程与电子技术, 2023, 45(5): 1 489-1 495 (Yu Deying, Li Houpu, Ji Bing, et al. Fast Satellite Selection Method Based on Grey Wolf Optimization Algorithm[J]. Systems Engineering and Electronics, 2023, 45(5): 1 489-1 495)
(  0) 0) |
| [9] |
王尔申, 杨迪, 王传云, 等. PSO选星算法参数分析与改进[J]. 北京航空航天大学学报, 2019, 45(11): 2 133-2 138 (Wang Ershen, Yang Di, Wang Chuanyun, et al. Parameter Analysis and Improvement of PSO Satellite Selection Algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(11): 2 133-2 138)
(  0) 0) |
| [10] |
王尔申, 贾超颖, 曲萍萍, 等. 基于混沌粒子群优化的北斗/GPS组合导航选星算法[J]. 北京航空航天大学学报, 2019, 45(2): 259-265 (Wang Ershen, Jia Chaoying, Qu Pingping, et al. BDS/GPS Integrated Navigation Satellite Selection Algorithm Based on Chaos Particle Swarm Optimization[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(2): 259-265)
(  0) 0) |
| [11] |
朱军, 许士杰, 李凯. 基于几何分布和差分进化的双模导航选星算法[J]. 北京邮电大学学报, 2021, 44(3): 9-14 (Zhu Jun, Xu Shijie, Li Kai. Dual-Mode Navigation Satellite Selection Algorithm Based on Differential Evolution and Geometry[J]. Journal of Beijing University of Posts and Telecommunications, 2021, 44(3): 9-14)
(  0) 0) |
| [12] |
肖人彬, 王磊. 人工免疫系统: 原理、模型、分析及展望[J]. 计算机学报, 2002, 25(12): 1 281-1 293 (Xiao Renbin, Wang Lei. Artificial Immune System: Principle, Models, Analysis and Perspectives[J]. Chinese Journal of Computers, 2002, 25(12): 1 281-1 293)
(  0) 0) |
| [13] |
Liu B, Teng Y L, Huang Q. GDOP Minimum in Multi-GNSS Positioning[J]. Advances in Space Research, 2017, 60(7): 1 400-1 403 DOI:10.1016/j.asr.2017.06.049
(  0) 0) |
| [14] |
何宏, 钱锋. 基于模糊自适应免疫算法的非线性系统模型参数估计[J]. 控制理论与应用, 2009, 26(5): 481-486 (He Hong, Qian Feng. Parameter Estimation of Nonlinear System Model Based on Fuzzy Adaptive Immune Algorithm[J]. Control Theory and Applications, 2009, 26(5): 481-486)
(  0) 0) |
2. Key Laboratory of Aviation-Aerospace-Ground Cooperative Monitoring and Early Warning of Coal Mining-Induced Disasters of Anhui Higher Education Institutes, Anhui University of Science and Technology, 168 Taifeng Street, Huainan 232001, China;
3. Coal Industry Engineering Research Center of Mining Area Environmental and Disaster Cooperative Monitoring, Anhui University of Science and Technology, 168 Taifeng Street, Huainan 232001, China
 2024, Vol. 44
2024, Vol. 44


