2. 地理信息工程国家重点实验室,西安市雁塔路中段1号,710054
高精度GNSS坐标序列中蕴含的构造运动和非构造运动信息已广泛应用于地壳运动研究、地下水储量反演和位移探测等领域[1-2],但GNSS坐标序列中存在着一种与时空特性相关的共模误差(CME),会使测站位置和速度估计产生偏差,导致解译出错误的地球物理信息。
目前,CME提取方法可分为区域滤波法、参考框架法和统计信号分解法3类,其中常用的统计信号分解法对CME提取效果最佳。区域滤波法前提需要假设CME空间分布均匀,但此假设与实际情况相悖。Wang等[3]基于PCA对CME提取进行研究,结果表明,PCA相比于区域滤波法有更好的效果。然而,PCA只能对符合高斯分布的信号进行提取,无法对具有非高斯特性的有色噪声进行识别。
ICA是一种顾及高阶统计信号的盲源分离方法。刘斌等[4]将ICA与PCA应用于垂向GNSS坐标序列的时空滤波,结果表明,二者提取的共模分量有着不同的时空分布特征;李斐等[5]基于ICA对GNSS坐标序列进行矩阵特征分解,重构共模分量,有效提取了坐标序列中的CME,但ICA分量顺序及其空间特性表现出随机性,并且ICA只能对一种高斯信号进行识别,这对共模分量确定和CME空间特征分析带来严重困扰。
vbICA是一种使用变分贝叶斯推理执行ICA的信号分解方法。目前,该方法在大地测量时间序列中的瞬态信号和季节性信号提取方面得到初步应用;Gao等[6]也初次使用该方法对云南、四川GNSS测站坐标序列进行有效滤波。针对PCA与ICA在CME提取方面的不足,本文采用vbICA对实验区20个GNSS测站坐标序列进行CME提取,并与PCA、ICA结果对比,分析vbICA方法的有效性和先进性,最后基于vbICA滤波估计速度场变化。
1 原理与方法 1.1 vbICA原理针对GNSS坐标序列中的有色噪声,建立带噪声的标准ICA混叠模型[7]:
| $ \boldsymbol{x}=\boldsymbol{As}+\boldsymbol{e} $ | (1) |
式中,x为观测坐标序列矩阵,s=[s1, s2, ⋯, sL]为信源向量,A为混合矩阵,e为高斯噪声向量。
基本流程为:首先,基于观测坐标序列矩阵x,引入贝叶斯定理将模型参数的先验概率分布转化为后验概率分布;其次,建立相关节点变量的贝叶斯模型,通过变分逼近方法求解各参数的后验概率分布,最终得到源信号最佳估值为
| $ \boldsymbol{X}=\boldsymbol{A} \hat{\boldsymbol{s}} $ | (2) |
式中,
| $ \lambda_k=\frac{\sum\limits_{i=1}^N\left(\boldsymbol{y}_k-\overline{\boldsymbol{y}}_k\right)^2}{\sum\limits_{k=1}^m \sum\limits_{i=1}^N\left(\boldsymbol{y}_k-\overline{\boldsymbol{y}}_k\right)^2} \times 100 \% $ | (3) |
式中,m为独立分量个数,N为观测历元总数,λk介于0~1区间。PCA的分量贡献率由特征值计算。
对所有独立分量贡献率按降序排列,选取贡献率最大的前p个独立分量表示最显著信号,最终CME可表示为:
| $ \mathrm{CME}_{\mathrm{vbICA}}=\sum\limits_{k=1}^p \boldsymbol{a}_k \hat{\boldsymbol{s}}_k $ | (4) |
由于环境负载会造成基准站周期性位移,致使GNSS坐标序列存在非线性信号。进行站间相关性分析的常用方法为Pearson相关系数法,其在分析残留有非线性信号的坐标残差序列时会导致相关性误差。因此,为准确反映扣除CME前后站间相关性变化,本文将采用能够衡量非线性变量之间相关程度的距离相关系数法[8]。
1.2.2 均方根变化| $ d_{\mathrm{RMS}}=\sqrt{\sum\limits_{i=1}^N \boldsymbol{x}_i^2 / N}-\sqrt{\sum\limits_{i=1}^N \overline{\boldsymbol{x}}_i^2 / N} $ | (5) |
式中,xi为原始坐标序列,xi为扣除CME后的坐标残差序列。
2 数据来源与预处理在PBO(plate boundary observatory)网络中选取均匀分布于俄勒冈州、内华达州、加利福利亚州内20个连续运行GNSS观测站,对其2009-01~2019-01期间的坐标序列进行处理。原始数据来源于Nevada Geodetic Laboratory,该数据采用GipsyX软件处理,同时加入极潮、海潮及固体潮等模型改正,并对电离层、对流层延迟、天线相位中心偏差进行校正,最终得到IGS2014框架下GNSS测站的三维坐标序列。经统计,20个测站数据完整率均在98%以上。
2.1 原始数据预处理由于受仪器故障和外界因素干扰,致使GNSS坐标序列不可避免地存在随机的数据缺失和粗差。首先,根据E、N、U方向上坐标序列的中误差设置阈值分别为20 mm、20 mm、30 mm进行初次粗差剔除;然后,利用3倍四分位数法进行二次粗差剔除;最终得到3个方向坐标序列最大缺失率分别为1.48%、1.51%、1.51%,且均发生在P059测站。为获得等时间间隔的坐标序列,采用三次样条插值对空缺位置数据进行恢复。此外,由于强震同震位移或设备更换等原因,可能会导致原始坐标序列中存在阶跃现象。根据Nevada Geodetic Laboratory提供的站点log文件,P386测站点在2016-10-13由于更换天线导致阶跃,其中N方向阶跃明显,约为10 mm。具体修正流程为:1)根据站点log文件确定站点阶跃时刻;2)利用Hector软件估计阶跃大小;3)将阶跃从原始坐标序列中扣除。对于其他存在阶跃的坐标序列,采用同样流程处理。
2.2 坐标残差序列获取经过预处理后,原始坐标序列将不含阶跃项和粗差。此时,任意t时刻,单站单方向的GNSS坐标序列y(t)可简化表示为:
| $ y(t)=a_0+a_1\left(t-t_0\right)+a_2(t)+a_3(t)+\varepsilon(t) $ | (6) |
式中,t0为起始历元,a0为初始位置,a1为线性趋势,a2为周期运动,a3为CME,ε为有色噪声。根据式(6),对原始坐标序列采用加权最小二乘拟合并扣除a1、a2,得到坐标残差序列。
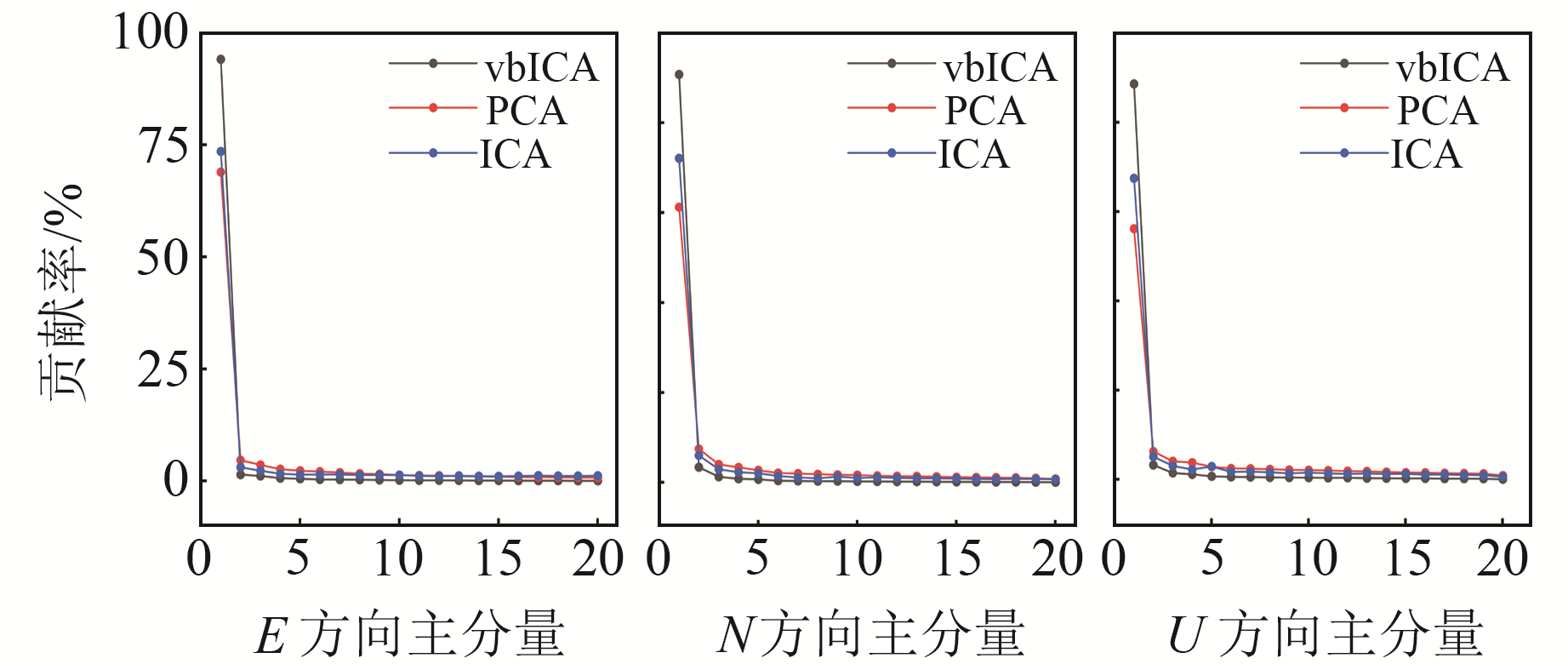
3 结果与分析 3.1 CME提取分析Dong等[9]基于PCA/KLE滤波方法对CME进行研究,提出利用共模模式进行CME判断,即被作为共模分量的主分量(principal component,PC)具有最高的分量占比,可认为是共模分量,贡献率最大的分量综合了原始坐标序列最多的信息。图 1为3个方向所有分量的贡献率统计结果。由图可知,vbICA、PCA和ICA分解后,3个方向第一主分量PC1贡献率均表现为最大,其中,E方向PC1贡献率分别为94.06%、68.92%、73.52%;N方向PC1贡献率为90.73%、61.21%、72.09%;U方向PC1贡献率为88.62%、56.18%、67.47%,分量PC2~PC20贡献率依次减小,且均小于10%。因此,本文以PC1作为共模分量重构CME,结果如图 2所示。
|
图 1 E、N、U方向主分量贡献率 Fig. 1 Contribution rate of PCS in E, N and U directions |
|
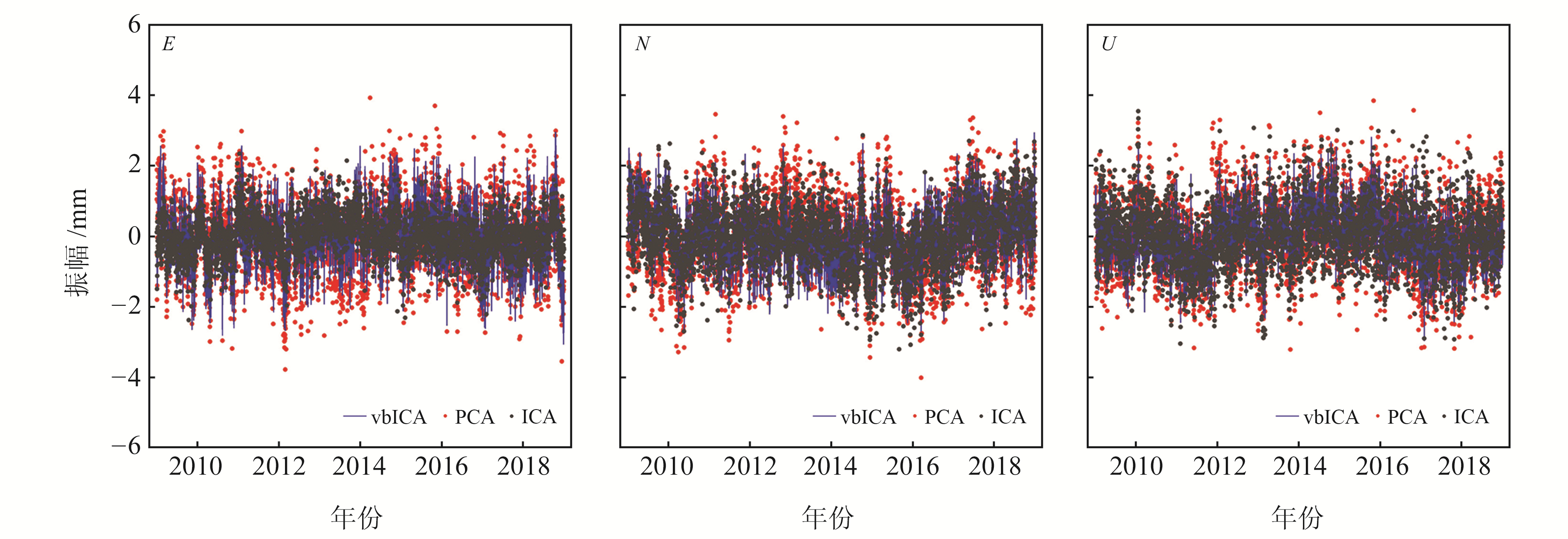
图 2 vbICA、PCA、ICA重构的CME Fig. 2 CME reconstructed by vbICA, PCA and ICA |
为对比vbICA与PCA和ICA提取的CEM差异,分别计算3个方向上CME之间的Pearson相似度。统计结果如表 1所示,可以看出,PCA与ICA的相似度较低,在E、U方向上相似度均低于0.6,根据ICA的高阶统计特性,说明PCA所得共模分量未考虑CME的高阶信息;vbICA重构的CME与PCA和ICA的结果具有较强的一致性,其最大相似度为0.80,最低为0.62,说明相同历元时刻的CME相近,且在整体表现为周期上的一致性。然而,vbICA与PCA在E方向的相似度较高,由于PCA存在潜在的“聚类”问题可能导致E方向PC1包含不同的物理模式,进而导致CME存在虚假信息,对于该现象后文将根据相关评价指标进一步分析。整体而言,以上结果初步证实了vbICA在提取CME方面的有效性。
|
|
表 1 CME相似度 Tab. 1 Similarity of CME |
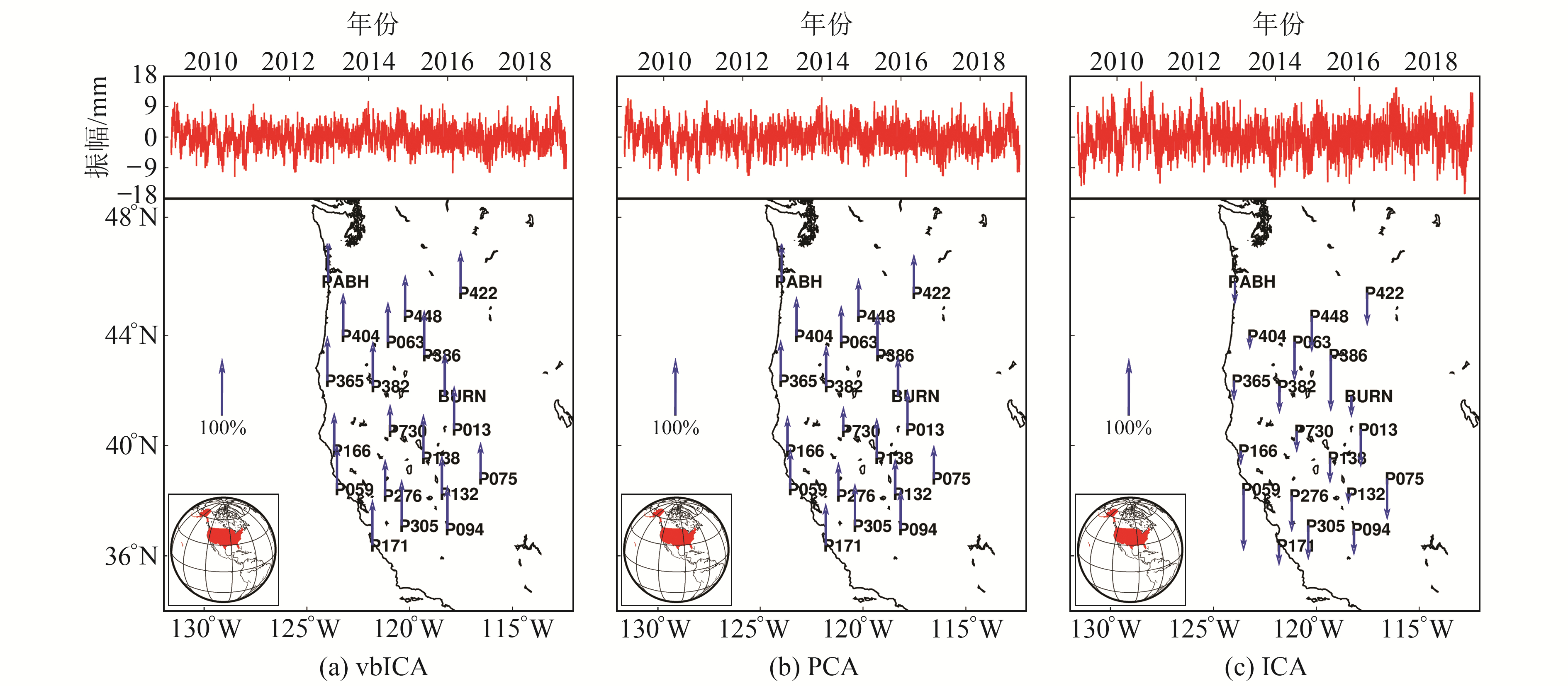
对3个方向20个主分量的空间响应(spatial response, SR)进行标准化。图 3分别为vbICA、PCA和ICA三种方法在E方向上的共模分量PC1及其空间响应SR1,箭头向上表示SR为正,向下为表示SR为负。由图可知,3种方法获取的共模分量PC1具有共同的周期特征,且所有站点的SR1表现一致,均为正响应或负响应;箭头大小表示SR大小,不同站点的SR1大小不同,表明所有测站的CME在空间分布上的不均匀性。
|
图 3 E方向PC1及其SR1 Fig. 3 PC1 and SR1 in the direction E |
对比图 3发现,vbICA和PCA在E方向上空间响应为正,ICA为负,且vbICA和PCA第一分量PC1方向相反。该现象的产生与算法自身特性密切相关:对于vbICA来说,信源模型选择是利用vbICA进行GNSS坐标序列分解的核心,而不同信源模型初始化先验信息具有唯一性,最终表现为当选定信源模型后,针对同一观测数据无论vbICA分解多少次,主分量及其空间响应符号均不会发生变化;而在ICA分解中,由于权重矩阵初始化采用的是随机矩阵,故而导致循环收敛后的混合矩阵具有随机性,最终重构的PC分量顺序也是随机的;PCA基于正交分解方差最大原则实现降维,在进行坐标序列特征分解时,并没有引入随机变量,其结果与vbICA表现一致。结合图 2,虽然不同方法所得空间响应SR符号和对应PC符号存在差异,但最终并不会对CME重构造成影响。
3.3 滤波效果分析为分析vbICA与PCA、ICA的CME提取效果差异,本文从原始坐标序列CME滤波前后均方根变化和测站间距离相关系数变化角度进行分析。
根据式(5)计算E、N、U方向CME滤波后各测站坐标残差序列RMS减少百分比变化,由于篇幅限制,仅对任意10个测站结果进行统计,如表 2(单位%)所示。由表可知,3种方法均可有效降低各测站E、N、U方向坐标残差序列的RMS,说明CME滤波后测站坐标序列离散程度降低、振幅减小。通过滤波前后3个方向RMS平均减少百分比可以发现,所有测站E、N、U方向上的坐标序列经vbICA滤波后RMS平均减小百分比分别为36.57%、31.63%、10.97%;经PCA滤波后RMS平均减小百分比分别为28.57%、22.77%、10.25%;经ICA滤波后RMS平均减小百分比分别为14.90%、23.34%、10.44%,显然vbICA结果明显好于PCA和ICA。针对上述vbICA与PCA相似度高的问题,由RMS结果可知,PCA提取的CME存在虚假信号。
|
|
表 2 滤波后各站RMS减少百分比 Tab. 2 Percentage reduction of RMS of each station after filtering |
进一步分析发现,P730经ICA滤波后E方向RMS变化为-0.16%,相比滤波前RMS增大,结合图 3(c)发现,P730测站空间特性明显;同理,vbICA和ICA对P166测站RMS改善也并不明显,说明测站的局部效应对于CME时空滤波具有不同程度的影响。垂直方向RMS变化明显低于水平方向,表明同一测站CME对该测站垂直和水平方向影响并不一致,且水平方向影响较大,主要原因为:垂直方向除CME以外,还受到非潮汐海洋负荷、环境负载以及基岩热膨胀效应等非线性变化因素的影响。
根据各测站距离的远近,以较远的PABH测站为基准,计算并统计其余19个测站相对于基准站在E、N、U方向上滤波前后的R变化百分比。整体而言,vbICA滤波后,E、N、U方向上R平均减小率分别为60.53%、56.84%、25.80%;ICA平均减小率为11.58%、33.54%、12.11%;PCA平均减小率为25.94%、22.79%、11.57%。由此可知,扣除vbICA提取的CME后,测站间相关性减弱程度明显高于ICA和PCA。此外,R在水平方向上的变化趋势较为明显,而在垂直方向上变化差异较小,一方面说明CME的影响因素在水平方向和垂直方向上存在差异,另一方面说明时间跨度长的GNSS坐标序列在水平方向受板块运动影响较大。
3.4 CME对速度场影响GNSS坐标序列CME滤波不仅可以获得更加精细的形变信息,还可以优化GNSS速度场,对于全球板块运动、mm级动态参考框架建立与维持等地学研究具有重要意义[1]。
根据黄立人等[10]相关学者研究结果,假设水平方向和垂向分别以FN+WN和FN+PL为最优噪声模型,采用极大似然估计法分别对测站3个方向原始坐标序列进行趋势项估计。表 3统计任意10个测站经vbICA滤波前后速度及其不确定度变化;图 4(a)、图 4(b)为滤波前后水平和垂向GNSS速度场及其不确定度变化,箭头长短表示速度的相对大小,圆圈大小表示不确定度的相对大小。对比分析可知,水平方向上,该区域整体向西南方向运动,且有涡旋趋势;在垂向上整体表现为地表下沉。剔除CME后,20个测站3个方向速度场估计的标准差平均降低52.71%、49.88%、18.04%。其中,水平速度场精度改善明显,不考虑个别特殊站,E方向测站速度平均变化不高于0.04 mm/a,N方向不高于0.01 mm/a。此外,滤波后P276测站的速度变化达到4.47 mm/a,P730变化达到了1.57 mm/a,且由图 4(b)可见,P305、P365测站运动速率为正,即垂直向上运动,说明垂向变化不仅与区域整体运动有关,局部形变因素也不容忽视。CME滤波可凸显局部效应较强的部分测站所隐藏的信号,提高GNSS速度场估计的可靠性,有助于地球物理现象的清晰解释。
|
|
表 3 CME滤波前后测站速度及其不确定度变化 Tab. 3 Velocity and uncertainty changes after CME filtering |

|
图 4 基于vbICA的GNSS速度场 Fig. 4 GNSS velocity field based on vbICA |
本文针对PCA、ICA在提取CME方面的不足,研究vbICA对CME的提取。通过对滤波前后坐标序列RMS值、距离相关性以及相似度等指标进行滤波效果分析,结果表明,vbICA方法滤波效果明显优于PCA和ICA;滤波后GNSS坐标序列的精度明显提高,且vbICA比ICA表现出更强的鲁棒性。
致谢: 感谢Nevada Geodetic Laboratory提供实验数据。
| [1] |
姜卫平, 王锴华, 李昭, 等. GNSS坐标时间序列分析理论与方法及展望[J]. 武汉大学学报: 信息科学版, 2018, 43(12): 2 112-2 123 (Jiang Weiping, Wang Kaihua, Li Zhao, et al. Prospect and Theory of GNSS Coordinate Time Series Analysis[J]. Geomatics and Information Science of Wuhan University, 2018, 43(12): 2 112-2 123)
(  0) 0) |
| [2] |
Wang J, Nie G G, Gao S J, et al. Landslide Deformation Prediction Based on a GNSS Time Series Analysis and Recurrent Neural Network Model[J]. Remote Sensing, 2021, 13(6): 1 055 DOI:10.3390/rs13061055
(  0) 0) |
| [3] |
Wang H, Li W H, Shu C F, et al. Assessment of Spatiotemporal Filtering Methods towards Optimising Crustal Movement Observation Network of China(CMONOC) GNSS Data Processing at Different Spatial Scales[J]. All Earth, 2022, 34(1): 107-119 DOI:10.1080/27669645.2022.2098611
(  0) 0) |
| [4] |
刘斌. 基于ICA的垂向GNSS坐标时间序列时空分析建模及反演的理论与方法[J]. 测绘学报, 2022, 51(5): 783 (Liu Bin. Theory and Method of Spatiotemporal Analysis, Modeling and Inversion of Vertical GNSS Coordinate Time Series Based on Independent Component Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2022, 51(5): 783)
(  0) 0) |
| [5] |
李斐, 李文浩, 张胜凯, 等. 基于独立分量分析的南极半岛GNSS网区域滤波[J]. 地球物理学报, 2019, 62(9): 3 279-3 295 (Li Fei, Li Wenhao, Zhang Shengkai, et al. Spatiotemporal Filtering for Regional GNSS Network in Antarctic Peninsula Using Independent Component Analysis[J]. Chinese Journal of Geophysics, 2019, 62(9): 3 279-3 295)
(  0) 0) |
| [6] |
Gao H, Kuang C L. Spatiotemporal Filtering of GNSS Coordinate Time Series Based on Variational Bayesian Independent Component Analysis[C]. China Satellite Navigation Conference(CSNC2022), Beijing, 2022
(  0) 0) |
| [7] |
Gualandi A, Serpelloni E, Belardinelli M E. Blind Source Separation Problem in GPS Time Series[J]. Journal of Geodesy, 2016, 90(4): 323-341 DOI:10.1007/s00190-015-0875-4
(  0) 0) |
| [8] |
Székely G J, Rizzo M L. Energy Statistics: A Class of Statistics Based on Distances[J]. Journal of Statistical Planning and Inference, 2013, 143(8): 1 249-1 272 DOI:10.1016/j.jspi.2013.03.018
(  0) 0) |
| [9] |
Dong D, Fang P, Bock Y, et al. Spatiotemporal Filtering Using Principal Component Analysis and Karhunen-Loeve Expansion Approaches for Regional GPS Network Analysis[J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B3)
(  0) 0) |
| [10] |
黄立人. GPS基准站坐标分量时间序列的噪声特性分析[J]. 大地测量与地球动力学, 2006, 26(2): 31-33 (Huang Liren. Noise Properties in Time Series of Coordinate Component at GPS Fiducial Stations[J]. Journal of Geodesy and Geodynamics, 2006, 26(2): 31-33)
(  0) 0) |
2. State Key Laboratory of Geo-Information Engineering, 1 Mid-Yanta Road, Xi'an 710054, China
 2024, Vol. 44
2024, Vol. 44


