2. 武汉地震科学仪器研究院有限公司,武汉市洪山侧路40号,430071
SS-Y伸缩仪是由中国地震局地震研究所自主研制,并在大地测量领域广泛应用的地壳表面两点因变量观测仪器,具有遥控标定、高精度、短基线等特点[1-2]。SS-Y伸缩仪映震能力较好,但易受到前置放大故障、供电故障、超量程等仪器内部故障或气压、温度、雷电等复杂外部环境因素的影响[3-8],出现数据曲线固体潮不清晰、局部不光滑等情况。自适应噪声完备集合经验模态分解(CEEMDAN)在信号去噪领域已取得显著成果。该方法通过自主分析信号质量,在信号分解过程中引入相匹配的白噪声,以改善传统EMD过程中常见的模态混叠现像,信号重构质量较高且去噪效果较好。基于CEEMDAN的改进的自适应噪声完备集合经验模态分解(ICEEMDAN)[9-11]能有效减少模态混叠现象和分解后虚假分量的产生,且针对信号在CEEMDAN处理过程中的问题进行优化改进,克服了某些本征模态函数中仍含有较多残余分量的现状,信号重构质量得到明显提升。
本文提出一种基于ICEEMDAN和分布熵(DistEn)[12]的SS-Y伸缩仪信号随机噪声压制方法。根据ICEEMDAN得到的各分量整体混乱程度,判断其是否为原始信号的有效成分或是否为含噪分量,进而采取处置手段;同时,设计仿真信号与SS-Y伸缩仪实测信号去噪对比及单轮与多轮去噪对比实验,结合多个指标评价去噪模型的性能。
1 信号去噪模型 1.1 ICEEMDAN原理1) 对原始信号x进行分解,构造原始信号的加噪合成信号:
| $ x^{(i)}=x+\beta_0 E_1\left(w^{(i)}\right) $ | (1) |
式中,β0为首次分解时的信噪比,w(i)为第i个被添加的高斯白噪声,E1(·)为EMD的首个IMF分量。
2) 重复步骤1)N次,得到N个x(i),并求全部局部均值函数值的均值,即首个残余分量:
| $ r_1=\frac{1}{N} \sum\limits_{i=1}^N M\left(x^{(i)}\right) $ | (2) |
式中,M(·)为局部均值函数。
3) 在原始信号的基础上减去首个残余分量,得到首个模态:
| $ d_1=x-r_1 $ | (3) |
4) 根据第k次分解后计算的局部均值函数值,得到第k个残余分量,并用上一个残余分量减去该残差结果,得到第k个模态dm:
| $ d_m=r_{k-1}-r_k $ | (4) |
| $ r_k=\frac{1}{N} \sum\limits_{i=1}^N M\left(r_{k-1}+\beta_{k-1} E_k\left(w^{(i)}\right)\right) $ | (5) |
5) 持续执行步骤4),直至满足分解停止条件。
1.2 DistEn原理DistEn[12]是对样本熵和近似熵的改进,可解决部分参数的高度依赖和非鲁棒性问题,一般计算步骤为:
1)设定信号
| $ \hat{\boldsymbol{x}}(i)=\{x(i), x(i+1), \cdots, x(i+p-1)\} $ | (6) |
2) 计算切比雪夫距离。分析向量
3) 利用直方图估算经验概率密度函数(EPDF,记作fk)。定义直方图柱数q,则直方图频数分布为
| $ f_k=n_k / \sum\limits_{k=1}^q n_k $ | (7) |
4) 计算分布熵:
| $ \text { DistEn }=-\sum\limits_{k=1}^q f_k \log _2 f_k $ | (8) |
ICEEMDAN-DistEn去噪模型步骤如下:
1) 对SS-Y伸缩仪信号进行ICEEMDAN处理,得到若干个IMF分量,并依据频率高低进行排序和标记。
2) 分别计算各IMF分量的DistEn,并设定阈值δ,对符合不同阈值区间的IMF分量作对应的差异化处理。
3) 当某个IMF的DistEn∈[δ, 1]时,表示该IMF分量内部几乎不包含随机噪声成分,属于原始信号的有效成分,可以直接参与线性重构。
4) 当某个IMF的DistEn∈[0, δ]时,表示该IMF分量基本为随机噪声成分,具有类似的随机振荡特性,可以直接舍弃。
5) 将步骤3)和4)所保留的全部IMF分量进行线性重构,即可得到SS-Y伸缩仪去噪后的数据。
由于ICEEMDAN方法属于CEEMDAN方法的改进,参考ICEEMDAN-DistEn去噪模型的核心原理得到CEEMDAN-DistEn去噪模型,作为SS-Y伸缩仪信号去噪实验的对照模型之一。
2 实验与分析设计3个实验分析ICEEMDAN-DistEn去噪模型的有效性,包括仿真信号的高、低频噪声去噪实验和SS-Y伸缩仪实测信号去噪实验,并利用相关系数、均方误差(MSE)及信噪比(SNR)等评价指标衡量模型的去噪效果。
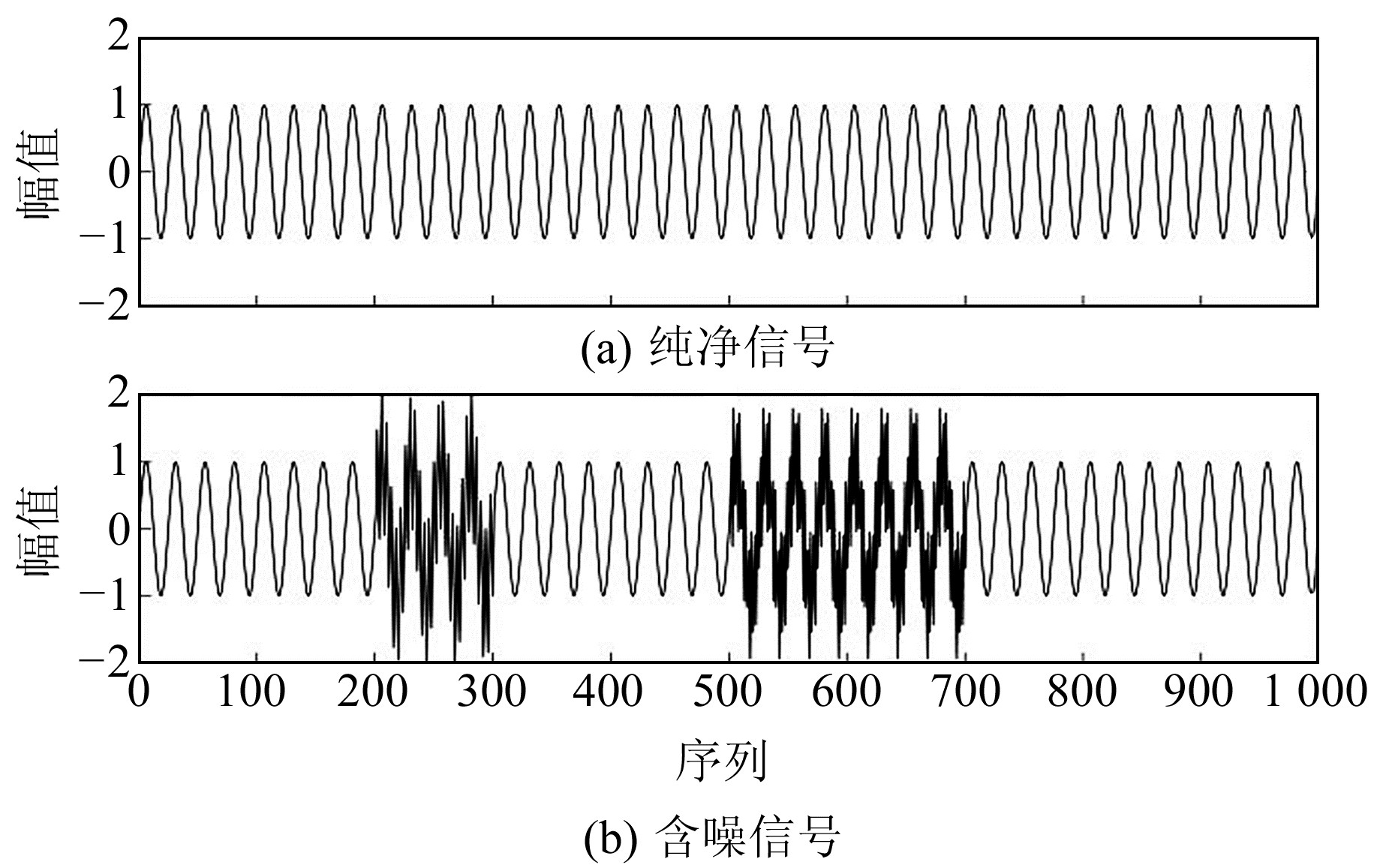
2.1 仿真信号的高频噪声去噪实验与分析设计仿真信号去噪实验,初始化一段纯净信号x1(t)和两段位置不同且幅值差异较大的噪声成分x2(t)和x3(t)(图 1),线性合成后构成需要处理的仿真含噪信号X(t),采样率为10 Hz。ICEEMDAN及ICEEMDAN-DistEn去噪波形如图 2和3所示:
|
图 1 利用MATLAB生成仿真纯净信号与加噪信号 Fig. 1 Simulation of pure signals and noise-added signals using MATLAB |
|
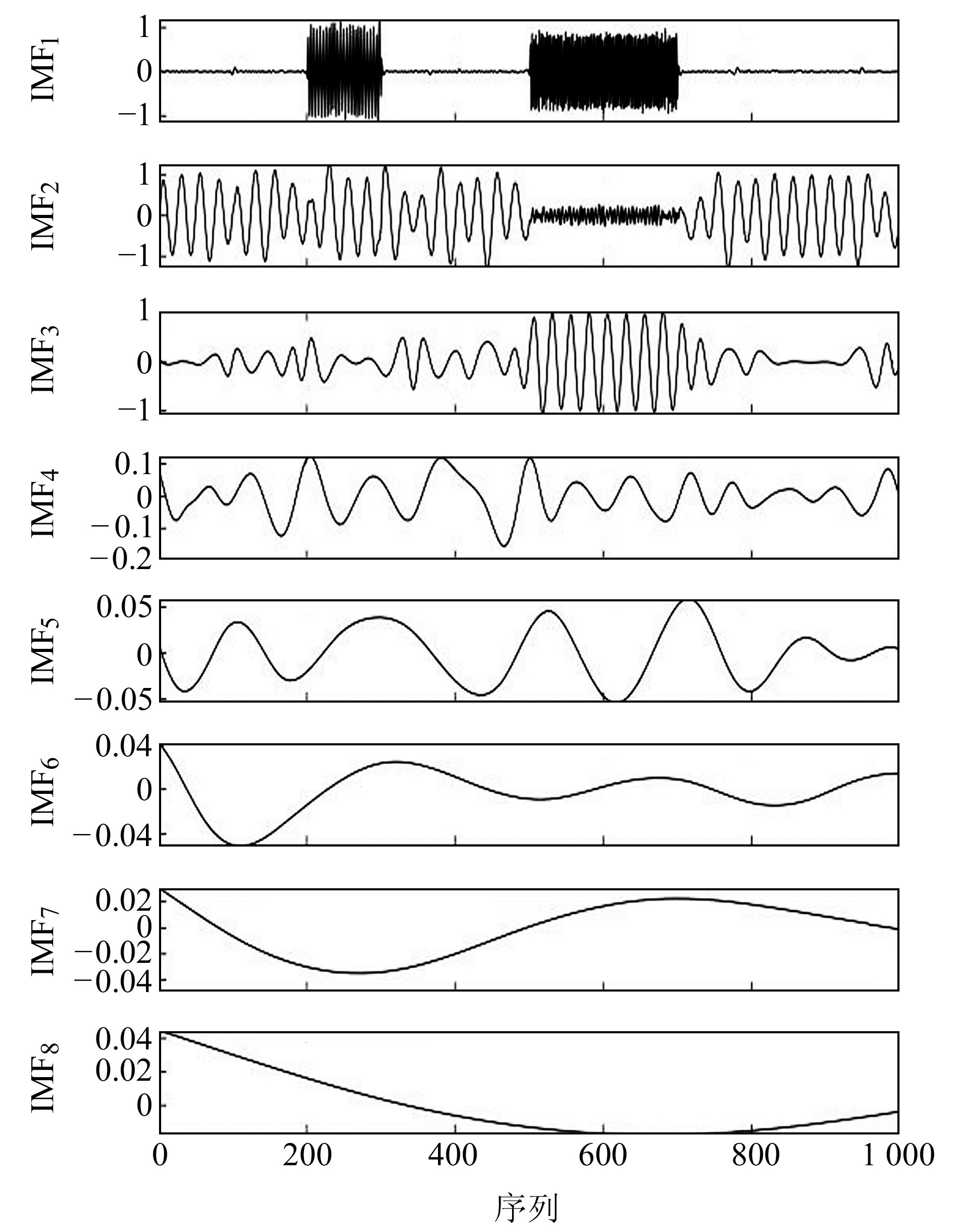
图 2 仿真含噪信号经过ICEEMDAN处理后得到的IMF Fig. 2 IMFs obtained from simulated noise-containing signals using ICEEMDAN |

|
图 3 基于ICEEMDAN-DistEn模型的仿真信号去噪结果 Fig. 3 Denoising results of simulated signals based on ICEEMDAN-DistEn model |
| $ X(t)=x_1(t)+x_2(t)+x_3(t) $ | (9) |
| $ \begin{gathered} x_1(t)=\sin (0.08 \pi t), \\ 1 \leqslant t \leqslant 1000 \end{gathered} $ | (10) |
| $ \begin{gathered} x_2(t)=\sin (0.5 \pi(t-201)), \\ 201 \leqslant t \leqslant 300 \end{gathered} $ | (11) |
| $ \begin{gathered} x_3(t)=\sin (0.8 \pi(t-301)), \\ 501 \leqslant t \leqslant 700 \end{gathered} $ | (12) |
图 2为仿真含噪信号的ICEEMDAN处理结果,包含8个IMF分量。可以看出,IMF1分量即可从原始含噪信号中分离出2个发生位置及持续时长完全不同的噪声成分,而IMF2分量和IMF3分量是原始纯净信号的主要幅值成分,其他IMF分量幅值较小,对去噪结果影响不大。
表 1为原始含噪信号经过ICEEMDAN处理后各IMF分量的分布熵值。可以看出,各IMF分量在最大幅值、混乱程度、局部变异、对称性等多个维度均存在极大差异,其中IMF1的分布熵值最小,IMF7的分布熵值最大,说明IMF1的局部噪声成分具有显著规律性和周期性,很容易被ICEEMDAN算法识别出。结合图 2和表 1可以发现,有规律性的高频噪声成分分布熵值较小,而作为原始含噪信号的有效成分由于已被ICEEMDAN处理为不同频率下的IMF分量,其分布熵值均较大,均可被用于线性重构。
|
|
表 1 仿真含噪信号经过ICEEMDAN处理后得到的各IMF分量的分布熵值 Tab. 1 Distributive entropy values of each IMF component obtained from simulated noise-containing signals using ICEEMDAN |
结合图 1和3可知,基于仿真含噪信号的ICEEMDAN-DistEn模型去噪效果较显著。为证明该模型的优越性,对比分析ICEEMDAN-DistEn、CEEMDAN-DistEn、卡尔曼滤波、小波去噪、70阶低通FIR滤波和Savitzky-Golay滤波等6个模型的去噪效果。表 2为6种去噪模型的含噪信号处理结果,表中相关系数、MSE、SNR等评价指标基于原始纯净信号和去噪后信号进行比较。由表可知,原始含噪信号相对于纯净信号的信噪比为5.228 8,6个模型中ICEEMDAN-DistEn、小波去噪、70阶低通FIR滤波和Savitzky-Golay滤波的去噪效果明显,SNR值大幅提高;综合相关系数和MSE来看,70阶低通FIR滤波模型的信号重构损失稍大,只有ICEEMDAN-DistEn模型的各指标均有相对均衡的去噪效果;卡尔曼滤波受制于状态方程参数设置的不确定性和随机性,去噪结果变化较大,本实验中没有得到预期效果。
|
|
表 2 不同去噪模型下的仿真含噪信号去噪结果 Tab. 2 Denoising results of simulated noise-containing signals with different denoising models |
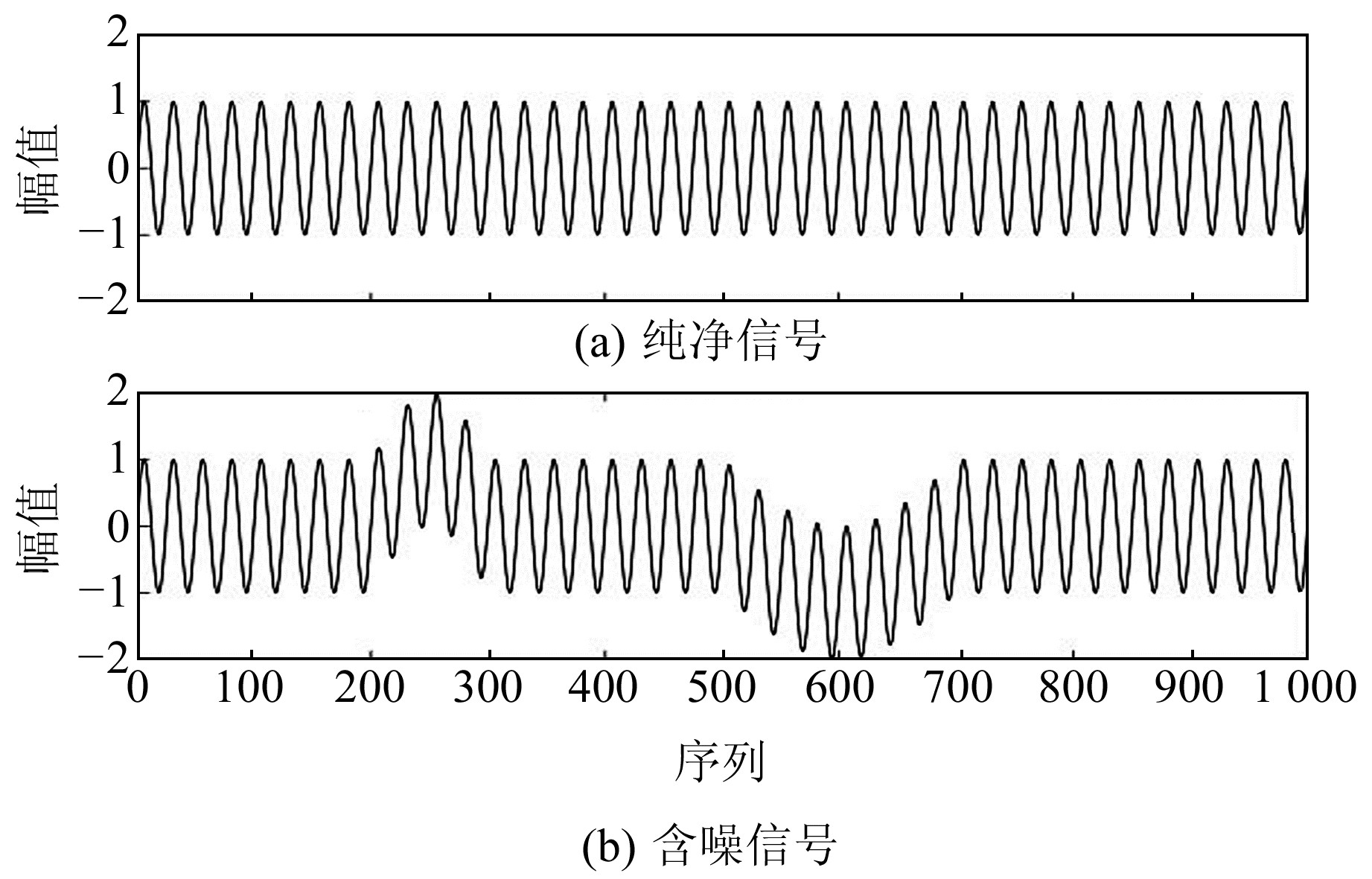
设计仿真含噪信号的相对低频噪声剔除实验(图 4),如式(13)~(16)所示,低频噪声信号的频率分别为0.005 Hz和0.002 5 Hz,远低于纯净信号的0.04 Hz:
|
图 4 利用MATLAB生成仿真纯净信号与低频噪声 Fig. 4 Pure signals and low frequency noise simulated by MATLAB |
| $ X^{\prime}(t)=x_1^{\prime}(t)+x_2^{\prime}(t)+x_3^{\prime}(t) $ | (13) |
| $ \begin{gathered} x_1^{\prime}(t)=\sin (0.08 \pi t), \\ 1 \leqslant t \leqslant 1000 \end{gathered} $ | (14) |
| $ \begin{gathered} x_2^{\prime}(t)=\sin (0.01 \pi(t-201)), \\ 201 \leqslant t \leqslant 300 \end{gathered} $ | (15) |
| $ \begin{gathered} x_3^{\prime}(t)=\sin (0.005 \pi(t-301)), \\ 501 \leqslant t \leqslant 700 \end{gathered} $ | (16) |
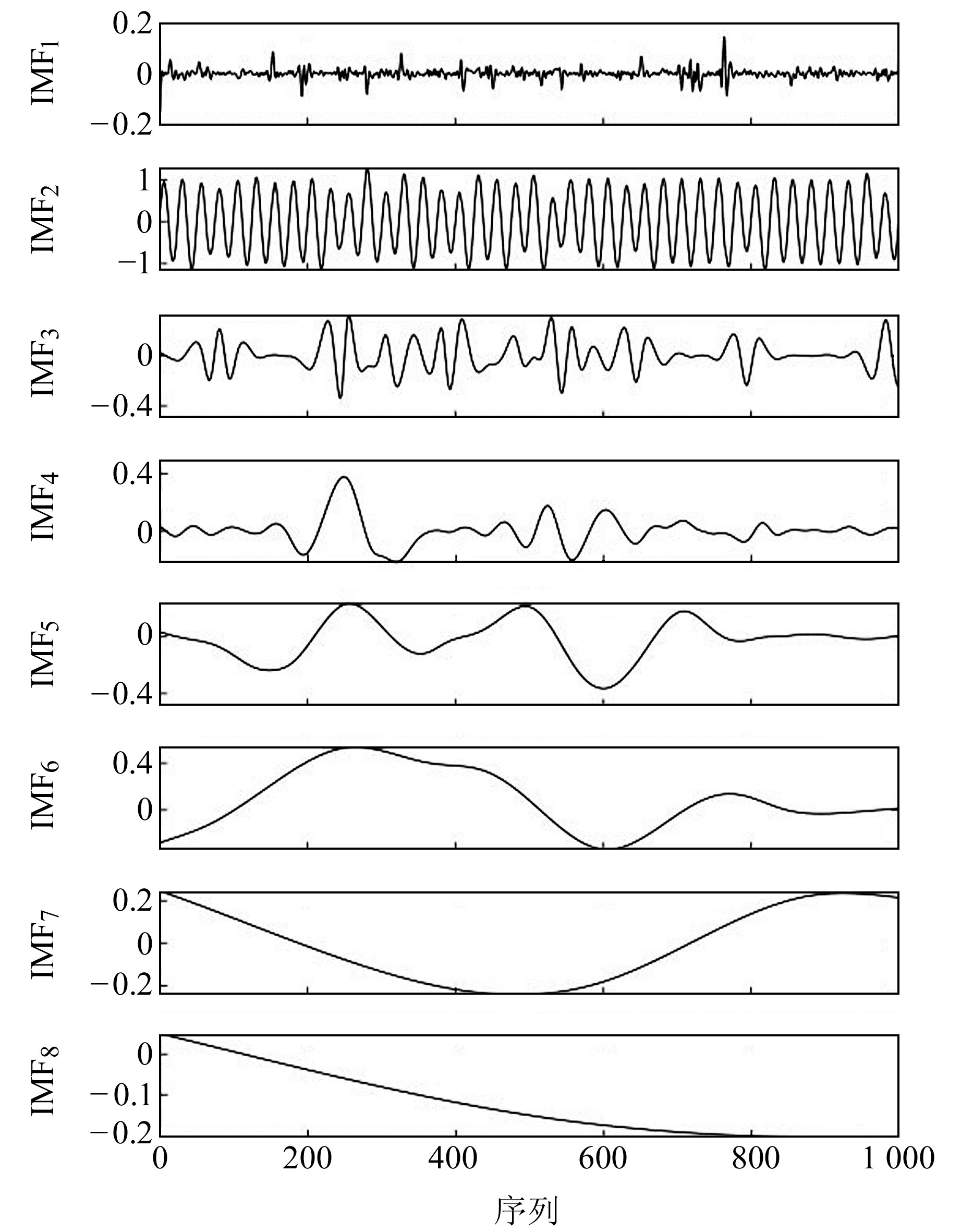
图 5为含低频噪声信号的ICEEMDAN处理结果。可以看出,IMF2分量与原始纯净信号的波形特征和幅值最为接近;IMF1分量的幅值整体较小且呈现无规律的尖刺现象,可判断为噪声成分;其他IMF分量的曲线较为光滑,需借助评价指标来判断优劣程度。由表 3可知,各IMF按照分布熵数值降序排列依次为IMF7、IMF8、IMF6、IMF2、IMF5、IMF3、IMF4、IMF1,分布熵值大于0.9的IMF分量有4个,含有极少的噪声,可以参与到后续的信号重构中。最终得到的去噪结果如图 6所示。
|
图 5 含低频噪声信号经过ICEEMDAN处理后得到的IMF Fig. 5 IMFs obtained from low-frequency noise-containing signals using ICEEMDAN |
|
|
表 3 仿真含低频噪声信号经过ICEEMDAN处理后得到的各IMF分量的分布熵值 Tab. 3 Distributive entropy values of each IMF component obtained from low-frequency noise-containing signals using ICEEMDAN |
|
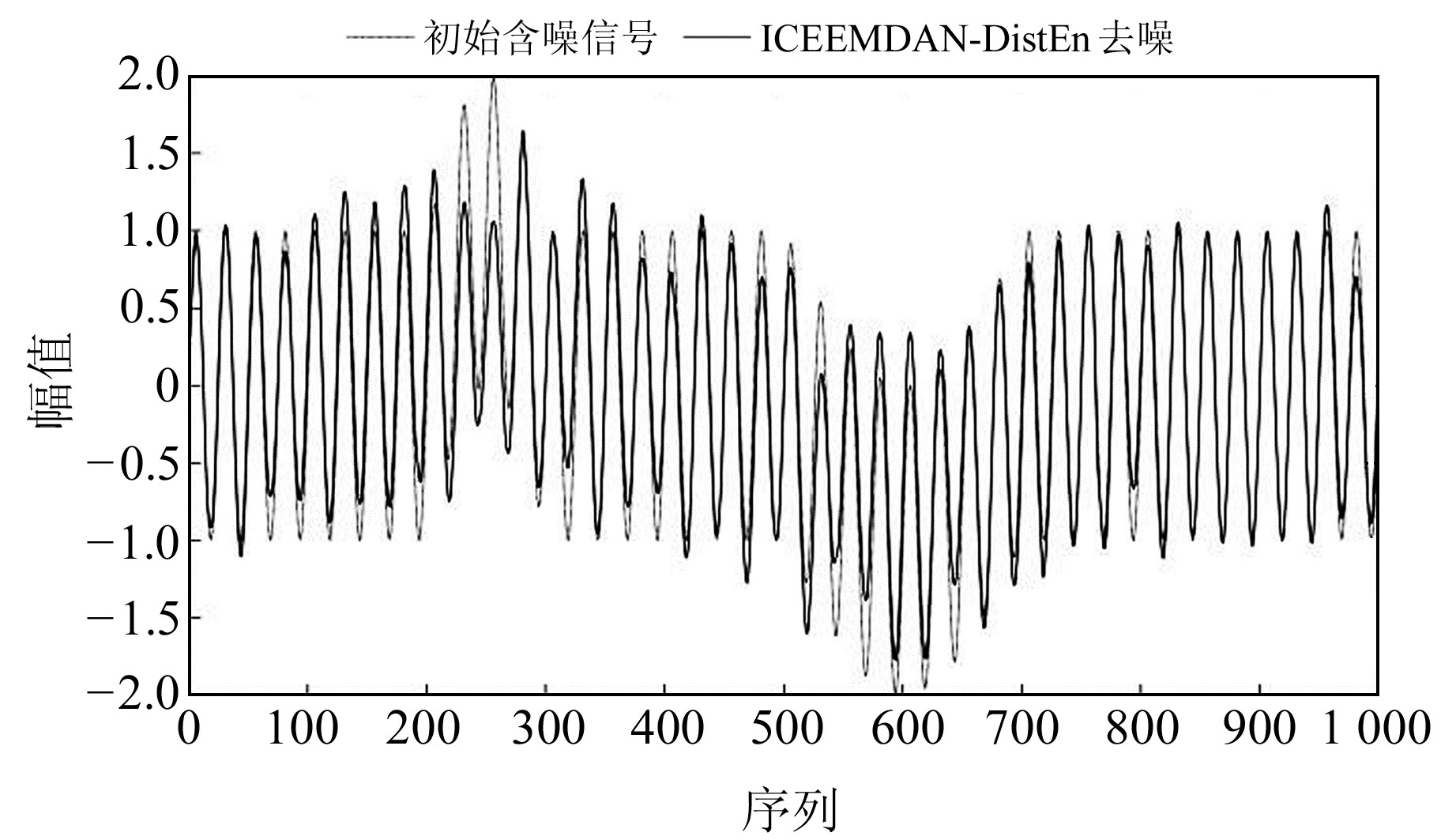
图 6 基于ICEEMDAN-DistEn模型的仿真低频噪声信号去噪结果 Fig. 6 Denoising results of simulated low-frequency noise-containing signals based on ICEEMDAN-DistEn model |
表 4为利用ICEEMDAN-DistEn、CEEMDAN-DistEn、卡尔曼滤波、小波去噪及Savitzky-Golay滤波等5个模型的去噪结果。可以看出,ICEEMDAN-DistEn模型在相关系数、MSE及SNR上皆显著优于其他去噪模型,能较好地抑制原始含噪信号中的低频噪声成分,一定程度上还原了初始纯净信号。
|
|
表 4 不同去噪模型下的仿真含低频噪声信号去噪结果 Tab. 4 Denoising results of simulated low-frequency noise-containing signals with different denoising models |
应用实测含噪信号进行ICEEMDAN-DistEn去噪实验,数据来自SS-Y伸缩仪,地点位于武汉地震中心站,时间为2022-05-31,文件格式为EPD,模型测试环境为MATLAB 2023a,实验结果如图 7~9和表 5~6所示。
|
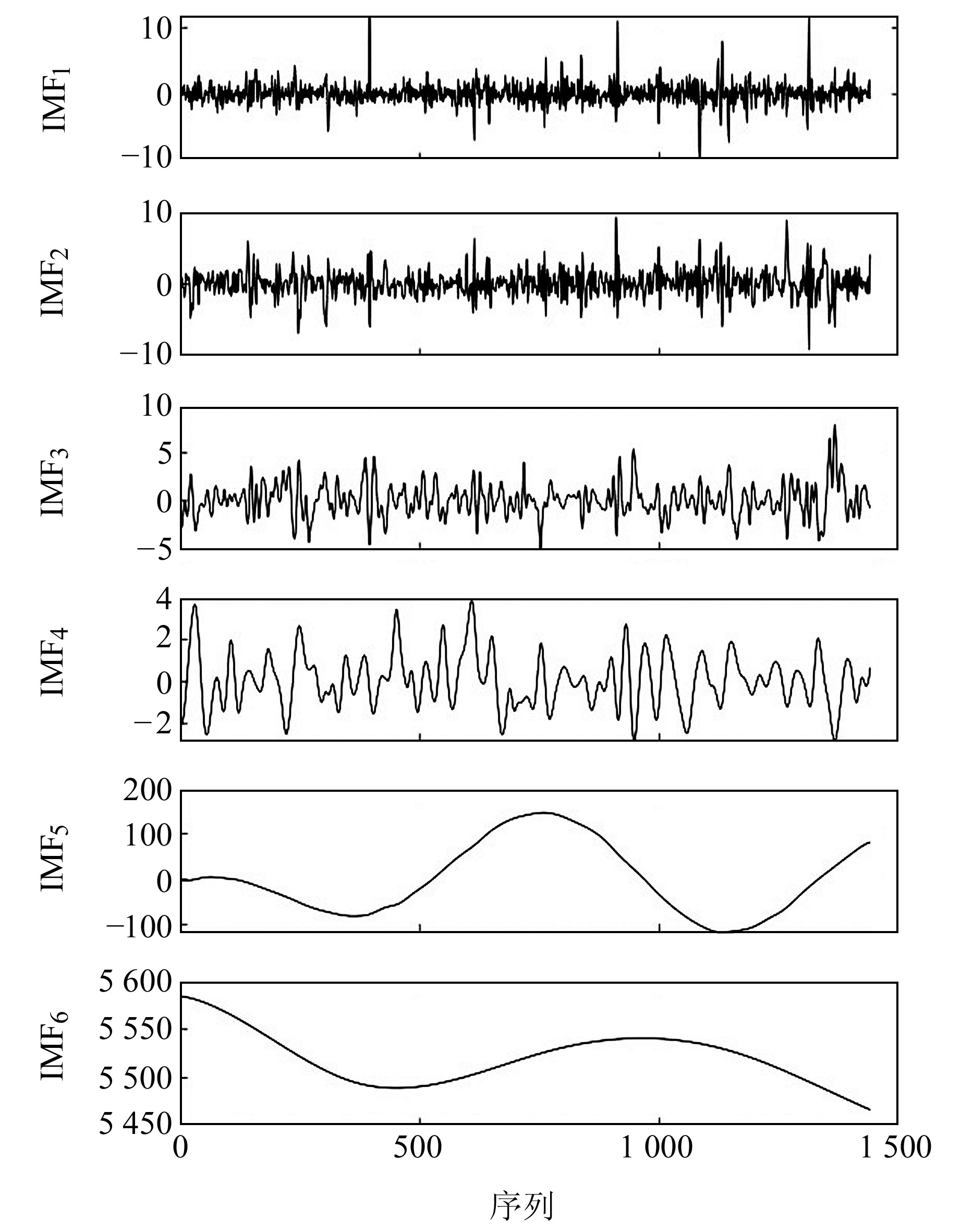
图 7 SS-Y伸缩仪信号经过ICEEMDAN处理后得到的IMF Fig. 7 IMFs obtained from SS-Y extensometer signals using ICEEMDAN |
|
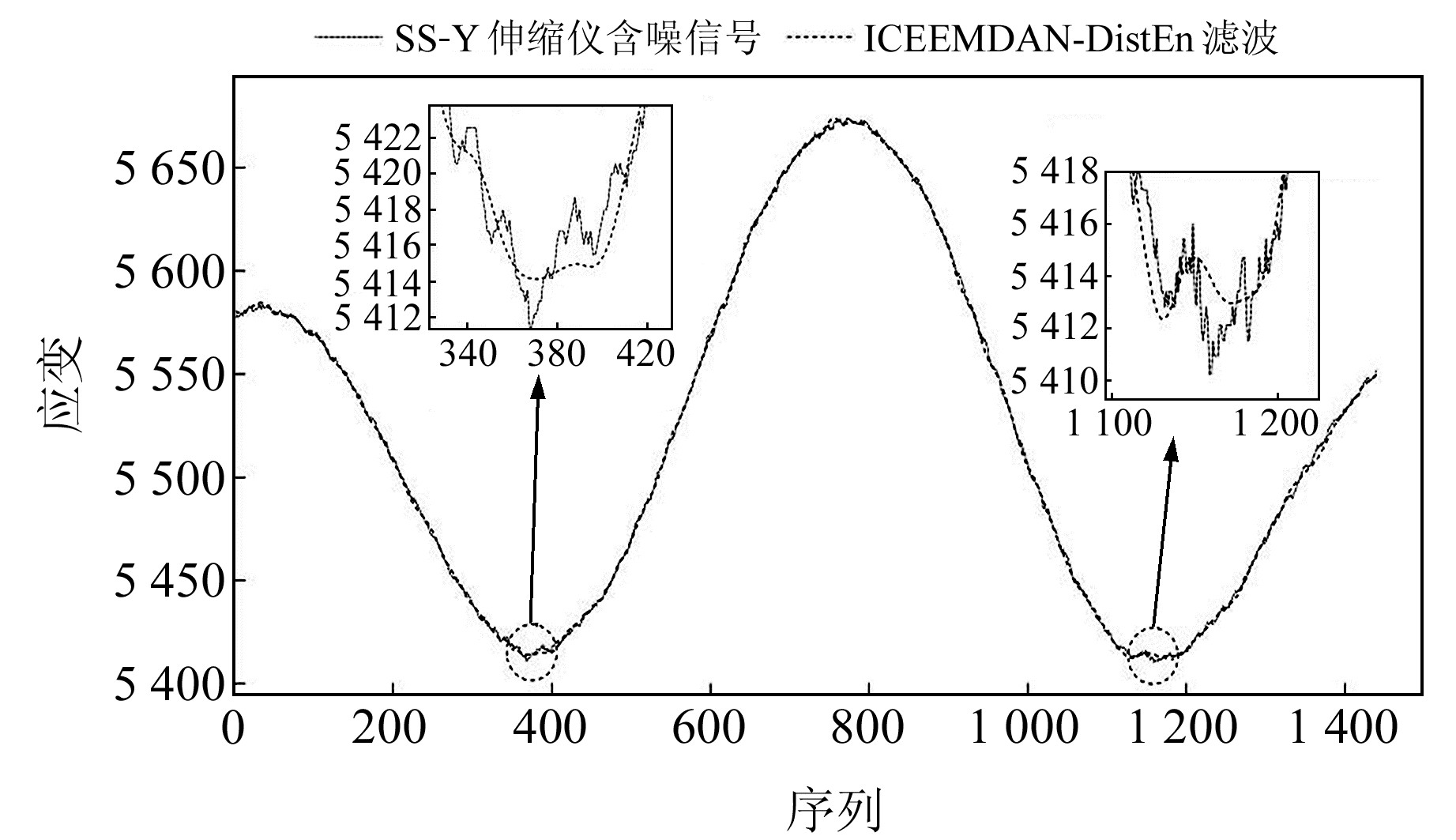
图 8 基于ICEEMDAN-DisEn模型的单条SS-Y伸缩仪信号去噪结果 Fig. 8 Denoising results of single SS-Y extensometer signals based on ICEEMDAN-DisEn model |
|
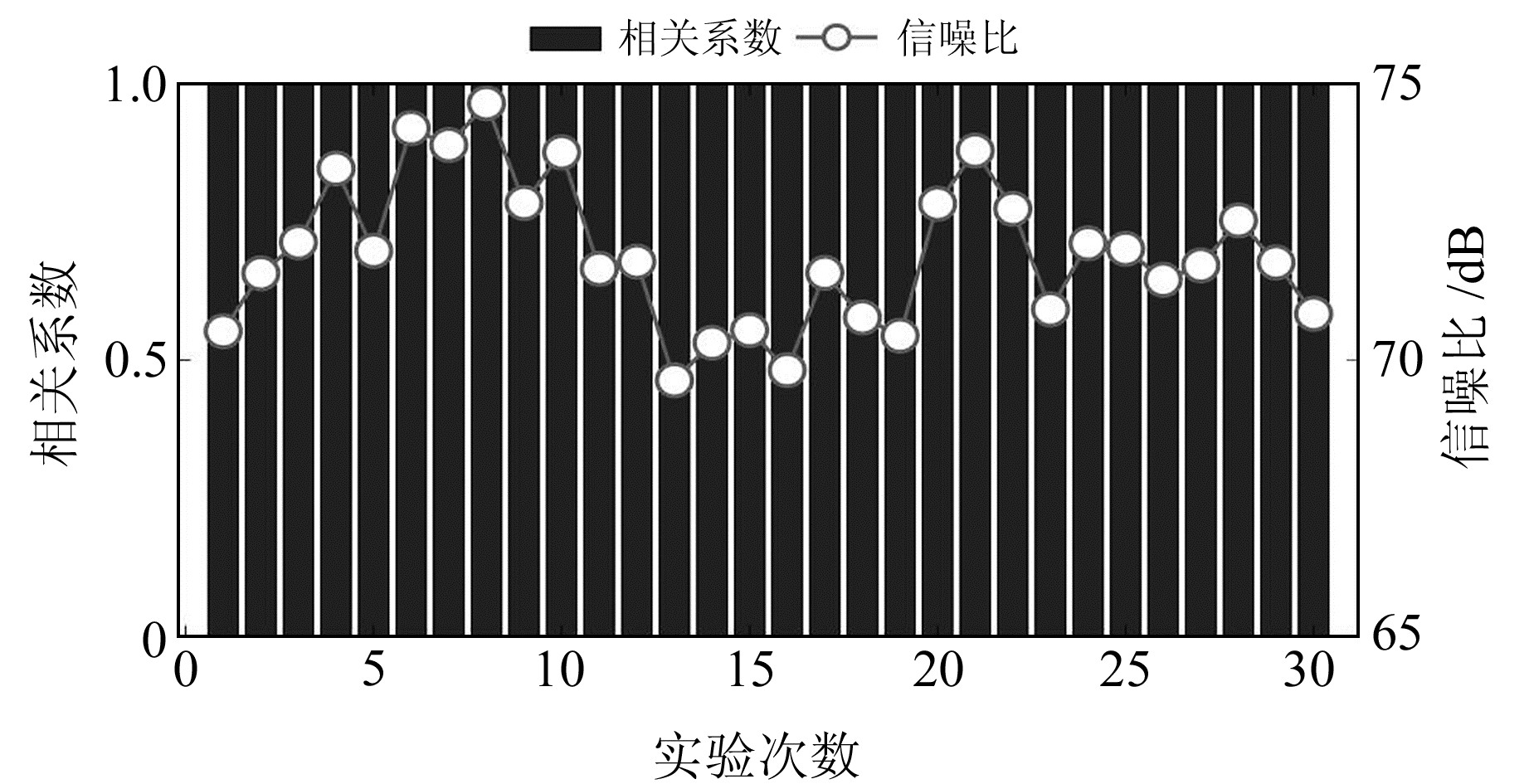
图 9 基于ICEEMDAN-DistEn模型的30 d SS-Y伸缩仪信号去噪结果 Fig. 9 Denoising results of 30 days SS-Y extensometer signals based on ICEEMDAN-DistEn model |
|
|
表 5 SS-Y伸缩仪信号经过ICEEMDAN处理后得到的各IMF分布熵值 Tab. 5 Distributive entropy values of IMFs obtained from SS-Y extensometer signals using ICEEMDAN |
|
|
表 6 不同去噪模型下SS-Y伸缩仪信号去噪结果 Tab. 6 Denoising results of SS-Y extensometer signals with different denoising models |
图 7为SS-Y伸缩仪信号经ICEEMDAN处理后得到的IMF结果。可以看出,IMF6分量拥有初始信号的主要能量;IMF1~IMF4分量的能量幅值极小,且波形极为杂乱,在零值上下剧烈振荡;IMF5分量的波形较光滑,最大幅值相对较小,对信号重构的影响不显著。表 5为各IMF分量的分布熵值,其中IMF4~IMF6分量的分布熵值皆超过0.8,而IMF1~IMF3分量分布熵值差异明显。
图 8为SS-Y伸缩仪单条信号的ICEEMDAN-DisEn去噪结果。从局部放大结果可以看出,该模型能有效地光滑曲线,且具有极好的信号还原性,线性重构结果较理想。引入CEEMDAN-DistEn、卡尔曼滤波、70阶低通FIR滤波等模型进行信号去噪对比,表 6为不同模型的信号去噪效果。可以看出,ICEEMDAN-DistEn模型的去噪效果相对最好;虽然CEEMDAN-DistEn模型的MSE值仅有0.800 5,表明其信号损失极小,但其SNR和相关系数都不理想,说明去噪过程中未处理真正的噪声成分;卡尔曼滤波和70阶低通FIR滤波模型的信噪比较高,但都出现极大的重构波形变异,结果完全失真。
2022-05的SS-Y伸缩仪信号去噪结果如图 9所示,其中柱状图为相关系数的分布统计,折线图为信噪比曲线。可以看出,几乎全部信号的信噪比都超过了70 dB,去噪前后的相关系数值也都接近于1。
3 结语本文提出一种结合ICEEMDAN和分布熵的SS-Y伸缩仪信号去噪方法,能够更精确地识别出噪声和有效信号,线性重构误差较小,无明显的失真现象,综合性能优于CEEMDAN和分布熵组建的去噪模型,并得到以下结论:
1) 作为2种完全不同的信号处理技术,ICEEMDAN和分布熵能分别提取和筛选出含噪信号中的噪声成分和有效成分,适当地对SS-Y伸缩仪含噪信号进行分解及熵值计算,剔除或保留信号并进行线性重构,可以有效地对信号进行去噪处理。
2) ICEEMDAN-DisEn模型有较明显的曲线光滑效果,不会造成严重的信号失真,同时可以将各种噪声的能量和位置准确地分离出来,便于后续开展SS-Y伸缩仪信号的异常检测,并与其他形变观测仪器进行同震响应分析。此外,本文设计的仿真信号去噪实验证明该模型既能剔除高频噪声,也能有效抑制低频噪声,是性能较为全面的去噪模型。
3) 由于观测环境和仪器布设地点的影响,ICEEMDAN-DisEn模型中的分布熵阈值并非固定值,应根据待去噪样本的数据特性预先设定一个值并检验其合理性,但阈值的选取原则应保持不变:较大分布熵值指示的IMF分量是有效成分的概率较大,较小分布熵值指示的IMF分量是噪声的概率较大。
针对SS-Y伸缩仪信号去噪结果的可靠性检验仍有一定的改进空间。后续将从固体潮调和分析入手,通过计算O1波和M2波的振幅因子和相位滞后等参数来佐证去噪结果的合理性。
| [1] |
张致伟, 程万正, 阮祥. 用SS-Y伸缩仪资料研究巨大远震引起的振荡波及谱[J]. 大地测量与地球动力学, 2008, 28(5): 27-33 (Zhang Zhiwei, Cheng Wanzheng, Ruan Xiang. On Oscillation Waves Induced by Great Far-Field Earthquake and Its Spectrum from SS-Y Extensometer Data[J]. Journal of Geodesy and Geodynamics, 2008, 28(5): 27-33)
(  0) 0) |
| [2] |
姜振海, 史小平. SSY-Ⅱ石英伸缩仪与SS-Y伸缩仪的对比分析[J]. 地震研究, 2010, 33(1): 63-67 (Jiang Zhenhai, Shi Xiaoping. Comparative Analysis of the SSY-Ⅱ Quartz Extensometer and the SS-Y Extensometer[J]. Journal of Seismological Research, 2010, 33(1): 63-67)
(  0) 0) |
| [3] |
张凯, 方宏芳, 张翊宁, 等. 漳州地震台SS-Y型伸缩仪资料干扰因素分析[J]. 地震地磁观测与研究, 2013, 34(增2): 156-161 (Zhang Kai, Fang Hongfang, Zhang Yining, et al. Preliminary Analysis of SS-Y Type Telescopic Instrument Data Interference Factors in Zhangzhou Seismic Station[J]. Seismological and Geomagnetic Observation and Research, 2013, 34(S2): 156-161)
(  0) 0) |
| [4] |
陈波. 信阳地震台SS-Y伸缩仪主要干扰因素分析[J]. 地下水, 2019, 41(3): 82-85 (Chen Bo. Analysis of Main Interference Factors of SS-Y Telescopic Instrument in Xinyang Seismic Station[J]. Ground Water, 2019, 41(3): 82-85)
(  0) 0) |
| [5] |
郝冉, 杨驰, 刘冬冬, 等. 徐州地震台伸缩仪观测干扰分析[J]. 地震科学进展, 2022, 52(12): 587-592 (Hao Ran, Yang Chi, Liu Dongdong, et al. Interference Analysis of the Extensometer Observation at Xuzhou Seismic Station[J]. Progress in Earthquake Sciences, 2022, 52(12): 587-592)
(  0) 0) |
| [6] |
张娜, 龚燕民. SS-Y型伸缩仪环境干扰的异常研究[J]. 地震科学进展, 2022, 52(2): 84-88 (Zhang Na, Gong Yanmin. Research on Environmental Disturbance of SS-Y Extensometer[J]. Progress in Earthquake Sciences, 2022, 52(2): 84-88)
(  0) 0) |
| [7] |
严吉, 樊冬, 李章, 等. 泾县台SS-Y型伸缩仪异常识别和干扰因素排查研究[J]. 科技资讯, 2020, 18(24): 46-48 (Yan Ji, Fan Dong, Li Zhang, et al. Study on Abnormal Recognition and Interference Factors Investigation of SS-Y Type Extensometer in Jingxian Station[J]. Science and Technology Information, 2020, 18(24): 46-48)
(  0) 0) |
| [8] |
张秀萍, 叶青, 张晓刚, 等. SS-Y型伸缩仪典型故障图像特征分析及处理[J]. 地震地磁观测与研究, 2022, 43(2): 134-144 (Zhang Xiuping, Ye Qing, Zhang Xiaogang, et al. Analysis and Process of Image Features of Typical Fault of SS-Y Type Extensometer[J]. Seismological and Geomagnetic Observation and Research, 2022, 43(2): 134-144)
(  0) 0) |
| [9] |
Zhao Y J, Yan S Q, He J L, et al. A Hybrid Denoising Algorithm for HIFU Echo Signal Based on ICEEMDAN Combined with MMSVC and WT[J]. Journal of Measurement Science and Instrumentation, 2023, 14(1): 35-44 DOI:10.62756/jmsi.1674-8042.2023005
(  0) 0) |
| [10] |
李聪康, 黄俊, 郑元杰. 基于ICEEMDAN的雷达生命信号检测方法[J]. 雷达科学与技术, 2023, 21(1): 105-112 (Li Congkang, Huang Jun, Zheng Yuanjie. Radar Life Signal Detection Method Based on ICEEMDAN[J]. Radar Science and Technology, 2023, 21(1): 105-112)
(  0) 0) |
| [11] |
赵桠松, 许辉群, 王泽峰, 等. 基于ICEEMDAN的曲波阈值地震数据去噪方法研究[J]. 工程地球物理学报, 2022, 19(2): 252-257 (Zhao Yasong, Xu Huiqun, Wang Zefeng, et al. Research on Curvelet Threshold Seismic Data Denoising Method Based on ICEEMDAN[J]. Chinese Journal of Engineering Geophysics, 2022, 19(2): 252-257)
(  0) 0) |
| [12] |
鲍明, 管鲁阳, 李晓东, 等. 基于欧氏距离分布熵的特征优化研究[J]. 电子学报, 2007, 35(3): 469-473 (Bao Ming, Guan Luyang, Li Xiaodong, et al. A Study on Optimum Classification Character Based on the Distributive Entropy of Euclidian Distance[J]. Acta Electronica Sinica, 2007, 35(3): 469-473)
(  0) 0) |
2. Wuhan Institute of Seismic Scientific Instruments Co Ltd, 40 Hongshance Road, Wuhan 430071, China
 2024, Vol. 44
2024, Vol. 44

