高精度、高分辨率的重力场模型在气候变化、资源勘探、灾害预防、国防安全等领域有着非常重要的作用。重力场解算的难度主要来源于庞大的计算量与巨大的内存占用。法方程的构建是重力场反演过程中的关键步骤,而法矩阵的规模与重力场阶数相关[1],是直接影响反演速度与内存占用的重要因素。当重力场阶数过大时,法方程的求解速度会大幅下降,故高阶重力场的解算尤为困难[2]。随着计算机技术的发展,已有一些新的技术与高性能算法可用于重力场的快速反演。邹贤才等[3]使用OpenMP对重力场解算过程进行并行化处理,计算速度提升近6倍;陈秋杰等[4]使用MKL(math kernel library)科学计算库与OpenMP并行计算库,显著提高了重力场解算的效率;周浩等[5-6]基于MPI并行技术对法方程构建、大规模矩阵相乘、求逆等关键节点引入并行计算,解算120阶重力场模型仅耗时40 min。
除CPU平台的并行计算方法与高性能算法外,近年来计算机图形学也得到快速发展,图形处理器(GPU)的计算能力甚至已经超过CPU。GPU编程工具的进步也使得各种算法成功移植到GPU上,混合计算平台已经实现了针对不同学科应用的大幅提速[7]。Hou等[8]提出一种结合CUDA和OpenMP的混合并行方法,能处理大规模的数据;刘世芳等[9]实现了基于MPI和CUDA的稠密对称矩阵三角化算法,取得了较好的加速效果。
上述研究均显示出并行计算在重力场相关研究中能起到显著作用。为提高使用最小二乘法反演重力场模型的解算速度,本文针对复杂的重力场反演流程,联合MPI与CUDA设计合理的并行方案,同时实现内存耗用与计算速度等多方面的优化。
1 基于动力积分法的重力场模型解算方法动力积分法是较早应用于重力场反演的基础方法之一,具有很高的求解精度,其计算流程可以概括为:
1) 使用先验力学模型计算各种摄动加速度对待估参数的偏导数,并通过积分器获得位置对各待估参数的偏导,构建设计矩阵;
2) 通过积分器获得参考轨道序列,并与实测数据作差,获得O-C残差序列b;
3) 使用最小二乘法求解方程Ax = b,获得卫星初始状态改进量ΔX和重力场位系数的改进量Δp;
4) 对初始状态和先验重力场模型进行改进,重复上述流程,直到残差满足收敛条件。
下面将详细阐述法方程的构建与求解过程,以便对线性的重力场反演任务进行分配与规划。
首先,将设计矩阵A按照参数类型进行分块,表示为:
| $ \boldsymbol{A}=\left[\begin{array}{ll} \boldsymbol{L} & \boldsymbol{G} \end{array}\right] $ | (1) |
式中,L为低轨卫星位置对局部参数的偏导数,局部参数是指如卫星初始状态向量、加速度计测定的非保守力等与时间有关的参数;G为低轨卫星位置对全局参数的偏导数,全局参数是指如重力场位系数等与时间无关的参数。通过该方式对A进行分块,有利于多弧段法方程的合并。
将分块后的单历元观测方程构建为法方程:
| $ \boldsymbol{A}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{x}=\boldsymbol{A}^{\mathrm{T}} \boldsymbol{y} $ | (2) |
| $ \left[\begin{array}{ll} \boldsymbol{L}^{\mathrm{T}} \boldsymbol{L} & \boldsymbol{L}^{\mathrm{T}} \boldsymbol{G} \\ \boldsymbol{G}^{\mathrm{T}} \boldsymbol{L} & \boldsymbol{G}^{\mathrm{T}} \boldsymbol{G} \end{array}\right]\left[\begin{array}{l} \Delta \boldsymbol{X} \\ \Delta \boldsymbol{p} \end{array}\right]=\left[\begin{array}{l} \boldsymbol{L}^{\mathrm{T}} \boldsymbol{y} \\ \boldsymbol{G}^{\mathrm{T}} \boldsymbol{y} \end{array}\right] $ | (3) |
式中,ΔX为局部参数的改正量,Δp为全局参数的改正量。上式简记为:
| $ \left[\begin{array}{ll} \boldsymbol{N}_{l l} & \boldsymbol{N}_{l g} \\ \boldsymbol{N}_{g l} & \boldsymbol{N}_{g g} \end{array}\right]\left[\begin{array}{l} \Delta \boldsymbol{X} \\ \Delta \boldsymbol{p} \end{array}\right]=\left[\begin{array}{l} \boldsymbol{R}_l \\ \boldsymbol{R}_g \end{array}\right] $ | (4) |
由于单个弧段的所有历元的待估参数完全一致,故单弧段的法方程形式与式(4)一致。但多弧段间的局部参数存在区别,需采用式(5)实现多弧段法方程合并:
| $ \left[\begin{array}{ccccc} \boldsymbol{L}_1 & & & & \boldsymbol{G}_1 \\ & \boldsymbol{L}_2 & & & \boldsymbol{G}_2 \\ & & \ddots & & \vdots \\ & & & \boldsymbol{L}_n & \boldsymbol{G}_n \end{array}\right]\left[\begin{array}{c} \Delta \boldsymbol{X}_1 \\ \Delta \boldsymbol{X}_2 \\ \vdots \\ \Delta \boldsymbol{X}_n \\ \Delta \boldsymbol{p} \end{array}\right]=\left[\begin{array}{c} \boldsymbol{y}_1 \\ \boldsymbol{y}_2 \\ \vdots \\ \boldsymbol{y}_n \end{array}\right] $ | (5) |
使用最小二乘法将式(5)整理成法方程形式并化简为:
| $ \begin{aligned} & {\left[\begin{array}{ccccc} \boldsymbol{N}_{l l}^1 & & & & \boldsymbol{N}_{l g}^1 \\ & \boldsymbol{N}_{l l}^2 & & & \boldsymbol{N}_{l g}^2 \\ & & \ddots & & \vdots \\ & & & \boldsymbol{N}_{l l}^n & \boldsymbol{N}_{l g}^n \\ \boldsymbol{N}_{k l}^1 & \boldsymbol{N}_{g l}^2 & \cdots & \boldsymbol{N}_{g l}^n & \sum\limits_1^n \boldsymbol{N}_{k g}^i \end{array}\right] \times} \\ & {\left[\begin{array}{c} \Delta \boldsymbol{X}_1 \\ \Delta \boldsymbol{X}_2 \\ \vdots \\ \Delta \boldsymbol{X}_n \\ \Delta \boldsymbol{p} \end{array}\right]=\left[\begin{array}{c} \boldsymbol{R}_1^1 \\ \boldsymbol{R}_1^2 \\ \vdots \\ \boldsymbol{R}_1^n \\ \sum\limits_1^n \boldsymbol{R}_g^i \end{array}\right]} \\ & \end{aligned} $ | (6) |
消去局部参数即可解得重力场位系数改进量:
| $ \begin{aligned} \Delta \boldsymbol{p}= & \left(\sum\limits_1^n \boldsymbol{N}_{g g}^i-\sum\limits_1^n \boldsymbol{N}_{g l}^i \boldsymbol{N}_{l l}^{i-1} \boldsymbol{N}_{l g}^i\right)^{-1} \times \\ & \left(\sum\limits_1^n \boldsymbol{R}_g^i-\sum\limits_1^n \boldsymbol{N}_{g l}^i \boldsymbol{N}_{l l}^{i-1} \boldsymbol{R}_l^i\right) \end{aligned} $ | (7) |
将式(7)代入式(6)即可求得卫星初始状态向量的改进量:
| $ \Delta \boldsymbol{X}=\boldsymbol{N}_u^{-1}\left(\boldsymbol{R}_1-\boldsymbol{N}_{l g} \Delta \boldsymbol{p}\right) $ | (8) |
动力法反演重力场模型的详细流程见图 1。
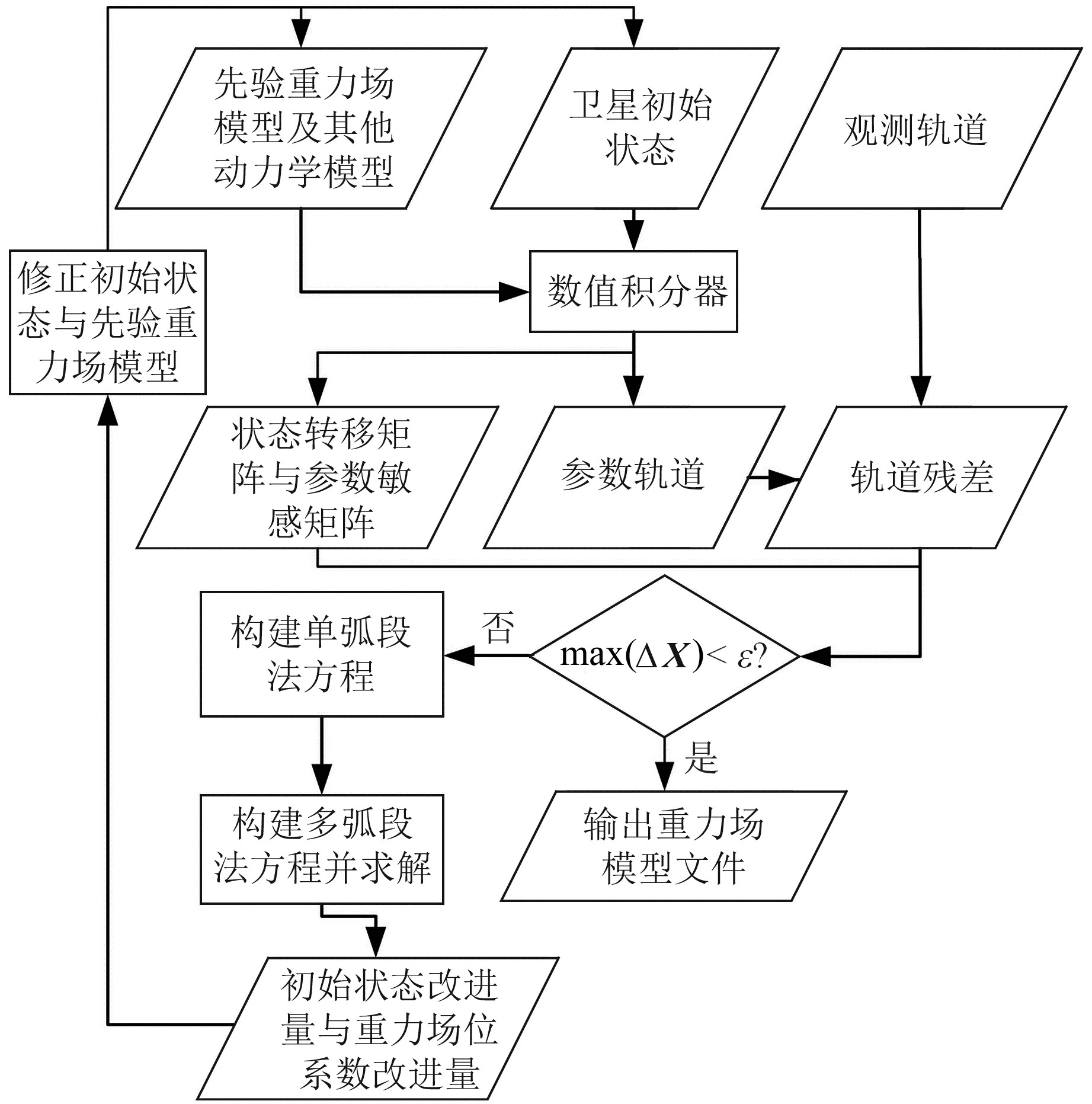
|
max(ΔX)表示卫星状态修正量在各个方向上的最大值,下同 图 1 地球重力场模型反演流程 Fig. 1 Flow chart of Earth gravity field model inversion |
经测试,解算过程中耗时最多的环节为数值积分器计算参考轨道、大规模矩阵相乘以及大规模矩阵求逆。除计算速度外,由于设计矩阵大小近似为3倍历元个数乘以n位系数,而n位系数又与重力场模型阶数n相关(式(9)),故当重力场模型阶数n过高时,设计矩阵的大小会剧增,需要兼顾计算过程中的内存及显存耗用,故有必要根据不同需求分别制定不同的并行加速策略:
| $ n_{\text {位系数 }}=(n+3)(n-1) $ | (9) |
MPI提供的各接口可以使不同进程间的信息相互传递[5],进而实现复杂任务的并行化处理。使用MPI实现按弧段并行构建设计矩阵及求解法方程,具体任务分配及运行流程见图 2。
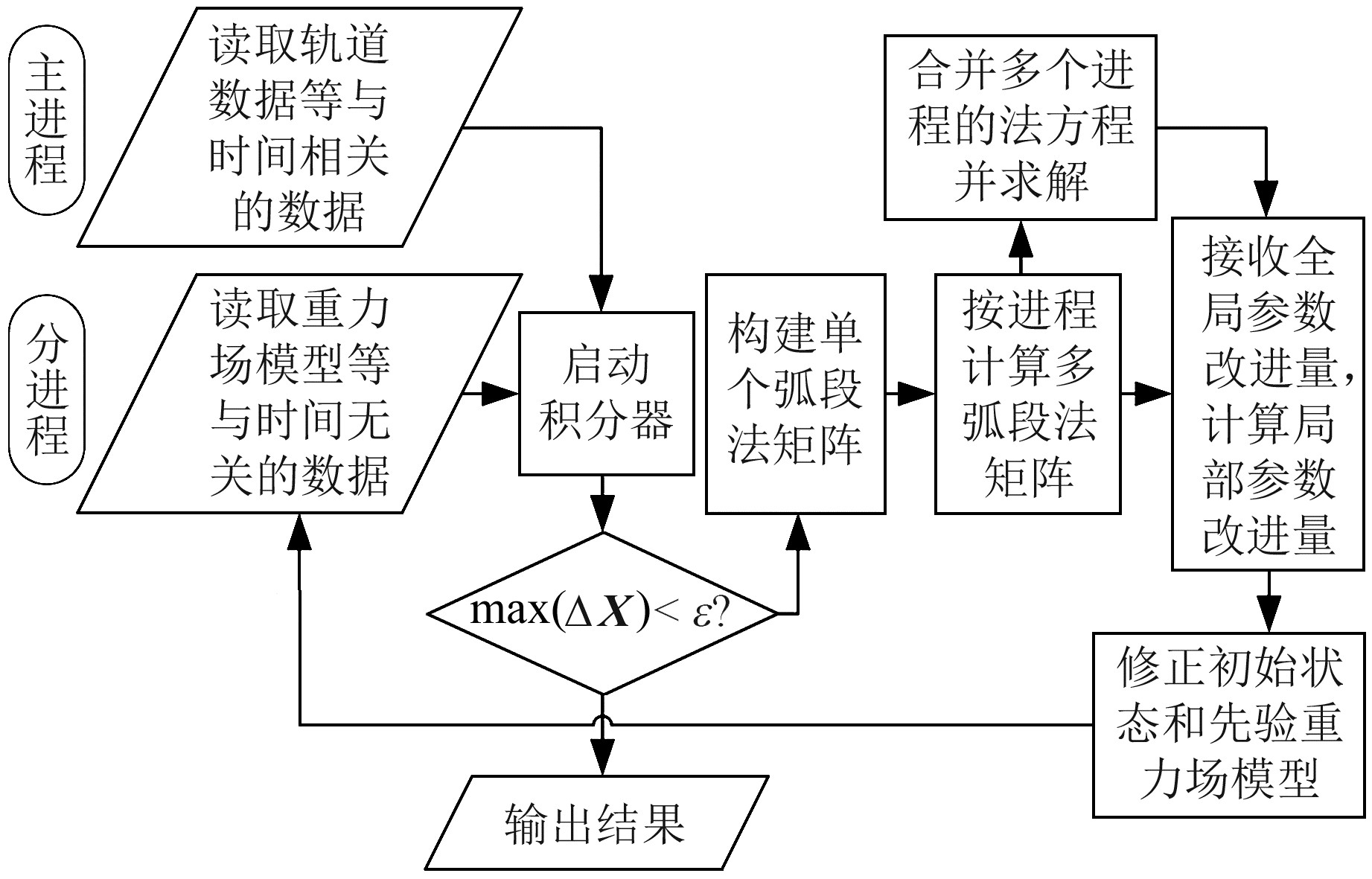
|
图 2 MPI任务分配及计算流程 Fig. 2 MPI task allocation and calculation process |
在MPI中,各进程编号通常为从0开始的整数。为便于表述,称0号进程为主进程,其他进程为分进程。由于轨道数据、加速度计数据、姿态数据等均按日期存储,故需要使用主进程读取各轨道文件,按弧段整理完毕后使用MPI_Send命令将数据发送到各分进程,再启动积分器执行后续任务。针对内存有限的单机计算,则可以按天数分配任务,为配合部分对数据连贯性有要求的函数(如批量读取加速度计数据的函数),直接由各分进程读取连续数日的数据文件,并按弧段进行存储。为使各分进程的任务均匀分配,分进程总数可定为任务总数的因数。
在计算法方程前,式(1)中低轨卫星位置对重力场位系数的偏导数矩阵G的内存耗用最大。以单弧段3 h共2 160个历元为例,不同重力场模型阶数n对应的矩阵G的规模见表 1。
|
|
表 1 不同阶数n对应的矩阵G的大小 Tab. 1 The size of matrix G corresponding to different order n |
一般而言,集群的单个节点内存在16 GB以上,故在解算法方程前可以保证内存充足,无需通过分块处理、写文件存储等方式防止内存溢出。
在使用最小二乘法求解时,需要通过式(2)构建法方程,单弧段法方程的构建结果见式(4)。当位系数个数充足时,式(4)中的Ngg大小将超过矩阵G。不同重力场模型阶数n对应的Ngg大小见表 2。
|
|
表 2 不同阶数n对应的矩阵Ngg的大小 Tab. 2 The size of matrix Ngg corresponding to different order n |
显然,当重力场模型阶数达到一定程度时,Ngg占用的内存会过大,需要使用合适的方法来控制其大小。
3 矩阵相乘的并行加速方法矩阵相乘是重力场解算流程中耗时最多、内存占用最大的环节。针对大规模矩阵相乘,可利用CUDA将程序编译为核函数(kernel)并发送至设备(device),进而在GPU上实现矩阵相乘的并行运算。CUDA是由NVIDIA推出的运算平台和编程模型,包含有CUDA指令集架构(ISA)与GPU内部的并行计算引擎,使开发者编写的程序能在GPU上高速运行。另外,当重力场阶数过大时,反演流程中的各矩阵,尤其是Ngg会占用大量显存,而显存容量一般较小,会严重限制可解算重力场阶数的上限。本节将利用CUDA和MPI实现大规模矩阵相乘的并行加速与内存压缩,同时解决耗时过长、内存与显存占用过大的问题。
法方程构建过程中涉及多个矩阵,其中以Ngg规模最大、占用内存最多,因此本文主要针对Ngg矩阵进行研究。
3.1 使用CUDA实现并行加速矩阵G的大小为3倍历元个数乘以n位系数,是设计矩阵A的主要成分。由式(9)可以推算出串行计算
整个过程在设备上进行,计算完毕后再将结果转移到主机。在GPU上计算的函数称为核函数,其逻辑见图 3。设线程的id为idx,则idx号线程负责的元素位置为(x/列数,y%列数),%为取模运算符;再将GT的第x行与G的第y列对应元素相乘后求和,即可求得Ngg的(x, y)号元素的值。
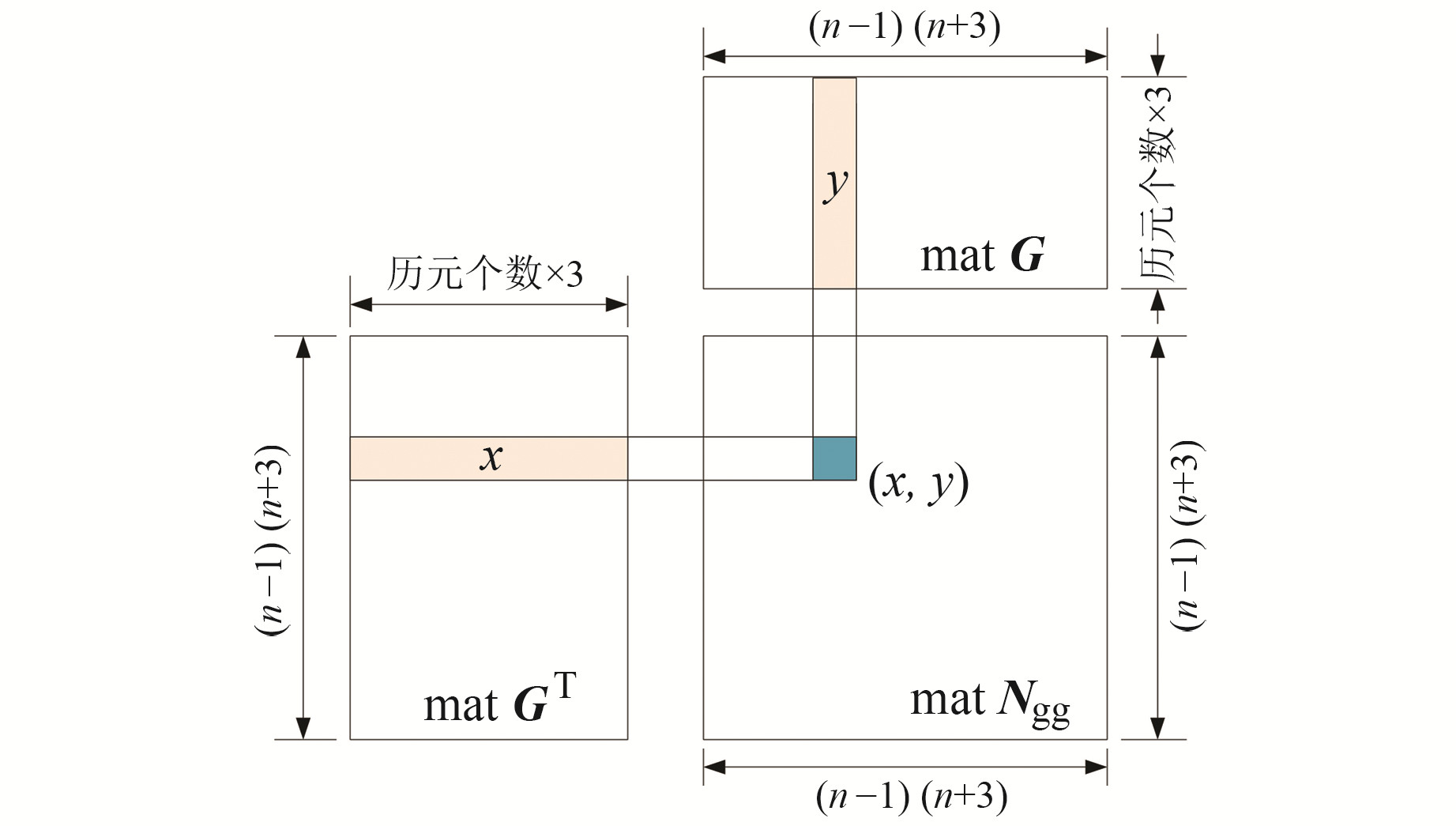
|
图 3 CUDA计算矩阵相乘的简单逻辑 Fig. 3 Simple logic for computing matrix multiplication in CUDA |
针对线性代数运算,CUDA提供了专门的子程序库cuBLAS(CUDA basic linear algebra subroutine library),其level-3函数cublasDgemm适用于double型常规矩阵相乘运算,比未经处理的简单矩阵并行相乘的核函数计算更快,后文的实验也将使用cuBLAS中的函数进行计算。
针对前述内存占用过大的问题,可根据Ngg的特殊性进行优化,主要有以下2点:
1) Ngg具有对称性,对于C = AAT型的矩阵相乘,cuBLAS提供了cublasDsyrk函数进行运算,并将结果矩阵以上三角或下三角的形式存储。但由于cublasDsyrk本身没有将结果再对称地运算,故可在CPU上完成对称操作。经过该处理后,显存耗用将减少一个矩阵G的大小,且计算量将减半。
2) 当Ngg占用内存接近或超过显存上限时,需要对矩阵G进行合适的分块处理。分块数量以及分块方式的差异都会对矩阵相乘的计算速度产生影响,可根据实际情况灵活调整。
3.2 使用MPI减少内存占用在矩阵相乘环节,采用矩阵分块计算的方法仅能控制显存,而无法压缩矩阵占用的内存。为进一步提高相同硬件配置下MPI并行进程的总数或能解算的重力场阶数上限,在上节的基础上,使用MPI进一步对重力场反演任务进行划分,通过去除直接计算Ngg的步骤实现分进程的内存压缩。主要流程(图 4)如下:

|
图 4 使用MPI减少分进程内存峰值的流程 Fig. 4 Flow chart of using MPI to reduce the peak memory of the subprocess |
1) 在分进程中,将G按列分块获得Gi,此后立刻销毁G,再计算其Ngg的子块Nggij(仅计算上三角矩阵),并使用类似的方法计算式(7)中第1个因式的对应子块,记为Nsubij,第2个因式不作处理,记为Rsub;
2) 将Nsubij和Rsub按弧段发送到主进程,且每计算完一个子块Nsubij便发送一次,同时销毁其占用的内存;
3) 主进程首先按弧段接收各分进程的Nsubij进行求和,再将Nsubij存储到大矩阵Nfin的对应位置,存储完毕后沿主对角线镜像,Rsub则直接按弧段接收并求和得到Rfin;
4) 代入式(7)计算最终结果。
该计算流程省去了分进程中Ngg占用的大部分内存,当重力场阶数较高时能将单进程内存峰值减少一半以上。同时,由于该过程不涉及文件读写,计算速度不会有明显的下降。
4 算例分析本节主要测试算法的加速效果。使用30 d仿真轨道数据模拟重力场月解的计算场景,解算不同阶数的时变重力场模型,“真实”重力场模型选用GGM05S,并不加入任何误差到仿真轨道数据中,先验重力场模型选用EGM96,弧长统一为3 h,共240个弧段。
使用的计算机配置如下:处理器为Intel(R) Xeon(R) W-2235 CPU @ 3.80 GHz,内存为32 GB,六核心,显卡为quadro P1000,显存为4 GB,CUDA核心共640个。
4.1 MPI并行加速效果本文程序基于Windows 10系统开发,使用微软的Microsoft MPI进行并行计算,为适配Visual Studio 2010,选用的MPI版本为8.1。
以30阶重力场解算为例,使用已经搭建完毕的重力场解算程序计算,仅修改并行的进程数量进行效率比对,统计结果见表 3与图 5。
|
|
表 3 启动不同数量分进程时的重力场解算耗时比较 Tab. 3 Comparison of the time consumption of gravity field calculation when starting different numbers of subprocesses |

|
图 5 启动不同数量分进程时的重力场解算耗时比较 Fig. 5 Comparison of the time consumption of gravity field calculation when starting different numbers of subprocesses |
结果显示,随着并行进程数量的增多,计算速度逐渐加快,但由于MPI并行本质上是逻辑的并行而非硬件层面的并行,计算速度仍然受到CPU性能的约束,所以进程数量越多,单进程的计算速度越慢。当进程数量超过CPU核心数目时,单进程的效率将大幅降低。在本实验中,分进程数量从5增加至10时,单进程计算耗时明显增加,而整体计算耗时并没有显著减少,内存峰值却加倍,造成了不必要的资源占用。故使用MPI进行并行计算时,应综合考虑实际任务需求与硬件性能进行适当的选择,建议总进程数量不超过CPU核数。
4.2 CUDA对矩阵相乘的加速效果本文使用的CUDA版本为8.0,主要用于大规模矩阵相乘环节。测试所使用矩阵G的大小均为2 160×N,N表示重力场位系数个数。分别计算30阶、60阶和120阶的重力场模型对应的Ngg,使用的方法包括串行计算和CUDA并行计算,后者又包括简单核函数并行以及cuBLAS库函数并行,计算结果见表 4。
|
|
表 4 不同方法计算矩阵相乘耗时比较 Tab. 4 Comparison of time consumption for matrix multiplication using different methods |
结果显示,使用CUDA并行计算矩阵相乘的速度远快于串行计算,且矩阵越大,加速效果越明显。但显存容量通常要比内存更小,在使用CUDA时应综合考虑显存限制与计算性能,对大矩阵进行合适的分块处理。
4.3 30阶和120阶重力场解算实例使用上述方法搭建动力学法反演重力场模型的并行计算平台。使用时长为30 d的仿真轨道数据进行测试,完成SST-HL模式下30阶重力场模型的解算,共迭代3次。使用GGM05S重力场模型进行外符合精度评估,计算出的位系数阶误差RMS见图 6。

|
图 6 30阶重力场解算结果阶误差RMS Fig. 6 RMS of order error of 30 order gravity field solution |
结果显示,30阶重力场模型的解算精度达到10-14量级,且从第2次迭代开始收敛。可认为本文搭建的重力场并行解算平台有足够的低阶重力场解算能力。本次共启用10个MPI分进程,单个弧段耗时3~6 s,迭代3次耗时约430 s。串行模式下单弧段耗时105~110 s,迭代3次耗时约81 600 s。对比可知,本文的并行计算程序在计算30阶重力场模型时可加速约180倍。
将重力场模型阶数提升到120阶,此时串行模式已经无法完成解算任务。使用与上一节仿真实验相同的条件,计算出的位系数阶误差RMS见图 7。
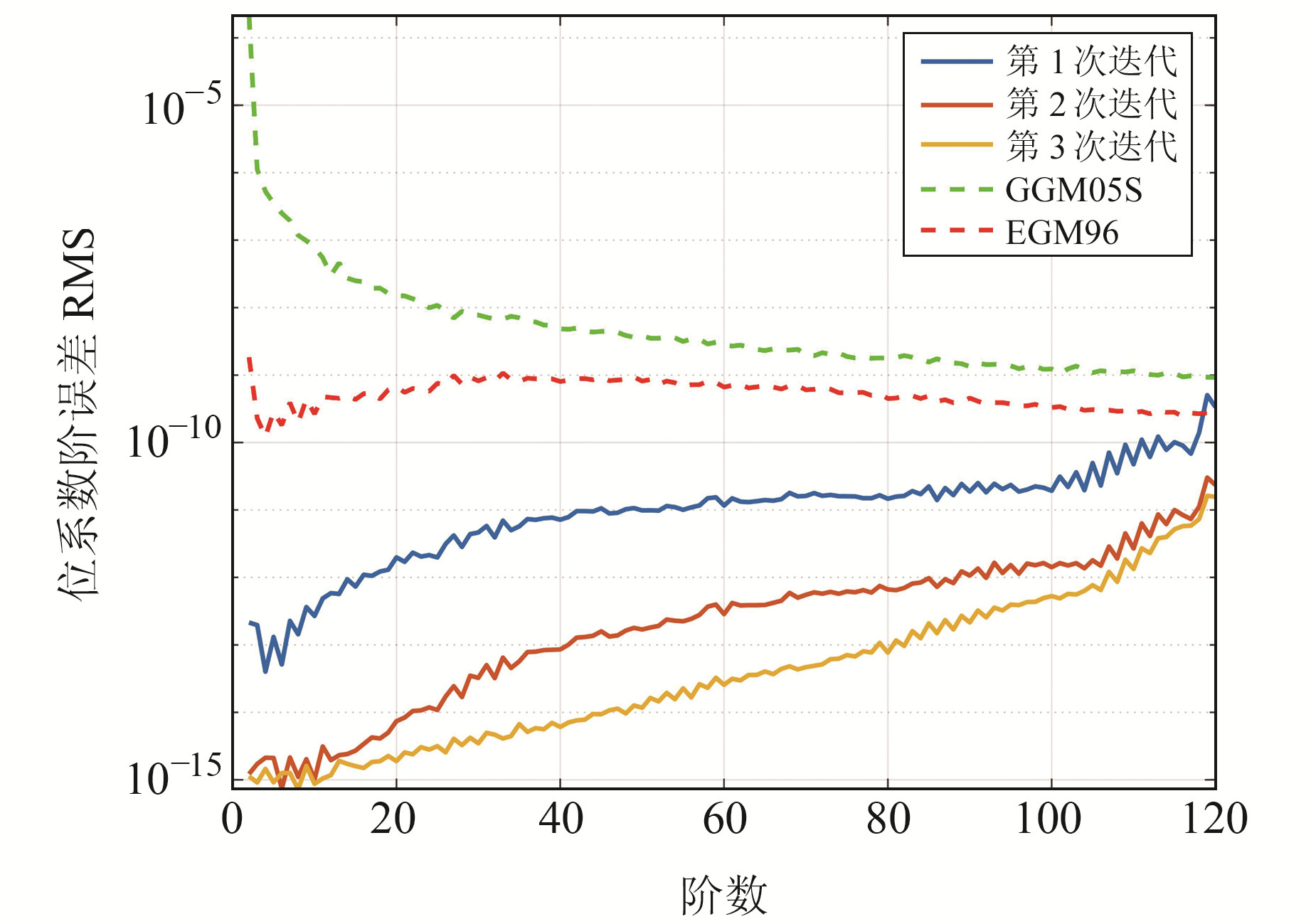
|
图 7 120阶重力场解算结果阶误差RMS Fig. 7 RMS of order error of 120 order gravity field solution |
结果显示,经过3次迭代得到的重力场模型的阶误差RMS可达10-13量级,证明了计算方法的正确性。该算例启用5个分进程进行计算,每个弧段耗时100~200 s不等,全过程耗时约6.3 h。同时,该结果仅由单机计算,对于高性能的集群同样适用。
5 结语本文针对基于最小二乘法的重力场模型解算过程,联合MPI与CUDA实现了并行加速。主要得出以下几点结论:
1) 使用MPI和CUDA可分别在全局和局部实现重力场解算过程的并行加速。前者负责重力场反演任务拆分,加速比与进程数正相关,但建议进程数量不超过CPU核数;后者负责法矩阵相关计算,加速比可达380以上。
2) 使用单机解算30阶重力场时加速比可达180;解算120阶重力场并迭代3次仅耗时约6.3 h,且该方法在高性能集群上同样适用。
| [1] |
王庆宾. 动力法反演地球重力场模型研究[D]. 郑州: 信息工程大学, 2009 (Wang Qingbin. Study on the Recovery of Gravitational Potential Model with Dynamical Method[D]. Zhengzhou: Information Engineering University, 2009)
(  0) 0) |
| [2] |
Fecher T, Pail R, Gruber T. Global Gravity Field Modeling Based on GOCE and Complementary Gravity Data[J]. International Journal of Applied Earth Observation and Geoinformation, 2015, 35: 120-127 DOI:10.1016/j.jag.2013.10.005
(  0) 0) |
| [3] |
邹贤才, 李建成, 汪海洪, 等. OpenMP并行计算在卫星重力数据处理中的应用[J]. 测绘学报, 2010, 39(6): 636-641 (Zou Xiancai, Li Jiancheng, Wang Haihong, et al. Application of Parallel Computing with OpenMP in Data Processing for Satellite Gravity[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(6): 636-641)
(  0) 0) |
| [4] |
陈秋杰, 沈云中, 张兴福. MKL和OpenMP多核并行算法解算高阶地球重力场的效率分析[J]. 大地测量与地球动力学, 2012, 32(5): 118-123 (Chen Qiujie, Shen Yunzhong, Zhang Xingfu. Analysis of Efficiency of Applying MKL and OpenMP Polynuclear Parallel Algorithms to Recovery of High Degree Earth's Gravity Field[J]. Journal of Geodesy and Geodynamics, 2012, 32(5): 118-123)
(  0) 0) |
| [5] |
周浩, 罗志才, 钟波, 等. 利用最小二乘直接法反演卫星重力场模型的MPI并行算法[J]. 测绘学报, 2015, 44(8): 833-839 (Zhou Hao, Luo Zhicai, Zhong Bo, et al. MPI Parallel Algorithm in Satellite Gravity Field Model Inversion on the Basis of Least Square Method[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(8): 833-839)
(  0) 0) |
| [6] |
周浩, 罗志才, 钟波. 大规模矩阵的MPI并行求逆算法设计与分析[J]. 大地测量与地球动力学, 2014, 34(5): 120-124 (Zhou Hao, Luo Zhicai, Zhong Bo. Design and Analysis of MPI Parallel Algorithm for Large-Scale Matrix Inversion[J]. Journal of Geodesy and Geodynamics, 2014, 34(5): 120-124)
(  0) 0) |
| [7] |
Mu D W, Chen P, Wang L Q. Accelerating the Discontinuous Galerkin Method for Seismic Wave Propagation Simulations Using Multiple GPUs with CUDA and MPI[J]. Earthquake Science, 2013, 26(6): 377-393 DOI:10.1007/s11589-013-0047-7
(  0) 0) |
| [8] |
Hou Z L, Huang D N. Multi-GPU Parallel Algorithm Design and Analysis for Improved Inversion of Probability Tomography with Gravity Gradiometry Data[J]. Journal of Applied Geophysics, 2017, 144: 18-27 DOI:10.1016/j.jappgeo.2017.06.009
(  0) 0) |
| [9] |
刘世芳, 赵永华, 于天禹, 等. 并行对称矩阵三对角化算法在GPU集群上的有效实现[J]. 计算机研究与发展, 2020, 57(12): 2 635-2 647 (Liu Shifang, Zhao Yonghua, Yu Tianyu, et al. Efficient Implementation of Parallel Symmetric Matrix Tridiagonalization Algorithm on GPU Cluster[J]. Journal of Computer Research and Development, 2020, 57(12): 2 635-2 647)
(  0) 0) |
 2024, Vol. 44
2024, Vol. 44

