2. 中国电建集团贵阳勘测设计研究院有限公司,贵阳市兴黔路16号,550081
GRACE及GRACE-FO卫星以前所未有的时空分辨率动态监测地球时变重力场变化,为分析陆地水循环、地下水消耗、地震活动、海平面变化、冰川冰盖消融等提供了重要的观测数据[1]。GRACE卫星因在任务前期处于调试运行阶段及在任务后期出现设备性能下降和供能不足等问题[2],导致任务期间存在部分月份的数据缺失。同时,GRACE与GRACE-FO卫星之间存在11个月的连续数据缺失(2017-10~2018-05)。数据缺失,尤其是连续数据缺失,破坏了卫星观测数据的连续性,阻碍了卫星重力数据的充分应用[3-4]。为构建长时间且连续的观测数据,学者们提出利用水文模型等资料,基于深度学习模型重构地表质量变化[5-9]。已有研究表明,基于深度学习的地表质量变化模型重构方法可有效填补现有的缺失数据,并为后期潜在的数据缺失提供解决方案。
基于深度学习重构的地表质量变化模型依赖于网络模型结构,因此现有研究主要侧重于优化网络模型结构来提升重构模型的精度。由于不同深度学习方法采用的模型结构及深度不同,导致其重构精度及适用性也存在差异。为此,本文采用贝叶斯三角帽(Bayesian three-cornered hat, BTCH)法,在模型不确定性评估的基础上,结合后验概率融合重构模型,构建一种组合模型,以进一步提升地表质量变化的重构精度。
1 数据及方法 1.1 研究数据现今发布的重构模型较多,本文仅选择以CSR Mascon(CSRM) 模型为参照目标的最新发布的重构模型为研究对象,模型方法、简称、驱动数据及时间跨度等信息见表 1。表中,Swarm为国际全球地球模型中心发布的最大阶次为40的重力场模型,ERA5-L是由欧洲中期天气预报中心发布的气候再分析数据,P和T分别代表降雨和温度,CWSC为累积蓄水量变化,TWSA为陆地质量变化异常[5]。考虑到各模型产品时间、空间覆盖范围不一致,本研究仅对公共时间段(2014-01~2020-12)和公共区域进行模型不确定性评估。
|
|
表 1 基于CSRM模型的重构地表质量变化产品 Tab. 1 Reconstruction products of surface mass change based on CSRM model |
BTCH方法被广泛用于卫星/地表土壤水观测数据融合、多源蒸散发数据融合、GRACE模型融合等方面[10-11]。其采用三角帽法评估单个模型的不确定性[12],使用模型的后验概率进行加权,并利用各模型时间序列的联合概率分布及代价函数获得最佳组合模型[10]:
| $ \boldsymbol{X}_{\text {true }}=\sum\limits_{i=1}^n \omega_i \boldsymbol{X}_i, \omega_i=\frac{\prod\limits_{k=1, k \neq i}^n \sigma_k^2}{\sum\limits_{i=1}^n \prod\limits_{k=1, k \neq i}^n \sigma_k^2} $ | (1) |
式中,Xtrue为时间序列最佳估值,ωi和σi分别为第i个模型时间序列的加权系数及标准差,n为重构模型个数。
1.3 评价指标使用皮尔逊相关系数(R)、均方根误差(RMSE)和纳什效率系数(NSE)评估各模型精度。其中,R和NSE值越接近于1,表明模型性能越好,且当R大于0.5时,可认为变量具有强相关性;RMSE越接近于0,表明模型性能越好。
2 广义三角帽法评估重构模型的不确定性 2.1 重构模型的相关性不同模型具有相同的真实信号和独立的噪声是广义三角帽法进行模型评估的前提。利用不同模型间相关系数纬度加权平均值衡量模型间的整体一致性水平,同时将所有的相关系数取平均得到多模型信号相关系数,如图 1(a)所示。可以看出,不同模型间的相关系数具有相似的空间分布,与多模型信号相关系数空间分布基本一致。对于大多数区域,由于重构模型具有相同的地表质量变化信号,所以两者的相关性较高;而在撒哈拉沙漠、阿拉伯等区域,由于陆地水储量变化信号较弱,且受观测噪声及重构误差的影响,其信噪比较低,故模型间相关性较弱。此外,将单一模型信号扣除各模型平均值后的差异作为概略噪声,利用概略噪声分析各模型的噪声相关性,并取平均得到多模型噪声相关系数,其空间分布如图 1(b)所示。多模型信号及噪声相关性分布表明,在全球绝大多数区域,不同模型基本包含了相同的地表质量变化信号,尤其是在高信号区域,模型信号具有强相关性;而不同模型噪声的相关性较弱。因此,可通过广义三角帽法进行模型精度评估。

|
图 1 模型信号和噪声相关系数 Fig. 1 Correlation coefficients of model signal and noise |
利用广义三角帽法评估DCAE、CNN、BCNN和BF模型的不确定性。结果表明,在撒哈拉沙漠等弱信号区域,各模型的不确定性均较小;在具有强烈水文质量变化的区域,尤其是亚马孙区域,各模型不确定性较大,且模型间的不确定性差异较为明显。基于深度学习重构的地表质量变化模型的不确定性与气候类型具有较强的相关性,在湿润区域的不确定性较高。利用各模型的纬度加权不确定性作为指标评价模型的总体不确定性,BCNN、DCAE、CNN和BF模型的整体不确定性分别为2.07 cm、2.59 cm、1.69 cm和2.83 cm。
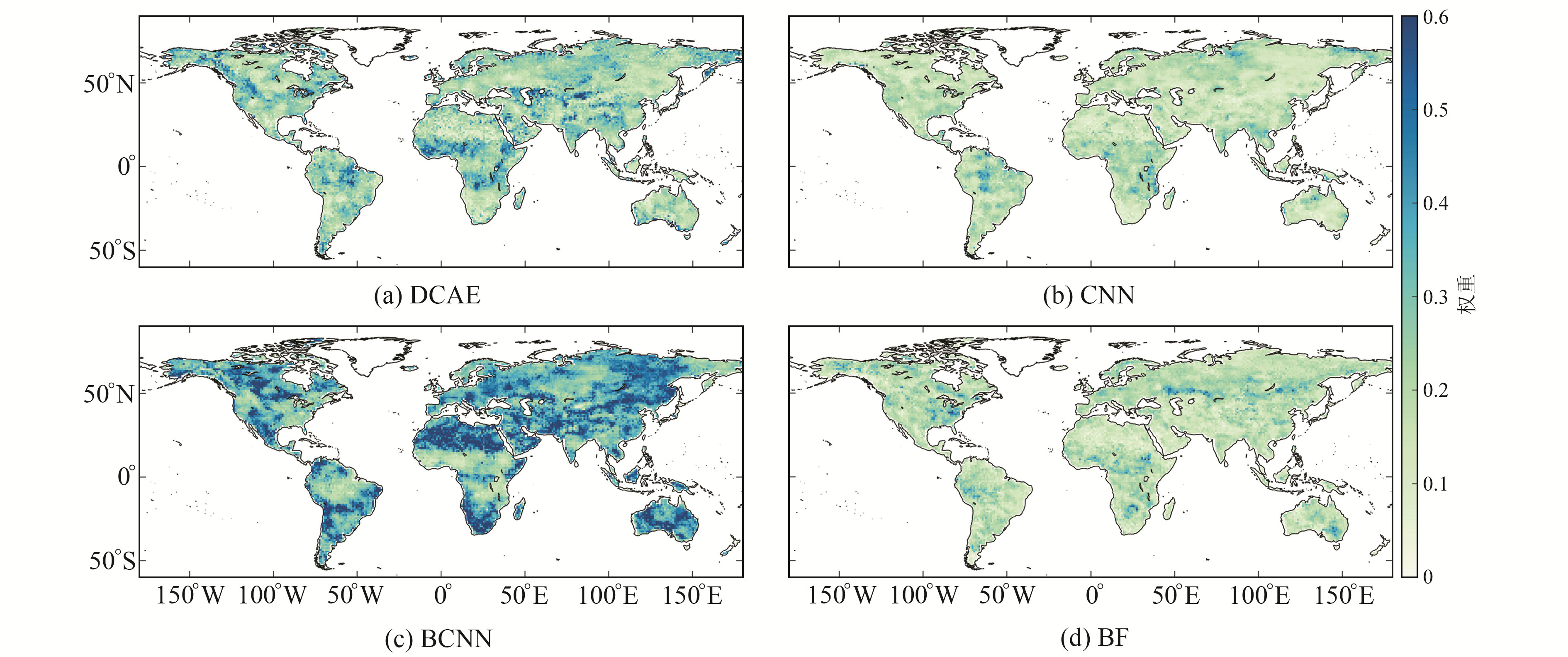
3 BTCH方法评估组合模型的不确定性 3.1 模型组合依据广义三角帽法评估模型的不确定性,通过式(1)确定各模型格网点权重,最终通过加权平均构建BTCH组合模型。各模型格网点权重如图 2所示。若模型格网点不确定性较低,则获得较高的权重;反之,则获得较低的权重。可以发现,4个重构模型中,BCNN模型在大多数区域权重较高,在非洲北部(撒哈拉沙漠)和南部、北美和南美中南部、澳洲和中亚等区域权重可达0.6,其权重纬度加权平均值为0.37;DCAE模型在南美中部(亚马孙盆地北部)、非洲中部等区域权重较高,可达到0.4,在澳洲及中亚等区域权重略低;CNN和BF模型由于不确定性较高,权重普遍较低。
|
图 2 各模型权重 Fig. 2 Weights of each model |
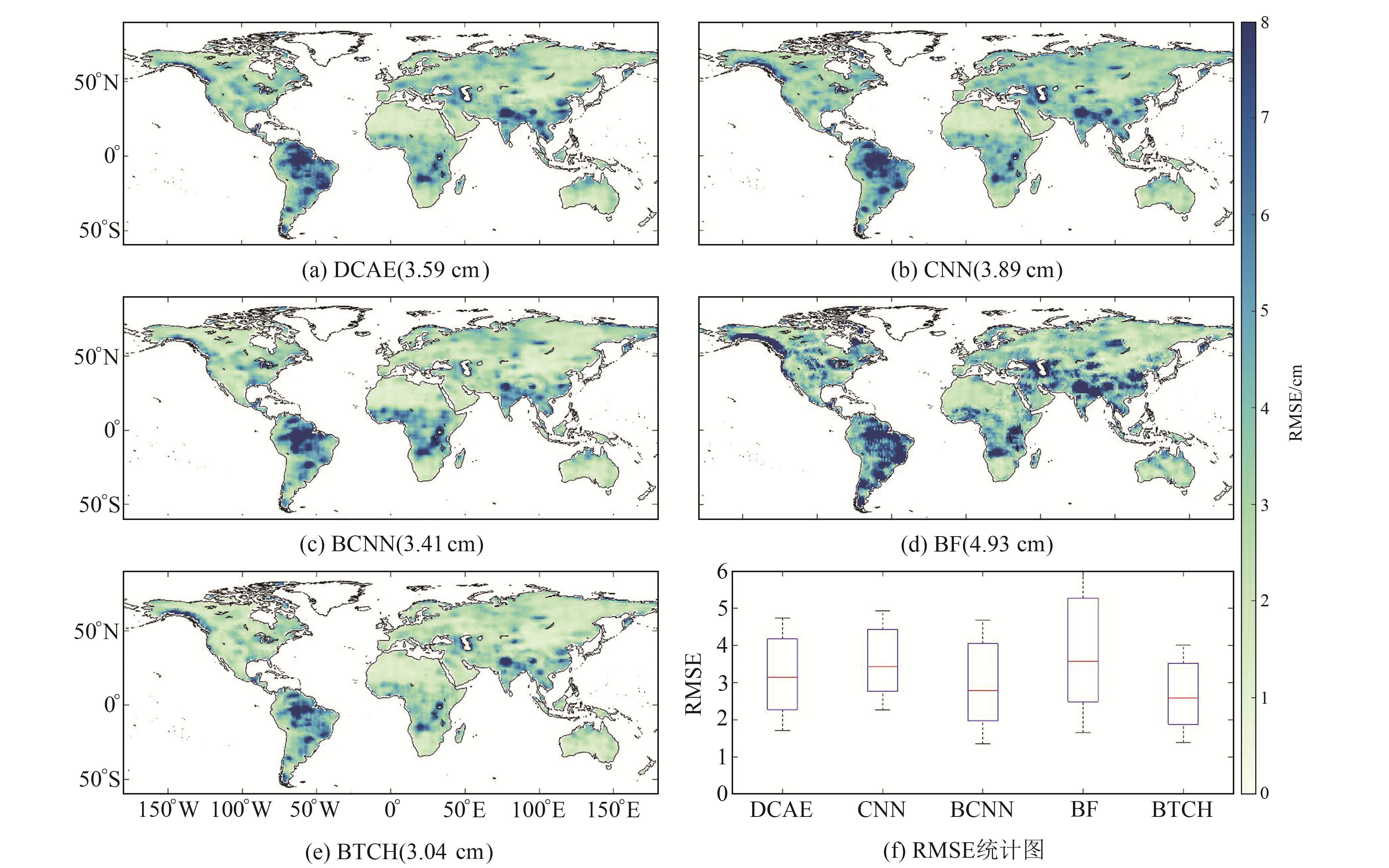
利用确定的各模型格网权阵,通过加权平均构建BTCH组合模型。为评价组合模型的精度,选取CSRM产品为参照模型,以2014-01~2020-12非间断期的各模型与参考模型数据的相关系数R、RMSE及NSE作为衡量精度的指标。限于篇幅,此处仅给出不同模型RMSE的空间分布(图 3)。可以看出,在具有强烈水文质量变化,尤其是季节性变化明显的区域,各模型与CSRM的RMSE较大。DCAE、CNN、BCNN、BF和BTCH模型的RMSE纬度加权平均值分别为3.59 cm、3.89 cm、3.41 cm、4.93 cm和3.04 cm,其中,BTCH模型在全球尺度上与CSRM模型一致性最佳,较最优的重构模型BCNN的误差降低约11%。各模型的RMSE格网箱体统计图如图 3(f)所示,红线为中位数,网箱顶边和底边为第75和25个百分位数,顶端和底端黑线对应最大和最小值。若箱体顶边与底边距离越短,则表明模型RMSE值分布越集中,结合中位数可反映该模型性能优劣。可以看出,BTCH模型的RMSE中位数略低于BCNN模型,且明显低于其他模型;同时,BTCH模型的RMSE分布较为集中,表明其在全球尺度上的适用性更强。
|
图 3 不同模型全球陆地水储量变化不确定性 Fig. 3 Uncertainty of different models of terrestrial water storage changes |
根据年平均干旱指数,将全球划分为超干旱(HA)、干旱(A)、半干旱(SA)、半湿润(SH)和湿润(H)5种气候类型区域[9],以评价组合模型及重构模型在不同气候类型区域的不确定性。2014-01~2020-12非间断期内不同气候类型区域的R、RMSE及NSE中位数如表 2所示。可以看出,模型预测结果受气候类型影响较大,R、RMSE和NSE均在超干旱/湿润区域取得最低/最高值,所有模型在超干旱/湿润区域的相关系数平均值分别为0.31/0.91,RMSE平均值分别为1.75 cm/3.71 cm,NSE平均值分别为-0.15/0.78。在超干旱和干旱区域,BTCH与CSRM模型的相关系数均略低于BCNN与CSRM模型的相关系数;而在半干旱、半湿润和湿润区域,二者的相关系数相当。非组合模型中,BCNN模型在各气候类型区域具有更低的RMSE和最高的NSE值。对于RMSE,BTCH模型在超干旱区域外的其他区域具有最佳结果,其中干旱、半干旱、半湿润和湿润区域的RMSE平均值较最优的单个重构模型结果分别下降约3%、9%、5%和13%。对于NSE,BTCH模型在半干旱、半湿润及湿润区域具有最优结果,NSE平均值较最优的单个重构模型性能分别提升约5%、5%和6%。整体而言,BTCH模型与CSRM模型具有更好的一致性,尤其是在湿润气候类型区域。综上,组合模型可降低重构模型中的误差,能够在大多数气候类型区域有效提升重构模型的精度。
|
|
表 2 不同气候类型区域的R、RMSE和NSE中位数统计 Tab. 2 Statistics of medians of R, RMSE and NSE for different climate regions |
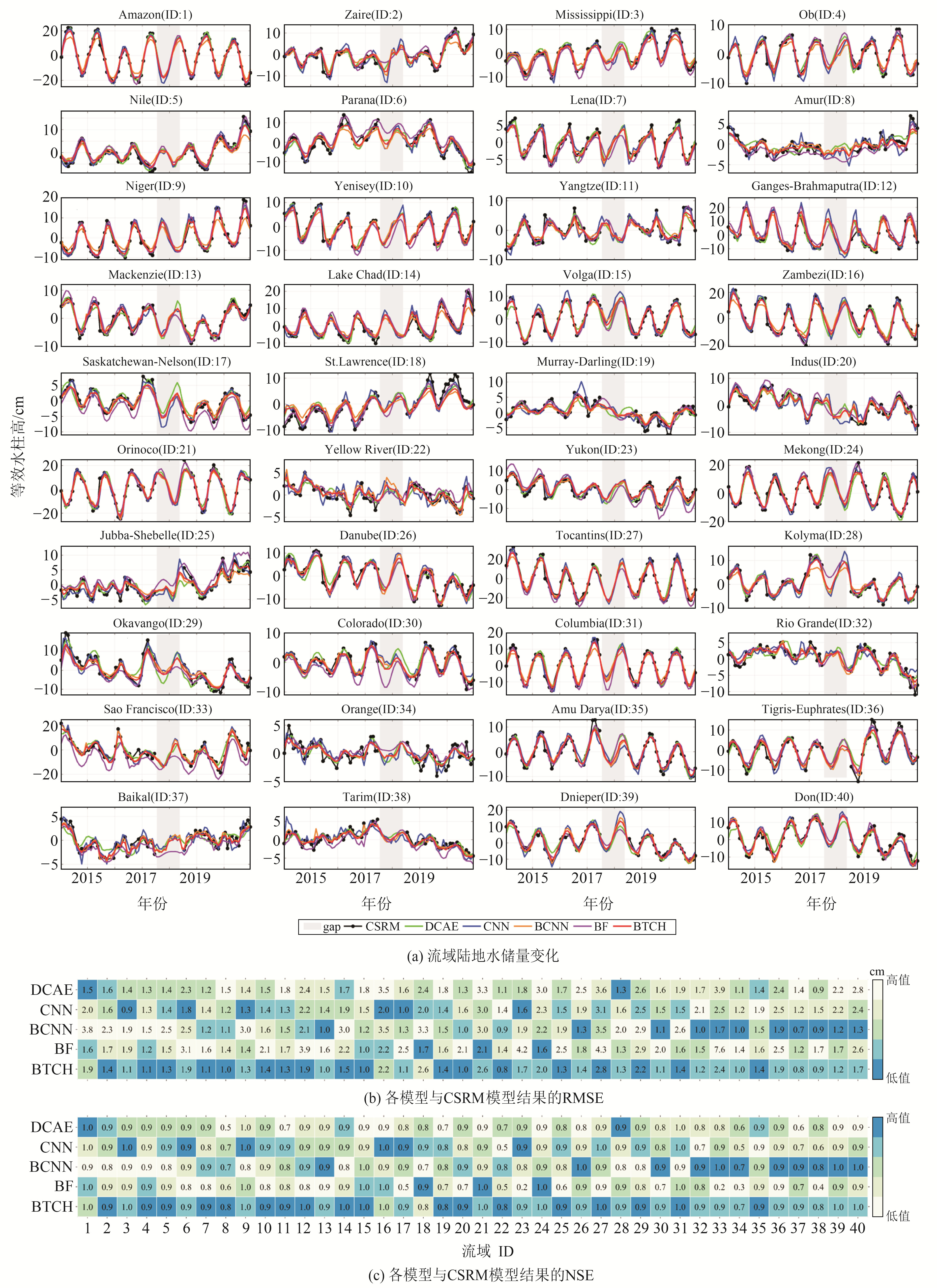
为进一步分析组合模型及重构模型的不确定性,选取全球前40个流域进行流域陆地质量变化统计,并将其与CSRM模型结果进行对比,如图 4(a)所示。可以看出,对于多数流域而言,重构模型和组合模型均与CSRM模型的结果表现出较强的相关性,但在Zaire、Parana等少数流域存在显著差异。为分析不同模型在流域尺度范围的优劣,利用其与CSRM模型结果的RMSE、NSE作为评价指标进行定量分析,结果如图 4(b)和4(c)所示。可以看出,BTCH与CSRM模型的结果在Zaire、Ob等18个流域一致性最佳;在Mississippi、Nile等19个流域一致性次佳。若以40个流域的RMSE平均值衡量重构模型在流域尺度上的不确定性,则DCAE、CNN、BCNN、BF和BTCH模型的流域平均不确定性分别为1.93 cm、1.76 cm、1.87 cm、2.13 cm和1.49 cm,组合模型不确定性较最优重构模型下降约15%。DCAE、CNN、BCNN、BF和BTCH模型在流域尺度上的平均NSE分别为0.85、0.86、0.87、0.78和0.91,组合模型较最优重构模型NSE指标提升约5%。综上,BTCH法能够有效降低因驱动数据、网络结构等不同引起的模型不确定性,融合不同重构模型的技术优势,进一步提升流域地表质量变化的精度。
|
图 4 流域陆地水储量变化时间序列及其不确定性 Fig. 4 Time series of basin-scale terrestrial water storage changes and their uncertainties |
本文利用广义三角帽法评估了近期发布的GRACE/GRACE-FO重构模型的不确定性,并基于贝叶斯模型平均方法确定组合模型。分析表明:
1) 组合模型估算的全球陆地水储量变化不确定性最低,BCNN模型次之,BF模型最差。各模型反演的陆地水储量变化受气候类型影响较大,在湿润区域具有最高不确定性;BTCH组合模型在超干旱区域以外的区域表现出更低的RMSE,较最优的单个重构模型RMSE下降约11%,在半干旱、半湿润及湿润区域具有最优NSE指标,较最优的单个重构模型性能提升约5%。
2) 重构模型及组合模型的流域质量变化与CSRM模型均表现出较强的相关性,但在Zaire、Parana等少数流域存在较大差异。对于选取的40个流域,组合模型BTCH在18个流域表现最佳,在19个流域表现次佳;组合模型不确定性较最优重构模型下降约15%,NSE指标较最优重构模型提升约5%。
3) 贝叶斯三角帽法能够有效融合重构的陆地水储量变化,进一步降低基于深度学习的地表质量变化重构模型的不确定性,为高精度填补及重构GRACE/GRACE-FO数据提供参考。
| [1] |
Tapley B D, Watkins M M, Flechtner F, et al. Contributions of GRACE to Understanding Climate Change[J]. Nature Climate Change, 2019, 9(5): 358-369 DOI:10.1038/s41558-019-0456-2
(  0) 0) |
| [2] |
石通, 刘新, 穆大鹏, 等. 基于多层感知机重建GRACE与GRACE-FO之间数据缺失的黄河流域陆地水储量变化[J]. 地球物理学报, 2022, 65(7): 2 448-2 463 (Shi Tong, Liu Xin, Mu Dapeng, et al. Reconstructing Gap Data between GRACE and GRACE-FO Based on Multi-Layer Perceptron and Analyzing Terrestrial Water Storage Changes in the Yellow River Basin[J]. Chinese Journal of Geophysics, 2022, 65(7): 2 448-2 463)
(  0) 0) |
| [3] |
Yang X C, Tian S Y, You W, et al. Reconstruction of Continuous GRACE/GRACE-FO Terrestrial Water Storage Anomalies Based on Time Series Decomposition[J]. Journal of Hydrology, 2021, 603
(  0) 0) |
| [4] |
Boergens E, Güntner A, Dobslaw H, et al. Quantifying the Central European Droughts in 2018 and 2019 with GRACE Follow-on[J]. Geophysical Research Letters, 2020, 47(14)
(  0) 0) |
| [5] |
Uz M, Atman K G, Akyilmaz O, et al. Bridging the Gap between GRACE and GRACE-FO Missions with Deep Learning Aided Water Storage Simulations[J]. Science of the Total Environment, 2022, 830
(  0) 0) |
| [6] |
Rateb A, Sun A, Scanlon B R, et al. Reconstruction of GRACE Mass Change Time Series Using a Bayesian Framework[J]. Earth and Space Science, 2022, 9(7)
(  0) 0) |
| [7] |
Zhang X, Li J B, Dong Q J, et al. Bridging the Gap between GRACE and GRACE-FO Using a Hydrological Model[J]. Science of the Total Environment, 2022, 822
(  0) 0) |
| [8] |
Lai Y, Zhang B, Yao Y B, et al. Reconstructing the Data Gap between GRACE and GRACE Follow-on at the Basin Scale Using Artificial Neural Network[J]. Science of the Total Environment, 2022, 823
(  0) 0) |
| [9] |
Mo S X, Zhong Y L, Forootan E, et al. Bayesian Convolutional Neural Networks for Predicting the Terrestrial Water Storage Anomalies during GRACE and GRACE-FO Gap[J]. Journal of Hydrology, 2022, 604
(  0) 0) |
| [10] |
He X L, Xu T R, Xia Y L, et al. A Bayesian Three-Cornered Hat(BTCH) Method: Improving the Terrestrial Evapotranspiration Estimation[J]. Remote Sensing, 2020, 12(5): 878 DOI:10.3390/rs12050878
(  0) 0) |
| [11] |
Yilmaz M T, Crow W T, Anderson M C, et al. An Objective Methodology for Merging Satellite- and Model-Based Soil Moisture Products[J]. Water Resources Research, 2012, 48(11)
(  0) 0) |
| [12] |
姚朝龙, 李琼, 罗志才, 等. 利用广义三角帽方法评估GRACE反演中国大陆地区水储量变化的不确定性[J]. 地球物理学报, 2019, 62(3): 883-897 (Yao Chaolong, Li Qiong, Luo Zhicai, et al. Uncertainties in GRACE-Derived Terrestrial Water Storage Changes over China's Mainland Based on a Generalized Three-Cornered Hat Method[J]. Chinese Journal of Geophysics, 2019, 62(3): 883-897)
(  0) 0) |
2. Guiyang Engineering Co Ltd, Power China, 16 Xingqian Road, Guiyang 550081, China
 2024, Vol. 44
2024, Vol. 44


