对变形监测数据进行及时分析,并对其未来变化趋势作出准确预测,可为工程建设的安全评估以及地质灾害的预测预报提供科学依据。用于变形监测的预测模型和方法很多,其中以GM(1, 1)模型为代表的灰色预测模型经过不断改进和完善,取得了较好的预测效果。从目前的研究来看,用于变形监测的灰色预测模型主要可以分为以下3类。
1) 传统GM(1, 1)模型及其改进模型[1-3]。由传统GM(1, 1)模型的建模原理可知,其仅适用于近似齐次指数序列的建模分析,本质上可等效为齐次指数函数模型。由于传统GM(1, 1)模型在建模原理上存在固有缺陷,即白化方程与灰微分方程的不匹配问题[4],研究人员往往会将其改进后再用于变形监测,如对背景值进行重构[2]或者采用无偏GM(1, 1)模型[3]。尽管改进后的GM(1, 1)模型能够提高传统GM(1, 1)模型的精度,但仍未能改变其模拟序列为齐次指数序列的本质。当用于滑坡临滑预测或变形体加速变形阶段预测时,GM(1, 1)模型可以得到较高的预测精度,但对于具有收敛特征的变形数据,如地基沉降数据,GM(1, 1)模型便不再适用[5]。
2) 非齐次灰色模型。非齐次灰色模型是指拟合函数为非齐次指数函数、拟合序列为非齐次指数序列的一类灰色预测模型。其拟合函数满足沉降的收敛特性,被广泛应用于沉降预测中。这类模型主要包括灰色线性组合模型[6]、无偏NGM(1, 1, k)模型[3, 5]和非等间隔GM(1, 1)模型[7]。除灰色线性组合模型以外,其余2种灰色模型都具备白指数率预测无偏性,可直接使用。其中,非等间隔GM(1, 1)模型解决了非等时距变形数据的建模问题[7]。非齐次灰色模型也可用于滑坡变形预测[3, 5],其预测精度往往高于GM(1, 1)模型。这是因为边坡临滑前的位移并不都完全服从近似齐次指数规律,许多数据具有非齐次指数规律[8]。
3) GM(1, 1)幂模型及其改进模型。GM(1, 1) 幂模型是一类非线性灰色预测模型,本质上可等效为生长曲线模型。当α=2时,GM(1, 1)幂模型即为灰色Verhulst模型[9]。当沉降趋于稳定或具有“S”型变化趋势时,可采用GM(1, 1)幂模型进行分析预测[9]。与GM(1, 1)模型类似,GM(1, 1)幂模型也存在背景值构造缺陷,需要将其改进后再用于变形预测[9-10]。在非等间隔GM(1, 1)模型的基础上,通过幂函数变换可建立非等间隔GM(1, 1)幂模型[9],以解决非等时距变形数据的建模问题。GM(1, 1)幂模型(主要是灰色Verhulst模型)也常用于边坡变形预测[11]。有学者[12-13]认为,采用Verhulst模型的反函数和GM(1, 1)幂模型的反函数来描述和拟合边坡变形特征更为合理。
此外,在变形监测中还有一些对数据处理进行改进的灰色预测模型,如残差修正GM(1, 1)模型[14-16]、灰色马尔科夫组合模型[17]、动态新陈代谢灰色模型[18]和卡尔曼滤波灰色模型[19]。但这些方法仍是以上述3类灰色预测模型为基础,只是在数据处理上进行改进,并未改变灰色预测模型的拟合函数。
综上所述,若不考虑数据处理方面的改进,仅从拟合函数的角度,变形监测灰色预测模型可分为3类:传统GM(1, 1)模型及其改进模型、非齐次灰色模型、GM(1, 1)幂模型及其改进模型。这3类模型的计算原理不同,特别是在拟合函数、是否适用于非等时距变形数据建模以及是否存在极限值等方面存在差异,这些差异对于选择变形监测预测模型非常重要,而现有研究缺少这方面的系统性探讨和总结。3类灰色预测模型本质上可等效为函数模型或曲线模型,但与一般的曲线拟合在参数计算上又存在差异,两者之间有何异同、曲线拟合函数是否可代替灰色预测模型用于变形监测也值得探讨。为此,本文以3类灰色预测模型为研究对象,以Origin拟合函数作为3类灰色预测模型的替代方法,基于理论分析和工程实例对比分析3类灰色预测模型及其替代方法,验证替代方法的可行性,并提出各类模型和方法的应用建议,为灰色预测模型在变形监测中的合理应用提供参考。
1 3类灰色预测模型的建模原理及替代方法虽然本文从拟合函数的角度将变形监测灰色预测模型分为3类,但由于改进方法繁多,每一类灰色预测模型都包含多种改进模型,所以本文仅选择其中有代表性的改进模型作为研究对象。具体按等时距和非等时距2种情况进行选择:等时距灰色预测模型适用于变形数据为等时距的情况,非等时距灰色预测模型适用于变形数据为非等时距的情况。
1) 等时距灰色预测模型的选择。文献[4]总结了GM(1, 1)模型的改进现状,认为白化方程参数重构的GM(1, 1)模型,即无偏GM(1, 1)模型建模相对简单、精度较高,故本文选用其作为第1类灰色预测模型的代表性模型。同样,选择改进原理相似的无偏NGM(1, 1, k)模型[3, 5]和无偏GM(1, 1)幂模型[9]作为第2类和第3类灰色预测模型的代表性模型。
2) 非等时距灰色预测模型的选择。传统非等间隔GM(1, 1)模型以时间间隔作为权重,对原始数据进行加权累加,其模拟序列并非齐次指数序列,而是不规则序列,并不适用于具有近似齐次指数趋势的变形数据[7]。因此,传统非等间隔GM(1, 1)模型与GM(1, 1)模型并不属于同一类模型。目前并未出现模拟序列为齐次指数序列的非等间隔GM(1, 1)模型,所以对于第1类灰色预测模型本文不考虑非等时距的情况。文献[7]提出一种非等间隔GM(1, 1)模型,其模拟序列为非齐次指数序列,可用于沉降的分析预测,本文将其作为第2类灰色预测模型的代表性模型。由幂函数变换结合非等间隔GM(1, 1)模型可建立非等间隔GM(1, 1)幂模型[9],本文将其作为第3类灰色预测模型的代表性模型。
1.1 等时距灰色预测模型 1.1.1 无偏GM(1, 1)模型记变形监测序列为X(0),其一次累加值为X(1)。无偏GM(1, 1)模型的灰微分方程为:
| $ x^{(0)}(k)+a z^{(1)}(k)=b $ | (1) |
式中,a为发展系数,b为灰作用量,z(1)(k)=0.5[x(1)(k)+x(1)(k-1)]。以最小二乘法估计参数a、b。
其白化方程为:
| $ \frac{\mathrm{d} x^{(1)}(t)}{\mathrm{d} t}+m x^{(1)}(t)=n $ | (2) |
时间响应式为:
| $ \hat{x}^{(1)}(k)=\left(x^{(1)}(1)-\frac{n}{m}\right) \mathrm{e}^{-m(k-1)}+\frac{n}{m} $ | (3) |
还原值为:
| $ \left\{\begin{array}{l} \hat{x}^{(0)}(1)=x^{(0)}(1) \\ \hat{x}^{(0)}(k)=\left(1-\mathrm{e}^m\right) \mathrm{e}^{-m(k-1)}\left(x^{(0)}(1)-\frac{n}{m}\right), \\ \quad k=2, 3, \cdots, n \end{array}\right. $ | (4) |
式中,m、n分别由参数变换公式
无偏NGM(1, 1, k)模型的建模原理与无偏GM(1, 1)模型相似,都是采用累加建模法。其灰微分方程为:
| $ x^{(0)}(k)+a z^{(1)}(k)=k b+c $ | (5) |
式中,a为发展系数,kb+c为灰作用量。同样以最小二乘法估计参数a、b、c。
其白化方程为:
| $ \frac{\mathrm{d} x^{(1)}(t)}{\mathrm{d} t}+m x^{(1)}(t)=n t+p $ | (6) |
时间响应式为:
| $ \begin{gathered} \hat{x}^{(1)}(k)=\left(x^{(1)}(1)-\frac{n}{m}+\frac{n}{m^2}-\frac{p}{m}\right) \mathrm{e}^{-m(k-1)}+ \\ \frac{n k}{m}-\frac{n}{m^2}+\frac{p}{m} \end{gathered} $ | (7) |
还原值为:
| $ \left\{\begin{array}{l} \hat{x}^{(0)}(1)=x^{(0)}(1) \\ \hat{x}^{(0)}(k)=\left(1-\mathrm{e}^m\right) \mathrm{e}^{-m(k-1)}\left(x^{(0)}(1)-\right. \\ \left.\frac{n}{m}+\frac{n}{m^2}-\frac{p}{m}\right)+\frac{n}{m}, k=2, 3, \cdots, n \end{array}\right. $ | (8) |
式中,m、n、p分别由参数变换公式
对无偏GM(1, 1)模型进行幂函数变换可建立无偏GM(1, 1)幂模型,但需将累加建模法改为直接建模法,其建模原理如下[9]。
令X′(1)为变形监测序列,幂函数变换后序列为X(1)=(X′(1))1-α(α≠1),其一次累减序列为X(0)。以序列X(0)和X(1)建立无偏GM(1, 1)模型得到预测值
| $ \begin{gathered} \hat{x}^{\prime(1)}(k)= \\ \left\{\left[\left(x^{\prime(1)}(1)\right)^{1-\alpha}-\frac{n}{m}\right] \mathrm{e}^{-m(k-1)}+\frac{n}{m}\right\}^{\frac{1}{1-\alpha}} \end{gathered} $ | (9) |
本文采用文献[9]的寻优算法,通过编制无偏GM(1, 1)幂模型的MATLAB程序,以拟合结果的平均相对误差最小作为优化目标,采用MATLAB直接搜索工具箱确定最优参数α。无偏GM(1, 1)幂模型满足白幂指数率预测无偏性[9]。由式(9)可见,无偏GM(1, 1)幂模型的拟合函数为生长曲线函数,可用于趋于稳定或具有“S”型变化趋势序列的分析和预测。
1.2 非等时距灰色预测模型 1.2.1 非等间隔GM(1, 1)模型非等间隔GM(1, 1)模型采用直接建模法,其建模原理如下[7]。
记变形监测序列为X(1),对应的时间序列为T(1),一次累减值为X(0)和T(0)。非等间隔GM(1, 1)模型的白化方程为:
| $ \frac{\mathrm{d} x^{(1)}}{\mathrm{d} t}+a x^{(1)}(t)=b $ | (10) |
时间响应式为:
| $ \begin{gathered} \hat{x}^{(1)}(k)=\left(x^{(1)}(1)-\frac{b}{a}\right) \cdot \\ \exp \left[-a\left(t^{(1)}(k)-t^{(1)}(1)\right)\right]+\frac{b}{a} \end{gathered} $ | (11) |
白化方程对应的灰微分方程为:
| $ \frac{x^{(0)}(k)}{t^{(0)}(k)}+a z^{(1)}(k)=b $ | (12) |
式中,z(1)(k)为背景值,计算公式为:
| $ z^{(1)}(k)=p x^{(1)}(k)+(1-p) x^{(1)}(k-1) $ | (13) |
式中,
参数β同样可采用文献[9]的寻优算法确定。非等间隔GM(1, 1)模型满足白指数率预测无偏性[7]。由式(11)可见,非等间隔GM(1, 1)模型的拟合函数为非齐次指数函数,可用于近似非齐次指数序列的分析和预测。
1.2.2 非等间隔GM(1, 1)幂模型由幂函数变换结合非等间隔GM(1, 1)模型可建立非等间隔GM(1, 1)幂模型[9]。
令X′(1)为沉降监测序列,幂函数变换后序列为X(1)=(X′(1))1-α(α≠1),对应的时间序列为T(1)。将幂函数变换后的沉降序列和时间序列进行一次累减,建立非等间隔GM(1, 1)模型得到预测值
| $ \begin{gathered} \hat{x}^{(1)}(k)=\left\{\left[\left(x'^{(1)}(1)\right)^{1-a}-\frac{b}{a}\right] \cdot\right. \\ \left.\exp \left[-a\left(t^{(1)}(k)-t^{(1)}(1)\right)\right]+\frac{b}{a}\right\}^{\frac{1}{1-a}} \end{gathered} $ | (14) |
除参数β以外,还需确定幂函数变换参数α。同样可采用文献[9]的寻优算法确定这2个参数。非等间隔GM(1, 1)幂模型满足白幂指数率预测无偏性[9]。由式(14)可见,非等间隔GM(1, 1)幂模型的拟合函数为生长曲线函数,可用于趋于稳定或具有“S”型变化趋势序列的分析和预测。
1.3 替代方法现有研究主要是在灰色建模法的基础上对灰色预测模型进行改进以提高模型的精度,少有研究避开灰色建模原理,直接求解拟合函数。鉴于灰色建模法求解参数的复杂性,笔者曾建议采用曲线拟合的方法直接求解灰色预测模型的拟合函数,即采用Origin软件提供的非线性拟合函数代替灰色预测模型,亦可实现其建模目标[3, 9]。可代替3类灰色预测模型的Origin拟合函数分别为:
| $ \text { Exp2PModl: } y=a \mathrm{e}^{b t} $ | (15) |
| $ \text { Exponential: } y=y_0+a \mathrm{e}^{b t} $ | (16) |
| $ \text { SRichards2 }: y=a\left[1+(d-1) \mathrm{e}^{-k\left(x-x_c\right)}\right]^{\frac{1}{(1-d)}} $ | (17) |
上述3种拟合函数分别为齐次指数函数、非齐次指数函数和生长曲线函数,与3类灰色预测模型的拟合函数相对应,可作为3类灰色预测模型的替代方法。下面从计算原理、建模数据和拟合效果3个方面对比分析灰色预测模型与Origin拟合函数。
1) 计算原理。灰色预测模型以最小二乘法为基础计算参数,对于无偏GM(1, 1)幂模型、非等间隔GM(1, 1)模型和非等间隔GM(1, 1)幂模型,还需采用寻优算法求解幂函数变换参数和背景值构造参数,而且寻优算法和最小二乘法属于嵌套计算,这就要求借助MATLAB等软件编制程序实现参数求解。Origin非线性拟合一般采用Levenberg-Marquardt优化算法,研究人员只要学会拟合操作即可,复杂的迭代过程交由Origin软件处理,在参数求解上更为简便[3, 9]。
2) 建模数据。灰色预测模型一般适用于小样本、少数据的建模[20],对数据量的要求较低,但数据量较大时会增加参数求解的难度。Origin拟合函数对数据量没有特殊要求,只要能实现参数计算即可。变形数据往往为非等时间间隔,而大部分灰色预测模型仅适用于等时距变形数据建模,适用于非等时距变形数据建模的非等间隔GM(1, 1)模型和非等间隔GM(1, 1)幂模型在参数求解上又存在一定难度。Origin拟合函数对变形数据的时间间隔没有要求,Origin软件可直接对非等时距变形数据进行非线性拟合。可见,当变形数据量较大或变形数据具有非等时距时,采用Origin拟合函数更具优势。
3) 拟合效果。灰色预测模型(不包括未改进的模型)和Origin拟合函数的拟合效果相当,在建模数据较多时,灰色预测模型的拟合效果可能不及Origin拟合函数[3, 9]。当采用寻优算法求解无偏GM(1, 1)幂模型等灰色预测模型的参数时,其优化目标可以根据实际情况进行调整,比如以平均相对误差最小作为优化目标[9],或者采用考虑数据新旧程度的目标误差函数[21]。Origin拟合函数一般不能实现这种特殊优化目标。
2 3类灰色预测模型的对比分析灰色预测模型的拟合函数属于何种类型、能否实现极限值的预测、是否适用于非等时距变形数据建模,这些性质对于变形监测都非常重要。因此,本文根据3类灰色预测模型的建模原理,从拟合函数、有无极限值、适合等时距或非等时距建模、替代方法和适用范围等5个方面进行对比分析,如表 1所示。
|
|
表 1 3类灰色预测模型的对比 Tab. 1 Comparison of three types of grey forecasting models |
1) 无偏GM(1, 1)模型的拟合函数为齐次指数函数y=aebx,b < 0时,极限值为0。对于变形数据,一般不存在极限值为0的情况,所以无偏GM(1, 1)模型不适合趋于稳定的沉降预测。b>0时,无极限值,且呈指数增长趋势,一般适用于滑坡临滑预测或变形体加速变形阶段的变形预测[9]。受建模原理的限制,无偏GM(1, 1)模型仅适合于等时距变形数据序列建模,若变形数据为非等时距,需要进行等时距的变换处理[3]。若采用Exp2PModl函数,则没有等时距的要求,且参数求解更简便。
2) 无偏NGM(1, 1, k)模型和非等间隔GM(1, 1)模型的拟合函数为非齐次指数函数y=aebx+m,b < 0时,极限值为m,适用于趋于稳定的沉降预测[7];b>0时,无极限值,且呈指数增长趋势,适用于滑坡临滑预测或变形体加速变形阶段的变形预测[3, 5]。受建模原理的限制,无偏NGM(1, 1, k)模型仅适合于等时距变形数据建模,若变形数据为非等时距,则需采用非等间隔GM(1, 1)模型。若采用Exponential函数,则无需考虑变形数据的时间间隔,且参数求解更简便。
3) 无偏GM(1, 1)幂模型和非等间隔GM(1, 1) 幂模型的拟合函数为生长曲线模型
文献[3, 9]对比分析了除非等间隔GM(1, 1)模型以外的代表性灰色预测模型与相应替代方法的拟合和预测精度。本文也采用文献[3, 9]中的3个实例。
1) 向家坡滑坡。以其位移监测资料为例[22],监测位移为等时距数据,可采用无偏GM(1, 1)模型和无偏NGM(1, 1, k)模型。以第1~7周位移数据分别建立上述2种灰色预测模型和Exp2PModl、Exponential函数,预测第8~9周位移,以对比各方法的拟合和预测精度。
2) 邵阳-怀化高速公路。以某软土路基断面12期总体沉降实测值为例[23],沉降实测值为等时距数据,可采用无偏NGM(1, 1, k)模型和无偏GM(1, 1)幂模型。分别建立上述2种灰色预测模型和Exponential、SRichards2函数,对比各方法的拟合精度。
3) 成绵乐铁路客运专线。以DK171+600测点的沉降观测结果为例[24],沉降实测值为非等时距数据,可采用非等间隔GM(1, 1)模型和非等间隔GM(1, 1)幂模型。分别建立上述2种灰色预测模型和Exponential、SRichards2函数,对比各方法的拟合精度。
若采用累加建模法建立灰色预测模型,会导致还原函数对初始值不具有拟合效果[25]。为进行合理对比,对于采用累加建模法的无偏GM(1, 1)模型、无偏NGM(1, 1, k)模型和无偏GM(1, 1)幂模型,在比较这些灰色预测模型和相应Origin拟合函数的拟合精度时,不考虑第1组数据,同时在求解Origin拟合函数时,也不考虑第1组数据。对于采用直接建模法的非等间隔GM(1, 1)模型和非等间隔GM(1, 1)幂模型,其拟合函数对初始值具有拟合效果,所以在进行拟合精度比较以及求解Origin拟合函数时,考虑第1组数据。
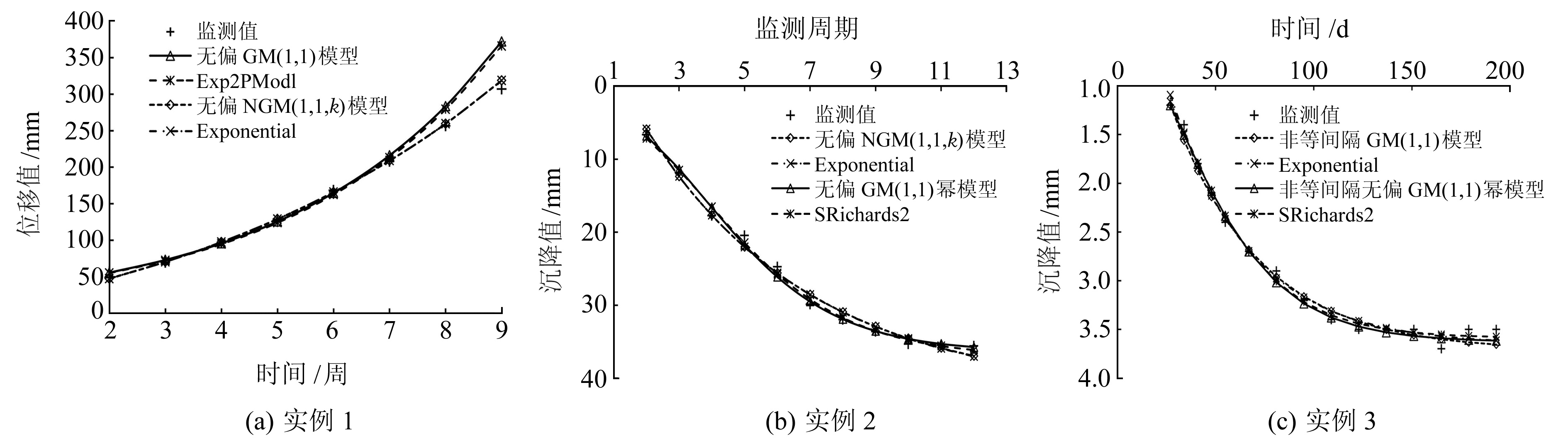
对于实例1,直接采用文献[3]中无偏GM(1, 1)模型、无偏NGM(1, 1, k)模型和Exponential函数的拟合结果。只需计算Exp2PModl函数的拟合结果。对于实例2,直接采用文献[9]中无偏GM(1, 1)幂模型的拟合结果,需去除第1组数据重新求解Exponential函数,同时还需计算无偏NGM(1, 1, k)模型和Exponential函数的拟合结果。对于实例3,直接采用文献[9]中非等间隔GM(1, 1)幂模型和SRichards2函数的拟合结果,需计算非等间隔GM(1, 1)模型和Exponential函数的拟合结果。其中,非等间隔GM(1, 1)模型的背景值构造参数采用文献[9]的寻优算法确定,在搜索参数β的最优值时,初值为0.1,参数范围为[-10, 10]。各模型的拟合预测结果如图 1所示,拟合公式和拟合(预测)精度如表 2所示,以均方差和平均相对误差衡量精度。
|
图 1 各模型的拟合(预测)结果与监测结果的对比 Fig. 1 Comparison of the fitted(predicted) results of each model with the monitoring results |
|
|
表 2 各模型的拟合公式和拟合(预测)精度 Tab. 2 Fitted formulas and fitted(predicted) accuracy of each model |
1) 对于实例1,与无偏GM(1, 1)模型相比,无偏NGM(1, 1, k)模型的拟合结果更接近于监测结果,其拟合预测精度更高,这说明向家坡滑坡的位移发展趋势更接近非齐次指数趋势。无偏GM(1, 1)模型与Exp2PModl函数的拟合预测效果相当,Exp2PModl函数拟合预测精度更高。无偏NGM(1, 1, k)模型与Exponential函数的拟合预测精度非常接近,两者的拟合预测效果几乎相同。
2) 对于实例2,与无偏NGM(1, 1, k)模型相比,无偏GM(1, 1)幂模型的拟合结果更接近于监测结果,其拟合精度更高,这说明沉降发展趋势更接近于“S”型变化。无偏NGM(1, 1, k)模型与Exponential函数的拟合精度非常接近,两者拟合效果相当。无偏GM(1, 1)幂模型与SRichards2函数的拟合精度较为接近,两者的拟合效果相差不大,SRichards2函数拟合的均方差更小,但其平均相对误差2.955%稍大于无偏GM(1, 1)幂模型的2.671%。
3) 对于实例3,非等间隔GM(1, 1)模型的均方差为0.109 mm2,平均相对误差为2.877%,拟合精度较高,说明沉降发展趋势比较接近于非齐次指数趋势。非等间隔GM(1, 1)幂模型的拟合精度更高,均方差为0.072 mm2,平均相对误差为2.146%。非等间隔GM(1, 1)模型和Exponential函数的拟合精度很接近,两者的拟合效果相差不大,Exponential函数拟合精度更高。非等间隔GM(1, 1)幂模型和SRichards2函数的拟合精度较为接近,两者拟合效果相差不大,SRichards2函数拟合精度更高。
3.2 讨论和建议 3.2.1 灰色预测模型的适用性从上述实例分析中可以看出,对于不同类型的监测数据,3类灰色预测模型的表现存在显著差异。3类灰色预测模型的拟合函数决定了它们分别适用于具有近似齐次指数、非齐次指数和“S”型变化趋势的变形数据。
第1类灰色预测模型的拟合函数为齐次指数函数,无法较好地拟合近似非齐次指数序列以及趋于稳定或具有“S”型变化趋势的序列,其适用性在3类灰色预测模型中最差。只有在边坡临滑或变形体加速变形阶段具有齐次指数发展趋势时,可采用第1类灰色预测模型。
第2类灰色预测模型属于非齐次灰色模型,不仅可用于具有非齐次指数增长趋势的滑坡位移建模,也可用于趋于稳定的沉降数据建模。当沉降发展趋势接近于非齐次指数趋势时,第2类灰色预测模型可以得到较好的拟合效果,比如本文实例3。
第3类灰色预测模型属于生长曲线模型,适用于趋于稳定或具有“S”型变化趋势的沉降预测。其模型结构比非齐次灰色模型更为复杂,但适用性更强,即使对于近似非齐次指数序列,也可以得到比非齐次灰色模型更高的拟合精度,比如本文实例3。
因此,建议在滑坡临滑预测或变形体加速变形阶段时,对第1类和第2类灰色预测模型的拟合效果进行对比,选择更能反映当前变形发展趋势的模型;在趋于稳定的沉降预测时,可直接采用第3类灰色预测模型。受地质条件和环境因素的影响,许多变形数据都具有波动性或者阶跃性[14, 16, 19, 26]。这种情况下,3类灰色预测模型可作为趋势分析模型,但需要根据变形的整体趋势特征选择合适的灰色预测模型。至于变形中的残余波动特征或者阶跃特征,可采用时间序列分析模型、BP神经网络等方法进行分析。
3.2.2 Origin拟合函数的替代性从本文实例来看,与3类灰色预测模型相比,Origin拟合函数可以得到相当甚至更高的拟合或预测精度。除实例2中SRichards2函数的平均相对误差稍大于无偏GM(1, 1)幂模型以外,其余实例中Origin拟合函数的均方差和平均相对误差都小于相应的灰色预测模型。无偏GM(1, 1)模型没有相应的非等时距模型,不能直接用于非等时距变形数据建模,其余2类灰色预测模型需要根据变形数据的时距特征选择相应的等时距或非等时距模型。相比之下,Origin拟合函数对变形数据的时间间隔没有要求,使用更为方便。
3类灰色预测模型采用最小二乘法计算参数a、b或a、b、c,需要进行矩阵运算,在参数辨识过程中可能出现病态性问题[27],影响模型的可靠性。无偏GM(1, 1)幂模型、非等间隔GM(1, 1)模型和非等间隔GM(1, 1)幂模型在采用寻优算法确定参数α或α、β时,需要合理选择待求参数的初始值和取值范围以及寻优算法的计算参数,以避免陷入局部最优解,影响计算结果。其中,非等间隔GM(1, 1)幂模型有2个寻优算法待求参数,计算难度相对较大,计算效率相对较低。相比之下,3种替代方法为Origin软件内置拟合函数,无需专门编制程序进行参数的优化求解,计算效率和可靠性相对更高。
综上,Origin拟合函数完全可以代替灰色预测模型用于变形监测。如果研究人员比较熟悉灰色预测模型的建模原理,也可根据数据特征选择合适的灰色预测模型进行预测分析。对于需要参数优化求解的非等间隔GM(1, 1)模型、无偏GM(1, 1)幂模型和非等间隔GM(1, 1)幂模型,可选择以平均相对误差最小作为优化目标或者采用考虑数据新旧程度的目标误差函数[21]等特殊优化目标,有时可以得到比Origin拟合函数更低的平均相对误差,比如本文实例2中的无偏GM(1, 1)幂模型。
4 结语将变形监测灰色预测模型分为传统GM(1, 1) 模型及其改进模型、非齐次灰色模型、GM(1, 1)幂模型及其改进模型3种类型,从拟合函数、有无极限值、适合等时距或非等时距建模和适用范围等方面对比3类灰色预测模型的代表性模型,给出3类灰色预测模型的应用建议,可为根据变形数据特征选择合适的灰色预测模型提供指导。
以Origin拟合函数Exp2PModl、Exponential和SRichards2作为3类灰色预测模型的替代方法。与3类灰色预测模型相比,Origin拟合函数在参数求解和建模数据要求上更具优势,而且可以得到相当甚至更高的拟合或预测精度,除需要编程实现的特殊优化目标外,可作为3类灰色预测模型的替代方法应用于变形监测。
| [1] |
盛建龙, 张鑫, 胡斌. 基于GM(1, 1)模型的老鹰嘴边坡位移变形预测[J]. 矿业研究与开发, 2022, 42(11): 82-87 (Sheng Jianlong, Zhang Xin, Hu Bin. Prediction on Displacement Deformation of Laoyingzui Slope Based on GM(1, 1) Model[J]. Mining Research and Development, 2022, 42(11): 82-87)
(  0) 0) |
| [2] |
王露. GM(1, 1)模型在凤山隧道变形预测中的应用[J]. 建筑技术, 2017, 48(9): 990-992 (Wang Lu. Application of GM(1, 1) Model to Deformation Prediction of Fengshan Tunnel[J]. Architecture Technology, 2017, 48(9): 990-992)
(  0) 0) |
| [3] |
陈鹏宇. 无偏灰色模型和Origin拟合函数在变形监测预报中的对比应用[J]. 大地测量与地球动力学, 2017, 37(3): 240-245 (Chen Pengyu. Comparison and Application of Unbiased Grey Model and Origin Fitting Functions on Deformation Monitoring and Prediction[J]. Journal of Geodesy and Geodynamics, 2017, 37(3): 240-245)
(  0) 0) |
| [4] |
陈鹏宇, 邓宏伟. GM(1, 1)模型的改进现状及应用[J]. 统计与决策, 2019, 35(6): 80-82 (Chen Pengyu, Deng Hongwei. Improvement and Application of GM(1, 1) Model[J]. Statistics and Decision, 2019, 35(6): 80-82)
(  0) 0) |
| [5] |
陈鹏宇. 一种无偏模型在变形监测中的应用[J]. 测绘科学, 2018, 43(3): 117-122 (Chen Pengyu. Application of an Unbiased Model in Deformation Monitoring[J]. Science of Surveying and Mapping, 2018, 43(3): 117-122)
(  0) 0) |
| [6] |
马保卿, 张荫. 地面沉降模拟计算的灰色模型[J]. 河南科技大学学报: 自然科学版, 2009, 30(1): 57-60 (Ma Baoqing, Zhang Yin. Grey Model for Ground Subsidence Simulation[J]. Journal of Henan University of Science and Technology: Natural Science, 2009, 30(1): 57-60)
(  0) 0) |
| [7] |
陈鹏宇. 非等距GM(1, 1)模型在沉降预测中的应用探讨[J]. 大地测量与地球动力学, 2017, 37(7): 709-714 (Chen Pengyu. Discussion of the Application of Non-Equidistant GM(1, 1) Models in Subsidence Prediction[J]. Journal of Geodesy and Geodynamics, 2017, 37(7): 709-714)
(  0) 0) |
| [8] |
谢金华. 滑坡变形临界预警方法及预测预报的灰色模型改进研究[D]. 厦门: 厦门大学, 2018 (Xie Jinhua. Critical Warning Method for Landslide Deformation and Improvement of Grey Model for Prediction[D]. Xiamen: Xiamen University, 2018)
(  0) 0) |
| [9] |
陈鹏宇. GM(1, 1)幂模型的改进及其在沉降预测中的应用[J]. 大地测量与地球动力学, 2020, 40(5): 464-469 (Chen Pengyu. Improvement of GM(1, 1) Power Model and Its Application on Settlement Prediction[J]. Journal of Geodesy and Geodynamics, 2020, 40(5): 464-469)
(  0) 0) |
| [10] |
王炳, 李培现, 张军, 等. 优化背景值的非等间距线性时变参数GM(1, 1)幂模型在变形监测中的应用[J]. 大地测量与地球动力学, 2022, 42(8): 823-828 (Wang Bing, Li Peixian, Zhang Jun, et al. Application of Non-Equidistant Linear Time-Varying Parameter GM(1, 1) Power Model with Optimized Background Value in Deformation Monitoring[J]. Journal of Geodesy and Geodynamics, 2022, 42(8): 823-828)
(  0) 0) |
| [11] |
李甲, 王文杰, 尹东. 基于改进灰色Verhulst模型的巷道变形破坏预警方法研究及应用[J]. 矿业安全与环保, 2022, 49(2): 66-71 (Li Jia, Wang Wenjie, Yin Dong. Research and Application of Early Warning Method of Roadway Deformation Based on Improved Grey Verhulst Model[J]. Mining Safety and Environmental Protection, 2022, 49(2): 66-71)
(  0) 0) |
| [12] |
李天斌, 陈明东. 滑坡时间预报的费尔哈斯反函数模型法[J]. 地质灾害与环境保护, 1996(3): 13-17 (Li Tianbin, Chen Mingdong. Time Prediction of Landslide Using Verhulst Inverse-Function Model[J]. Journal of Geological Hazards and Environment Preservation, 1996(3): 13-17)
(  0) 0) |
| [13] |
贺小黑. 边坡变形预测与失稳预报研究[D]. 北京: 中国科学院大学, 2013 (He Xiaohei. Research on Slope Deformation Prediction and Instability Forecasting[D]. Beijing: University of Chinese Academy of Sciences, 2013)
(  0) 0) |
| [14] |
薛永安, 冀哲, 张文志. 基于残差修正GM(1, 1)模型的采空区残余变形预测研究[J]. 煤矿安全, 2023, 54(1): 101-108 (Xue Yongan, Ji Zhe, Zhang Wenzhi. Study on Residual Deformation Prediction of Goaf Based on Residual Modified GM(1, 1)Model[J]. Safety in Coal Mines, 2023, 54(1): 101-108)
(  0) 0) |
| [15] |
杨小虎, 朱庆伟, 沈宇恒, 等. 改进灰色时序模型在建筑物变形监测中的应用[J]. 西安科技大学学报, 2020, 40(5): 919-926 (Yang Xiaohu, Zhu Qingwei, Shen Yuheng, et al. Application of Improved Grey-Time Series Model in Monitoring Building Deformation[J]. Journal of Xi'an University of Science and Technology, 2020, 40(5): 919-926)
(  0) 0) |
| [16] |
胡圣武. 遗传算法的灰色神经网络在基坑变形中的应用[J]. 测绘科学, 2019, 44(3): 91-94 (Hu Shengwu. Study on Deformation of Foundation Pit Based on Grey Neural Network Model of Genetic Algorithm[J]. Science of Surveying and Mapping, 2019, 44(3): 91-94)
(  0) 0) |
| [17] |
张英豪, 刘晓青, 宁昕扬. 灰色-马尔科夫模型在南俄5水电站大坝变形预测中的应用研究[J]. 水利水电技术, 2018, 49(2): 139-143 (Zhang Yinghao, Liu Xiaoqing, Ning Xinyang. Application of Grey Markov Model to Deformation Prediction of Dam for Nam Ngum 5 Hydropower Station[J]. Water Resources and Hydropower Engineering, 2018, 49(2): 139-143)
(  0) 0) |
| [18] |
李昂, 王旭, 蒋代军. 基于Verhulst动态新陈代谢的邻近铁路基坑变形预测[J]. 铁道科学与工程学报, 2017, 14(4): 739-744 (Li Ang, Wang Xu, Jiang Daijun. Prediction of Foundation Pit Deformation near by the Railway Based on Verhulst Dynamic Metabolism[J]. Journal of Railway Science and Engineering, 2017, 14(4): 739-744)
(  0) 0) |
| [19] |
文鸿雁, 周吕, 韩亚坤, 等. 基于卡尔曼滤波的GM(1, 1)模型在高铁隧道沉降变形分析中的应用[J]. 大地测量与地球动力学, 2014, 34(1): 88-91 (Wen Hongyan, Zhou Lü, Han Yakun, et al. Application of GM(1, 1) Model Based on Kalman Filter to the Subsiding Analysis of High-Speed Railway Tunnel[J]. Journal of Geodesy and Geodynamics, 2014, 34(1): 88-91)
(  0) 0) |
| [20] |
刘思峰. 灰色系统理论的产生与发展[J]. 南京航空航天大学学报, 2004(2): 267-272 (Liu Sifeng. Emergence and Development of Grey System Theory and Its Forward Trends[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2004(2): 267-272)
(  0) 0) |
| [21] |
曹文贵, 印鹏, 贺敏, 等. 考虑实测数据新旧程度的工后沉降单项模型预测方法[J]. 水文地质工程地质, 2015, 42(6): 65-70 (Cao Wengui, Yin Peng, He Min, et al. A Prediction Method for Post-Construction Settlement of a Single Model with the Consideration of the New or Old Degree of the Measured Data[J]. Hydrogeology and Engineering Geology, 2015, 42(6): 65-70)
(  0) 0) |
| [22] |
王朝阳, 许强, 范宣梅, 等. 灰色新陈代谢GM(1, 1)模型在滑坡变形预测中的应用[J]. 水文地质工程地质, 2009(2): 108-111 (Wang Zhaoyang, Xu Qiang, Fan Xuanmei, et al. Application of Renewal Gray GM(1, 1) Model to Prediction of Landslide Deformation with Two Case Studies[J]. Hydrogeology and Engineering Geology, 2009(2): 108-111)
(  0) 0) |
| [23] |
唐利民, 朱建军. 软土路基沉降泊松模型的正则化牛顿迭代法[J]. 武汉大学学报: 信息科学版, 2013, 38(1): 69-73 (Tang Limin, Zhu Jianjun. Regularized Newton Iterative Algorithm for Poisson Model of Soft Clay Embankment Settlement[J]. Geomatics and Information Science of Wuhan University, 2013, 38(1): 69-73)
(  0) 0) |
| [24] |
肖霞林. 路基沉降变形评估与非等间隔灰色Verhulst模型[J]. 铁道建筑, 2011(4): 86-88 (Xiao Xialin. Evaluation of Subgrade Settlement Deformation and Unequal Interval Grey Verhulst Model[J]. Railway Engineering, 2011(4): 86-88)
(  0) 0) |
| [25] |
顾乐民. 对GM灰色模型及理论的质疑[J]. 计算机工程与应用, 2011, 47(30): 58-63 (Gu Lemin. To the GM Grey Model and Theory Question[J]. Computer Engineering and Applications, 2011, 47(30): 58-63)
(  0) 0) |
| [26] |
李小伟, 王琳, 王力, 等. 阶跃型滑坡的位移预测方法研究——以三峡库区树坪滑坡为例[J]. 三峡大学学报: 自然科学版, 2021, 43(1): 38-42 (Li Xiaowei, Wang Lin, Wang Li, et al. Research on Displacement Prediction Method of Step Type Landslide-Taking Shuping Landslide in Three Gorges Reservoir Area as an Example[J]. Journal of China Three Gorges University: Natural Sciences, 2021, 43(1): 38-42)
(  0) 0) |
| [27] |
王正新, 党耀国, 刘思峰. GM(1, 1)幂模型的病态性[J]. 系统工程理论与实践, 2013, 33(7): 1 859-1 866 (Wang Zhengxin, Dang Yaoguo, Liu Sifeng. The Morbidity of GM(1, 1) Power Model[J]. Systems Engineering-Theory and Practice, 2013, 33(7): 1 859-1 866)
(  0) 0) |
 2024, Vol. 44
2024, Vol. 44

