2. 河北省地质矿产勘查开发局国土资源勘查中心,石家庄市中山西路800号,050081
地球自转参数(Earth rotation parameters,ERP)包括极移运动(polar motion,PM)、UT1-UTC和日长变化(length of day,LOD),是实现天球坐标系与地球坐标系相互转换的必要参数,在GNSS和地球科学等领域有重要的应用价值[1-3]。许多实际应用需要实时获取ERP参数,但这十分困难。因此,有必要进行地球自转参数预报[4-5]。目前主流的研究方向是基于最小二乘法(least squares,LS)和自回归模型(autoregressive model,AR)组合预报地球自转参数[2-3]。一些学者引入流体激发函数、遗忘因子等对LS+AR模型进行改进,极大提高了极移、UT1-UTC预报的精度和可靠性[6-8]。Akyilmaz等[9-10]基于模糊推理系统构建一种易于实现且预报精度较高的地球自转参数预报模型,并将模糊推理系统与小波分析算法进行结合,在ERP短期预报方面具有优势。随着神经网络的发展,一些学者将其引入到地球自转参数预报,如王宇谱等[11]和王宗建[12]分别基于小波神经网络与反向传播(back propagation,BP)神经网络进行日长变化预报与极移预报。
通过分析上述研究发现,组合预报模型相比于单一预报模型有更好的泛用性与更高的预报精度,但不同的预报模型有各自的优缺点,它们的适用性和预报效果尚未得到很好的验证和分析。本文利用2019~2022年的ERP数据,以最小二乘法、小波去噪、小波神经网络和BP神经网络为基础,构建9种不同组合的地球自转参数预报模型,对极移和日长变化进行预报和分析。
1 数据源与研究方法本文使用的ERP数据来自国际地球自转服务(international Earth rotation and reference systems service,IERS)。
1.1 最小二乘法模型最小二乘法模型简单且精度较高,可以较好地拟合ERP参数时间序列的趋势项和周期项。在目前地球自转参数预报中,该模型常与其他预报模型进行组合,用于拟合趋势项与周期项,其他模型则预报剩余数据。具体模型如下:
| $ \begin{gathered} f(t)=a_0+a_1 t+ \\ \sum\limits_{i=1}^k\left(A_i \sin \left(\frac{2 \pi t}{R_i}\right)+B_i \cos \left(\frac{2 \pi t}{R_i}\right)\right)+\varepsilon_t \end{gathered} $ | (1) |
式中,a0和a1为趋势项的拟合系数,k为参与最小二乘拟合的主要周期数量,Ri为第i个周期项的周期值,Ai和Bi为模型拟合参数,εt为0均值的白噪声。
1.2 自回归模型自回归模型是一种常见的时间序列处理方法,其优点是所需数据不多,可用自身变数数列来进行预测,对于地球自转参数这种受自身历史数据影响较大的时间序列有较好的预报效果。自回归模型的预报效果与模型阶数p的选择有极大关系,本文采用最终预测误差准则(FPE)来确定模型阶数。自回归模型表达式可总结为:
| $ z_t=\sum\limits_{t=1}^p \varphi_i z_{t-i}+\varepsilon_t $ | (2) |
式中,p为AR模型的阶数,φi为模型参数,εt为t时刻的白噪声。该公式称为p阶自回归模型,记为AR(p)。
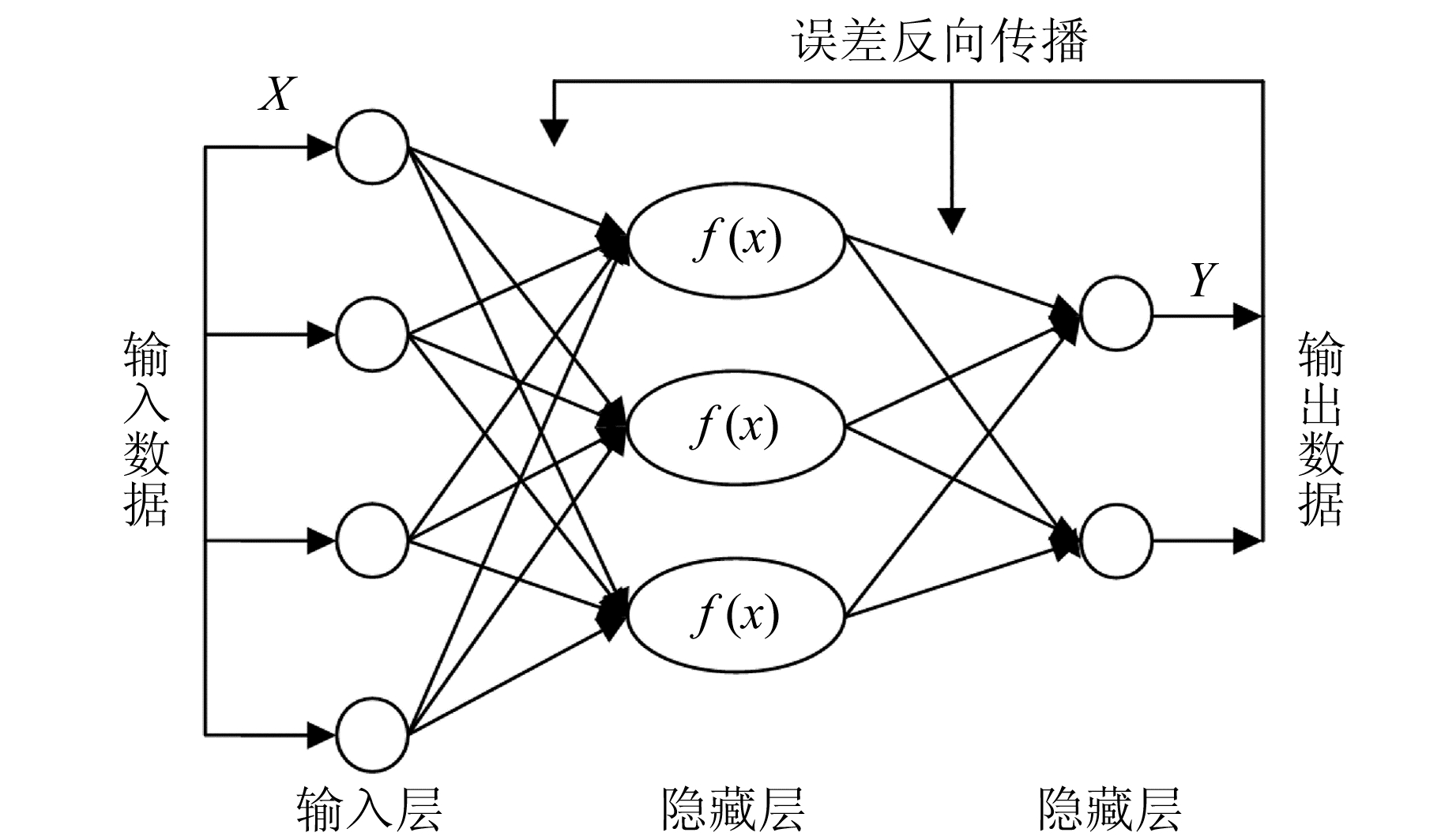
1.3 BP神经网络BP神经网络是一种依托误差反向传播进行训练的多层前馈网络,包含输入层、输出层和隐藏层。其基本思想是梯度下降法,数据作为输入向量输入后,在该层进行处理,并将处理后的输出值作为下一层的输入值,经过逐层处理得到最终的输出值,并计算输出值与期望值的差值,根据差值不断调整每个隐藏节点的权值。重复上述过程,直到差值达到要求(图 1)。BP神经网络具有很强的非线性映射能力和柔性的网络结构,同时具有强大的自学习、自适应能力,可以自动分析学习时间序列本身蕴含的周期项,对于时间序列预报具有较好的效果。
|
图 1 BP神经网络结构 Fig. 1 Structure of BP neural network |
确定BP神经网络的输入层节点数和隐藏层节点数对地球自转参数预报有重要影响。以极移X为例,对比分析不同输入层节点数和隐藏层节点数时BP神经网络的预报效果(表 1,单位mas)。
|
|
表 1 不同输入层节点数和隐藏层节点数时BP神经网络30 d极移X预报RMSE Tab. 1 RMSE of 30-day polar motion X prediction for BP neural network with different input layer node numbers and hidden layer node numbers |
根据表 1的预测结果可知,当输入层节点数为60、隐藏层节点数为12时,RMSE最小,BP神经网络对极移X的预报效果最好。以同样的方式可得输入层节点数为60、隐藏层个数为1、隐藏层节点数为12时,BP神经网络进行极移Y和LOD预报的效果最佳。
1.4 小波去噪本文采用基于小波包变换的小波分解重构去噪,其可以同时对低频和高频信号进行有效分解。由于仪器本身固有的精度问题,基于现代空间大地测量手段获取的地球自转参数往往会含有一定的噪声,小波分解重构去噪可以通过去除序列中高频项的方式去除这部分噪声,同时也会删去部分地球自转参数序列中固有的高频项,使地球自转参数序列更加平滑。
1.5 小波神经网络小波神经网络(wavelet neural network,WNN)是小波变换和人工神经网络的结合。以BP神经网络为基础,以小波基函数代替BP神经网络相邻两层之间的传递函数,即可得到小波神经网络。小波神经网络具有自学习能力和非线性映射能力较强等特点,同时具有小波变换对信号时频分析和处理的能力,对时间序列有很好的预测效果,其拟合函数为:
| $ \hat{S}(x)=\sum\limits_{n=1}^n w_n f\left(\frac{x_i-b_n}{a_n}\right) $ | (3) |
式中,
由于小波神经网络与BP神经网络有类似的结构,故对小波神经网络各项参数的选择也与BP神经网络类似。以极移X为例,对比分析不同输入层节点数和隐藏层节点数时小波神经网络的预报效果(表 2,单位mas)。
|
|
表 2 不同输入层节点数和隐藏层节点数时小波神经网络30 d极移X预报RMSE统计 Tab. 2 RMSE statistics of 30-day polar motion X prediction for wavelet neural network with different input layer node numbers and hidden layer node numbers |
根据表 2的预测结果可知,当输入层节点数为70、隐藏层节点数为10时,RMSE最小,小波神经网络对极移X的预报效果最好。以同样方式确定当输入层节点数为60、隐藏层个数为1和隐藏层节点数为10时,小波神经网络对极移Y的预报效果最佳。但LOD预报与极移预报最佳参数略有不同,当隐藏层节点数为12时,小波神经网络对LOD的预报效果最好。
1.6 ERP预报方案设计本文利用最小二乘法(LS)、小波去噪、线性自回归(AR)、BP神经网络和小波神经网络(WNN)构建9种ERP预报方案,使用2019~2022年极移和日长变化序列进行学习训练,然后对极移X(PMX)、极移Y(PMY)和日长变化值(LOD)进行30 d短期预报。由于BP神经网络和WNN本身的随机性,取独立10次预报结果的平均值作为最终预报结果。构建LS+BP和LS+WNN地球自转参数预报模型时,首先基于LS模型拟合ERP周期项和趋势项,然后使用BP神经网络模型和WNN对ERP残差项进行预报。顾及到极移和日长变化序列本身的特点,对使用小波分解重构去噪适当消去高频项是否有助于提高精度进行探讨。
9种方案具体为:方案1,基于LS+AR模型的ERP预报;方案2,基于BP神经网络模型的ERP预报;方案3,基于WNN模型的ERP预报;方案4,基于LS+BP模型的ERP预报;方案5,基于LS+WNN模型的ERP预报;方案6,利用小波去噪后,基于BP神经网络模型的ERP预报;方案7,利用小波去噪后,基于WNN的ERP预报;方案8,利用小波去噪后,基于LS+BP模型的ERP预报;方案9,利用小波去噪后,基于LS+WNN模型的ERP预报。
2 结果 2.1 小波去噪前ERP预报精度对比小波去噪前不同组合方案ERP预报精度统计结果见图 2和表 3。

|
图 2 小波去噪前各方案ERP预报精度 Fig. 2 ERP prediction accuracy of each scheme before wavelet denoising |
|
|
表 3 各ERP预报方案的RMSE Tab. 3 RMSE of each ERP prediction scheme |
由图 2可知,对于极移X坐标,0~5 d预报范围内,方案1、3、5的预测效果较好,与真值有很好的一致性;对于极移Y坐标,0~5 d预报范围内,方案1、3、4、5的预测效果较好。0~30 d内预报范围内,方案5的预报结果与真值最为接近,方案2的预报结果与真值有较大的差异;方案1、3曲线高度相似,可见直接使用WNN和常规LS+AR的预报效果相近;方案2的预报结果与真值的偏差最大,表明BP神经网络预测效果最差。
对于日长变化,0~30 d内预报范围内,方案2、3的曲线具有较高的相似度,且偏差变化平稳,与真值一致性高,而方案4、5的预报结果与真值差异较大,表明直接使用WNN和BP神经网络的预报效果较好,使用高频残差项预报的效果较差;方案5的预测效果最差,方案1、4的预测效果较差,方案2的预测效果较好,方案3预报效果最好。不难发现,最小二乘法消去主要周期项后,人工神经网络对高频数据的学习效果得到提升,使极移预报的预报精度提高,日长变化的预报精度下降,说明增加高频数据的学习不利于对日长变化的预报,这与韩恒星等[3]的结论一致。
2.2 小波去噪后ERP预报精度对比小波去噪后不同组合方案ERP预报精度统计结果见图 3和表 3。
|
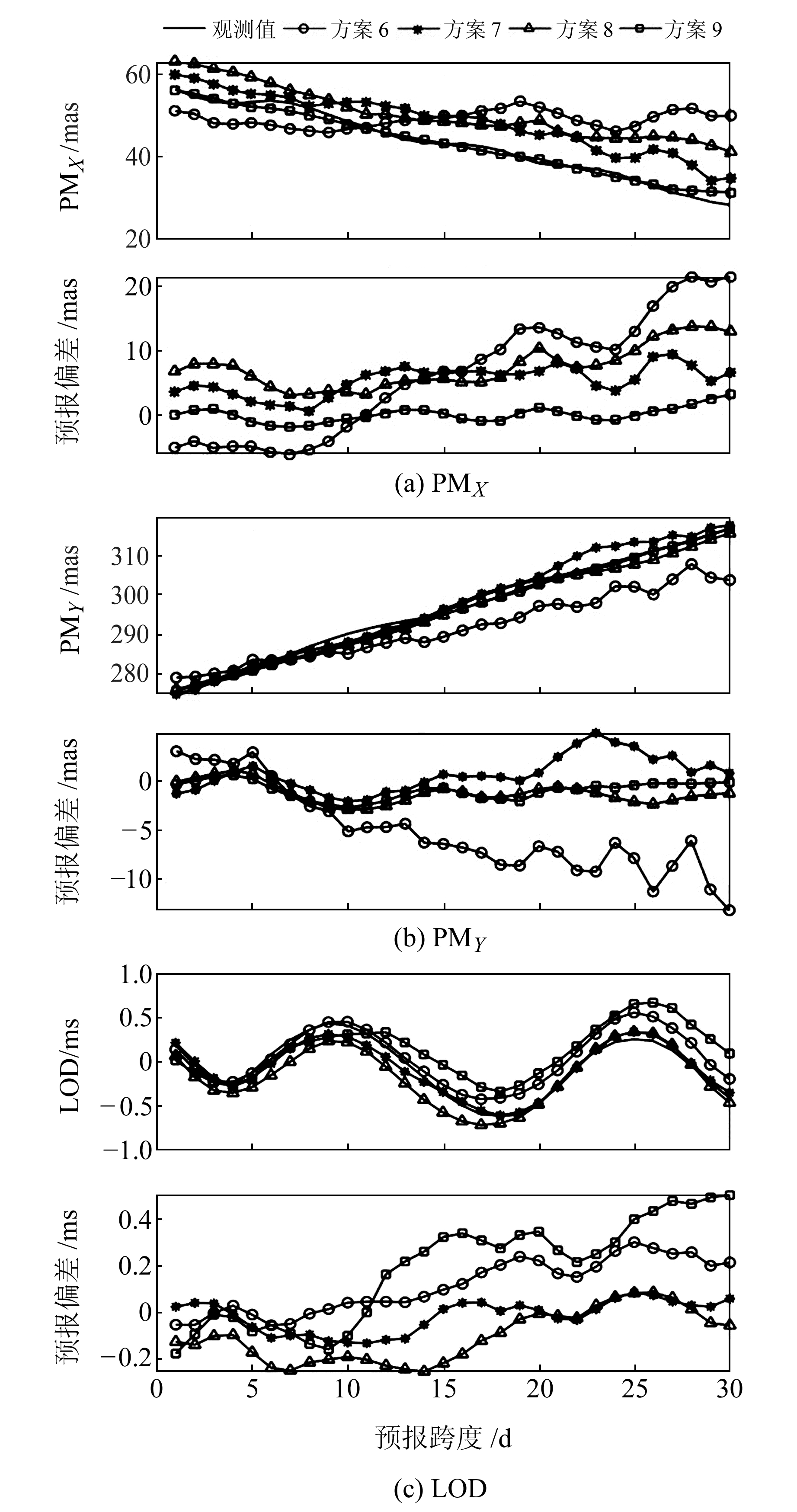
图 3 小波去噪后各方案ERP预报精度 Fig. 3 ERP prediction accuracy of each scheme after wavelet denoising |
由图 3可知,对于极移坐标,在0~5 d预报范围内,除方案6外,其他方案与真值一致性较好。在0~30 d预报范围内,方案9的预报结果与真值最接近,方案6的预报结果与真值差异较大,方案7、8曲线相似,可见LS+BP神经网络预报与WNN预报效果近似。
对于日长变化,在0~30 d预报范围内,预测效果从优到差依次为方案7、方案6、方案8、方案9。不难发现,小波去噪前后各方案之间的关系变化不大,小波去噪对ERP预报效果的影响明显小于预报模型不同带来的影响。
由表 3可见,对于极移X坐标和极移Y坐标,方案5、9的RMSE小于1.4 mas,表明LS+WNN模型对极移残差预报的效果较好;其他方案的RMSE都大于1.6 mas。小波去噪后的方案相比于小波去噪前的方案,预报结果具有一致性,精度有少量提升,但提升效果不明显。总体而言,方案9的精度最高,表明小波去噪后使用LS+WNN对极移残差项的预报效果最好。
对于日长变化预报,方案3、7的RMSE较小,小于0.12 ms,表明WNN的日长变化预报效果较好,其他方案的RMSE均大于0.13 ms。方案5、9的日长变化残差预报的效果较差,其RMSE大于0.18 ms,说明对残差项进行预测不适用于日长变化预报。小波去噪后的方案相比于小波去噪前的方案,预报结果具有一致性,精度有明显提高。总体上,方案7的精度最高,表明小波去噪后直接使用WNN进行日长变化预报的效果最好。
3 结语本文利用LS、线性自回归、BP神经网络和WNN构建了9种地球自转参数预报模型,使用2019~2022年极移和日长变化序列进行学习训练,然后对极移X、极移Y和日长变化值进行30 d短期预报,主要得到以下结论:
1) 对于极移X、Y坐标而言,LS+WNN模型的预报效果较好,其RMSE小于1.4 mas;BP神经网络模型的RMSE最大,尤其在进行极移X坐标预报时,其RMSE大于26 mas。小波去噪后,预报精度有少量提高。
2) 对于日长变化预报,WNN模型的RMSE小于0.12 ms,表明其日长变化预报效果较好;其他4种预报方案的的RMSE都大于0.13 ms,尤其是LS+WNN模型的RMSE大于0.28 ms,表明LS+WNN模型在预测日长变化方面效果较差。小波去噪后,预报精度有明显提高,WNN预报模型的RMSE为0.07 ms,预报效果最好。
| [1] |
孙张振. 高精度地球自转参数预报模型与算法研究[D]. 济南: 山东大学, 2020 (Sun Zhangzhen. Research on High-Precision Prediction Model and Algorithm of Earth Rotation Parameters[D]. Ji'nan: Shandong University, 2020)
(  0) 0) |
| [2] |
雷雨. 地球自转参数高精度预报方法研究[D]. 北京: 中国科学院大学, 2016 (Lei Yu. Research on High-Precision Prediction Method of Earth Rotation Parameters[D]. Beijing: University of Chinese Academy of Sciences, 2016)
(  0) 0) |
| [3] |
韩恒星, 党亚民, 许长辉, 等. 地球自转参数的LS+AR超短期预报方法[J]. 测绘通报, 2017(7): 1-4 (Han Hengxing, Dang Yamin, Xu Changhui, et al. Ultra Short-Term Forecasting of Earth Rotation Parameters Based on LS+AR[J]. Bulletin of Surveying and Mapping, 2017(7): 1-4)
(  0) 0) |
| [4] |
李军, 赵德军, 陈永祥. 利用LS+AR模型和激发函数预报地球自转参数[J]. 大地测量与地球动力学, 2015, 35(3): 457-459 (Li Jun, Zhao Dejun, Chen Yongxiang. Prediction of Earth Rotation Parameters Using LS+AR Model and Excited Functions[J]. Journal of Geodesy and Geodynamics, 2015, 35(3): 457-459)
(  0) 0) |
| [5] |
严凤, 姚宜斌. 地球自转参数短期预报方法及其实现[J]. 大地测量与地球动力学, 2012, 32(4): 71-75 (Yan Feng, Yao Yibin. Short-Term Prediction Methods and Realization of Earth Rotation Parameters[J]. Journal of Geodesy and Geodynamics, 2012, 32(4): 71-75)
(  0) 0) |
| [6] |
吴飞. 几种改进的地球自转参数预报方法[D]. 徐州: 中国矿业大学, 2019 (Wu Fei. Several Improved Prediction Methods of Earth Rotation Parameters[D]. Xuzhou: China University of Mining and Technology, 2019)
(  0) 0) |
| [7] |
韩恒星, 党亚民, 许长辉. 地球自转参数的RFFLS短期预报算法研究[J]. 测绘通报, 2017(9): 15-18 (Han Hengxing, Dang Yamin, Xu Changhui. Short-Term Forecasting of Earth Rotation Parameter Based on Forgetting Factor Recursive Least Squares[J]. Bulletin of Surveying and Mapping, 2017(9): 15-18)
(  0) 0) |
| [8] |
加松. 地球自转参数高精度预报理论与算法研究[D]. 西安: 长安大学, 2017 (Jia Song. Research on Theory and Algorithm of High Precision Prediction of Earth Rotation Parameters[D]. Xi'an: Chang'an University, 2017)
(  0) 0) |
| [9] |
Akyilmaz O, Kutterer H. Prediction of Earth Rotation Parameters by Fuzzy Inference Systems[J]. Journal of Geodesy, 2004, 78(1-2): 82-93
(  0) 0) |
| [10] |
Akyilmaz O, Kutterer H, Shum C K, et al. Fuzzy-Wavelet Based Prediction of Earth Rotation Parameters[J]. Applied Soft Computing, 2011, 11(1): 837-841 DOI:10.1016/j.asoc.2010.01.003
(  0) 0) |
| [11] |
王宇谱, 吕志平. 小波神经网络日长预报算法研究[J]. 大地测量与地球动力学, 2012, 32(1): 127-131 (Wang Yupu, Lü Zhiping. Research on Algorith of Wavelet Neural Network for Forecasting Length of Day[J]. Journal of Geodesy and Geodynamics, 2012, 32(1): 127-131)
(  0) 0) |
| [12] |
王宗建. 基于BP神经网络的地球自转参数短期预测[D]. 西安: 长安大学, 2015 (Wang Zongjian. Short-Term Prediction of Earth Rotation Parameters Based on BP Neural Network[D]. Xi'an: Chang'an University, 2015)
(  0) 0) |
2. Land and Resources Exploration Center of Hebei Bureau of Geology and Mineral Resources Exploration, 800 West-Zhongshan Road, Shijiazhuang 050081, China
 2024, Vol. 44
2024, Vol. 44


