2. 中国科学院大学,北京市玉泉路19号甲,100049;
3. 探索数据科技(深圳)有限公司,深圳市留仙洞路33号,518055
提高导航卫星精密定轨解算效率是GNSS卫星精密定轨技术的研究重点之一[1-2]。Ge等[3]采用消参方法,在每个历元时刻消去法方程中的过时参数,极大地减少了最终法方程解算参数的个数,从而有效提高了导航卫星精密定轨解算的效率,该方法是从算法层面对解算效率进行优化。随着CPU的迭代发展,部分学者开展基于CPU技术提高计算效率的研究,包括基于CPU的多核、多线程并行运算技术[4-5]和基于CPU分层存储架构的方法[6]。
目前,关于提高GNSS数据处理软件计算效率的研究几乎都是基于X86架构的Intel CPU,涉及国产ARM架构CPU[7]上效率提升的实验和研究很少。在科学计算中,线性代数库是运行效率优化的重要工具,Lapack能以高效的方式实现科学计算的接口规范[8],并且适用于X86、ARM和PowerPC等不同架构平台。Intel CPU发展至今已经很成熟,Intel可实现适应其CPU的高效运算库Intel Math Kernel Library(MKL)。表 1为导航卫星精密定轨处理软件分别运行于Intel CPU中性能突出的X86架构Intel(R) Xeon(R) Gold 6134 CPU(表中Intel)和国产CPU中性能突出的飞腾ARM FT-2000+CPU(表中ARM)的运行耗时,软件运行时采用相同的数据和场景。可以看出,采用Lapack时,Intel CPU的解算效率是ARM CPU的3倍多;采用MKL后,Intel CPU的解算效率是ARM CPU的5倍多。由此可知,ARM CPU还需要寻求更合适的优化方法以提升导航卫星精密定轨的解算效率。
|
|
表 1 Intel CPU和ARM CPU单次迭代平均耗时 Tab. 1 Average time consuming on Intel CPU and ARM CPU |
本文选取国产飞腾CPU的最新型号FT-2000+进行卫星精密定轨解算效率优化研究。
1 GNSS卫星精密定轨解算 1.1 解算原理设历元i的第j条观测是接收机r与卫星s的伪距相位观测,添加动力学约束的观测方程为:
| $ \begin{gathered} P_j\left(t_i\right)=f\left(\vec{X}_{\mathrm{s}}, \vec{X}_{\mathrm{r}}, \overrightarrow{\mathrm{ERP}}\right)+\mathrm{ZTD}_{\mathrm{r}} \cdot \operatorname{map}+ \\ \mathrm{AMB}_{\mathrm{r}}^{\mathrm{s}}+\mathrm{clk}_{\mathrm{r}}\left(t_i\right)+\mathrm{clk}_{\mathrm{s}}\left(t_i\right)+\varepsilon \end{gathered} $ | (1) |
式中,Pj(ti)为相位值的双频无电离层组合(伪距与之相同,不同的是右方程无模糊度参数);
将式(1)在近似值处线性化得到:
| $\begin{aligned} P_j\left(t_i\right)= & f\left(\Delta \vec{X}_{\mathrm{s}}, \Delta \vec{X}_{\mathrm{r}}, \Delta \overrightarrow{\mathrm{ERP}}\right)+\mathrm{ZTD}_{\mathrm{r}} \cdot \mathrm{map}+ \\ & \mathrm{AMB}_{\mathrm{r}}^{\mathrm{s}}+\operatorname{clk}_{\mathrm{r}}\left(t_i\right)+\operatorname{clk}_{\mathrm{s}}\left(t_i\right)+ \\ & f\left(\vec{X}_{0 \mathrm{~s}}, \vec{X}_{0 \mathrm{r}}, \overrightarrow{\mathrm{ERP}}_0\right)+\varepsilon\end{aligned}$ | (2) |
式中,
|
|
表 2 GNSS精密定轨中待估参数的时效性 Tab. 2 Validity period of estimated parameters in GNSS precise orbit determination |
由表 2可以看出,卫星钟差参数和接收机钟差参数个数总量远大于其他待估参数个数。然而钟差参数的有效期仅为一个历元,属于局部参数,因此将其约化处理进行定轨解算。式(2)的向量形式可表示为:
| $\begin{array}{c} P_j\left(t_i\right)= \\ {\left[\begin{array}{lllll}\frac{\partial f}{\partial \Delta \vec{X}_{\mathrm{s}}} & \frac{\partial f}{\partial \Delta \vec{X}_{\mathrm{r}}} & \frac{\partial f}{\partial \Delta \overrightarrow{\mathrm{ERP}}} & \text { map } & 1\end{array}\right]\left[\begin{array}{c}\Delta \vec{X}_{\mathrm{s}} \\ \Delta \vec{X}_{\mathrm{r}} \\ \Delta \overrightarrow{\mathrm{ERP}} \\ \mathrm{ZTD}_{\mathrm{r}} \\ \mathrm{AMB}_{\mathrm{r}}^{\mathrm{s}}\end{array}\right]+} \\ {\left[\begin{array}{ll}-1 & 1\end{array}\right]\left[\begin{array}{l}\mathrm{clk}_{\mathrm{s}}\left(t_i\right) \\ \operatorname{clk}_{\mathrm{r}}\left(t_i\right)\end{array}\right]+f\left(\vec{X}_{0 \mathrm{~s}}, \vec{X}_{0 \mathrm{r}}, \overrightarrow{\mathrm{ERP}}_0\right)+\varepsilon} \end{array}$ | (3) |
更一般地,历元i第j条观测的观测向量方程可表示为:
| $ \left\{ \begin{array}{l} {Y_{i, j}} = {\mathit{\boldsymbol{B}}_{i, j}}\mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{B}}_{Gi, j}}}&{{\mathit{\boldsymbol{B}}_{Ri, j}}} \end{array}} \right]\left[ {{{\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{X}}_G}}&{\mathit{\boldsymbol{X}}_R^i} \end{array}}^{\rm{T}}}} \right.\\ {{\bf{B}}_{Gi, j}} = \left[ {\frac{{\partial f}}{{\partial \Delta {{\vec X}_{\rm{s}}}}}\;\;\; \cdots \;\;\;\frac{{\partial f}}{{\partial \Delta {{\vec X}_{\rm{r}}}}}\;\;\; \cdots } \right.\\ \left. {\;\;\;\;\;\frac{{\partial f}}{{\partial \Delta \overrightarrow {{\rm{ERP}}} }}\;\;\;{\mathop{\rm map}\nolimits} \;\;\;1\;\;\; \cdots } \right]\\ {\mathit{\boldsymbol{B}}_{Ri, j}} = \left[ {\begin{array}{*{20}{l}} \cdots &{ - 1}&1& \cdots \end{array}} \right]\\ {\mathit{\boldsymbol{X}}_G} = \left[ {\begin{array}{*{20}{l}} {\Delta {{\vec X}_{\rm{s}}}}& \cdots &{\Delta {{\vec X}_{\rm{r}}}}& \cdots &{\Delta \overrightarrow {{\rm{ERP}}} } \end{array}} \right.\\ \;\;\;{\left. {\begin{array}{*{20}{l}} {{\rm{ZT}}{{\rm{D}}_{\rm{r}}}}&{{\rm{AMB}}_{\rm{r}}^{\rm{s}}}& \cdots \end{array}} \right]^{\rm{T}}}\\ \mathit{\boldsymbol{X}}_R^i = {\left[ {\begin{array}{*{20}{l}} \cdots &{{{{\mathop{\rm clk}\nolimits} }_{\rm{s}}}\left( {{t_i}} \right)}&{{\rm{cl}}{{\rm{k}}_{\rm{r}}}\left( {{t_i}} \right)}& \cdots \end{array}} \right]^{\rm{T}}}\\ {Y_{i, j}} = {P_j}\left( {{t_i}} \right) - f\left( {{{\vec X}_{0{\rm{s}}}}, {{\vec X}_{0{\rm{r}}}}, {{\overrightarrow {{\rm{ERP}}} }_0}} \right) \end{array} \right. $ | (4) |
式中,系数矩阵Bi, j=[BGi, j BRi, j]为历元i第j条观测的系数矩阵,其中BGi, j为该观测的全局变量系数矩阵,BRi, j为该观测的局部变量系数矩阵;待估参数向量X=[XG XRi]T,其中XG为所有待估全局待变量,XRi为仅在i历元时刻有效的待估参数;Yi, j为观测常值。
基于式(4)、最小二乘原理及矩阵运算原理可知,历元i法方程NbbiX=Wi中,矩阵Nbbi和Wi可分别对历元i各观测法方程系数矩阵Nbbij和右矩阵Wij叠加计算获得:
| $ \begin{gathered} \boldsymbol{N}_{b b}^i=\sum\limits_{j=1}^m \boldsymbol{N}_{b b}^{i j}=\sum\limits_{j=1}^m\left(\boldsymbol{B}_{i, j}^{\mathrm{T}} \boldsymbol{B}_{i, j}\right)= \\ \sum\limits_{j=1}^m\left[\begin{array}{ll} \boldsymbol{B}_{G i, j}^{\mathrm{T}} \boldsymbol{B}_{G i, j} & \boldsymbol{B}_{G i, j}^{\mathrm{T}} \boldsymbol{B}_{R i, j} \\ \boldsymbol{B}_{R i, j}^{\mathrm{T}} \boldsymbol{B}_{G i, j} & \boldsymbol{B}_{R i, j}^{\mathrm{T}} \boldsymbol{B}_{R i, j} \end{array}\right]=\\ {\left[\begin{array}{cc} \sum\limits_{j=1}^m\left(\boldsymbol{B}_{G i, j}^{\mathrm{T}} \boldsymbol{B}_{G i, j}\right) & \sum\limits_{j=1}^m\left(\boldsymbol{B}_{G i, j}^{\mathrm{T}} \boldsymbol{B}_{R i, j}\right) \\ \sum\limits_{j=1}^m\left(\boldsymbol{B}_{R i, j}^{\mathrm{T}} \boldsymbol{B}_{G i, j}\right) & \sum\limits_{j=1}^m\left(\boldsymbol{B}_{R i, j}^{\mathrm{T}} \boldsymbol{B}_{R i, j}\right) \end{array}\right]=} \\ {\left[\begin{array}{ll} \boldsymbol{N}_{b b G G i} & \boldsymbol{N}_{b b G R i} \\ \boldsymbol{N}_{b b R G i} & \boldsymbol{N}_{b b R R i} \end{array}\right]} \end{gathered} $ | (5) |
| $ \begin{gathered} \boldsymbol{W}^i=\sum\limits_{j=1}^m \boldsymbol{W}^{i j}=\sum\limits_{j=1}^m\left(\boldsymbol{B}_{i, j}^{\mathrm{T}} Y_{i, j}\right)= \\ \sum\limits_{j=1}^m\left[\begin{array}{l} \boldsymbol{B}_{G i, j}^{\mathrm{T}} Y_{i, j} \\ \boldsymbol{B}_{R i, j}^{\mathrm{T}} Y_{i, j} \end{array}\right]=\left[\begin{array}{l} \sum\limits_{j=1}^m \boldsymbol{B}_{G i, j}^{\mathrm{T}} Y_{i, j} \\ \sum\limits_{j=1}^m \boldsymbol{B}_{R i, j}^{\mathrm{T}} Y_{i, j} \end{array}\right]=\left[\begin{array}{l} \boldsymbol{W}_G^i \\ \boldsymbol{W}_R^i \end{array}\right] \end{gathered} $ | (6) |
式中,m为历元i中的观测数量。根据式(5)和(6),历元i的法方程可写为:
| $ \left[\begin{array}{ll} \boldsymbol{N}_{b b G G i} & \boldsymbol{N}_{b b G R i} \\ \boldsymbol{N}_{b b R G i} & \boldsymbol{N}_{b b R R i} \end{array}\right]\left[\begin{array}{l} \boldsymbol{X}_G \\ \boldsymbol{X}_R^i \end{array}\right]=\left[\begin{array}{l} \boldsymbol{W}_G^i \\ \boldsymbol{W}_R^i \end{array}\right] $ | (7) |
根据式(7)可得:
| $ \boldsymbol{X}_R^i=\left(\boldsymbol{N}_{b b R R i}\right)^{-1}\left(\boldsymbol{W}_R^i-\boldsymbol{N}_{b b R G i} \boldsymbol{X}_G\right) $ | (8) |
将式(8)代入式(7),可获得消去局部钟差参数后的历元i的法方程:
| $ \left\{\begin{array}{l} \boldsymbol{N}_{b b G G i^{\prime}} \boldsymbol{X}_G=\boldsymbol{W}_{G^{\prime}}^i \\ \boldsymbol{N}_{b b G G i^{\prime}}=\left(\boldsymbol{N}_{b b G G i}-\boldsymbol{N}_{b b G R i}\left(\boldsymbol{N}_{b b R R i}\right)^{-1} \boldsymbol{N}_{b b R G i}\right) \\ \boldsymbol{W}_{G^{\prime}}^i=\boldsymbol{W}_G^i-\boldsymbol{N}_{b b G R i}\left(\boldsymbol{N}_{b b R R i}\right)^{-1} \boldsymbol{W}_R^i \end{array}\right. $ | (9) |
根据式(9)对各历元法方程进行叠加,可建立所有历元观测数据统一的法方程:
| $ \left.\sum\limits_{i=1}^n \boldsymbol{N}_{b b G G i^{\prime}}\right) \boldsymbol{X}_G=\sum\limits_{i=1}^n \boldsymbol{W}_{G^{\prime}}^i $ | (10) |
式中,n为历元个数。对上式求逆解算可得:
| $ \left.\boldsymbol{X}_G=\sum\limits_{i=1}^n \boldsymbol{N}_{b b G G i^{\prime}}\right)^{-1} \quad \sum\limits_{i=1}^n \boldsymbol{W}_{G^{\prime}}^i $ | (11) |
式中,XG为最小二乘全局参数最优解。将XG代入式(8)可得到各历元时刻的局部参数解。
1.2 解算耗时分析通过软件进行导航卫星精密定轨解算是基于式(5)~(11)分步实现的,其实质是对矩阵NbbGGi、NbbRRi、NbbGRi、NbbRGi、(NbbRRi)-1、NbbGRi(NbbRRi)-1NbbRGi和
|
|
表 3 导航卫星精密定轨解算各环节复杂度分析 Tab. 3 Analysis of the complexity of each calculation processes in GNSS precise orbit determination |
为充分发挥ARM架构CPU的计算效能,采用基于CPU的多核、多线程并行运算技术和基于CPU的分层存储架构对上述2个计算耗时最长的矩阵进行优化。采用多线程方法对钟差参数约化解算部分进行优化,采用OpenBlas对统一方法求逆部分进行优化。OpenBlas是同时采用上述2种方法实现矩阵运算效率提升的开源高性能科学计算库。
2.1 基于多线程的消参并行解算优化通过式(5)可以获得NbbGRi、NbbGRi和NbbRRi,然后计算NbbGRi(NbbRRi)-1NbbRGi,最后完成式(9)的计算。由此可知,钟差参数约化解算部分NbbGRi(NbbRRi)-1NbbRGi在解算过程中是完全独立的,可以单独对其进行优化。优化过程为:首先优化矩阵运算NbbGRi(NbbRRi)-1,然后优化矩阵运算NbbGRi(NbbRRi)-1NbbRGi,这2步的优化方法一致。矩阵乘法运算可表示为CI×J=AI×PBP×J。软件中代码实现是对浮点数的一个3层循环运算,见图 1,图中aip、bpj、cij分别为矩阵A、B、C的元素,是一个串行执行过程。
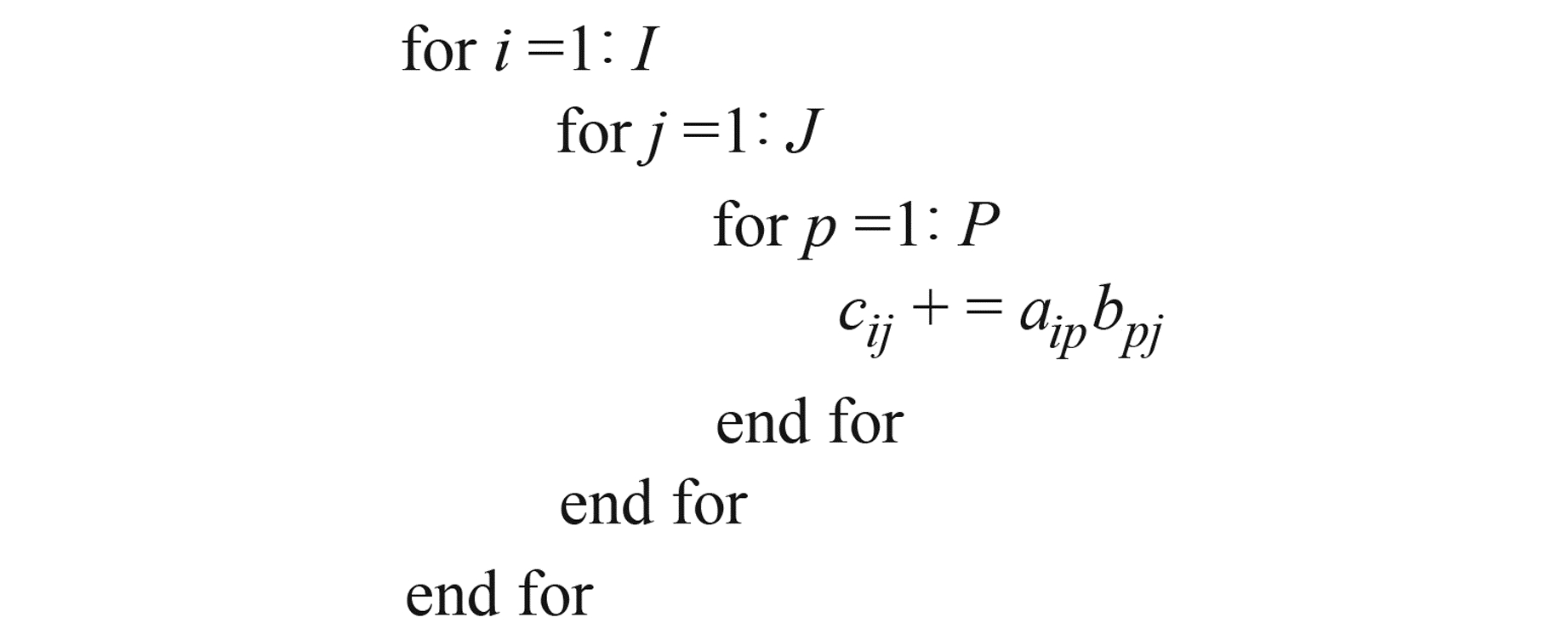
|
图 1 矩阵乘法的3层循环实现 Fig. 1 Implementation of matrix multiplication with three layer loops |
根据矩阵乘法特点,可对图 1中最外2层循环(即矩阵A的行和矩阵B的列)进行拆分,分解为多个独立的运算任务,进而采用多线程并行优化。假如采用n(n≤I)个线程进行并行运算,对每个线程分配最外层循环个数可表示为:
通过式(9)和(10)分别获得矩阵
Lapack相比基础线性代数程序从算法层面进行了许多优化,OpenBlas继承了这些优点,并进一步采用前文基于CPU技术特点的2个优化方法对矩阵运算进行优化。基于CPU分层存储架构优化计算效率的具体思路见文献[9]。
在多线程并行优化方面,OpenBlas采用仅将矩阵B作列拆分的方式进行多线程优化[10]。在此基础上,考虑每个线程独有的缓存资源以及共享缓存资源,根据线程数调整内核GEBP[9]的大小,使内核GEBP适合缓存大小,以减少缓存不命中的情况,详细过程见文献[10]。
3 实验分析CPU具体架构信息见表 4,GNSS卫星精密定轨软件的具体解算策略见表 5。采用32颗卫星和不同数目的测站检验精密定轨解算优化情况,每次定轨解算执行8次迭代,每次迭代均重复执行消参和法方程求逆解算。
|
|
表 4 国产飞腾CPU和Intel CPU架构信息 Tab. 4 Architecture information of domestic Feiteng CPU and Intel CPU |
|
|
表 5 GNSS卫星精密定轨软件解算策略 Tab. 5 Solution strategy for GNSS precise orbit determination software |
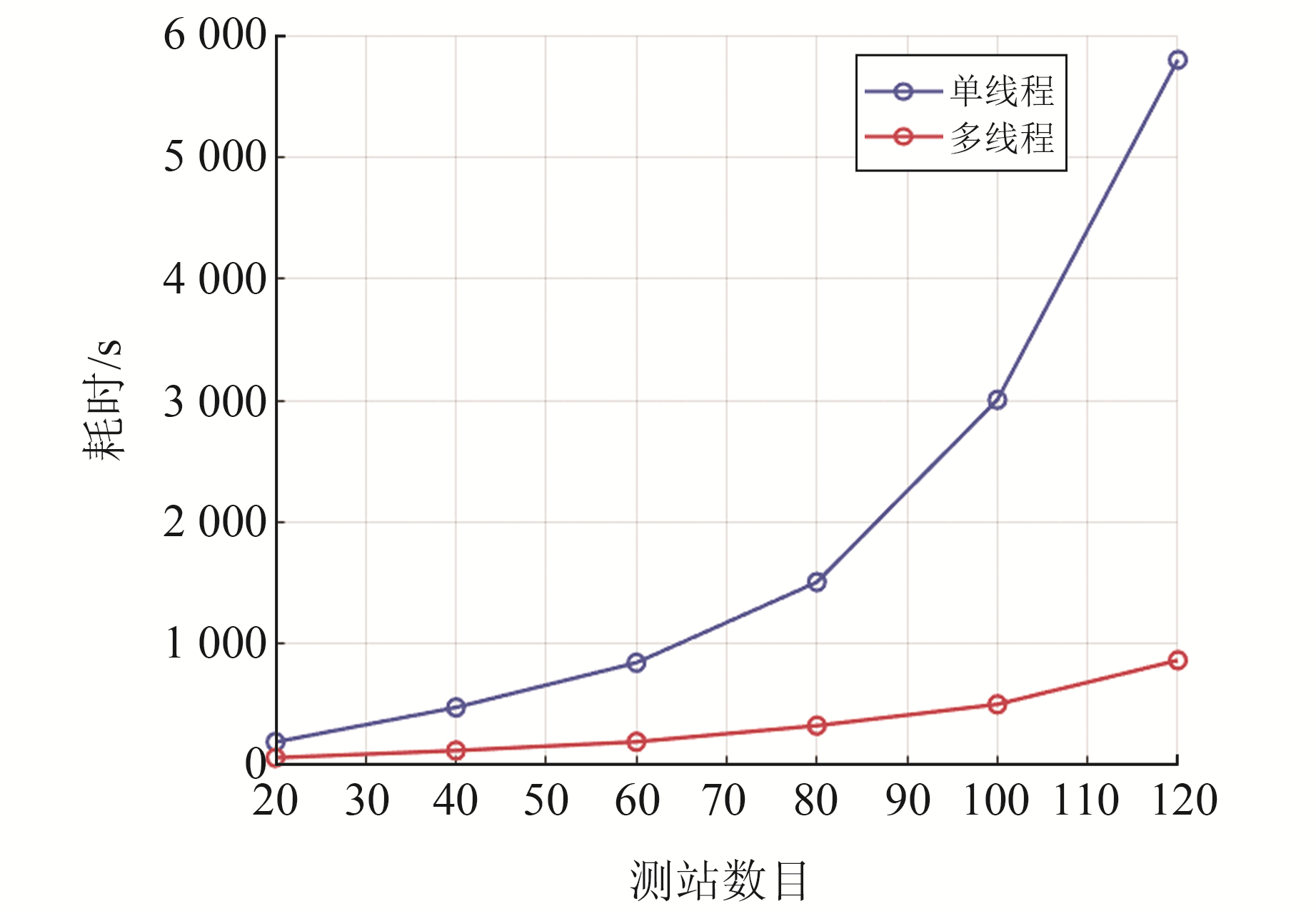
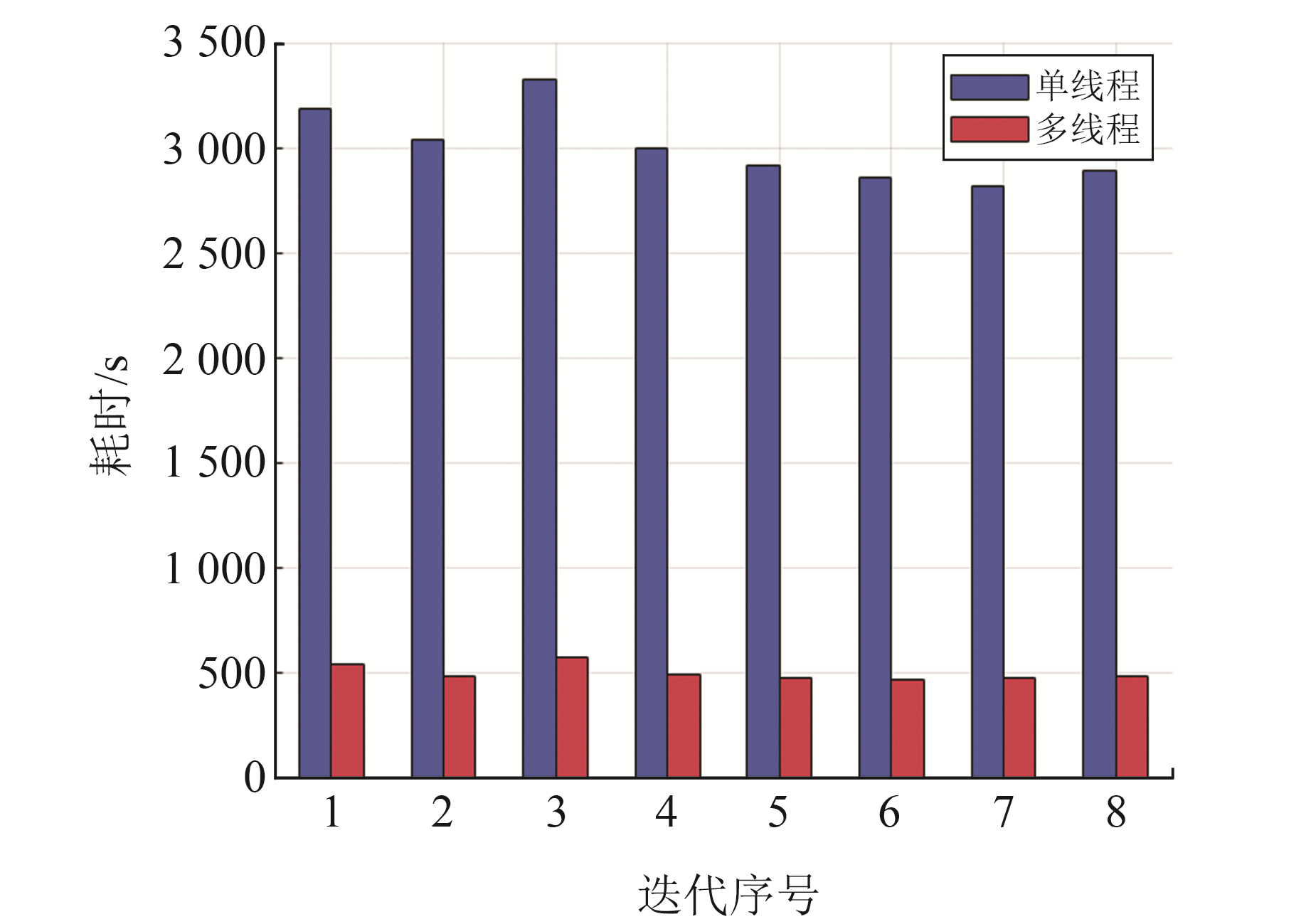
在飞腾CPU上进行解算时,采用16个线程的多线程方法对消参部分进行优化,优化前后解算效率对比见图 2。可以看出,相比于原始单线程,采用多线程后消参解算效率大幅提升。随着测站数量的增加,采用单线程消参解算耗时急剧上升,而多线程解算耗时平缓上升,且多线程解算效率提升效果更明显。在100个测站的情况下,统计第1次迭代中各历元单线程和多线程消参解算耗时。单线程解算1个历元平均耗时1.105 s,而多线程仅为0.188 s。100个测站情况下所有8次迭代消参耗时情况见图 3。由图可知,与第1次迭代耗时情况一致,多线程解算效率约为单线程解算效率的6倍。
|
图 2 消参部分采用单线程和多线程解算耗时对比 Fig. 2 Comparison of time consuming between single-threaded and multi-threaded for parameter elimination |
|
图 3 100个测站解算8次迭代消参耗时 Fig. 3 Time consuming for parameter elimination in 8 iterations with 100 stations |
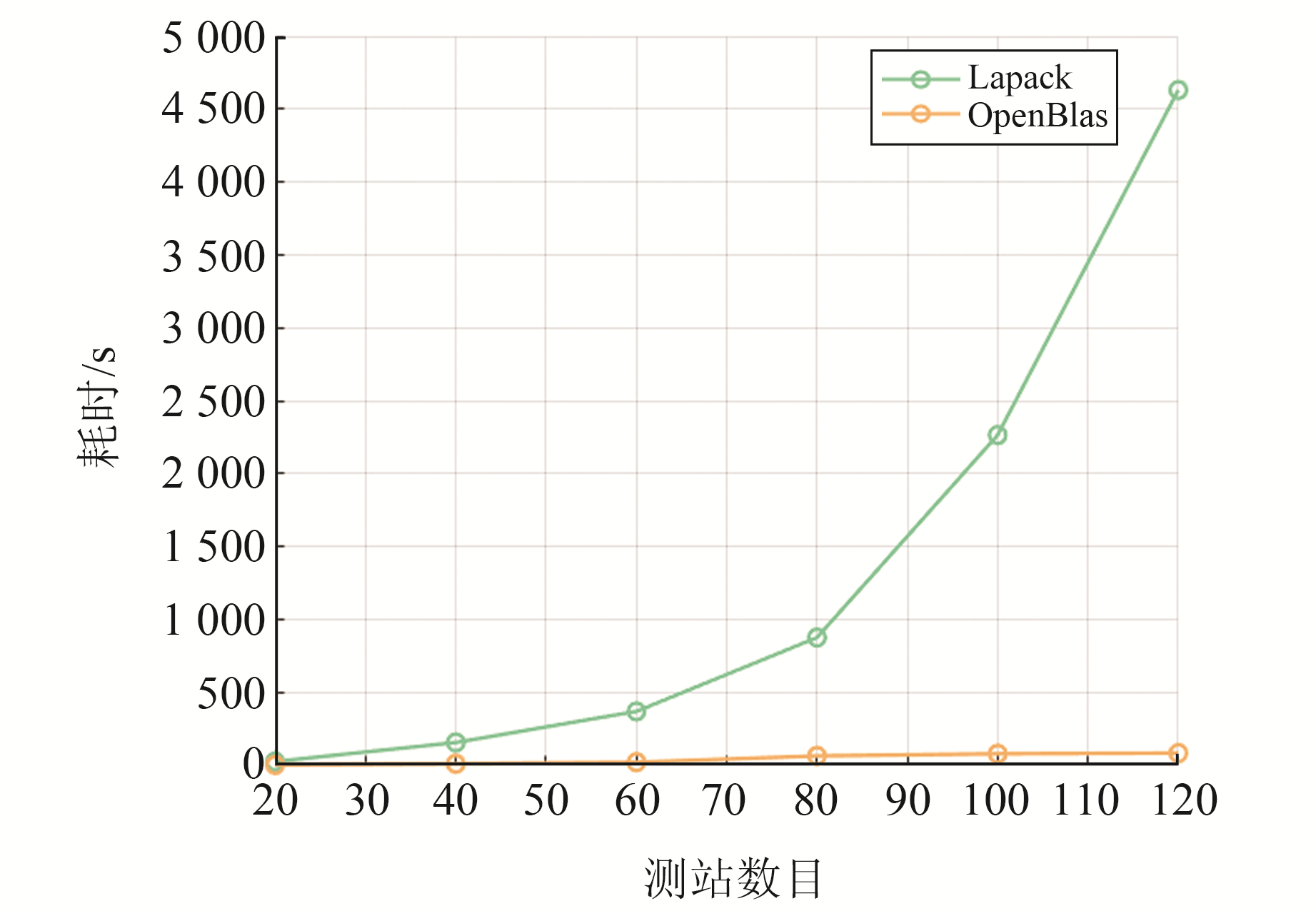
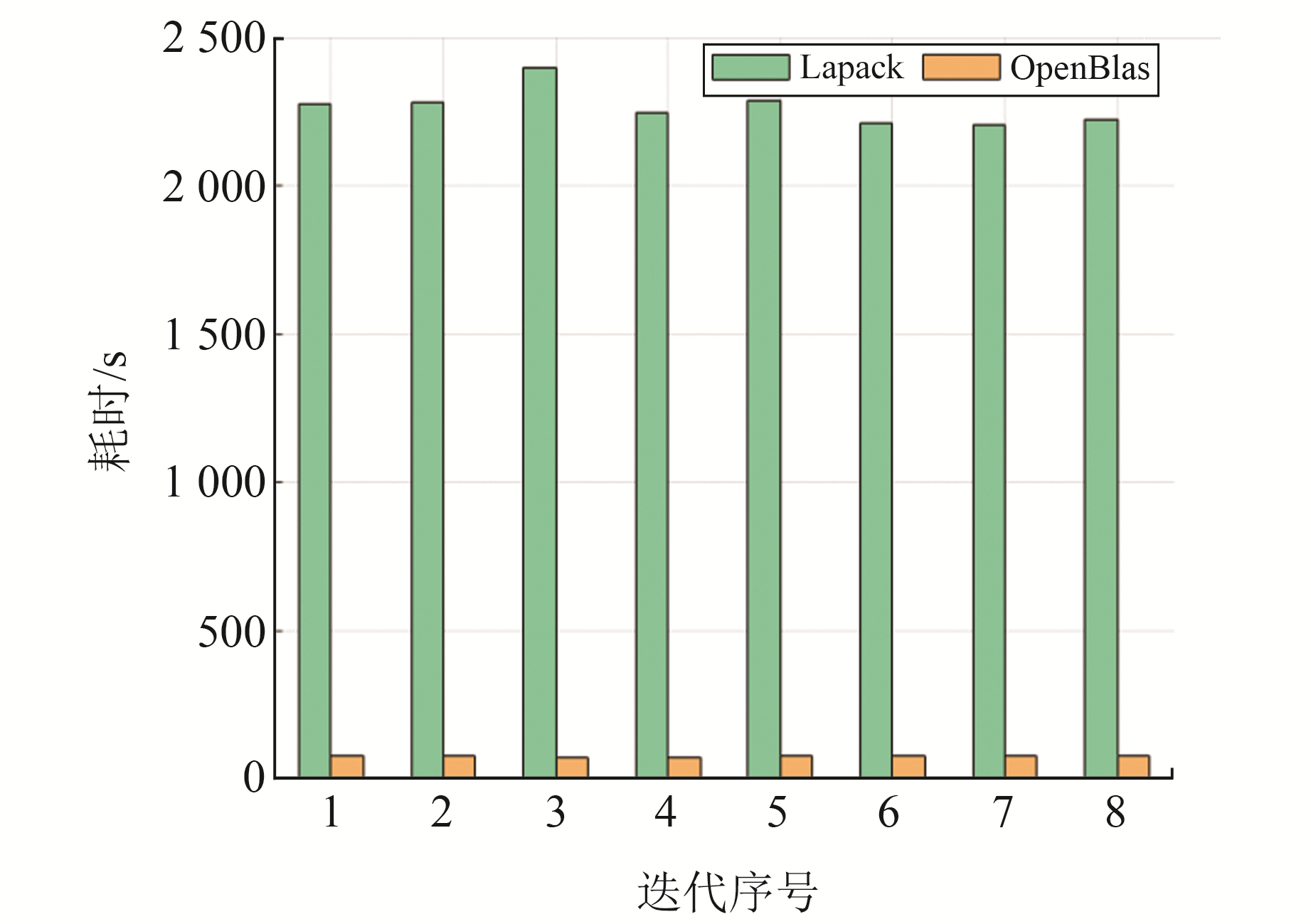
对于求逆解算,将采用单线程和多线程矩阵运算优化方法的OpenBlas库和原始Lapack库进行解算对比。OpenBlas库采用16线程,统计每次解算中8次迭代统一法方程求逆耗时的平均值,图 4为不同测站情况下采用Lapack库和OpenBlas库法方程求逆平均耗时对比。可以看出,OpenBlas库解算效率明显优于Lapack库,且随着测站数目的增加,OpenBlas库的优势更加明显。图 5为在100个测站情况下,8次迭代中二者法方程求逆解算耗时对比。经统计,采用Lapack库平均耗时为2 264 s,采用OpenBlas库平均耗时仅为78 s。
|
图 4 采用Lapack库和OpenBlas库法方程求逆平均耗时对比 Fig. 4 Comparison of average time consuming of solving inverse equations using Lapack library and OpenBlas library |
|
图 5 8次迭代法方程求逆耗时对比 Fig. 5 Comparison of time consuming of solving inverse equations in 8 iterations |
表 6为本文优化策略下使用ARM CPU和Intel CPU单次定轨的平均迭代时间。由表可知,在ARM CPU上通过上述2种方法优化(ARM+多线程+OpenBlas)的定轨解算效率为表 1中原始定轨处理(ARM+Lapack)的6倍左右,并且超过原始软件在Intel CPU(Intel+MKL)上的解算效率。本文优化方法在Intel CPU上也可以提高解算效率,采用MKL(Intel+多线程+MKL)时解算效率还是最高的。ARM CPU上最优解算耗时与Intel CPU上最优解算耗时相比,从原来的5倍缩小到3倍,说明本文方法可以提升ARM CPU的计算效能,提高导航卫星定轨解算效率。
|
|
表 6 优化后ARM CPU和Intel CPU单次定轨的平均迭代时间 Tab. 6 Single average orbit determination iteration time on ARM CPU and Intel CPU after optimizing |
以国产飞腾CPU为例,讨论在国产ARM架构CPU基础上的导航卫星精密定轨解算效率优化方法。影响导航卫星精密定轨解算效率的最主要因素为钟差参数约化和法方程求逆运算,对前者采用多线程优化方法,对后者采用OpenBlas开源库进行优化。优化后,2个部分的解算效率均大幅提升,且随着所需解算参数的增加,效率提升的倍数不断增加。在100个测站32颗卫星和OpenBlas采用16线程的情况下,针对矩阵乘法同时进行单线程和多线程运算优化的法方程求逆解算时,OpenBlas库的解算效率为Lapack库的29倍,这个优化倍数已突破仅通过多线程优化所能达到的最理想倍数(16倍),说明OpenBlas中单线程矩阵运算优化同样可以大幅提升解算效率。后续研究将进一步根据ARM CPU的架构特点和OpenBlas的原理,针对ARM架构对OpenBlas内部参数进行适配性调整,以进一步提升ARM CPU解算卫星精密轨道的效能。
| [1] |
Tang C P, Hu X G, Chen J P, et al. Orbit Determination, Clock Estimation and Performance Evaluation of BDS-3 PPP-B2b Service[J]. Journal of Geodesy, 2022, 96(9)
(  0) 0) |
| [2] |
Zhao X L, Zhou S S, Ci Y, et al. High-Precision Orbit Determination for a LEO Nanosatellite Using BDS-3[J]. GPS Solutions, 2020, 24(4)
(  0) 0) |
| [3] |
Ge M, Gendt G, Dick G, et al. A New Data Processing Strategy for Huge GNSS Global Networks[J]. Journal of Geodesy, 2006, 80(4): 199-203 DOI:10.1007/s00190-006-0044-x
(  0) 0) |
| [4] |
Gao K, Zhang S J, Li J C, et al. Real-Time GPS Satellite Clock Estimation Based on OpenMP[C]. The 8th China Satellite Navigation Conference, Shanghai, 2017
(  0) 0) |
| [5] |
Kuang K F, Zhang S J, Li J C. Real-Time GPS Satellite Orbit and Clock Estimation Based on OpenMP[J]. Advances in Space Research, 2019, 63(8): 2378-2386 DOI:10.1016/j.asr.2019.01.009
(  0) 0) |
| [6] |
Chen X H, Ge M R, Hugentobler U, et al. A New Parallel Algorithm for Improving the Computational Efficiency of Multi-GNSS Precise Orbit Determination[J]. GPS Solutions, 2022, 26(3)
(  0) 0) |
| [7] |
马威, 姚静波, 常永胜, 等. 国产CPU发展的现状与展望[J]. 集成电路应用, 2019, 36(4): 5-8 (Ma Wei, Yao Jingbo, Chang Yongsheng, et al. Current Situation and Prospect of CPU Development in China[J]. Application of IC, 2019, 36(4): 5-8)
(  0) 0) |
| [8] |
李玉成. Lapack中的分块算法及其效果[J]. 数值计算与计算机应用, 2001, 22(3): 172-180 (Li Yucheng. Block Algorithms and Their Effect in Lapack[J]. Journal of Unmerical Methods and Computer Applications, 2001, 22(3): 172-180)
(  0) 0) |
| [9] |
Goto K, Geijn R. High-Performance Implementation of the Level-3 BLAS[J]. ACM Transactions on Mathematical Software, 2008, 35(1)
(  0) 0) |
| [10] |
Zhang X Y, Wang Q, Zhang Y Q. Model-Driven Level 3 BLAS Performance Optimization on Loongson 3A Processor[C]. 2012 IEEE 18th International Conference on Parallel and Distributed Systems, Singapore, 2013
(  0) 0) |
2. University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China;
3. Insight Data Technology(Shenzhen) Co Ltd, 33 Liuxiandong Road, Shenzhen 518055, China
 2024, Vol. 44
2024, Vol. 44


