2. 东华理工大学自然资源部环鄱阳湖区域矿山环境监测与治理重点实验室,南昌市广兰大道 418号,330013
受多路径效应、钟差、电离层延迟等因素的影响,GNSS坐标时间序列存在各种噪声[1-2],呈现明显的非线性变化,不能准确反映测站的实际运动信息。常用的GNSS坐标时序降噪方法主要有小波分解(WD)[3-4]、经验模态分解(EMD)[5]等。EMD在处理非线性、非平稳信号方面应用广泛,但存在一定的端点效应和模态混叠现象,影响降噪效果。Wu等[6]和Yeh等[7]对EMD进行优化和改进,分别提出集合经验模态分解(EEMD)和互补集合经验模态分解(CEEMD)。两者都能有效抑制模态混叠现象,但计算效率低且过程繁琐。Dragomiretskiy等[8]提出一种新的信号时频分析处理方法——变分模态分解(VMD),该方法可以有效分离IMF分量、划分信号的频域,避免了EMD方法中模态混叠等缺陷,具有较好的鲁棒性。鲁铁定等[9]将VMD应用到变形监测数据的降噪中,效果显著。但VMD方法需要预先设置模态分解个数K和二次惩罚因子α,这2个参数在大多数情况下是依据经验选取的,然而实测信号复杂多变,若参数设定不当会对分解效果产生严重影响。
基于以上研究,本文先利用麻雀搜索算法(SSA)优化VMD,然后结合WD方法提出一种GNSS坐标时间序列降噪方法IVMD-WD,并结合仿真信号和GNSS实测数据实验验证该方法的有效性。
1 算法原理 1.1 VMD基本原理VMD处理非线性和非平稳信号时效果较好[8],其实质是一个变分问题的构造和求解过程。VMD构造的约束变分问题可表示为[9]:
| $ \begin{gathered} \min _{\left\{u_k\right\}, \left\{\omega_k\right\}}\left\{\sum\limits_k\left\|\partial t\left[\left(\delta(t)+\frac{\mathrm{j}}{\pi}\right) u_k(t)\right] \mathrm{e}^{-\mathrm{j} \omega_k t}\right\|_2^2\right\} \\ \text { s.t. } \sum\limits_k u_k=f \end{gathered} $ | (1) |
式中,t为时间,f为原始信号,uk为模态函数,ωk为各模态的实际中心频率,e-jωkt为每个解析信号的预估中心频率,‖·‖2为求L2范数,s.t.表示约束条件。
使用二次惩罚因子α和Lagrange乘子λ(t),将约束变分问题转换为无约束变分问题,进而求得式(1)的最优解,得到增广Lagrange表达式为:
| $ \begin{gathered} L\left(\left\{u_k\right\}, \left\{\omega_k\right\}, \lambda\right)= \\ \alpha \sum\limits_k\left\|\partial t\left[\left(\delta(t)+\frac{\mathrm{j}}{\pi t}\right) u_k(t)\right] \mathrm{e}^{-\mathrm{j} \omega_k t}\right\|_2^2+ \\ \left\|f(t)-\sum\limits_k u_k(t)\right\|_2^2+\left\langle\lambda(t), f(t)-\sum\limits_k u_k(t)\right\rangle \end{gathered} $ | (2) |
利用交替方向乘子算法,通过迭代更新ukn+1、ωkn+1、λn+1求得式(2)的鞍点,即为式(1)的最优解。详细计算过程参见文献[10]。
1.2 SSA基本原理SSA是Xue等[11]受麻雀觅食行为启发而提出的一种新型群体智能优化算法。相较于粒子群算法、遗传算法等优化算法,SSA收敛速度更快、求解精度更高、稳定性和鲁棒性更好[11-12]。麻雀种群按其职能分为发现者和追随者,发现者一般占比为10%~20%,主要负责为种群寻找食物和提供觅食的区域和方向,剩余麻雀均为依赖发现者来获取食物的追随者。此外,部分麻雀带有预警机制,一般占比为10%~20%,当遇到危险时,会发出报警信号,麻雀会进行反捕食。详细过程参见文献[12]。
1.3 SSA优化VMD对VMD计算结果影响较大的是模态分解数K和惩罚因子α,其余参数一般设置为默认值。当K过小时,会使信号欠分解;当K过大时,会造成信号过分解并产生模态混叠现象[10]。本文利用SSA对VMD的参数K和α进行优化,可快速准确地获取优化后的参数。
选用包络熵为SSA优化VMD的适应度函数。包络熵可以较好地反映原始信号的稀疏特性和不确定性,当信号中噪声较多时,熵值较大;反之,熵值较小。包络熵的原理[10]为:
| $ \left\{\begin{array}{l} E_p=-\sum\limits_{j=1}^N p_j \lg p_j \\ p_j=a(j) / \sum\limits_{j-1}^N a(j) \end{array}\right. $ | (3) |
式中,N为信号的采样点数,pj为a(j)的归一化形式,a(j)为信号x(j)经Hilbert解调后得到的包络信号。
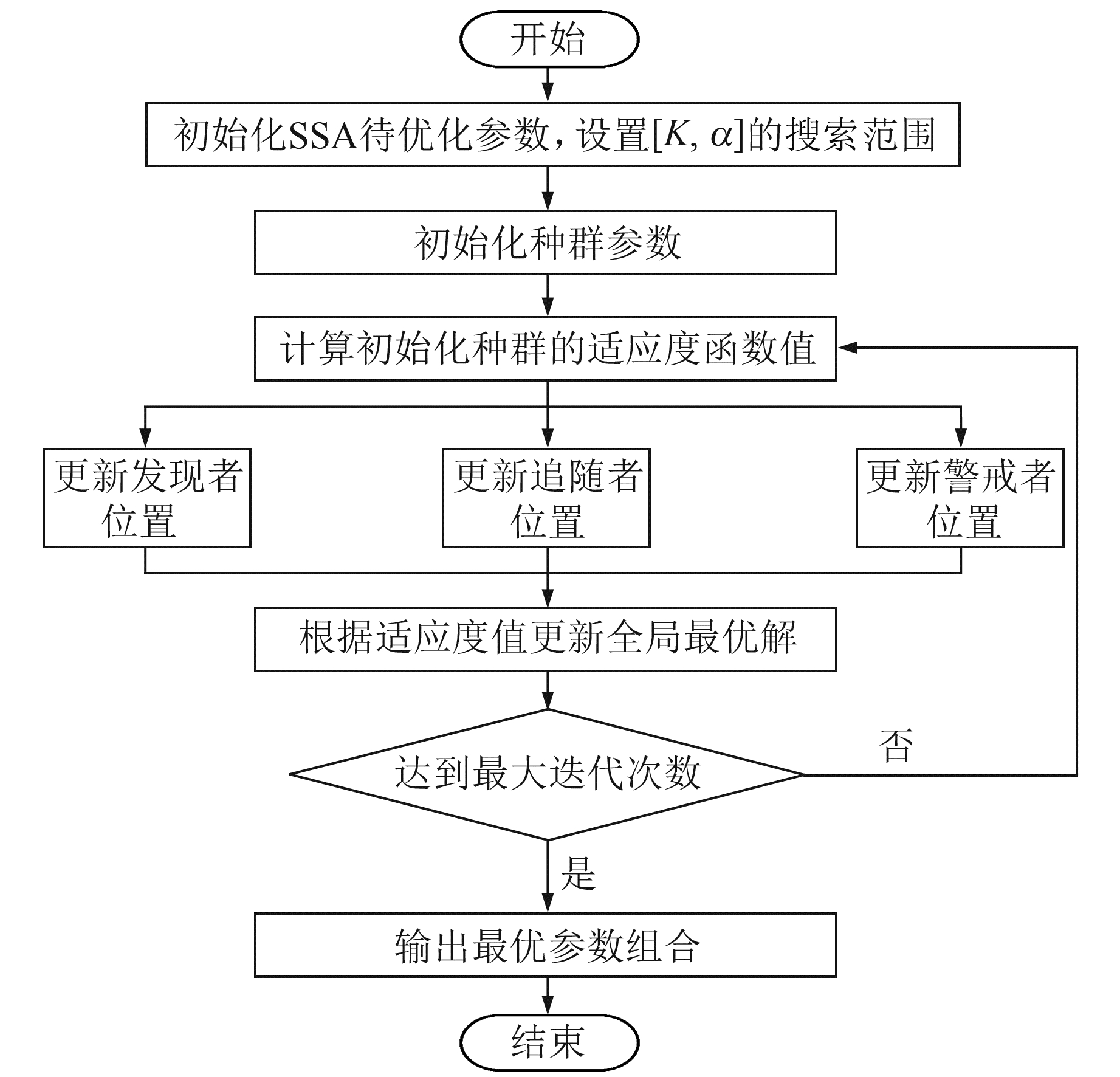
SSA优化VMD的过程见图 1。
|
图 1 SSA优化VMD的流程 Fig. 1 Flowchart of VMD optimization using SSA |
WD可以避免传统傅里叶变换的缺陷,具有较好的时频局部分析和多分辨率分析性能,因此在非线性非平稳信号研究中应用广泛[3, 5]。
WD通过一组高通和低通滤波器将原始信号分解为低频和高频分量,然后将低频分量分解。小波基函数表示为[13]:
| $ \left\{\begin{array}{l} W_f(a, b)=\left|\frac{1}{\sqrt{a}}\right| \int_{-\infty}^{+\infty} f(t) \varphi\left(\frac{t-b}{a}\right) \mathrm{d} t \\ \varphi_{a, b}(t)=\left|\frac{1}{\sqrt{a}}\right| \varphi\left(\frac{t-b}{a}\right) \end{array}\right. $ | (4) |
式中,φ(t)为基小波或者母小波函数,经过尺度因子a和平移因子b变换后的φa, b(t)统称为小波函数。
小波分解过程中最重要的就是确定小波基函数和分解层数,本文选用正则性较好的db4小波进行分解,最佳层数由文献[3]的方法确定。
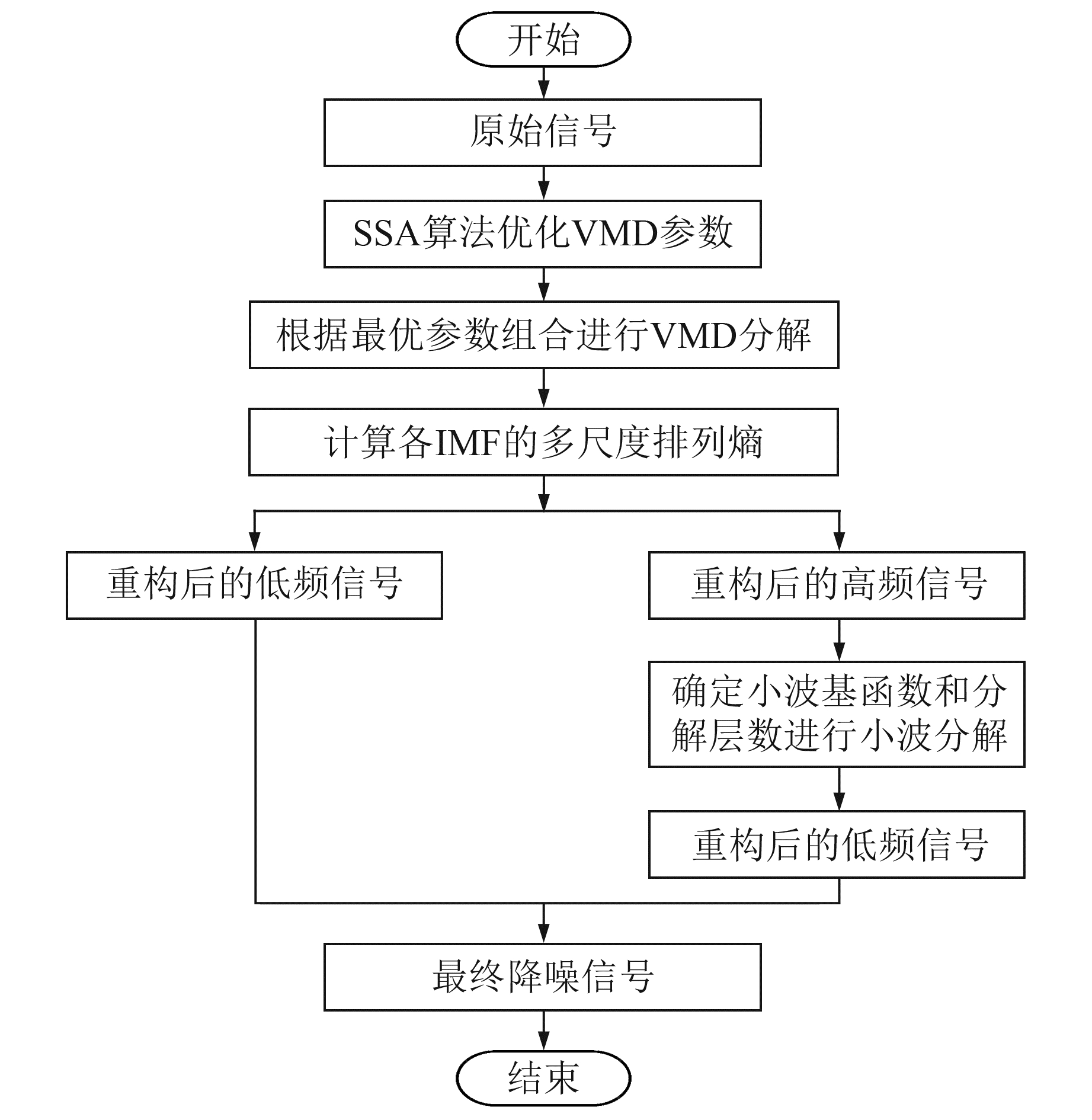
1.5 IVMD-WD方法构建使用SSA优化影响VMD分解效果的2个关键参数K和α。对于VMD分解后的多个IMF分量,采用多尺度排列熵(multi-scale permutation entropy,MPE)作为判断噪声和信号的标准,具体计算步骤参考文献[14]。IVMD-WD方法的降噪流程见图 2,具体步骤如下:
|
图 2 IVMD-WD方法的降噪流程 Fig. 2 Noise reduction flowchart of IVMD-WD method |
1) 初始化SSA参数,设置麻雀种群数量为30,最大迭代次数为10,考虑计算效率和算法精度,将K的取值范围设为[3, 10],α的取值范围设为[100,3 500]。
2) 根据得到的最优参数组合[K, α],对原参考信号进行VMD处理,得到K个IMF。
3) 计算各IMF的MPE,设定MPE的阈值,根据阈值大小判断出有效IMF并重构为信号,剩余IMF重构为噪声。
4) 将步骤3)中重构后的高频噪声部分利用小波分解再次降噪,利用相关系数判断得到有效信号,将步骤3)中得到的低频信号与小波分解处理后的信号重构为最终的降噪信号。
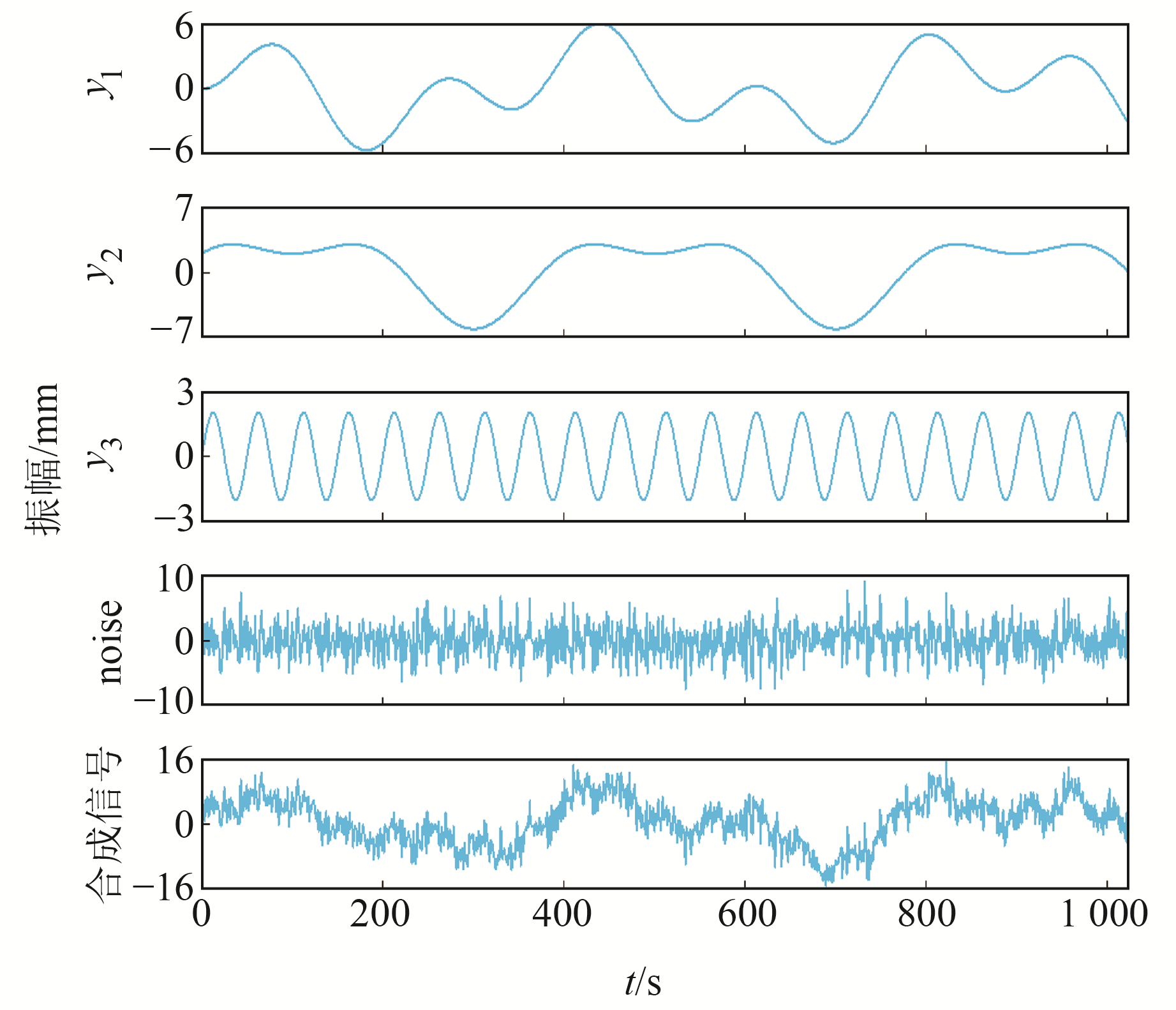
2 仿真信号算例分析 2.1 仿真信号降噪实验进行仿真信号实验,并将IVMD-WD方法与EMD、WD和EEMD方法进行对比。实验过程中,EMD、WD和EEMD方法均利用相关系数法分离噪声和信号。仿真信号由3个周期项和高斯白噪声组成,采样间隔设置为1 s,采样点数为1 024,并加入信噪比(signal noise ratio, SNR)为6 dB的高斯白噪声,仿真信号的分量波形见图 3,表达式如式(5)所示:
| $ \left\{\begin{array}{l} y_1=6 \sin (2 \pi t / 600) \sin (2 \pi t / 250) \\ y_2=4 \sin (2 \pi t / 400)+2 \cos (2 \pi t / 200) \\ y_3=2 \sin (2 \pi t / 50)+\sin (16 \pi t) \cos (150 \pi t) \\ \varepsilon=\text { noise } \\ y=y_1+y_2+y_3+\varepsilon \end{array}\right. $ | (5) |
|
图 3 仿真信号各分量波形 Fig. 3 Waveforms of each component of simulated signal |
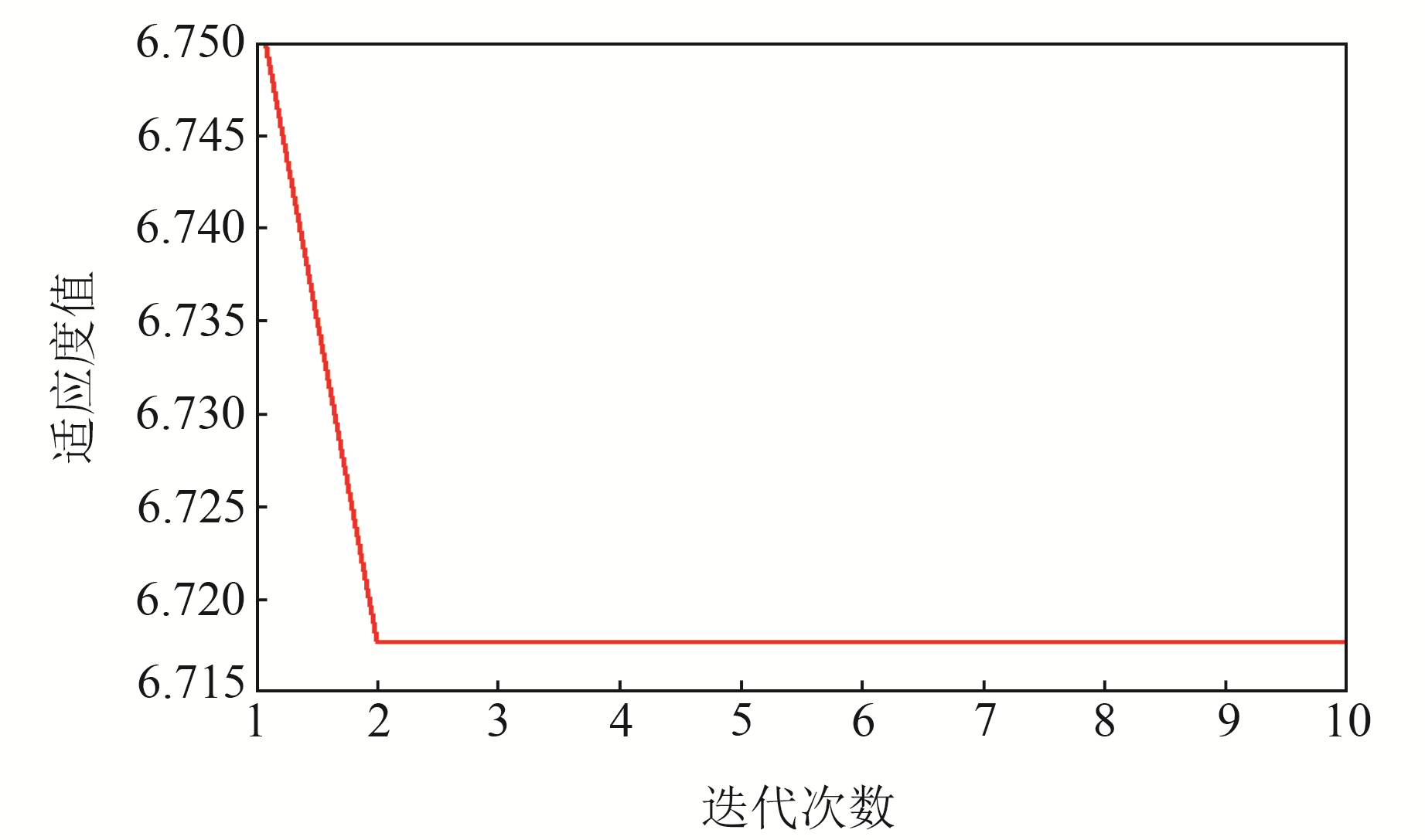
本文方法进行降噪时需先利用SSA寻找VMD的最优参数组合,采用包络熵作为适应度函数,适应度函数值在SSA寻优过程中随迭代次数的变化见图 4。由图 4可知,适应度值在迭代到第2次时达到最小,此时对应的[K, α]=[7, 2 730]为最优参数组合。
|
图 4 适应度值收敛图 Fig. 4 Convergence diagram of fitness values |
利用SSA得到的最优参数组合对信号进行VMD处理,得到的7个IMF见图 5。由图 5可知,低频分量主要集中在前2阶模态中。

|
图 5 IVMD分解图 Fig. 5 IVMD decomposition diagram |
为有效分离出低频信号和高频噪声,需计算出各IMF的MPE值。计算MPE时需设置适当的参数,本文参考文献[15]对关键参数进行设定:尺度因子s=12、嵌入维数m=6、延迟时间τ=1。计算不同尺度因子下各IMF的排列熵均值作为最终的MPE值,MPE值越接近于1,表明时间序列具有越大的随机波动性和不规则性。MPE阈值一般取0.6,将大于0.6的IMF视为噪声分量,小于0.6的视为低频信号分量[15]。VMD得到的各IMF的MPE值见表 1。
|
|
表 1 IVMD得到的各IMF的MPE值 Tab. 1 MPE values of each IMF component obtained by IVMD |
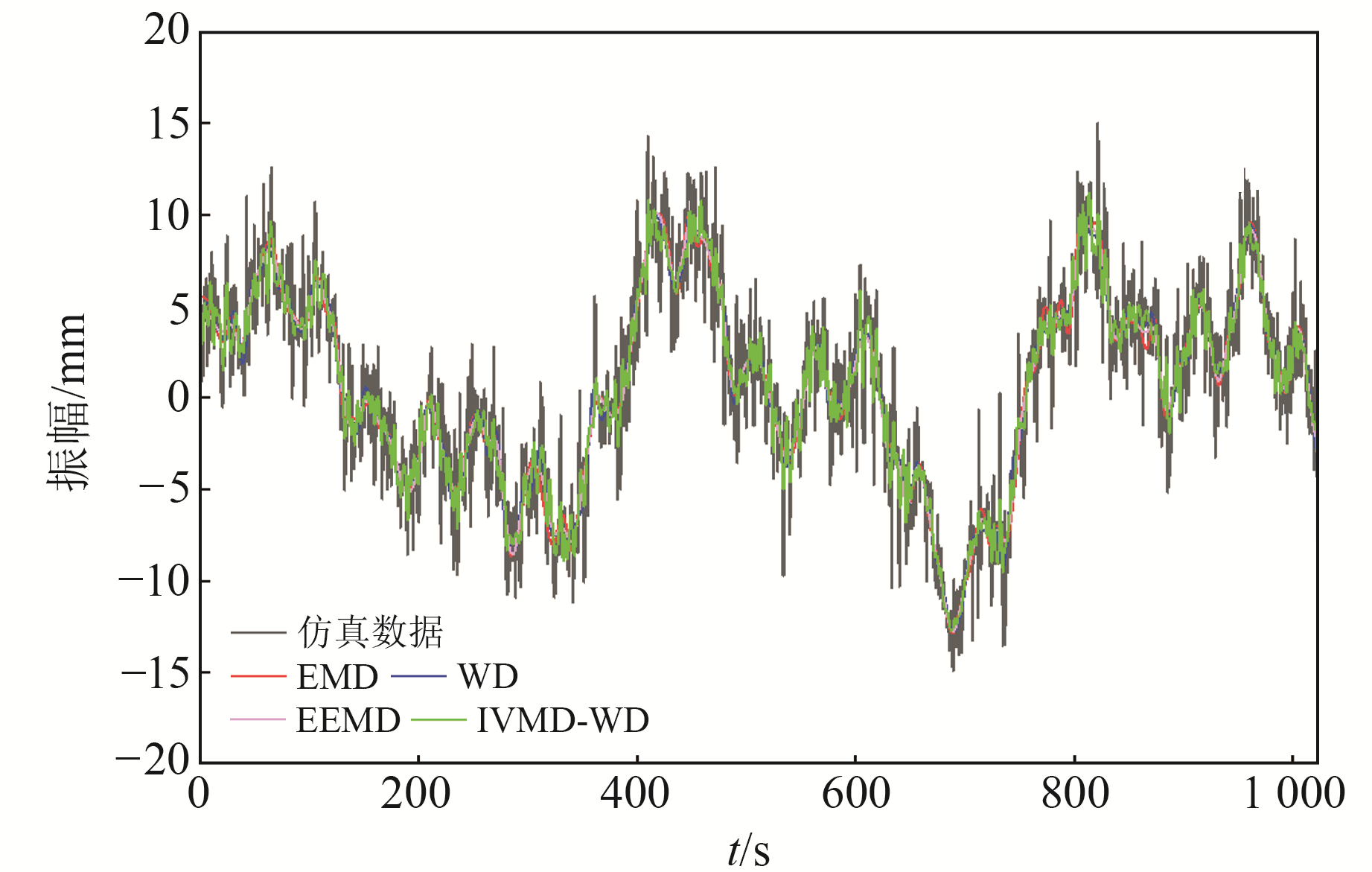
由表 1可见,IMF1~IMF7的MPE值逐渐增大,表明序列的随机波动性越来越大,噪声成分逐渐增多,符合图 5的波形描述。IMF1、IMF2的MPE值均小于0.6,因此,将IMF1、IMF2重构为低频信号,IMF3~IMF7重构为高频噪声,然后利用小波分解处理高频噪声部分。同时,使用EMD、WD、EEMD方法对仿真信号进行降噪处理,并与本文方法进行对比,见图 6。可以看出,EMD、WD、EEMD方法降噪后,信号波形与原始序列拟合效果较差,而本文方法降噪后的波形与仿真信号更加接近,曲线更为光滑,避免了EMD降噪过程中的端点效应和模态混叠问题,能够提取更多的有效信号,降噪效果更好。
|
图 6 4种降噪信号波形对比 Fig. 6 Waveform comparison among four types of noise reduction signals |
为了评价上述4种方法的降噪效果,选取均方根误差(RMSE)、信噪比(SNR)、平均绝对误差(MAE)和互相关系数(R)作为评价指标:
| $ \mathrm{RMSE}=\sqrt{\frac{1}{N} \sum\limits_{i=1}^N\left(x_i-y_i\right)^2} $ | (6) |
| $ \operatorname{SNR}=10 \lg \left(\frac{\sum\limits_{i=1}^N x_i^2}{\sum\limits_{i=1}^N\left(x_i-y_i\right)^2}\right) $ | (7) |
| $ \mathrm{MAE}=\frac{1}{N} \sum\limits_{i=1}^N\left|\left(x_i-y_i\right)\right| $ | (8) |
| $ R(x, y)=\frac{\sum\limits_{i=1}^N\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum\limits_{i=1}^N\left(x_i-\bar{x}\right)^2} \sqrt{\sum\limits_{i=1}^N\left(y_i-\bar{y}\right)^2}} $ | (9) |
式中,i为历元时刻,x、y分别为降噪后信号和原始信号,x、y分别x和y的平均值,N为数据长度。4种降噪方法的评价指标结果见表 2。
|
|
表 2 4种方法的降噪效果 Tab. 2 Noise reduction effect for four methods |
由表 2可见,WD降噪效果略优于EMD和EEMD,而本文方法相比于EMD、WD和EEMD方法,各降噪评价指标均为最优,RMSE分别降低15.42%、14.35%和15.06%,MAE分别降低15.62%、13.37%和15.18%,SNR分别提高1.44 dB、1.35 dB和1.48 dB, R分别提高0.028 2、0.025 6和0.027 0。IVMD-WD方法的RMSE和MAE最小,表明其降噪后的序列偏差更小;SNR和R最大,表明其提取的有效信号最多,降噪信号波形与原始信号波形更相似,拟合度更高。仿真信号实验结果表明,IVMD-WD方法的降噪效果优于EMD、WD和EEMD方法。
3 GNSS实测数据降噪分析为进一步验证本文方法的可靠性和适用性,选取SOPAC(Scrips Orbit and Permanent Array Center) 提供的美国西海岸10个GNSS基准站网原始坐标时间序列进行分析,观测时间为2000~2023年,采样间隔为1/365.25 a。
限于篇幅,仅以GOBS站为例进行详细分析,图 7为该站N、E、U方向的原始时间序列与经4种方法降噪后的信号对比结果。可以看出,EMD、WD和EEMD降噪后信号波形与原始时间序列的波形存在一定差异,而IVMD-WD方法去噪后的时间序列能够更好地拟合原始时间序列,可以有效地反映局部运动趋势,且周期振荡较小。图 8为利用4种方法得到的降噪信号与原始时间序列的残差对比。由图可知,IVMD-WD方法的平均残差最小,表明本文方法有效滤除了高频噪声,降噪效果最显著。

|
图 7 GOBS站点3个方向降噪效果对比 Fig. 7 Comparison of noise reduction effects in three directions at GOBS station |

|
图 8 降噪信号与原始信号的残差结果 Fig. 8 Residual results between the noise reduction signals and the original signals |
图 9为10个站点采用上述4种方法降噪后信号的4种评价指标值对比。由图 9(a)和9(b)可知,EMD方法降噪效果在部分站点上要优于EEMD,整体来说,两者降噪效果相差不大;WD降噪效果整体上略低于EMD,略优于EEMD;相比于EMD、WD和EEMD方法,本文方法降噪后得到的RMSE和MAE最小。由图 9(c)和9(d)可知,本文方法降噪后的SNR和R最大。综合可知,本文IVMD-WD方法降噪后的各项评价指标均为最优,表明本文方法降噪效果最显著,能够有效提取出更多的有用信号。

|
图 9 4种降噪方法的评价指标 Fig. 9 Evaluation indicators for four noise reduction methods |
本文针对GNSS坐标时间序列的非线性、非平稳特性构建了一种新的降噪算法IVMD-WD。该方法利用麻雀搜索算法优化VMD参数,使用多尺度排列熵作为噪声和信号的筛选标准,结合小波分解算法对VMD进行改进。通过仿真信号和10个GNSS基准站的实测数据进行降噪分析。结果表明,与传统的EMD、WD和EEMD方法相比,本文IVMD-WD方法降噪后的各指标均为最优,能够更有效地剔除原始时间序列中的高频噪声并保留有用信号,在降噪性能上具有明显优势。
| [1] |
李昭, 姜卫平, 刘鸿飞, 等. 中国区域IGS基准站坐标时间序列噪声模型建立与分析[J]. 测绘学报, 2012, 41(4): 496-503 (Li Zhao, Jiang Weiping, Liu Hongfei, et al. Noise Model Establishment and Analysis of IGS Reference Station Coordinate Time Series inside China[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 496-503)
(  0) 0) |
| [2] |
姜卫平, 李昭, 刘万科, 等. 顾及非线性变化的地球参考框架建立与维持的思考[J]. 武汉大学学报: 信息科学版, 2010, 35(6): 665-669 (Jiang Weiping, Li Zhao, Liu Wanke, et al. Thoughts on the Establishment and Maintenance of the Earth Reference Frame Considering Nonlinear Changes[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6): 665-669)
(  0) 0) |
| [3] |
李宗春, 邓勇, 张冠宇, 等. 变形测量异常数据处理中小波变换最佳级数的确定[J]. 武汉大学学报: 信息科学版, 2011, 36(3): 285-288 (Li Zongchun, Deng Yong, Zhang Guanyu, et al. Determination of Optimal Series of Wavelet Transform in Abnormal Data Processing of Deformation Measurement[J]. Geomatics and Information Science of Wuhan University, 2011, 36(3): 285-288)
(  0) 0) |
| [4] |
马俊, 曹成度, 姜卫平, 等. 利用小波包系数信息熵去除GNSS站坐标时间序列有色噪声[J]. 武汉大学学报: 信息科学版, 2021, 46(9): 1309-1317 (Ma Jun, Cao Chengdu, Jiang Weiping, et al. Elimination of Colored Noise in GNSS Station Coordinate Time Series by Using Wavelet Packet Coefficient Information Entropy[J]. Geomatics and Information Science of Wuhan University, 2021, 46(9): 1309-1317)
(  0) 0) |
| [5] |
Huang N E, Shen Z, Long S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J]. Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995 DOI:10.1098/rspa.1998.0193
(  0) 0) |
| [6] |
Wu Z H, Huang N E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41 DOI:10.1142/S1793536909000047
(  0) 0) |
| [7] |
Yeh J R, Shieh J S, Huang N E. Complementary Ensemble Empirical Mode Decomposition: A Novel Noise Enhanced Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2010, 2(2): 135-156 DOI:10.1142/S1793536910000422
(  0) 0) |
| [8] |
Dragomiretskiy K, Zosso D. Variational Mode Decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544 DOI:10.1109/TSP.2013.2288675
(  0) 0) |
| [9] |
鲁铁定, 谢建雄. 变分模态分解结合样本熵的变形监测数据降噪[J]. 大地测量与地球动力学, 2021, 41(1): 1-6 (Lu Tieding, Xie Jianxiong. Deformation Monitoring Data De-Noising Method Based on Variational Mode Decomposition Combined with Sample Entropy[J]. Journal of Geodesy and Geodynamics, 2021, 41(1): 1-6)
(  0) 0) |
| [10] |
唐贵基, 王晓龙. 参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J]. 西安交通大学学报, 2015, 49(5): 73-81 (Tang Guiji, Wang Xiaolong. Parameter Optimized Variational Mode Decomposition Method with Application to Incipient Fault Diagnosis of Rolling Bearing[J]. Journal of Xi'an Jiaotong University, 2015, 49(5): 73-81)
(  0) 0) |
| [11] |
Xue J K, Shen B. A Novel Swarm Intelligence Optimization Approach: Sparrow Search Algorithm[J]. Systems Science and Control Engineering, 2020, 8(1): 22-34 DOI:10.1080/21642583.2019.1708830
(  0) 0) |
| [12] |
王瑞, 徐新超, 逯静. 基于麻雀搜索算法优化变分模态分解和混合核极限学习机的短期风电功率预测[J]. 信息与控制, 2023, 52(4): 444-454 (Wang Rui, Xu Xinchao, Lu Jing. Short-Term Wind Power Prediction Based on SSA Optimized Variational Mode Decomposition and Hybrid Kernel Extreme Learning Machine[J]. Information and Control, 2023, 52(4): 444-454)
(  0) 0) |
| [13] |
王江, 史元浩, 郭正玉, 等. 融合小波分解和LSTM的目标轨迹预测[J]. 电子测量与仪器学报, 2023, 37(1): 204-211 (Wang Jiang, Shi Yuanhao, Guo Zhengyu, et al. Target Trajectory Prediction by Fusing Wavelet Decomposition and LSTM[J]. Journal of Electronic Measurement and Instrumentation, 2023, 37(1): 204-211)
(  0) 0) |
| [14] |
李瑞, 范玉刚. 基于CEEMDAN多尺度排列熵和SO-RELM的高压隔膜泵单向阀故障诊断[J]. 振动与冲击, 2023, 42(5): 127-135 (Li Rui, Fan Yugang. Fault Diagnosis of One-Way Valve of High-Pressure Diaphragm Pump Based on CEEMDAN Multi-Scale Permutation Entropy and SO-RELM[J]. Journal of Vibration and Shock, 2023, 42(5): 127-135)
(  0) 0) |
| [15] |
陈祥, 杨志强, 田镇, 等. GA-VMD与多尺度排列熵结合的GNSS坐标时序降噪方法[J]. 武汉大学学报: 信息科学版, 2023, 48(9): 1425-1434 (Chen Xiang, Yang Zhiqiang, Tian Zhen, et al. Denoising Method for GNSS Time Series Based on GA-VMD and Multi-Scale Permutation Entropy[J]. Geomatics and Information Science of Wuhan University, 2023, 48(9): 1425-1434)
(  0) 0) |
2. Key Laboratory of Mine Environmental Monitoring and Improving around Poyang Lake, MNR, East China University of Technology, 418 Guanglan Road, Nanchang 330013, China
 2024, Vol. 44
2024, Vol. 44


