2. 西安测绘研究所,西安市雁塔路中段1号,710054
地月空间平动点是圆形限制性三体问题的5个特解,包括3个共线平动点L1、L2和L3以及2个三角平动点L4和L5。由于特殊的位置特性和动力学特性,在平动点附近存在大量的周期、拟周期轨道,对中继通信、空间中转站、星际低能转移等具有独特的优势。共线平动点附近的轨道类型主要有Halo轨道、Lissajous轨道和Lyapunov轨道3类。
众多学者对共线平动点附近周期轨道进行过研究[1-5],但由于圆形限制性三体问题在理论模型、参数设置、数值计算等方面均存在误差,因此获得的解析轨道均为近似值。例如在圆形限制性三体问题中将地月质心距离作为固定参数处理,但实际上受地月质量分布、太阳摄动等因素的影响,地月质心相对位置是不断变化的。相应的变化信息主要依赖于美国DE系列、法国INPOP系列和俄罗斯EPM系列数值星历表,这3种星历表代表了目前世界上数值星历表的领先水平。张文昭等[6]对比以上3种历表中大行星(包含月球)相对地球和相对太阳系质心的位置坐标差最大值及均方根。结果表明,相对于地心的位置偏差,月球历表的精度在dm~m级,3个历表之间的差别可从侧面反映当前行星位置的测量精度。李萌萌等[7]对比不同版本的JPL历表对地球及其他天体天球坐标转换及月固坐标系与月心天球坐标系的影响。刘婉逸等[8]基于DE405、DE421、DE430、DE440星历计算各大行星在地球质心及太阳系质心惯性系中的位置,比较其他星历相对于DE440星历的位置精度。地月历表是地月空间轨道的时空基准,分析其误差对研究地月空间轨道误差至关重要,但目前尚无学者针对此问题进行深入、系统的研究。
根据误差传播定律,地月历表的误差会引起平动点的位置误差,而共线平动点具有弱稳定性,其附近的轨道对初值和扰动非常敏感。故分析地月历表误差对平动点,尤其是共线平动点附近轨道不同空间位置的影响特性,对于航天器入轨点选择、入轨速度确定、测控支持等具有一定的参考意义。本文首先研究圆形限制性三体问题的建模与求解,分析不同初值条件下的轨道演化特性,再研究地月历表误差对地月共线平动点周期轨道在不同初值及初值误差时的影响。
1 圆形限制性三体问题圆形限制性三体问题是深空探测中考察探测器运动状态时常用的基本力学模型之一,其描述一个质量可忽略的小天体(如探测器)在2个作相互圆周运动的大天体(主天体)的引力作用下的运动状态[9]。求解圆形限制性三体问题通常用到质心惯性坐标系和质心旋转坐标系(也称会合坐标系)[10]。质心惯性坐标系的定义为:坐标原点位于2个主天体质心,X轴指向惯性空间某固定方向,Z轴指向主天体轨道运动的角动量方向,Y轴与X、Z轴构成右手系。会合坐标系的定义是:坐标原点位于2个主天体质心,x轴由大天体指向小天体,z轴指向主天体轨道运动的角动量方向,y轴与x、z轴构成右手系(图 1)。会合坐标系绕质心惯性坐标系作匀速圆周运动,其周期与2个主天体绕质心运动的周期相同。在会合坐标系中,设i、j、k分别为x轴、y轴和z轴方向的单位矢量,3个质点P1、P2和P3的位置矢量分别为(x1, 0, 0)、(x2, 0, 0)和(x, y, z)。
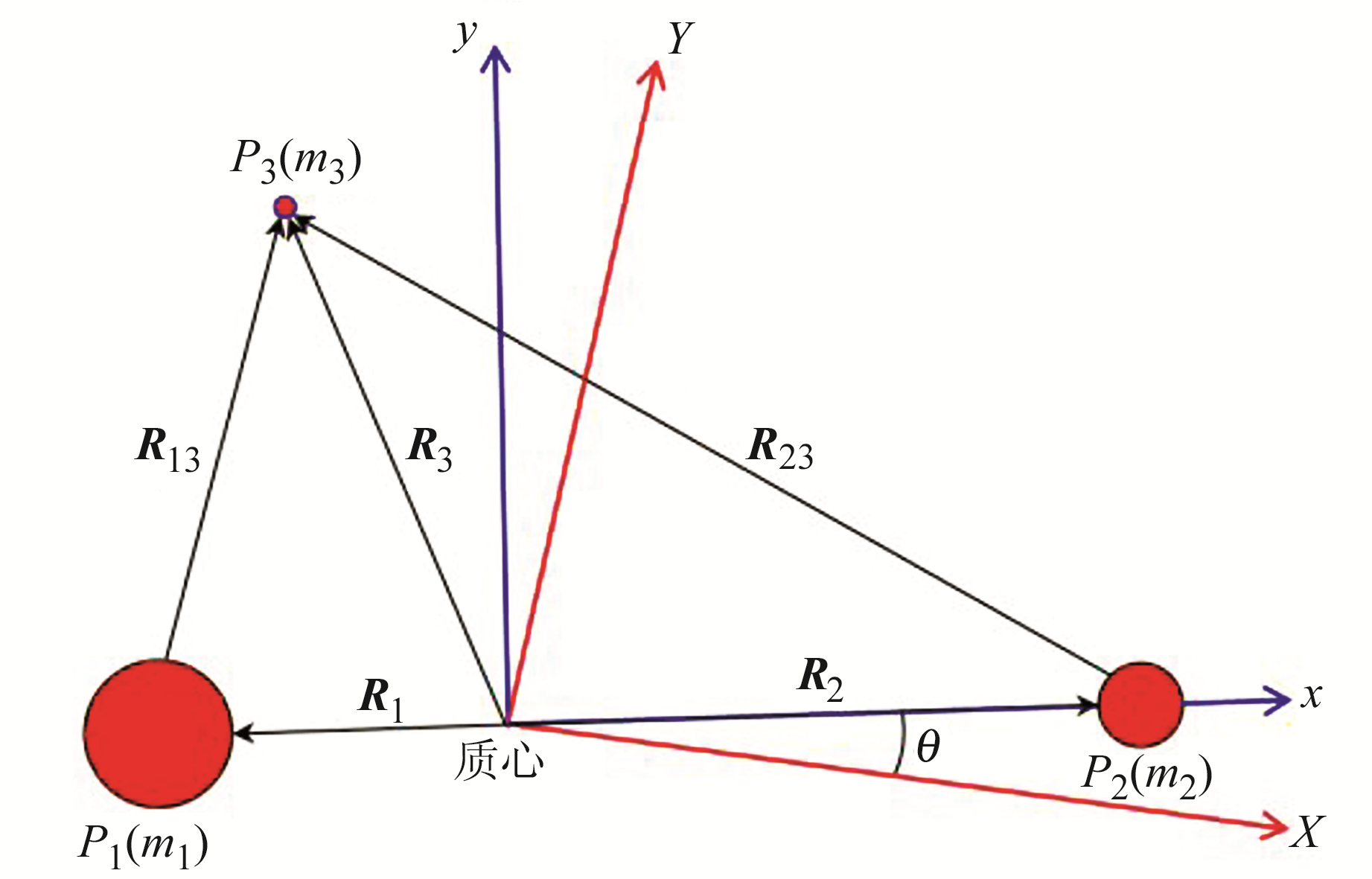
|
图 1 会合坐标系 Fig. 1 Converging coordinate system |
在会合坐标系中,圆形限制性三体问题的标量形式为[10]:
| $ \left\{\begin{array}{l} \ddot{x}-2 \omega \dot{y}-\omega^2 x=-\frac{G m_1}{r_1^2}\left(x_1-x\right)- \\ \quad \frac{G m_2}{r_2^2}\left(x_2-x\right) \\ \ddot{y}+2 \dot{\omega x}-\omega^2 y=-\frac{G m_1}{r_1^2} y-\frac{G m_2}{r_2^2} y \\ \ddot{z}=-\frac{G m_1}{r_1^2} z-\frac{G m_2}{r_2^2} z \end{array}\right. $ | (1) |
式中, r1和r2可写为
为简化动力学方程的表达形式,对式(1)进行无量纲化处理,得到无量纲化的动力学方程[9]:
| $\left\{\begin{array}{l}\ddot{x}-2 \dot{y}=\frac{\partial \varOmega}{\partial x} \\ \ddot{y}+2 \dot{x}=\frac{\partial \varOmega}{\partial y} \\ \ddot{z}=\frac{\partial \varOmega}{\partial z}\end{array}\right.$ | (2) |
式中,Ω为等效势能函数,且[9]
| $\left\{\begin{array}{l}\varOmega=\frac{1}{2}\left(x^2+y^2+z^2\right)+\frac{1-\mu}{r_1}+\frac{\mu}{r_2} \\ r_1=\sqrt{(x+\mu)^2+y^2+z^2} \\ r_2=\sqrt{(x-1+\mu)^2+y^2+z^2}\end{array}\right.$ | (3) |
拉格朗日点是在会合坐标系中速度和加速度均为0的位置,相对于2个主天体静止不动。式(1)中,令
| $ \left\{\begin{array}{l} \frac{\partial \varOmega}{\partial x}=x-\frac{1-\mu}{r_1^3}(x+\mu)- \\ \quad\frac{\mu}{r_2^3}(x-1+\mu)=0 \\ \frac{\partial \varOmega}{\partial y}=y\left(1-\frac{1-\mu}{r_1^3}-\frac{\mu}{r_2^3}\right)=0 \\ \frac{\partial \varOmega}{\partial z}=-z\left(\frac{1-\mu}{r_1^3}-\frac{\mu}{r_2^3}\right)=0 \end{array}\right. $ | (4) |
方程(4)有以下2种情况[10]:
| $ y=0, \left\{\begin{array}{l} x+\frac{1-\mu}{(x-\mu)^2}-\frac{\mu}{(x+1-\mu)^2}=0\left(L_1\right) \\ x+\frac{1-\mu}{(x-\mu)^2}+\frac{\mu}{(x+1-\mu)^2}=0\left(L_2\right) \\ x-\frac{1-\mu}{(x-\mu)^2}-\frac{\mu}{(x+1-\mu)^2}=0\left(L_3\right) \end{array}\right. $ | (5) |
| $ \begin{array}{c} y \ne 0, \\ \left\{ \begin{array}{l} 1 - \frac{{1 - \mu }}{{r_1^3}} - \frac{\mu }{{r_2^3}} = 0\\ x - \frac{{1 - \mu }}{{r_1^3}}(x + \mu ) - \frac{\mu }{{r_2^3}}(x - 1 + \mu ) = 0 \end{array} \right.\left( {{L_4}, {L_5}} \right) \end{array} $ | (6) |
求解方程(5)和(6)可得到拉格朗日点的位置,如图 2所示,L1、L2、L3为共线平动点,L4、L5为三角平动点。
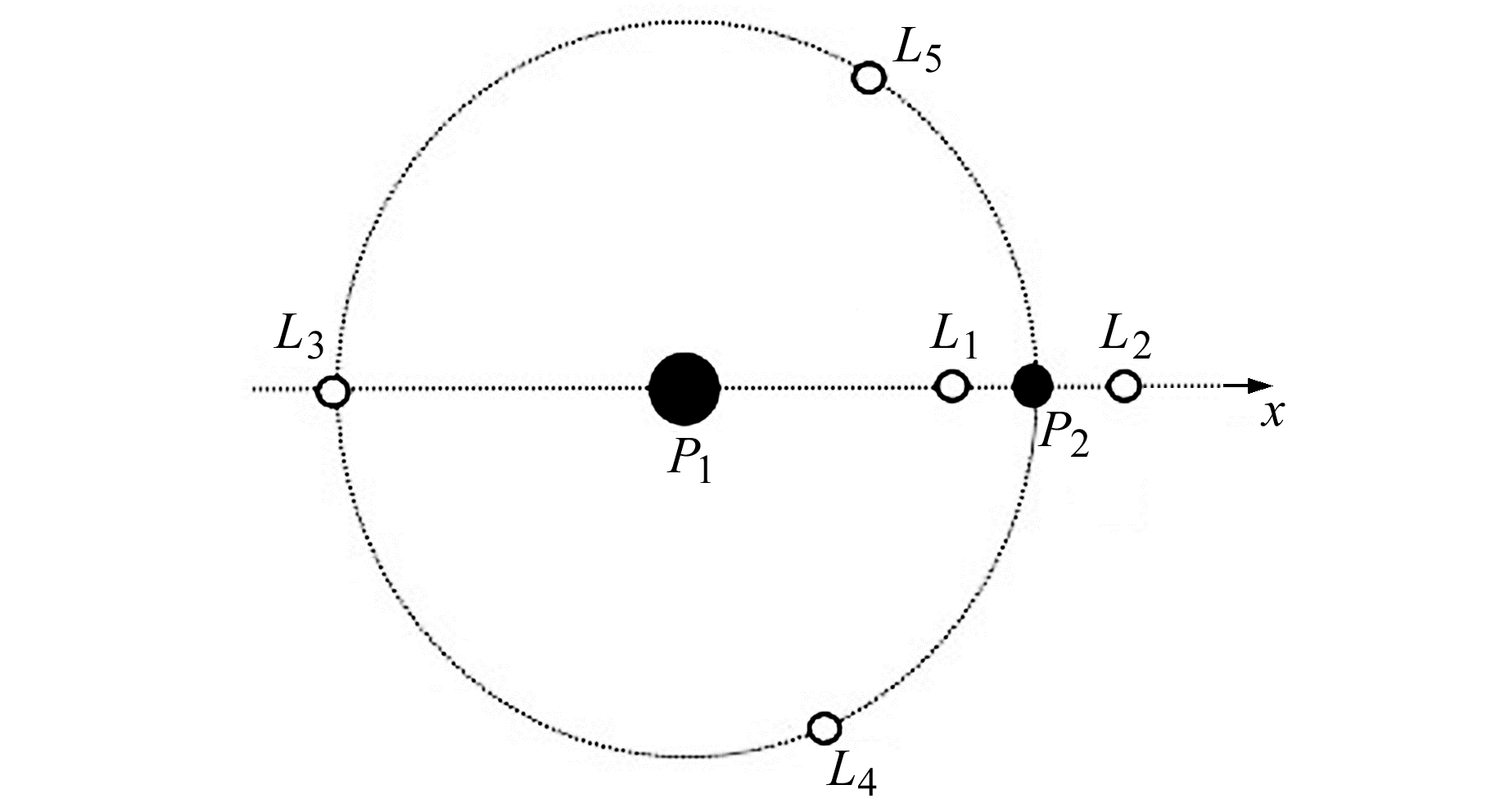
|
图 2 平动点位置图 Fig. 2 Location map of libration points |
利用文献[11]给出的3阶解析解分析共线平动点附近的周期轨道:
| $ \left\{\begin{array}{l} x(\tau)=-A \cos u-\frac{1}{4}\left(2 A^2+B^2\right)+\frac{1}{2} A^2 \cos 2 u+ \\ \quad\frac{1}{4} B^2 \cos 2 v+\frac{1}{8} A B^2 \cos (u+2 v)+\frac{3}{8} A^3 \cos 3 u \\ y(\tau)=2 A \cos u+\frac{1}{4} \sin 2 u-\frac{1}{4} B^2 \sin 2 v- \\ \quad\frac{1}{8} A B^2 \sin \cos (u+2 v)+\frac{7}{24} A^3 \sin 3 u+ \\ \quad\frac{3}{8} A B^2 \sin (u-2 v)-\frac{9}{8} A^3 \sin u \\ z(\tau)=B \sin v+\frac{1}{2} A B[\sin (u+v)- \\ \quad 3 \sin (v-u)]+\frac{3}{8} A^2 B \sin (2 u+v) \end{array}\right. $ | (7) |
式中,A、B、φ、ψ由初始条件决定[11],u=τ+φ, v=τ+ψ。
| $ \left\{\begin{array}{l} A=\sqrt{a_3^2+a_4^2} \\ B=\sqrt{a_5^2+a_6^2} \\ \varphi=\arccos \frac{a_3}{\sqrt{a_3^2+a_4^2}} \\ \psi=\arcsin \frac{a_5}{\sqrt{a_5^2+a_6^2}} \end{array}\right. $ | (8) |
| $ \left\{\begin{array}{l} a_3=x_0 \\ a_4=x_0^{\prime} \\ a_5=z_0 \\ a_6=z_0^{\prime} \end{array}\right. $ | (9) |
此外,为了消除轨道解析解中的非周期项,初始条件中还需满足[11]:
| $ \left\{\begin{array}{l} y_0=2 x_0^{\prime} \\ y_0^{\prime}=-2 x_0 \end{array}\right. $ | (10) |
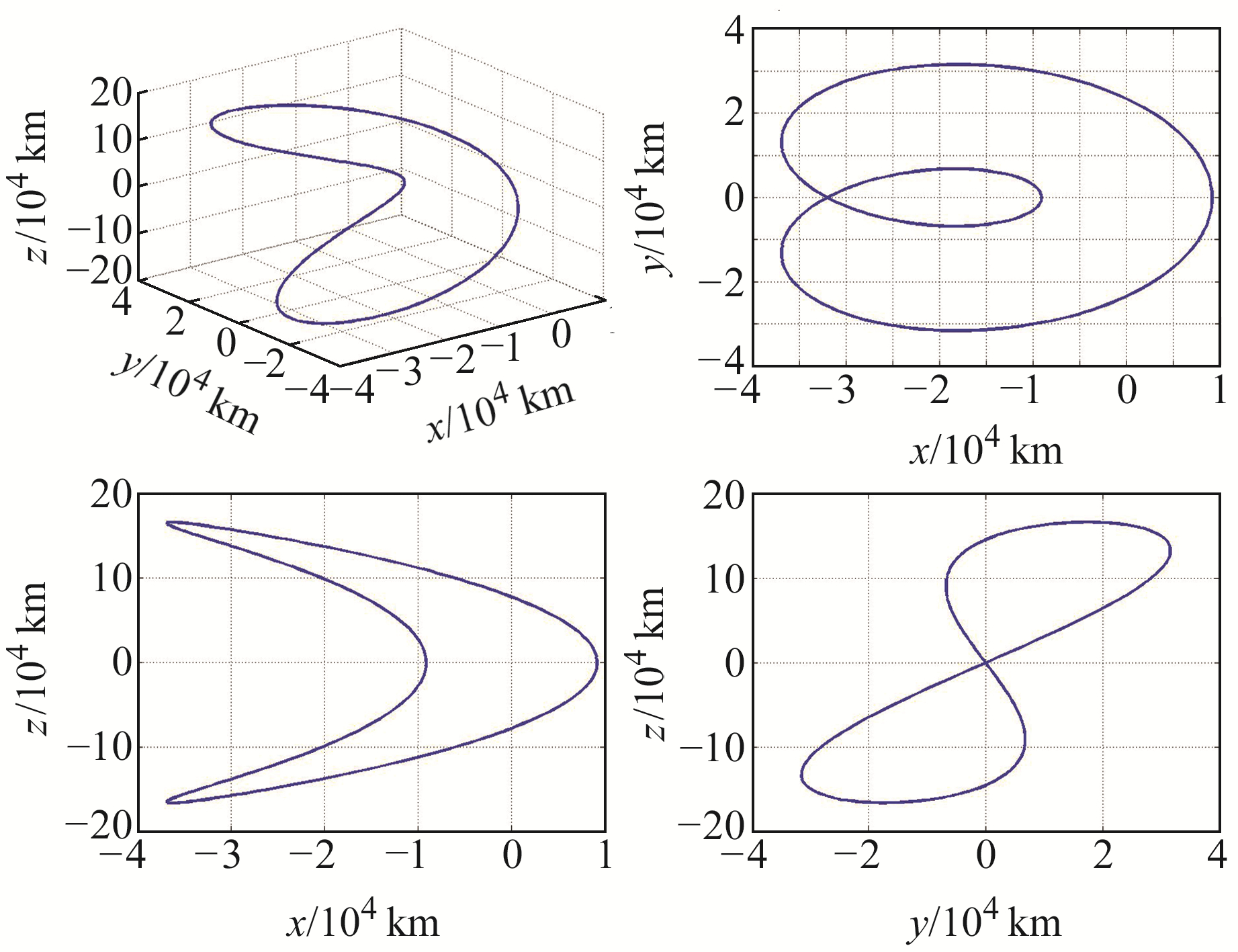
需要说明的是,式(10)均为无量纲形式。图 3~5给出不同初始条件(表 1)的三维轨道图及在xy、xz和yz平面的投影。
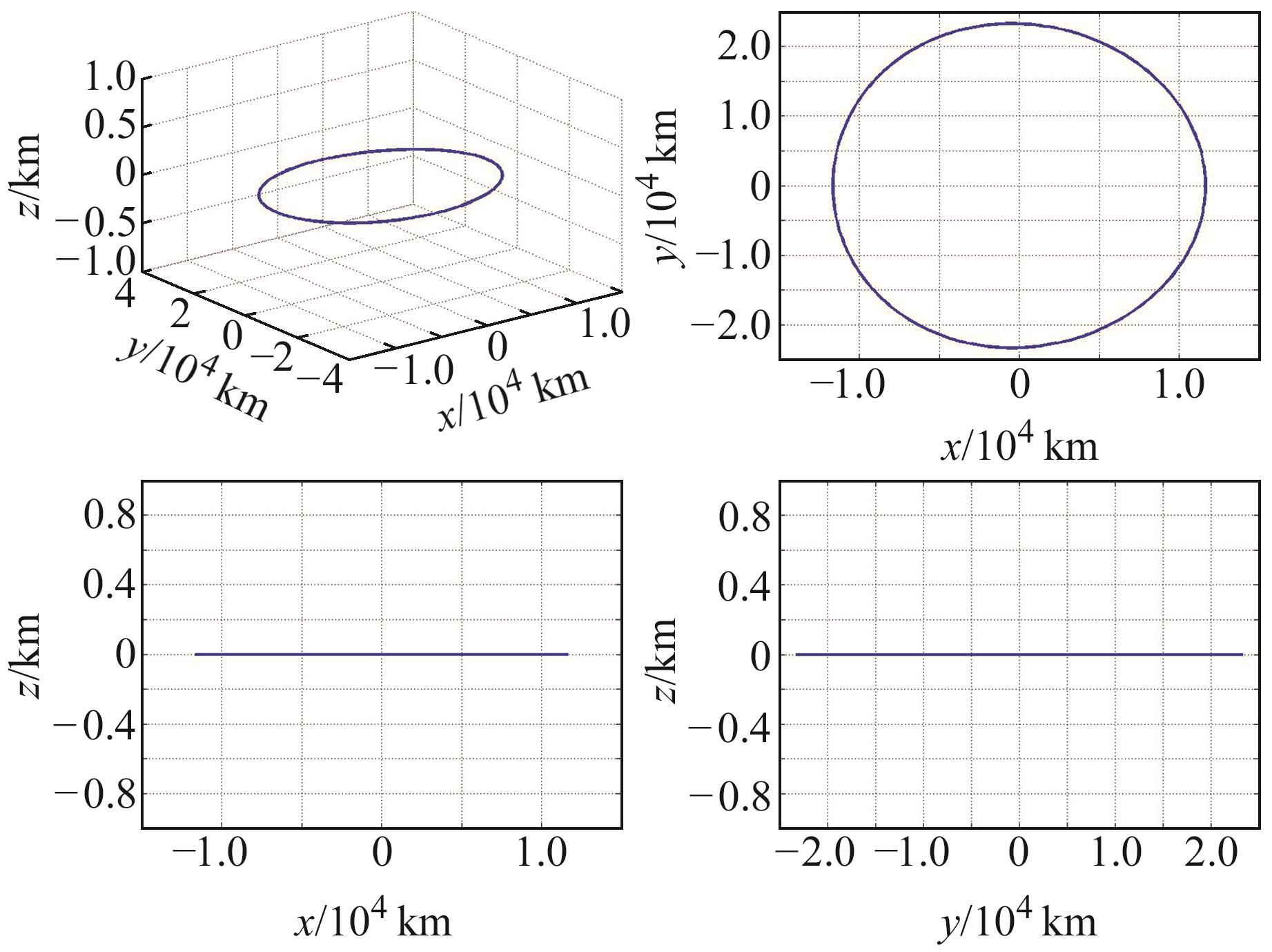
|
图 3 共线平动点周期轨道T1 Fig. 3 Periodic orbit T1 of libration points |
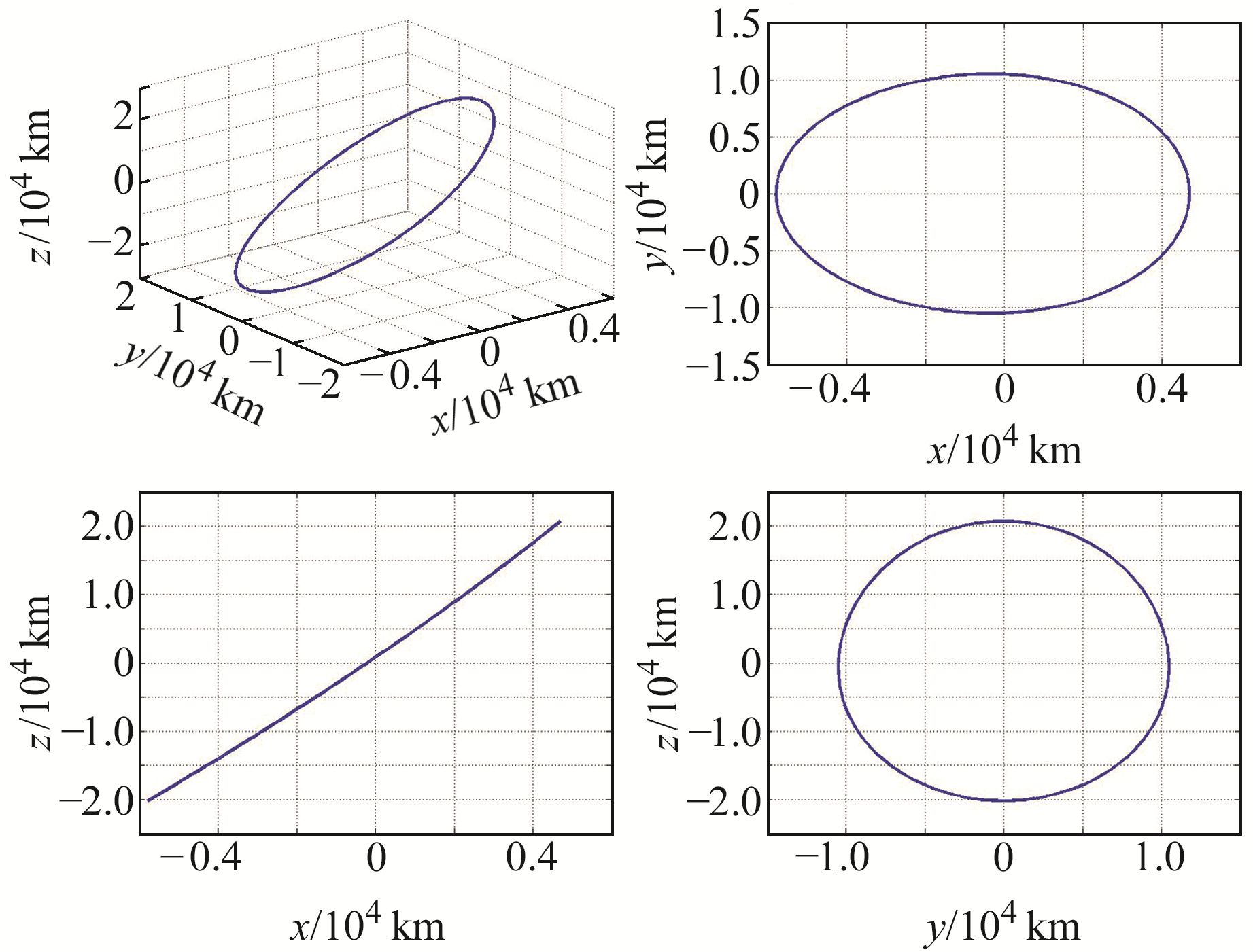
|
图 4 共线平动点周期轨道T2 Fig. 4 Periodic orbit T2 of libration points |
|
图 5 共线平动点周期轨道T3 Fig. 5 Periodic orbit T3 of libration points |
|
|
表 1 不同初始条件 Tab. 1 Different initial conditions |
当z方向初始位置和初始速度均为0时,轨道为水平Lyapunov轨道(图 3),其在xy平面投影为椭圆,在xz和yz平面投影为一条直线;当z方向初始位置不为0、初始速为0时,轨道为Halo轨道(图 4),其在xy平面和yz平面投影为椭圆,在xz平面投影为一条直线;当z方向初始位置为0、初始速度不为0时,轨道为垂直Lyapunov轨道(图 5)。
2.2 地月历表误差对平动点周期轨道的影响轨道的选择需要考虑3向振幅、轨道周期、入轨位置、入轨速度等特征。由轨道的3阶解析解可知,振幅和初始相位由x和z方向的初始位置和初始速度决定,y方向的初始位置和初始速度由x方向的初始位置和初始速度决定。地月历表误差引起的平动点的位置误差可认为是轨道的初始误差,设地月历表误差为R0=(dx0 dz0)T,则由地月历表误差引起的各方向的轨道误差R=(dx dy dz)T可表示为
轨道总误差值
式(7)中,x(τ)、y(τ)、z(τ)分别对x0、z0求偏导,可得:
| $ \left\{ \begin{array}{l} \frac{\partial x}{\partial x_0}=\left[-\cos u-A+A \cos 2 u+\frac{1}{8} B^2 \cos (u+2 v)+\frac{9}{8} A^2 \cos 3 u\right] \frac{a_3}{\sqrt{a_3^2+a_4^2}}+ \\ \quad\left[A \sin u-A^2 \sin 2 u-\frac{1}{8} A B^2 \sin (u+2 v)-\frac{9}{8} A^3 \sin 3 u\right]\left(-a_4\right) \\ \frac{\partial y}{\partial x_0}=\left[2 \cos u-\frac{1}{8} B^2 \sin (u+2 v)+\frac{7}{8} A^2 \sin 3 u+\frac{3}{8} B^2 \sin (u-2 v)-\frac{27}{8} A^2 \sin u\right] \frac{a_3}{\sqrt{a_3^2+a_4^2}}+ \\ \quad\left[-2 A \sin u+\frac{1}{2} \cos 2 u-\frac{1}{8} A B^2 \cos (u+2 v)+\frac{7}{8} A^3 \cos 3 u+\frac{3}{8} A B^2 \cos (u-2 v)-\frac{27}{8} A^3 \cos u\right]\left(-a_4\right) \\ \frac{\partial z}{\partial x_0}=\left[\frac{1}{2} B(\sin (u+v)-3 \sin (v-u))+\frac{3}{4} A B \sin (2 u+v)\right] \frac{a_3}{\sqrt{a_3^2+a_4^2}}+ \\ \left.\quad \frac{1}{2} A B(\cos (u+v)+3 \cos (v-u))+\frac{3}{4} A^2 B \cos (2 u+v)\right]\left(-a_4\right) \\ \frac{\partial x}{\partial z_0}=\left[-\frac{1}{2} B+\frac{1}{2} B \cos 2 v+\frac{1}{4} A B \cos (u+2 v)\right] \frac{a_5}{\sqrt{a_5^2+a_6^2}}+\left[-\frac{1}{2} B^2 \sin 2 v-\frac{1}{4} A B^2 \sin (u+2 v)\right] a_6 \\ \frac{\partial y}{\partial z_0}=\left[-\frac{1}{2} B \sin 2 v-\frac{1}{4} A B \sin (u+2 v)+\frac{3}{4} A B \sin (u-2 v)\right] \frac{a_5}{\sqrt{a_5^2+a_6^2}+} \\ \quad{\left[-\frac{1}{4} B^2 \cos 2 v-\frac{1}{4} A B^2 \cos (u+2 v)-\frac{3}{4} A B^2 \cos (u-2 v)\right] a_6} \\ \frac{\partial z}{\partial z_0}=\left[\sin v+\frac{1}{2} A(\sin (u+v)-3 \sin (v-u))+\frac{3}{8} B \sin (2 u+v)\right] \frac{a_5}{\sqrt{a_5^2+a_6^2}}+ \\ \quad{\left[B \cos v+\frac{1}{2} A B(\cos (u+v)-3 \cos (v-u))+\frac{3}{8} A^2 B \cos (2 u+v)\right] a_6} \end{array} \right. $ | (11) |
由文献[7]可知,对于月球在地心天球坐标系中的位置,DE405与DE430的位置差异最大值约为18.73 m,均方根为1.363 m;DE421、DE423、DE418与DE430的位置差异最大值约为0.56 m、1.61 m、1.76 m,均方根为1.12 m、0.82 m、0.88 m。文献[8]以DE440为参考,分析其他不同历表(DE405、DE421、DE430)的误差。其中,DE405、DE421、DE430的月球地心位置精度分别约为7 m、1.5 m、1.3 m,用于月球探测器从月惯性系转换为月固系产生的坐标误差分别为30 m、1.3 m、1 m。以上分析表明,历表对于月球坐标系转换的影响为m级,并表现出一定的周期性和随机性。
假设地月历表误差均为随机噪声,分析T1、T2、T3三种轨道分别在以下4种误差条件下的轨道误差:1) [dx0 dz0]T均值为[10 m 10 m]T,标准差为[1 m 1 m]T;2) [dx0 dz0]T均值为[20 m 20 m]T,标准差为[1 m 1 m]T;3) [dx0 dz0]T均值为[10 m 10 m]T,标准差为[2 m 2 m]T;4) [dx0 dz0]T均值为[0 0]T,标准差为[1 m 1 m]T。
图 6~11给出T1、T2、T3轨道在不同地月历表误差条件下不同位置的轨道误差及轨道误差随时间的变化,图中圆圈直径表示误差的大小。综合分析图 6~11可知:1)同一条轨道不同位置的轨道误差有较大差别,平面Lyapunov轨道误差的峰值点位于或接近X向最大值与最小值处,在x=0处最小;Halo轨道误差的峰值点位于或接近轨道Z向最大值与最小值处,在z=0处误差值最小;垂直Lyapunov轨道误差的峰值点位于或接近z=0处,在Z向最大值与最小值处误差最小。2)地月历表误差对于轨道误差的影响表现为随时间周期性变化,其无量纲的周期约为π,为轨道周期的0.5倍(无量纲轨道周期为2π)。3)轨道误差的值与地月历表误差的值在同一个量级,当地月历表误差的均值不为0时,轨道误差的峰值约为地月历表误差均值的2.5倍。

|
图 6 T1轨道在第1种地月历表误差下的轨道误差 Fig. 6 Orbit error under the first kind of cislunar ephemerides error of T1 orbit |

|
图 7 T2轨道在第1种地月历表误差下的轨道误差 Fig. 7 Orbit error under the first kind of cislunar ephemerides error of T2 orbit |

|
图 8 T3轨道在第1种地月历表误差下的轨道误差 Fig. 8 Orbit error under the first kind of cislunar ephemerides error of T3 orbit |
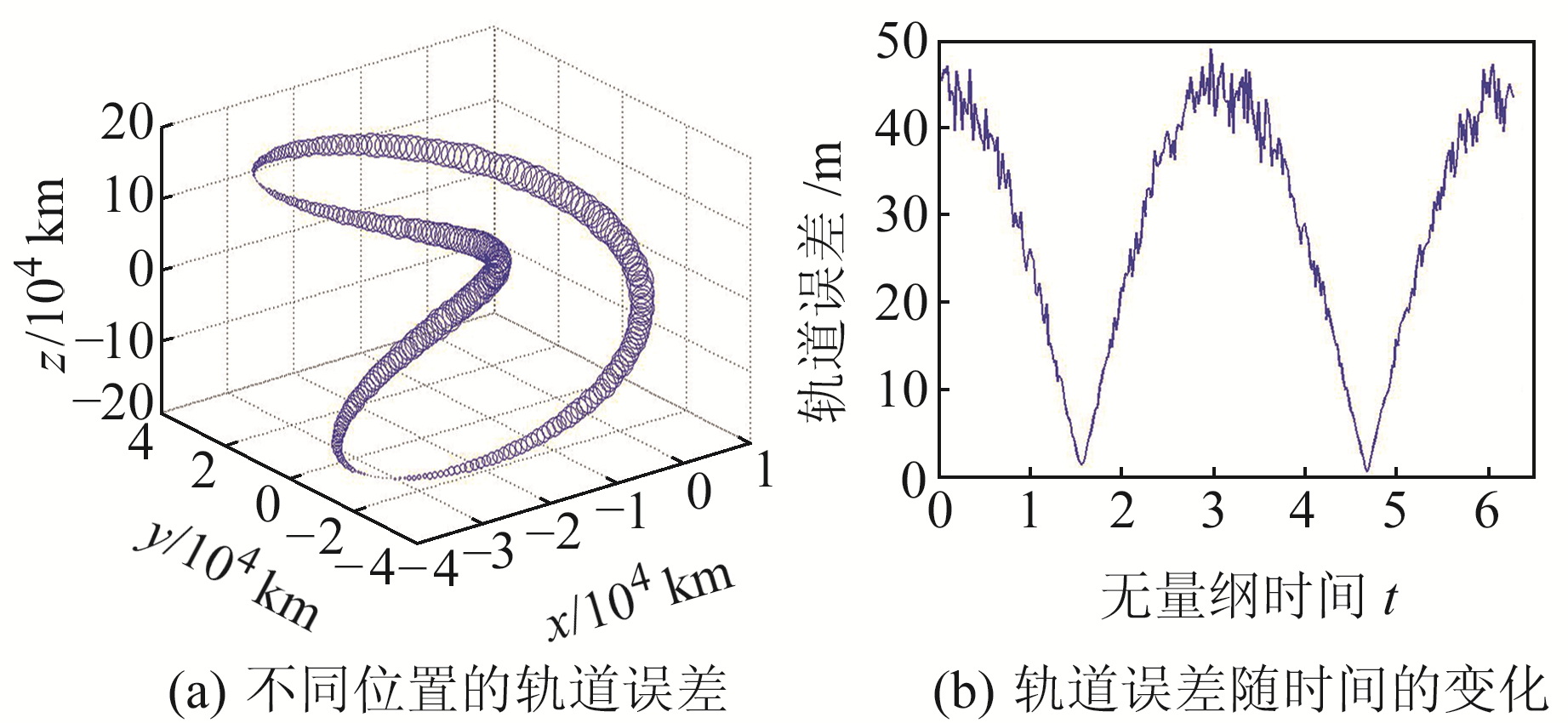
|
图 9 T3轨道在第2种地月历表误差下的轨道误差 Fig. 9 Orbit error under the second kind of cislunar ephemerides error of T3 orbit |
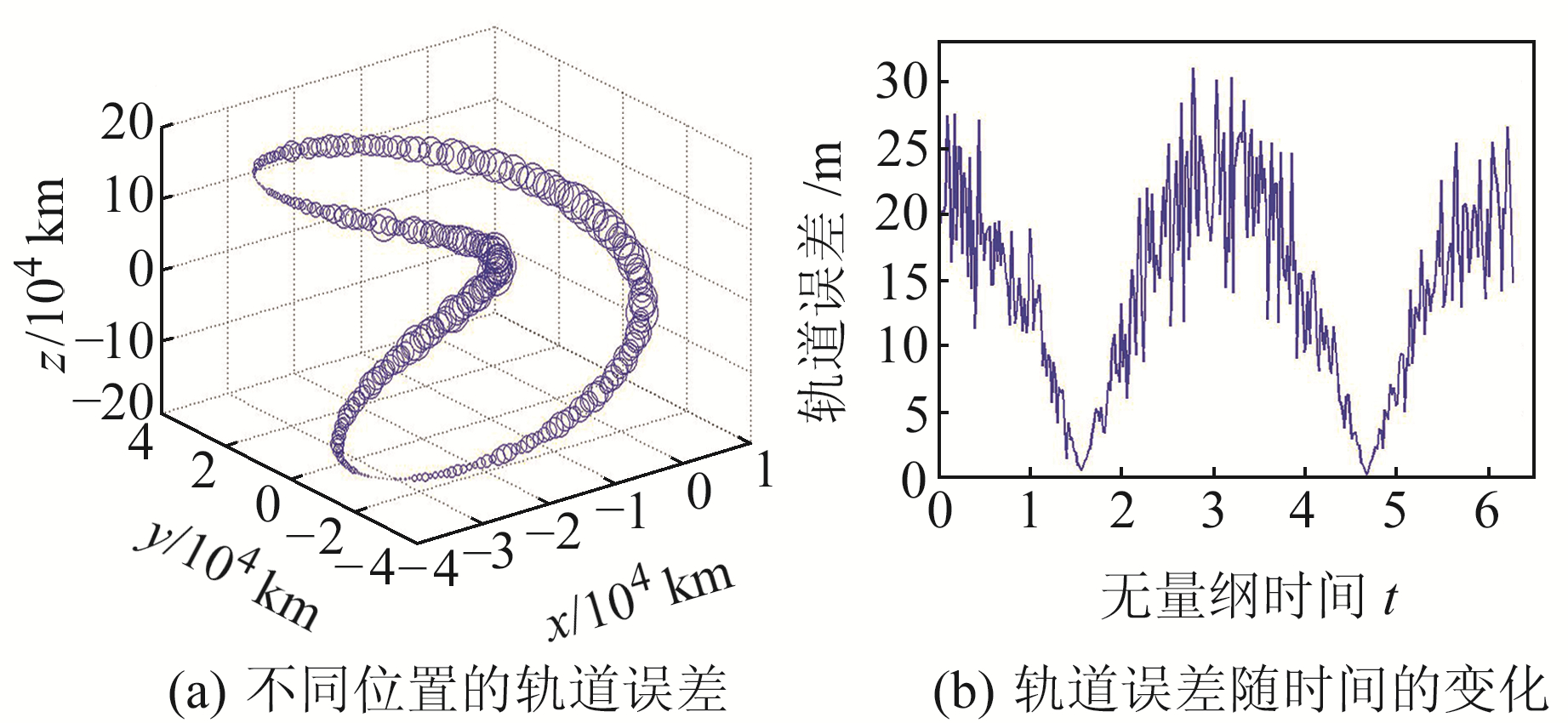
|
图 10 T3轨道在第3种地月历表误差下的轨道误差 Fig. 10 Orbit error under the third kind of cislunar ephemerides error of T3 orbit |
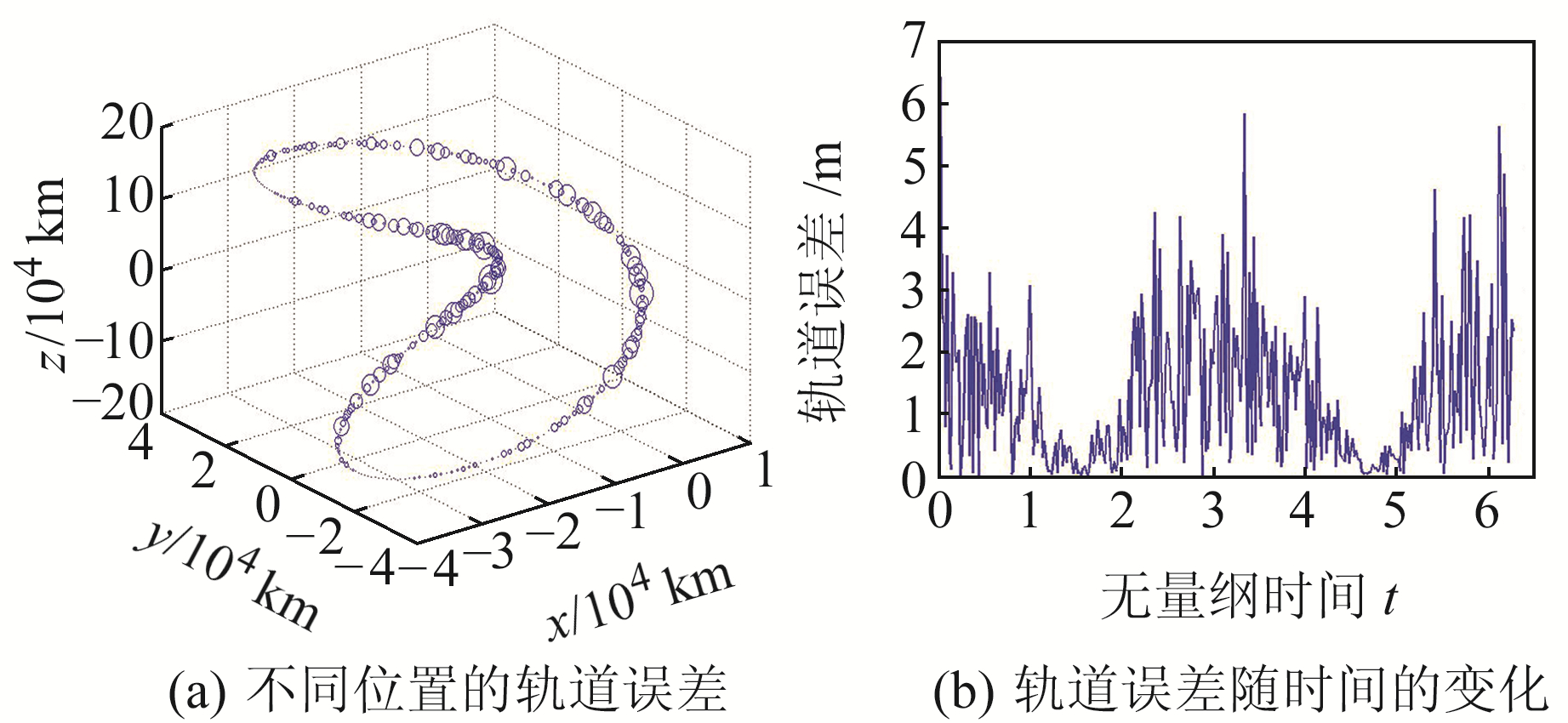
|
图 11 T3轨道在第4种地月历表误差下的轨道误差 Fig. 11 Orbit error under the forth kind of cislunar ephemerides error of T3 orbit |
本文面向深空探测任务的实际工程需求,基于圆形限制性三体问题下地月平动点的3阶轨道解析解,分析不同初值条件下的轨道演化特性。基于误差传播理论,研究地月历表误差对地月共线平动点周期轨道在不同初值及初值误差时的影响。主要结论为:
1) 轨道误差与地月历表误差在同一个量级,其峰值大约为地月历表误差的2.5倍;
2) 地月历表误差对轨道误差的影响表现为周期性,其随时间变化的无量纲周期约为轨道无量纲周期的0.5倍;
3) 在同一条轨道的不同位置,地月历表误差影响存在很大差异,对于不同类型的轨道,其误差表现形式也不尽相同。
本文主要基于限制性三体问题的3阶解析解进行分析,但基于解析解的误差分析与真实轨道之间存在一定差异,因此具有一定的局限性,后续将开展基于太阳系力模型的数值轨道分析。
| [1] |
Richardson D L. Analytic Construction of Periodic Orbits about the Collinear Points[J]. Celestial Mechanics, 1980, 22(3): 241-253 DOI:10.1007/BF01229511
(  0) 0) |
| [2] |
Howell K C. Families of Orbits in the Vicinity of the Collinear Libration Points[J]. The Journal of the Astronautical Sciences, 2001, 49(1): 107-125 DOI:10.1007/BF03546339
(  0) 0) |
| [3] |
梁伟光, 周文艳, 雪丹, 等. 解析计算在月球中继卫星Halo轨道设计中的应用[J]. 宇航学报, 2016, 37(10): 1171-1178 (Liang Weiguang, Zhou Wenyan, Xue Dan, et al. Application of Analytical Calculation in Lunar Relay Satellite Halo Orbit Design[J]. Journal of Astronautics, 2016, 37(10): 1171-1178)
(  0) 0) |
| [4] |
周敬, 胡军, 张斌. 限制性三体问题共线平动点轨道近似解析解[J]. 深空探测学报, 2020, 7(1): 93-101 (Zhou Jing, Hu Jun, Zhang Bin. Approximate Analytical Solutions of Motion near the Collinear Libration-Points in Restricted Three-Body Problem[J]. Journal of Deep Space Exploration, 2020, 7(1): 93-101)
(  0) 0) |
| [5] |
刘刚, 黄静, 郭思岩. 星历模型地月系统平动点拟周期轨道设计研究[J]. 上海航天, 2017, 34(5): 16-22 (Liu Gang, Huang Jing, Guo Siyan. Quasi-Periodic Orbit Design around Earth-Moon Libration Points Using Ephemeris Model[J]. Aerospace Shanghai, 2017, 34(5): 16-22)
(  0) 0) |
| [6] |
张文昭, 平劲松, 李文潇. 3种典型的太阳系大行星历表的对比分析[J]. 中国科学院大学学报, 2021, 38(1): 114-120 (Zhang Wenzhao, Ping Jinsong, Li Wenxiao. Comparison and Analysis of Three Kinds of Typical Solar System Planetary Ephemeris[J]. Journal of University of Chinese Academy of Sciences, 2021, 38(1): 114-120)
(  0) 0) |
| [7] |
李萌萌, 王潜心, 程彤, 等. 不同版本JPL历表对天体坐标转换影响的分析[J]. 合肥工业大学学报: 自然科学版, 2021, 44(10): 1397-1405 (Li Mengmeng, Wang Qianxin, Cheng Tong, et al. Analysis on the Influence of Different JPL Ephemerides Versions on Celestial Coordinate Conversion[J]. Journal of Hefei University of Technology: Natural Science, 2021, 44(10): 1397-1405)
(  0) 0) |
| [8] |
刘婉逸, 邹贤才, 衷路萍. JPL行星历表的发展及比较[J]. 大地测量与地球动力学, 2022, 42(9): 925-930 (Liu Wanyi, Zou Xiancai, Zhong Luping. Development and Comparison of JPL Planetary Ephemerides[J]. Journal of Geodesy and Geodynamics, 2022, 42(9): 925-930)
(  0) 0) |
| [9] |
刘林, 侯锡云. 深空探测器轨道力学[M]. 北京: 电子工业出版社, 2012 (Liu Lin, Hou Xiyun. Orbital Mechanics of Deep Space Probe[M]. Beijing: Publishing House of Electronics Industry, 2012)
(  0) 0) |
| [10] |
周建华, 徐波, 冯全胜. 轨道力学[M]. 北京: 科学出版社, 2009 (Zhou Jianhua, Xu Bo, Feng Quansheng. Orbital Mechanics[M]. Beijing: Science Press, 2009)
(  0) 0) |
| [11] |
Richardson D, Mitchell J W. A Third-Order Analytical Solution for Relative Motion with a Circular Reference Orbit[J]. Journal of the Astronautical Sciences, 2003, 51: 1-12 DOI:10.1007/BF03546312
(  0) 0) |
2. Xi'an Research Institute of Surveying and Mapping, 1 Mid-Yanta Road, Xi'an 710054, China
 2024, Vol. 44
2024, Vol. 44

